1. Introduction
Structural health monitoring (SHM) by using guided ultrasonic waves (GUW) has been the subject of research for several years. Due to their low attenuation behavior, GUW propagate over large distances without severe signal loss and can be used to monitor large areas. Their property to interact with structural inhomogeneities such as cracks and delaminations makes them suitable for structural monitoring.
GUW appear in two different wave modes, the symmetric and the antisymmetric wave modes [
1]. These two modes differ in the direction of the displacement with respect to the midplane of the plate. Regarding the out-of-plane component of the symmetric mode, the phase relation between the structure’s surfaces corresponds to the point symmetry relation of an odd function such as the sine-function [
2]. This can be interpreted as a phase shift between the upper and lower surface of
. In contrast, the out-of-plane component of the antisymmetric mode behaves like a symmetric function such as the cosine function. This means that the upper and lower surface oscillate in phase [
1]. In anisotropic laminates i.e., fiber-reinforced composites, the calculated displacement fields show the same phase relation as described in detail in [
2]. In contrast to these displacement field symmetry conditions, the propagation of GUW in honeycomb and foam sandwich structures behaves differently. They show the behavior of Rayleigh surface waves for undamaged structures without penetrating the core when higher excitation frequencies are used. In [
3], sandwich structures with different core height as well as a honeycomb structure with debonded areas are investigated. Propagation of GUW in these structures shows mode conversion from GUW to Rayleigh surface waves for higher frequencies [
3], which results in the change of wavelengths. It was also shown that for higher frequencies, the energy transferred from one specimen surface through the core to the other specimen surface for the GUW is damped throughout the thickness of the sandwich structure i.e., fed to the Rayleigh surface wave [
3].
The GUW signals that are captured via different measurement methods need further signal analysis and processing to allow an interpretation of the wave propagation properties. In the literature, numerous different signal processing techniques can be found as some are presented in an exemplary manner in [
4], offering the time-frequency representation (TFR) as a powerful tool for the analysis of signal features.
The Fourier transformation (FT) is used to gain knowledge about the frequency spectrum of a time signal [
5]. The FT assumes that all oscillations can be represented by a summation of sinusoidal oscillations of different frequency, magnitude, and instantaneous oscillation phase [
5]. The short-time Fourier transformation (STFT) applies the FT to a small, windowed time signal element whereas the rest of the signal is disregarded. The energy spectrum of the complete signal is created by moving the segment window forward until the complete signal is analyzed. This procedure has a drawback in terms of precision because the window size stays constant [
6]. The continuous wavelet transformation (CWT) is a well-known transformation procedure for processing GUWs that uses two parameters, scale, and time to adjust a time-limited wavelet function to the course of a time signal [
6]. In comparison to the STFT, a variable window size is used, which is adjusted to the instantaneous size of the signal segment under investigation. This leads to a higher precision in both the time- and frequency-domain simultaneously [
6]. It offers full signal information and allows a localization in time and frequency domain [
6]. Therefore, it is used for the evaluation of energy distribution in signals over time. This serves the identification of damage when the absolute values of the complex-valued transformation are taken into account [
6]. The CWT leads to complex-valued CWT coefficients. The absolute value of these represent the energy distribution. In addition to this, the complex values of the CWT also contain instantaneous phase angle information per frequency per point in time. Little research has been done regarding and using the phase angle gained by CWT applications so far. One aspect that has been dealt with is the concept of the instantaneous phase (IP) gained by the Hilbert transformation (HT). In this method, the phase angle is obtained from an analytic complex signal, which is built from the real-valued time signal
and its real-valued Hilbert transform
. Deducing an envelope function
and a phase function
leads to the complex representation
from which the instantaneous Hilbert phase can be derived for the real-valued time domain signal
[
7]. Although it is hardly established in engineering applications, the concept of IP has found its way into neuroscience, where it is used intensively to evaluate signals like captured fast transitory signals of brain activity. The need for the synchrony estimation between biological signals has initiated the search for methods that allow the comparison of signal phases. One example is the estimation of phase-locking between two distant brain recordings (i.e., they are recorded by EEG, meaning the detection of a constant phase difference between two signals for a limited time window [
8]). Because some noise and fluctuation is to be expected in the brain signals, statistical methods need to be added to allow statements about signal synchrony. This means that the estimation of the IP of the signals must be followed by statistical procedures that allow quantification of the phase relation. The estimation of the IP by using HT and convolution with a complex wavelet are presented in [
8] as two principle approaches for the quantification of phase synchrony between neuronal signals. The authors compared the two methods on different signal sets regarding their suitability for the study of neuroelectrical signals. In [
9], an algorithmic method is developed for the extraction of instantaneous frequency and IP information in captured oscillations in the olfactory system of rats. The processed signals contained one or more oscillatory frequencies. The method is based on the CWT and was tested on a synthetic signal to extract the IP. A comparison with the state-of-the-art HT was performed. Although the neuroelectrical signals occur in frequencies between approx. 10–80 Hz [
9] (in the olfactory system in rats) and approx. 1–100 Hz [
8] (brain activity in humans), the engineering applications using GUW reach to much higher frequencies.
The concept of the IP has also been used for damage detection in the engineering field. In [
7], the change in the phase and the time-of-flight of propagating longitudinal wave modes is investigated in damaged and undamaged pipes. This approach is a qualitative method for damage identification and independent from the quality of the transducer bonding, i.e., independent from the signal strength. The sensitivity of GUW modes to delaminations in laminated aluminum plates is investigated in [
10]. In the work, the time signal is first processed through a method of mode decomposition to allow the application of the HT as suggested. After having decomposed the time signal into several parts, the HT has been applied to each mode and the IP per mode has been estimated. Subsequently, the IPs per mode are summed to build a total IP which has the property of increasing monotonically as a function of time. The time course of the IP can give indications for existing delaminations showing specific variations.
Another application case is the compensation of temperature effects as a change of the temperature and hence, the material properties influences the GUW propagation. As described in [
11], the comparison of a baseline measurement and a measurement under temperature influence may lead to a mismatch in the wave modes due to signal stretching in the time domain. Hence, the authors have developed a method for temperature compensation, which is based also on the time signals’ IP derived by the HT. The mismatch, i.e., stretch between the baseline signal and a signal under thermal influence are identified as a change of the IP of the signals. Knowing the phase relation, the shift of the signals can then be compensated mathematically. The analytical signals are converted back to the time domain afterwards, which offers a temperature compensation [
11].
In [
12], a method for wave mode identification in the context of acoustic emission monitoring is developed. The authors use the phase in combination with the instantaneous frequency information to determine the different wave modes in complex structures. Due to the complexity of the carbon fiber-reinforced polymer (CFRP) structure used, the reflected waves overlap and therefore cannot be distinguished in the time domain. The sensitivity of the method to small changes in phase, the simple implementation of the HT and the independence of the signals’ amplitudes allow the occuring wave modes to be reliably identified. In [
13], adhesive defects on a glass fiber-reinforced polymer (GFRP) sample are located, sized and characterized using different signal processing techniques for GUW applications. The authors also apply the HT, but use the derived instantaneous amplitude instead of the phase information. It is noted that in GUW processing there is the necessity to decompose harmonics properly to apply the HT. In [
14], the authors develop a GUW-based damage imaging condition method for the detection of barely visible impact damages. Therefore, the interaction of the GUW with the damaged area is observed. The interacting waves show a change in the wave number at the damaged location which are identified by using the Riesz transform (RT). The RT is a 2D-HT from which instantaneous amplitudes and phases can be derived for further processing and interpretation of instantaneous 2D wave field images. The IPs used in the work are derived in reference to the direction normal to the propagating wavefront in a 2D representation. A method for defect detection in anisotropic plates by using GUW is proposed in [
15]. In the presented work, the HT is used to derive the phase relation between an emitter and receiver via emitter–receiver signal combinations by using a linear sensor array consisting of several piezoelectric elements [
15]. In [
16], the IP characteristics of shear horizontal waves are used for the detection of various defects in an aluminum specimen. The shift in the IP of the shear horizontal waves shows different patterns for different defects. In geophysics, Yuan et al. [
4] define the concept of the exponentiated phase (EP) by using a normalization of the HT by its corresponding time-dependent envelope function. This concept allows a steady application to seismic signals.
Examples that the phase information derived by the CWT, which cover the field of medical research and civil engineering, are presented in the following. In [
17], the CWT is used for electroencephalography signals to extract magnitude and phase information at the same time. With both the magnitude and phase information, neural networks are trained. In the field of civil engineering, the complex continuous wavelet transformation (CCWT) is utilized to decompose a single time domain signal and to separate it into different time domain signals per frequency [
18]. The phase information per time domain signal is used for phase observation. CCWT is used to identify defects in piles by observing phase changes in the 3D phase spectogram. In this context, the 3D phase spectrogram is the IP angle derived from the CWT coefficients [
18]. With the information about the location of the phase inversion in the time domain, damage is detected. The time difference allows one to derive defect location. Furthermore, the wavelet transformation based on a modified complex Morlet wavelet with variable center frequency is applied to seismic response data to gain the phase information [
19]. Again, the objective is to detect damage. This is done considering the phase of each measurement, i.e., the phase of each sensing node for different test cases. The phase angles of the individual analyzed frequencies of the recorded signals show changes in case of damage. The location of damage is derived by the sensing node position in which a phase angle change occurs [
19]. The major objective is the reconstruction of the time signal of an earthquake response from the complex wavelet coefficients. Therefore, the calculation of the unwrapped phase is performed by selecting frequency bands of interest. For this, the complex values along the bandwidth are summed, which leads to a coefficient sum per time step. These obtained complex values are then used to calculate the IP at each particular time step [
19]. It is shown that the concept of an IP gained from analytical signals mostly created by the HT are used in wavefield analysis especially in damage detection applications and neuroscience. However, it needs to be verified whether the approaches used in neuroscience can be transferred to GUW at higher frequencies. In [
9], the IP extracted by HT and the wavelet transformation are compared. As a drawback of IP that uses the angle of the HT, it is found that the time signals require an appropriate filtering before transformation to obtain accurate estimates of the phase. Good phase results can be obtained by filtering, but at the cost of losing time and frequency information [
9].
However, phase evaluation methods based on the Hilbert IP do not consider the phase relation of different frequency components, but evaluate a time signal as such. For a multifrequency signal, it needs to be taken into account that different frequency components may have different phase relations. Furthermore, the description of the oscillation phase relation in GUW has so far been valid for isotropic and anisotropic materials. It is to be examined whether this assumption can be transferred from GUW to fiber metal laminates (FML). It was shown experimentally that the oscillation in FML not only propagate through the covering layer but also penetrate the thickness of the laminate, so there is no experimental verification about possible phase delays and shifts of the surface oscillations [
20].
The major objective of this work is therefore, the investigation whether there is a phase shift between the upper and lower surface oscillation of plate-like structure fabricated from FML. This is of particular interest because FML consist of the combination of materials with very different wave propagation velocities. Wave propagation behavior remains to be characterized depending on the difference in acoustic impedances and their change within the laminates. Because the HT is insufficient when a signal shows many wave modes overlapping, different approaches will be investigated in this work [
6]. Regarding signal transformation procedures such as STFT and CWT, it can be seen that IP angle information is stored in the transformation parameters and therefore is evaluated with regard to the suitability for phase angle evaluation.
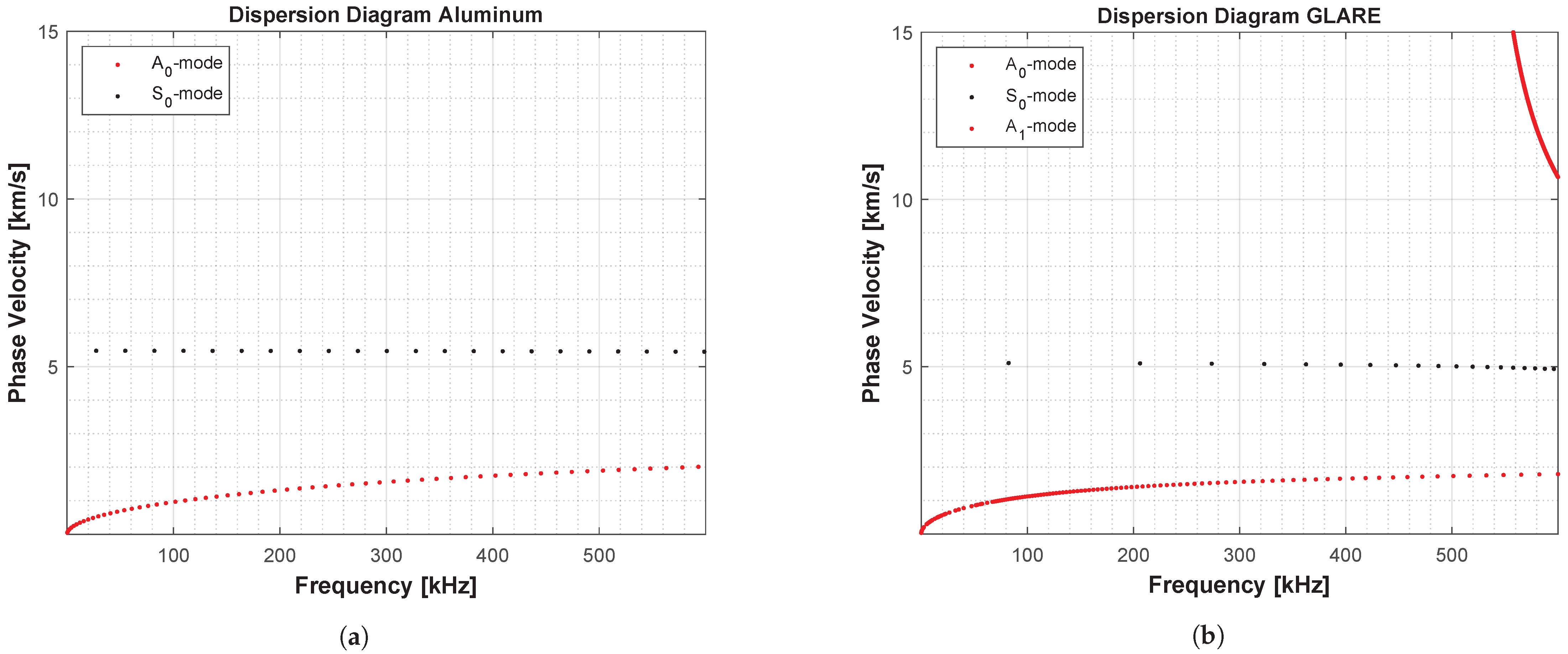
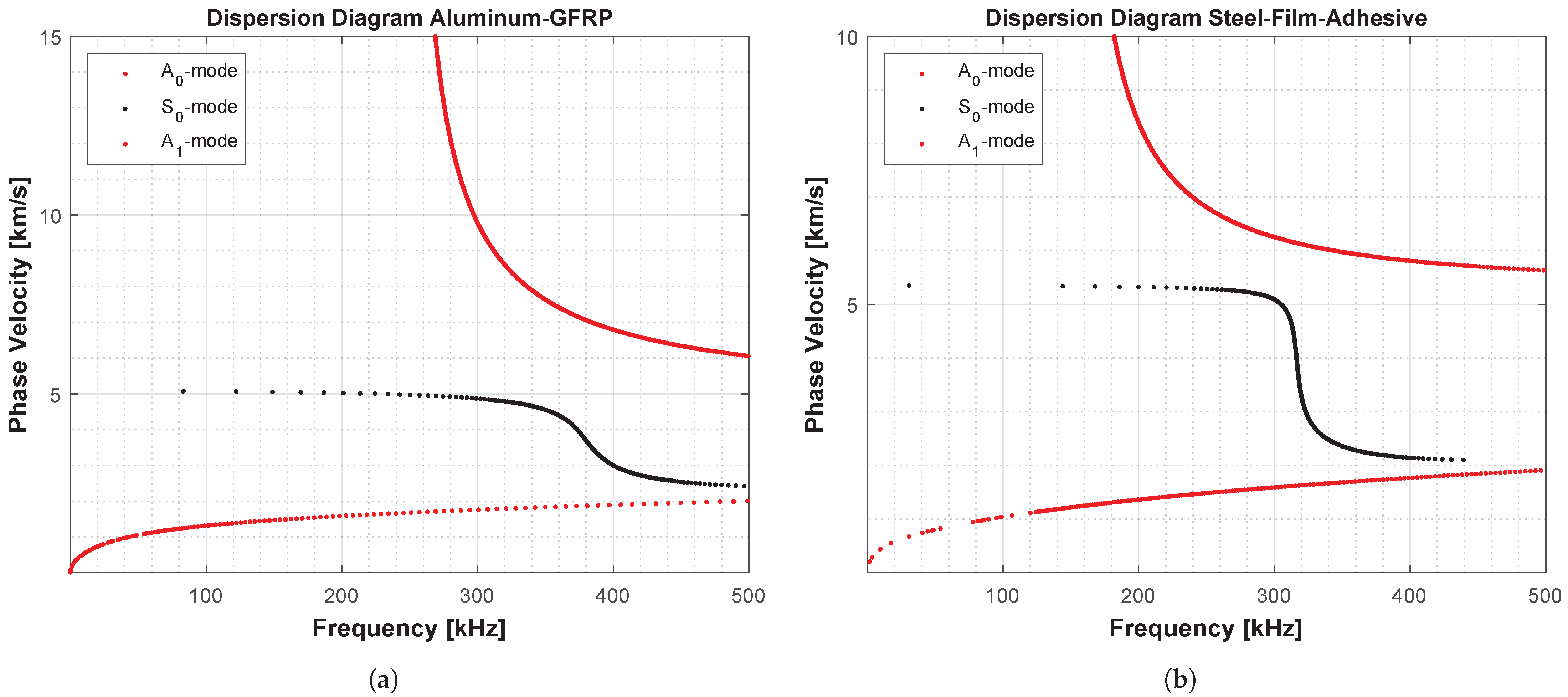
Following the different wave propagation patterns of GUW in pure fiber-reinforced polymer (FRP) and sandwich structures as well as the suitability of the CWT to extract phase information over time of a signal, the CWT is evaluated in this work to analyze the wave propagation characteristics in structures with different grades of complexity and impedance changes over the thickness. Hence, the work focuses on both experimental and numerical investigation based on laminates made from different solid materials. It is analyzed whether the propagating wave modes show the same oscillation phase behavior at the surface as described in the analytical framework of GUW. In this context, phase angles different from or 0 indicate a wave propagation behavior that differs significantly from the analytical framework of GUW in thin-walled structures.
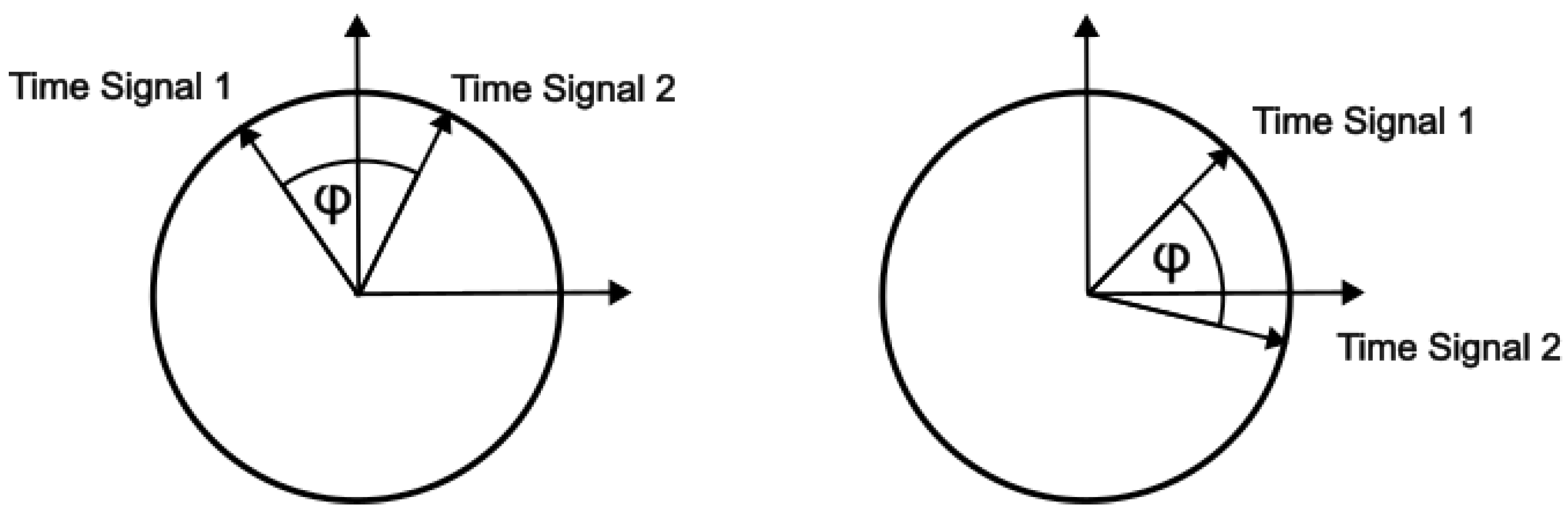
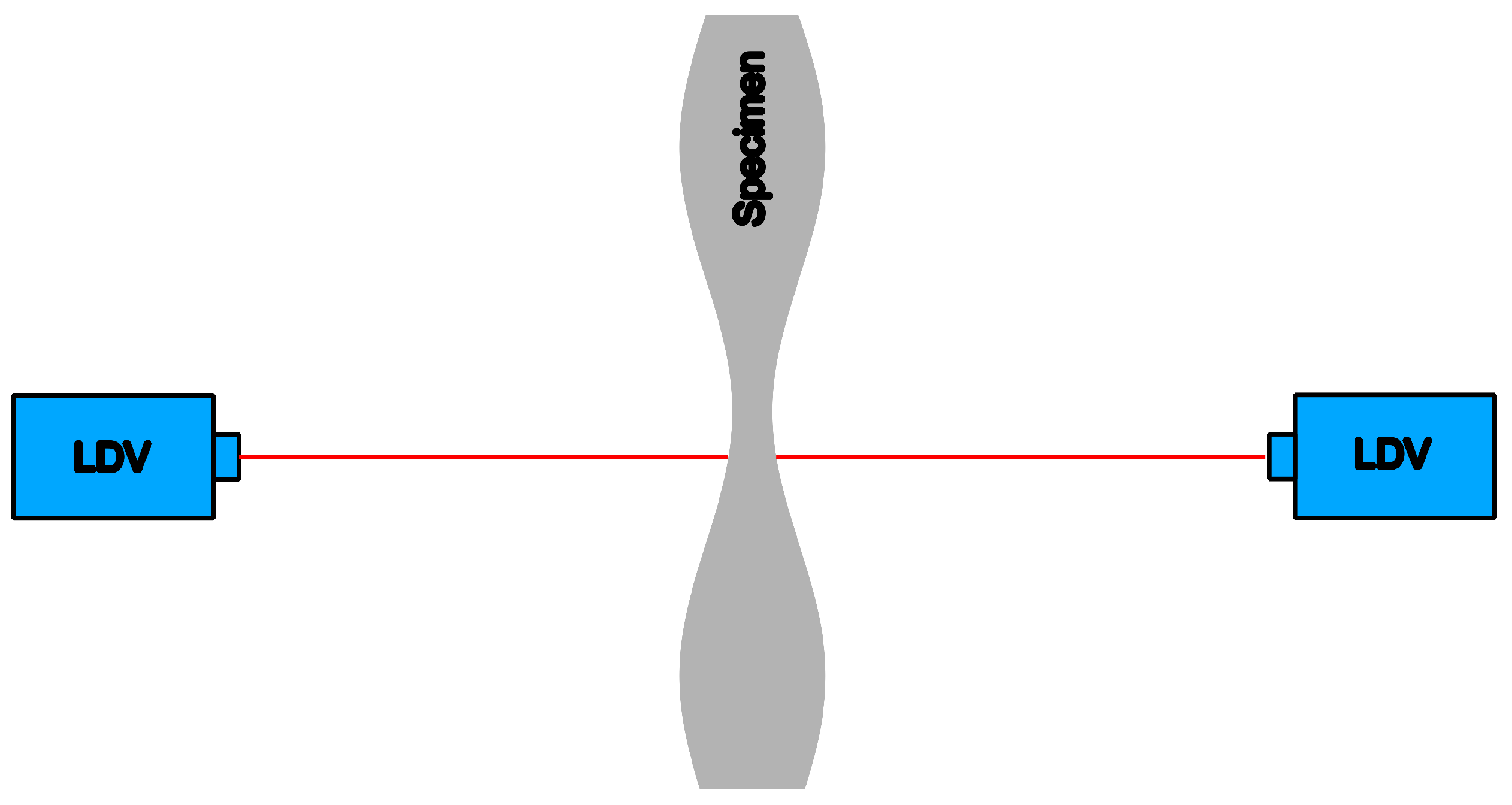
This work addresses two objectives. The first is the development of a procedure to compare the oscillation phases of time signals across a certain bandwidth while allowing a reference to time segments of the analyzed signals. The second objective is to investigate whether FML show the same surface oscillation behavior under GUW excitation as composites or metals. In the first step, two methods of oscillation phase angle evaluation are derived and presented. As mentioned above, a method based on the CWT comparing the oscillation time signals of the two surfaces of plate-like structures and the STFT. In this approach, the upper and lower structure surface spectra thus obtained are related by subtracting them and interpreting the phase difference in terms of the analytic phase relation for GUW.
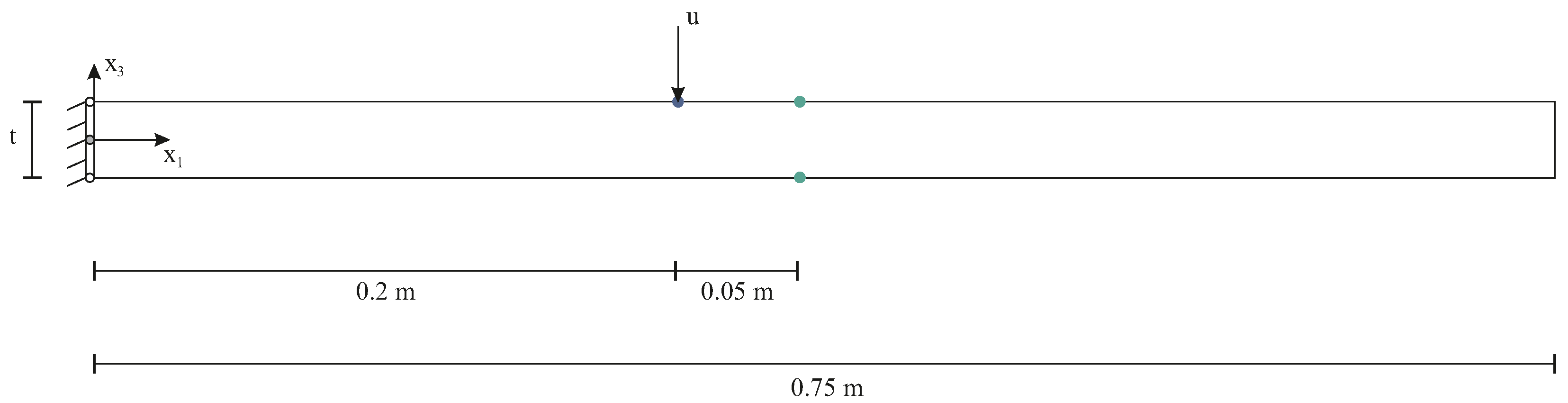
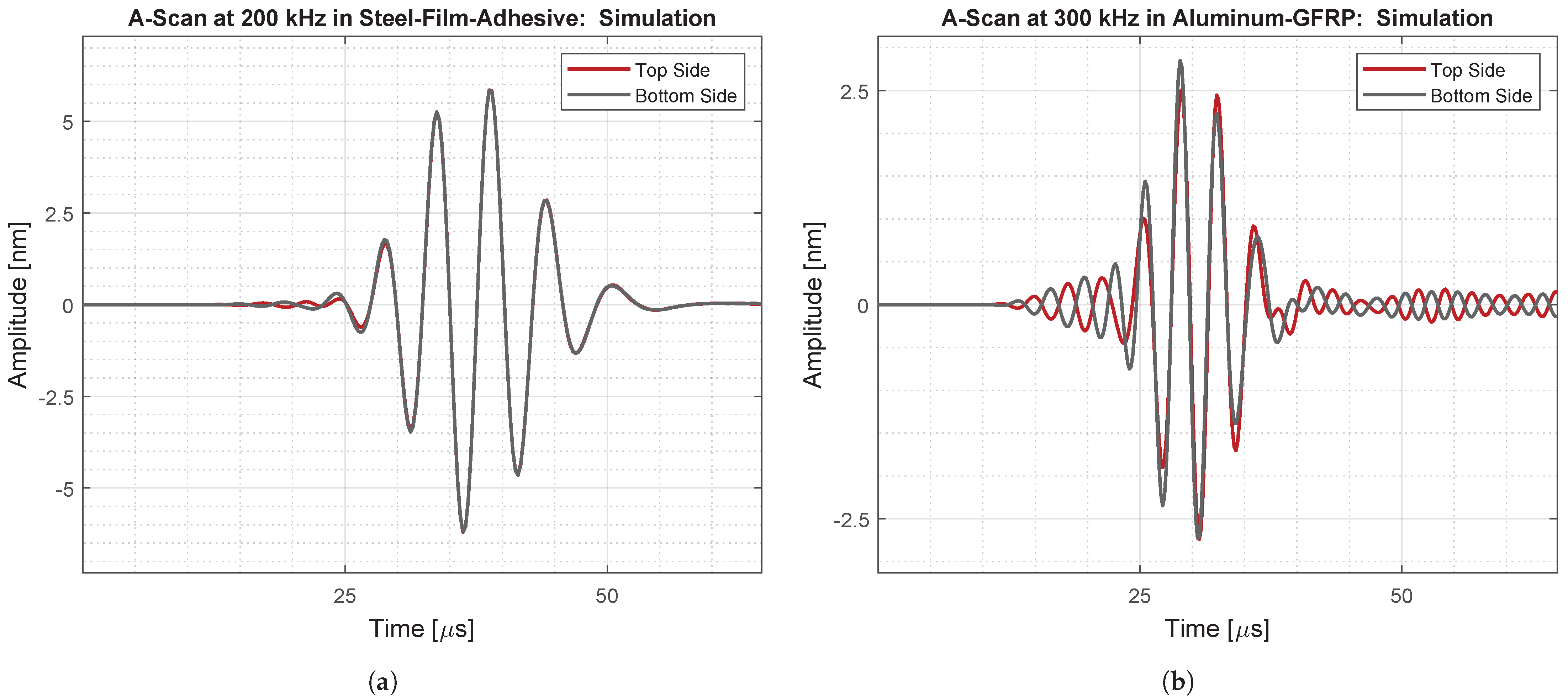
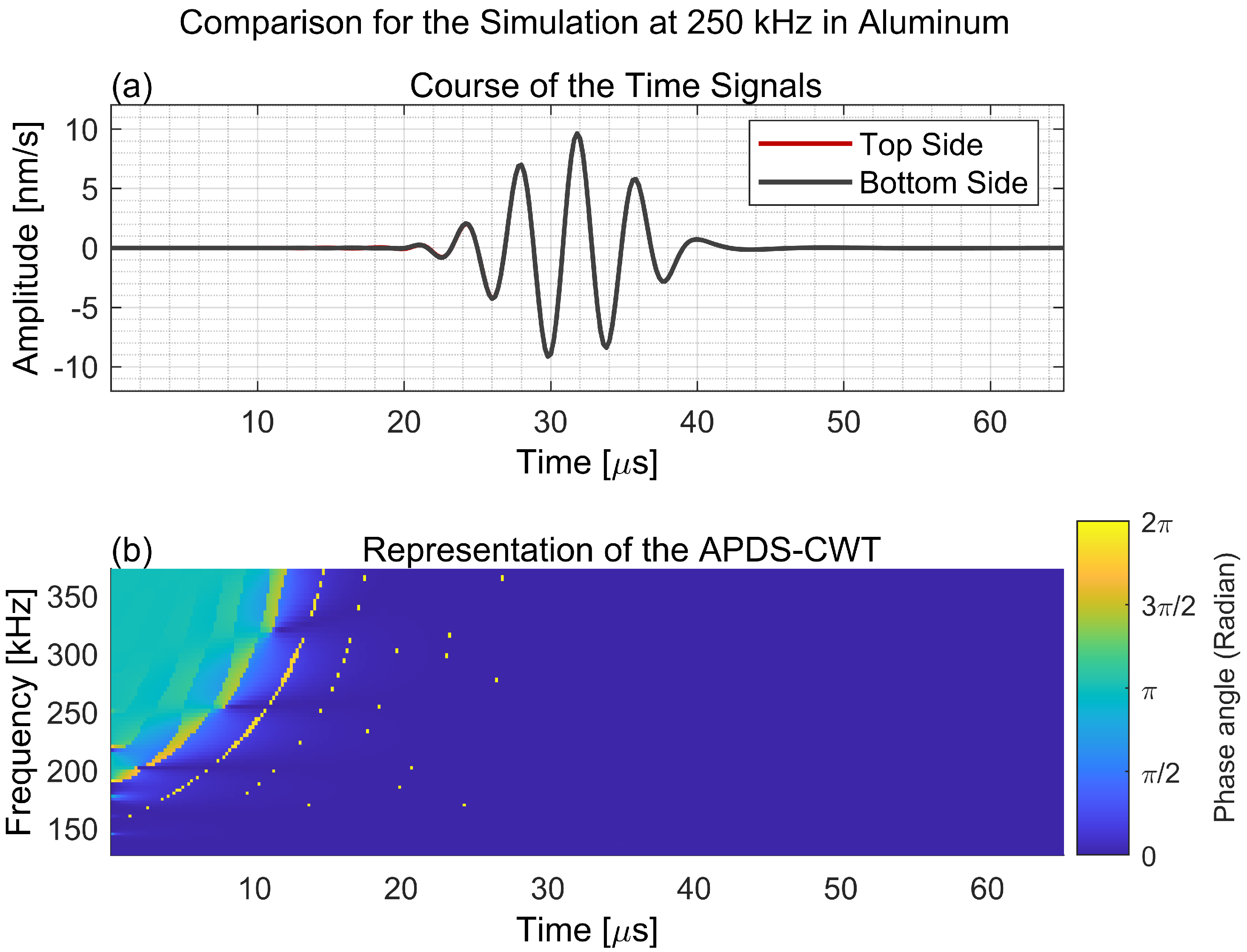
In the second step, the developed evaluation methods are applied to numerically obtained time signals showing the noise-free GUW propagation in four different specimen material setups for the upper and lower structure surface. The specimens prepared from different material settings are considered to identify various possible factors influencing the phase angle relation. The plate specimens differ regarding the amount of material interfaces, stiffness characteristics, amount of materials and fiber content to enable a step-by-step examination of the different settings.
In the third step, the wave propagation is measured on FML test specimens to gain experimental time signal data and to validate the approach. The derived methods are then applied to the authentic measurements. They are evaluated with regard to their oscillation signals on the upper and lower surface. The work closes with an evaluation of the work and outlook of future work.
6. Conclusions
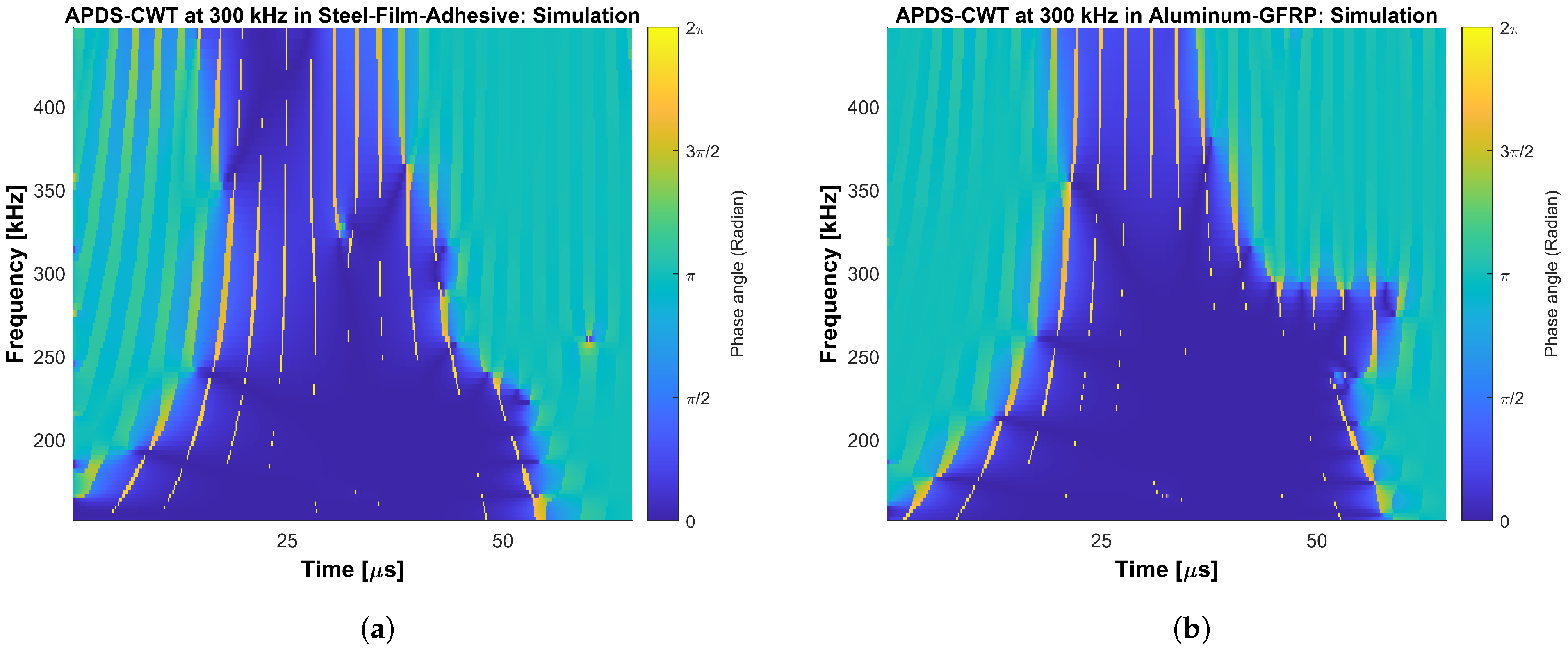
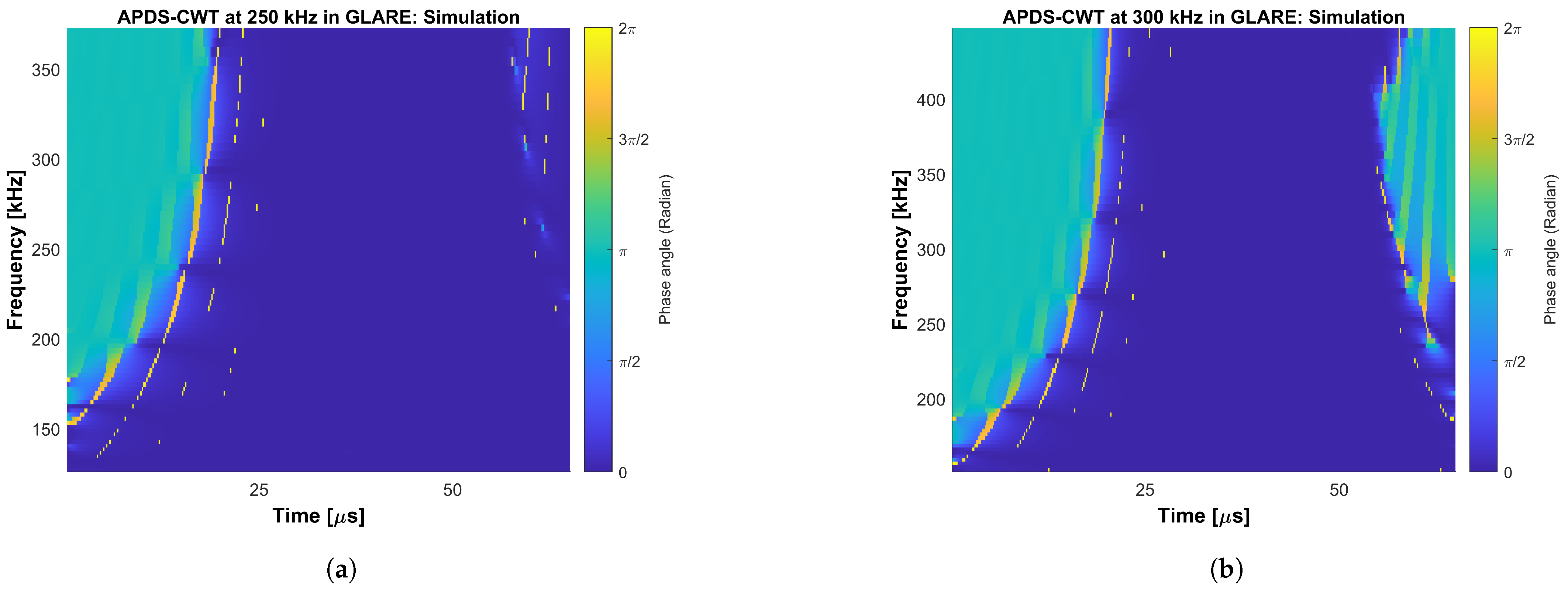
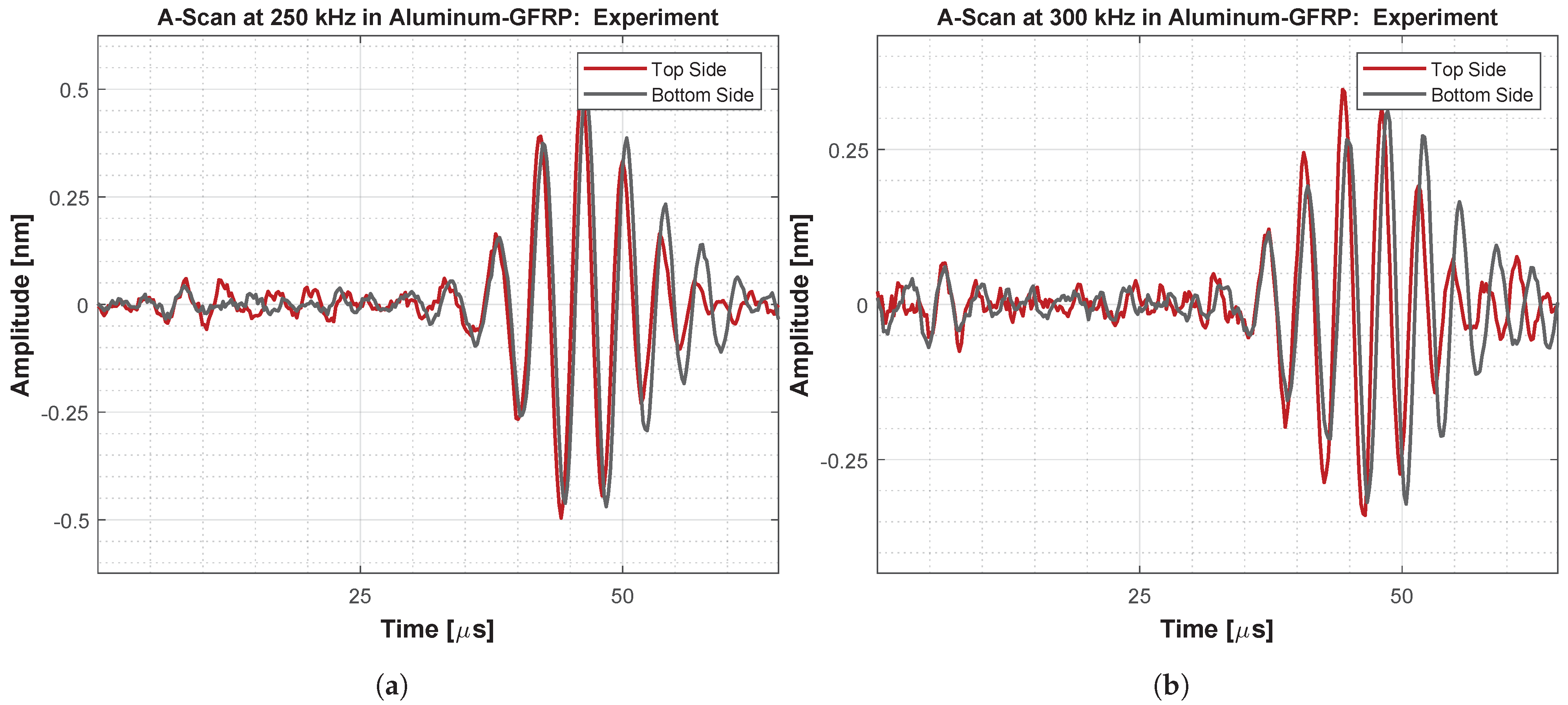
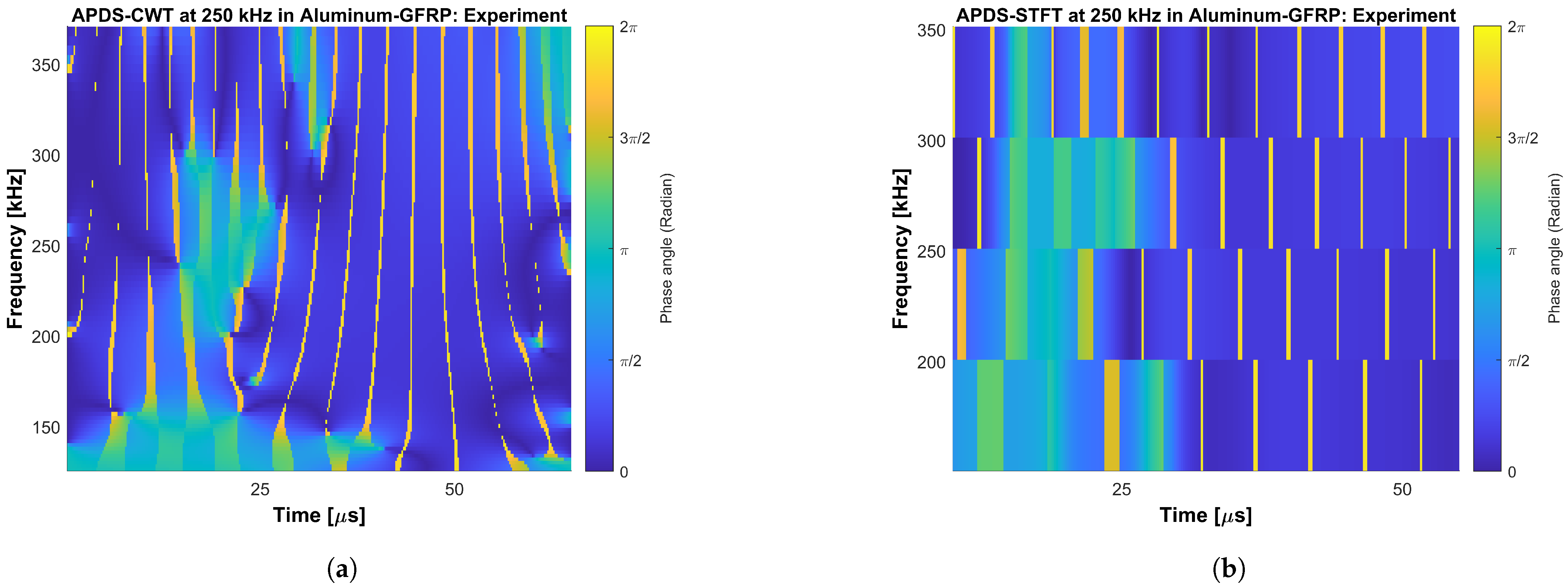
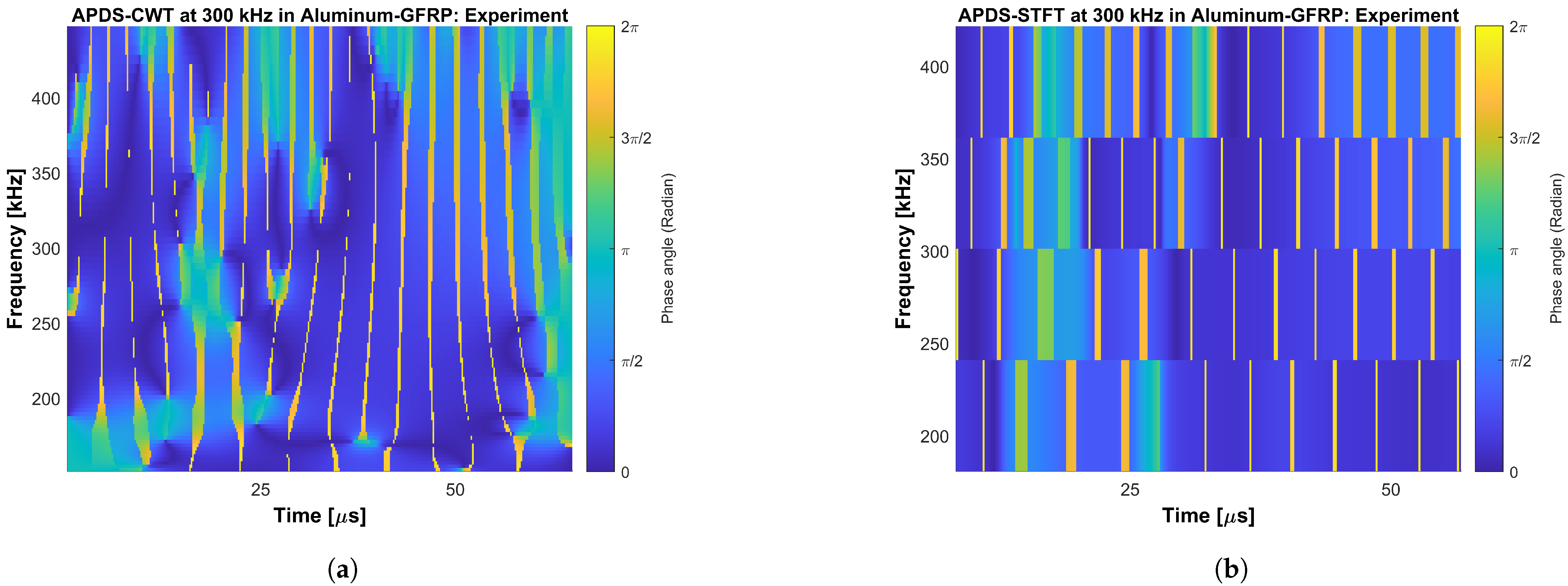
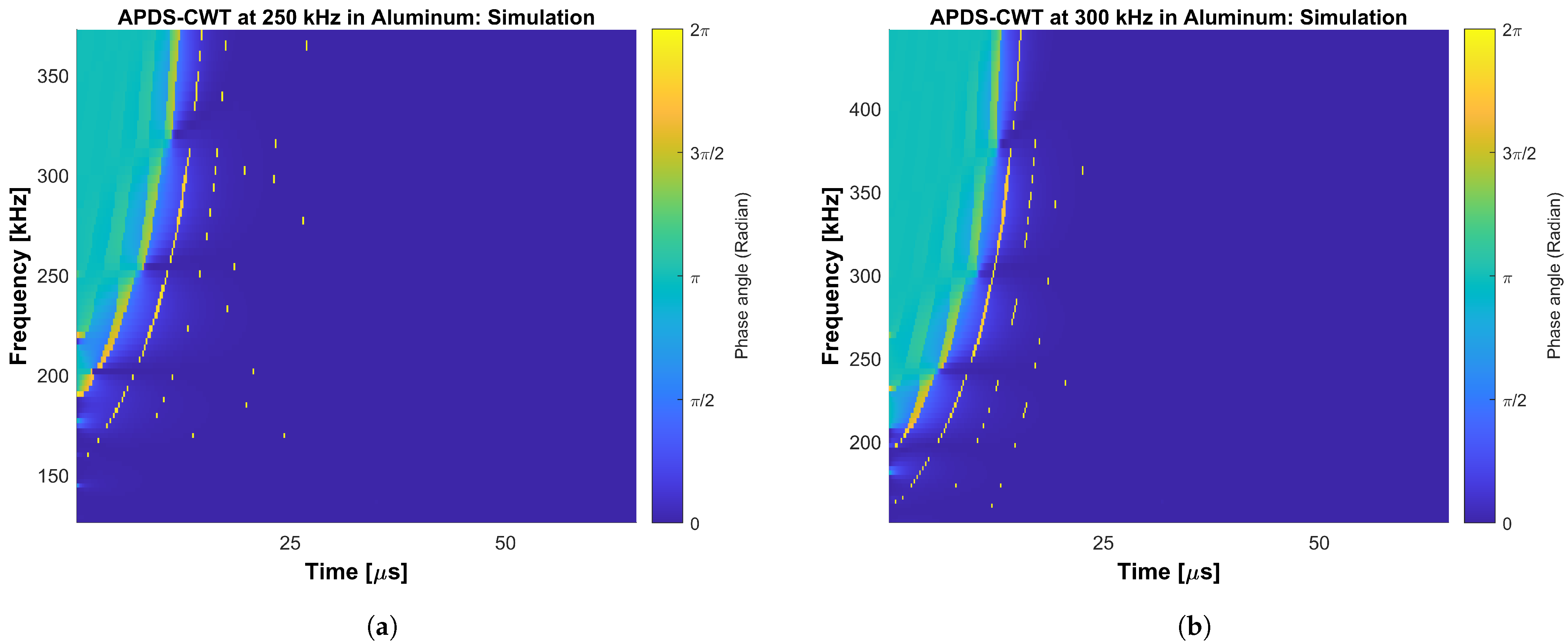
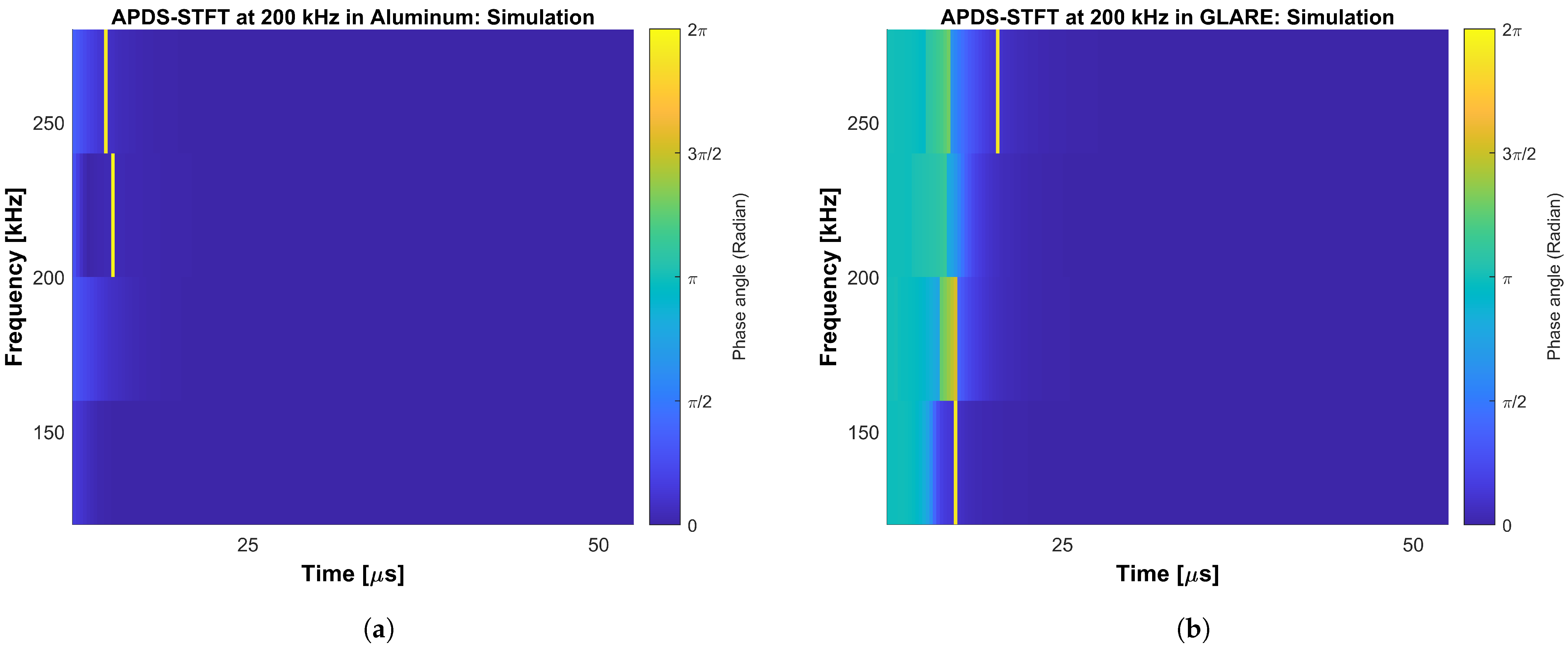
The main objective of this work is to answer the question of whether the oscillation phase relation on the upper and lower surface of plate-like structures made of FML under GUW wave propagation shows the same behavior as for GUW in metals or composites. Hence, two different frequency-time analysis methods are derived and used to evaluate segment-wise time signals’ oscillation phase angles. One method is based on the CWT and its IP information stored in the complex transformation parameters. The second methods is based on the STFT. Phase difference spectra are extracted and compared regarding their capability of identifying the phase relation between in-phase wave modes and wave modes shifted by an angle of . Properties like the uncertainty principle during transformation are taken into account because a good adjustment between the time axes allows a quick comparison of the gained spectra with the underlying time signals. During the evaluation, the main focus for the interpretation of the spectra lies on the excitation signal’s bandwidth for both numerical and experimental data. Furthermore, the spectra cover the bandwidth of the excitation burst signal because these are the frequencies in which the wave modes physically appear on the excited structures. Higher and lower frequencies bands in the spectra can be interpreted as relicts of the transformation itself. It should be taken into account that numerical errors as well as effects of the boundary conditions in the simulation can lead to local variations in the phase and transition behavior between the phase and 0. If not the absolute value of the difference is used, the order of the summands influences the later sign of the difference. Therefore, values of and can be interpreted the same as a phase shift of and as an indication for local symmetric oscillation behavior. Due to numerical boundary conditions, low-amplitude oscillations can appear in the time signals. Their phase angle changes are present in the spectra of the numerical captured time signals. This shows that the spectra do not replace a critical interpretation of the results. This also applies for experimental errors such as positioning inaccuracies of the vibrometer’s measuring laser. When interpreting the spectra, it needs to be taken into account that the APDS do not distinguish between signals of lower amplitude, i.e., structural vibration, measurement noise or numerical relicts. Because noise occurs randomly, its representation in the APDS is shown as random phase relations of slight extension.
This work proves that the oscillation phase relation between the upper and lower surface of FML shows the same wave propagation behavior of GUW in composites and metals resp. the GUW in FML form the same surface oscillation characteristics as the Lamb waves in metals or composites as presented in
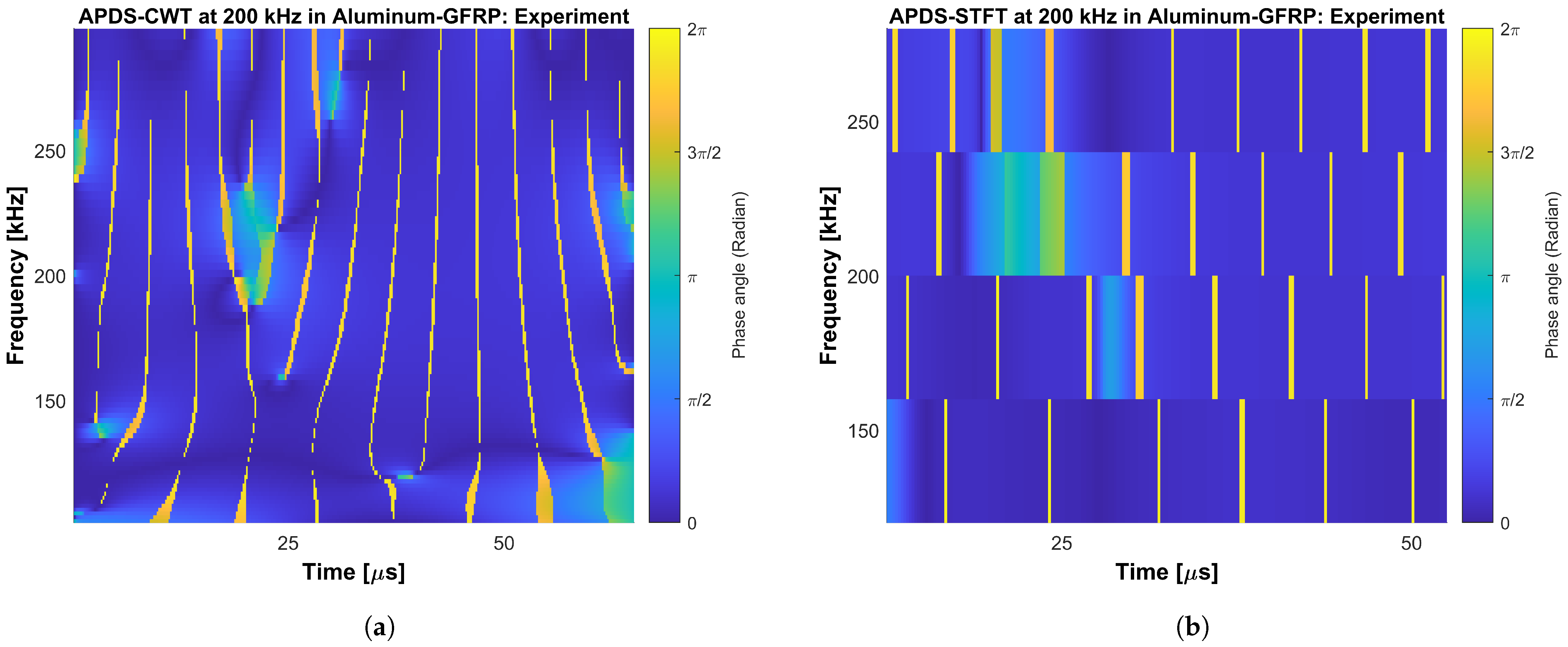
Section 1. The existence of Lamb waves in FML is thus proven. The CWT is found suitable to gain phase information by comparing oscillation signals from plates’ upper and lower surfaces. The work also illustrates with the help of concrete examples that positioning accuracy is crucial in experiments. The effect of noise in the experimentally captured time signals significantly influences the APDS, because the evaluation procedures are magnitude-independent. Time signals being in phase can clearly be identified in all cases in the APDS. The narrow lines in the APDS-CWT and APDS-STFT which occur intensely when evaluating the experimental data (i.e., in
Figure A6a,b) show phase jumps of approx.
and are caused by noise in the captured time signals. Profound filtering of the time signals as well as the implementation of thresholds in the methods will smooth the APDS representation of both methods. At this stage of the work, an estimation of the oscillation phase relation between transient time signals can be performed by using the concept of the APDS-STFT and a more detailed observation via the APDS-CWT. To gain a better adjustment between the points in time in the time domain and the points in time in the frequency-domain, it is recommended to set the STFT to the maximum possible overlap and then use, in the CWT, as many scales per octave as is feasible.
In future work, the optimization of the presented methods will be adressed. The APDS-CWT as well as the APDS-STFT will be adjusted in their settings until the best possible agreement between time domain and frequency domain is found. When applied to measured data, background noise and superimposing errors need to be taken into account. Because noise shows in the APDS as a small, discontinuous phase, postprocessing will help insmoothing the representation. Thresholds will be implemented as well to smooth the representation when noisy experimental data is used.