The Spherical Harmonic Family of Beampatterns
Abstract
1. Introduction
2. Theory
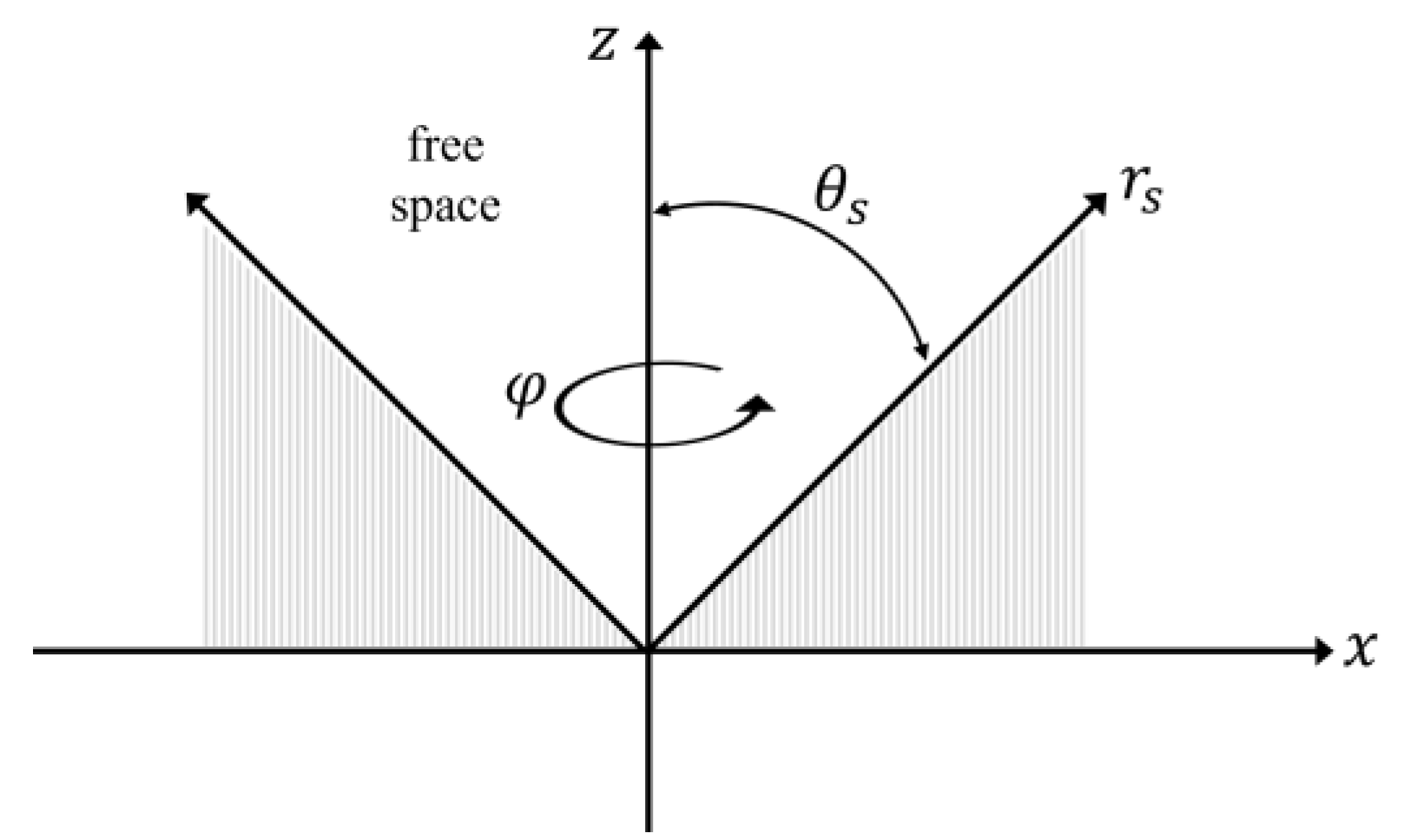
2.1. General Solution
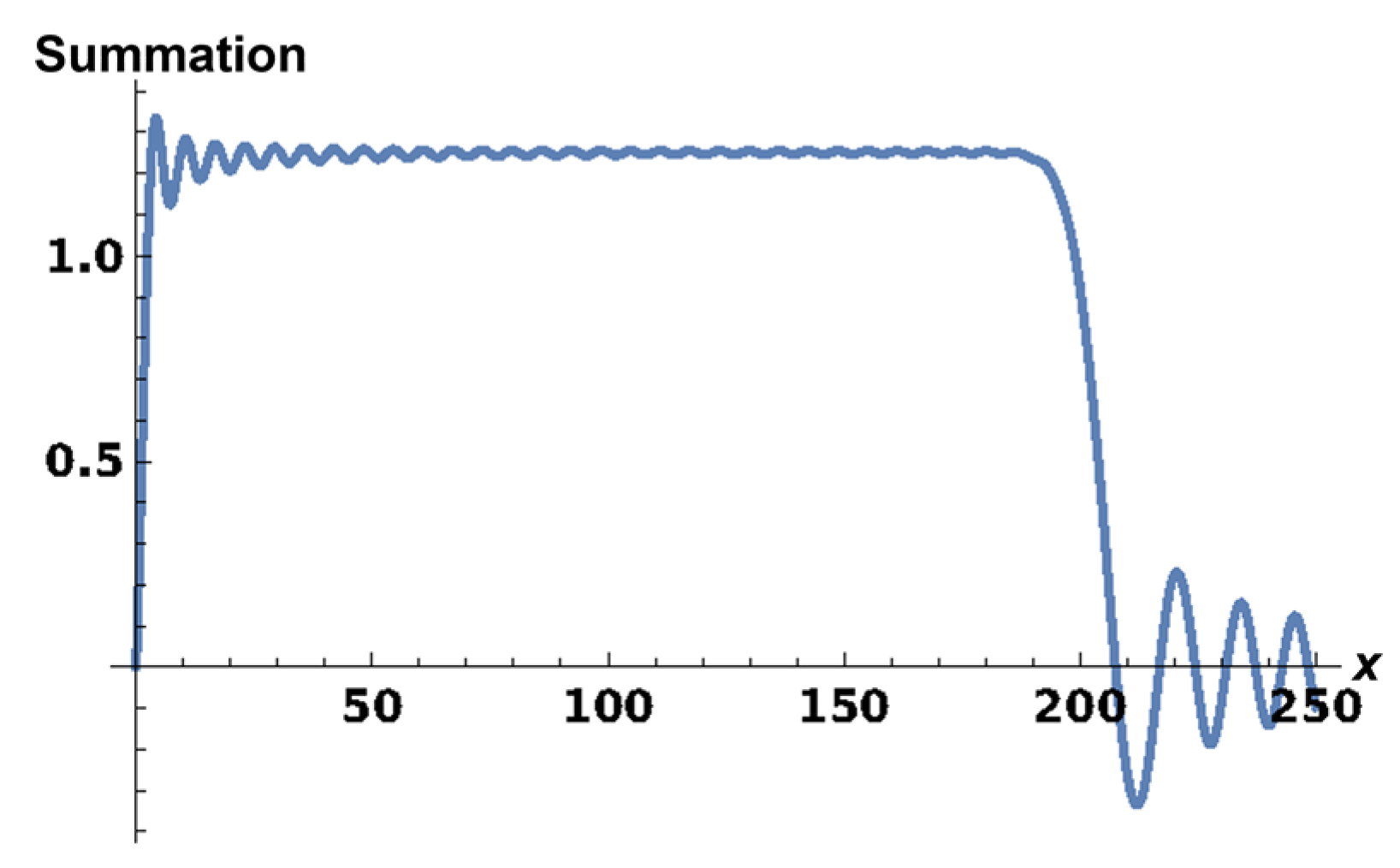
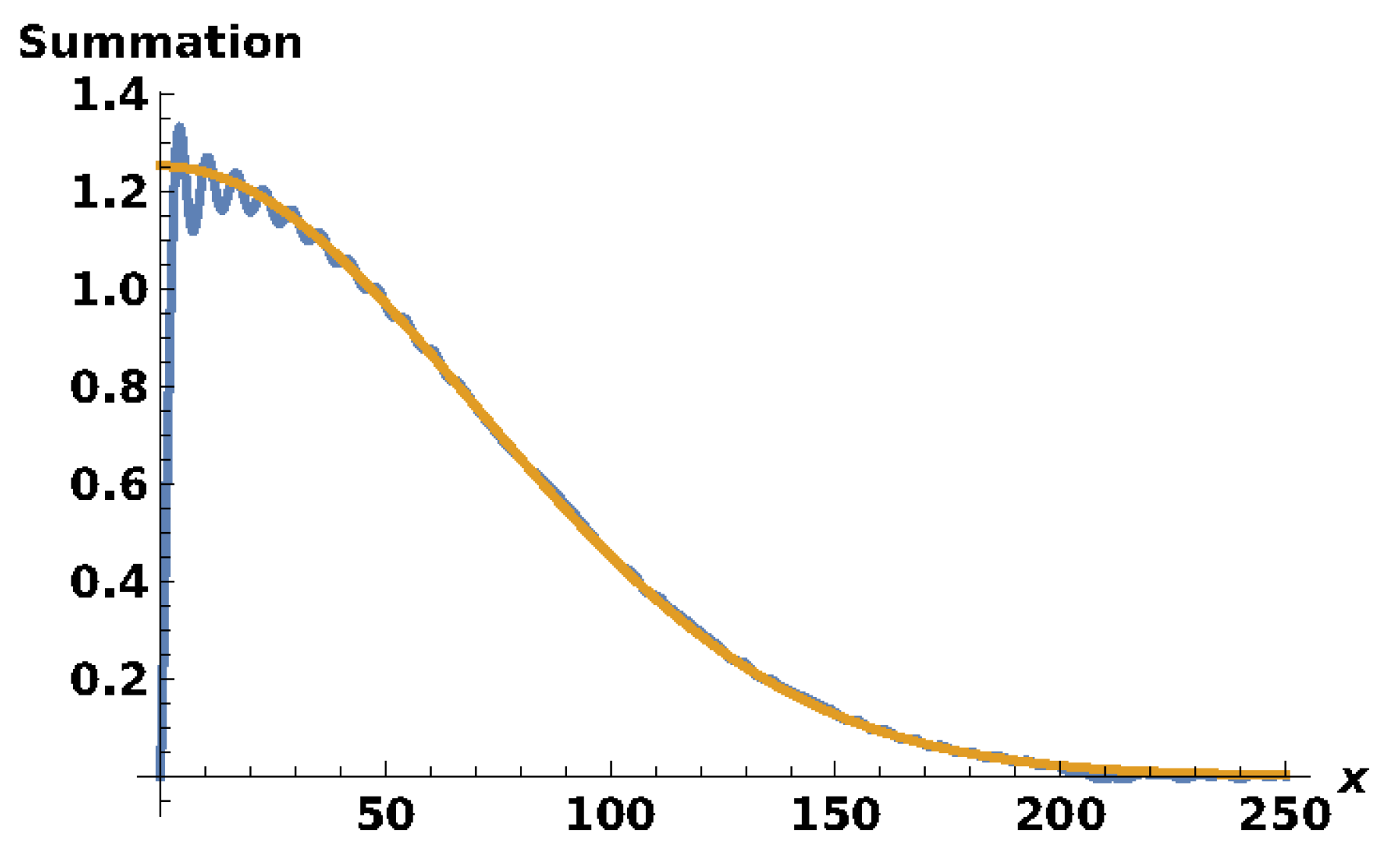
2.2. Special Properties of Sums of Spherical Bessel Functions
2.3. Modifications via Imaginary Shift in Coordinates
2.4. Other Simple Modifications and Properties
3. Methods
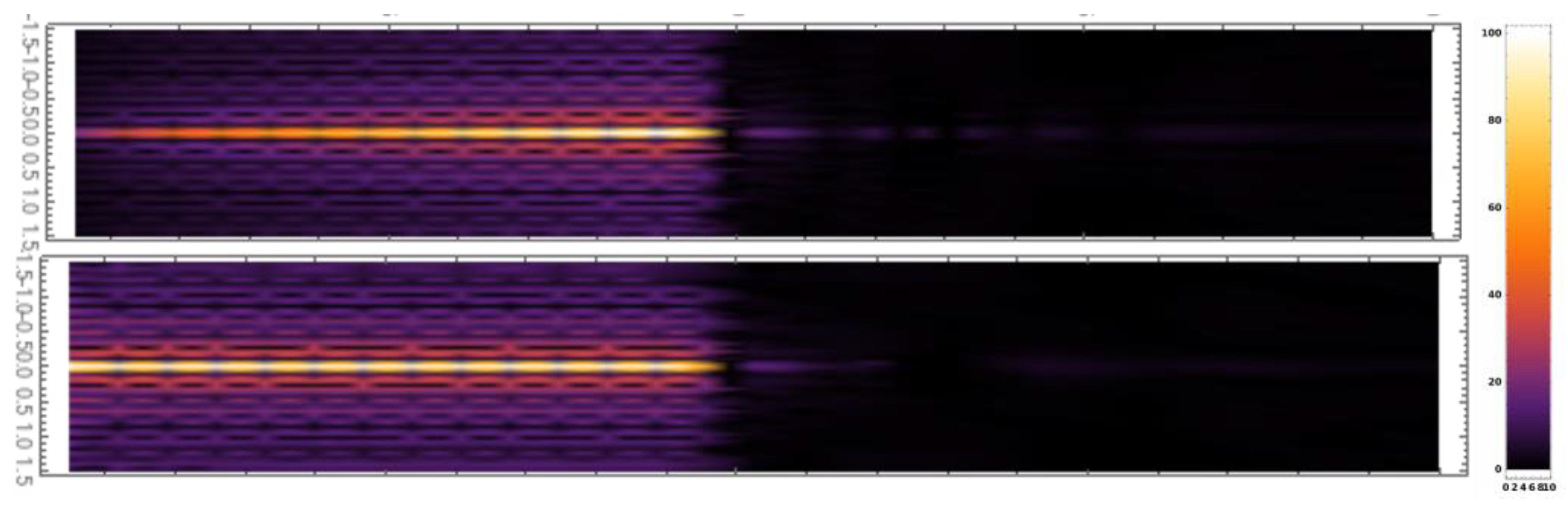
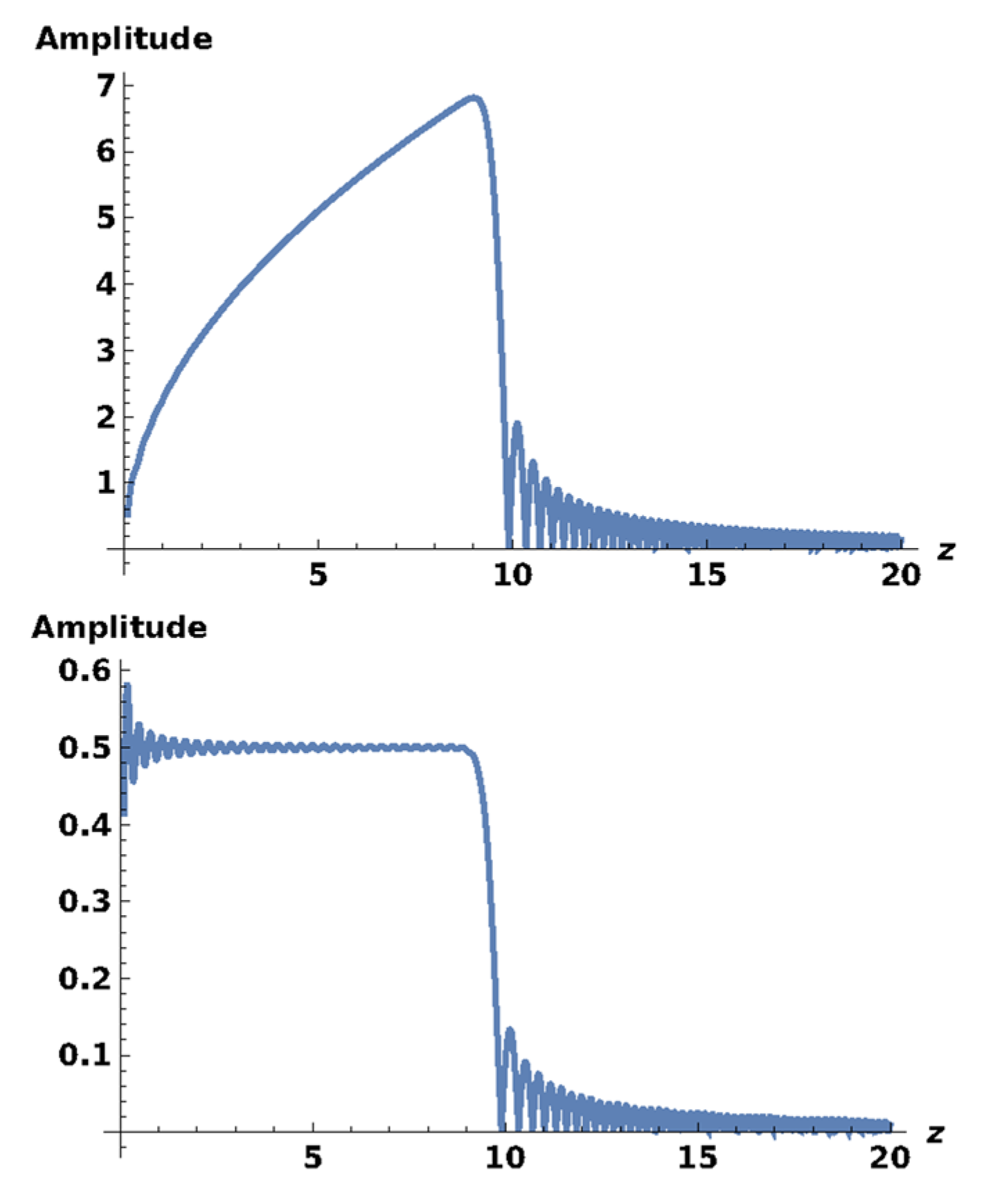
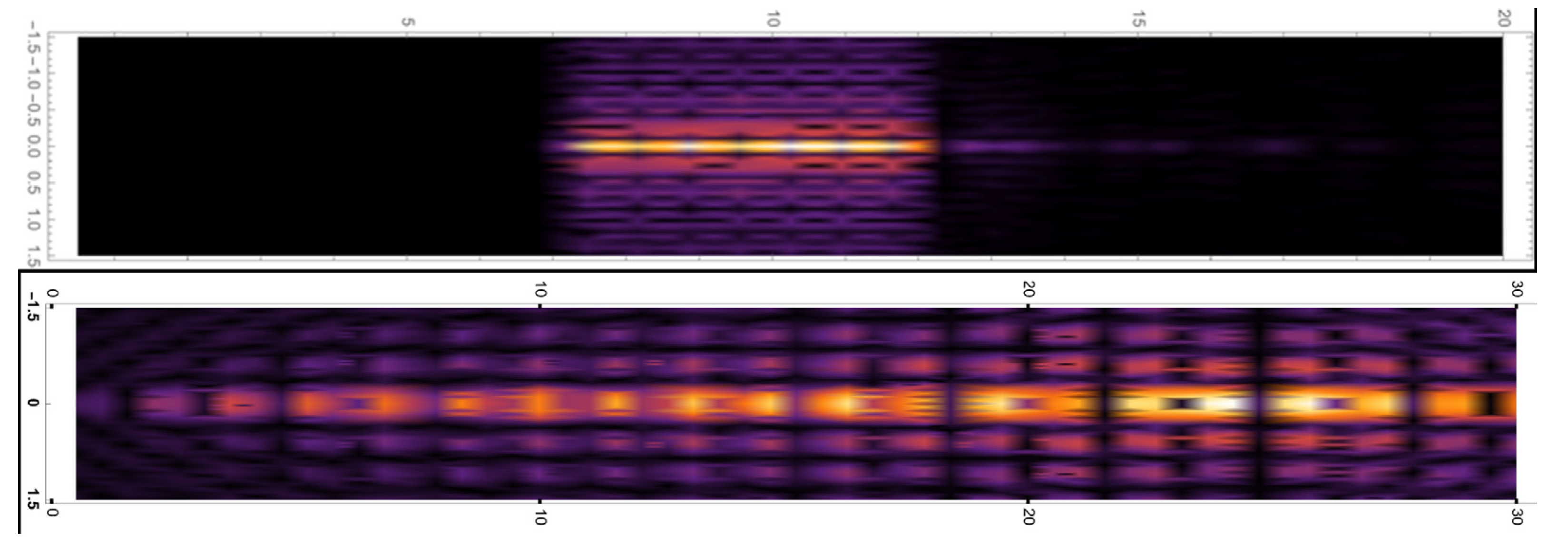
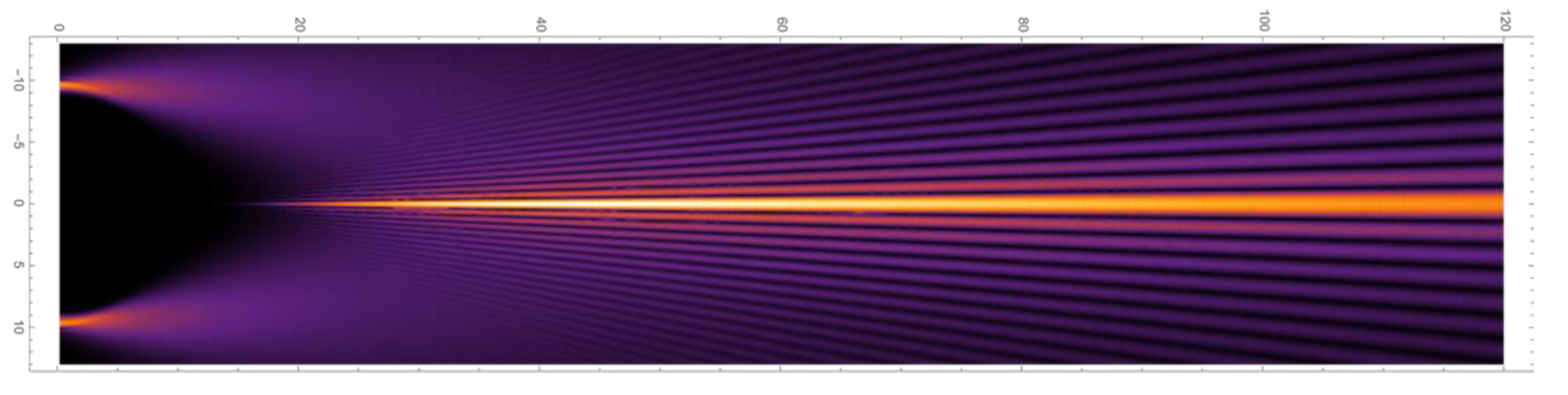
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hernández-Figueroa, H.E.; Zamboni-Rached, M.; Recami, E. Localized Waves; IEEE Press: Hoboken, NJ, USA, 2008. [Google Scholar]
- Durnin, J. Exact solutions for nondiffracting beams. I. The scalar theory. JOSA 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli, J., Jr.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.Y.; Greenleaf, J.F. Nondiffracting X waves-exact solutions to free-space scalar wave equation and their finite aperture realizations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 19–31. [Google Scholar] [CrossRef]
- Parker, K.J.; Chen, S.; Alonso, M.A. The ultrasound needle pulse. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2017, 64, 1045–1049. [Google Scholar] [CrossRef] [PubMed]
- Cobbold, R.S.C. Foundations of Biomedical Ultrasound; Oxford University Press: New York, NY, USA, 2007. [Google Scholar]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Elsevier Academic Press: Burlington, MA, USA, 2004. [Google Scholar]
- Parker, K.J. Correspondence: Apodization and windowing functions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1263–1271. [Google Scholar] [CrossRef] [PubMed]
- Parker, K.J. Correspondence: Apodization and windowing eigenfunctions. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 1575–1579. [Google Scholar] [CrossRef] [PubMed]
- Williams, E.G. Fourier Acoustics: Sound Radiation and Nearfield Acoustical Holography; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Co.: Englewood, CO, USA, 2005. [Google Scholar]
- Sheppard, C.J.R.; Alonso, M.A.; Moore, N.J. Localization measures for high-aperture wavefields based on pupil moments. J. Opt. A Pure Appl. Opt. 2008, 10, 033001. [Google Scholar] [CrossRef]
- Boyer, C.P.; Kalnins, E.G.; Miller, W. Symmetry and separation of variables for the Helmholtz and Laplace equations. Nagoya Math. J. 1976, 60, 35–80. [Google Scholar] [CrossRef]
- Baddour, N. Multidimensional wave field signal theory: Mathematical foundations. AIP Adv. 2011, 1, 022120. [Google Scholar] [CrossRef]
- Baddour, N. Multidimensional wave field signal theory: Transfer function relationships. Math. Probl. Eng. 2012, 2012, 478295. [Google Scholar] [CrossRef]
- Baddour, N. The derivative-free Fourier shell identity for photoacoustics. Springerplus 2016, 5, 1597. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; U.S. Government Publishing Office: Washington, WA, USA, 1964; p. 1046.
- Morse, P.M.; Ingard, K.U. Theoretical Acoustics, Chapter 7; Princeton University Press: Princeton, NJ, USA, 1987. [Google Scholar]
- Wang, Z.; Wu, S.F. Helmholtz equation-least-squares method for reconstructing the acoustic pressure field. J. Acoust. Soc. Am. 1997, 102, 2020–2032. [Google Scholar] [CrossRef]
- Wolf, E.; Marchand, E.W. Comparison of the Kirchhoff and the Rayleigh–Sommerfeld theories of diffraction at an aperture. JOSA 1964, 54, 587–594. [Google Scholar] [CrossRef]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; McGraw-Hill Book Co.: New York, NY, USA, 1981. [Google Scholar]
- Watson, G.N. A Treatise on the Theory of Bessel Functions, Chapter XVI; Cambridge University Press: London, UK, 1922. [Google Scholar]
- Alonso, M.A.; Borghi, R.; Santarsiero, M. New basis for rotationally symmetric nonparaxial fields in terms of spherical waves with complex foci. Opt. Express 2006, 14, 6894–6905. [Google Scholar] [CrossRef] [PubMed]
- Cizmár, T.; Dholakia, K. Tunable Bessel light modes: Engineering the axial propagation. Opt. Express 2009, 17, 15558–15570. [Google Scholar] [CrossRef] [PubMed]
- Devaney, A.J.; Wolf, E. Multipole expansions and plane wave representations of the electromagnetic field. J. Math. Phys. 1974, 15, 234–244. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, K.J.; Alonso, M.A. The Spherical Harmonic Family of Beampatterns. Acoustics 2022, 4, 958-966. https://doi.org/10.3390/acoustics4040059
Parker KJ, Alonso MA. The Spherical Harmonic Family of Beampatterns. Acoustics. 2022; 4(4):958-966. https://doi.org/10.3390/acoustics4040059
Chicago/Turabian StyleParker, Kevin J., and Miguel A. Alonso. 2022. "The Spherical Harmonic Family of Beampatterns" Acoustics 4, no. 4: 958-966. https://doi.org/10.3390/acoustics4040059
APA StyleParker, K. J., & Alonso, M. A. (2022). The Spherical Harmonic Family of Beampatterns. Acoustics, 4(4), 958-966. https://doi.org/10.3390/acoustics4040059





