Phasor Wave-Field Simulation Providing Direct Access to Instantaneous Frequency: A Demonstration for a Damped Elastic Wave Simulation
Abstract
:1. Introduction
2. Materials and Methods
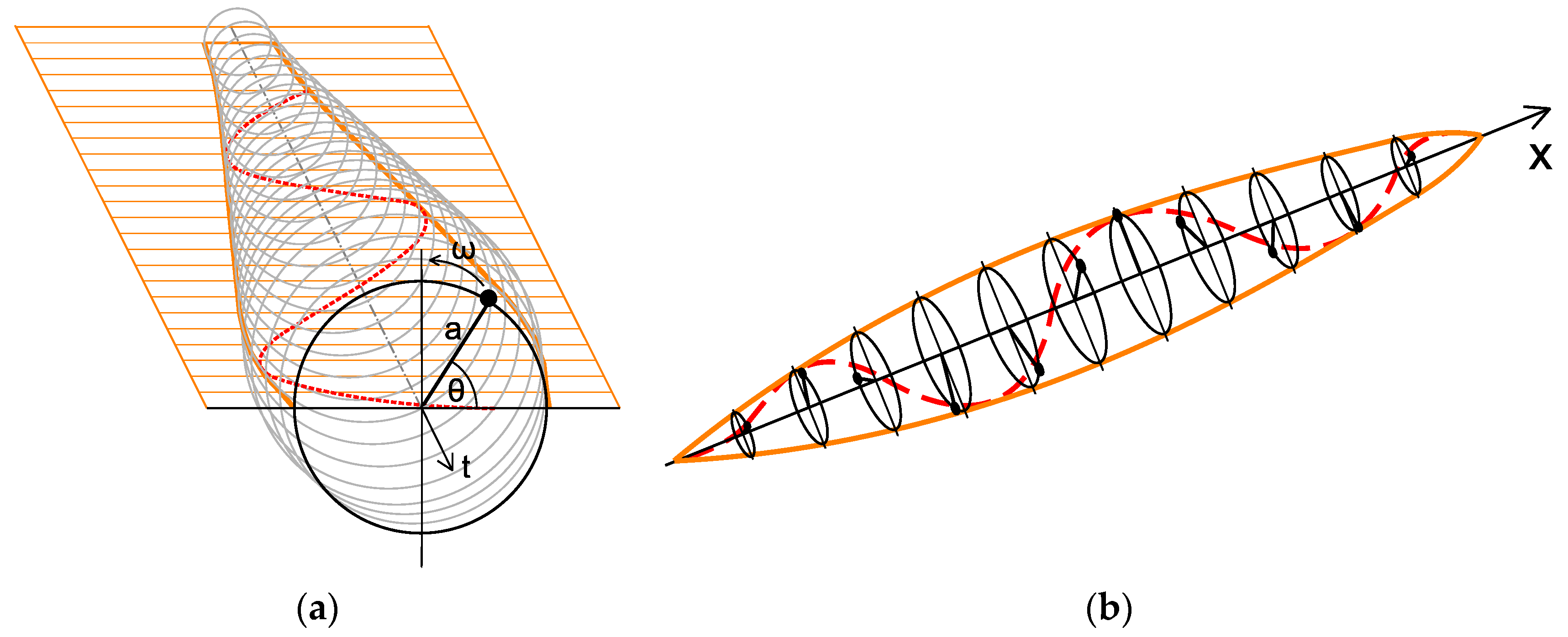
2.1. The Phasor Concept
2.2. The Instantaneous Frequency Concept
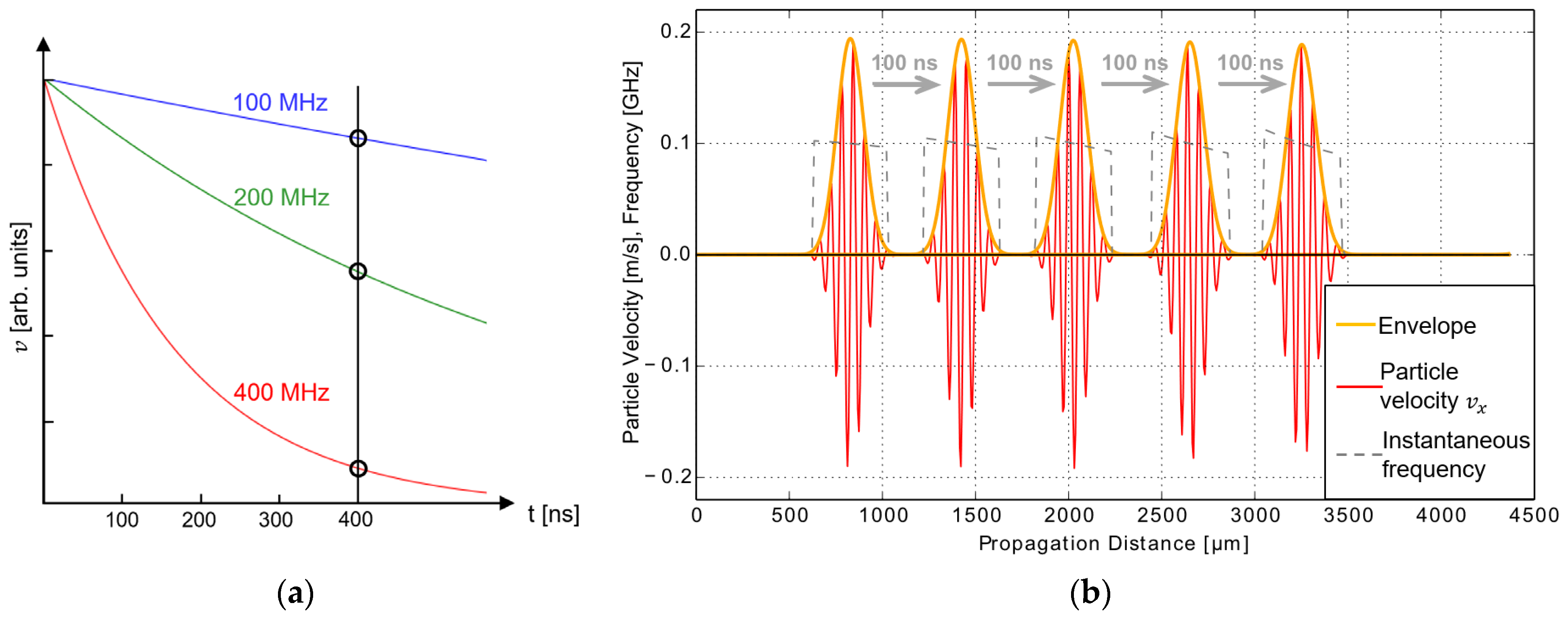
2.3. The Wave Attenuation Concept
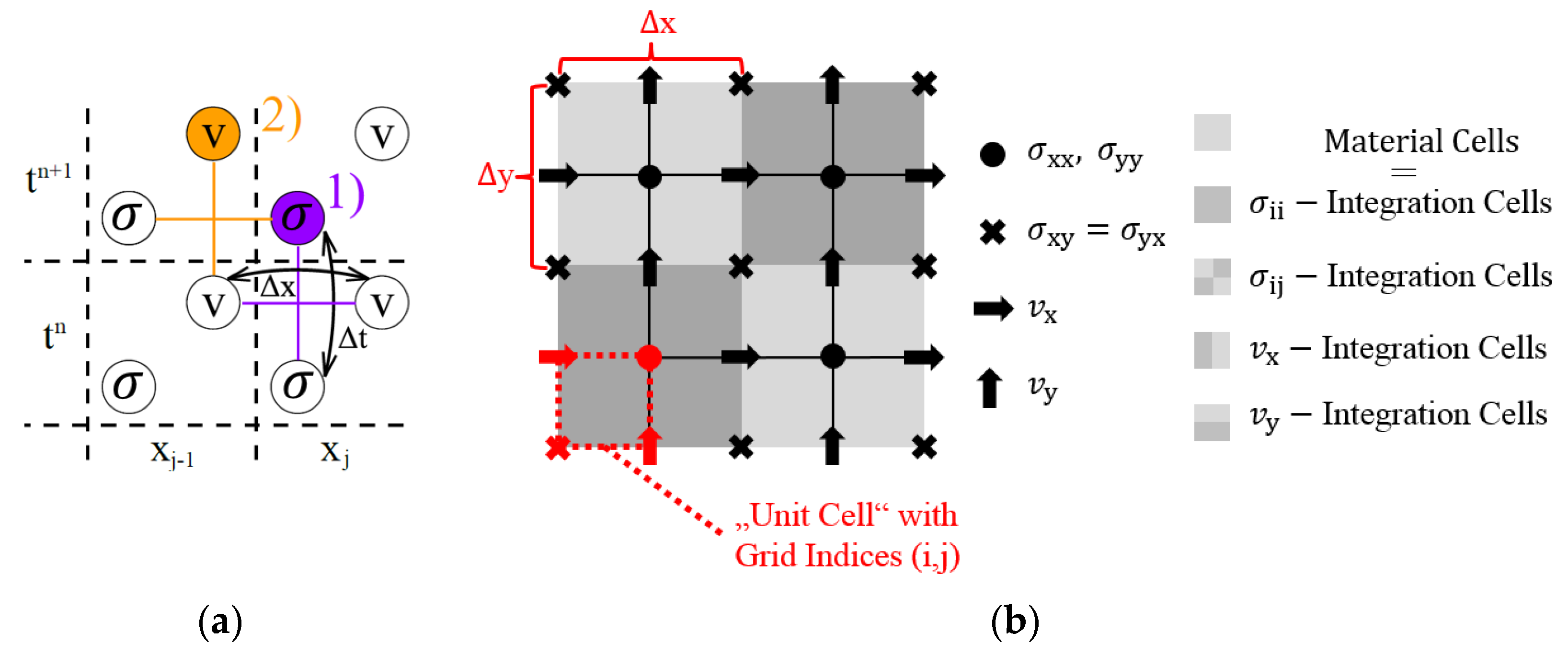
3. The Use Case, Elastic Wave Propagation
- The kinetics which has its origin in Newton’s second law and is also called the Cauchy momentum equation , where the particle velocity field is the first derivative of the displacement field with respect to time, stands for the mass density, and represents the body forces (like gravity, electro-magnetic forces, etc.);
- The kinematics, relating the velocities of a material point to the strain rates ;
- The material law relating stress and strain , here shown for an isotropic material with λ and μ being the first and second Lame constants representing the stiffness of the material.
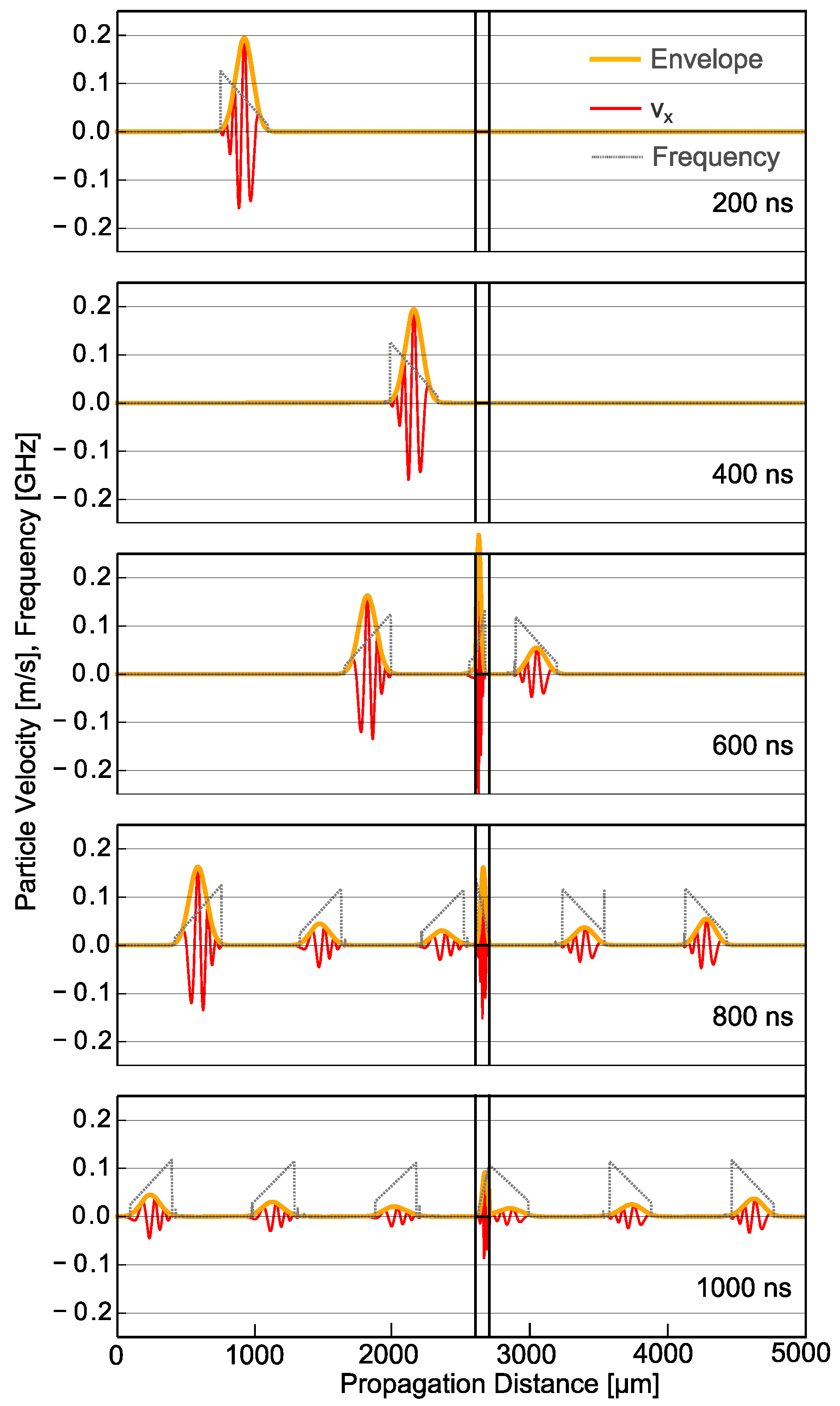
4. Results
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Achenbach, J. Wave Propagation in Elastic Solids; Elsevier BV: Amsterdam, The Netherlands, 1975. [Google Scholar] [CrossRef] [Green Version]
- Virieux, J. SH-wave propagation in heterogeneous media: Velocity-stress finite-difference method. Geophysics 1984, 49, 1933–1942. [Google Scholar] [CrossRef]
- Magnoni, F.; Casarotti, E.; Michelini, A.; Piersanti, A.; Komatitsch, D.; Peter, D.; Tromp, J. Spectral-Element Simulations of Seismic Waves Generated by the 2009 L’Aquila Earthquake. Bull. Seism. Soc. Am. 2013, 104, 73–94. [Google Scholar] [CrossRef] [Green Version]
- Etgen, J.; Gray, S.H.; Zhang, Y. An overview of depth imaging in exploration geophysics. Geophysics 2009, 74, WCA5–WCA17. [Google Scholar] [CrossRef]
- Paltauf, G.; Nuster, R.; Haltmeier, M.; Burgholzer, P. Photoacoustic tomography using a Mach-Zehnder interferometer as an acoustic line detector. Appl. Opt. 2007, 46, 3352–3358. [Google Scholar] [CrossRef]
- E Kennedy, J.; Ter Haar, G.R.; Cranston, D. High intensity focused ultrasound: Surgery of the future? Br. J. Radiol. 2003, 76, 590–599. [Google Scholar] [CrossRef] [PubMed]
- Sehra, G.; Cole, M.; Gardner, J. Miniature taste sensing system based on dual SH-SAW sensor device: An electronic tongue. Sens. Actuators B Chem. 2004, 103, 233–239. [Google Scholar] [CrossRef]
- Rodríguez-Madrid, J.; Iriarte, G.F.; Williams, O.; Calle, F. High precision pressure sensors based on SAW devices in the GHz range. Sens. Actuators A Phys. 2013, 189, 364–369. [Google Scholar] [CrossRef] [Green Version]
- Hoshi, T.; Takahashi, M.; Iwamoto, T.; Shinoda, H. Noncontact Tactile Display Based on Radiation Pressure of Airborne Ultrasound. IEEE Trans. Haptics 2010, 3, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Pandey, D.; Pandey, S. Ultrasonics: A Technique of Material Characterization; InTech: Rijeka, Croatia, 2010. [Google Scholar] [CrossRef] [Green Version]
- Rose, J.L. Ultrasonic Guided Waves in Solid Media; Cambridge University Press (CUP): Cambridge, UK, 2014. [Google Scholar] [CrossRef]
- Toozandehjani, M.; Matori, K.A.; Ostovan, F.; Mustapha, F.; Zahari, N.I.; Oskoueian, A. On the correlation between microstructural evolution and ultrasonic properties: A review. J. Mater. Sci. 2015, 50, 2643–2665. [Google Scholar] [CrossRef]
- McClements, D.; Gunasekaran, S. Ultrasonic characterization of foods and drinks: Principles, methods, and applications. Crit. Rev. Food Sci. Nutr. 1997, 37, 1–46. [Google Scholar] [CrossRef]
- Grünwald, E.; Hammer, R.; Rosc, J.; Maier, G.; Bärnthaler, M.; Cordill, M.; Brand, S.; Nuster, R.; Krivec, T.; Brunner, R. Advanced 3D failure characterization in multi-layered PCBs. NDT E Int. 2016, 84, 99–107. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; She, W.; Ma, L.; Zhu, W. Ultrasound monitoring of setting and hardening process of ultra-high performance cementitious materials. NDT E Int. 2012, 47, 177–184. [Google Scholar] [CrossRef]
- Grünwald, E.; Rosc, J.; Hammer, R.; Czurratis, P.; Koch, M.; Kraft, J.; Schrank, F.; Brunner, R. Automatized failure analysis of tungsten coated TSVs via scanning acoustic microscopy. Microelectron. Reliab. 2016, 64, 370–374. [Google Scholar] [CrossRef]
- Brand, S.; Appenroth, T.; Naumann, F.; Steller, W.; Wolf, M.J.; Czurratis, P.; Altmann, F.; Petzold, M. Acoustic GHz-microscopy and its potential applications in 3D-integration technologies. In Proceedings of the 2015 IEEE 65th Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 26–29 May 2015; pp. 46–53. [Google Scholar] [CrossRef]
- Sledzinska, M.; Graczykowski, B.; Maire, J.; Chavez-Angel, E.; Sotomayor-Torres, C.M.; Alzina, F. 2D Phononic Crystals: Progress and Prospects in Hypersound and Thermal Transport Engineering. Adv. Funct. Mater. 2020, 30, 1–12. [Google Scholar] [CrossRef]
- Yuan, S.; Song, X.; Cai, W.; Hu, Y. Analysis of attenuation and dispersion of Rayleigh waves in viscoelastic media by finite-difference modeling. J. Appl. Geophys. 2018, 148, 115–126. [Google Scholar] [CrossRef]
- Vishnevsky, D.M.; Solovyev, S.A.; Lisitsa, V.V. Numerical Simulation of Wave Propagation in 3D Elastic Media with Viscoelastic Formations. Lobachevskii J. Math. 2020, 41, 1603–1614. [Google Scholar] [CrossRef]
- Tie, B.; Mouronval, A.-S.; Nguyen, V.-D.; Series, L.; Aubry, D. A unified variational framework for the space discontinuous Galerkin method for elastic wave propagation in anisotropic and piecewise homogeneous media. Comput. Methods Appl. Mech. Eng. 2018, 338, 299–332. [Google Scholar] [CrossRef]
- Emmerich, H.; Korn, M. Incorporation of attenuation into time-domain computations of seismic wave fields. Geophysics 1987, 52, 1252–1264. [Google Scholar] [CrossRef]
- Blanch, J.O.; Robertsson, J.O.A.; Symes, W.W. Modeling of a constant Q: Methodology and algorithm for an efficient and optimally inexpensive viscoelastic technique. Geophysics 1995, 60, 176–184. [Google Scholar] [CrossRef] [Green Version]
- Moczo, P.; Robertsson, J.O.; Eisner, L. The Finite-Difference Time-Domain Method for Modeling of Seismic Wave Propagation. Adv. Geophys. 2007, 48, 421–516. [Google Scholar] [CrossRef]
- Boashash, B. The Instantaneous Frequency of a Signal—Part 1: Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z.; Long, S.R.; Arnold, K.C.; Chen, X.; Blank, K. On Instantaneous Frequency. Adv. Adapt. Data Anal. 2009, 1, 177–229. [Google Scholar] [CrossRef]
- Fellinger, P.; Marklein, R.; Langenberg, K.; Klaholz, S. Numerical modeling of elastic wave propagation and scattering with EFIT—elastodynamic finite integration technique. Wave Motion 1995, 21, 47–66. [Google Scholar] [CrossRef]
- Hsu, M.K.; Sheu, J.C.; Hsue, C. Overcoming the negative frequencies—Instantaneous frequency and amplitude estimation using Osculating Circle method. J. Mar. Sci. Technol. 2011, 19, 514–521. [Google Scholar]
- Hahn, S. Hilbert Transforms in Signal Processing; Artech House Inc.: Boston, MA, USA, 1996. [Google Scholar]
- Hammer, R.; Pötz, W.; Arnold, A. A dispersion and norm preserving finite difference scheme with transparent boundary conditions for the Dirac equation in(1+1)D. J. Comput. Phys. 2014, 256, 728–747. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Jeong, H.; Cho, S.; Li, X. Measurement of attenuation coefficients of the fundamental and second harmonic waves in water. AIP Conf. Proc. 2016, 1706. [Google Scholar] [CrossRef]
| Material | Mass Density | 1st Lame Const. | 2nd Lame Const | Damping 1 |
|---|---|---|---|---|
| ρ [kg/m3] | λ [GPa] | μ [GPa] | β [Neper/(s Hz2] | |
| Aluminum | 2700 | 55.5 | 26.1 | - |
| Water | 1000 | 2.08 | 0 | 3.7 × 10−11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hammer, R.; Mitterhuber, L.; Brunner, R. Phasor Wave-Field Simulation Providing Direct Access to Instantaneous Frequency: A Demonstration for a Damped Elastic Wave Simulation. Acoustics 2021, 3, 485-492. https://doi.org/10.3390/acoustics3030032
Hammer R, Mitterhuber L, Brunner R. Phasor Wave-Field Simulation Providing Direct Access to Instantaneous Frequency: A Demonstration for a Damped Elastic Wave Simulation. Acoustics. 2021; 3(3):485-492. https://doi.org/10.3390/acoustics3030032
Chicago/Turabian StyleHammer, René, Lisa Mitterhuber, and Roland Brunner. 2021. "Phasor Wave-Field Simulation Providing Direct Access to Instantaneous Frequency: A Demonstration for a Damped Elastic Wave Simulation" Acoustics 3, no. 3: 485-492. https://doi.org/10.3390/acoustics3030032
APA StyleHammer, R., Mitterhuber, L., & Brunner, R. (2021). Phasor Wave-Field Simulation Providing Direct Access to Instantaneous Frequency: A Demonstration for a Damped Elastic Wave Simulation. Acoustics, 3(3), 485-492. https://doi.org/10.3390/acoustics3030032







