Preliminary Determination of the Optimal Parameters When Using an Ultrasonic Probe to Measure Cavern Geometry Where a Metal Borehole Pipe Is Present
Abstract
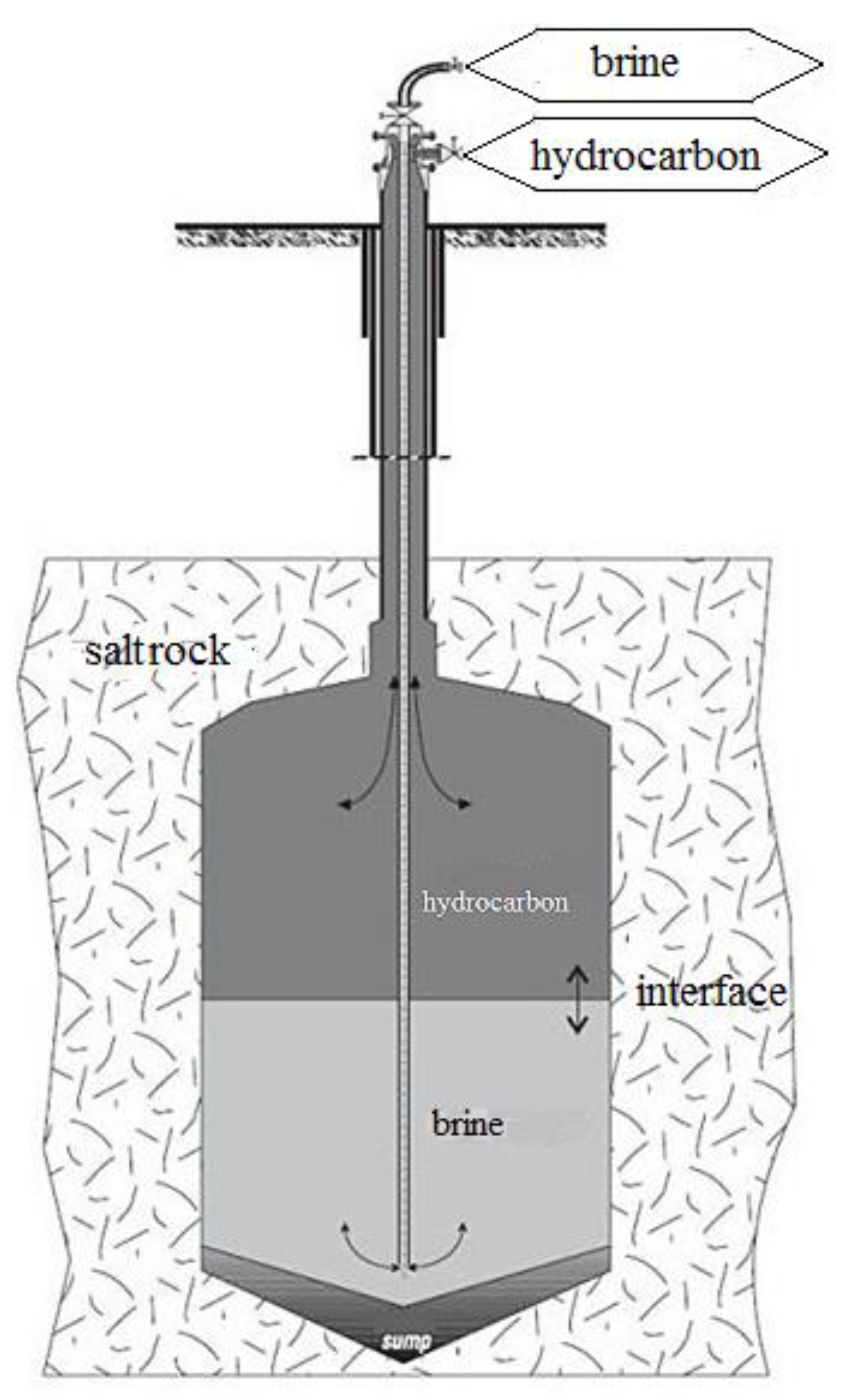
1. Physical Background
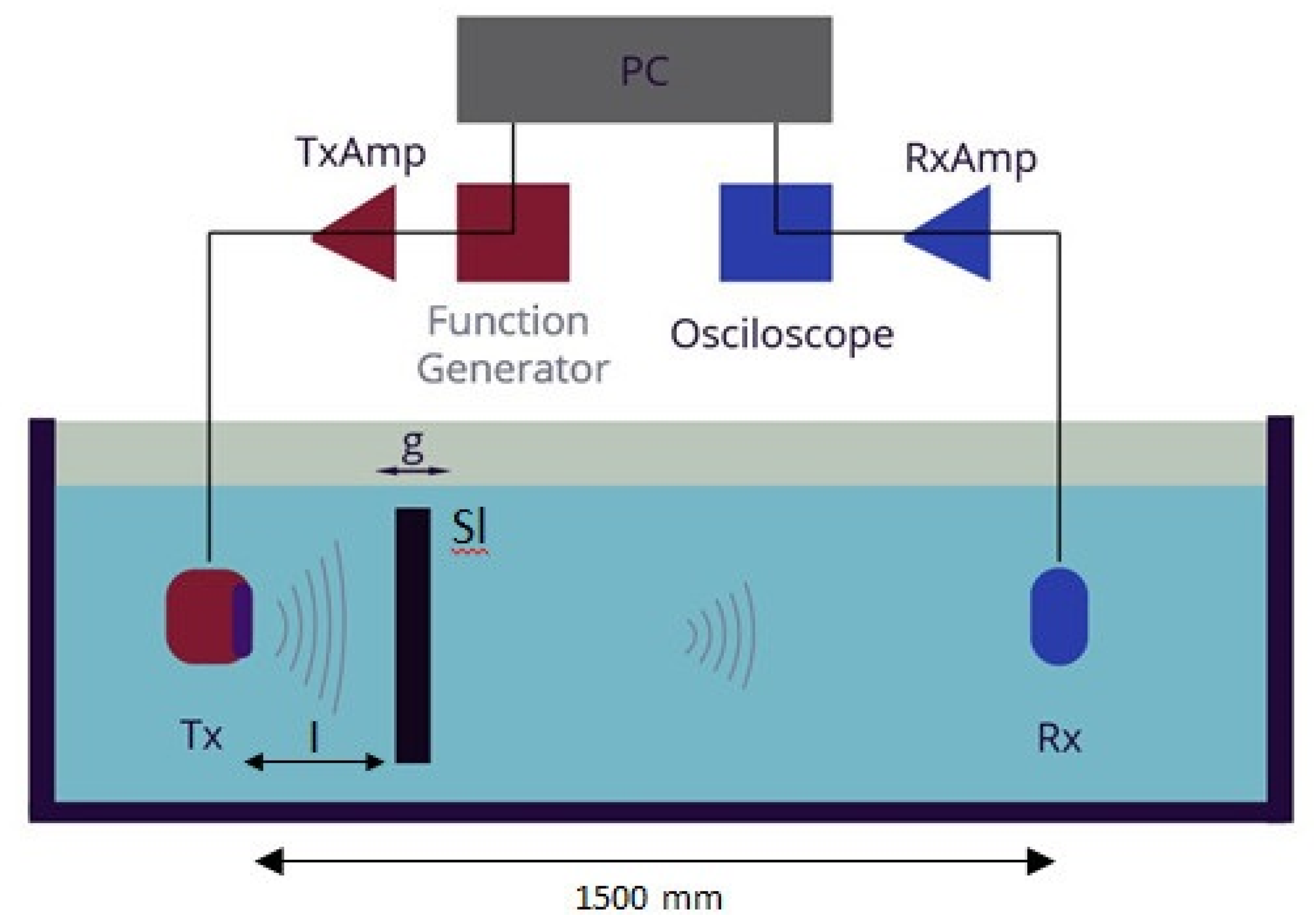
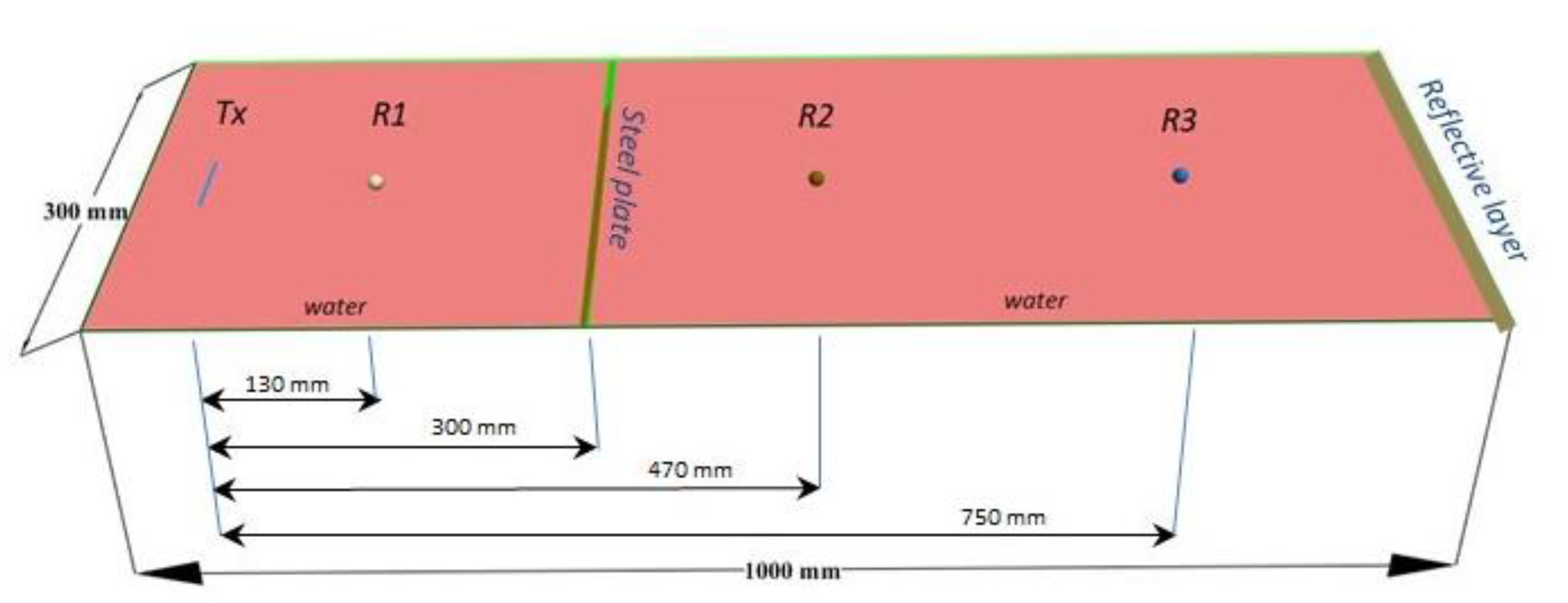
2. Experiments
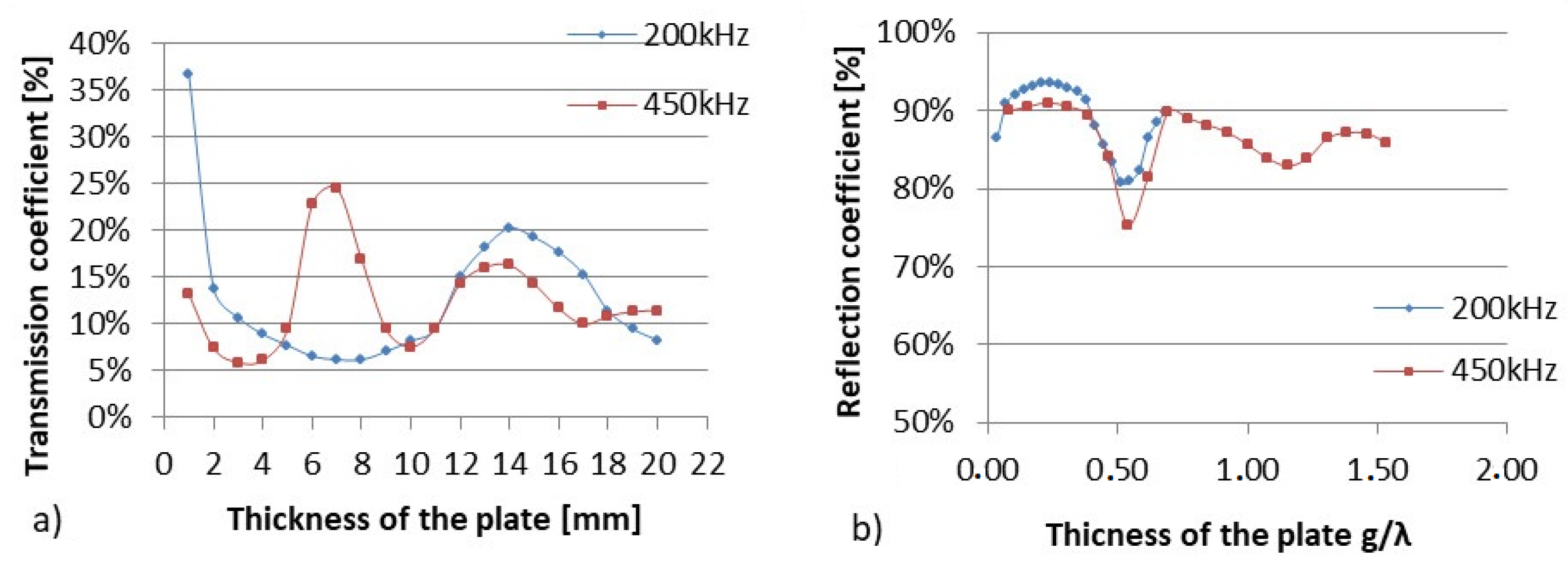
2.1. Influence of the Thickness of the Steel Plate Barrier on the Ultrasonic Wave Transmitted
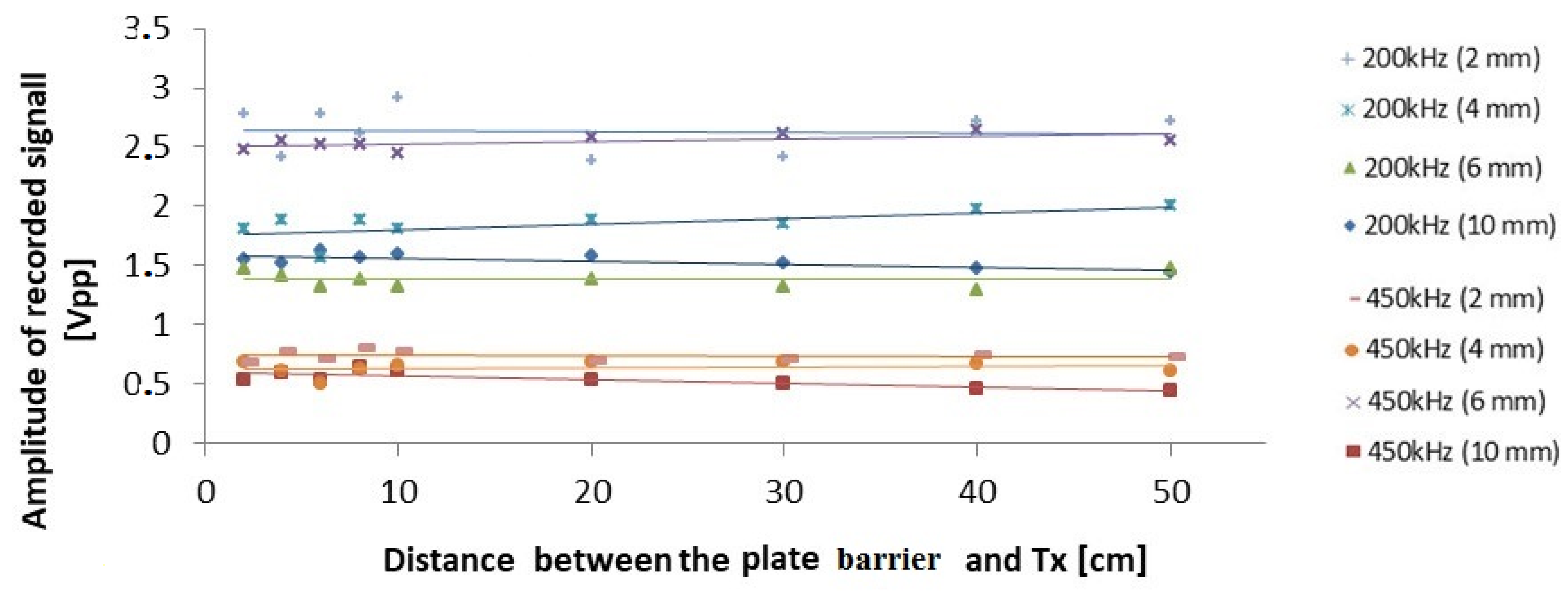
2.2. Influence of the Distance between the Transducer and the Plate Barrier on the Transmitted Signal
3. Computer Simulations
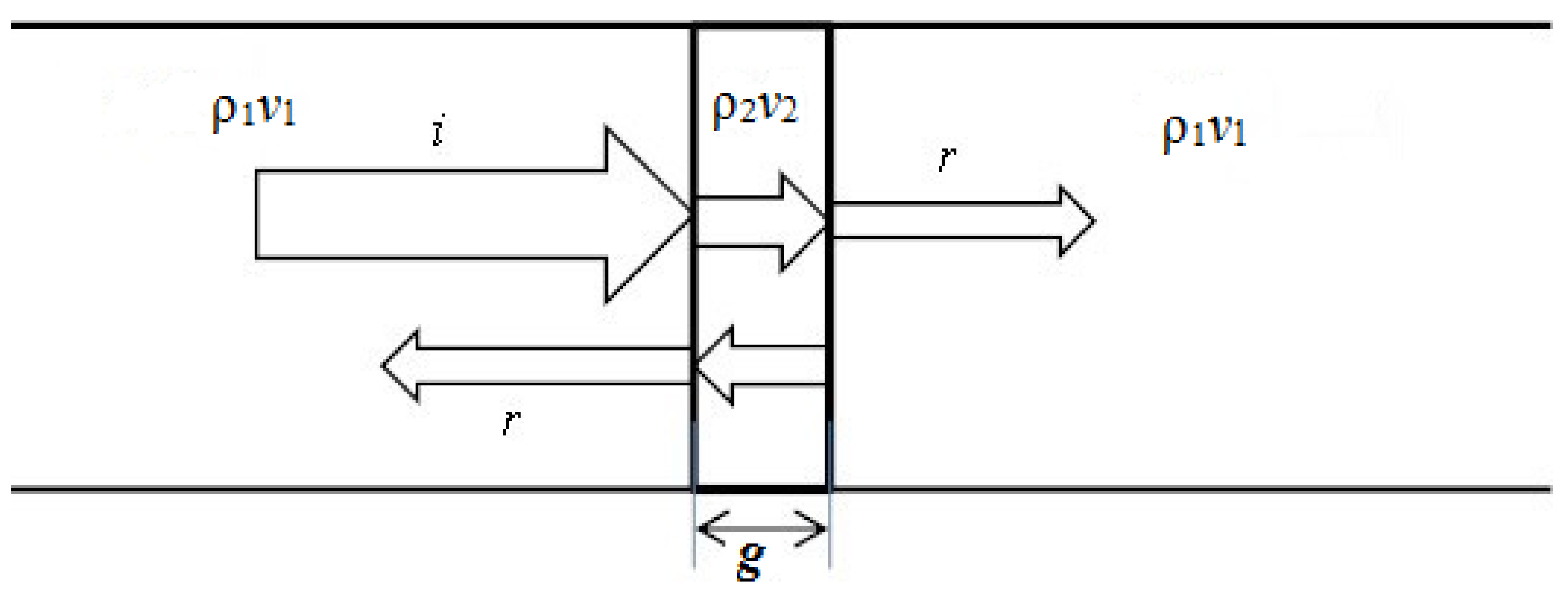
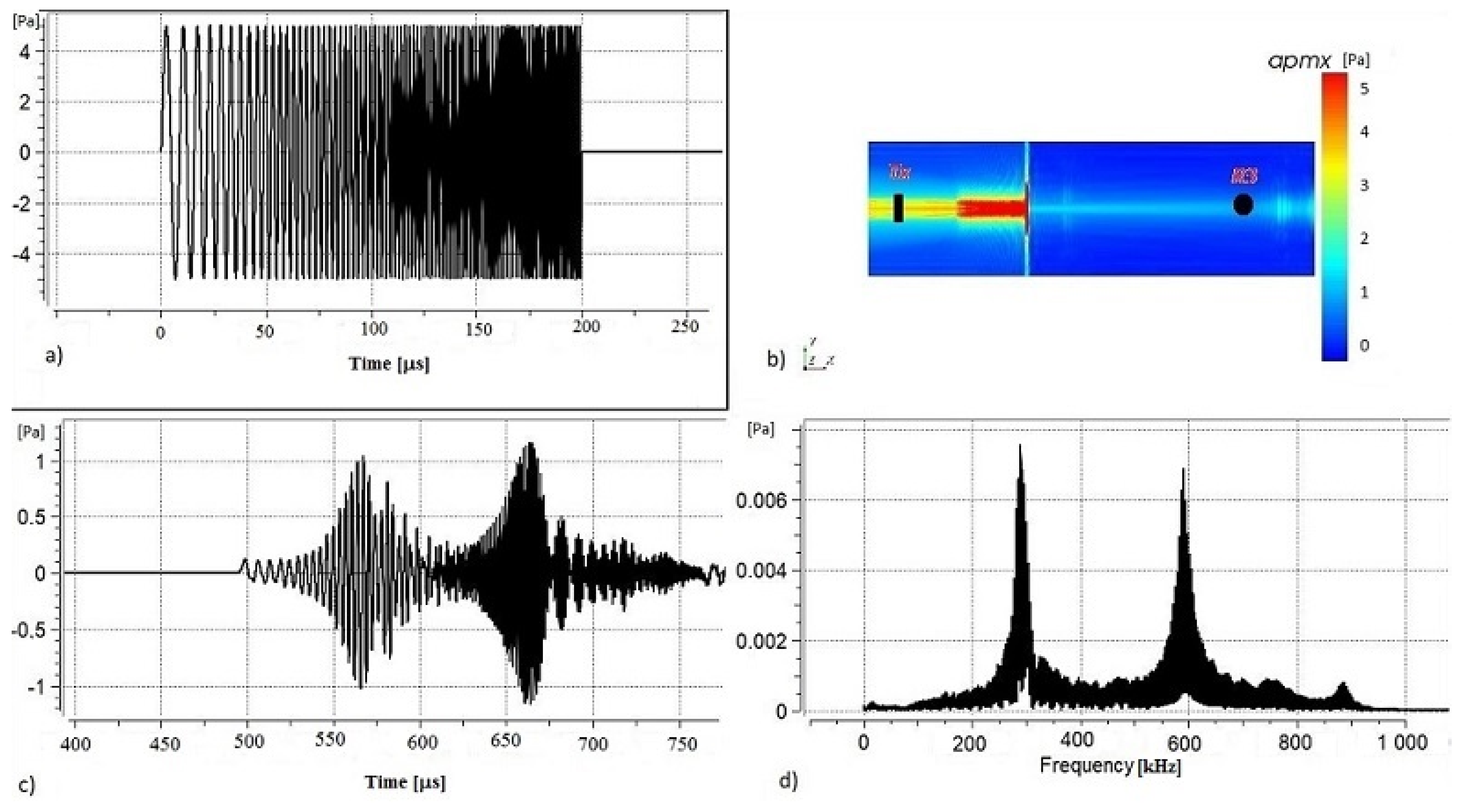
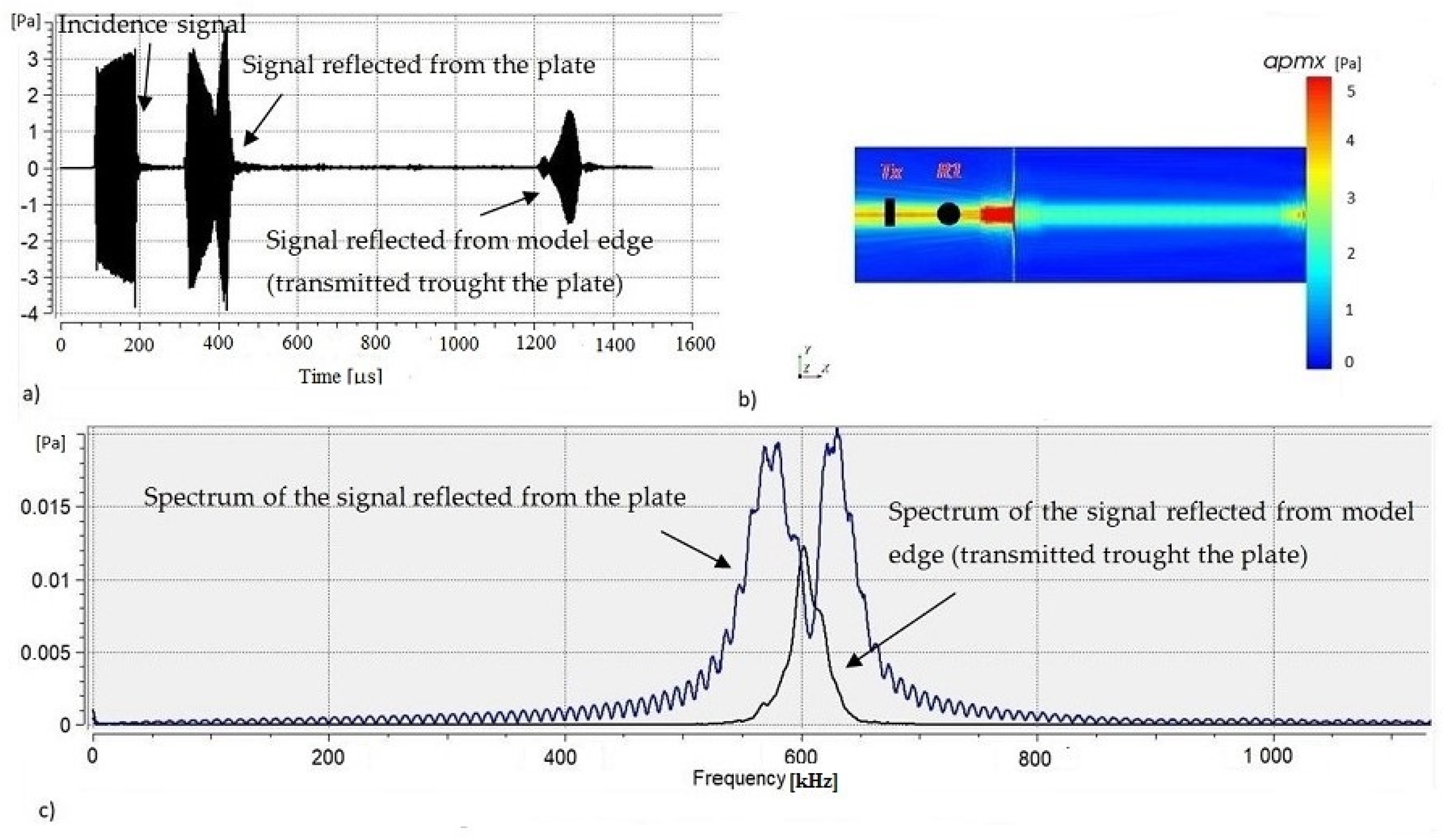
3.1. Transmission through the Barrier Plate and Reflection from Both Plate and Reflective Layer
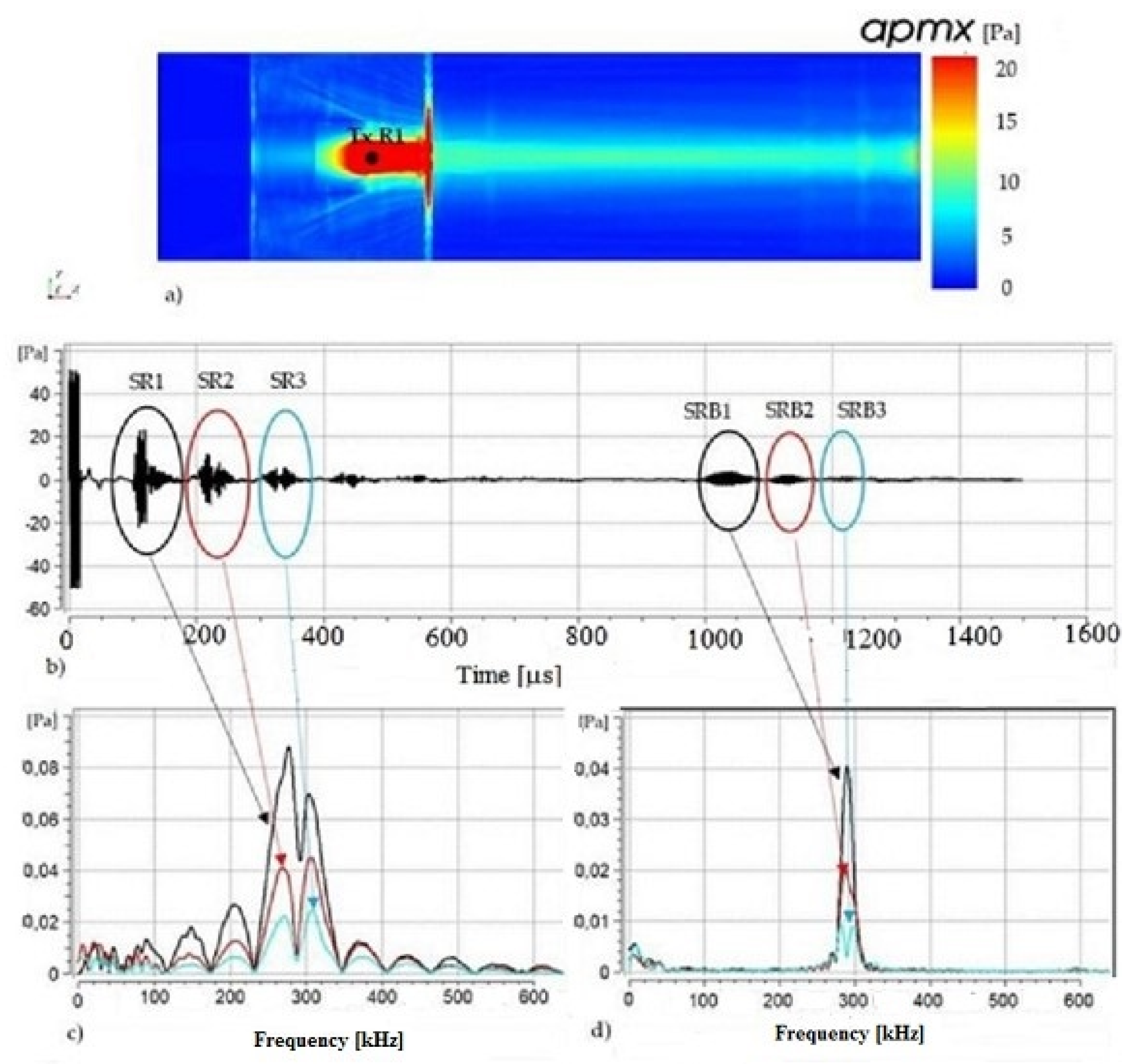
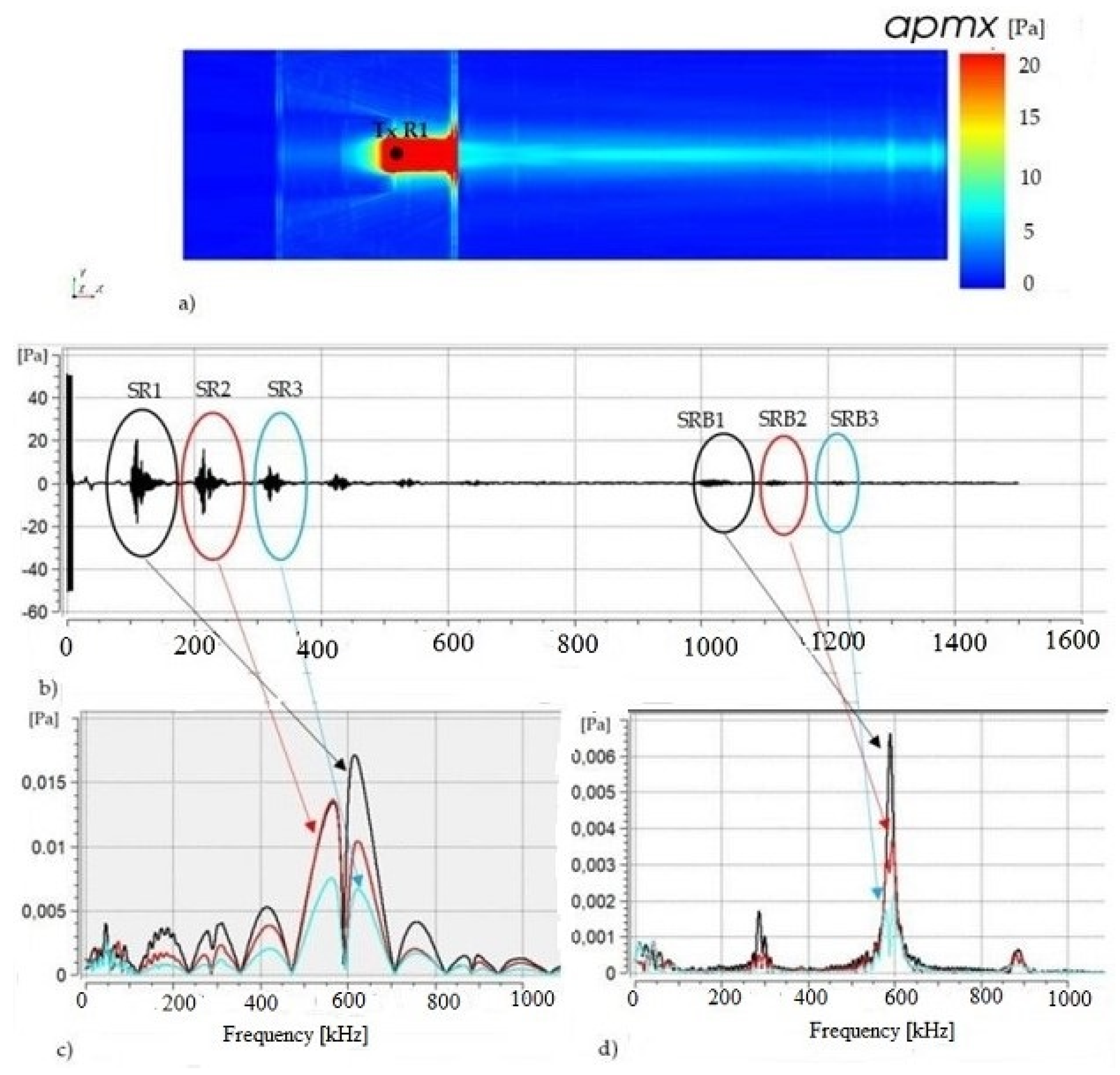
3.2. Reverberation of Ultrasonic Waves in the Zone within the Plates
4. Results and Discussion
4.1. Experimental Results
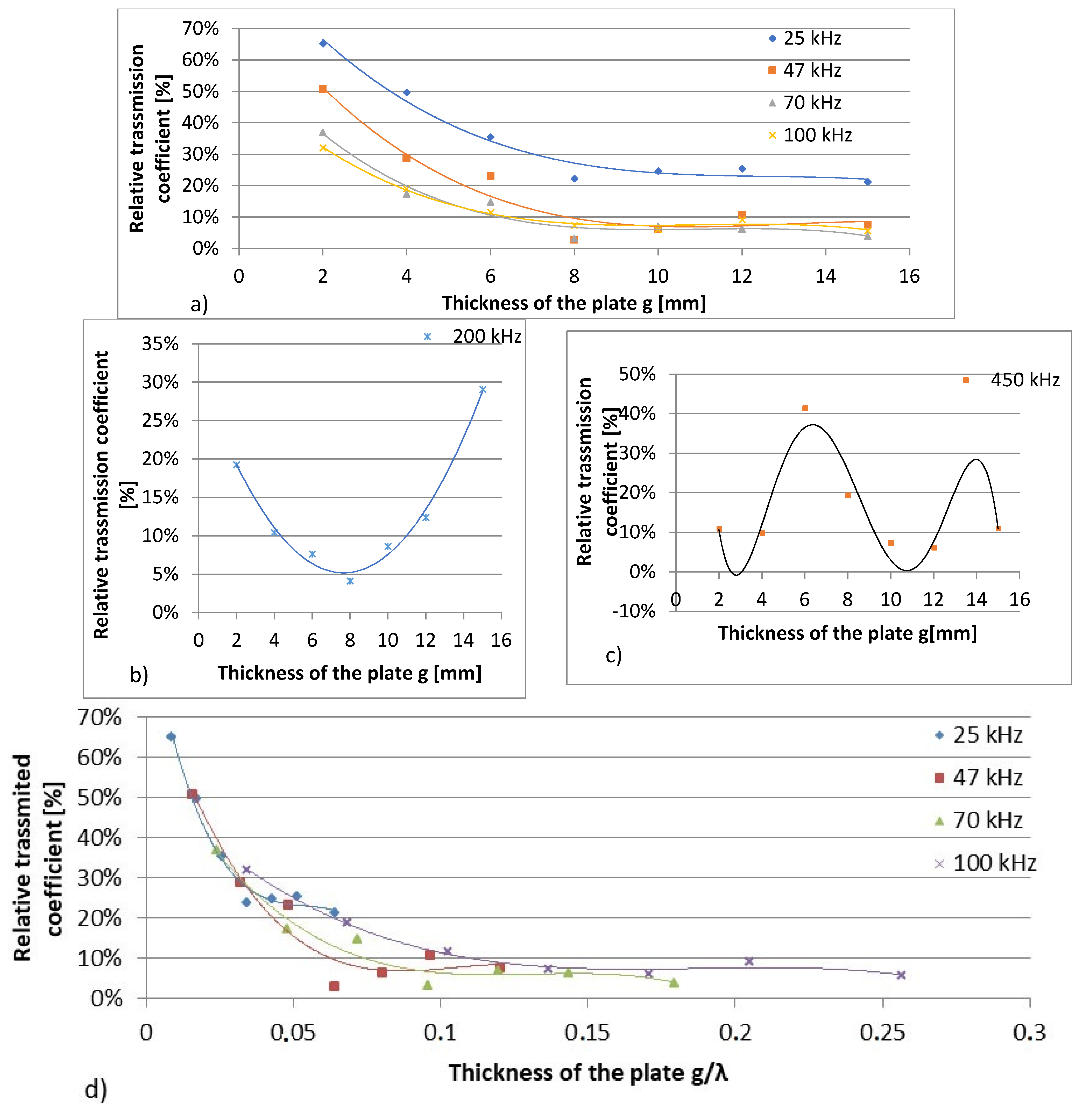
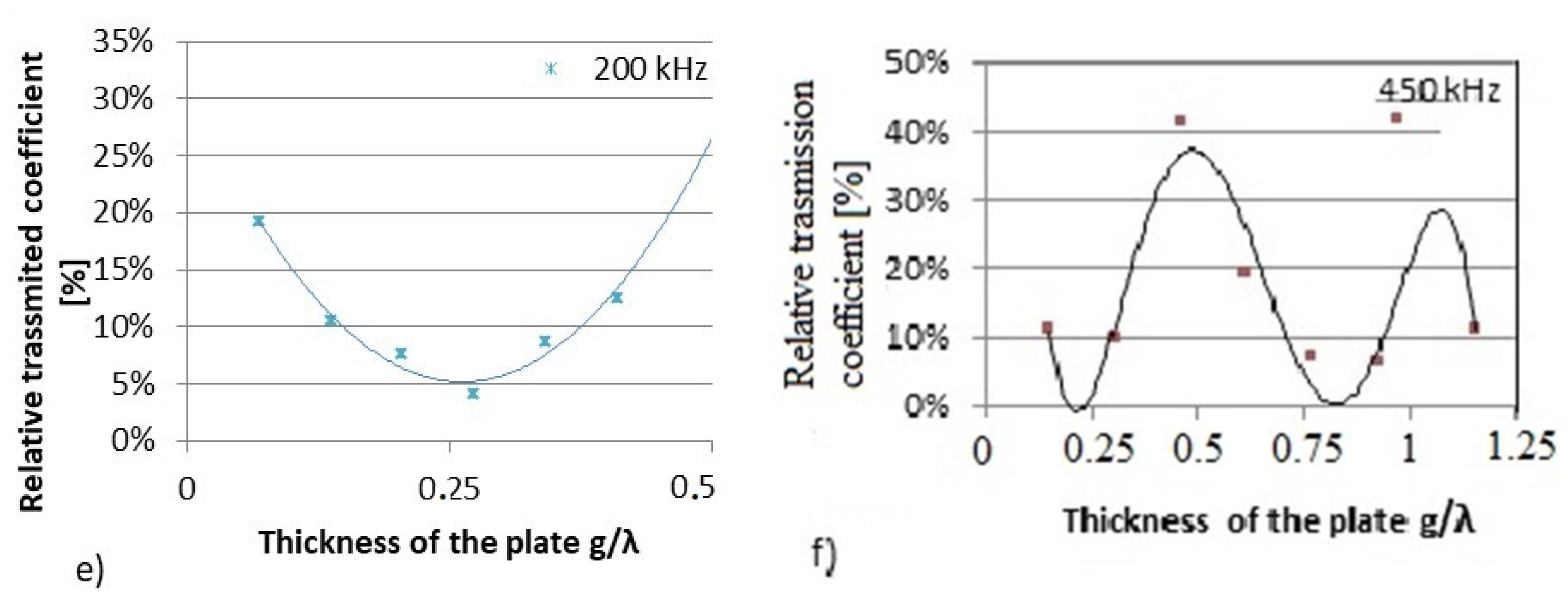
4.1.1. Influence of the Thickness of the Plate Barrier on the Transmitted Signal
4.1.2. The Influence of the Distance between the Plate Barrier and the Transducer Tx on the Transmitted Signal
4.2. Simulation Results
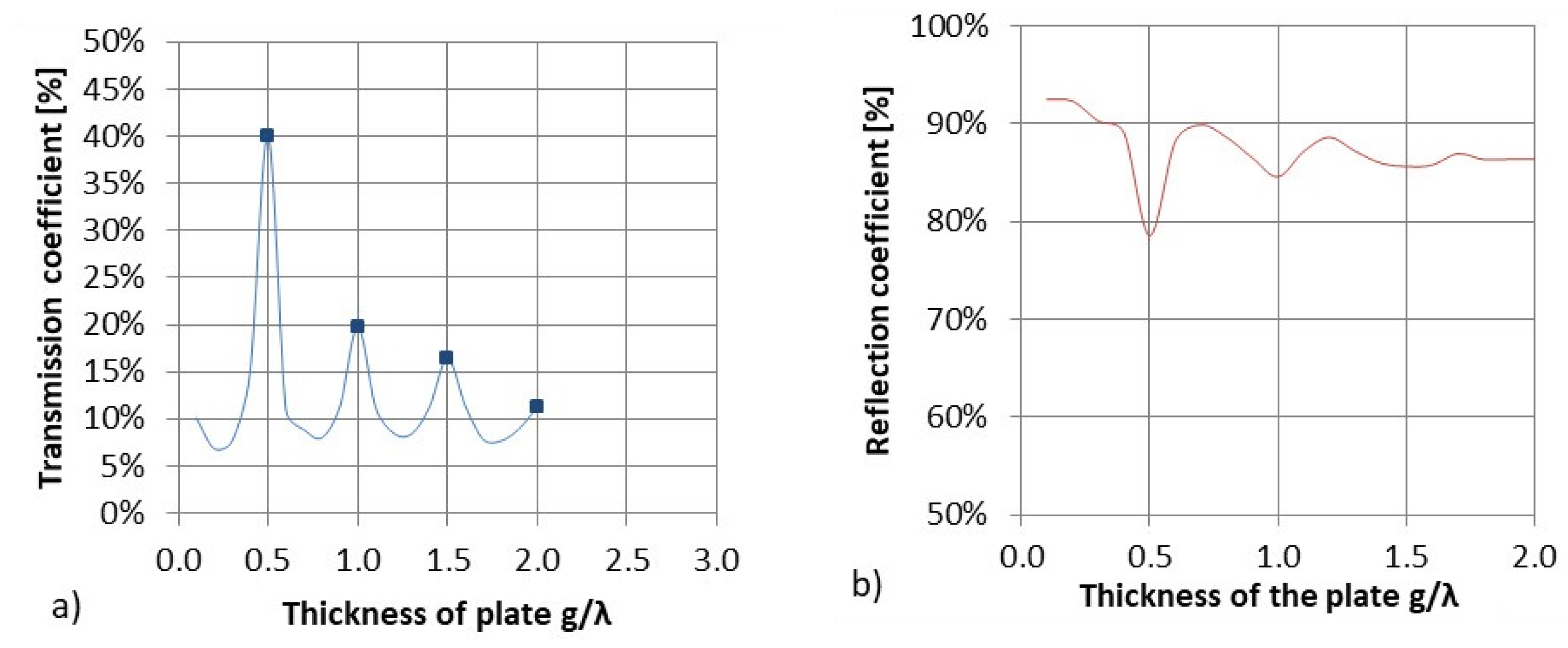
4.2.1. Influence of the Thickness of the Plate Barrier on the Transmitted Signal and Weakness Coefficient of the Plate Material
4.2.2. Transducer and Receiver Placed on One Side of the Barrier
4.2.3. Transducer and Receiver Placed in the Zone between the Two Barrier Plates
5. Conclusions
- Generally, the transmission coefficient of the ultrasonic wave decreases with increase in barrier thickness and wave frequency.
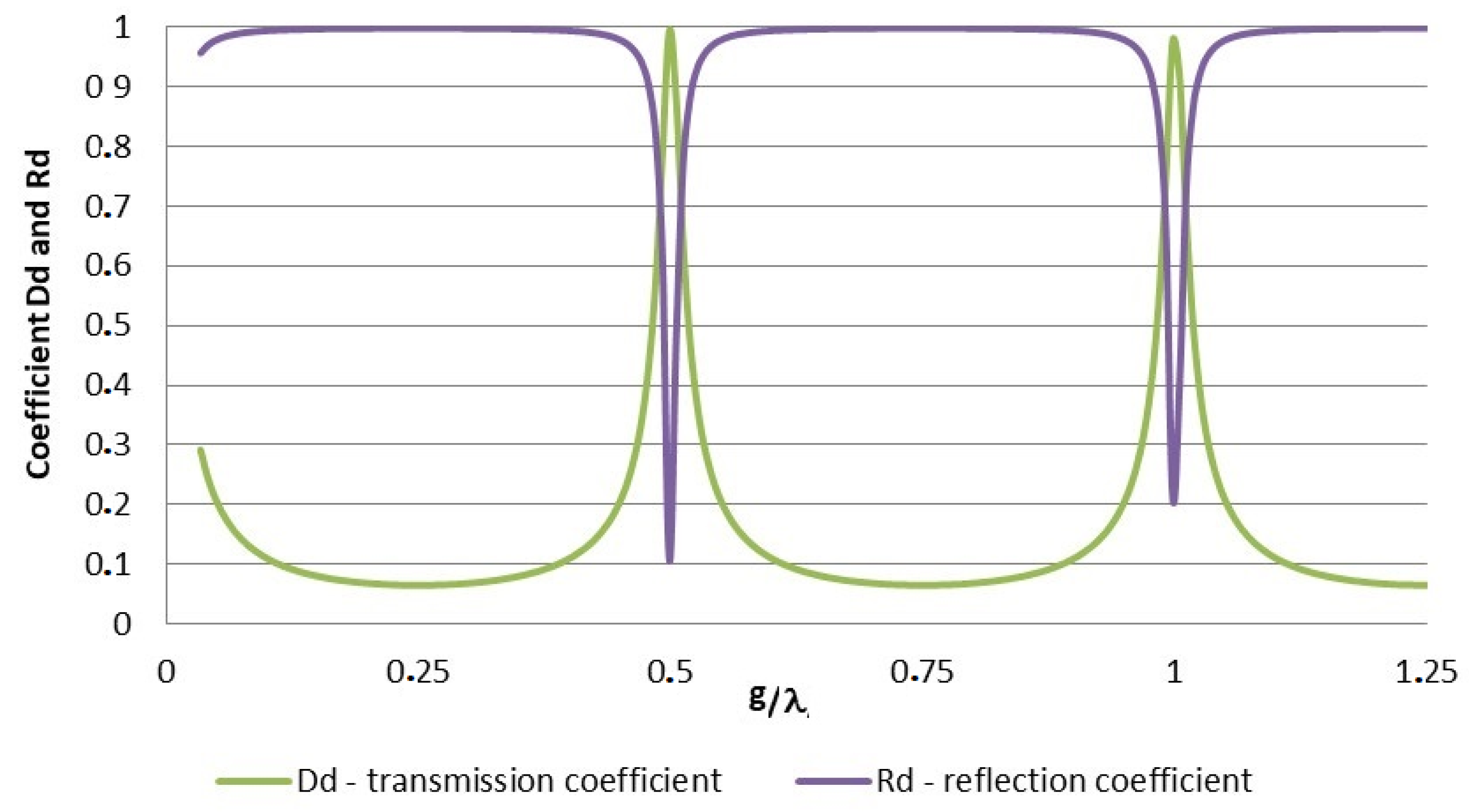
- The transmission coefficient reaches maximal values for a plate with a thickness equal to a multiple of half of the wavelength of the wave propagating in the barrier material. This conclusion confirms the results of the theoretical background.
- In the case where the distance from transducer and receiver is constant, the influence of the position of the plate in mentioned section on the transmitted signal recorded is not significant.
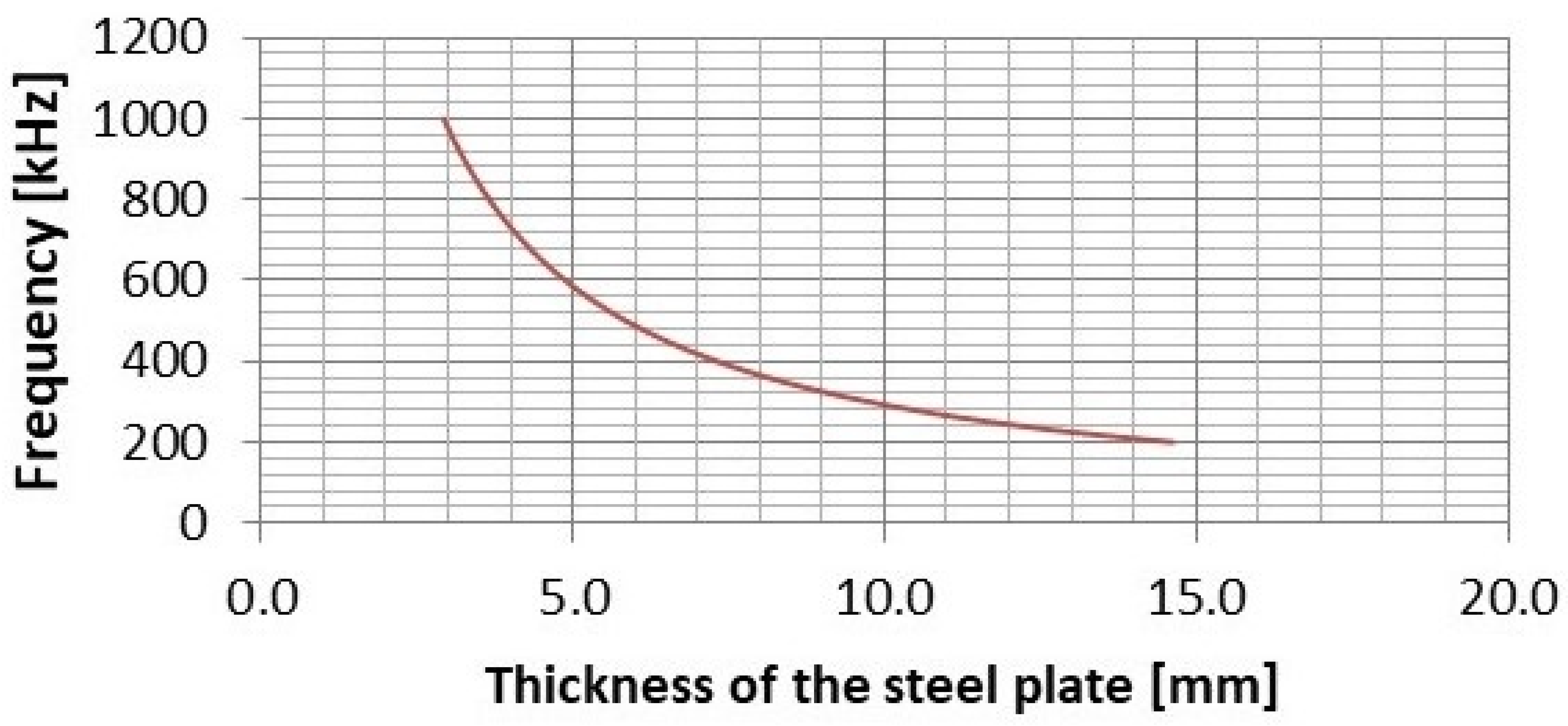
- Knowledge of the thickness of the plate barrier makes it possible to select an appropriate frequency for the signal to be emitted;
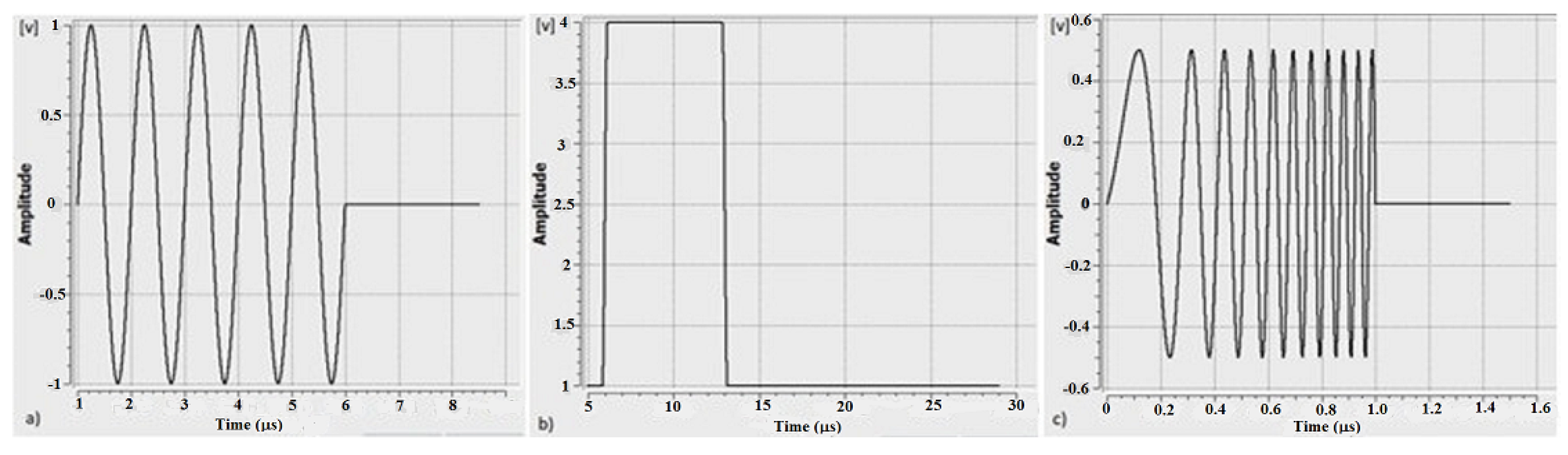
- In cases where the thickness of the plate barrier is unknown, the signal should be generated with a linearly modulated frequency LFM. The relative standard deviation is near 7%.
- Frequency analysis of the transmitted and reflected signals received makes it possible to determine the frequency of the signals which are least attenuated by the plate barrier.
- The reverberation of the ultrasonic wave between two barrier plates (pipe diameter) clearly influences on the recorded signals and in the case of cavern filled water the distance between the ultrasonic probe and the cavern wall must be at least longer than three times of the distance between the two places (pipe diameter). The relative standard deviation of the determined distance is near 5%.
- It is planned to extend the tests of both the transmitted and the reflected signals to cases where the measuring probe is inside single or double service pipes. Such cases are more and more frequently encountered in the exploration of salt domes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaliski, M.; Janusz, P.; Szurlej, A. Underground storage as an element ensuring the continuity of underground gas. Wiertnictwo. Nafta Gaz (Drill. Oil Gas) 2000, 27, 193–205. (In Polish) [Google Scholar]
- Kepplinger, J.; Crotogino, F.; Donadei, S.; Wohlers, M. Present Trends in Compressed Air Energy and Hydrogen Storage in Germany. In Proceedings of the Solution Mining Research Institute Fall 2011, Technical Conference, York, UK, 3–4 October 2011. [Google Scholar]
- Niu, C.K.; Tan, Y.F.; Li, J.N.; Song, C.L. Model validation and stability analysis for operation projects in Jintan Salt Cavern for strategic oil storage of China. J. Pet. Sci. Eng. 2015, 127, 44–52. [Google Scholar] [CrossRef]
- He, W.; Luo, X.; Evans, D.; Busby, J.; Garvey, S.; Parkes, D.; Wanga, J. Exergy storage of compressed air in cavern and cavern volume estimation of the large-scale compressed air energy storage system. Appl. Energy 2017, 208, 745–757. [Google Scholar] [CrossRef]
- Szabłowski, Ł.; Krawczyk, P.; Badyda, K.; Karellas, S.; Kakaras, E.; Bujalski, W. Energy and exergy analysis of adiabatic compressed air energy storage system. Energy 2017, 138, 12–18. [Google Scholar] [CrossRef]
- Tarkowski, R. Wybrane aspekty podziemnego magazynowania wodoru. Przegląd Geol. 2017, 65, 281–291. [Google Scholar]
- Wołowicz, M.; Krawczyk, P.; Gruszecka, M.; Mikołajczak, A. Wykorzystanie kawernowych magazynów gazu ziemnego, jako wysokopojemnościowych magazynów energii elektrycznej. Rynek Energii 2017, Nr 5, 45–48. [Google Scholar]
- Costa, A.; Costa, P.; Azevedo, O. Potential of storing gas with high CO2 content in salt caverns built in ultra-deep water in Brazil. Greenh. Gas Sci. Technol. 2019, 9, 79–94. [Google Scholar]
- Kukiałka, P. Salt caverns in Province of Alberta, Western Canada. Przegląd Solny Salt Rev. 2015, 11, 83–90. [Google Scholar]
- Hasselkus, F.; Reitze, A. Sonar surveys under challenging conditions in gas at very low pressure and in crude oil. Salt Rev. 2015, 11, 109–115. [Google Scholar]
- Nguyen, D.C.; Kubacka, T.; Figarski, M. Possibilities of using the echoprobe CHEMKOP and large cavernometer in measurement of geometry of caverns. Przegląd Górniczy 2019, 75, 1–7. (In Polish) [Google Scholar]
- Figarski, M.; Kubacka, T. Pomiary echometryczne kawern solnych wypełnionych gazem przy użyciu echosondy CHEMKOP. Przegląd Solny 2017, 13, 130–134. (In Polish) [Google Scholar]
- Leong, T.; Coventry, M.; Swiergon, P.; Knoerzer, K.; Juliano, P. Ultrasound pressure distributions generated by high frequency transducers in large reactors. Ultrason. Sonochem. 2015, 27, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Gómez Álvarez-Arenas, T.E. Simultaneous determination of the ultrasound velocity and the thickness of solid plates from the analysis of thickness resonances using air-coupled ultrasound. Ultrasonic 2010, 50, 104–109. [Google Scholar] [CrossRef] [PubMed]
- Gooberman, G.L. Ultrasonics Theory and Application; The English Universities Press: London, UK, 1968. [Google Scholar]
- Kunstman, A.; Poborska-Młynarska, K.; Urbańczyk, K. Geological and mining aspects of building salt storage caverns. Przegląd Geologiczny 2009, 57, 819–828. (In Polish) [Google Scholar]
- Wang, H.; Samuel, R. 3D Geomechanical Modeling of Salt Creep Behavior on Well bore Casing for Presalt Reservoirs. SPE Drill. Complet. 2016, 1, 261–272. [Google Scholar] [CrossRef]
- Ren, Y.; Wang, Y.; Wang, M.; Wu, S.; Wei, B. A Measuring System for Well Logging Attitude and Method of Sensor Calibration. Sensors 2014, 14, 9256–9270. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, P.B.; Gunn, D.A.; Holyoake, S.; Dashwood, B.A.J.; Brett, C.R.; Rees, J.G. A Low frequency acoustic and ultrasound waves to characterize layered media. NDT E Int. 2018, 96, 35–46. [Google Scholar] [CrossRef]
- Obraz, J. Ultrasonic Wave in Measurement Techniques; Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 1983; pp. 45–47. [Google Scholar]
- Jagodziński, Z. Ultrasonic Transducers; Wydawnictwo Komunikacji i Łączności: Warszawa, Poland, 1997; p. 150. (In Polish) [Google Scholar]
- Rossing, T.D.; Fletcher, N.H. Principles of Vibration and Sound, 2nd ed.; Springer: New York, NY, USA, 2004; p. 148. [Google Scholar]
- Michaud, M.; Leong, T.; Swiergon, P.; Juliano, P.; Knoerzer, K. Design parameters of stainless steel plates for maximizing high frequency ultrasound wave transmission. Ultrason. Sonochem. 2015, 26, 56–63. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarek, M.; Piwakowski, B.; Drelich, R. Ultrasonic reflectometry in air: Errors of sample positioning. J. Acoust. Soc. Am. 2015, 137, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Misaridis, T.; Jensen, J.A. Use of Modulated Excitation Signals in Medical Ultrasound. Part II: Design and Performance for Medical Imaging Applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 192–207. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.chemkop.pl (accessed on 12 June 2021).
- Available online: https://www.Adash.com (accessed on 12 June 2021).
- Available online: https://www.echologger.com (accessed on 12 June 2021).
- Durmuş, H.O.; Karaböce, B.; Ҫetin, E.; Özdingiş, M. Investigating of the effect of tungsten used in backing materials of ultrasound probes on acoustical parameters. In Proceedings of the 2019 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Istanbul, Turkey, 26–28 June 2019; pp. 1–6. [Google Scholar]


| Parameter/Medium | Water | Steel |
|---|---|---|
| Density [kg∙m−3] | 1000 | 7800 |
| Wave speed [ms−1] | 1483 | 5850 |
| Acoustic impedance [kgs−1m−2] | 1.48 × 106 | 45.63 × 106 |
| Thickness | 2 mm | 4 mm | 6 mm | 8 mm | 10 mm | 12 mm | 15 mm |
|---|---|---|---|---|---|---|---|
| Frequency (Wavelength a) | Rx | Rx | Rx | Rx | Rx | Rx | Rx |
| 25 kHz (234 mm) | 65% | 50% | 35% | 22% | 25% | 25% | 21% |
| 47 kHz (124 mm) | 51% | 29% | 23% | 3% | 11% | 11% | 8% |
| 70 kHz (83.6 mm) | 37% | 17% | 25% | 3% | 6% | 6% | 4% |
| 100 kHz (58.5 mm) | 32% | 19% | 12% | 7% | 7% | 9% | 6% |
| 200 kHz (29.25 mm) | 19% | 10% | 8% | 4% | 9% | 12% | 29% |
| 450 kHz (13 mm) | 11% | 10% | 41% | 19% | 7% | 6% | 11% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kubacka, T.; Dinh, C.N. Preliminary Determination of the Optimal Parameters When Using an Ultrasonic Probe to Measure Cavern Geometry Where a Metal Borehole Pipe Is Present. Acoustics 2021, 3, 425-441. https://doi.org/10.3390/acoustics3020028
Kubacka T, Dinh CN. Preliminary Determination of the Optimal Parameters When Using an Ultrasonic Probe to Measure Cavern Geometry Where a Metal Borehole Pipe Is Present. Acoustics. 2021; 3(2):425-441. https://doi.org/10.3390/acoustics3020028
Chicago/Turabian StyleKubacka, Tomasz, and Chau Nguyen Dinh. 2021. "Preliminary Determination of the Optimal Parameters When Using an Ultrasonic Probe to Measure Cavern Geometry Where a Metal Borehole Pipe Is Present" Acoustics 3, no. 2: 425-441. https://doi.org/10.3390/acoustics3020028
APA StyleKubacka, T., & Dinh, C. N. (2021). Preliminary Determination of the Optimal Parameters When Using an Ultrasonic Probe to Measure Cavern Geometry Where a Metal Borehole Pipe Is Present. Acoustics, 3(2), 425-441. https://doi.org/10.3390/acoustics3020028





