Factorized One-Way Wave Equations
Abstract
:1. Introduction
2. Method of PDE Factorization
3. Results
3.1. PDE Factorization - Waves in Inhomogeneous Media
3.2. PDE Factorization - Transversal Waves
3.3. PDE Factorization - Further Mechanical and Electromagnetic Waves
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angus, D.A. The One-Way Wave Equation: A Full-Waveform Tool for Modeling Seismic Body Wave Phenomena. Surv. Geophys. 2014, 35, 359–393. [Google Scholar] [CrossRef] [Green Version]
- Luo, M.; Jin, S. Halliburton Energy Services: Hybrid One-Way and Full-Way Wave Equation Migration. U.S. Patent Nr. 8116168B1, 14 February 2012. [Google Scholar]
- Yan, J.; Anderson, J.E.; Lu, R.; Marcinkovich, C.M. Exxonmobile Upstream Research Company. Efficient Seismic Attribute Gather Generation With Data Synthesis Furthermore, Expectation Method. WO-Patent Nr. 2017136133A1, 10 August 2017. [Google Scholar]
- Zhou, M. China Petrol & Chemical Corporation: Method and Device for Enhanced Seismic Imaging Based on One-Way Wave Equation. U.S. Patent Nr. 10962669B2, 30 March 2021. [Google Scholar]
- Bai, J.; Yilmaz, O. Emerson Paradigm Holding LLC. Seismic Migration Techniques for Improved Image Accuracy. U.S. Patent Nr. 2021215824A1, 15 July 2021. [Google Scholar]
- Schlesinger, L. Handbuch der Theorie der Linearen Differentialgleichungen; Teubner Verlag: Leipzig, Germany, 1897. [Google Scholar]
- Kamke, E. Differentialgleichungen: Lösungsmethoden und Lösungen; Akademische Verlagsgesellschaft: Leipzig, Germany, 1965. [Google Scholar]
- Davis, J.L. Mathematics of Wave Propagation; Princeton University Press: Princeton, NJ, USA, 2000; p. 85. [Google Scholar]
- Garrett, S.L. Understanding Acoustics; An Experimentalist’s View of Acoustics and Vibration; Springer: Berlin, Germany, 2017; p. 136. [Google Scholar]
- Olver, P.J. Introduction to Partial Differential Equations; Springer: Berlin, Germany, 2016; p. 51. [Google Scholar]
- Elsevier, B.V. Wave Propagation in Inhomogeneous Media. Int. Geophys. 1972, 17, 223–307. [Google Scholar]
- Seriani, G.; Oliveira, S.P. Numerical modeling of mechanical wave propagation. Riv. Nuovo C 2020, 43, 460. [Google Scholar] [CrossRef]
- Lamoureux, M.P. The Mathematics of PDEs and the Wave Equation; Seismic Imaging Summer School, University of Calgary: Calgary, AB, Canada, 2006. [Google Scholar]
- Bschorr, O.; Raida, H.-J. Transversal One-Way Wave Equation. In Proceedings of the DAGA, Hannover, Germany, 16–19 March 2020; pp. 1075–1076. [Google Scholar]
- Bschorr, O.; Raida, H.-J. One-Way Wave Equation Derived from Impedance Theorem. Acoustics 2020, 2, 12. [Google Scholar] [CrossRef] [Green Version]
- Bschorr, O.; Raida, H.-J. Spherical One-Way Wave Equation. Acoustics 2021, 3, 21. [Google Scholar] [CrossRef]
| 2nd Order Wave Equation | 1st Order Wave Equation | 1st Order Wave Equation |
|---|---|---|
| Two Solutions: | Unique Solution: | Unique Solution: |
| Standing Waves | Propagating Wave -dir. | Propagating Wave -dir. |
 | 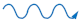 | 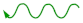 |
 | ||
| Propagating Wave -dir. | ||
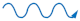 | ||
| Propagating Wave -dir. | ||
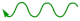 |
| Wave Type | Conventional Wave Equation =2nd Order PDE | Factorized Wave Equation =1st Order PDE | Factorized Wave Wave Direction +xi Transversal dir. j,k | Wave Velocity |
|---|---|---|---|---|
| Longitudinal Wave | ||||
| Transversal Wave | ||||
| Torsional Wave | ||||
| String Wave | ||||
| Moens/Korteweg Wave | ||||
| Bending Wave | ||||
| Electromagnetic | ||||
| Transversal Wave | ||||
| Longitudinal | ||||
| Telegraph Wave | ||||
| Electromagnetic | ||||
| Longitudinal Wave |
| Equation | Concept | SI Units | PDE Type | Variable | Solutions for Inhomogeneity |
|---|---|---|---|---|---|
| Cauchy’s 1st Eq. of Motion: | |||||
| Force Equilibrium | N/m | 2nd order | Analytical solutions given for some simple functions | ||
| Force Unit: N | kgm/s | (Two-way) | |||
| Factorization: | |||||
| Impulse Equilibrium | N/ms | 1st order | General analytical solution: | ||
| Impulse Unit: Ns | kgm/s | (One-way) |
| Mathematical/Physical Approach | Starting Equation | Conversion/ Insertion | Scalar One-Way Wave Equation | Traveling Wave Solution |
|---|---|---|---|---|
| (a) PDE Factorization | ||||
| (b) Impedance Theorem | ;; | |||
| (c) Impulse Equilibrium | ;;; |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bschorr, O.; Raida, H.-J. Factorized One-Way Wave Equations. Acoustics 2021, 3, 717-722. https://doi.org/10.3390/acoustics3040045
Bschorr O, Raida H-J. Factorized One-Way Wave Equations. Acoustics. 2021; 3(4):717-722. https://doi.org/10.3390/acoustics3040045
Chicago/Turabian StyleBschorr, Oskar, and Hans-Joachim Raida. 2021. "Factorized One-Way Wave Equations" Acoustics 3, no. 4: 717-722. https://doi.org/10.3390/acoustics3040045
APA StyleBschorr, O., & Raida, H.-J. (2021). Factorized One-Way Wave Equations. Acoustics, 3(4), 717-722. https://doi.org/10.3390/acoustics3040045






