ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models
Abstract
1. Introduction
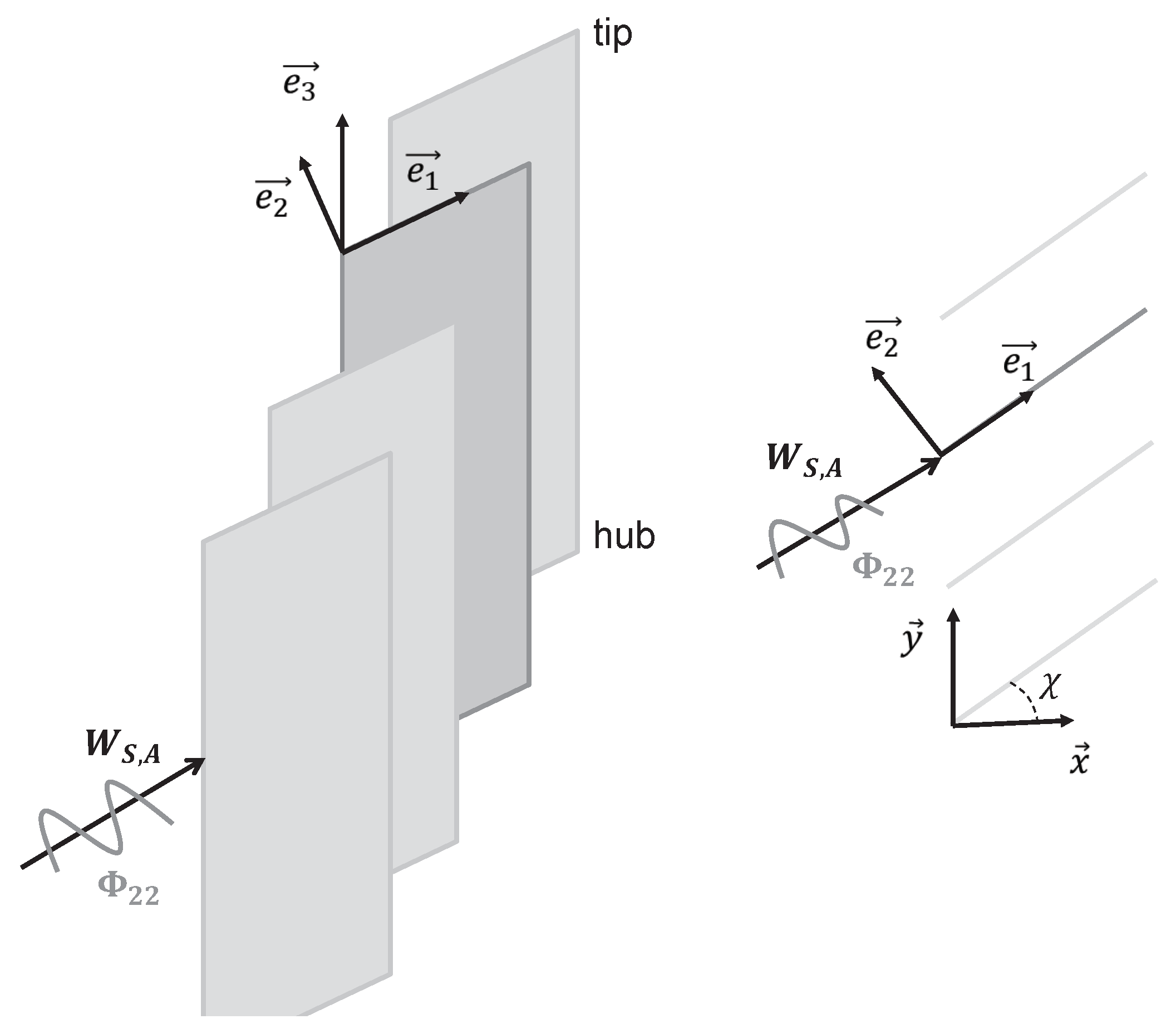
- and refer respectively to a cartesian and a cylindrical coordinate system, where the x-axis corresponds to the duct axis.
- are indexes referring to the streamwise, upwash and spanwise components of flow.
- The variable K refers to convective wavenumbers (of the incoming gust).
- The variable k refers to acoustic wavenumbers (of the radiated pressure waves).
2. Benchmark Preparation
2.1. ACAT1 Fan Benchmark Data
2.1.1. Tests at AneCom AeroTest
2.1.2. Acoustic Data
2.2. Input for the Analytical Models
2.2.1. RANS Calculations
2.2.2. RANS Data Processing
3. Acoustic Models
3.1. Preamble
- All methods of the benchmark are formulated in the frequency domain. They target a representation of broadband noise in the form of a frequency spectrum but not as a time signal.
- It was assumed that broadband noise was generated by the interaction of the incoming turbulence with the blades. Other sources of broadband noise like rotor self-noise, stator self-noise and rotor–ESS interaction noise were ignored for the benchmark.
- The turbulence was assumed to be homogeneous, isotropic turbulence at each radial position/for each strip. In all calculations, the turbulence was imposed as if it were a background turbulence but of course using the equivalent TKE and TLS values of the benchmark, which include the wake and background contributions.
- Either the von Kármán or the Liepmann model was used to describe the turbulence. The difference between the two models is rather small. In fact, the differences are smaller than 1 dB for the one-dimenional wavenumber spectrum. As observed by Grace [24], the agreement with experiments is better using the Liepmann model than using the Gaussian model.
- Most of the methods are mathematical expressions containing integrals and summations. A few methods resort to a very complex modelling of RSI noise, which has a direct impact on computation time. The latter can potentially exceed one day as reported by Grace [24]. The solution labelled BB1 is partly numerical as it used a CAA solver to calculate the acoustic response of the stator. That method was the only one able to account for the real blade profile including the effects from the mean flow.
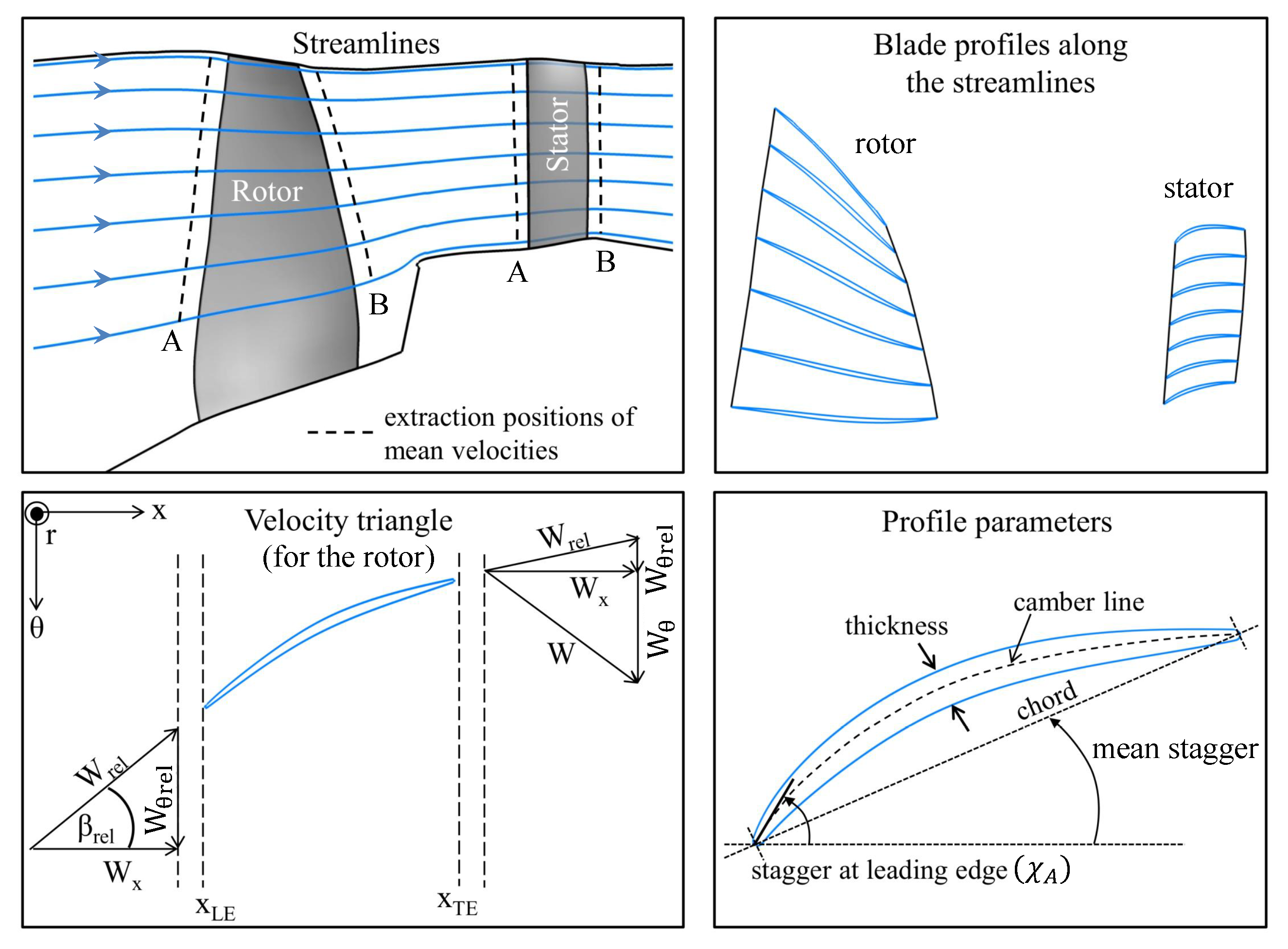
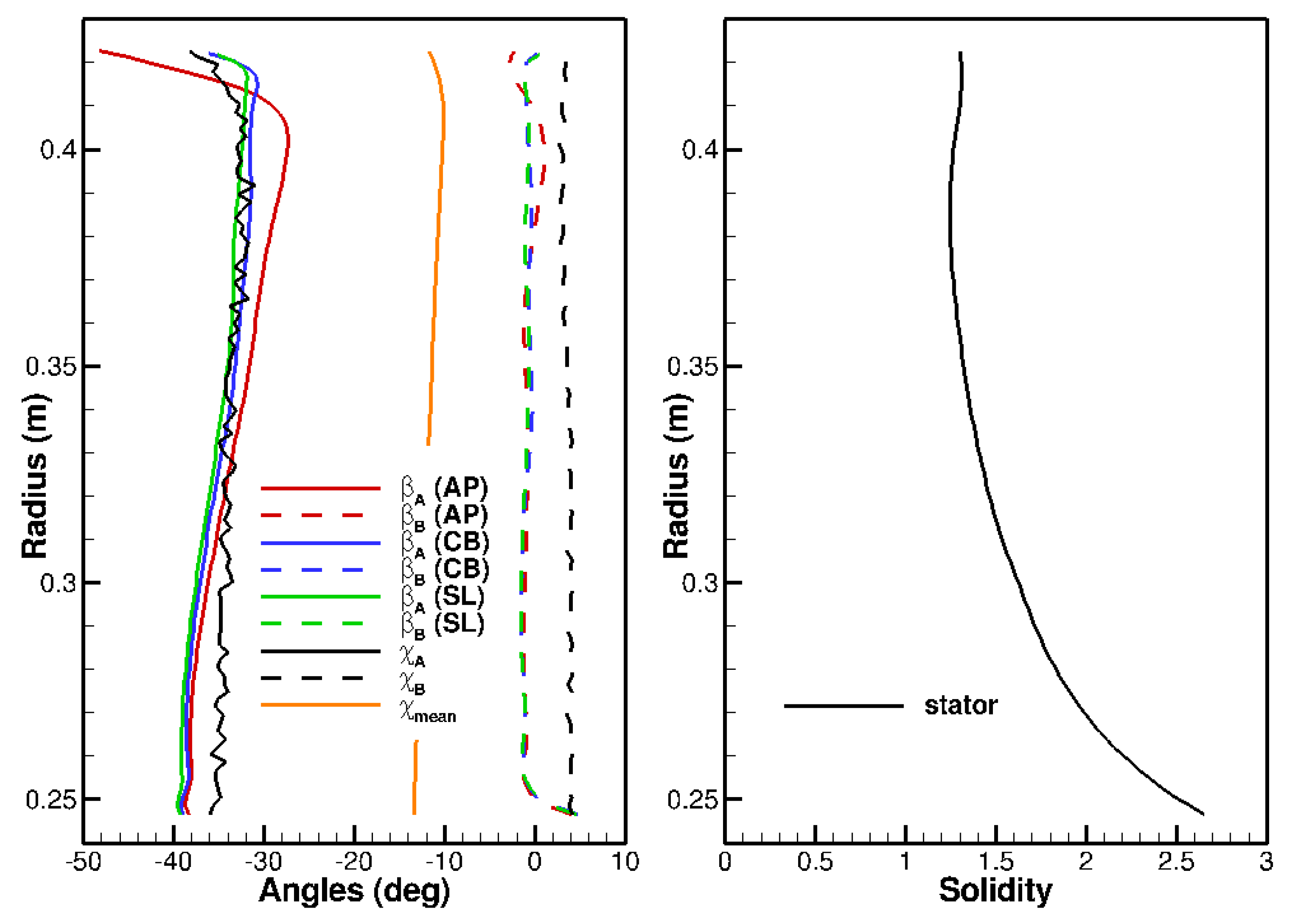
- All other methods replaced the stator vanes by flat plates as isolated airfoils or arranged in a cascade. The “flat plate” hypothesis implies that the most representative stagger angle is used. All the methods relied on the angle at the leading edge except for results TA1 and TA2, which considered the inflow angle. As the flow incidence is small at the stator leading edge, no strong effect is expected from that choice, even though the stagger angle is known to be a sensitive modelling parameter.
3.2. Classification of the Methods
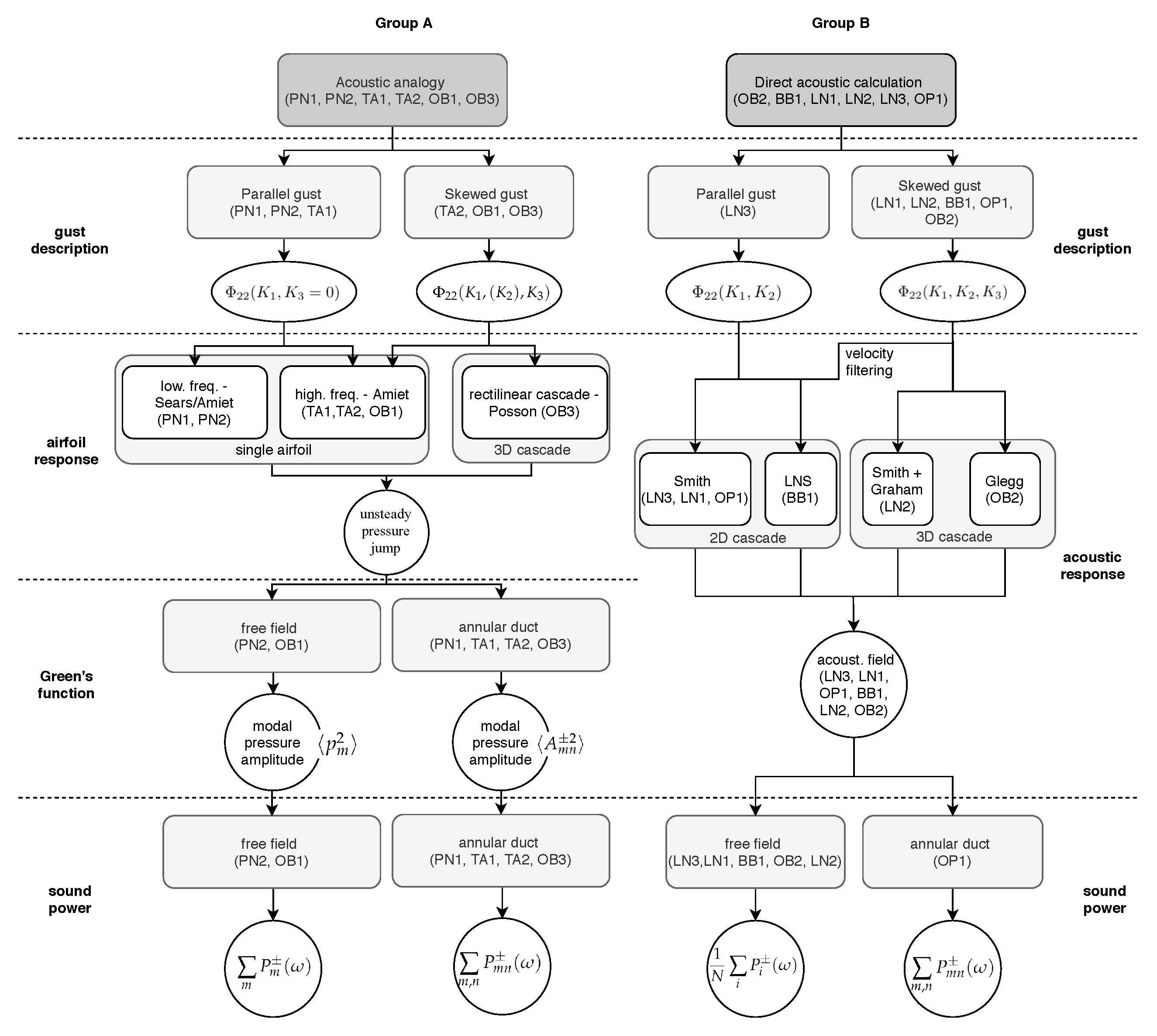
- Methods based on the acoustic analogy were assembled in Group A. The models use a source term (the unsteady lift produced by the turbulence on the blade surface) in combination with a Green’s function to calculate the acoustic pressure. They either make the assumption of a single, isolated airfoil or consider a cascade of airfoils.
- The methods of Group B follow a different approach. They rely on a direct calculation of the acoustic pressure response of the cascade of blades without requiring a source term. Therefore there is one step less in the workflow represented in Figure 8. All of the studied methods account for the cascade by considering separate radial strips. These strips are then unwrapped to match the theoretical case.
3.3. Methods Based on the Acoustic Analogy (Group A)
3.3.1. Solutions PN1 and PN2
- In-duct formulation (PN1): Based on , a modal power amplitude is calculated for each cut-on mode using the equations in Appendix B. For each frequency, the sound power is obtained by summing the modal contributions: .
- Free-field formulation (PN2): The pressure amplitude for the azimuthal mode m is used to calculate the sound power by integrating the sound intensity along the polar arc. The sound intensity is obtained by applying the Blokhintsev invariant technique [43,45]. The sound power integrated between the polar angle and corresponds to the downstream radiation, and the part between and to the upstream one. The sound power for each frequency is integrated by summation over m: .
3.3.2. Solutions TA1 and TA2
3.3.3. Solution OB1
3.3.4. Solution OB3
3.4. Methods Based on a Direct Calculation of the Acoustics (Group B)
3.4.1. Solution OB2
3.4.2. Solution LN3
3.4.3. Solution LN1
3.4.4. Solution BB1
- The cascade response is independent of the value and is set equal to the response obtained for . Grace [24] showed that using that simplification leads to a good agreement at high frequency but an overestimation of the sound power at low frequency.
- To counteract that effect, convective modes that are acoustically cut-off (subcritical waves) are discarded to avoid having their contribution included.
- The resulting pressure is assumed constant over the radius.
- The sound power is calculated through the integration of the intensity over the cascade faces without accounting for the presence of the duct.
3.4.5. Solution LN2
3.4.6. Solution OP1
- (1)
- The simplest approach uses a 2D -wavenumber spectrum obtained by integrating Liepmann’s 3D wavenumber spectrum over the spanwise component .
- (2)
- An a priori correction is applied, which consists in filtering the 2D wavenumber spectrum by discarding gusts, whose contributions are known to be acoustically cut-off. This automatically lowers acoustic levels.
- (3)
- The results of three-dimensional CAA calculations performed for few selected gust modes and frequencies are combined to develop an a priori correction of the turbulence content.
- (a)
- The 2D acoustic power is calculated and then assumed to be constant over the span. The final solution is obtained by statistically averaging the contributions of all strips.
- (b)
- The pressure amplitudes are averaged and then distributed in acoustic duct modes according to a certain model (equal energy distribution, equal energy density distribution, etc.). This emulates the approach used to determine sound power based on experimental data.
- (c)
- An acoustic mean pressure is calculated by averaging the results of all the strips. The radial pressure distribution is represented by a complex function, whose amplitude is constant to the averaged value and the phase is randomly varied along the span. This radial pressure is fitted to the basis of induct acoustic eigenmodes in order to determine the amplitudes . Finally, the modal sound power is calculated following the method described in Appendix A.
4. Results and Discussion
4.1. Overall Comparisons
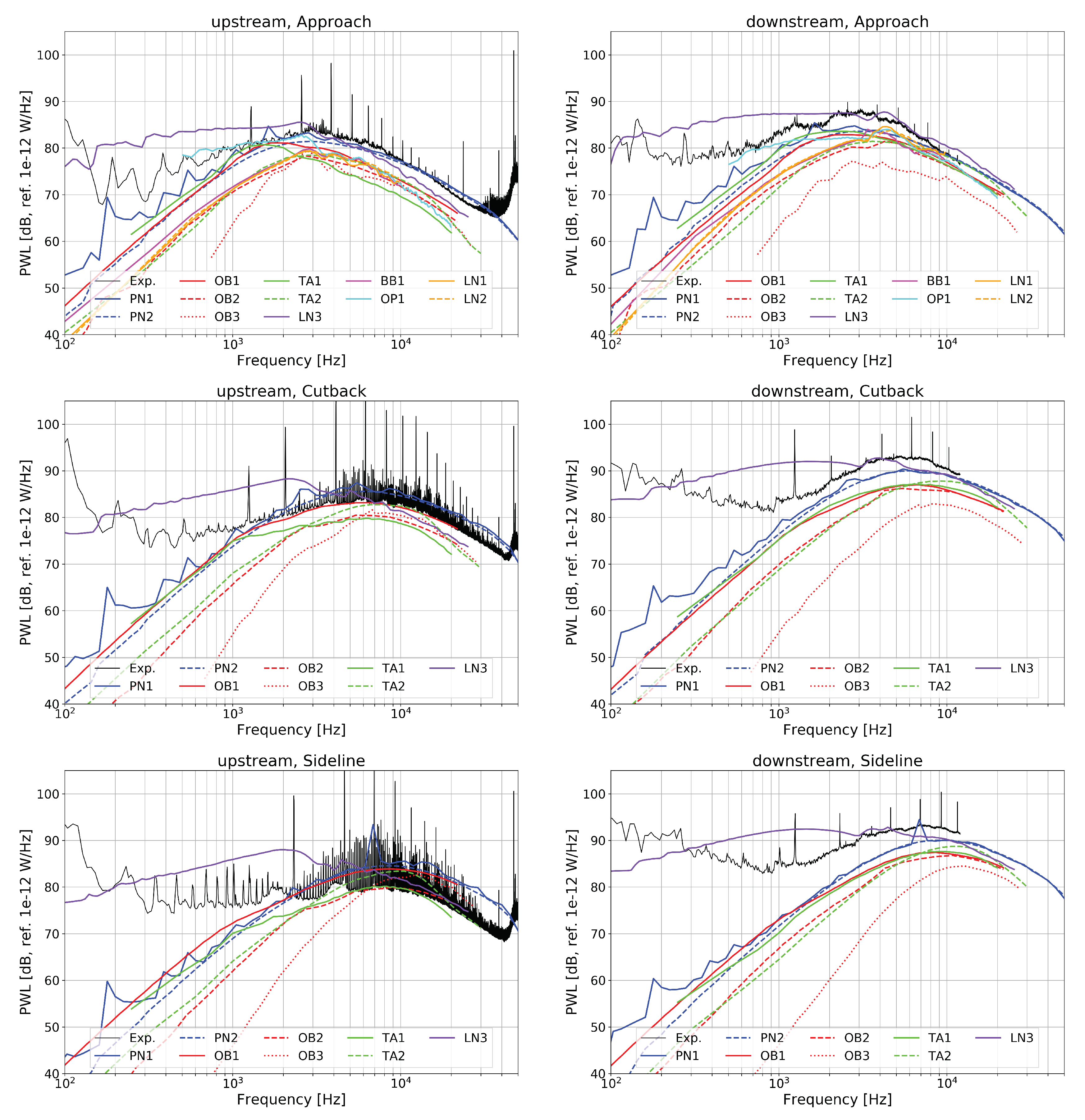
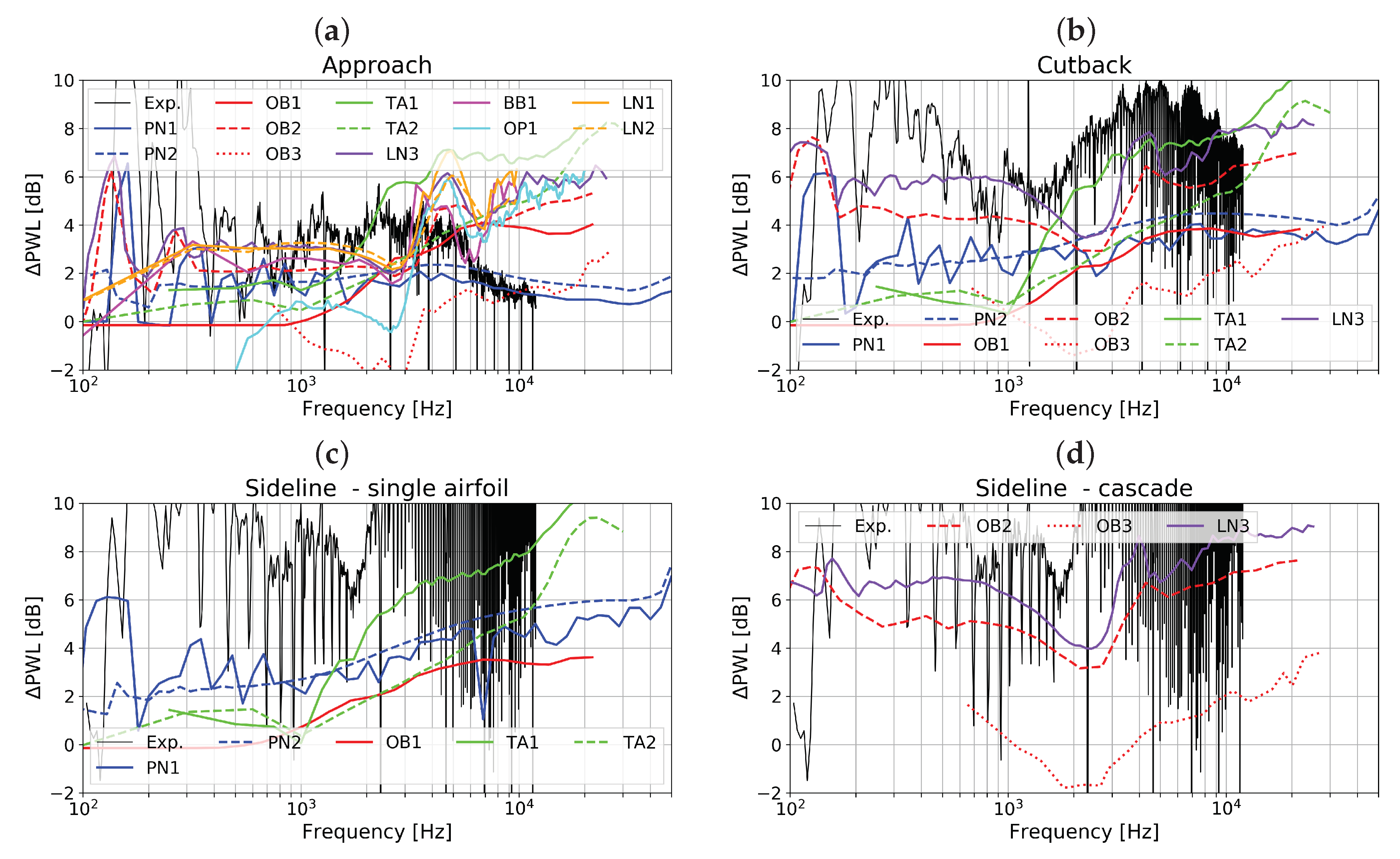
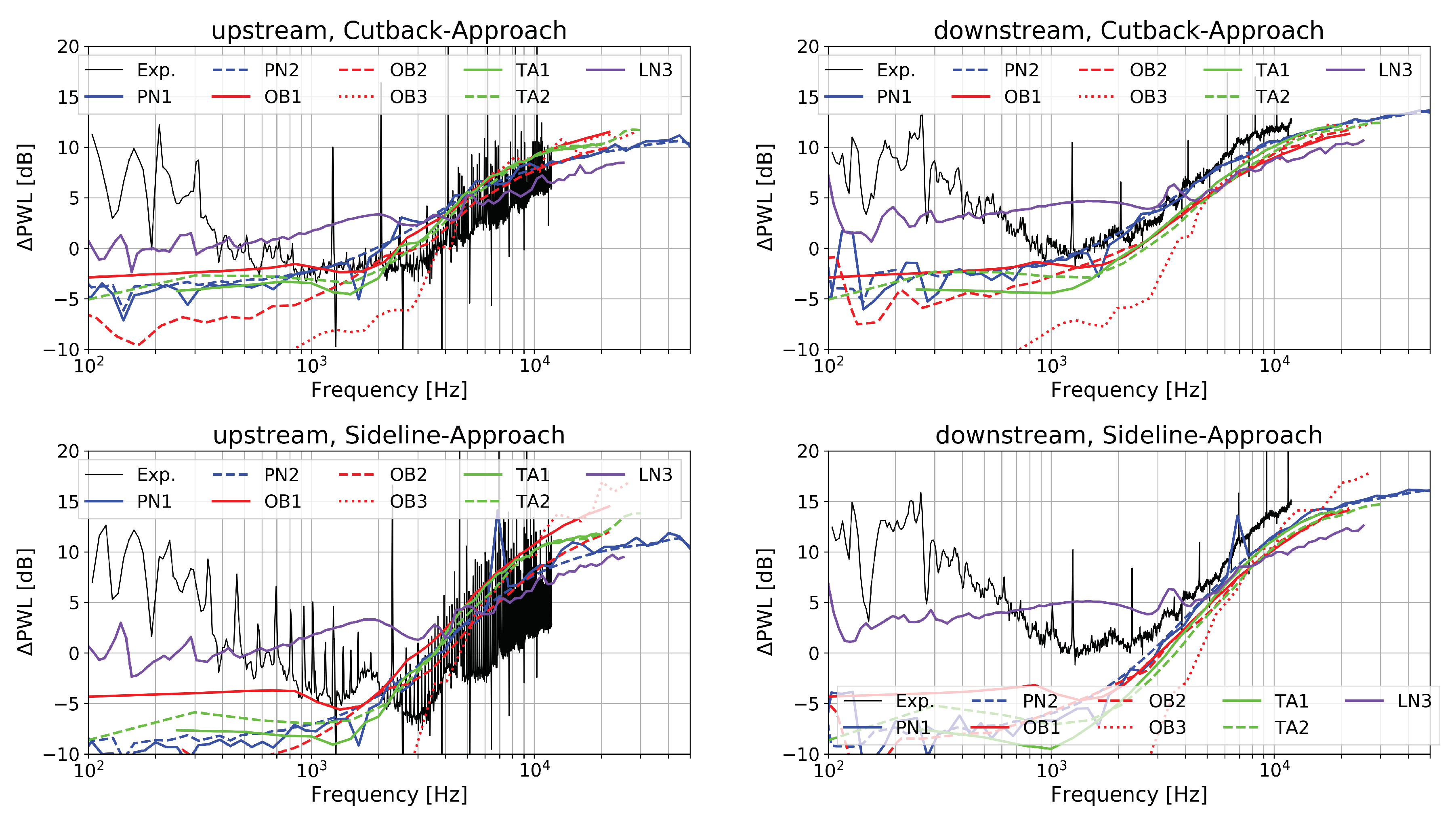
- The prediction curves match satisfactorily with the experimental results at mid and high frequencies. All but one result deviate by less than ±3 dB in that frequency range compared to a hypothetic median solution. The predicted peak frequency agrees with the experimental data, indicating that the RANS prediction of the integral length scale was acceptable.
- Greater differences are visible at low frequencies, yet most results remain within a similar range. The solutions LN3 and OB3 represent two extrema, respectively much higher and lower than the other ones.
- In general, the differences between two prediction curves remain the same for the up- and downstream positions.
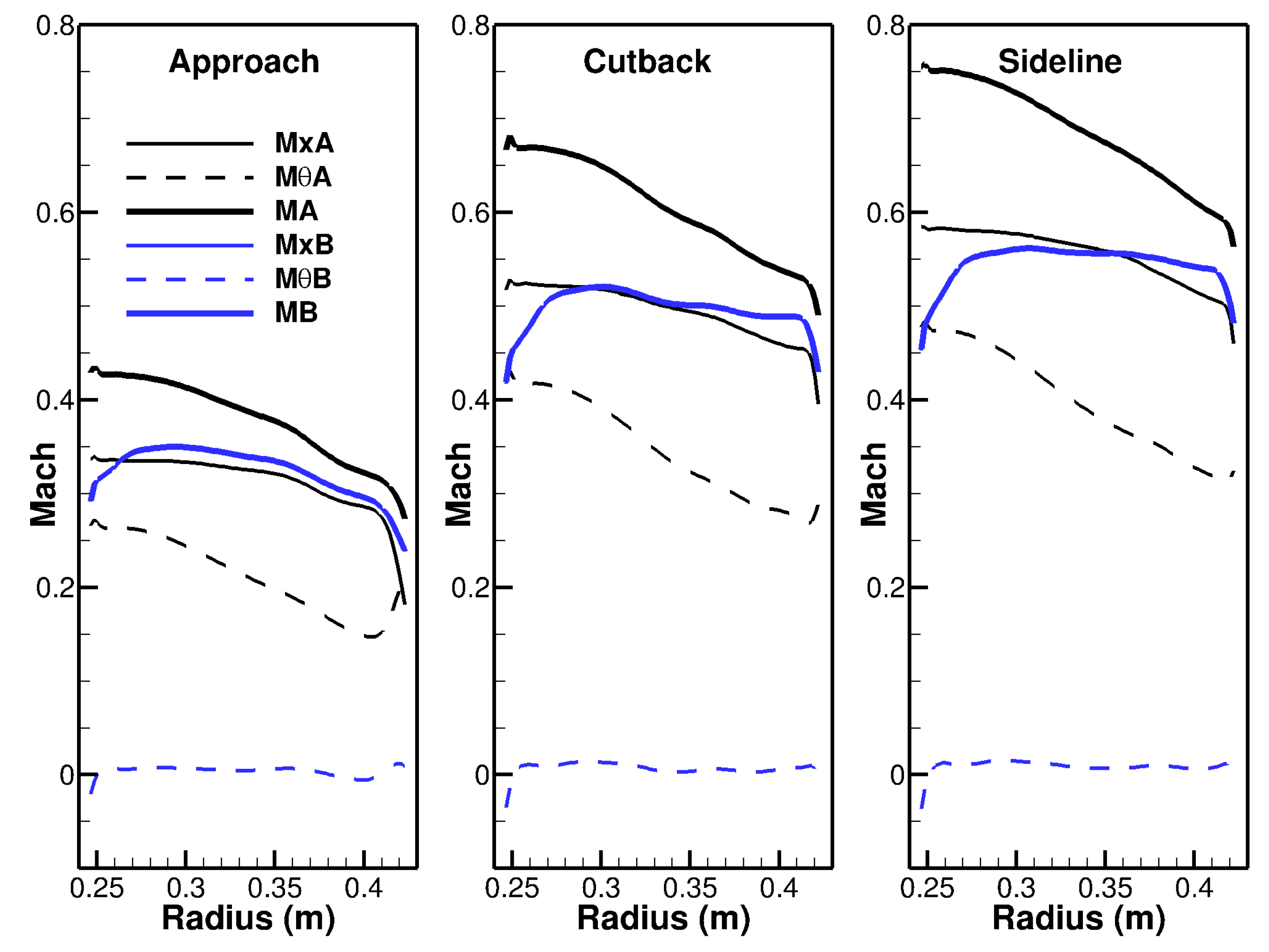
- Compared to the experimental data, the predicted levels are underestimated downstream of the stator, except for LN3. At the upstream position, amplitudes are slightly overestimated in some of the results at high speed. This is possibly related to the fact that rotor shielding was not included in any of the simulations. At the higher speeds, the formation of shocks on the rotor blades blocks the transmission of RSI noise in the direction of the inlet (see the investigation by Blázquez and Corral [56] regarding the importance of blockage for the ACAT1 fan). This effect explains that the amplitudes measured at Sideline in the forward arc are lower than those obtained at Cutback. A model accounting for rotor shielding would be necessary to improve the comparison with the far-field data in the forward arc.
4.2. Trends in Sound Power Split and by Speed Variation
- (1)
- Previous studies [7,20,22,23,24] showed the sensitivity of sound power to the choice of the stagger angle, in particular in the upstream direction. The flat plate assumption with the use of the leading edge stagger angle for inclination tends to overestimate the upstream contribution and underestimate the downstream contribution.
- (2)
- The rotor shielding and to a lesser extent the swirl effect influence the balance in energy between the upstream and downstream radiations too.
- (3)
- Finally, the mismatch between the unsteady loading formulation and the Green’s function in methods of Group A is also a source of error.
4.3. Detailed Comparisons
4.3.1. Effect of Acoustic Boundary Conditions
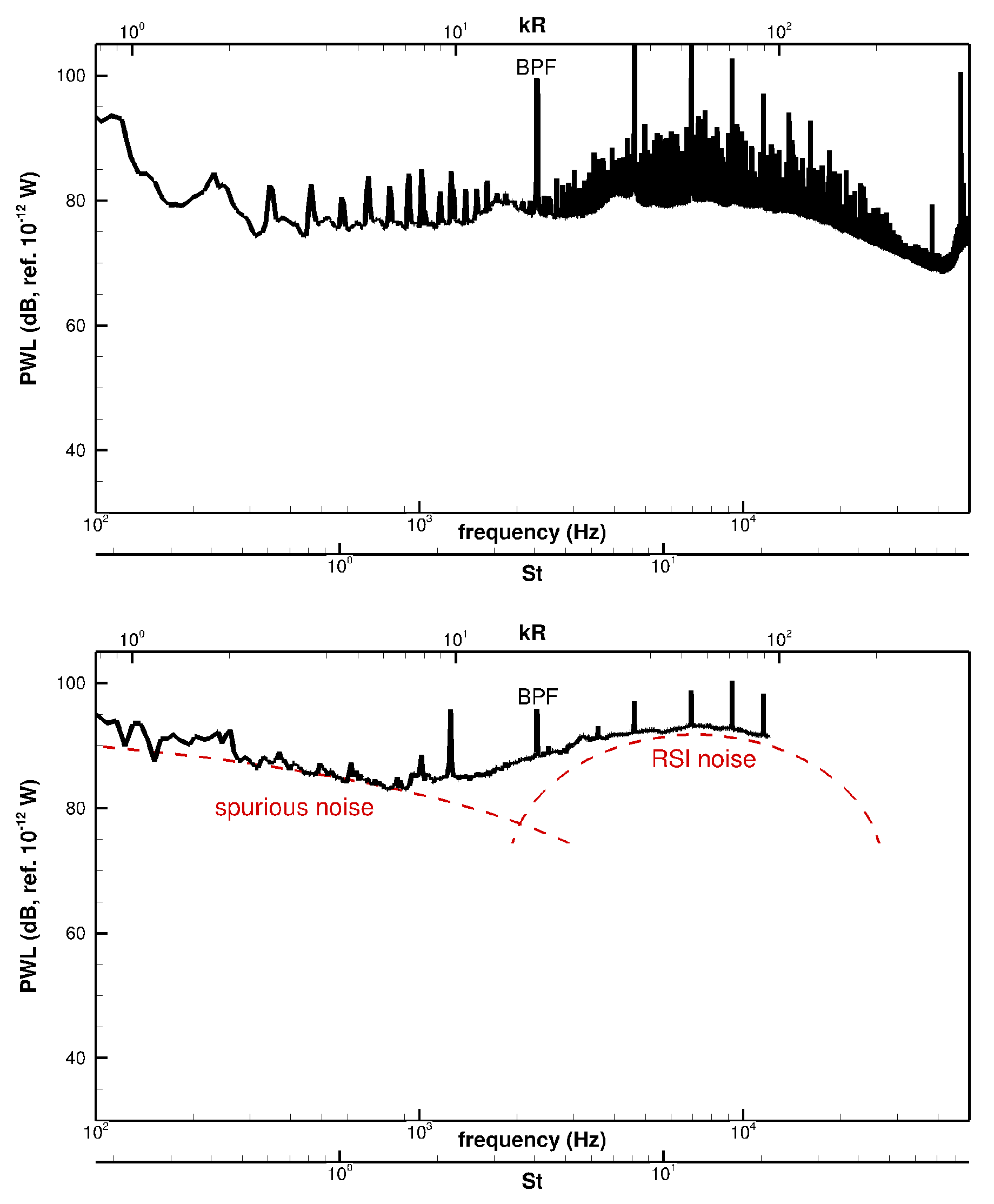
- The solutions PN1 and PN2 based on the in-duct and free-field formulations for the Green’s function converge asymptotically at high frequency (see Figure 9, Figure 10 and Figure 11) as expected from for example, Moreau and Guérin [43]. The in-duct solution PN1 exhibits some peaks in the low-frequency range, which occur when new in-duct acoustic modes become cut-on. These peaks are clearly visible in the measurements, not only in the in-duct data downstream but also in the far-field data upstream.
- Unfortunately, the comparison between TA1 and PN1 does not allow for a definite conclusion regarding the importance of swirl as the two solutions also differ with respect to the Green’s function, the stagger angle, and the blade response. The agreement between TA1 and PN1 is generally good (within 1–2 dB) at low frequency and fair (within 3 dB) at the downstream position at high frequency. In the upstream direction, the mismatch is significant at high frequency exceeding up to 8 dB. Supposedly, this behaviour is due to the different definition of the stagger angle and the use of a different blade response function and is likely not related to the effect of swirl.
- The swirl effect accounted for in the solution PN1 has no significant impact on the predicted noise spectra. Compared to PN2, only a slight noise increase is observed at low frequency. By considering the swirl, the acoustic modal content is changed. For example, swirl shifts the cut-on limit of acoustic modes (see Equation A7). But once the modal contributions of the same frequency band are summed up, the impact on the resulting broadband noise spectrum is rather small at medium and high frequencies due to the statistically large number of cut-on modes. Based on this result, the authors argue that accounting for the swirl may not be essential to achieve a reasonable prediction of RSI broadband noise levels. (This statement does not hold for the prediction of RSI tones since they can be composed of only a few propagative modes.) This finding conflicts with the results presented by Moreau [5] about the extension of Posson’s model to sheared swirling flow. A noise diminution of up to 4–5 dB was reported over a large frequency range in the forward arc for the SDT fan at the Approach condition.
4.3.2. Effect of Gusts Model
- The simulations TA1 and TA2 differ in the wavenumber representation of the gusts. In the first simulation, all gusts are assumed to impinge on the stator with a wavefront parallel to the leading edge (). For the second case the spanwise component is included in the simulations. The two models produce results, which differ significantly, in particular at low frequency. Considering the oblique component leads to a decrease in sound power level by more than 5 dB at low frequency and an increase by up to 3 dB in the mid range. The inversion point is located slightly below the peak frequency. At high frequencies, the two solutions are more alike. A similar trend was reported by Reboul [47] for a single airfoil in free field with a low aspect ratio. Thus, the assumption that the contribution of oblique gusts is negligible as proposed by Amiet [6] is not applicable to our case. Presumably, the levels are lower at low frequency in TA2, because subcritical gusts are properly considered. Such an effect was also observed on cascade models when accounting or removing subcritical gusts on the SDT case [24,25].
- A similar comparison can be done between the results LN1 (parallel gusts) and LN2 (oblique gusts) for the cascade model. Contrary to the previous example, the results are close. This is due to the fact that the subcritical gusts were removed a priori from the two-dimensional wavenumber velocity spectrum used to calculate the solution LN1.
- The agreement between LN3 (two-dimensional representation of the turbulence spectrum) and LN1 (two-dimensional representation of the turbulence spectrum with filtering of the subcritical gusts) is good at high frequency but poor at low frequency, which supports the previous claims. Note that the trends at low frequency presented by Cheong et al. [52] for a model test may seem to be different from those shown here using the same code: unlike for the present ACAT1 benchmark, the shape of the spectra corresponded to an inverse parabolic curve, typical of RSI broadband noise. Compared to the present study, the only differences in Cheong’s paper were (i) the representation in one-third octave bands, which changes the trend at low frequency compared to a representation in narrow bands, and (ii) the fact that turbulence length-scale and intensity were adjusted to provide the best possible match to the measured data at high frequencies.
4.3.3. Impact of Airfoil-Response Model
- In-duct Isolated Airfoil: The results PN1 and TA1 can be analysed regarding the impact of the lift-response function. For that, the effect of swirl on the in-duct Green’s function must be assumed neglected. The solution PN1 applies the low-frequency Sears’ model enhanced by an acoustic, non-compact term [9], whereas TA1 relies on the Amiet’s high-frequency approximation [48]. In the downstream section of the duct, there is a difference of approximately 3–4 dB between the two results. In the upstream section, the discrepancy is larger and increases with the Mach number. It is not clear whether it is due to the lift-response function or to the definition of the stagger angle, which is a sensitive parameter for the upstream results as alluded before. Recall that PropNoise uses the leading-edge angle and TinA1D the mean flow angle to define the inclination of the plate (see Table A1).
- Free-field Isolated Airfoil: The comparison between PN2 and OB1 allows to further compare Sears and Amiet. One additional difference is that, unlike PN2, OB1 works with the two-dimensional wavenumber spectrum. The two results are in good agreement for all simulations in both directions of propagation. The discrepancy does not exceed 3 dB.
- Isolated Airfoil vs. Cascade of Airfoils: As the solidity (chord-to-pitch ratio) grows, the cascade effect is expected to play an increasing role in noise. Moreau and Roger [60] considered that the isolated-airfoil approximation should be applicable for values of solidity below one and without overlap. When these conditions are not satisfied, they recommend the use of the cascade response. Note that this analysis does not include the wavenumber of the incoming gust and as a consequence does not account for the potentially differing trends towards low and high frequency. The stator solidity of the ACAT1 stator varies between 2.5 at the hub and 1.4 at the tip (see Figure 7) and the overlap, which depends on the choice of the stagger angle, is positive. According to Moreau and Roger’s criteria, it should be preferable to account for the cascade effect for the ACAT1. Concerning the role of the cascade effect in broadband noise, contrary trends between open and in-duct configurations, two and three-dimensional simulations can be found in the literature. Hanson [7], using the three-dimensional cascade-response model in free field, found little impact on his results, even at low frequency, when he varied the solidity in the range 0.8 to 2.5, while keeping the blade count constant. These findings are not in agreement with Grace’s results [61] for a shrouded configuration. Indeed, she observed differences superior to 5 dB at high frequency on the baseline configuration of the SDT fan but comparable levels at low frequency. The same conclusion can be drawn from de Laborderie’s results [27] for the same fan. Comparing the single airfoil model to the cascade model in 2D, Blandeau et al. [23] reported potentially severe differences between the two solutions at frequencies below a critical value. Above that critical frequency, blade-to-blade interactions are weak and the contribution of all blades to the radiated sound power are additive. By neglecting the cascade effect, the results obtained below the critical limit become increasingly unsuitable as the solidity augments. For a 2D cascade, the critical frequency [52] is given by:where and are the axial and tangential Mach numbers, , and s is the pitch. At the Approach condition, the following values are found in the benchmark data at midspan: , , m/s and m. This yields as critical frequency Hz. A convergence at high frequency, starting in a frequency range not too far from that predicted by Cheong et al. is observed between OB1 (single airfoil) and OB2 (3D cascade). The solution OB3 (3D cascade) also converges to the isolated case but at a much higher frequency. A reduction of the noise levels in the low-frequency range is observable for the OB2, OB3, LN1 and LN2 simulations but not for the LN3 and OP1 curves. The LN3 solution is 2D, which produces the difference as already explained. Concerning OP1, no strong reduction of the noise levels in the low-frequency range is observed because the number of CAA calculations used to derive the a priori correction of the turbulence content were not enough. Only a small amount of CAA simulations were performed and it seems that those were sufficient to reproduce the results at high frequency but insufficient to better account for the low-frequency behaviour. Also note that the TA2 results, which do not consider the cascade effect but do account for the oblique gusts, are very similar to OB2. Thus, it is not clear whether the effect of oblique gusts is dominant over the cascade effect.
- Cascade of Flat Plates vs. Cascade of Thick, Cambered Airfoils: The comparison between BB1 and LN1 at the condition Approach indicates that considering the real blade geometry does not significantly modify the results. Using a solution valid upstream of the cascade, Evers and Peake [62] also found that considering thickness and camber has a relatively small impact on broadband noise, which is no longer true for tonal noise. Grace [61], using the asymptotic solution for an isolated single blade provided by Ayton and Peake [63], investigated the effect of thickness, camber and angle of attack. For a realistic choice of parameters, the differences reported by Grace did not exceed 3 dB. Using a synthetic turbulence method coupled to a CAA solver, Gea-Aguilera et al. [64] found similar results for fan RSI noise.
5. Conclusions
- Similar to the RANS turbulence model, the chosen approach to model acoustics may have a significant impact on the predictions of RSI broadband noise. At frequencies higher than the peak frequency, differences of up to ±3 dB were observed between the results and the median solution. At lower frequencies, the deviation was even more substantial, mainly for two reasons: the presence of subcritical gusts and the cut-off effect of acoustic modes, which are both important to consider when the number of contributing waves is small.
- Compared to experiments, the predicted levels were usually lower by some decibels, even though the turbulence intensity was overestimated by the RANS simulations.
- The choice of the turbulence spectrum (whether Liepmann or von Kármán) was not of primary importance for the results.
- Depending whether the open or the in-duct formulation was used for the Green’s function, the results differed at low frequency. The relative impact due to the choice of the Green’s function was found to be stronger by considering the cascade effect.
- For the case investigated at the lowest Mach number, it could be shown that replacing the real blade geometry by a flat plate is an acceptable assumption for broadband noise. This is likely totally different for tonal noise predictions as the chordwise distribution of the pressure jump is known to be different for real airfoils.
- The trends predicted by increasing the rotor speed were similar for almost all models. They were principally driven by the changes in the turbulence velocity spectrum.
- Two-dimensional cascade-based models have inherent difficulties to account for the third, that is, the spanwise, dimension. Several solutions were developed by the participants to overcome that problem. Without these corrections, broadband noise is overestimated at low frequency. With this respect, the single airfoil theory considering the oblique component produces better results.
- The split between the up- and downstream power levels exhibited different trends for the single-airfoil and the cascade response results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ACAT1 | AneCom AeroTest Rotor 1 |
| AP | Approach |
| BPF | Blade Passing Frequency |
| CAA | Computational AeroAcoustics |
| CB | Cutback |
| CFD | Computational Fluid Dynamics |
| ESS | Engine Support Stator |
| HW | Hot Wire (anemometry) |
| LE | Leading edge |
| NASA | National Aeronautics and Space Administration |
| PWL | Sound Power Level |
| RANS | Reynolds Averaged Navier-Stokes |
| rpm | round per minute |
| RSI | Rotor–Stator Interaction |
| SDT | Source Diagnostic Test (fan rig) |
| SL | Sideline |
| SLS | Sea Level Static (working line) |
| TE | Trailing edge |
| TKE | Turbulence Kinetic Energy |
| TLS | Turbulence Length Scale |
| TNBB | EU founded project TurboNoiseBB |
| UFFA | Universal Fan Facility for Acoustics |
| Latin letters | |
| A | pressure mode amplitude (Pa) |
| c | speed of sound (m/s) or blade chord (m) |
| unsteady lift coefficient (-) | |
| f | frequency (1/s) |
| g | Green’s function |
| k | acoustic wavenumber (1/m) or turbulence kinetic energy (m2/s2) |
| turbulence kinetic energy from RANS (m2/s2) | |
| K | convective wavenumber (1/m) |
| radial correlation length (m) | |
| M | Mach number (-) |
| N | number of strips (-) |
| P | sound power (W) |
| r | radial position (m) |
| R | duct radius (m) or cascade response function |
| s | pitch (m) (for stator: s = 2r/V) |
| S | Sears function |
| Strouhal number (-) | |
| turbulent velocity fluctuation (m/s) | |
| V | number of stator vanes (-) |
| W | mean flow velocity (m/s) |
| x | axial position (m) |
| Greek letters | |
| cut-on factor (-) | |
| mean flow angle relative to blade (deg) | |
| swirl factor (-) | |
| turbulence dissipation rate (m2/s3) | |
| hub-to-tip ratio (-) | |
| azimuthal angle (deg) | |
| turbulence integral length scale from RANS (m) | |
| density (kg/m3) | |
| source term (Pa) | |
| turbulence spectrum (m2/s2) | |
| polar angle (deg) | |
| chordwise correlation (-) | |
| stagger angle (deg) | |
| angular frequency (rad/s) | |
| specific turbulence dissipation rate (1/s) | |
| rotational angular speed of a solid body swirl (rad/s) | |
| Subscripts | |
| 0 | ambient mean flow value |
| 1, 2, 3 | streamwise, upwash, spanwise |
| A, B | at/upstream of LE, at/downstream of TE |
| L | unsteady loading |
| azimuthal, radial mode order | |
| rel | relative to blade |
| R, S | rotor, stator |
| x, r, | axial, radial, tangential |
| ⊥, l | normal, parallel to blade chord |
| Superscripts | |
| ± | direction of propagation: (+) downstream, (−) upstream |
| averaged value |
Appendix A. Summary of the Acoustic Models
| Code | ID | Turbulence Spectrum | Blade Model | Gust | Acoustic Conditions | |
|---|---|---|---|---|---|---|
| Mean Flow | Boundaries | |||||
| PropNoise [42,43] | PN1 | v. Kármán | isolated flat plate with [9] | parallel | axial uniform + solid body swirl | infinite duct with hard walls |
| PN2 | axial uniform | free field | ||||
| OPTIBRUI [27] | OB1 [50] | Liepmann | isolated flat plate with [9] | oblique | axial uniform | free field |
| OB2 [7] | cascade of flat plates with [12] | stripwise swirling flow | ||||
| OB3 [25] | axial uniform | infinite duct with hard walls | ||||
| BBNANEMS | BB1 [56] | Liepmann | cascade of real blades [57] | parallel | stripwise swirling flow | free field |
| LN1 [55] | cascade of flat plates with [53] | |||||
| LN2 | cascade of flat plates with [14,53] | oblique | ||||
| TinA [46,47] | TA1 | v. Kármán | isolated flat plate with [9] | parallel | axial uniform | infinite duct with hard walls |
| TA2 | oblique | |||||
| Orpheus [59] | OP1 | Liepmann | cascade of flat plates with [53] | oblique | axial uniform strip based | infinite duct with hard walls |
| LINSUB | LN3 [52] | Liepmann | cascade of flat plates with [53] | parallel | stripwise swirling flow | free field |
| ID | Number of Strips | Number of Frequencies | Approximate Computation Time |
|---|---|---|---|
| PN1 | 97 | 100 | 1 min |
| PN2 | 97 | 100 | 1 min |
| OB1 | 25 | 25 | 1 min |
| OB2 | 25 | 25 | 3 h on 24 cores |
| OB3 | 25 | 25 | 2 h on 240 cores |
| BB1 | 5 | 39 | 170 GPU h/8500 CPU h |
| LN1 | 5 | 39 | 2 min |
| LN2 | 5 | 39 | 10 min |
| TA1 | 97 | 24 | 1 min |
| TA2 | 10 | 24 | 1 h |
| OP1 | 9 | 315 | 25 min |
| LN3 | 49 | 100 | 8 h |
Appendix B. Modal Sound Power Amplitude
References
- Kissner, C.; Guérin, S.; Seeler, P.; Billson, M.; Chaitanya, P.; Laraña, P.C.; de Laborderie, H.; François, B.; Lefarth, K.; Lewis, D.; et al. ACAT1 benchmark of RANS-informed analytical methods for fan noise prediction: Part I—Influence of the RANS Simulation. Acoustics 2020, 2, 539–578. [Google Scholar] [CrossRef]
- Rienstra, S. Sound transmission in slowly varying circular and annular lined ducts with flow ducts. J. Fluid Mech. 1999, 380, 279–296. [Google Scholar] [CrossRef]
- Ribner, H.S. Shock-Turbulence Interaction and the Generation of Noise; NACA Technical Note 3255; NACA: Washington, DC, USA, 1954. [Google Scholar]
- Posson, H.; Roger, M.; Moreau, S. On a uniformly valid analytical rectilinear cascade response function. J. Fluid Mech. 2010, 663, 22–52. [Google Scholar] [CrossRef]
- Moreau, S. Turbomachinery Noise Predictions: Present and Future. Acoustics 2019, 1, 92–116. [Google Scholar] [CrossRef]
- Amiet, R. Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vib. 1975, 41, 407–420. [Google Scholar] [CrossRef]
- Hanson, D. Theory for Broadband Noise of Rotor and Stator Cascades with Inhomogeneous Inflow Turbulence Including Effects of Lean and Sweep; NASA CR-2001-210762; NASA: Cleveland, OH, USA, 2001. [Google Scholar]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. 1955, 231, 505–514. [Google Scholar]
- Amiet, R. Compressibility effects in unsteady thin-airfoil theory. AIAA J. 1974, 12, 252–254. [Google Scholar] [CrossRef]
- Sears, W. Some aspects of non-stationary airfoil theory and its practical applications. J. Aeronaut. Sci. 1941, 8, 104–108. [Google Scholar] [CrossRef]
- Adamczyk, J.J. The Passage of an Infinite Swept Airfoil through an Oblique Gust; NASA CR-2395; NASA: Wahington, DC, USA, 1974. [Google Scholar]
- Glegg, S. The response of a swept blade row to a three-dimensional gust. J. Sound Vib. 1999, 227, 29–64. [Google Scholar] [CrossRef]
- Goldstein, M. Aeroacoustics; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Graham, J. Similarity rules for thin aerofoils in non-stationary subsonic flows. J. Fluid Mech. 1970, 43, 753–766. [Google Scholar] [CrossRef]
- Kerschen, E.; Gliebe, P. Fan Noise Caused by Ingestion of Anisotropic Turbulence—A Model Based on Axisymmetric Turbulence Theory. In Proceedings of the 6th AIAA Aeroacoustics Conference, Hartford, CT, USA, 4–6 June 1980. [Google Scholar]
- Ventres, C.; Theobald, M.; Mark, W. Turbofan Noise Generation. Volume 1: Analysis; NASA CR-167952; NASA: Cleveland, OH, USA, 1982. [Google Scholar]
- Nallasamy, M.; Envia, E. Computation of rotor wake turbulence noise. J. Sound Vib. 2005, 282, 649–678. [Google Scholar] [CrossRef]
- Grace, S.; Wixom, A.; Winkler, J.; Sondak, D.; Logue, M.M. Fan Broadband Interaction Noise Modeling. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference, Colorado Springs, CO, USA, 4–6 June 2012. [Google Scholar]
- Kissner, C.A.; Guérin, S. Influence of Wake and Background Turbulence on Predicted Fan Broadband Noise. AIAA J. 2019, 58. [Google Scholar] [CrossRef]
- Grace, S.; Maunus, J.; Sondak, D. Effect of CFD Wake Prediction in a Hybrid Simulation of Fan Broadband Interaction Noise. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2011. [Google Scholar]
- Moreau, A.; Guérin, S. The impact of low-speed fan design on noise: An exploratory study. J. Turbomach. 2016, 138, 081006. [Google Scholar] [CrossRef]
- Jaron, R.; Herthum, H.; Franke, M.; Moreau, A.; Guérin, S. Impact of turbulence models on RANS-informed prediction of fan broadband noise. In Proceedings of the 12th European Conference on Turbomachinery Fluid dynamics and Thermodynamics, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Blandeau, V.P.; Joseph, P.F.; Jenkins, G.; Powles, C.J. Comparison of sound power radiation from isolated airfoils and cascades in a turbulent flow. J Acoust. Soc. Am. 2011, 129, 3521–3530. [Google Scholar] [CrossRef] [PubMed]
- Grace, S. Fan broadband interaction noise modeling using a low-order method. J. Sound Vib. 2015, 346, 402–423. [Google Scholar] [CrossRef]
- Posson, H.; Moreau, S.; Roger, M. Broadband noise prediction of fan outlet guide vane using a cascade response function. J. Sound Vib. 2011, 330, 6153–6183. [Google Scholar] [CrossRef]
- Posson, H.; Moreau, S.; Roger, M. On the use of a uniformly valid analytical cascade response function for fan broadband noise predictions. J. Sound Vib. 2011, 329, 3721–3743. [Google Scholar] [CrossRef]
- de Laborderie, J. Approches Analytiques et NuméRiques pour la PréDiction du Bruit Tonal et Large Bande de Soufflantes de Turboréacteurs. Ph.D. Thesis, Université de Sherbrooke, Sherbrooke, QC, Canada, 2013. [Google Scholar]
- Lewis, D.; Moreau, S.; Jacob, M. On the use of RANS-informed analytical models to perform broadband rotor-stator interaction noise predictions. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- TurboNoiseBB. European Union’s Horizon 2020 Research and Innovation Programme. Available online: http://dlr.de/at/turbonoisebb (accessed on 9 May 2020).
- Guérin, S.; Kissner, C.; Kajasa, B.; Jaron, R.; Behn, M.; Hakansson, S.; Pardowitz, B.; Tapken, U.; Meyer, R.; Enghardt, L. Noise prediction of the ACAT1 fan with a RANS-informed analytical method: Success and challenge. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Meyer, R.; Hakansson, S.; Hage, W.; Enghardt, L. Instantaneous flow field measurements in the interstage section between a fan and the outlet guiding vanes at different axial positions. In Proceedings of the 13th European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar]
- Tapken, U.; Behn, M.; Spitalny, M.; Pardowitz, B. Radial mode breakdown of the ACAT1 fan broadband noise generation in the bypass duct using a sparse sensor array. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Tapken, U.; Pardowitz, B.; Behn, M. Radial mode analysis of fan broadband noise. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Behn, M.; Pardowitz, B.; Tapken, U. Separation of tonal and broadband noise components by cyclostationary analysis of the modal sound field in a low-speed fan test rig. In Proceedings of the International Conference of Fan Noise, Aerodynamics, Applications and Systems 2018, Darmstadt, Germany, 18–20 April 2018. [Google Scholar]
- Joseph, P.; Morfey, C.; Lowis, C. Multi-mode sound transmission in duts with flow. J. Sound Vib. 2003, 264, 523–544. [Google Scholar] [CrossRef]
- Pereira, A.; Jacob, M. Experimental assessement of in-duct modal content of fan broadband noise via iterative Bayesian inverse approach. In Proceedings of the Berlin Beamforming Conference, Berlin, Germany, 2–3 March 2020. [Google Scholar]
- Heidmann, M. Interim Prediction Method for Fan and Compressor Source Noise; NASA TM X-71763; NASA: Cleveland, OH, USA, 1979. [Google Scholar]
- Becker, K.; Heitkamp, K.; Kügeler, E. Recent Progress in a Hybrid Grid CFD Solver for Turbomachinery Flows. In Proceedings of the Fifth European Conference on Computational Fluid Dynamics, Lisbon, Portugal, 14–17 June 2010. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Jaron, R. Aeroakustische Auslegung Von Triebwerksfans Mittels Multidisziplinärer Optimierungen. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2018. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Moreau, A. A Unified Analytical Approach for the Acoustic Conceptual Design of Fans of Modern Aero-Engines. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2017. [Google Scholar]
- Moreau, A.; Guérin, S. Similarities of the in-duct and free-field formulations in rotor noise problems. In Proceedings of the 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA, 5–8 June 2011. [Google Scholar]
- Hanson, D.B. Helicoidal surface theory for harmonic noise of propellers in the far field. AIAA J. 1980, 18, 1213–1220. [Google Scholar] [CrossRef]
- Blokhinstev, D. The propagation of sound in an inhomogeneous and moving medium. J. Acoust. Soc. Am. 1946, 18, 322–328. [Google Scholar] [CrossRef]
- Reboul, G.; Polacsek, C.; Léwy, S.; Heib, S. Ducted-Fan Broadband Noise Simulations Using Unsteady or Averaged Data. In Proceedings of the 37th International Congress and Exposition on Noise Control Engineering, Shanghai, China, 26–29 October 2008. [Google Scholar]
- Reboul, G. Modélisation du Bruit à Large Bande de Soufflante de Turboréacteur. Ph.D. Thesis, École Centrale de Lyon, Lyon, France, 2010. [Google Scholar]
- Amiet, R. High-frequency thin-airfoil theory for subsonic flow. AIAA J. 1976, 14, 1076–1082. [Google Scholar] [CrossRef]
- Guérin, S.; Moreau, A.; Tapken, U. Relation between source models and acoustic duct modes. In Proceedings of the 15th AIAA/CEAS Aeroacoustics Conference, Miami, FL, USA, 11–13 May 2009. [Google Scholar]
- Amiet, R.; Egolf, C.; Simonich, J. Noise Produced by Turbulent Flow into a Rotor: Users Manual for Noise Calculation; NASA CR-181790; NASA: Hampton, VA, USA, 1989. [Google Scholar]
- Hanson, D.; Horan, K. Turbulence/cascade interaction, spectra of inflow, cascade response, and noise. In Proceedings of the AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998. [Google Scholar]
- Cheong, C.; Joseph, P.; Lee, S. High frequency formulation for the acoustic power spectrum due to cascade-turbulence interaction. J. Acoust. Soc. Am. 2006, 119, 108–122. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, D. AGARD Manual on Aeroelasticity in Axial-Flow Turbomachines. Volume 1: Unsteady Turbomachinery Aerodynamics, Classical Two-Dimensional Methods; AGARD-AG-298; AGARD: Neuilly sur Seine, France, 1987. [Google Scholar]
- Smith, S.N. Discrete Frequency Sound Generation in Axial Flow Turbomachines; Aeronautical Research Council Reports and Memoranda; Reports and Memoranda No. 3709; Her Majesty’s Stationery Office: London, UK, 1970. [Google Scholar]
- Blázquez, R.; Corral, R. Efficient Fan Broadband Noise Prediction using Navier-Stokes Linearized Analysis. In Proceedings of the 25th AIAA/CEAS Aeroacoustics Conference, Delft, The Netherlands, 20–23 May 2019. [Google Scholar]
- Blázquez, R.; Corral, R. Prediction of fan acoustic blockage on fan-outlet guide vanes broadband interaction noise. In Proceedings of the 15th Turbomachinery Technical Conference and Exposition, London, UK, 22–26 June 2020. [Google Scholar]
- Corral, R.; Escribano, A.; Gisbert, F.; Serrano, A.; Vasco, C. Validation of a linear multigrid accelerated un structured Navier-Stokes solver for the computation of turbine blades on hybrid grids. In Proceedings of the 9th AIAA/CEAS Aeroa Coustics Conference, Hilton Head, SC, USA, 12–14 May 2003. [Google Scholar]
- Wohlbrandt, A.; Kissner, C.; Guérin, S. Impact of cyclostationarity on fan broadband noise prediction. J. Sound Vib. 2018, 420, 142–164. [Google Scholar] [CrossRef]
- Carrasco Laraña, P.C.; Serrano, A. A Frequency Domain Model for Turbine Interaction Broadband Noise: Comparison with Measurements. In Proceedings of the 24th AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Moreau, S.; Roger, M. Advanced noise modeling for future propulsion systems. Int. J. Aeroacoust. 2018, 17, 576–599. [Google Scholar] [CrossRef]
- Grace, S. Further Investigations into a Low-Order Model of Fan Broadband Noise. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar]
- Evers, I.; Peake, N. On sound generation by the interaction between turbulence and a cascade of airfoils with non-uniform mean flow. J. Fluid Mech. 2002, 463, 25–52. [Google Scholar] [CrossRef]
- Ayton, L.J.; Peake, N. On high-frequency noise scattering by aerofoils in Flow. J. Fluid Mech. 2013, 734, 144–182. [Google Scholar] [CrossRef]
- Gea-Aguilera, F.; Gill, J.; Zhang, X. On the effects of fan wake modelling and vane design on cascade noise. J. Sound Vib. 2019, 459, 114859. [Google Scholar] [CrossRef]
- Morse, M.; Ingard, K. Theoretical Acoustics; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Morfey, C. Sound transmission and generation in ducts with flow. J. Sound Vib. 1971, 14, 37–55. [Google Scholar] [CrossRef]


| Short Gap | Approach (AP) | Cutback (CB) | Sideline (SL) |
|---|---|---|---|
| rpm massflow (kg/s) | 3856.1 (50%) 54.85 | 6175.1 (80%) 88.80 | 6945.7 (90%) 101.32 |
| corr. rpm corr. massflow (kg/s) | 3797.9 56.48 | 6077.3 91.61 | 6836.5 104.53 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guérin, S.; Kissner, C.; Seeler, P.; Blázquez, R.; Carrasco Laraña, P.; de Laborderie, H.; Lewis, D.; Chaitanya, P.; Polacsek, C.; Thisse, J. ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models. Acoustics 2020, 2, 617-649. https://doi.org/10.3390/acoustics2030033
Guérin S, Kissner C, Seeler P, Blázquez R, Carrasco Laraña P, de Laborderie H, Lewis D, Chaitanya P, Polacsek C, Thisse J. ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models. Acoustics. 2020; 2(3):617-649. https://doi.org/10.3390/acoustics2030033
Chicago/Turabian StyleGuérin, Sébastien, Carolin Kissner, Pascal Seeler, Ricardo Blázquez, Pedro Carrasco Laraña, Hélène de Laborderie, Danny Lewis, Paruchuri Chaitanya, Cyril Polacsek, and Johan Thisse. 2020. "ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models" Acoustics 2, no. 3: 617-649. https://doi.org/10.3390/acoustics2030033
APA StyleGuérin, S., Kissner, C., Seeler, P., Blázquez, R., Carrasco Laraña, P., de Laborderie, H., Lewis, D., Chaitanya, P., Polacsek, C., & Thisse, J. (2020). ACAT1 Benchmark of RANS-Informed Analytical Methods for Fan Broadband Noise Prediction: Part II—Influence of the Acoustic Models. Acoustics, 2(3), 617-649. https://doi.org/10.3390/acoustics2030033






