Abstract
A physical process is characterized as complex when it is difficult to analyze and explain in a simple way, and even more difficult to predict. The complexity within an art painting is expected to be high, possibly comparable to that of nature. Herein, we apply a 2D stochastic methodology to images of both portrait photography and artistic portraits, the latter belonging to different genres of art, with the aim to better understand their variability in quantitative terms. To quantify the dependence structure and variability, we estimate the Hurst parameter, which is a common dependence metric for hydrometeorological processes. We also seek connections between the identified stochastic patterns and the desideratum that each art movement aimed to express. Results show remarkable stochastic similarities between portrait paintings, linked to philosophical, cultural and theological characteristics of each period.
1. Introduction
The aesthetic evaluation of art paintings typically involves the physical procedure of visual examination of an image [1,2,3,4,5,6,7,8,9]. This approach is considered highly subjective and celebrated as such, with its outcomes being the subject of philosophy of art, and in particular of the philosophical branch known as aesthetics [10]. In an attempt to conceive an alternative and objective procedure for the aesthetic analysis, artificial intelligence and mathematical tools are the subject of a plethora of related publications [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44].
The mathematical field of Stochastics has been introduced as an alternative to deterministic approaches and is used to model the so-called random, i.e., complex, unexplained or unpredictable, fluctuations observed in (but not limited to) non-linear geophysical processes [45,46,47]. Stochastics helps develop a unified perception for natural phenomena and expel dichotomies like random vs. deterministic. Under the viewpoint of stochastics, there is no such thing as a virus of randomness that infects some phenomena to make them random, leaving other phenomena unaffected. Rather, it seems that both randomness and predictability coexist and are intrinsic to natural systems, which can be deterministic and random at the same time, depending on the prediction horizon and the time scale [48]. On this basis, the uncertainty in art, in line with other natural processes, could be considered both aleatory and epistemic, since, in principle, in this case as well, we do not know perfectly well the underlying causal mechanisms. By applying the methods of stochastics, we can quantify this uncertainty treating the unpredictable fluctuations of art works as realizations of complex stochastic processes.
A physical process is characterized as complex when it is difficult to analyze or explain in a completely predictive way. Likewise, constructions by artists (e.g., paintings, music, literature, etc.) are also expected to be of high complexity since they are produced by numerous human (e.g., logic, intuition, emotions, etc.) and non-human (e.g., quality of paints, paper, tools, etc.) processes interacting with each other in a complex manner. Art paintings are thus likely to resemble a stochastic process of increased uncertainty and variability. Such a process deviates from a purely White-Noise behavior, i.e., unstructured randomness, as its aesthetic attributes are likely to appear in clusters by a highly non-predictive manner.
Even though beauty is difficult or even impossible to quantify [49,50,51] stochastic analysis may offer new insights into aesthetical issues and a basis for their objective evaluation. The stochastic analysis of the examined artworks is performed using the 2D-climacogram (2D-C), a stochastic tool evaluating the degree of variability vs. spatial scale. As case studies, we use multiple images of art paintings depicting human portraits, and seek whether there exist stochastic similarities in the ways the human face has been depicted by various art movements.
2. Quantifying the Variability in Art Painting through the 2D Climacogram
A stochastic computational tool called 2D-C [52,53,54,55,56,57,58] is used to analyze images of art paintings quantifying the variability of the brightness vs. scale in a specific image and in a group of images as well. Here, we refer to spatial (not time) scale, defined as the ratio of the area of k × k adjacent cells (i.e., scale k) that are averaged to form the (scaled) spatial field, over the spatial resolution of the original field (i.e., at scale 1). The term climacogram [59,60] comes from the Greek word κλιμαξ (pronounced: climax meaning scale). It is defined as the (plot of) variance of the averaged process (assuming stationary) versus averaging scale k, and is denoted as γ(k). The climacogram is useful for detecting the long-term change (or else dependence, persistence, clustering) of a process, which emerges particularly in complex systems as opposed to white noise (absence of dependence) of even Markov (i.e., short-term persistence) behavior [61].
In order to obtain a quantitative characterization of the artwork, its image is digitized in 2D and each pixel is assigned a grayscale color intensity (white = 1, black = 0). Assuming that our sample is an area nΔ × nΔ, where n is the number of intervals (e.g., pixels) along each spatial direction and Δ is the discretization unit determined by the image resolution, (e.g., pixel length), the empirical classical estimator of the climacogram for a 2D process can be expressed as:
where the ‘^’ over γ denotes estimation, is the the dimensionless spatial scale, represents a local average of the space-averaged process at scale κ, at grid cell (i, j), and, is the global average of the process of interest. Note that the maximum available scale for this estimator is n/2. The difference between the value in each element and the field mean is raised to the power of 2, since we are mostly interested in the magnitude of the difference rather than its sign. Thus, the climacogram expresses in each scale the diversity in the greyscale intensity among the different elements. In this manner, we may quantify the uncertainty of the brightness intensities at each scale by measuring their spatial variability.
An important property of stochastic processes is the Hurst–Kolmogorov (HK) dynamics (usually known in hydrometeorological processes as Long-Term Persistence, or LTP), which can be summarized by the Hurst parameter as estimated in large scales. This parameter is estimated by minimizing the fitting error of the logarithmic slope of the tail (i.e., the last 50 scales in the presented applications) of the observed (from data through Equation (1)) and the modelled (Equation (2)) climacogram. The isotropic HK process with an arbitrary marginal distribution (e.g., for the Gaussian one, this results in the well-known fractional-Gaussian-noise, as described by Mandelbrot and van Ness [62]), i.e., the power-law decay of variance as a function of scale, is defined for a 1D or 2D process as:
where is the variance at scale k = κΔ, d is the dimension of the process/field (i.e., for a 1D process d = 1, for a 2D field d = 2, etc.), and H is the Hurst parameter (0 < H < 1). For 0 < H < 0.5 the HK process exhibits an anti-persistent behavior, H = 0.5 corresponds to the white noise process, and for 0.5 < H < 1 the process exhibits LTP (clustering). In the case of clustering behavior, due to the non-uniform heterogeneity of the brightness of the painting, the high variability in brightness persists even in large scales. This clustering effect may substantially increase the diversity between the brightness in each pixel of the image, a phenomenon also observed in hydrometeorological processes (such as temperature, precipitation, wind etc.), natural landscapes and music [63].
The algorithm that generates the climacogram in 2D was developed in MATLAB for rectangular images [64]. In particular, for the current analysis, the images are cropped to 400 × 400 pixels, 14.11 cm × 14.11 cm, in 72 dpi (dots per inch). In particular, for the current analysis, the images are cropped to 400 × 400 pixels, 14.11 cm × 14.11 cm, in 72 dpi (dots per inch). The values assigned to each pixel are the grayscale color intensity (white = 1, black = 0) of the image. In Figure 1, we present three images for benchmark image analysis: (a) white noise; (b) image with clustering; and (c) an art painting. In Figure 2, we describe the steps in our analysis, and show how grouped pixels at scales k = 2, 4, 8, 16, 20, 25, 40, 50, 80, 100 and 200, are used to calculate the climacogram in Figure 3. In Figure 3, we also depict the standardized climacogram, which is defined as the ratio , and is also a function of scale k but without having any effect from the marginal variance of the process.

Figure 1.
Benchmark of image analysis; (a) White noise, average brightness 0.5; (b) Image with clustering, average brightness 0.54; (c) Photo of Audrey Hepburn, average brightness 0.57.

Figure 2.
Example of stochastic analysis of 2D picture; steps. Grouped pixels at different scales used to calculate the climacogram; (a) White noise; (b) Image with clustering; (c) Photo.
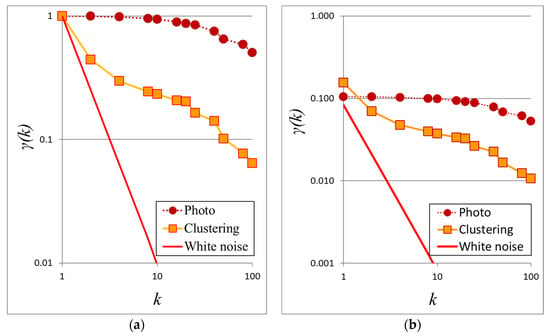
Figure 3.
(a) Climacograms of the benchmark images; (b) Standardized climacograms of the benchmark images.
The presence of clustering is reflected in the climacogram, which shows a marked difference compared to independent pixels as in white noise processes (Figure 3). Specifically, the variance of the clustered images is notably higher than that of white noise at all scales, indicating a greater degree of variability and uncertainty of the process. Likewise, comparing the clustered image and the art painting, the latter has the most pronounced clustering behavior and a higher degree of variability.
3. Stochastic Evaluation in Arts
Art’s functions are vital for our society on multiple levels. A work of art is not only (and perhaps not necessarily) something pleasing to the eye, but also a medium that portrays our emotions. Although each artist’s work contains a unique message, the field of art creates a cultural process; aesthetics: a communication channel between the artist and the observer.
Cartesian rationalism, which was derived from the French philosopher Rene Descartes, does not regard aesthetic quality as an inherent quality of a physical object, but instead as the distinction of mind and nature, paving the way for humans to appreciate the role of their own subjective feelings in determining their aesthetic preferences. Other philosophers, such as Leibniz, believed that there is a norm behind every aesthetic feeling, which we simply do not know yet how to measure [65].
The most common stochastic attribute in natural processes is the long-term persistence behavior or HK-behavior, which is identified in global-scale analyses including billions of records, and in over-centennial timeseries of the most important hydrometeorological processes (i.e., temperature, humidity, wind, solar radiation, river discharge, atmospheric pressure, and precipitation), [58,59], and expressed through the climacogram for large scales as shown in Equation (2). Remarkably, the shape of the dependence structure, as visualized through the climacogram, exhibits similarities among natural processes, having a Markov-type behavior at small scales and a long-term persistence behavior (i.e., a power-law function of scale) at large scales, described by the expression , where q is now a scale-parameter indicative of the transition point between the short-term (roughness) and long-term (persistence) behaviours in the climacogram (Figure 4). The latter behavior can be quantified by the Hurst parameter, which is defined as the semi log-log slope plus one, i.e., H = s/2+1, where s is the slope in logarithmic axes of the climacogram at large scales (as shown in Equation (2)).
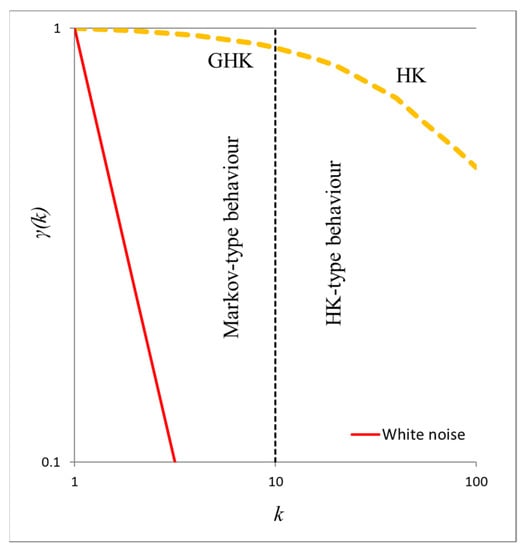
Figure 4.
Illustration of the Hurst-Kolmogorov dynamics model visualized through the climacogram, γ, vs. scale, k, and expanding from micro (GHK behavior) to macro (HK behavior) scales.
Although art is a mix of determinism (e.g., certain rules have to be followed) and stochasticity (e.g., creativity and inspiration), we treat artistic works as a natural process and test whether art paintings share a similar structure of dependence as do various natural processes.
In art paintings portraying human faces, the face is a focus point which condenses the feeling of the painting. In order to evaluate how nature depicts in 2D we first examine the climacogram of photographs of human faces [66,67,68], shown in Figure 5. Then, we analyze portraits from various artistic genres dating from medieval to recent times (data from: [69,70,71,72,73,74,75,76,77]), i.e., of Byzantine art, Renaissance and Baroque, and 20th century modern art. We also analyze the self-portraits of Rembrandt Harmenszoon van Rijn [78] and Pablo Picasso [79] made in different periods of their lives. Each 2D photo and painting is digitized based on a grayscale color intensity and the climacogram is estimated based on the geometric scale rather than the average one (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16). The Hurst parameter is estimated for each image set and shown in Table 1.

Figure 5.
Images of portrait photography. Photos courtesy of Kostas Mountrichas.
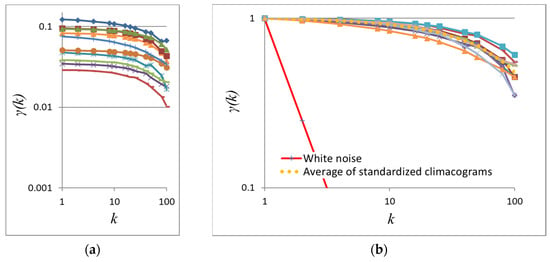
Figure 6.
(a) Climacograms and (b) standardized climacograms of the images in Figure 5 (Hurst parameters ranging from 0.76 for the lower left image to 0.91 for the upper right, averaging to 0.87).

Figure 7.
Images of portrait paintings from the Renaissance and Baroque periods.
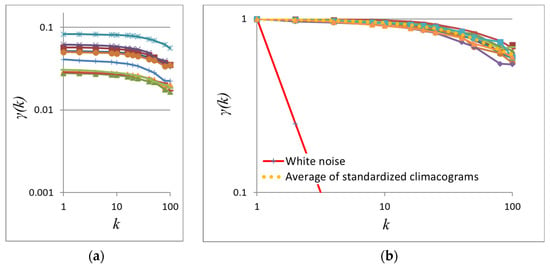
Figure 8.
(a) Climacograms and (b) standardized climacograms of the paintings in Figure 7 (Hurst parameters ranging from 0.90 for the lower left image to 0.94 for the lower right, averaging to 0.92).

Figure 9.
Self-portraits of Rembrandt in chronological order.
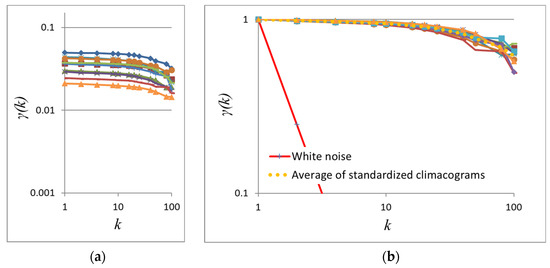
Figure 10.
(a) Climacograms and (b) standardized climacograms of the paintings in Figure 9 (Hurst parameters ranging from 0.87 for the lower right image to 0.95 for the upper left, averaging to 0.92).

Figure 11.
Images of portrait paintings of 20th century art.
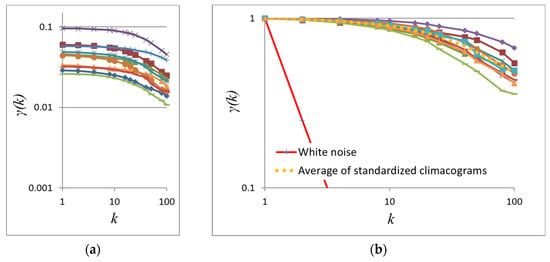
Figure 12.
(a) Climacograms and (b) standardized climacograms of the paintings in Figure 11 (Hurst parameters ranging from 0.88 for the lower left image to 0.93 for the upper left, averaging to 0.90).

Figure 13.
Self-portraits of Pablo Picasso in chronological order.
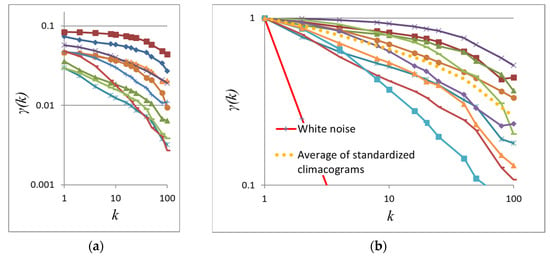
Figure 14.
(a) Climacograms and (b) standardized climacograms of the paintings in Figure 13 (Hurst parameters ranging from 0.73 lower second from the left image to 0.91 lower in the middle, averaging to 0.83).

Figure 15.
Images of portrait paintings of Byzantine art, fresco.
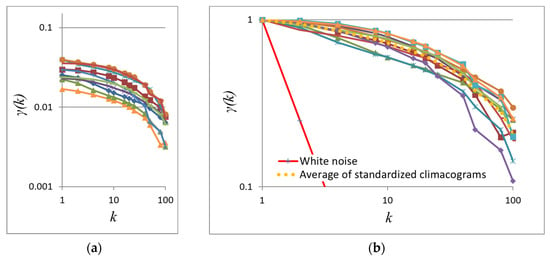
Figure 16.
(a) Climacograms and (b) standardized climacograms of the paintings in Figure 15 (Hurst parameters ranging from 0.72 for the lower left image to 0.86 for the upper right, averaging to 0.79).

Table 1.
Average Hurst parameter H and coefficient of variation of the climacograms g(k) of the exanimated sets.
For each painting, we calculated the coefficient of variation of the original image at scale 1, which, by definition, is the standard deviation of brightness divided by the average. We then calculated the average of all the images of each set. A high value of the coefficient of variation shows that, in each set there is a broad range of brightness in paintings for the same average brightness. The average coefficient of variation of each set is presented in Table 1.
In order to evaluate the different sets, averages of climacograms thereof are plotted (Figure 17a). To quantify the range of fluctuations of the climacograms, for each scale k we calculated the coefficient of variation of all standardized climacograms, g(k). Figure 17b shows the graphs of g(k) vs. k for all examined cases, indicating the range of fluctuations from the average climacogram of each set.
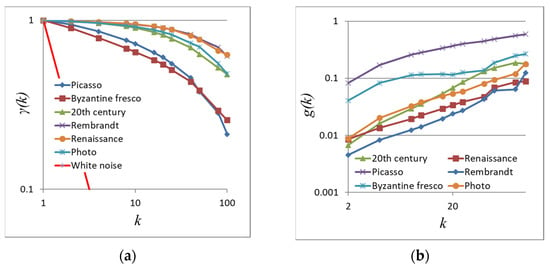
Figure 17.
(a) Average of standardized climacograms of different sets; (b) Coefficient of variation of the climacograms of the different image sets.
Results show an interesting insight. Renaissance/Baroque and Rembrandt’s self-portraits which follow the most naturalistic aesthetic approach, have a strong dependence structure similar to that of photos and of various hydrometeorological processes (estimated H ≈ 0.9). A strong dependence structure is also observed in the portraits of 20th century (estimated H ≈ 0.9) and Picasso’s self-portraits (estimated H ≈ 0.85), yet with a bigger range of fluctuations, indicative of the artistically freer and nonrepresentational approach of modern art. The most interesting insight, however, is that the portraits belonging to the Byzantine art period show a weaker dependence structure (estimated H ≈ 0.8), which is closer to white noise. This attribute seems consistent with the theology of Christian’s Orthodox dogma dictating a specific type of representation of saints and religious figures.
4. Discussion
Since prehistoric art creations, art was related to, and inspired by natural forms. Aristotle said that “art takes nature as its model”, and “…not only imitates nature, but also completes its deficiencies” [80]. Furthermore, Plato connected arts with ideas, the soul and the idealistic expression [81,82].
Around the 20th century, artists embraced an alternative way of expression by focusing more on modern society’s habits and deviating from naturalistic themes and related representation. Even more, artists then found Nature’s complexity obsolete. Paul Klee noted that “Nature is garrulous to the point of confusion, let the artist be truly taciturn.” [83]. One may argue however that the uncertainty within ourselves that drives all forms of art is the same inherent uncertainty of nature that was used subconsciously as inspiration. If this is true, then we should be able to find stochastic similarities between art projects and natural processes imprinted in the estimated variability vs. scale.
The results of this study provide grounds to this hypothesis as patterns can be observed in the dependence structure in photographs and portraits of Renaissance/Baroque which represent the most naturalistic approach, having similar moderate structure (photo, average H ≈ 0.87; Renaissance/Baroque, average H ≈ 0.92). A similar Hurst parameter was estimated by Hurst in his pioneering work on the stage of the river Nile [84,85,86] and, additionally, in global-scale analyses of the long annual records of key hydrometeorological processes such as temperature and wind speed as well as of small-scale processes recorded in the laboratory such as grid-turbulence and turbulent jets [59]. An overall Hurst parameter (H) equal to 0.9 is observed in all hydrometeorological processes (after adjusting for bias; a task that is often neglected in stochastic analysis [87,88,89]).
Patterns can also be observed in the art portraits of 20th century yet with a bigger range of fluctuation as modern artists wanted to express their ‘own’ view of nature away from what they perceived as “nature’s monotony” [90,91]. Interestingly, though, although the aesthetic means employed are indeed markedly different from older naturalistic paintings, the stochastic variability of modern art portraits is still on average close to the one found both in the most naturalistic paintings and in natural processes itself, revealing an overall Hurst parameter (H) equal to 0.9.
Another related validation is the evaluation of self-portraits during the lifetime of Rembrandt’s and Picasso. Rembrandt’s works exhibit stochastic similarities and a strong dependence structure (average H = 0.92) whereas Picasso’s self-portraits show a wider range of fluctuation (Figure 17b).
Sant Gregory of Nyssa (Άγιος Γρηγόριος Νύσσης) (died c. 395 AD) describes how the creation of Byzantine art is connected with the spirituality of the artist “man is the painter of his life, creator of paintings is artists’ motive”«της ιδίας έκαστος ζωής εστί ζωγράφος, τεχνίτης δε της [ζωγραφικής] δημιουργίας ταύτης εστίν η προαίρεσις» [92] Byzantine art, is a religious art serving the purposes of the Christian’s Orthodox dogma. An interesting note is that Byzantine art portraits correspond to a weaker dependence structure (0.7 < H < 0.85) than that of the other genres, with wide range of fluctuation at small scales and small range of fluctuation at large scales, closer to white noise. This might be explained considering that these paintings depict religious figures being in divine states of mine, often praying [93,94]. The meaning of pray in Orthodox dogma is described in one of the most important theological books of Orthodox, Philokalia (Φιλοκαλία) [95], which contains the writings of the Eastern Fathers from the fourth to the fifteenth centuries. In this work, Saint Nilus of Sinai (Άγιος Νείλος ο Σιναΐτης) (died c. 430 AD), teaches that the mind must be “deaf and mute during prayer” «Aγωνίσου να κρατάς το νού σου την ώρα της προσευχής κουφό και άλαλο.» and “when you pray, do not accept any form or shape…” «Μην επιδιώκεις να δεχτείς την ώρα της προσευχής με κανένα τρόπο μορφή ή σχήμα». The identified stochastic structure corresponds to this theology as this ideal of religious figures experiencing a divine humbling experience is better delivered with weaker dependence structures.
5. Conclusions
In recent years, artificial intelligence processes and mathematical computational tools have been used to develop methods for classification and evaluation of aesthetics. Scale-variant methods similar to the presented stochastic analysis have also been used, but they usually include very complex processes and algorithms not easily understood by non-experts.
With the presented 2D-C methodology quantifying the brightness’s variability over scales of pixels, we can observe stochastic patterns among different groups of art paintings. In this work, we have focused on paintings and photos depicting the human face. We identified dependence structures similar to that of natural processes, with an average H ≈ 0.9, in photographs of faces, as well as in portraits belonging to the Renaissance/Baroque period and Rembrandt’s self-portraits. Modern art portraits and Picasso’s portraits also have an average H ≈ 0.9 implying underlining strong dependence structures, but showing a wider range of fluctuations indicative of the pursuit of freer artistic expression during these years. On the contrary, the stricter dogma-inspired Byzantine figures exhibit an overall weaker dependence structure (average H ≈ 0.8) and the smaller coefficient of variation (0.379) among the other sets.
These findings suggest that the presented methodology can capture the interrelation between the stochastic expression of the art paintings and the philosophical issues they want to describe (desideratum). This aspect is encouraging for the use of stochastics in the analysis of art paintings and their relation to wider philosophical and cultural issues.
Author Contributions
Conceptualization, G.-F.S.; methodology, G.-F.S. and P.D.; software, P.D.; validation, G.-F.S.; formal analysis, G.-F.S.; investigation, G.-F.S.; resources, G.-F.S.; data curation, G.-F.S.; writing—original draft preparation, G.-F.S., and P.D.; writing—review and editing, T.I. and D.K.; visualization, G.-F.S.; supervision, D.K.; project administration, G.-F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
We thank the editors of Heritage-MDPI for the invitation of this paper and the processing of the paper, as well as one anonymous reviewer for comments that helped improve and enrich the manuscript and a second anonymous reviewer for the enthusiastic review.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berlyne, D.E. Reviewed Work: Studies in the New Experimental Aesthetics: Steps toward an Objective Psychology of Aesthetic Appreciation. J. Aesthet. Art Crit. 1975, 34, 86–87. [Google Scholar]
- Fayn, K.; Silvia, P.J.; Erbas, Y.; Tiliopoulos, N.; Kuppens, P. Nuanced aesthetic emotions: Emotion differentiation is related to knowledge of the arts and curiosity. Cogn. Emot. 2017, 32, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Mulkay, M.; Chaplin, E. Aesthetics and the Artistic Career: A Study of Anomie in Fine-Art Painting. Sociol. Q. 1982, 23, 117–138. [Google Scholar] [CrossRef]
- Gordon, D.A. Methodology in the Study of Art Evaluation. J. Aesthet. Art Crit. 1952, 10, 338. [Google Scholar] [CrossRef]
- Bourgeon-Renault, D. Evaluating Consumer Behaviour in the Field of Arts and Culture Marketing. Int. J. Arts Manag. 2000, 3, 4–18. [Google Scholar]
- Lombardi, T.E. The Classification of Style in Fine-Art Painting, School of Computer Science and Information Systems; Pace University: New York, NY, USA, 2005. [Google Scholar]
- Thomasson, A.L. The Ontology of Art and Knowledge in Aesthetics. J. Aesthet. Art Crit. 2005, 63, 221–229. [Google Scholar] [CrossRef]
- Swami, V. Context matters: Investigating the impact of contextual information on aesthetic appreciation of paintings by Max Ernst and Pablo Picasso. Psychol. Aesthet. Creat. Arts 2013, 7, 285–295. [Google Scholar] [CrossRef]
- Winston, A.S.; Cupchik, G.C. The evaluation of high art and popular art by naive and experienced viewers. Visual Arts Research 1992, 18, 1–14. [Google Scholar]
- Chiotinis, Μ. Beauty in Architecture As an Experience of Ontological Donation; National Technichal University of Athens: Athens, Greece, 2018. [Google Scholar] [CrossRef]
- Augello, A.; Infantino, I.; Maniscalco, U.; Pilato, G.; Rizzo, R.; Vella, F. Robotic intelligence and computational creativity. Encycl. Semantic Comput. Robot. Intell. 2018, 2, 1850011. [Google Scholar] [CrossRef]
- Carbonneau, M.-A.; Cheplygina, V.; Granger, E.; Gagnon, G. Multiple Instance Learning: A Survey of Problem Characteristics and Applications. Pattern Recognit. 2018, 77, 329–353. [Google Scholar] [CrossRef]
- Castellano, G.; Vessio, G. Towards a Tool for Visual Link Retrieval and Knowledge Discovery in Painting Datasets. In Digital Libraries: The Era of Big Data and Data Science; Ceci, M., Ferilli, S., Poggi, A., Eds.; IRCDL 2020, Communications in Computer and Information Science; Springer: Cham, Switzerland, 2021; Volume 1177. [Google Scholar]
- Collomosse, J.; Bui, T.; Wilber, M.; Fang, C.; Jin, H. Sketching with Style: Visual Search with Sketches and Aesthetic Context. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2679–2687. [Google Scholar]
- Jboor, N.H.; Belhi, A.; Al-Ali, A.K.; Bouras, A.; Jaoua, A. Towards an Inpainting Framework for Visual Cultural Heritage. In Proceedings of the 2019 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 9–11 April 2019; pp. 602–607. [Google Scholar]
- Correia, J.; Machado, P.; Romero, J.; Martins, P. Amílcar Cardoso F. Breaking the Mould An Evolutionary Quest for Innovation Through Style Change. In Computational Creativity. Computational Synthesis and Creative Systems; Veale, T., Cardoso, F., Eds.; Springer: Cham, Swizterland, 2019. [Google Scholar]
- Neumann, A.; Alexander, B.; Neumann, F. Evolutionary Image Transition and Painting Using Random Walks. Evol. Comput. 2020, 28, 643–675. [Google Scholar] [CrossRef] [PubMed]
- Carballal, A.; Santos, A.; Romero, J.; Machado, J.T.A.P.; Correia, J.; Castro, L. Distinguishing paintings from photographs by complexity estimates. Neural Comput. Appl. 2018, 30, 1957–1969. [Google Scholar] [CrossRef]
- De Caro, L.; Matricciani, E.; Fanti, G. Imaging Analysis and Digital Restoration of the Holy Face of Manoppello—Part II. Heritage 2018, 1, 349–364. [Google Scholar] [CrossRef]
- Shen, J. Stochastic modeling western paintings for effective classification. Pattern Recognit. 2009, 42, 293–301. [Google Scholar] [CrossRef]
- Florea, C.; Gieseke, F. Artistic movement recognition by consensus of boosted SVM based experts. J. Vis. Commun. Image Represent. 2018, 56, 220–233. [Google Scholar] [CrossRef]
- Tan, W.R.; Chan, C.S.; Aguirre, H.E.; Tanaka, K. Ceci n’est pas une pipe: A deep convolutional network for fine-art paintings classification. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3703–3707. [Google Scholar]
- Van Noord, N.; Postma, E. Learning scale-variant and scale-invariant features for deep image classification. Pattern Recognit. 2017, 61, 583–592. [Google Scholar] [CrossRef]
- Tan, W.R.; Chan, C.S.; Aguirre, H.E.; Tanaka, K. ArtGAN: Artwork synthesis with conditional categorical GANs. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3760–3764. [Google Scholar]
- Fuchs, R.; Hauser, H. Visualization of Multi-Variate Scientific Data. Comput. Graph. Forum 2009, 28, 1670–1690. [Google Scholar] [CrossRef]
- Lecoutre, A.; Negrevergne, B.; Yger, F. Recognizing Art Style Automatically in Painting with Deep Learning. JMLR Workshop Conf. Proc. 2017, 80, 1–17. [Google Scholar]
- Cetinic, E.; Lipic, T.; Grgic, S. Fine-tuning Convolutional Neural Networks for fine art classification. Expert Syst. Appl. 2018, 114, 107–118. [Google Scholar] [CrossRef]
- Cetinic, E.; Lipic, T.; Grgic, S. Learning the Principles of Art History with convolutional neural networks. Pattern Recognit. Lett. 2020, 129, 56–62. [Google Scholar] [CrossRef]
- Babak, S.; Elgammal, A. Large-Scale Classification of Fine-Art Paintings: Learning the Right Metric on the Right Feature. Int. J. Digit. Art Hist. 2016, 2, 70–93. [Google Scholar]
- Sandoval, C.; Pirogova, E.; Lech, M. Two-Stage Deep Learning Approach to the Classification of Fine-Art Paintings. IEEE Access 2019, 7, 41770–41781. [Google Scholar] [CrossRef]
- Wang, Z.; Lian, J.; Song, C.; Zhang, Z.; Zheng, W.; Yue, S.; Ji, S. SAS: Painting Detection and Recognition via Smart Art System with Mobile Devices. IEEE Access 2019, 7, 135563–135572. [Google Scholar] [CrossRef]
- Cetinic, E.; Lipic, T.; Grgic, S. A Deep Learning Perspective on Beauty, Sentiment, and Remembrance of Art. IEEE Access 2019, 7, 73694–73710. [Google Scholar] [CrossRef]
- Hayn-Leichsenring, G.U.; Lehmann, T.; Redies, C. Subjective Ratings of Beauty and Aesthetics: Correlations With Statistical Image Properties in Western Oil Paintings. i-Perception 2017, 8. [Google Scholar] [CrossRef] [PubMed]
- Sigaki, H.Y.D.; Perc, M.; Ribeiro, H.V. History of art paintings through the lens of entropy and complexity. Proc. Natl. Acad. Sci. USA 2018, 115, E8585–E8594. [Google Scholar] [CrossRef] [PubMed]
- Oomen, E. Classification of Painting Style with Transfer Learning. Master’s Thesis, Tilburg University, Tilburg, The Netherlands, 2018. [Google Scholar]
- Sabatelli, M.; Kestemont, M.; Daelemans, W.; Geurts, P. Deep Transfer Learning for Art Classification Problems; Springer Nature: London, UK, 2019; pp. 631–646. [Google Scholar]
- Carneiro, G.; da Silva, N.P.; Del Bue, A.; Costeira, J.P. Artistic Image Classification: An Analysis on the PRINTART Database. In Computer Vision—ECCV 2012; Fitzgibbon, A., Lazebnik, S., Perona, P., Sato, Y., Schmid, C., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7575. [Google Scholar]
- Crowley, E.J. Visual Recognition in Art using Machine Learning. Ph.D. Thesis, University of Oxford, Oxford, UK, 2016. [Google Scholar]
- Jafarpour, S.; Polatkan, G.; Brevdo, E.; Hughes, S.; Brasoveanu, A.; Daubechies, I. Stylistic Analysis of Paintings Usingwavelets and Machine Learning. In Proceedings of the 2009 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1220–1224. [Google Scholar]
- Johnson, C.R.; Hendriks, E.; Berezhnoy, I.J.; Brevdo, E.; Hughes, S.M.; Daubechies, I.; Li, J.; Postma, E.; Wang, J.Z. Image processing for artist identification. IEEE Signal Process. Mag. 2008, 25, 37–48. [Google Scholar] [CrossRef]
- Yiyu, H.; Jongweon, K. Art Painting Identification using Convolutional Neural Network. Int. J. Appl. Eng. Res. 2017, 12, 532–539. [Google Scholar]
- Li, C.; Chen, T. Aesthetic Visual Quality Assessment of Paintings. IEEE J. Sel. Top. Signal Process. 2009, 3, 236–252. [Google Scholar] [CrossRef]
- Puthenputhussery, A.; Liu, Q.; Liu, C. Color multi-fusion fisher vector feature for fine art painting categorization and influence analysis. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–9. [Google Scholar]
- Galanter, P. Computational Aesthetic Evaluation: Past and Future. In Computers and Creativity; McCormack, J., d’Inverno, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Koutsoyiannis, D. HESS Opinions “A random walk on water”. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk; National Technical University of Athens: Athens, Greece, 2020; 330p. [Google Scholar]
- Dimitriadis, P. Hurst-Kolmogorov dynamics in hydrometeorological processes and in the microscale of turbulence. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2017. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D.; Tzouka, K. Predictability in dice motion: How does it differ from hydrometeorological processes? Hydrol. Sci. J. 2016, 61, 1611–1622. [Google Scholar] [CrossRef]
- Christofides, A.; Efstratiadis, A.; Koutsoyiannis, D.; Sargentis, G.-F.; Hadjibiros, K. Resolving conflicting objectives in the management of the Plastiras Lake: Can we quantify beauty? Hydrol. Earth Syst. Sci. 2005, 9, 507–515. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Hadjibiros, K.; Christofides, A. Plastiras Lake: The impact of water level on the aesthetic value of the landscape. In Proceedings of the 9th International Conference on Environmental Science and Technology, Rhodes, Greece, 1–3 September 2005. [Google Scholar]
- Sargentis, G.-F.; Hadjibiros, K.; Papagiannakis, I.; Papagiannakis, E. Plastiras Lake: Influence of the relief on the revelation of the water presence. In Proceedings of the 9th International Conference on Environmental Science and Technology, Rhodes, Greece, 1–3 September 2005. [Google Scholar]
- Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installa-tions and Civil Works. Energies 2019, 12, 2817. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Koutsoyiannis, D. Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage 2020, 3, 283–305. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Iliopoulou, T.; Sigourou, S.; Dimitriadis, P.; Koutsoyiannis, D. Evolution of Clustering Quantified by a Stochastic Method—Case Studies on Natural and Human Social Structures. Sustainability 2020, 12, 7972. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Ioannidis, R.; Iliopoulou, T.; Dimitriadis, P.; Koutsoyiannis, D. Landscape Planning of Infrastructure through Focus Points’ Clustering Analysis. Case Study: Plastiras Artificial Lake (Greece). Infrastructures 2021, 6, 12. [Google Scholar] [CrossRef]
- Ioannidis, R.; Dimitriadis, P.; Meletopoulos, I.T.; Sargentis, G.-F.; Koutsoyiannis, D. Investigating the spatial characteristics of GIS visibility analyses and their correlation to visual impact perception with stochastic tools. In EGU General Assembly Conference Abstracts; European Geosciences Union: Vienna, Austria, 2020; p. 18212. [Google Scholar]
- Manta, E.; Ioannidis, R.; Sargentis, G.-F.; Efstratiadis, A. Aesthetic Evaluation of Wind Turbines in Stochastic Setting: Case Study of Tinos Island, Greece. In European Geosciences Union General Assembly 2020, Geophysical Research Abstracts; EGU2020-5484; European Geosciences Union: Vienna, Austria, 2020; Volume 22. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Ioannidis, R.; Meletopoulos, I.T.; Dimitriadis, P.; Koutsoyiannis, D. Aesthetical issues with stochastic evaluation. In European Geosciences Union General Assembly 2020, Geophysical Research Abstracts; EGU2020-19832; European Geosciences Union: Vienna, Austria, 2020; Volume 22. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Encolpion of stochastics: Fundamentals of Stochastic Processes; National Technical University of Athens: Athens, Greece, 2013; 12p. [Google Scholar]
- Koutsoyiannis, D. Climacogram-Based Pseudospectrum: A Simple Tool to Assess Scaling Properties. In European Geosciences Union General Assembly 2013, Geophysical Research Abstracts; EGU2013-4209; European Geosciences Union: Vienna, Austria, 2013; Volume 15. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst–Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Iliopoulou, T.; Ioannidis, R.; Koutsoyiannis, D. Stochastic investigation of the Hurst-Kolmogorov behaviour in arts. In European Geosciences Union General Assembly 2018, Geophysical Research Abstracts; EGU2018-17082; European Geosciences Union: Vienna, Austria, 2018; Volume 20. [Google Scholar]
- Dimitriadis, P.; Tzouka, K.; Koutsoyiannis, D.; Tyralis, H.; Kalamioti, A.; Lerias, E.; Voudouris, P. Stochastic investigation of long-term persistence in two-dimensional images of rocks. Spat. Stat. 2019, 29, 177–191. [Google Scholar] [CrossRef]
- Beardsley, M.C. Aesthetics from Classical Greece to the Present: A Short History; University of Alabama Press: Tuscaloosa, AL, USA, 1975. [Google Scholar]
- Portrait Photographers. Available online: https://fixthephoto.com/best-portrait-photographers.html (accessed on 2 January 2021).
- Top 10 Photographers. Available online: https://www.bwvision.com/top-10-photographers/ (accessed on 2 January 2021).
- The 10 Most Famous Portrait Photographers in the World. Available online: https://blazepress.com/2014/12/10-famous-portrait-photographers-world/ (accessed on 2 January 2021).
- Painting. Available online: https://en.wikipedia.org/wiki/Painting (accessed on 2 January 2021).
- Portrait Painting. Available online: https://en.wikipedia.org/wiki/Portrait_painting (accessed on 2 January 2021).
- Speranzas Spyridon (Byzantine Artist). Available online: https://paletaart.wordpress.com/ (accessed on 2 January 2021).
- Cretan School. Available online: https://en.wikipedia.org/wiki/Cretan_School (accessed on 2 January 2021).
- Italian Renaissance Painting. Available online: https://en.wikipedia.org/wiki/Italian_Renaissance_painting (accessed on 2 January 2021).
- Albrecht Dürer. Available online: https://en.wikipedia.org/wiki/Albrecht_D%C3%BCrer (accessed on 2 January 2021).
- Titian. Available online: https://en.wikipedia.org/wiki/Titian (accessed on 2 January 2021).
- Impressionism. Available online: https://en.wikipedia.org/wiki/Impressionism (accessed on 2 January 2021).
- 20th-Century Art. Available online: https://en.wikipedia.org/wiki/20th-century_art (accessed on 2 January 2021).
- Rembrandt. Available online: https://en.wikipedia.org/wiki/Rembrandt (accessed on 2 January 2021).
- Pablo Picasso Self-Portraits. Available online: https://mymodernmet.com/pablo-picasso-self-portraits/ (accessed on 2 January 2021).
- John, B.; Patrick, A. (Eds.) Aristoteles, Poetics, Aριστοτέλης, Ποιητική 1447a. In Translated and with a Commentary by George Whalley; McGill-Queen’s University Press: London, UK, 1997; pp. 19–23. [Google Scholar]
- Beardsley, M.C.; Tatarkiewicz, W.; Czerniawski, A.; Czerniawski, A.; Harrell, J.; Montgomery, R.M.; Kisiel, C.A.; Besemeres, J.F.; Petsch, D. Tatarkiewicz’ History of Aesthetics. J. Hist. Ideas 1976, 37, 549. [Google Scholar] [CrossRef]
- Sargentis, G.-F. Use and Technical Aspects of Materials in Sculpture. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2005. [Google Scholar] [CrossRef]
- Klee, P. Diary entry (Munich, 1909), # 857. In The Diaries of Paul Klee, 1898–1918; University of California Press: Berkeley, CA, USA, 1968; p. 236. [Google Scholar]
- Hurst, H.E. The Problem Of Long-Term Storage in Reservoirs. Int. Assoc. Sci. Hydrol. Bull. 1956, 1, 13–27. [Google Scholar] [CrossRef]
- Cohn, T.A.; Lins, H.F. Nature’s style: Naturally trendy. Geophys. Res. Lett. 2005, 32, L23402. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods/Prévision du débit du Nil à moyen terme: Une comparaison de méthodes stochastiques et déterministes. Hydrol. Sci. J. 2008, 53, 142–164. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. The mode of the climacogram estimator for a Gaussian Hurst-Kolmogorov process. J. Hydroinform. 2019, 22, 160–169. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef]
- Ioannidis, R.; Dimitriadis, P.; Sargentis, G.-F.; Frangedaki, E.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic similarities between natural processes and art: Application in the analysis and optimization of landscape aesthetics of renewable energy and civil works. In Geophysical Research Abstracts; European Geosciences Union: Vienna, Austria, 2019; Volume 21. [Google Scholar]
- Apollinaire, G. Les Peintres Cubistes: Méditations Esthétiques; Tous Les Arts: Paris, France, 1913. [Google Scholar]
- Sargentis, G.-F. Aesthetic Element in Water, Hydraulic Works and Dams. Master’s Thesis, National Technical University of Athens, Athens, Greece, 1998. [Google Scholar] [CrossRef]
- Sant Gregory of Nyssa (Άγιος Γρηγόριος Νύσσης), About Christian Perfection (Περί Χριστιανικής Τελειότητος), Tertios, Katerini. 1980. Available online: https://en.wikipedia.org/wiki/Gregory_of_Nyssa (accessed on 4 February 2021).
- Gerontos Paisiou Agioritou (Γέροντος Παϊσίου Aγιορείτου), For prayer (Περί Προσευχής), Ieron Isichastirio Evangelistis Iwannis o Theologos (Ιερόν Hσυχαστήριο «Ευαγγελιστής Ιωάννης ο Θεολόγος»), Sourot. 2012. Available online: https://www.politeianet.gr/ekdotis/ieron-isuchastirion-euaggelistis-ioannis-theologos-2852 (accessed on 4 February 2021).
- Holy Bible, New Testament, Mathew (Κατά Ματθαίον) 22,37; Mark (Κατά Μάρκον) 12,30; Luke (Κατά Λουκά) 10,27. Available online: http://www.apostoliki-diakonia.gr/bible/bible.asp?contents=new_testament/contents.asp&main= (accessed on 4 February 2021).
- Philocalia (Φιλοκαλία), edt. Ioannou Mavrogordatou (Ιωάννου Μαυρογορδάτου), Venice 1782, Greek Translation. Available online: https://greekdownloads.wordpress.com/φιλοκαλία/ (accessed on 2 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).