Structural Health Monitoring in Historical Buildings: A Network Approach †
Abstract
:1. Introduction
2. Past Related Work
3. System Definition
3.1. Arduino
3.2. Wireless SD Shield
3.3. XBee Modules
3.4. Accelerometer
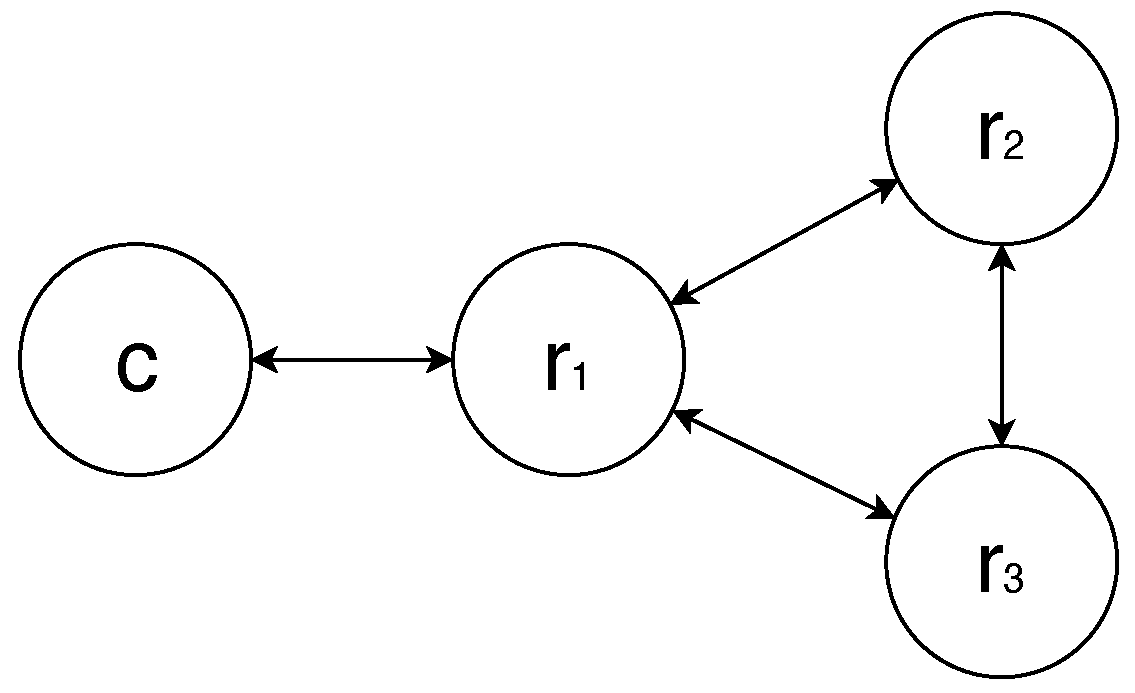
3.5. WSN Node
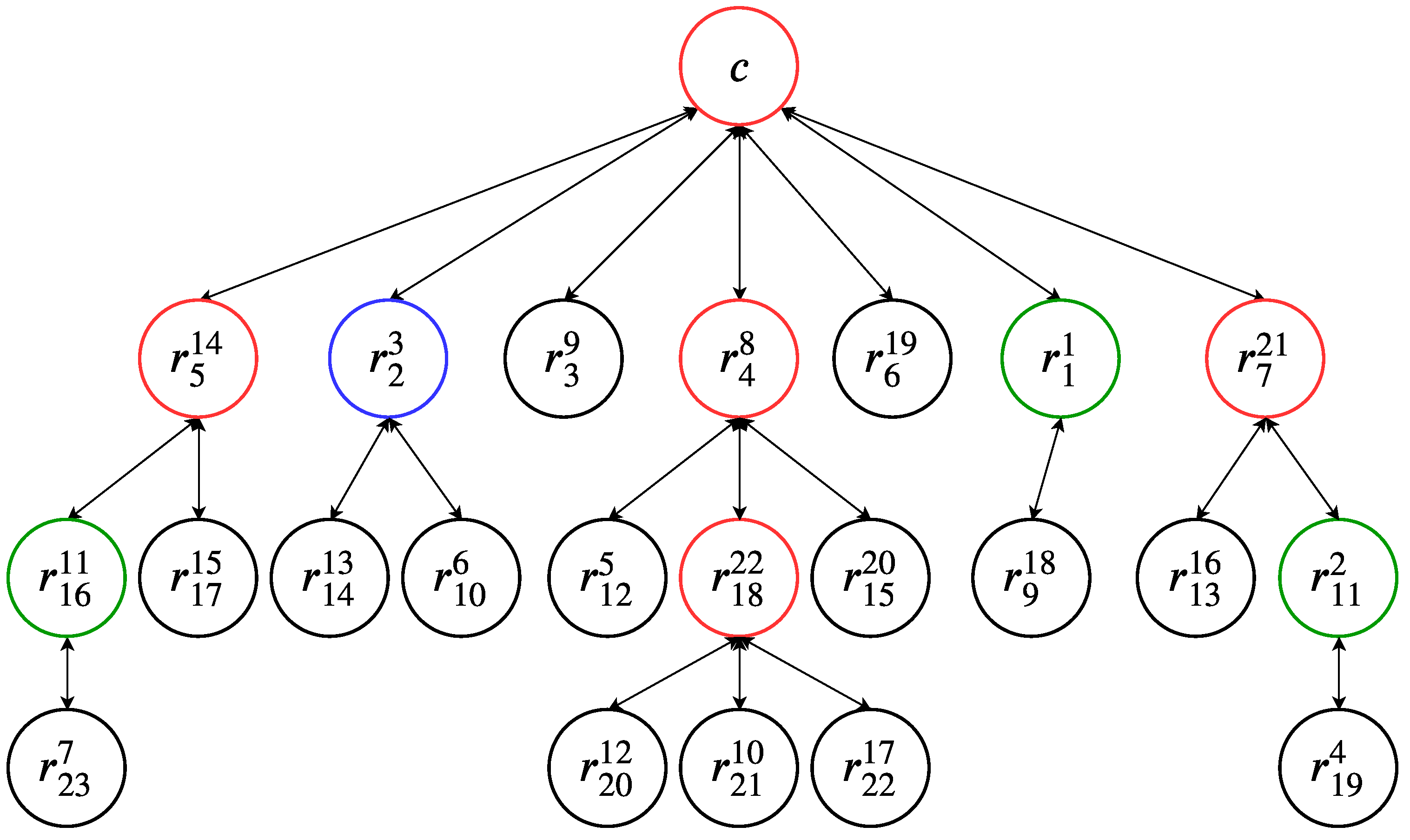
4. Synchronization of the WSN
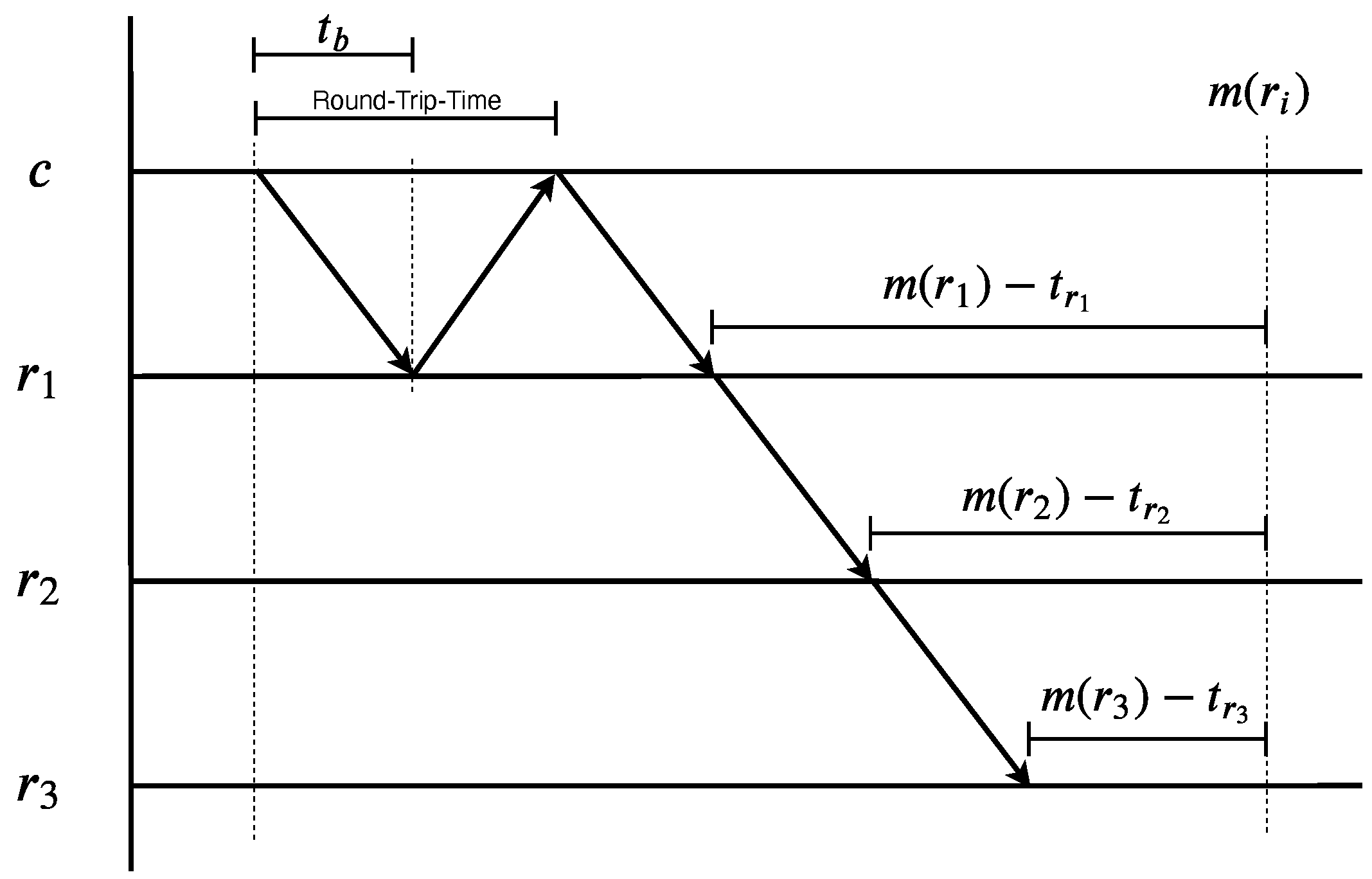
4.1. Synchronization Model
4.2. The Synchronization Algorithm
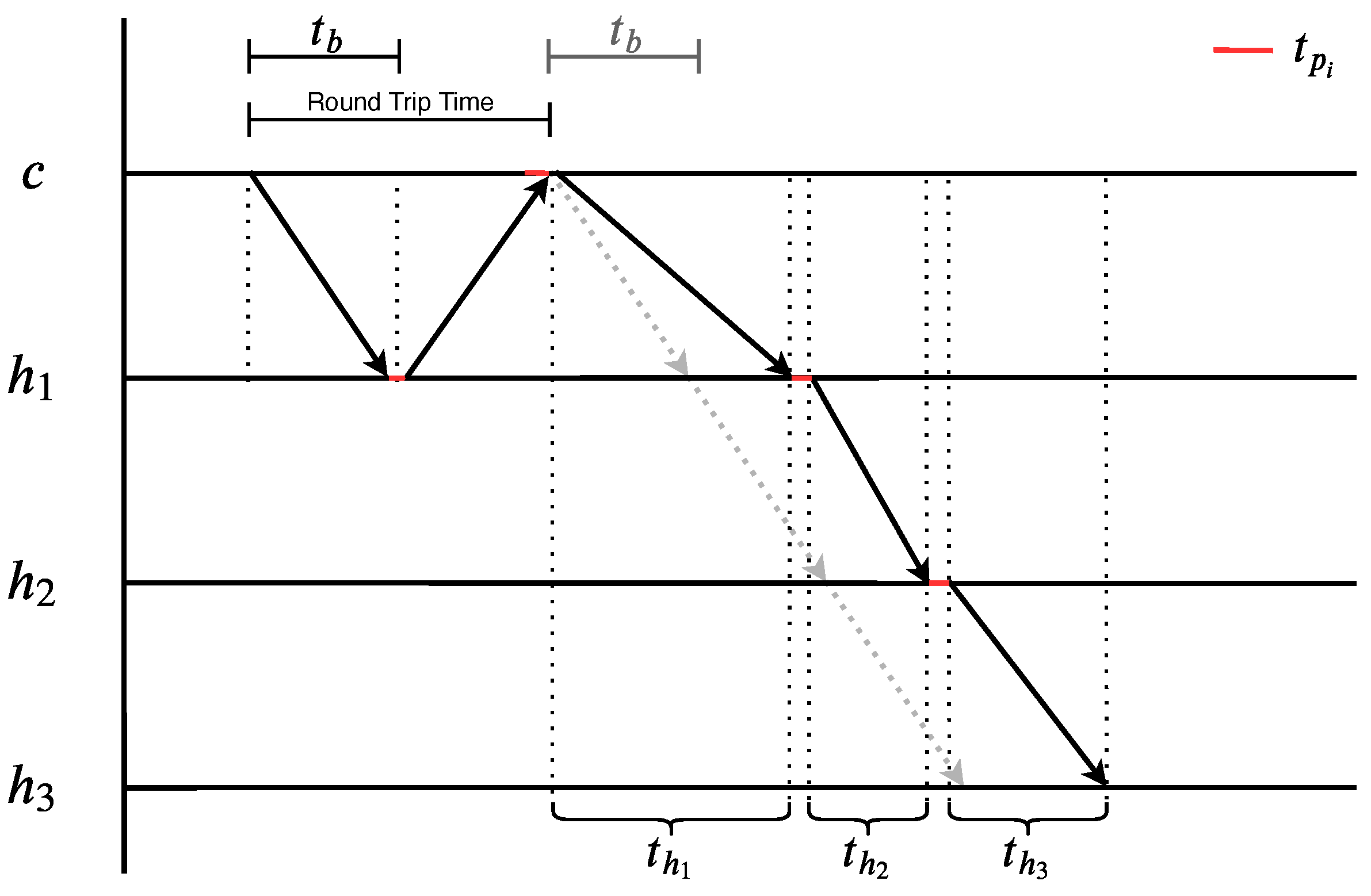
4.3. Synchronized Measurement Initialization
5. Experiments and Results
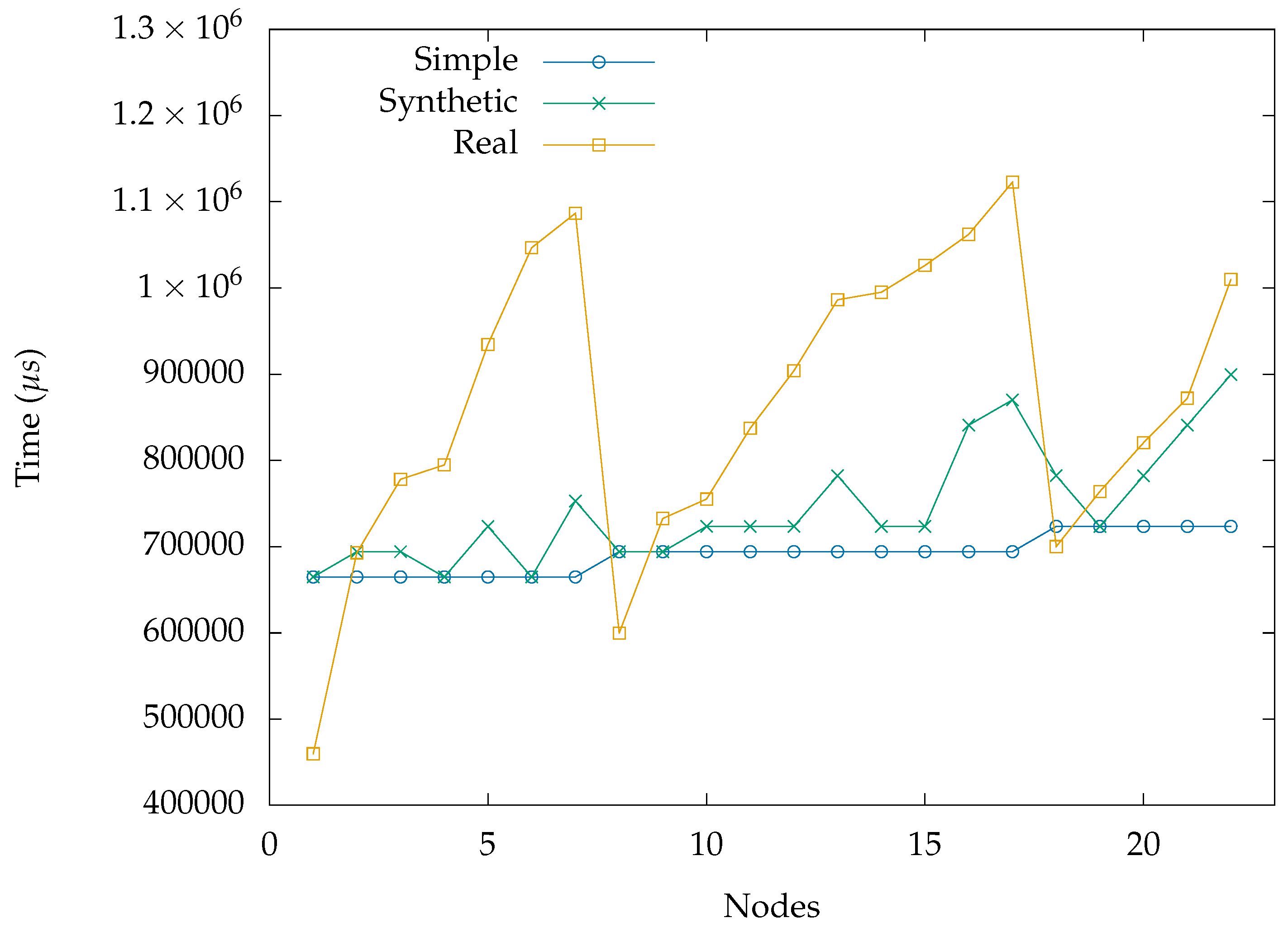
5.1. Multiple Synchronizations and Interrupt Events
5.2. Remote Synchronization Evaluation on Per-Hop-Basis Time-Stamping
6. Discussion
7. Conclusions and Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| SHM | Structural Health Monitoring |
| LAN | Local Area Network |
| WSN | Wireless Sensor Network |
| CSMA/CA | Carrier Sense Multiple Access/Collision Avoidance |
| MLE | Maximum Likelihood Estimation |
| FTSP | Flooding Time Synchronization Protocol |
| TTME | Two-Way Time Message Exchange |
| RTS | Ready To Send |
| CTS | Clear To Send |
References
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 365, 303–315. [Google Scholar] [CrossRef]
- Janapati, V.; Kopsaftopoulos, F.; Li, F.; Lee, S.J.; Chang, F.K. Damage detection sensitivity characterization of acousto-ultrasound-based structural health monitoring techniques. Struct. Health Monit. 2016, 15, 143–161. [Google Scholar] [CrossRef]
- Deivasigamani, A.; Daliri, A.; Wang, C.; John, S. A review of passive wireless sensors for structural health monitoring. Mod. Appl. Sci. 2013, 7, 57–76. [Google Scholar] [CrossRef]
- Jo, H.; Rice, J.A.; Spencer, B.F., Jr.; Nagayama, T. Development of high-sensitivity accelerometer board for structural health monitoring. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2010; International Society for Optics and Photonics: San Diego, CA, USA, 2010; Volume 7647, p. 764706. [Google Scholar]
- Rashid, R.A.; Ahmad, A.G. Overview of maintenance approaches of historical buildings in Kuala Lumpur–a current practice. Procedia Eng. 2011, 20, 425–434. [Google Scholar] [CrossRef] [Green Version]
- Celebi, M. Seismic Instrumentation of Buildings (with Emphasis on Federal Buildings); Technical Report; Citeseer: Menlo Park, CA, USA, 2002. [Google Scholar]
- Ishikawa, K.I.; Mita, A. Time synchronization of a wired sensor network for structural health monitoring. Smart Mater. Struct. 2007, 17, 015016. [Google Scholar] [CrossRef] [Green Version]
- Akyildiz, I.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef] [Green Version]
- Oikonomou, K.; Koufoudakis, G.; Kavvadia, E.; Chrissikopoulos, V. A wireless sensor network innovative architecture for ambient vibrations structural monitoring. In Key Engineering Materials; Trans Tech Publ.: Zurich, Switzerland, 2015; Volume 628, pp. 218–224. [Google Scholar]
- Seah, W.K.; Eu, Z.A.; Tan, H.P. Wireless sensor networks powered by ambient energy harvesting (WSN-HEAP)-Survey and challenges. In Proceedings of the IEEE 2009 1st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace & Electronic Systems Technology, Aalborg, Denmark, 17–20 May 2009; pp. 1–5. [Google Scholar]
- Shaikh, F.K.; Zeadally, S. Energy harvesting in wireless sensor networks: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 55, 1041–1054. [Google Scholar] [CrossRef]
- Tokognon, C.A.; Gao, B.; Tian, G.Y.; Yan, Y. Structural health monitoring framework based on Internet of Things: A survey. IEEE Internet Things J. 2017, 4, 619–635. [Google Scholar] [CrossRef]
- Orenday-Tapia, E.E.; Pacheco-Martínez, J.; Padilla-Ceniceros, R.; López-Doncel, R.A. In situ and nondestructive characterization of mechanical properties of heritage stone masonry. Environ. Earth Sci. 2018, 77, 286. [Google Scholar] [CrossRef]
- Bezas, K.; Komianos, V.; Oikonomou, K.; Koufoudakis, G.; Tsoumanis, G. Structural Health Monitoring in Historical Buildings Using A Low Cost Wireless Sensor Network. In Proceedings of the 2019 South Eastern European Design Automation, Computer Engineering, Computer Networks and Social Media Conference (SEEDA-CECNSM), Piraeus, Greece, 20–22 September 2019. [Google Scholar]
- De Stefano, A.; Matta, E.; Clemente, P. Structural health monitoring of historical heritage in Italy: Some relevant experiences. J. Civ. Struct. Health Monit. 2016, 6, 83–106. [Google Scholar] [CrossRef]
- De Stefano, A.; Clemente, P. SHM on historical heritage. Robust methods to face large uncertainties. In Proceedings of the 1st International Conference on Structural Condition Assessment, Monitoring and Improvement, Perth, Australia, 12–14 December 2005; pp. 12–14. [Google Scholar]
- Boscato, G.; Dal Cin, A.; Russo, S.; Sciarretta, F. SHM of historic damaged churches. In Advanced Materials Research; Trans Tech Publ.: Zurich, Switzerland, 2014; Volume 838, pp. 2071–2078. [Google Scholar]
- Gattulli, V.; Lepidi, M.; Potenza, F. Dynamic testing and health monitoring of historic and modern civil structures in Italy. Struct. Monit. Maint. 2016, 3, 71. [Google Scholar] [CrossRef]
- Pierdicca, A.; Clementi, F.; Isidori, D.; Concettoni, E.; Cristalli, C.; Lenci, S. Numerical model upgrading of a historical masonry palace monitored with a wireless sensor network. Int. J. Mason. Res. Innov. 2016, 1, 74–98. [Google Scholar] [CrossRef]
- Noel, A.B.; Abdaoui, A.; Elfouly, T.; Ahmed, M.H.; Badawy, A.; Shehata, M.S. Structural health monitoring using wireless sensor networks: A comprehensive survey. IEEE Commun. Surv. Tutor. 2017, 19, 1403–1423. [Google Scholar] [CrossRef]
- Riggio, M.; Dilmaghani, M. Structural health monitoring of timber buildings: A literature survey. Build. Res. Inf. 2019, 1–21. [Google Scholar] [CrossRef]
- Sadler, B.M.; Swami, A. Synchronization in sensor networks: An overview. In Proceedings of the MILCOM 2006–2006 IEEE Military Communications Conference, Washington, DC, USA, 23–25 October 2006; pp. 1–6. [Google Scholar]
- Lasassmeh, S.M.; Conrad, J.M. Time synchronization in wireless sensor networks: A survey. In Proceedings of the IEEE SoutheastCon 2010 (SoutheastCon), Concord, NC, USA, 18–21 March 2010; pp. 242–245. [Google Scholar] [CrossRef]
- Swain, A.R.; Hansdah, R. A model for the classification and survey of clock synchronization protocols in WSNs. Ad Hoc Netw. 2015, 27, 219–241. [Google Scholar] [CrossRef]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 147–163. [Google Scholar] [CrossRef]
- Noh, K.; Serpedin, E.; Qaraqe, K. A New Approach for Time Synchronization in Wireless Sensor Networks: Pairwise Broadcast Synchronization. IEEE Trans. Wirel. Commun. 2008, 7, 3318–3322. [Google Scholar] [CrossRef]
- Kim, S.; Pakzad, S.; Culler, D.; Demmel, J.; Fenves, G.; Glaser, S.; Turon, M. Health monitoring of civil infrastructures using wireless sensor networks. In Proceedings of the 6th International Conference on Information Processing in Sensor Networks, Cambridge, MA, USA, 25–27 April 2007; pp. 254–263. [Google Scholar]
- Maróti, M.; Kusy, B.; Simon, G.; Lédeczi, Á. The flooding time synchronization protocol. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 39–49. [Google Scholar]
- Mock, M.; Frings, R.; Nett, E.; Trikaliotis, S. Continuous clock synchronization in wireless real-time applications. In Proceedings of the 19th IEEE Symposium on Reliable Distributed Systems SRDS-2000, Nurnberg, Germany, 16–18 October 2000; pp. 125–132. [Google Scholar]
- Shi, F.; Tuo, X.; Yang, S.; Li, H.; Shi, R. Multiple two-way time message exchange (ttme) time synchronization for bridge monitoring wireless sensor networks. Sensors 2017, 17, 1027. [Google Scholar] [CrossRef] [Green Version]
- Xu, N.; Rangwala, S.; Chintalapudi, K.K.; Ganesan, D.; Broad, A.; Govindan, R.; Estrin, D. A wireless sensor network for structural monitoring. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 3–5 November 2004; pp. 13–24. [Google Scholar]
- Wang, Y.; Lynch, J.P.; Law, K.H. A wireless structural health monitoring system with multithreaded sensing devices: Design and validation. Struct. Infrastruct. Eng. 2007, 3, 103–120. [Google Scholar] [CrossRef] [Green Version]
- Shannon, J.; Melvin, H.; Ruzzelli, A.G. Dynamic flooding time synchronisation protocol for WSNs. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 365–371. [Google Scholar]
- Su, W.; Akyildiz, I.F. Time-diffusion synchronization protocol for wireless sensor networks. IEEE/ACM Trans. Netw. (TON) 2005, 13, 384–397. [Google Scholar] [CrossRef]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-sync protocol for sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, 5–7 November 2003; pp. 138–149. [Google Scholar]
- Sommer, P.; Wattenhofer, R. Gradient clock synchronization in wireless sensor networks. In Proceedings of the 2009 International Conference on Information Processing in Sensor Networks. IEEE Computer Society, San Francisco, CA, USA, 13–16 April 2009; pp. 37–48. [Google Scholar]
- Li, Q.; Rus, D. Global clock synchronization in sensor networks. IEEE Trans. Comput. 2006, 55, 214–226. [Google Scholar]
- PalChaudhuri, S.; Saha, A.K.; Johnson, D.B. Adaptive Clock Synchronization in Sensor Networks. In Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, 27 April 2004; IPSN ’04. ACM: New York, NY, USA, 2004; pp. 340–348. [Google Scholar] [CrossRef] [Green Version]
- Phanish, D.; Garver, P.; Matalkah, G.; Landes, T.; Shen, F.; Dumond, J.; Abler, R.; Zhu, D.; Dong, X.; Wang, Y.; et al. A wireless sensor network for monitoring the structural health of a football stadium. In Proceedings of the 2015 IEEE 2nd World Forum on Internet of Things (WF-IoT), Milan, Italy, 14–16 December 2015; pp. 471–477. [Google Scholar]
- Chen, Z.; Li, D.; Huang, Y.; Tang, C. Event-triggered communication for time synchronization in WSNs. Neurocomputing 2016, 177, 416–426. [Google Scholar] [CrossRef]
- Fanarioti, S.; Tsipis, A.; Giannakis, K.; Koufoudakis, G.; Christopoulou, E.; Oikonomou, K.; Stavrakakis, I. A Proposed Algorithm for Data Measurements Synchronization in Wireless Sensor Networks. In Proceedings of the Second International Balkan Conference on Communications and Networking 2018 (BalkanCom’18), Podgorica, Montenegro, 6–8 June 2018; pp. 1–5. [Google Scholar]
- Casarin, F.; Modena, C.; Aoki, T.; da Porto, F.; Lorenzoni, F. Structural Health Monitoring of historical buildings: Preventive and post-earthquake controls. In Proceedings of the 5th International Conference on Structural Health Monitoring of Intelligent Infrastructure (SHMII-5), Cancun, Mexico, 11–15 December 2011; pp. 11–15. [Google Scholar]
- Arduino. Arduino Mega 2560 Rev3. Available online: https://store.arduino.cc/mega-2560-r3 (accessed on 17 March 2020).
- Arduino. Arduino Wireless SD Shield. Available online: https://store.arduino.cc/arduino-wirelss-sd-shield (accessed on 17 March 2020).
- Digi. XBee-PRO Zigbee Through-Hole (Wire Antenna). Available online: https://www.digi.com/products/models/xbp24cz7wit-004 (accessed on 17 March 2020).
- Andrewrapp. andrewrapp/xbee-arduino. Available online: https://github.com/andrewrapp/xbee-arduino (accessed on 17 March 2020).
- InvenSense. MPU-6050 Six-Axis (Gyro + Accelerometer) MEMS MotionTracking™ Devices. Available online: https://www.invensense.com/products/motion-tracking/6-axis/mpu-6050/ (accessed on 17 March 2020).
- Alvanou, A.G.; Zervopoulos, A.; Papamichail, A.; Bezas, K.; Vergis, S.; Stylidou, A.; Tsipis, A.; Komianos, V.; Tsoumanis, G.; Koufoudakis, G.; et al. CaBIUs: Description of the Enhanced Wireless Campus Testbed of the Ionian University. Electronics 2020, 9, 454. [Google Scholar] [CrossRef] [Green Version]







© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezas, K.; Komianos, V.; Koufoudakis, G.; Tsoumanis, G.; Kabassi, K.; Oikonomou, K. Structural Health Monitoring in Historical Buildings: A Network Approach. Heritage 2020, 3, 796-818. https://doi.org/10.3390/heritage3030044
Bezas K, Komianos V, Koufoudakis G, Tsoumanis G, Kabassi K, Oikonomou K. Structural Health Monitoring in Historical Buildings: A Network Approach. Heritage. 2020; 3(3):796-818. https://doi.org/10.3390/heritage3030044
Chicago/Turabian StyleBezas, Konstantinos, Vasileios Komianos, George Koufoudakis, Georgios Tsoumanis, Katerina Kabassi, and Konstantinos Oikonomou. 2020. "Structural Health Monitoring in Historical Buildings: A Network Approach" Heritage 3, no. 3: 796-818. https://doi.org/10.3390/heritage3030044
APA StyleBezas, K., Komianos, V., Koufoudakis, G., Tsoumanis, G., Kabassi, K., & Oikonomou, K. (2020). Structural Health Monitoring in Historical Buildings: A Network Approach. Heritage, 3(3), 796-818. https://doi.org/10.3390/heritage3030044








