Abstract
Games of chance have historically played a critical role in the development and teaching of probability theory and game theory, and, in the modern age, computer programming and reinforcement learning. In this paper, we derive the optimal strategy for playing the two-dice game Pig, both the standard version and its variant with doubles, coined “Double-Trouble”, using certain fundamental concepts of reinforcement learning, especially the Markov decision process and dynamic programming. We further compare the newly derived optimal strategy to other popular play strategies in terms of the winning chances and the order of play. In particular, we compare to the popular “hold at n” strategy, which is considered to be close to the optimal strategy, especially for the best n, for each type of Pig Game. For the standard two-player, two-dice, sequential Pig Game examined here, we found that “hold at 23” is the best choice, with the average winning chance against the optimal strategy being 0.4747. For the “Double-Trouble” version, we found that the “hold at 18” is the best choice, with the average winning chance against the optimal strategy being 0.4733. Furthermore, time in terms of turns to play each type of game is also examined for practical purposes. For optimal vs. optimal or optimal vs. the best “hold at n” strategy, we found that the average number of turns is 19, 23, and 24 for one-die Pig, standard two-dice Pig, and the “Double-Trouble” two-dice Pig games, respectively. We hope our work will inspire students of all ages to invest in the field of reinforcement learning, which is crucial for the development of artificial intelligence and robotics and, subsequently, for the future of humanity.
1. Introduction
Games of chance have always played a crucial role in the development and teaching of
probability (Dagobert, 1946; Rubel, 2008) [1,2], game theory (Brokaw and Mertz, 2004) [3] and now, increasingly, computer programming (Dlab and Hoic-Bozic, 2021) [4], machine learning (Hazra and Anjaria, 2022) [5], and especially reinforcement learning (Konstantia et al., 2018; Zha et al., 2021) [6,7]. Games of chance can be viewed as simplified versions of real-world problems. Developing algorithms for their optimal solutions can often inspire the subsequent solutions to real-world problems, as shown in AlphaGo (Silver et al., 2016) [8] and AlphaFold (Jumper et al., 2021) [9]. Among the various games of chance, one common type is dice games in which six-sided dice are involved prominently in the play of the game. There are over 40 common types of dice games, including Yahtzee, backgammon, and the dice game Pig, which we shall focus on in this work. Back in 1979, a reinforcement learning algorithm-based AI backgammon player famously beat the world champion at all games for the first time (Berliner, 1980) [10]. This was tremendous and has since inspired and propelled the development of increasingly more-sophisticated reinforcement learning algorithms and applications not only in games, but also various real-world applications [11,12,13,14,15,16,17,18,19,20]. In the following, we focus on developing optimal play strategies for the two-dice game of Pig using ingredients of reinforcement learning.
The dice game Pig was first documented in the book Scarne on Dice by the American magician John Scarne in 1945 [21]. There, Scarne introduced the one-die Pig game with a simple rule of play: Two players race to reach a certain point total, say 100 points, and the first one to reach the said total wins the game. At each turn, a player repeatedly rolls a die until either a one is rolled (and the player scores nothing for that turn and it becomes the opponent’s turn), or the player holds out of his/her own volition and scores the sum of all the rolls in that turn. That is, at any time during a player’s turn, the player is faced with two decisions: roll or hold. If the player rolls a 1, he/she must stop, and the turn total will be 0. If the player rolls a number other than 1, namely, 2 to 6, this number will be added to the turn total, and the player can again choose to roll or hold; if they choose to hold, it becomes the opponent’s turn. Pig is a “jeopardy dice game”, as one can jeopardize his/her previous gains by continuing to roll for greater gains (if the next roll is not 1) or ruin (if 1 is rolled) [22]. The one-die Pig game is simple, but the optimal strategy to play this simple game is not so simple and has only been solved in recent years using the Markov decision process and dynamic programming [23,24]. These authors even wrote an online interactive app so that people can play one-die Pig with the computer:http://cs.gettysburg.edu/projects/pig/piggame.html (accessed on 1 June 2022)
The one-die Pig game has since evolved into several variations, with the most popular one being the two-dice Pig game, where two dice are rolled instead of one. Commercial variants of the two-dice Pig game include Pass the Pigs, Pig Dice, and Skunk. Being a more complicated setting than the one-die Pig game, the optimal strategy of two-dice Pig had not been derived prior to our work. The only attempt back in 1973 yielded sub-optimal strategies [25]. In this work, we derive the optimal strategy for the original version of the two-dice Pig game using the Markov decision process and dynamic programming. The objective of two-dice Pig remains the same as the one-die game: the first player to reach the said total points, say 100 points, wins. Each player’s turn consists of repeatedly rolling two dice. After each roll, the player is faced with the same two choices: roll or hold. The rules of play for the standard two-dice Pig are summarized in Figure 1:
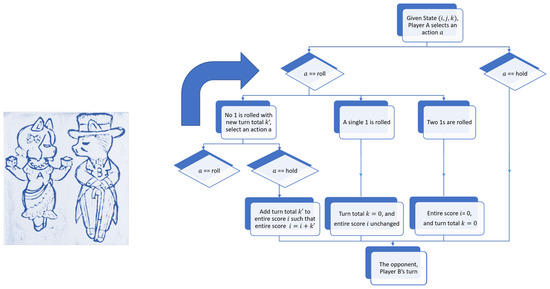
Figure 1.
Rules of play for standard two-dice Pig.
If the player holds, the turn total, which is defined as the sum of the rolls during the turn, is added to the player’s score, and it becomes the opponent’s turn.
If the player rolls, then one of the following applies: If neither die shows a one, his/her sum is added to the turn total, and the player’s turn continues. If a single one is rolled, the player’s turn ends with the loss of his/her turn total. If two ones are rolled, the player’s turn ends with the loss of his/her turn total as well as his/her entire score.
2. Reinforcement Learning
2.1. General Background
Reinforcement learning is a computational approach to understanding and automating goal-directed learning and sequential decision making. It starts with a complete, interactive, goal-seeking agent. An interactive environment for reinforcement learning is formally described as a Markov decision process (MDP). An agent may include one or more of the following components: 1. Policy, which determines how the agent will behave; 2. Value function, which measures how good a state or a state-action pair is; and 3. Model, which predicts what the environment will do next, reflecting the agent’s representation of the environment. Inclusion or exclusion of Component 3 divides the reinforcement learning methods into two categories: model-based methods and model-free methods. For model-based methods, the key feature is that the transition probability from the current state to next state is known. Dynamic programming (DP) is then one of the general solutions for such planning problems. On the other hand, if full knowledge of an MDP cannot be obtained, e.g., the transition probability is unknown, then Monte Carlo (MC) learning and temporal difference (TD) learning are two powerful approaches to both estimating and optimizing the value function of an unknown MDP. Unlike DP, which performs computations with its model, these two methods learn directly from episodes of experience.
2.2. Markov Decision Process Formulation and Value Iteration
The standard two-dice Pig game can be solved using reinforcement learning, as we are interested in the long-term reward—winning the game. In particular, we can model the game process as an agent–environment interaction. Furthermore, the game can be viewed as an MDP as, given the current state, the action is independent of the past states. The state contains three elements: Player A’s entire score i, the opponent Player B’s score j, and the turn total k. Given such state s, Player A has two options: roll or hold. The roll action is coded as 1, while the hold action is coded as 0, i.e., . For any two states (not necessarily different) and any action , there is a transition probability such that taking action a will change the state from s to . The immediate reward on each transition from s to under action a is defined as , with if is a winning state, and if is a not-winning state. The winning state has the property because the player reaching the winning state can simply hold and then wins the game. Because the only situation obtaining the positive reward is winning the game, there is no discount factor () needed to ensure convergence.
After a finite MDP is formulated, there are several reinforcement learning methods to solve the problem, such as DP and deep reinforcement learning (DRL). The main idea of DRL is to utilize deep neural networks such as the deep Q-network to approximate the value function. On the other hand, the key idea of DP in reinforcement learning is to use value functions to organize and structure the search for good policies (or an optimal strategy). Once we have found the optimal value functions , which satisfy the Bellman optimality equations: , the optimal policy can be easily obtained by . One difference between DRL and DP is that for DRL, the value function is approximate, thus rendering the optimal strategy to be less accurate than that of DP; meanwhile, by taking the DP approach to this problem, we obtain the exact optimal strategy. Under the DP setting, combining policy evaluation and policy improvement together, we have policy iteration [26]. Once a policy has been evaluated by the value function , we can improve the current policy to generate a better policy using . Next, we compute and improve it again to yield an even better policy ; we repeat this process until the policy cannot be improved anymore. We then have the following sequence of monotonically improving policies and value functions:
where denotes a policy evaluation and denotes a policy improvement. Because a finite MDP has only a finite number of policies, convergence to an optimal policy and optimal value function is guaranteed in a finite number of iterations for the standard two-dice Pig game.
For policy iteration, each evaluation needs multiple sweeps through the state set to converge in terms of limits. If we wait for the exact convergence of every evaluation, the computational cost for policy iteration is too high. In fact, policy iteration still converges to the final optimal policy even if the policy evaluation is stopped after only one update of every state. This algorithm is called value iteration.
3. Optimal Strategy for the Standard Two-Dice Pig Game
Throughout this paper, the default goal is 100 unless otherwise specified. For a given policy , define the winning probability for a given state to be . For another policy , we say policy is no better than policy if, for all states :
The value for state s given policy is defined as the winning probability:
where and are the winning probabilities for rolling and holding, respectively, for policy . For the standard two-dice Pig game, these probabilities together with the policy are:
If both players are rational, i.e., Player A and the opponent Player B both play optimally, then the solution of in the above system is the Nash equilibrium, or the optimal policy . The optimal policy can be obtained through value iteration (Algorithm 1).
| Algorithm 1: Value Iteration Algorithm |
|
Figure 2 shows the roll/hold boundary for each possible state s. As Opponent B’s score approaches the goal of 100, Player A plays more aggressively on each turn, especially when Player A’s score is relatively low. On the contrary, when Opponent B’s score is close to 0, Player A plays conservatively. Figure 3 shows the decision boundary given Player A’s score when Opponent B’s score is fixed. For a better comparison, we combine these results in Figure 4 with the additional case of an opponent score of 90. This produces the same observation we mentioned above. At the extreme case of an opponent score of 90, Player A’s optimal strategy is to simply reach the goal of 100 in one turn, as Opponent B has a very high probability of winning the game in his/her turn.
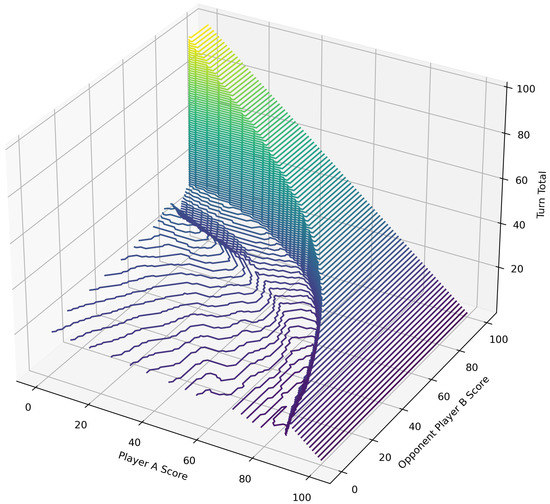
Figure 2.
The roll/hold boundary for each state (Player A Score, Opponent Player B Score, and Turn Total) for Player A who goes first. The line shown is the boundary between states in which Player A should roll (below the line) and states in which Player A should hold (above the line).
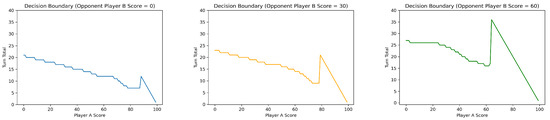
Figure 3.
The roll/hold boundary for Player A who goes first when the opponent Player B’s score is fixed.
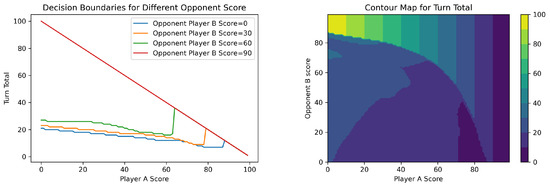
Figure 4.
Left: Comparison between different boundary curves for Player A who goes first when the opponent Player B’s score changes. Right: contour for the turn total given Player A’s score and the opponent Player B’s score.
Intuitively, we believe that the player who goes first has some advantage. Figure 5 shows the winning probabilities of the first player, Player A, when the goal is increasing. Indeed, the first player has a certain advantage in terms of a higher winning probability, and such advantage vanishes gradually as we increase the goal. When the goal is 100, the winning probability for Player A is 52.18%, while the winning probability drops to 50.76% when the goal is 200. Detailed winning probabilities for the first player when both players play optimally are summarized in Table A1.
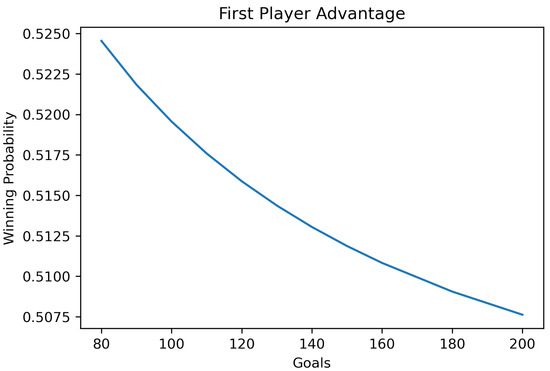
Figure 5.
The winning probability of the first player when both players play optimally.
If the opponent Player B tries to fool us by playing less than optimally, shall Player A still use the optimal strategy? Will the optimal strategy further increase Player A’s winning chance?
Let and denote the winning probabilities of Player A with policy and the opponent Player B with policy , respectively. Further assume the optimal policy is . Then, we have for any other policy . In particular, for all state . Define to be the winning probability for Player A under policy with the opponent Player B under policy for state ; then
Therefore, no matter how the opponent Player B plays, which is unknown to Player A, Player A should always play with the optimal strategy. The worse the opponent Player B plays, the higher the winning chance for Player A. However, if the opponent Player B’s strategy is known, there may exist a better strategy for Player A such that the winning probability for Player A is maximized against .
A simple policy is the “hold at 20” policy, where a player holds as soon as the turn total reaches at least 20 if the score needed to reach the goal is more than 20 (otherwise hold the score needed to reach the goal). This generalizes to the strategy of “hold at n”, where n can be any integer number between 0 and the goal, say 100. Barring large and small values of n not meaningful for the “hold at n” strategy, we examine the range of n from 10 to 35. Figure 6 demonstrates that for the standard two-dice Pig game, the best scenario is to “hold at 23”, as the winning probability of the optimal strategy is lowest among all those values of n. However the optimal strategy wins over all “hold at n” strategies. Even when the player who uses the optimal strategy goes second, his/her winning probability is still higher than 50% for all n. Detailed winning probabilities against “hold at n” are summarized in Table A2.
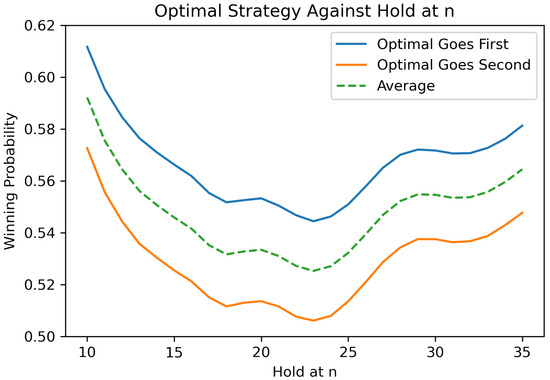
Figure 6.
Winning probabilities of the optimal strategy developed in this work against the traditional “hold at n” strategy for the standard two-dice Pig game.
4. “Double Trouble”, a Variation of the Standard Two-Dice Pig
This variation is the same as the standard two-dice Pig except for the addition of Rule #4 below (summarized in Figure 7 with red boxes indicating the difference between the standard two-dice Pig and the “Double Trouble” variation):
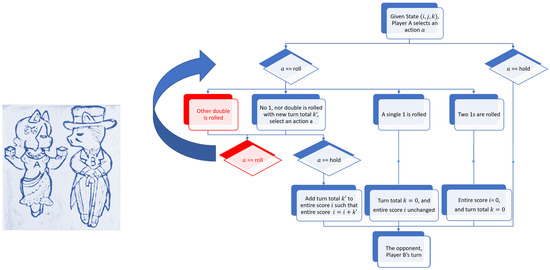
Figure 7.
Rules of play for the “Double Trouble” variation of the two-dice Pig game.
1. Two standard dice are rolled. If neither shows a one, the sum is added to the player’s turn total.
2. If a single one is rolled, the player scores nothing and the turn ends.
3. If two ones are rolled, the player’s entire score is lost, and the turn ends.
4. If a double other than two ones is rolled, the point total is added to the turn total as with any roll, but the player is obligated to roll again.
With Rule #4 added to the standard two-dice Pig game, the framework for finding the optimal strategy needs to be changed accordingly. Indeed, such change is not trivial, as explained below, and, hence, we nickname this variation “Double Trouble”.
To apply value iteration, there are two issues we need to address first:
1. Insufficient information. Suppose the current state is (30, 10, 20), indicating Player A’s entire score is 30, the opponent Player B’s entire score is 10, and the turn total for Player A is 20. Further, assume Player A decides to roll again (there is nothing special if Player A chooses to hold). The new rolls {3, 5} and {4, 4} are totally different, although the turn totals are the same: . According to the optimal strategy obtained by the standard two-dice Pig game, Player A is supposed to hold in both cases. However, with the addition of Rule #4, Player A is forced to roll again in the latter situation, while for the first case, Player A can hold to increase his/her entire score. Therefore, for the “Double Trouble” variation, by looking at the turn total even without rolling a single one, one does not have enough information to decide whether to roll or to hold.
2. Infinite states. For the standard two-dice Pig game, we have the constraints that and that correspond to the winning condition and losing condition, respectively. As a result, the states are finite. By adding Rule #4, this variation has the potential to cause an infinite states problem. Assume the current state is (90, 20, 10) and Player A rolls {5, 5} in this turn. Originally, Player A could simply hold and win the game. In “Double Trouble”, unfortunately, Player A is not allowed to hold when a double (other than two ones) occurs. Player A has to roll again. Imagine Player A keeps on rolling doubles (other than two ones) without the opportunity to hold. In theory, Player A could reach a state even like (90, 20, 1000) with extremely low probability. Therefore, the turn total k here may blow up to infinity, and is no longer the winning condition.
To distinguish whether a double (other than two ones) has been rolled, as the decision depends on this information, we need to introduce another element to track the information. Instead of the original three-element tuple state , here, we propose a four-element tuple to represent the state, where the first three elements stay the same, and the fourth element l is a binary variable recording whether a non-ones double has been rolled in the most recent roll, where means no other double has occurred, and indicates a non-ones double has been rolled. The new probabilities at each given state can be calculated by:
where
When a player decides to roll, there are four different situations: (i) a single one; (ii) two ones; (iii) a non-ones double; or (iv) none of the above. We shall prove that (iv) is a necessary and sufficient condition for winning the game with the next single roll given state with . Suppose Player A’s next roll has two different faces and neither of them is one, which is exactly situation (iv). Since , Player A can simply hold and win. To win the game in one roll, the player must be able to hold, rendering doubles impossible. After the player holds, the winning condition must be satisfied to win the game. Thus, the new rolled faces cannot include a one, otherwise so that (here we do not consider because it is meaningless). Therefore, (iv) is also a necessary condition. Through the above simple proof, as long as , the probability of winning with the next roll for a state does not depend on the exact value of k, since the probability of situation (iv) is always independent of k.
To avoid the infinite state space, which only occurs when , we claim that under the condition , the turn total k no longer matters for winning the game. For situations (i) and (ii), the new turn total will become 0 regardless of the current turn total k. For situation (iv), the player can hold and win the game no matter what the current turn total k is, because . For situation (iii), the turn total k will increase and the player is obligated to roll again. If situation (iii) keeps happening, the turn total k becomes irrelevant because the player can do nothing except roll. The probability that situation (iii) lasts forever is . Once one of the situations (i), (ii), or (iv) happen (with probability of one), the turn total k does not matter according to the previous result. Therefore, the turn total k is important only when . After that, we can ignore the exact value of k.
As the value of k is no longer important for determining the winning probability when , we have for any satisfying and . In particular, for any . Therefore, for ,
By doing so, we reduce the number of states to be finite so that there is no need to consider the case during the value iteration, but we set it as one of the boundary conditions. The boundary conditions under the “Double Trouble” setting are:
The optimal strategy can thence be found using value iteration with the new updates (3) and (4), as well as the new boundary conditions (6). Figure 8 shows the winning probabilities of the optimal strategy against the “hold at n” strategy considering both optimal strategies for the player going first vs. second. Like with standard two-dice Pig, even if the player goes second, the optimal strategy outperforms the “hold at n” strategy for any choice of n. Table A3 shows the detailed winning probabilities of the optimal strategy against the “hold at n” strategy. The best n for this “Double Trouble” variation is 18. In fact, from the plot we can conclude that the winning probabilities from hold at 18 to hold at 23 are very close. It is reasonable that the best n decreases from 23 in the standard two-dice Pig game to 18 in this variant, as any non-ones double will force the player to roll again. In real game play, hold at 18 does not indicate that in each turn a player holds at exactly 18, as this is impossible. Considering the non-ones double case, the turn total can be much larger than 18, even if the player adopts the “hold at 18” strategy.
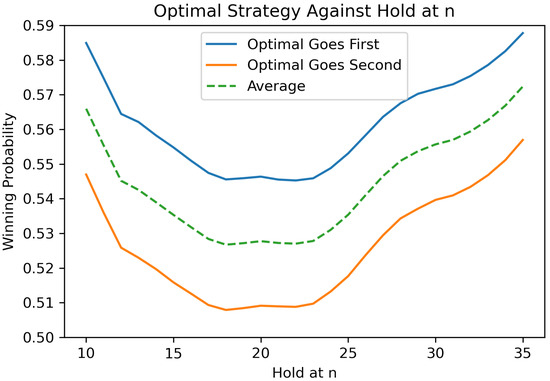
Figure 8.
Winning probabilities of the optimal strategy developed in this work against the traditional “hold at n” strategy for “Double Trouble”, a variation of the standard two-dice Pig game.
Will forcing a player to roll again when a non-ones double occurs speed up game-play in terms of fewer total turns? Here total turns is defined as the sum of the number of turns that each player has played. We simulate 10,000,000 games, assuming one player using the optimal strategy and the other player using the “hold at 25” strategy, and the average number of turns played in one-die Pig is 19.19 if the optimal strategy player goes first; the average number of turns played in one-die Pig is 19.15 if the optimal strategy player goes second. Meanwhile, the average number of turns played increases slightly to 19.25 if both players adopt the optimal strategy. For the standard two-dice Pig game, the average number of turns played is 23.38 for the optimal strategy against the “hold at 23” strategy. If the “hold at 23” strategy goes first, the average number of turns played is 23.35. If both players play optimally, the average number of turns increases slightly to 23.68. For the two-dice variation Pig, “Double Trouble”, the average number of turns played for the optimal strategy player going first and second are 24.23 and 24.21, respectively, versus “hold at 18”. If both players play optimally, the average number of turns increases slightly to 24.49. Whether the optimal strategy goes first or goes second does not impact the total turns significantly, but the optimal strategy going second always has a smaller number of turns compared to that of the optimal strategy going first. As for the standard deviation, both versions of the two-dice Pig game (approximately 11.0) have much larger standard deviations than the one-die Pig game (approximately 6.5), which is consistent with our intuition, as more dice cause higher randomness. In particular, the “Double Trouble” two-dice Pig variation (around 11.3) has a larger standard deviation than the standard two-dice Pig game (around 10.8). The exact means and standard deviations for each strategy combination are summarized in Table 1.

Table 1.
The average number of turns played in different strategy combinations, simulated by 10,000,000 games. Numbers in the parenthesis are the standard deviations. The choice of n is determined by the best n in each scenario. For one-die Pig, n = 25; for standard two-dice pig, n = 23; for “Double Trouble”, the two-dice Pig variation, n = 18.
One interesting fact is that both players playing optimally does not reduce the number of turns in all three case, especially in both versions of the two-dice Pig game. This phenomenon is due to the rolling one penalty, since any ones will at least lose the turn total, especially the “snake eyes” rule: double ones drop the entire set score to zero. For one-die Pig, the entire score can never decrease, which is not true for the two-dice Pig game. We refer to playing optimally in this paper as maximizing the probability of winning rather than minimizing the number of turns played. Maximizing the winning probability may also increase the chances of rolling ones, including the “snake eyes”, which increases the number of turns played. Another fact is that the two-dice Pig variation, “Double Trouble”, will have more turns on average compared to the standard two-dice Pig. Instead of reaching the goal more quickly, forcing a player to roll again in non-ones doubles increases the risk of rolling ones, rendering the turn total to be zero (or even resetting the set total if double ones are rolled), and thus the turn is wasted.
5. Discussion
In this work, we successfully derived the optimal play strategy for the two-dice Pig game, both the standard and “Double Trouble” variations, using the Markov decision process (MDP) and dynamic programming (DP), which are classical components of reinforcement learning (RL). Like our previous work published in Stats [27], we could have chosen to use Q-learning instead of DP to derive the optimal play strategy for the two-dice Pig game. Both DP and Q-learning are RL algorithms, each developed to maximize a reward in a given environment, usually by the MDP (except for rare situations with hidden states, for instance [28]). Both Q-learning and Value Iteration (a DP technique) use similar update rules based on the Bellman optimality equations. The difference lies in that DP requires the entire equation system, including all the transition probabilities—while the benefit is that the optimal solutions derived are usually the exact optimal solutions and not the approximate ones provided by Q-learning. This benefit can be substantial in a problem with a limited number of states such as the two-dice Pig game. Fortunately, we were able to derive all the transition probabilities and thereby provide the explicit model to deploy the DP algorithm and obtain the exact optimal play strategy for the two-dice Pig game. The usefulness of the MDP and DP solutions to the Pig dice games goes beyond merely providing the optimal play strategies for these games. Rather, this line of work can help inspire people, especially young people, to learn and to excel in STEM subjects critical to AI and robotics, including probability and statistics, game theory, computer programming, and machine learning. We shall continue our work along this line by developing online two-dice Pig games and finding the optimal play strategies for multiple-player Pig games.
Author Contributions
Conceptualization, T.Z. and M.H.M.; methodology, T.Z. and M.H.M.; software, T.Z. and M.H.M.; validation, T.Z. and M.H.M.; formal analysis, T.Z. and M.H.M.; investigation, T.Z. and M.H.M.; resources, T.Z. and M.H.M.; data curation, T.Z. and M.H.M.; writing—original draft preparation, T.Z.; writing—review and editing, M.H.M.; visualization, T.Z. and M.H.M.; supervision, T.Z. and M.H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Zhenhua Liu for many helpful discussions, and Todd Neller for the one-die optimal play Java code.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Detailed winning probabilities of the first player when both players play optimally, for the standard two-dice Pig game.
Table A1.
Detailed winning probabilities of the first player when both players play optimally, for the standard two-dice Pig game.
| Goal | Winning Probability |
|---|---|
| 80 | 0.5245 |
| 90 | 0.5218 |
| 100 | 0.5196 |
| 110 | 0.5176 |
| 120 | 0.5159 |
| 130 | 0.5144 |
| 140 | 0.5130 |
| 150 | 0.5119 |
| 160 | 0.5108 |
| 180 | 0.5091 |
| 200 | 0.5076 |

Table A2.
Detailed winning probabilities of the optimal strategy against the “hold at n” strategy, for the standard two-dice Pig game. Here the “hold at 23” is the best choice with the average winning chance against the optimal strategy being 0.4747 (= 1 − 0.5253).
Table A2.
Detailed winning probabilities of the optimal strategy against the “hold at n” strategy, for the standard two-dice Pig game. Here the “hold at 23” is the best choice with the average winning chance against the optimal strategy being 0.4747 (= 1 − 0.5253).
| Hold at n | Optimal Goes First | Optimal Goes Second | Average Probability |
|---|---|---|---|
| 10 | 0.6117 | 0.5726 | 0.5922 |
| 11 | 0.5955 | 0.5558 | 0.5756 |
| 12 | 0.5847 | 0.5444 | 0.5645 |
| 13 | 0.5765 | 0.5358 | 0.5561 |
| 14 | 0.5710 | 0.5304 | 0.5507 |
| 15 | 0.5663 | 0.5255 | 0.5459 |
| 16 | 0.5618 | 0.5212 | 0.5415 |
| 17 | 0.5553 | 0.5151 | 0.5352 |
| 18 | 0.5517 | 0.5116 | 0.5317 |
| 19 | 0.5526 | 0.5130 | 0.5328 |
| 20 | 0.5533 | 0.5136 | 0.5334 |
| 21 | 0.5505 | 0.5116 | 0.5310 |
| 22 | 0.5468 | 0.5077 | 0.5272 |
| 23 | 0.5444 | 0.5061 | 0.5253 |
| 24 | 0.5463 | 0.5079 | 0.5271 |
| 25 | 0.5509 | 0.5136 | 0.5323 |
| 26 | 0.5578 | 0.5209 | 0.5394 |
| 27 | 0.5651 | 0.5287 | 0.5469 |
| 28 | 0.5701 | 0.5344 | 0.5522 |
| 29 | 0.5721 | 0.5375 | 0.5548 |
| 30 | 0.5717 | 0.5375 | 0.5546 |
| 31 | 0.5706 | 0.5363 | 0.5535 |
| 32 | 0.5707 | 0.5367 | 0.5537 |
| 33 | 0.5727 | 0.5387 | 0.5557 |
| 34 | 0.5762 | 0.5429 | 0.5595 |
| 35 | 0.5813 | 0.5477 | 0.5645 |

Table A3.
Detailed winning probabilities of the optimal strategy against the “hold at n” strategy, for “Double Trouble”, a variation of the standard two-dice Pig game. Here the “hold at 18” is the best choice with the average winning chance against the optimal strategy being 0.4733 (= 1 − 0.5267).
Table A3.
Detailed winning probabilities of the optimal strategy against the “hold at n” strategy, for “Double Trouble”, a variation of the standard two-dice Pig game. Here the “hold at 18” is the best choice with the average winning chance against the optimal strategy being 0.4733 (= 1 − 0.5267).
| Hold at n | Optimal Goes First | Optimal Goes Second | Average Probability |
|---|---|---|---|
| 10 | 0.5849 | 0.5470 | 0.5659 |
| 11 | 0.5748 | 0.5360 | 0.5554 |
| 12 | 0.5645 | 0.5259 | 0.5452 |
| 13 | 0.5621 | 0.5230 | 0.5425 |
| 14 | 0.5583 | 0.5197 | 0.5390 |
| 15 | 0.5548 | 0.5159 | 0.5353 |
| 16 | 0.5510 | 0.5126 | 0.5318 |
| 17 | 0.5474 | 0.5093 | 0.5284 |
| 18 | 0.5456 | 0.5079 | 0.5267 |
| 19 | 0.5459 | 0.5084 | 0.5272 |
| 20 | 0.5464 | 0.5091 | 0.5277 |
| 21 | 0.5455 | 0.5089 | 0.5272 |
| 22 | 0.5453 | 0.5088 | 0.5270 |
| 23 | 0.5459 | 0.5097 | 0.5278 |
| 24 | 0.5488 | 0.5132 | 0.5310 |
| 25 | 0.5531 | 0.5177 | 0.5354 |
| 26 | 0.5583 | 0.5237 | 0.5410 |
| 27 | 0.5636 | 0.5295 | 0.5465 |
| 28 | 0.5675 | 0.5343 | 0.5509 |
| 29 | 0.5703 | 0.5371 | 0.5537 |
| 30 | 0.5717 | 0.5396 | 0.5557 |
| 31 | 0.5730 | 0.5410 | 0.5570 |
| 32 | 0.5754 | 0.5434 | 0.5594 |
| 33 | 0.5785 | 0.5468 | 0.5627 |
| 34 | 0.5826 | 0.5511 | 0.5668 |
| 35 | 0.5878 | 0.5569 | 0.5724 |
References
- Dagobert, E.B. Mathematical Probabilities in Games of Chance The Game of Sevens. Math. Teach. 1946, 39, 155–158. [Google Scholar] [CrossRef]
- Rubel, L. Book Review: Teaching With Games of Chance: A Review of The Mathematics of Games and Gambling. J. Res. Math. Educ. 2008, 39, 343–346. [Google Scholar]
- Brokaw, A.J.; Merz, T.E. Active learning with Monty Hall in a game theory class. J. Econ. Educ. 2004, 35, 259–268. [Google Scholar] [CrossRef]
- Holenko Dlab, M.; Hoic-Bozic, N. Effectiveness of game development-based learning for acquiring programming skills in lower secondary education in Croatia. Educ. Inf. Technol. 2021, 26, 4433–4456. [Google Scholar] [CrossRef] [PubMed]
- Hazra, T.; Anjaria, K. Applications of game theory in deep learning: A survey. Multimed. Tools Appl. 2022, 81, 8963–8994. [Google Scholar] [CrossRef]
- Xenou, K.; Chalkiadakis, G.; Afantenos, S. Deep reinforcement learning in strategic board game environments. In Proceedings of the European Conference on Multi-Agent Systems, Bergen, Norway, 6–7 December 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 233–248. [Google Scholar]
- Zha, D.; Xie, J.; Ma, W.; Zhang, S.; Lian, X.; Hu, X.; Liu, J. Douzero: Mastering doudizhu with self-play deep reinforcement learning. In Proceedings of the International Conference on Machine Learning, Online, 18–24 July 2021; PMLR: Brookline, MA, USA, 2021; pp. 12333–12344. [Google Scholar]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Berliner, H.J. Backgammon computer program beats world champion. Artif. Intell. 1980, 14, 205–220. [Google Scholar] [CrossRef]
- Tesauro, G. Temporal difference learning of backgammon strategy. In Machine Learning Proceedings 1992; Elsevier: Amsterdam, The Netherlands, 1992; pp. 451–457. [Google Scholar]
- Tesauro, G. TD-Gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 1994, 6, 215–219. [Google Scholar] [CrossRef]
- Tesauro, G. Temporal difference learning and TD-Gammon. Commun. ACM 1995, 38, 58–68. [Google Scholar] [CrossRef]
- Kormushev, P.; Calinon, S.; Caldwell, D.G. Reinforcement learning in robotics: Applications and real-world challenges. Robotics 2013, 2, 122–148. [Google Scholar] [CrossRef]
- Nian, R.; Liu, J.; Huang, B. A review on reinforcement learning: Introduction and applications in industrial process control. Comput. Chem. Eng. 2020, 139, 106886. [Google Scholar] [CrossRef]
- Magdy, R.; Rashad, S.; Hany, S.; Tarek, M.; Hassan, M.A.; Mohammed, A. Deep reinforcement learning approach for augmented reality games. In Proceedings of the 2021 International Mobile, Intelligent, and Ubiquitous Computing Conference (MIUCC), Cairo, Egypt, 26–27 May 2021; pp. 330–336. [Google Scholar]
- Dobre, G.C.; Gillies, M.; Pan, X. Immersive machine learning for social attitude detection in virtual reality narrative games. Virtual Reality 2022, 26, 1–20. [Google Scholar] [CrossRef]
- Guo, P.; Xiao, K.; Ye, Z.; Zhu, W. Route optimization via environment-aware deep network and reinforcement learning. ACM Trans. Intell. Syst. Technol. (TIST) 2021, 12, 1–21. [Google Scholar] [CrossRef]
- Guo, P.; Xiao, K.; Ye, Z.; Zhu, H.; Zhu, W. Intelligent career planning via stochastic subsampling reinforcement learning. Sci. Rep. 2022, 12, 1–16. [Google Scholar]
- Singh, B.; Kumar, R.; Singh, V.P. Reinforcement learning in robotic applications: A comprehensive survey. Artif. Intell. Rev. 2021, 55, 945–990. [Google Scholar] [CrossRef]
- Scarne, J. Scarne on Dice; Military Service Publishing Co.: Harrisburg, PA, USA, 1945. [Google Scholar]
- Knizia, R. Dice Games Properly Explained; Elliot Right-Way Books: London, UK, 1999. [Google Scholar]
- Neller, T.W.; Presser, C.G. Optimal play of the dice game Pig. UMAP J. 2004, 25, 25–47. [Google Scholar]
- Neller, T.W.; Presser, C.G. Practical play of the dice game pig. UMAP J. 2010, 31, 5–19. [Google Scholar]
- Elliott, N.L. A Mathematical Approach to an Optimal Strategy for the Dice Game Pig. Ph.D. Thesis, University of North Carolina at Greensboro, Greensboro, NC, USA, 1973. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Zhu, T.; Zhu, W. Quantitative Trading through Random Perturbation Q-Network with Nonlinear Transaction Costs. Stats 2022, 5, 546–560. [Google Scholar] [CrossRef]
- Whitehead, S.D.; Lin, L.J. Reinforcement learning of non-Markov decision processes. Artif. Intell. 1995, 73, 271–306. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).