Integration of Lattice Structures into the Boring Bars as a Passive Chatter Suppression Technique: Concepualization, Modelling and Simulation
Abstract
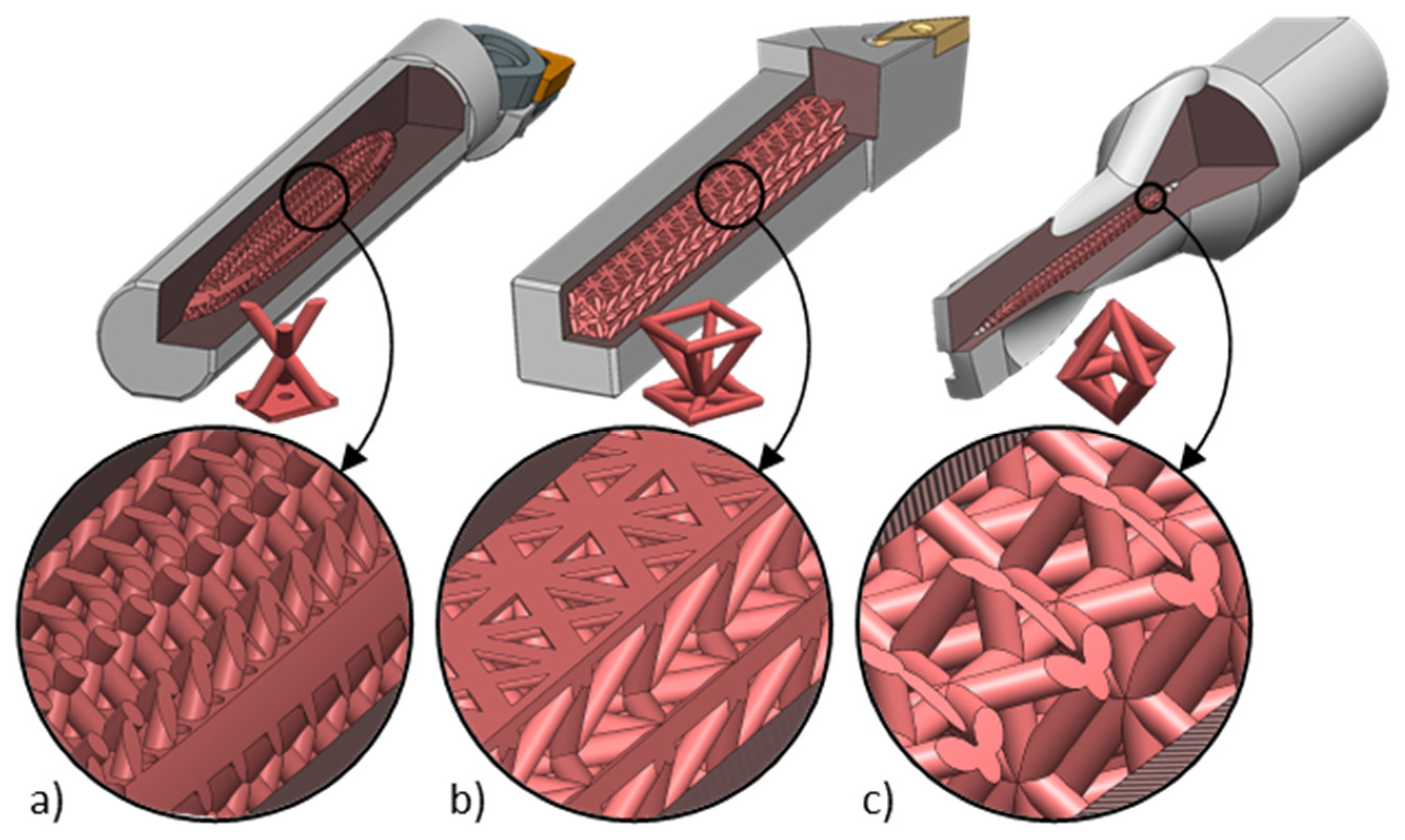
1. Introduction
- calculate a suitable design space for a mold with an existing boring bar base body
- make it available in a simulation model in order to
- ○
- fill this design space with 3D lattice structures and
- ○
- use the finite element method (FEM) simulation to determine whether and on what approximate scale the undesirable vibrations during machining could be reduced using this method.
2. Determination of an Optimal Design Space and Testing 3D Lattices Simulation Model
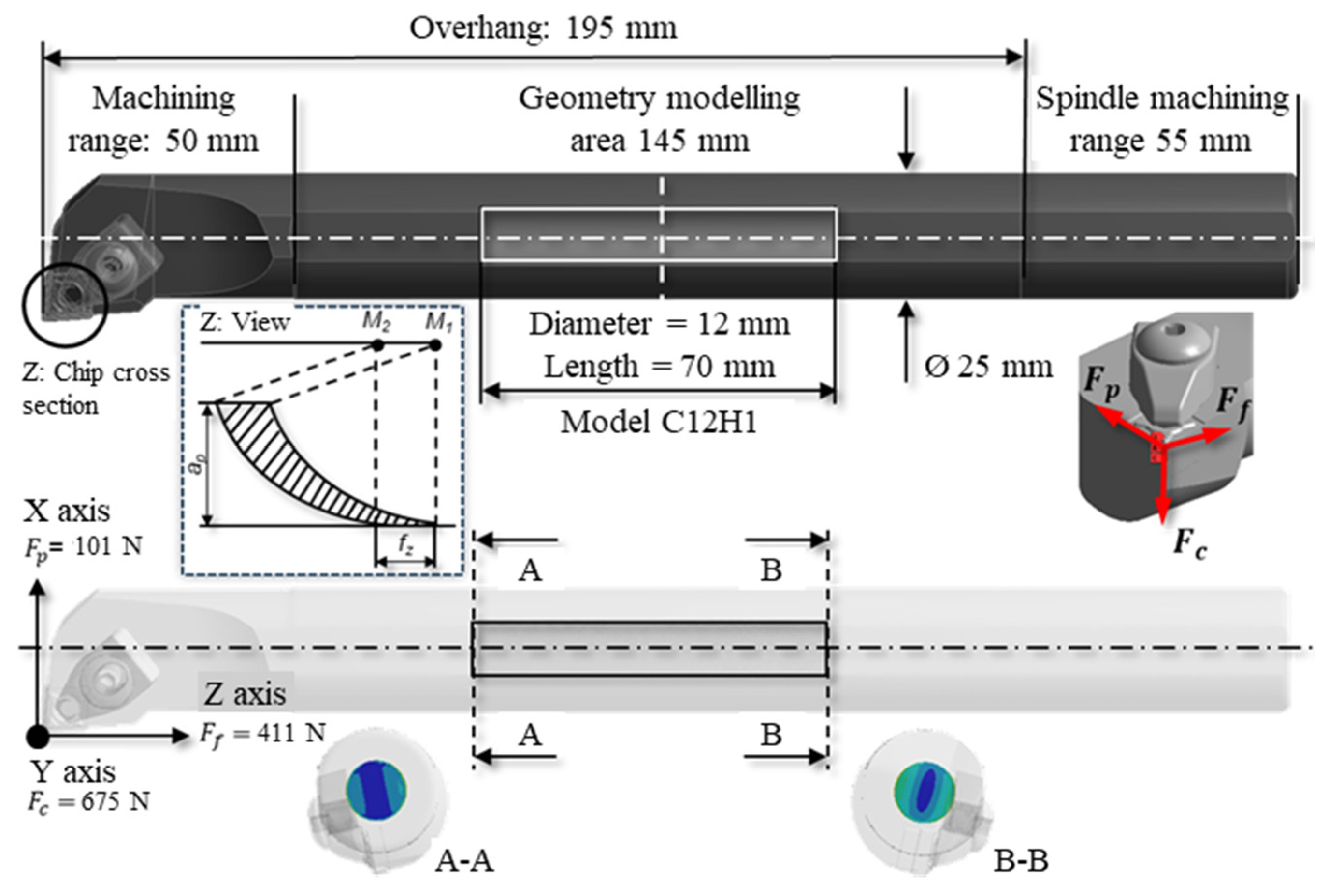
2.1. Experimental Setup for First Step
2.2. Modal Analysis and Harmonic Response Analysis with ANSYS
2.3. Development of a Simulation Model
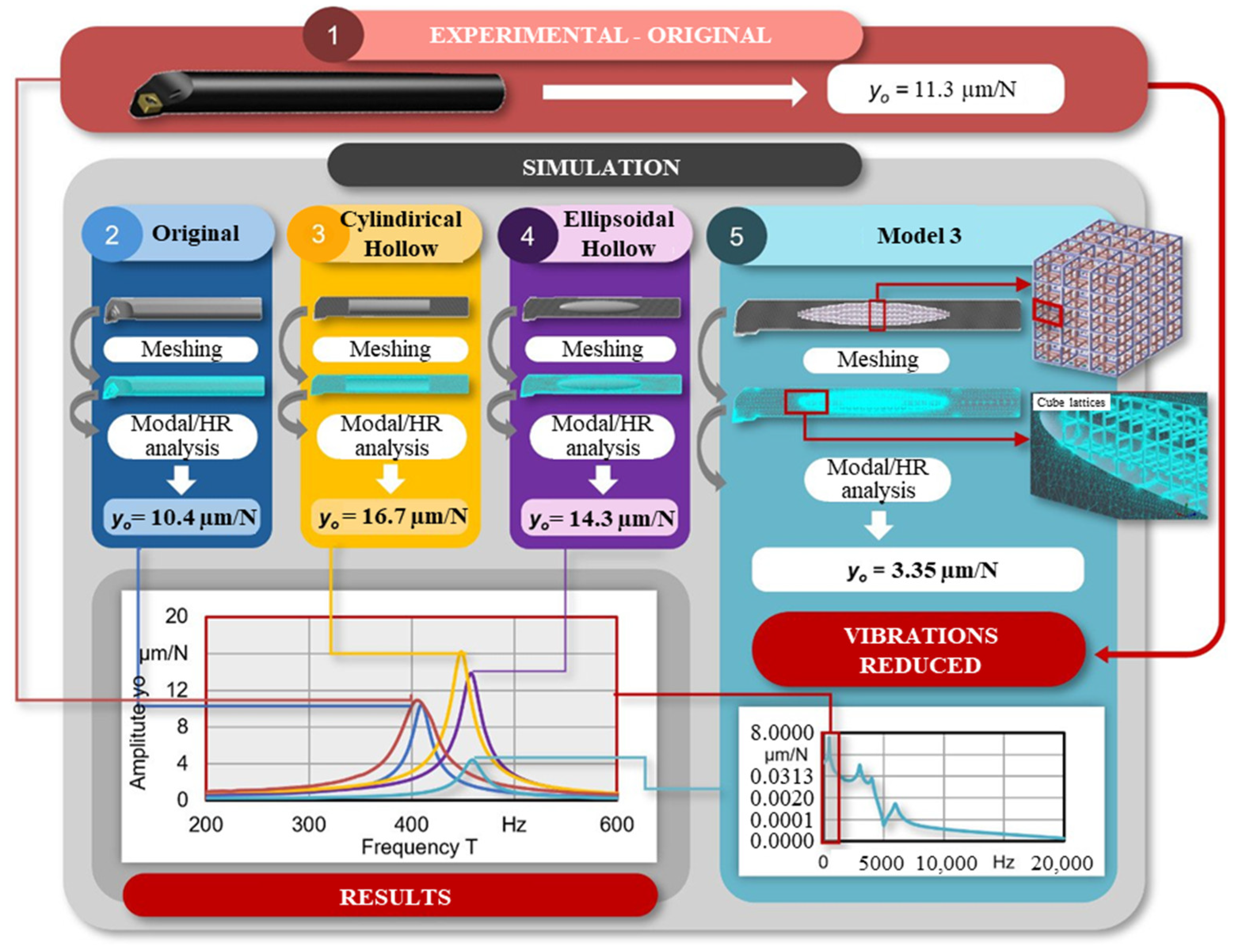
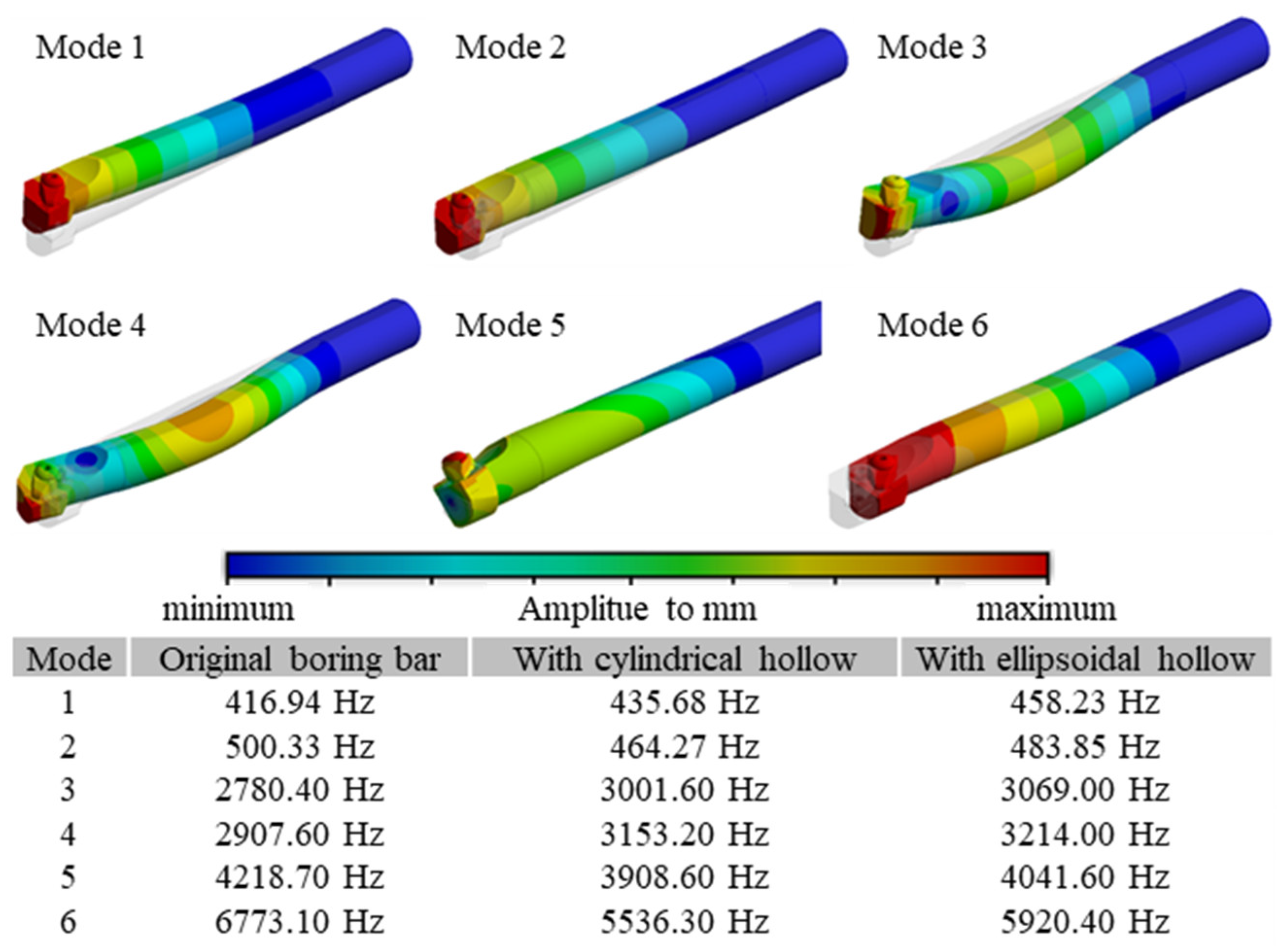
2.4. Determination of the Maximum Hollow Volume by FEM Simulation
- reference model (original boring bar) was calculated analytically with = 42.90 MPa. This value is far below the permissible bending stress = 183.3 MPa, which means that the criterion is fulfilled.
- The cylindrical hollow space was also calculated analytically. This value is also far below the allowable bending stress with = 45.30 MPa.
- The simulation of the reference model (original boring bar) resulted in a value of = 43.30 MPa for the existing bending stress. Validated with the analytical value, a very good agreement was achieved with only a marginal deviation of 0.92%.
- Based on the validated reference model, the simulation of the cylindrical hollow was performed and an existing bending stress of = 47.76 MPa was achieved. Validated with the analytical value, a very good agreement was also obtained by a small deviation of 5.15%.
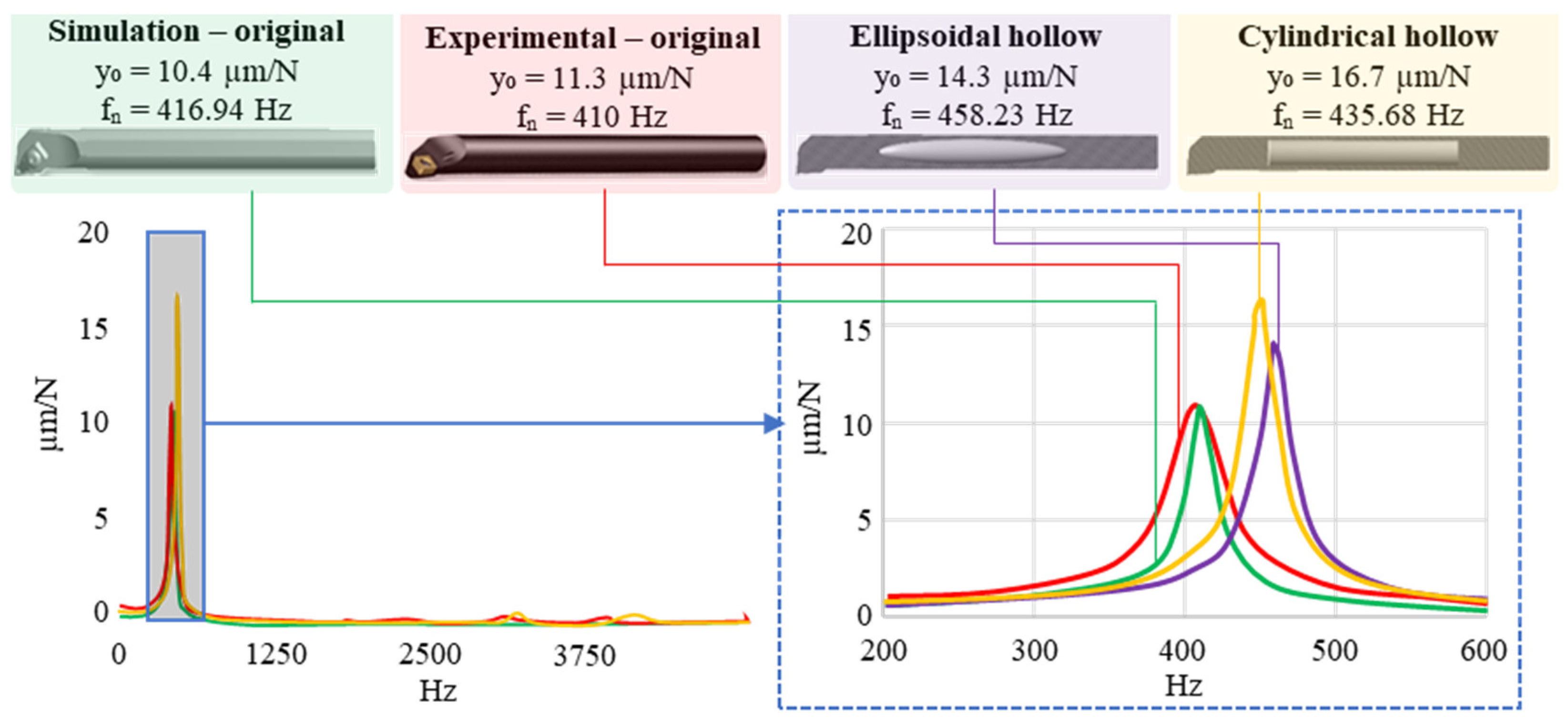
2.5. Modal Analysis and Harmonic Response Analysis of the Modified Hollow
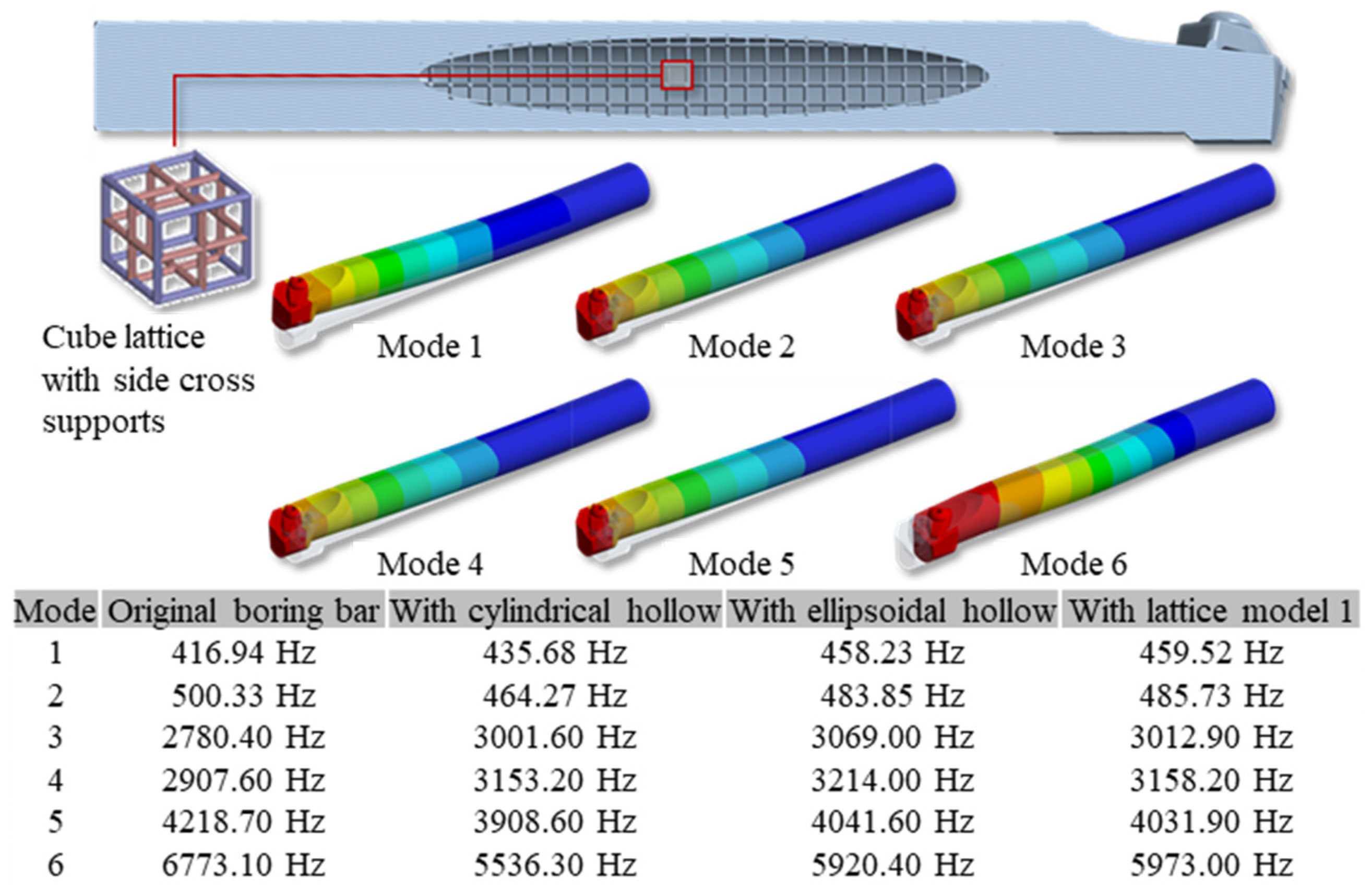
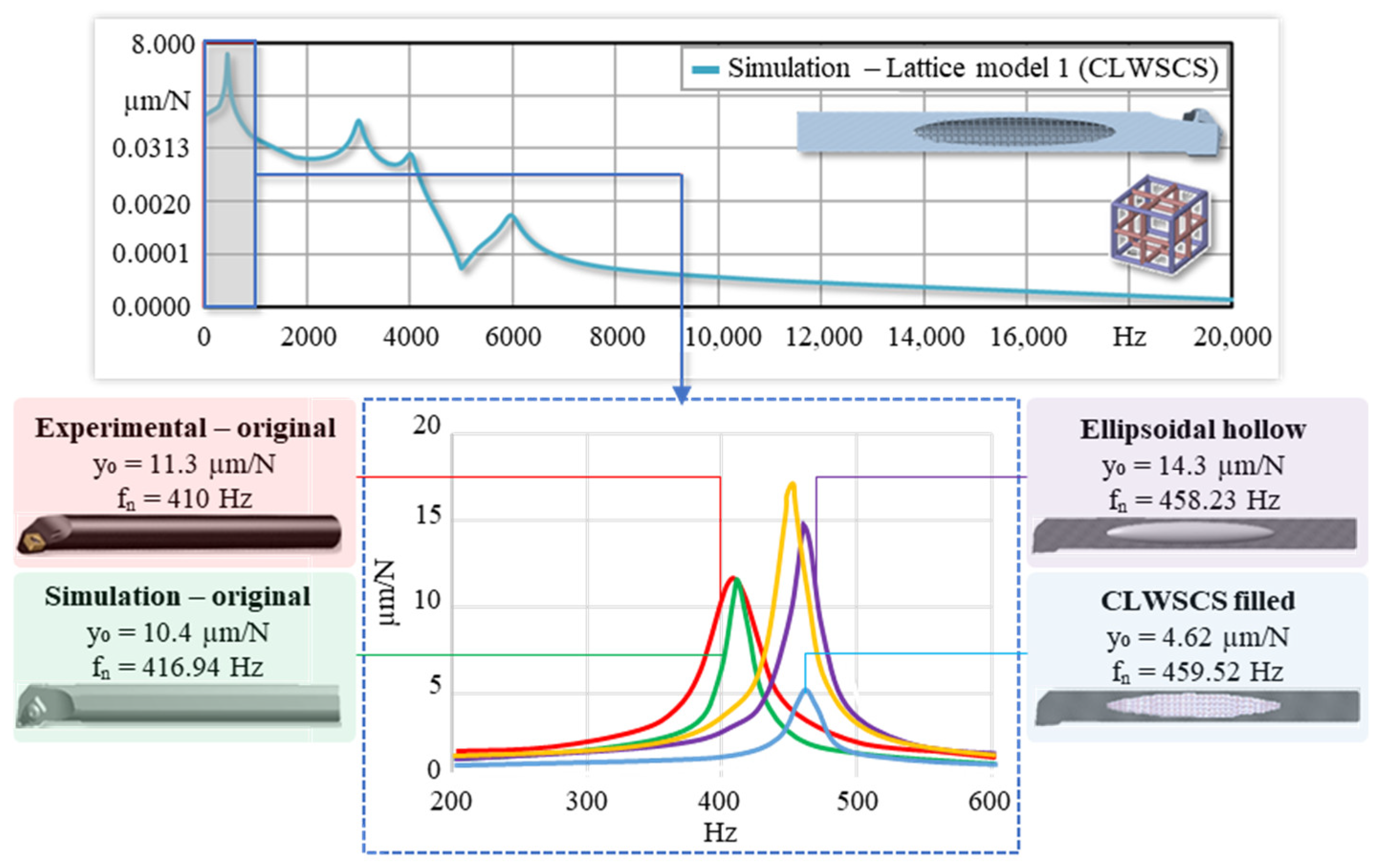
2.6. FEM Reference Model Damping Analysis with Lattice Cube
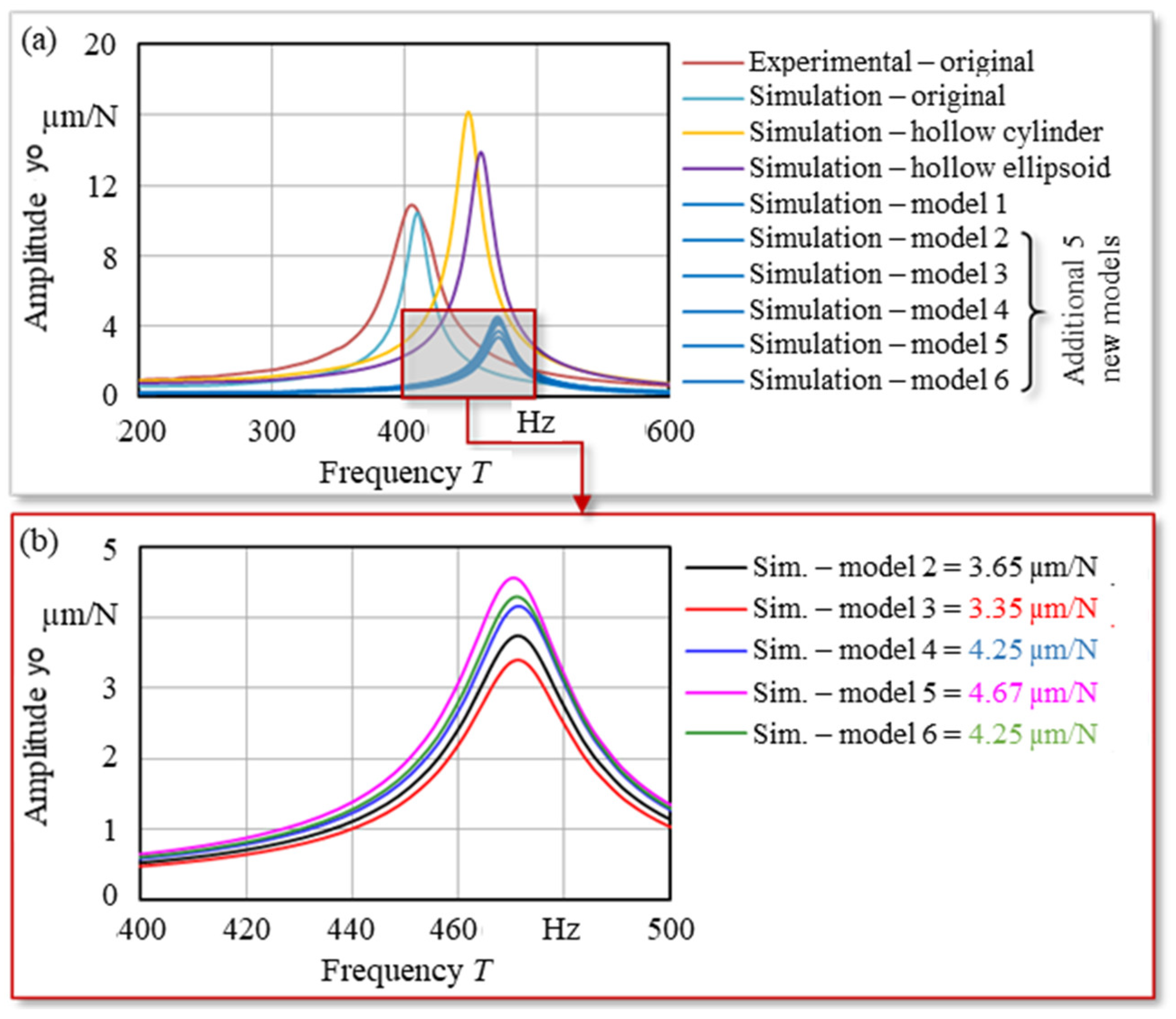
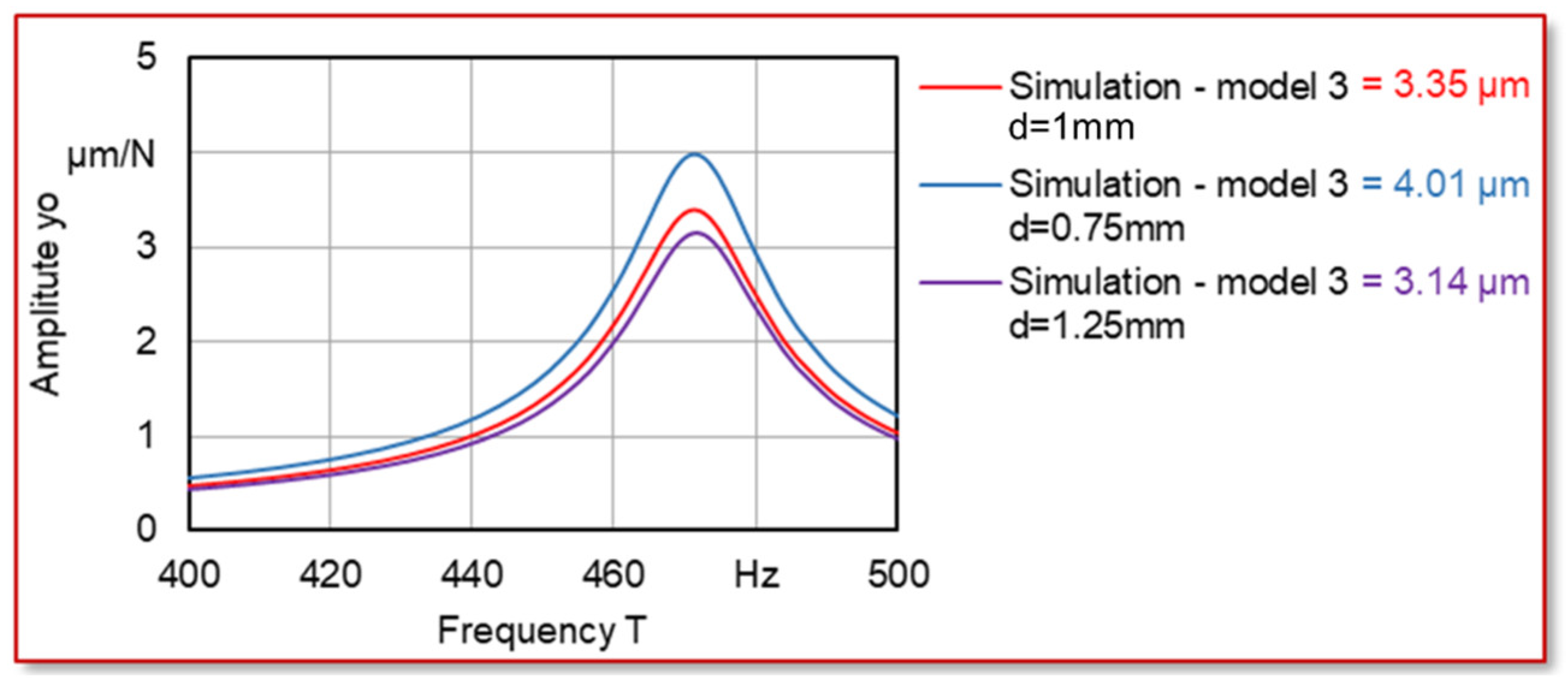
2.7. Testing of Different 3D Lattice Structures
2.8. Computation Time for the Simulations
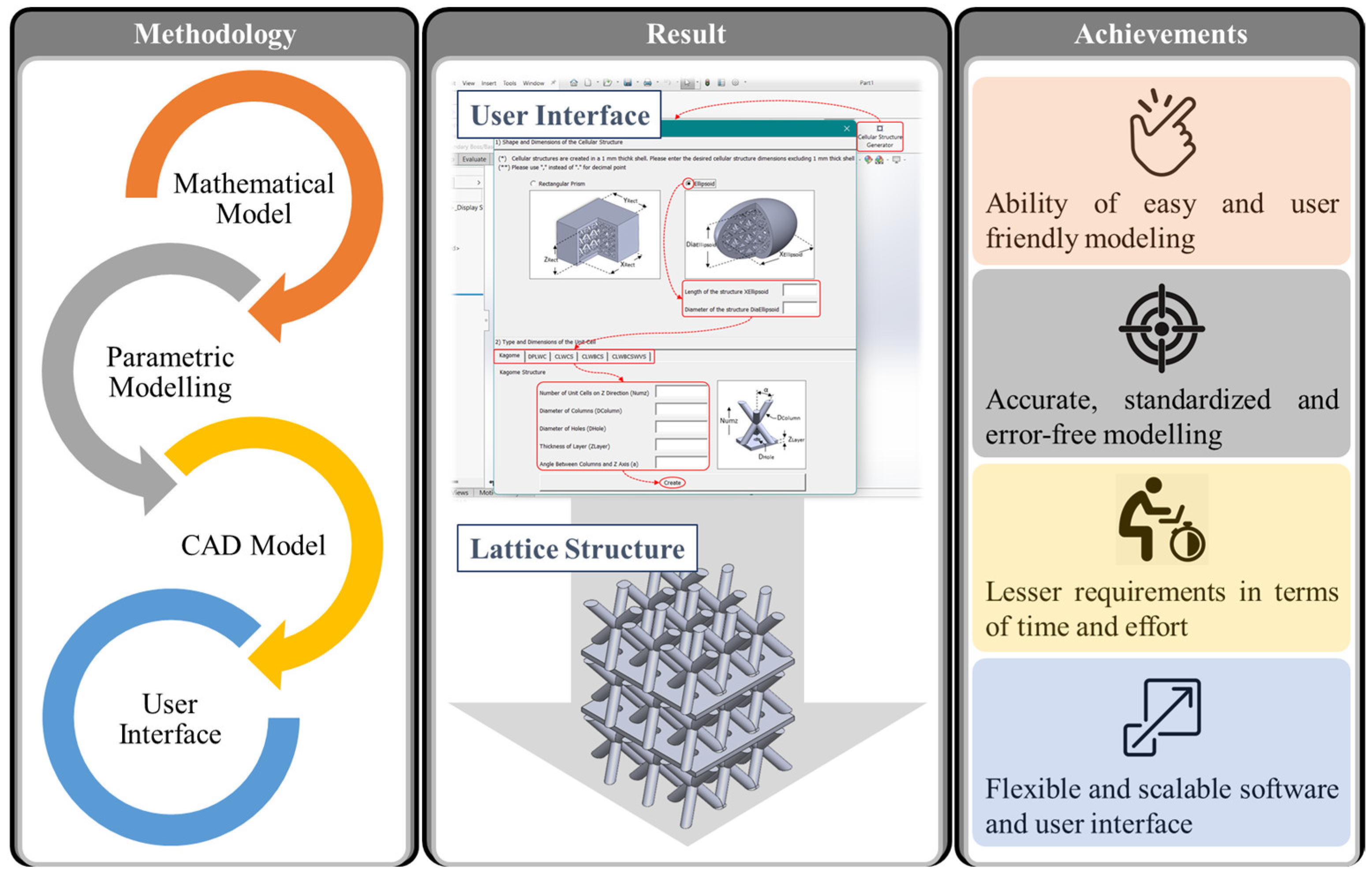
3. Development of a Specific Parametric CAD Software Tool
3.1. Methodology
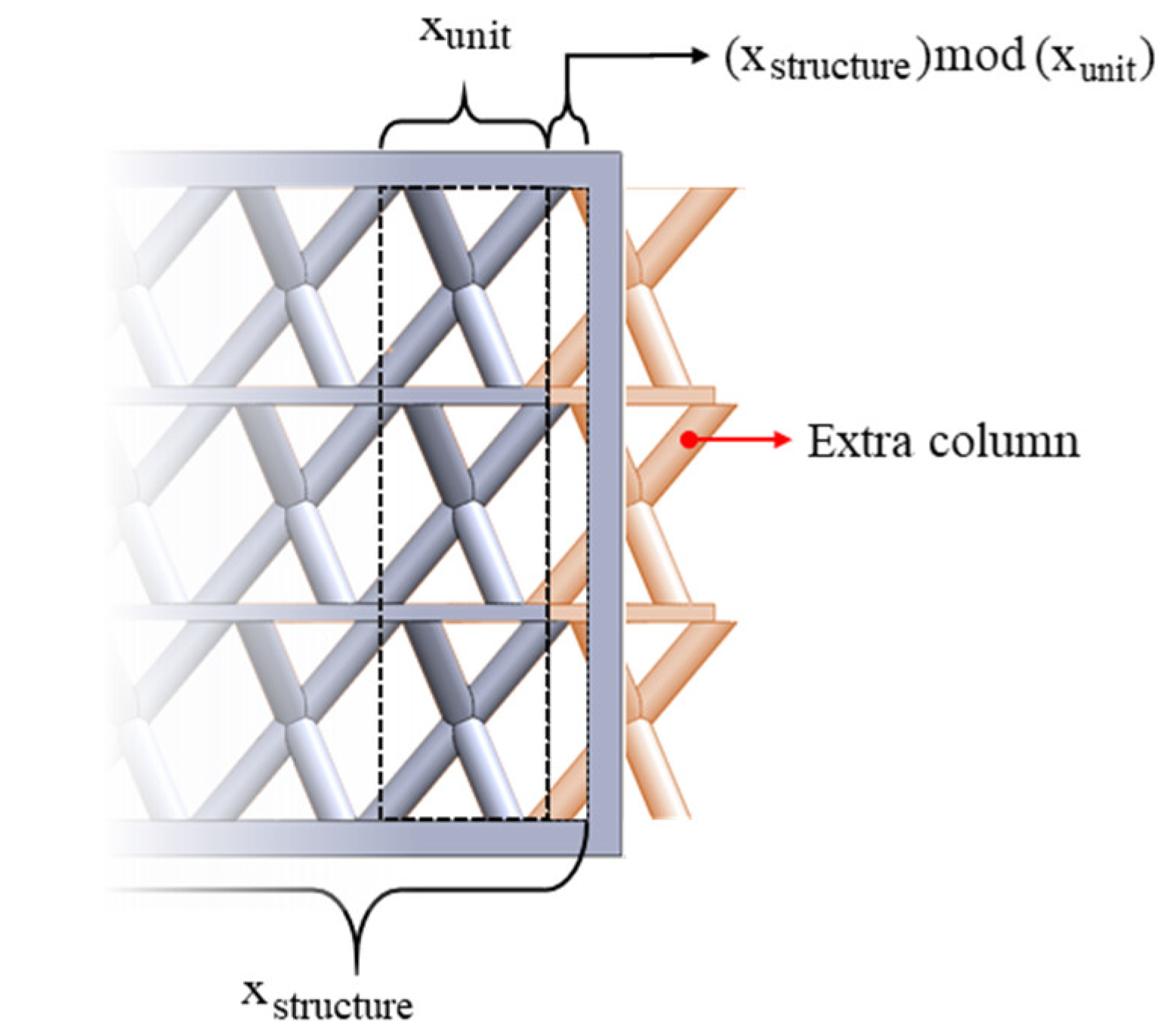
3.2. Mathematical Model of 3D Lattice Structures
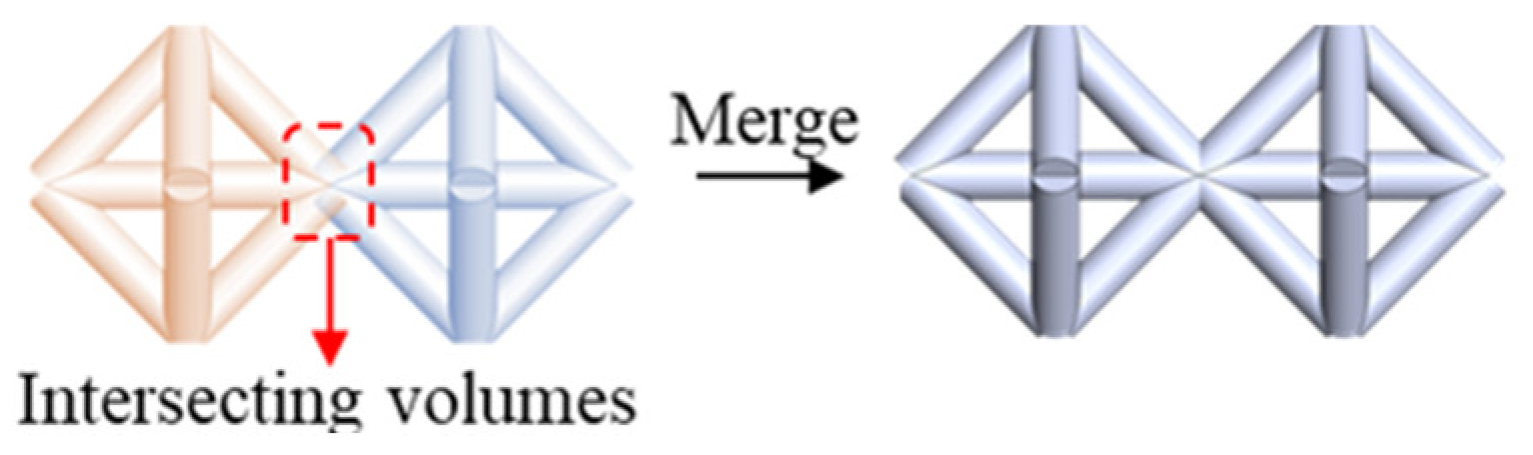
3.3. Lattice Structure Generation
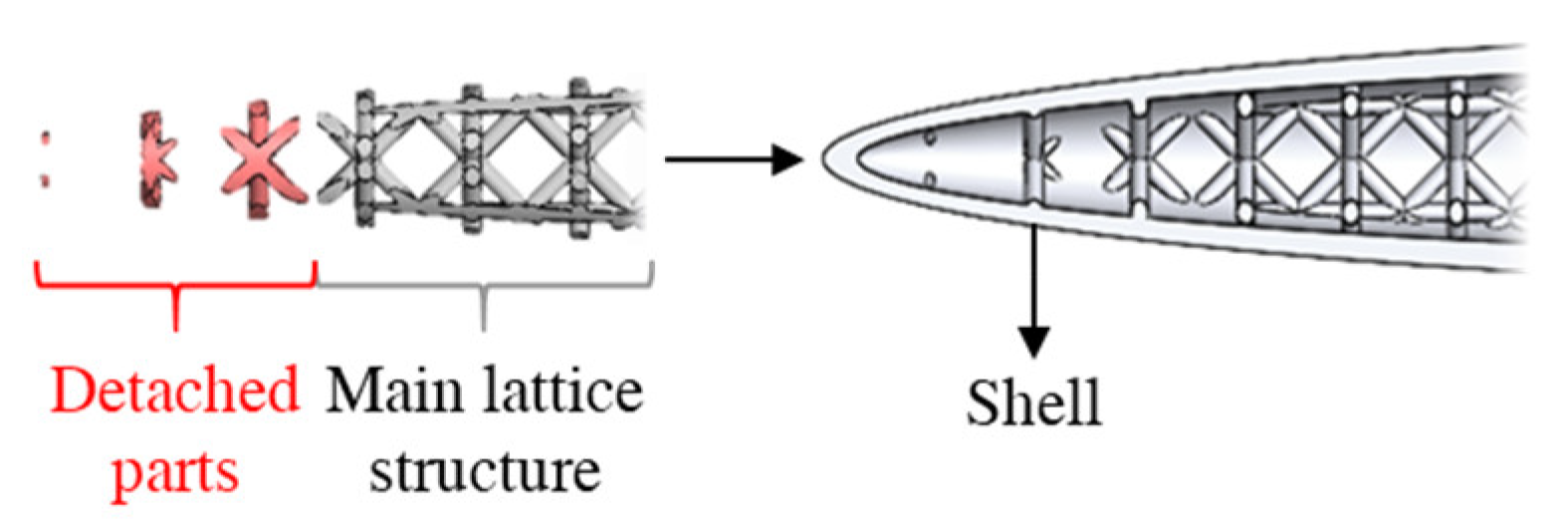
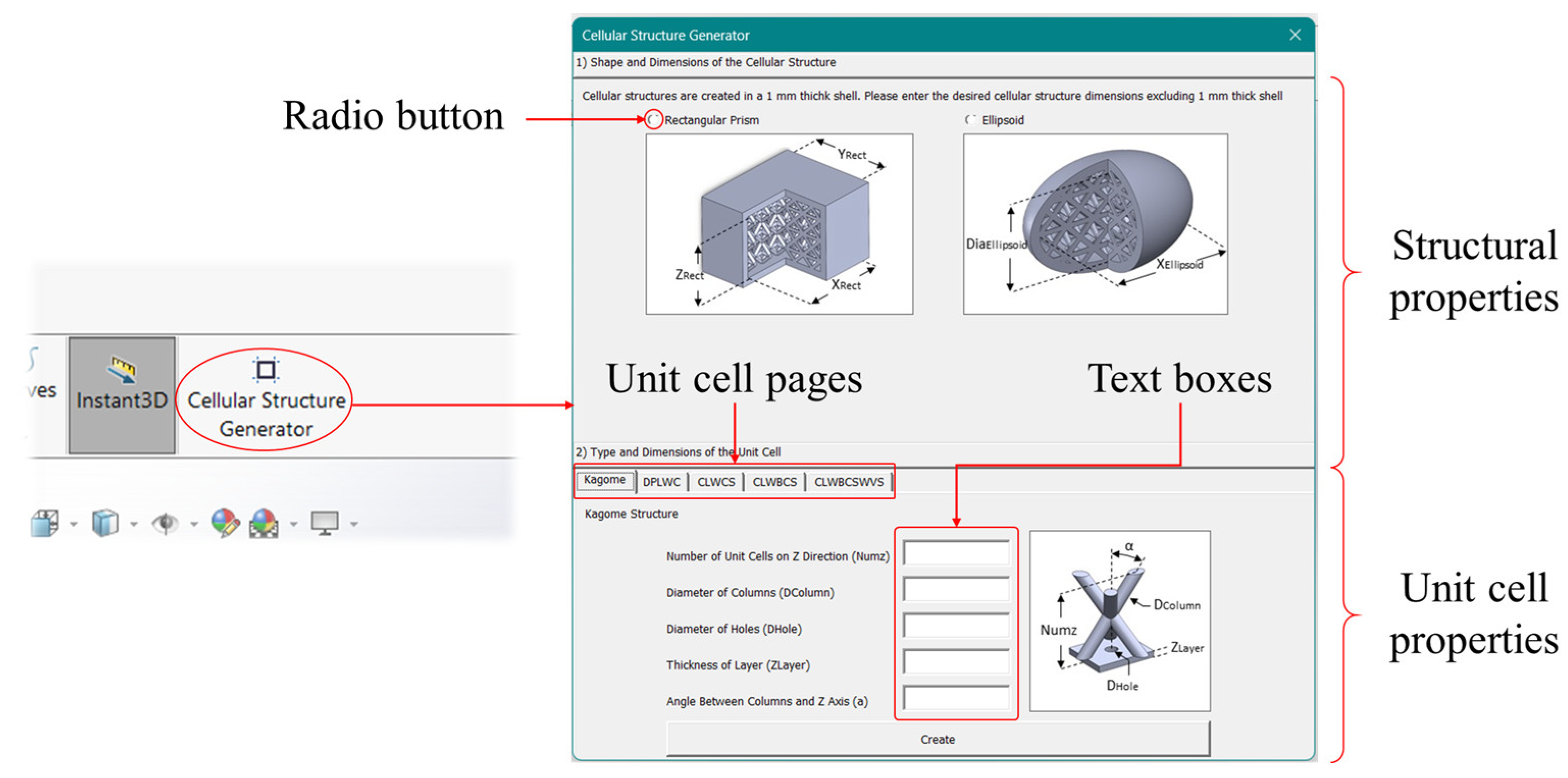
3.4. Modelling in the Specific Parametric CAD Software Tool
3.5. Computer Aided Parametric Modelling
- lattice unit generation,
- multiplication,
- shell generation,
- trimming, and
- scaling.
- Start Event (
) indicates the start of the process;
- The exclusive gateway (
) directs sequence flows to only one of the outgoing branches. When merging flows, the exclusive gateway waits for an incoming branch to complete before continuing the flow;
- The parallel gateway (
) directs the process path down multiple outbound sequence flows to be followed in parallel. When merging flows, the parallel gateway acts as a synchronization mechanism, waiting for all branches to complete before continuing the flow; and
- End event (
) indicates where a path will end.
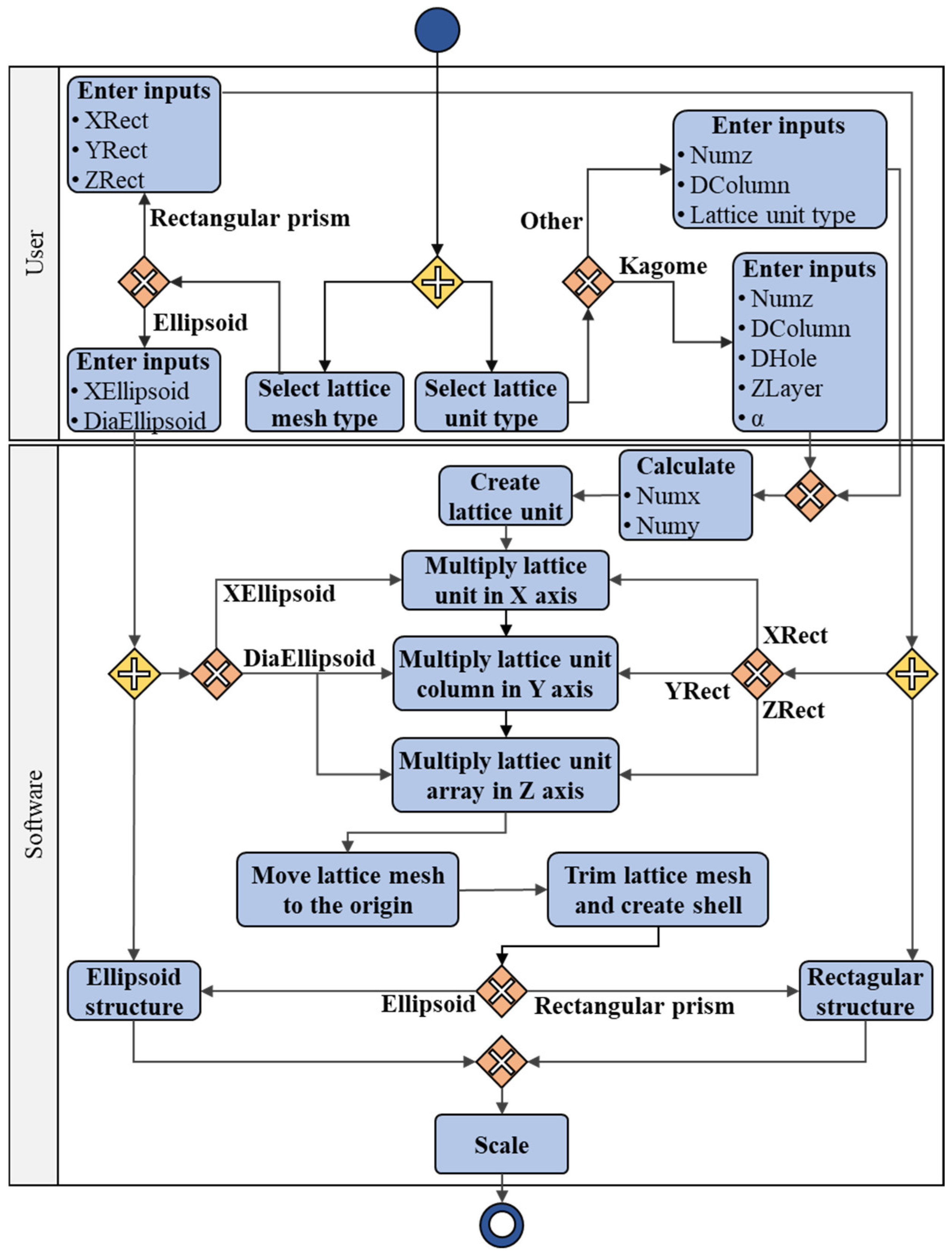
3.6. The User Interface
4. Discussion
5. Conclusions
- A validated FEM-based simulation model was developed, accurately predicting the dynamic behavior of the boring bar.
- In comparison with the cylindrical hollow, the optimal design was determined as ellipsoidal hollow shape by considering natural frequency and decrease in vibration amplitude.
- Six different lattice structures were designed, modelled, and analyzed, with the best-performing design achieving up to a 69.81% reduction in vibration amplitude.
- A dedicated parametric CAD simulation tool was developed to enable rapid and error-free generation of complex lattice structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |||
| 2D | Two Dimensional | FE | Finite Element |
| 3D | Three Dimensional | FEM | Finite Element Method |
| AM | Additive Manufacturing | GUI | Graphical User Interface |
| API | Application Programming Interface | HRA | Harmonic Response Analysis |
| BPMN | Business Process Model and Notation | ISO | International Organization for Standardization |
| C | Carbon | Mn | Manganese |
| CAD | Computer Aided Design | NURBS | Non-uniform Rational Basis Spline |
| CLWBCS | Cube Lattice with Bottom Centre Supports | P | Phosphorus |
| CLWBCWVS | Cube Lattice with Bottom Centre Without Vertical Supports | S | Sulphide |
| CLWCS | Cube Lattice with Centre Supports | Si | Silicon |
| CNC | Computer Numeric Control | TPMS | Triply Periodic Minimal Surfaces |
| Cr | Chromium | V | Vanadium |
| DAQ | Data acquisition | VBA | Visual Basic for Applications |
| DPLWC | Double Pyramid Lattice with Cross | ||
| Latin Letters | |||
| A | Cross sectional area | Numy | Number of lattice units in the y-axis direction |
| ap | Depth of cut (mm) | Numz | Number of lattice units in the z-axis direction |
| C | Damping matrix | Vc | Cutting speed (m/min) |
| d | Diameter (mm) | xstructure | Length of the lattice structure in x-axis direction (mm) |
| dcolumn | Diameter of the columns (mm) | xunit | Length of the lattice unit in x-axis direction (mm) |
| dhole | Diameter of the holes (mm) | y0 | Vibration amplitude (µm/N) |
| E | Modulus of elasticity | ystructure | Length of the lattice structure in y-axis direction (mm) |
| ej | Sinusoidal motion | yunit | Length of the lattice unit in y-axis direction (mm) |
| F | Force (N) | zlayer | Thickness of the separation layer between the lattice rows (mm) |
| f | Feed (mm/rev) | zstructure | Length of the lattice structure in z-axis direction (mm) |
| K | Stiffness matrix | zunit | Length of the lattice unit in z-axis direction (mm) |
| L | Length (mm) | T | Vibration frequency (Hz) |
| L/d | Slenderness ratio | t | Time (s) |
| Numx | Number of lattice units in the x-axis direction | ||
| Greek Letters | |||
| α | Angle between a support and vertical axis for kagome lattice (°) | σb | Bending stress (MPa) |
| θ | Phase shift | ψ | Force shift |
| ρ | Density (kg/m3) | Ω | Excitation frequency |
| σ | Stress (MPa) | ||
References
- Yadav, A.; Talaviya, D.; Bansal, A.; Law, M. Design of chatter-resistant damped boring bars using a receptance coupling approach. J. Manuf. Mater. Process. 2020, 4, 53. [Google Scholar] [CrossRef]
- Altintas, Y. Manufacturing Automation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Beri, B.; Meszaros, G.; Stepan, G. Machining of slender workpieces subjected to time-periodic axial force: Stability and chatter suppression. J. Sound Vib. 2021, 504, 116114. [Google Scholar] [CrossRef]
- Baklouti, W.; Mrad, C.; Nasri, R. Numerical study of the chatter phenomenon in orthogonal turning. Int. J. Adv. Manuf. Technol. 2018, 99, 755–764. [Google Scholar] [CrossRef]
- Yıldırım, G. Milli savaş uçağı KAAN, ASELSAN ile “BİLGE KAAN” olacak. 2024. Available online: https://www.aa.com.tr/tr/savunma-sanayisi/milli-savas-ucagi-kaan-aselsan-ile-bilge-kaan-olacak/3145409 (accessed on 28 April 2025).
- TEI-TF10000 Turbofan Motoru n.d. Available online: https://www.tei.com.tr/urunler/tei-tf10000-turbofan-motoru (accessed on 28 April 2025).
- Kubilay. TEI-TF6000 Turbofan Uçak Motoru. 2023. Available online: https://www.yerlivemilliteknoloji.com/tei-tf6000-turbofan-ucak-motoru/ (accessed on 28 April 2025).
- Şahin, G.; Aslanoğlu, V. Karadeniz’de yeni sondajlar yeni keşifler yolda. 2020. Available online: https://www.star.com.tr/acik-gorus/karadenizde-yeni-sondajlar-yeni-kesifler-yolda-haber-1568927/ (accessed on 28 April 2025).
- Türkiye’nin ilk yerli rüzgar gülü Bursa’daki RES’te. 2017. Available online: https://www.hurriyet.com.tr/ekonomi/turkiyenin-ilk-yerli-ruzgar-gulu-bursadaki-reste-40548746 (accessed on 28 April 2025).
- Medical Implants n.d. Available online: https://www.hiperbaric.com/en/hip-technology/hip-sectors/medical-implants/ (accessed on 28 April 2025).
- Diagnosis of Chatter Marks n.d. Available online: https://www.planlauf.com/en/measurement/diagnosis-of-chatter-marks/ (accessed on 28 April 2025).
- Keep a Close Eye on Piston Scuffing to Prevent Scoring and Seizing n.d. Available online: https://gesrepair.com/keep-a-close-eye-on-piston-scuffing-to-prevent-scoring-and-seizing/ (accessed on 28 April 2025).
- Parus, A.; Pajor, M.; Hoffmann, M. Suppression of self-excited vibration in cutting process using piezoelectric and electromagnetic actuators. Adv. Manuf. Sci. Technol. 2009, 33, 35–50. [Google Scholar]
- Quintana, G.; Ciurana, J. Chatter in machining processes: A review. Int. J. Mach. Tools Manuf. 2011, 51, 363–376. [Google Scholar] [CrossRef]
- Sun, Y.; Zheng, M.; Jiang, S.; Zhan, D.; Wang, R. A State-of-the-Art Review on Chatter Stability in Machining Thin−Walled Parts. Machines 2023, 11, 359. [Google Scholar] [CrossRef]
- Mehrabadi, I.M.; Nouri, M.; Madoliat, R. Investigating chatter vibration in deep drilling, including process damping and the gyroscopic effect. Int. J. Mach. Tools Manuf. 2009, 49, 939–946. [Google Scholar] [CrossRef]
- Muhammad, B.B.; Wan, M.; Feng, J.; Zhang, W.H. Dynamic damping of machining vibration: A review. Int. J. Adv. Manuf. Technol. 2017, 89, 2935–2952. [Google Scholar] [CrossRef]
- Munoa, J.; Beudaert, X.; Dombovari, Z.; Altintas, Y.; Budak, E.; Brecher, C.; Stepan, G. Chatter suppression techniques in metal cutting. CIRP Ann. 2016, 65, 785–808. [Google Scholar] [CrossRef]
- Khatake, P.; Nitnaware, P.T. Vibration mitigation using passive damper in machining. Int. J. Mod. 2013, 3, 3649–3652. [Google Scholar]
- Thomas, W.; Fulop, Z.; Szilágyi, A. Passive Damping Techniques for Vibration Suppression in Boring Operation with Long Overhangs. In Vehicle and Automotive Engineering 3; Jármai, K., Voith, K., Eds.; Springer: Singapore, 2021; Volume 22, pp. 256–264. [Google Scholar] [CrossRef]
- Vogel, F.A.M.; Berger, S.; Özkaya, E.; Biermann, D. Vibration suppression in turning TiAl6V4 using additively manufactured tool holders with specially structured, particle filled hollow elements. Procedia Manuf. 2019, 40, 32–37. [Google Scholar] [CrossRef]
- Aggogeri, F.; Borboni, A.; Merlo, A.; Pellegrini, N.; Ricatto, R. Vibration damping analysis of lightweight structures in machine tools. Materials 2017, 10, 297. [Google Scholar] [CrossRef] [PubMed]
- Szuba, P.; Zou, Q.; Barber, G.C.; Yang, L. Optimization of hollow cantilevered boring bar stiffness. Mach. Sci. Technol. 2005, 9, 325–343. [Google Scholar] [CrossRef]
- Nguyen, D.S. Design of lattice structure for additive manufacturing in CAD environment. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, 19-00175. [Google Scholar] [CrossRef]
- Thalhamer, A.; Fleisch, M.; Schuecker, C.; Fuchs, P.F.; Schlögl, S.; Berer, M. A black-box optimization strategy for customizable global elastic deformation behavior of unit cell-based tri-anti-chiral metamaterials. Adv. Eng. Softw. 2023, 186, 103553. [Google Scholar] [CrossRef]
- Chen, K.; Fang, S.; Gao, Q.; Zou, D.; Cao, J.; Liao, W.H. An enhanced nonlinear piezoelectric energy harvester with multiple rotating square unit cells. Mech. Syst. Signal Process. 2022, 173, 109065. [Google Scholar] [CrossRef]
- Chen, X.; Ren, W.; Sun, Y.; Zhang, J.; Yang, J.; Wang, K.; Gong, Y.; Zhang, Z.; Bai, L. Adjusting unit cell three-dimensional posture and mirror array: A novel lattice structure design approach. Mater. Des. 2022, 221, 110852. [Google Scholar] [CrossRef]
- Fongsamootr, T.; Suttakul, P.; Tippayawong, N.; Nanakorn, P.; Cappellini, C. Bending behavior of 2D periodic plates with different unit cells: Numerical and experimental investigations. Mater. Today Commun. 2022, 31, 103774. [Google Scholar] [CrossRef]
- Préve, D.; Lenarda, P.; Maskery, I.; Paggi, M. A comprehensive characterization of fracture in unit cell open foams generated from Triply Periodic Minimal Surfaces. Eng. Fract. Mech. 2023, 277, 108949. [Google Scholar] [CrossRef]
- Sauermoser-Yri, M.; Veldurthi, N.; Wölfle, C.H.; Svartvatn, P.J.; Flo Hoem, S.O.; Lid, M.J.; Bock, R.; Palko, J.W.; Torgersen, J. On the porosity-dependent permeability and conductivity of triply periodic minimal surface based porous media. J. Mater. Res. Technol. 2023, 27, 585–599. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Tang, M.; Cai, C.; Wu, J.; Zhang, Z.; Shi, Y. Field-driven design and performance evaluation of dual functionally graded triply periodic minimal surface structures for additive manufacturing. Mater. Des. 2023, 233, 112257. [Google Scholar] [CrossRef]
- Yan, K.; Wang, J.; Li, L.; Deng, H. Numerical investigation into thermo-hydraulic characteristics and mixing performance of triply periodic minimal surface-structured heat exchangers. Appl. Therm. Eng. 2023, 230, 120748. [Google Scholar] [CrossRef]
- Kaur, I.; Singh, P. Flow and Thermal Transport Through Unit Cell Topologies of Cubic and Octahedron Families. Int. J. Heat Mass Transf. 2020, 158, 119784. [Google Scholar] [CrossRef]
- Dharmaraj, M.; Kumar, K.V.S.; Sridhar, C. Crashworthiness unit cell design investigation for energy absorption analysis. Mater. Today Proc. 2021, 50, 1282–1290. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Butscher, A.; Watts, S.; Tortorelli, D.A. Anisotropic yield models for lattice unit cell structures exploiting orthotropic symmetry. Comput. Methods Appl. Mech. Eng. 2022, 394, 114935. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, L.; Gain, A.K. A novel auxetic unit cell for 3D metamaterials of designated negative Poisson’s ratio. Int. J. Mech. Sci. 2023, 260, 108614. [Google Scholar] [CrossRef]
- Deshmukh, S.; Kumar, S.; Wagh, A.; Krishnan, S.; Ramamoorthy, S. Selection of periodic cellular structures for multifunctional applications directly based on their unit cell geometry. Int. J. Mech. Sci. 2022, 220, 107133. [Google Scholar] [CrossRef]
- Corbett, T.M.; Thole, K.A. Large eddy simulations of kagome and body centered cubic lattice cells. Int. J. Heat Mass Transf. 2024, 218, 124808. [Google Scholar] [CrossRef]
- An, X.; Sun, G.; Yuan, X.; Tian, Y.; Hou, X.; Fan, H. Design of Kagome lattice composite sandwich metastructures with high load bearing and low frequency vibration reduction properties. Compos. Part A Appl. Sci. Manuf. 2023, 174, 107716. [Google Scholar] [CrossRef]
- Xu, W.; Yu, A.; Lu, X.; Tamaddon, M.; Wang, M.; Zhang, J.; Zhang, J.; Qu, X.; Liu, C.; Su, B. Design and performance evaluation of additively manufactured composite lattice structures of commercially pure Ti (CP–Ti). Bioact. Mater. 2021, 6, 1215–1222. [Google Scholar] [CrossRef]
- Yao, J.; Su, Y.; Scarpa, F.; Li, Y. An optimization approach to design deformation patterns in perforated mechanical metamaterials using distributions of Poisson’s ratio-based unit cells. Compos. Struct. 2022, 281, 115015. [Google Scholar] [CrossRef]
- Seto, Y.; Ullah, A.S.; Kubo, A.; D’Addona, D.M.; Teti, R. On the Porous Structuring using Unit Cells. Procedia CIRP 2021, 99, 381–386. [Google Scholar] [CrossRef]
- Maskery, I.; Parry, L.A.; Padrão, D.; Hague, R.J.M.; Ashcroft, I.A. FLatt Pack: A research-focussed lattice design program. Addit. Manuf. 2022, 49, 102510. [Google Scholar] [CrossRef]
- Geyer, S.; Hölzl, C. Comparison of CAD Software for Designing Cellular Structures for Additive Manufacturing. Appl. Sci. 2024, 14, 3360. [Google Scholar] [CrossRef]
- Azman, A.H.; Vignat, F.; Villeneuve, F. Evaluating current cad tools performances in the context of design for additive manufacturing. In Proceedings of the Joint Conference on Mechanical, Design Engineering & Advanced Manufacturing, Toulouse, France, 18–20 June 2014; pp. 1–7. [Google Scholar]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for Additive Manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Liu, H.C.; Wan, M.; Zhang, W.H. A new cutting tool filled with metallic lattice and design method for vibration suppression in milling. Mech. Syst. Signal Process. 2024, 212, 111310. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.-L.; Yuan, J.-W.; Kong, W.-L.; Wan, M.; Zang, W.-H. Development of an anti-vibration cutting tool combining the lattice structures infill with damping particles. Mech. Syst. Signal Process. 2025, 228, 112425. [Google Scholar] [CrossRef]
- Jared, B.H.; Aguilo, M.A.; Beghini, L.L.; Boyce, B.L.; Clark, B.W.; Cook, A.; Kaehr, B.J.; Robbins, J. Additive manufacturing: Toward holistic design. Scr. Mater. 2017, 135, 141–147. [Google Scholar] [CrossRef]
- Robbins, J.; Owen, S.J.; Clark, B.W.; Voth, T.E. An efficient and scalable approach for generating topologically optimized cellular structures for additive manufacturing. Addit. Manuf. 2016, 12, 296–304. [Google Scholar] [CrossRef]
- Azman, A.H.; Vignat, F.; Villeneuve, F. Cad tools and file format performance evaluation in designing lattice structures for additive manufacturing. J. Teknol. 2018, 80, 87–95. [Google Scholar] [CrossRef]
- Downing, D.; McMillan, M.; Brandt, M.; Leary, M. Programmatic lattice generation tools for additive manufacture [Formula presented]. Softw. Impacts 2022, 12, 100262. [Google Scholar] [CrossRef]
- Manufacturing Automation Laboratories n.d. Available online: https://www.malinc.com/ (accessed on 28 April 2025).
- Budak, E.; Ozlu, E. Analytical Modeling of Chatter Stability in Turning and Boring Operations: A Multi-Dimensional Approach. CIRP Ann. 2007, 56, 401–404. [Google Scholar] [CrossRef]
- Ozlu, E.; Budak, E. Analytical modeling of chatter stability in turning and boring operations—Part I: Model development. J. Manuf. Sci. Eng. 2007, 129, 726–732. [Google Scholar] [CrossRef]
- Lanczos, C. An Iteration Method for the Solution of the Eigenvalue Problem of Linear Differentail and Integral Operators. J. Res. Natl. Bur. Stand. 1950, 45, 255–282. [Google Scholar] [CrossRef]
- Astarloa, A.; Comak, A.; Mancisidor, I.; Fernandes, M.H.; Munoa, J.; Dombovari, Z. Improvement of boring operations by means of mode coupling effect. CIRP J. Manuf. Sci. Technol. 2022, 37, 633–644. [Google Scholar] [CrossRef]
- Houck, L.; Schmitz, T.L.; Smith, K.S. A tuned holder for increased boring bar dynamic stiffness. J. Manuf. Process. 2011, 13, 24–29. [Google Scholar] [CrossRef]
- Cheng, L.; Liang, X.; Belski, E.; Wang, X.; Sietins, J.M.; Ludwick, S.; To, A.C. Natural frequency optimization of variable-density additive manufactured lattice structure: Theory and experimental validation. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 105002. [Google Scholar] [CrossRef]
- Nightingale, M.; Hewson, R.; Santer, M. Multiscale optimisation of resonant frequencies for lattice-based additive manufactured structures. Struct. Multidiscip. Optim. 2021, 63, 1187–1201. [Google Scholar] [CrossRef]
- Xia, Q.; Shi, T.; Wang, M.Y. A level set based shape and topology optimization method for maximizing the simple or repeated first eigenvalue of structure vibration. Struct. Multidiscip. Optim. 2011, 43, 473–485. [Google Scholar] [CrossRef]
- Elmadih, W.A.; Syam, W.P.; Maskery, I.; Leach, R. Additively manufactured lattice structures for precision engineering applications. In Proceedings of the 32nd Annual Meeting of American Society for Precision Engineering, Charlotte, NC, USA, 29 October–3 November 2017; pp. 164–169. [Google Scholar]
- Huang, Y.; Wan, A.R.O.; Schmidt, K.; Sefont, P.; Singamneni, S.; Chen, Z.W. Effects of cell orientation on compressive behaviour of electron beam powder bed fusion Ti6Al4V lattice structures. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Li, Y.; Pavier, M.; Coules, H. Fracture behaviour of octet-truss lattices in different orientations. Procedia Struct. Integr. 2022, 37, 49–56. [Google Scholar] [CrossRef]

















| Vibration Damping | Characteristics |
|---|---|
| Active Methods | Installation of additional devices, such as actuators |
| Use of advanced and complex control algorithms | |
| Knowledge of vibrations eigen-frequencies | |
| Model-based strategy | |
| Passive Methods | Based on viscoelastic materials, viscous fluids, magnetic, or passive piezoelectric, lightweight materials |
| Vibration energy dissipation or redirection | |
| Cost effective | |
| Dampers are usually small size and easy to install |
| Physical | Tensile Strength | Yield Point | Elongation | Contraction | Impact Resistance | Elasticity Modulus | Density | Poisson’s Ratio |
|---|---|---|---|---|---|---|---|---|
| 1000–1200 MPa | >550 MPa | >10% | >45% | >30 J | 210 × 103 MPa | 7.7 kg/dm3 | 0.29 | |
| Chemical | C % | Si % | Mn % | P % | S % | Cr % | V % | |
| Minimum | 0.47 | - | 0.70 | - | - | 0.90 | 0.10 | |
| Maximum | 0.55 | 0.40 | 1.10 | 0.025 | 0.025 | 1.20 | 0.25 |
| Model | Modified Diameter | Length | Bending Stress in Section A-A | Bending Stress in Section B-B |
|---|---|---|---|---|
| C12H1 | 12 mm | 70 mm | 47.768 MPa | 63.119 MPa |
| C12H2 | 12 mm | 100 mm | 36.219 MPa | 65.659 MPa |
| C12H3 | 12 mm | 130 mm | 32.275 MPa | 59.626 MPa |
| C15H1 | 15 mm | 70 mm | 60.100 MPa | 81.006 MPa |
| C15H2 | 15 mm | 100 mm | 48.598 MPa | 92.165 MPa |
| C15H3 | 15 mm | 130 mm | 46.153 MPa | 94.645 MPa |
| C18H1 | 18 mm | 70 mm | 81.493 MPa | 118.690 MPa |
| C18H2 | 18 mm | 100 mm | 71.630 MPa | 128.910 MPa |
| C18H3 | 18 mm | 130 mm | 62.477 MPa | 131.050 MPa |
| C21H1 | 21 mm | 70 mm | 121.370 MPa | 175.840 MPa |
| C21H2 | 21 mm | 100 mm | 102.110 MPa | 217.450 MPa |
| C21H3 | 21 mm | 130 mm | 90.315 MPa | 255.730 MPa |
 | ||||
| Node | Elements | Data Size | Simulation Time | |
|---|---|---|---|---|
| High-End Workstation Features | HP Z800 2× CPU Intel Xeon W5580, 3.50 GHz, 8 MB L3, 1333 MHz Memory, 130W32 144 GB (4 × 12 GB; 6 × 16 GB) DDR3-1333 ECC Registered RAM 2-CPU NVIDIA Quadro FX 5800 4 GB PCIe Graphics Card 1110 W 89% (SILVER) Efficient wide-ranging, active Power Factor Correction | |||
| FEM- MODAL/HRA reference model (full) | 1855.120 | 1360.492 | 47.54 GB | 4 h 22 min |
| FEM- MODAL/HRA cylindrical hollow model | 1470.612 | 960.958 | 51.55 GB | 5 h 38 min |
| FEM- MODAL/HRA ellipsoidal hollow model | 1201.598 | 798.921 | 54.29 GB | 12 h 59 min |
| FEM static/mechanical analysis 13 models (see Table 3) | - | - | 120.18 GB | 32 d 10 h 46 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 1 | 28,816.225 | 19,167.250 | 277.15 GB | 10 d 21 h 27 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 2 | 27,972.315 | 18,245.017 | 263.27 GB | 10 d 10 h 13 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 3 | 28,012.064 | 18,644.344 | 265.05 GB | 11 d 7 h 38 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 4 | 29,106.924 | 19,909.789 | 281.98 GB | 11 d 13 h 3 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 5 | 29,181.181 | 19,960.379 | 282.23 GB | 11 d 33 h 42 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 6 | 28,776.861 | 19,227.129 | 278.33 GB | 11 d 47 h 7 min |
| FEM-MODAL/HRA ellipsoidal hollow with simulation model 3 d = 0.75 mm | 27,004.154 | 17,991.879 | 259.85 GB | 10 d 1 h 41 min |
| FEM- MODAL/HRA ellipsoidal hollow with simulation model 3 d = 1.25 mm | 29,914.361 | 20,044.485 | 291.96 GB | 12 d 5 h 52 min |
| # | Type of Lattice Unit | Model | # | Type of Lattice Unit | Model |
|---|---|---|---|---|---|
| 1 | Kagome |  | 4 | CLWBCWVS (Cube Lattice with Bottom Centre Without Vertical Supports) |  |
| 2 | CLWCS (Cube Lattice with Center Supports) |  | 5 | DPLWC (Double Pyramid Lattice with Cross) |  |
| 3 | CLWBCS (Cube Lattice with Bottom Center Supports) |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oezkaya, E.; Aslantas, K.; Çiçek, A.; Çetindağ, H.A. Integration of Lattice Structures into the Boring Bars as a Passive Chatter Suppression Technique: Concepualization, Modelling and Simulation. Vibration 2025, 8, 29. https://doi.org/10.3390/vibration8020029
Oezkaya E, Aslantas K, Çiçek A, Çetindağ HA. Integration of Lattice Structures into the Boring Bars as a Passive Chatter Suppression Technique: Concepualization, Modelling and Simulation. Vibration. 2025; 8(2):29. https://doi.org/10.3390/vibration8020029
Chicago/Turabian StyleOezkaya, Ekrem, Kubilay Aslantas, Adem Çiçek, and Hüseyin Alp Çetindağ. 2025. "Integration of Lattice Structures into the Boring Bars as a Passive Chatter Suppression Technique: Concepualization, Modelling and Simulation" Vibration 8, no. 2: 29. https://doi.org/10.3390/vibration8020029
APA StyleOezkaya, E., Aslantas, K., Çiçek, A., & Çetindağ, H. A. (2025). Integration of Lattice Structures into the Boring Bars as a Passive Chatter Suppression Technique: Concepualization, Modelling and Simulation. Vibration, 8(2), 29. https://doi.org/10.3390/vibration8020029














