Abstract
The optimal design methodology for a Maxwell–Coulomb friction damper is proposed to minimize the resonant vibration of dynamic structures. The simple Coulomb friction damper has the problem of zero or little damping effect of the vibration of the spring–mass dynamic system at resonance. This problem is solved in the case of the Maxwell–Coulomb friction damper, which is formed by combining a Coulomb friction damper with a spring element in series. However, the design and analysis of the Maxwell–Coulomb friction damper become much more complicated. The optimal design methodology for this nonlinear damper is proposed in this article. The nonlinear equations of motion of the proposed damper are modelled, and its hysteresis loop can be constructed by combining four different cases of stick–slide motion. Motion responses of the turbine blade with the proposed damper are solved by a central difference solver. Optimal paths of damping and stiffness ratios are determined by the central difference Newton search method. The optimal experimental design is ascertained using a prototype damper test. Close correlation with its numerical simulations is observed in our hysteresis loop comparison. The performance of the proposed damper is also compared to that of a viscous damper in the seismic response design of adjacent single-story buildings.
1. Introduction
The response of a single-degree-of-freedom (SDOF) system with a tuned mass damper with traditional linear stiffness and a dry friction damping arrangement subjected to harmonic excitation was considered by Ricciardelli and Vickery [1]. In the traditional Coulomb damper, the optimal solution delivered a standard response curve, which almost flat in a broad range of frequencies. However, its response became singular at resonances leading to instability or excessive vibration of the primary system. A tunable friction damper was established by Lee et al. [2] using viscous and Coulomb elements in a parallel arrangement. It was designed to work as a friction damper while the mass slips and as a vibration absorber while the mass sticks. However, it involved a more complicated and expensive viscous component. The frictional force was coupled with the vibration amplitude. This reduced the peak amplitude, and it reduced the offsets in both the frictional force and vibration amplitude. In our turbine blade vibration simulation, these offsets are inessential to damper design. A similar report was given on dual blades [2], with minimum coupling being applied to reduce their effects. However, these offsets are essential to actual Maxwell–Coulomb (MC) friction damper testing.
In the work of Brizard et al. [3], a friction damper was designed and a prototype was built to reduce engine vibrations on a space launcher. The friction damper was modeled by a spring in series with a friction element. The damper prototype proved to efficiently dampen the rocket engine vibrations. The design method used for dimensioning the friction damper gave an approximation of the optimal sliding force of the damper. The adaptive friction damper prototype enables the sliding force to be adjusted by controlling the normal force. For our optimal design process, the damper spring and friction element are arranged in the Maxwell configuration similarly. However, we do not consider just the energies related to the damper. The performance of its transmissibility is one of the key factors used in our design. Its derivative at the specific level is employed to optimize its stiffness ratio as another factor. Simultaneously, its damping ratio is optimized using the force ratio between the Coulomb force and the applied force.
Research efforts have been directed toward perfecting the Maxwell-type damper arrangement in dynamic vibration absorber (DVA) research. The response of the SDOF spring mass system connected to a vibration absorber with a flexible friction damper and subjected to sinusoidal excitation was considered by Sinha and Trikutam [4]. Its flexible friction damper was of Maxwell configuration in the two-DOF system. Meanwhile, its motion equations were derived with the Lindstedt–Poincaré (LP) method, commonly used in nonlinear vibration. As approximate one-term ODEs were derived without considering stick–slip motion cases, only simple sinusoidal motion responses were generated without stick–slip motion features. Then, they were solved numerically by an ordinary differential equation (ODE) method. The friction damper was used by Wang and Chen [5] to reduce the maximum vibration of an engine blade. Although the harmonic balance method (HBM) is a well-known method for studying nonlinear vibration problems, generally, only a one-term approximation is proposed to study the nonlinear vibration of a frictionally damped blade. In their work, an HMB procedure with a multi-term approximation was proposed. The results showed that the steady-state response and other related behavior of a frictionally damped blade were predicted accurately and quickly by an HBM with a multi-term approximation. An accurate frictional damping loop was simulated with stick–slip motions. In this analysis, a similar turbine blade is implemented to demonstrate the correctness of the hysteresis loop generated by the central difference solution. Various unconstrained central difference search methods are developed to optimize turbine blade friction and stiffness. They are well adapted, according to the finite-difference ODE solutions.
A numerical method was developed by Hatada et al. [6] for the dynamic analysis of a tall building structure with viscous dampers in the Maxwell configuration. Viscous dampers were installed between the top of an inverted V-shaped brace and the upper beam on each story to reduce vibrations during strong disturbances like earthquakes. A third-order differential equation was established. The computational method was formulated by incorporating a finite element of the Maxwell model into the second-order ODE of motion. Forward-difference forms of restoring force and velocity were implemented to approximate its solution. Bhaskararao and Jangid [7] investigated the dynamic behavior of two identical adjacent structures connected with viscous dampers under base acceleration. Peak displacements and minimum inter-story damping were obtained. Closed-form expressions for the optimum damping of undamped structures were applied to the damped structure. The governing differential equations of motion of the coupled system were derived and solved for relative displacement and absolute acceleration responses by Patel and Jangid [8]. Parametric study was conducted to study the influence of important system parameters (such as excitation frequency, mass ratio, and stiffness ratio) on the response behavior of damper connected structures. Chen and Wu [9] investigated the seismic performance of two adjacent towers and podiums connected by viscous dampers. Three types of damper placement were discussed, including installing dampers within a single building, connecting two buildings at the same floor level, and connecting two buildings at the inter-story level. In this effort, the Maxwell–Coulomb damper is applied to suppress the maximum displacement of adjacent towers and podiums subjected to ground motions. Its performance is compared with viscous damper using equivalent damping ratios.
In this SDOF design, we discover that the commonly used viscous damper is less effective for lower range damping ratio application. From the shape of contour graph, it appeared to produce straight lines. On the other side, the Maxwell–Coulomb damper displays a concave downward contour as the damping ratio decreases. Compared to the viscous damper, its performance is better at lower range. Thus, this damper can be a better alternative than the viscous damper because of its low cost and ease of maintenance. However, the friction damper was not as commonly used as viscous damper because its design involved nonlinear dynamics analysis. Also, the pure Coulomb friction damper had the problem of zero or little damping effect on the vibration of a spring–mass dynamic system at resonance where singularity is occurring. With the combination of a Maxwell spring, these gaps can be addressed by a relatively convenient conversion using a viscous equivalent damping coefficient, resulting in less drastic and more stable motion under additional stiffness.
A mesh-free least-squares-based finite difference method was applied by Wu et al. [10] for solving the large-amplitude free vibration problem of arbitrarily shaped thin plates. Spatial derivatives of a function at a point are expressed as weighted sums of the function values of a group of supporting points. A string/slider nonlinear coupling system with a time-dependent boundary condition was considered by Fung and Chang [11]. The finite difference method with a variable grid was employed to show the numerical results of the coupling effect between the string and slider. The three-dimensional dynamics of long pipes towed underwater were analyzed by Kheiri et al. [12]. In their finite difference scheme, partial differential equations of motion and boundary conditions were converted into a set of first-order ODEs. In our analysis, ODEs from four case models were solved separately using the central difference method. Then, they were sequentially connected by initial displacements and velocities.
2. System Modeling and Central Difference Solver of Coulomb Dampers
2.1. System Modeling of Rigid Coulomb Friction Damper
Figure 1 illustrates a single-degree-of-freedom system of mass M and stiffness K with a Coulomb friction damper of equivalent viscous damping factor excited by a harmonic force of amplitude .
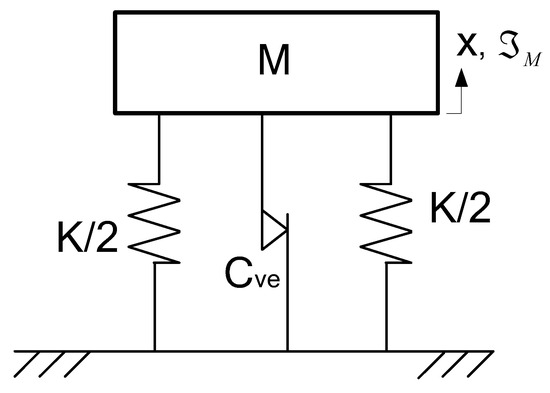
Figure 1.
Modeling of structural system with a rigid Coulomb friction damper.
The general form of a steady state vibration amplitude X of displacement x under harmonic excitation frequency can be represented as
Its energy dissipation per cycle is
Its motion equation can be written as
When only Coulomb friction is considered, its hysteresis loop being rectangular, its energy dissipation per cycle can be expressed as
where is the friction coefficient and is the damper normal force. Under constant normal force and equating Equations (2) and (4), one can obtain
Substituting of Equation (5) to Equation (1), its transmissibility can be written as
where is the excitation force ratio and is the frequency ratio. In Equation (6), singularity exist at = 1, leading to its infinite amplitude of the mass M at resonance.
Furthermore, we can investigate the transmissibility of a traditional viscous damper using Equation (1). By extracting K, it becomes
in which constant viscous damping ratio is . Without loss of generality, one can assume that the mass displays resonance at maximum displacement. Hence, at = 1, the maximum transmissibility becomes
2.2. Central Difference Solver for Stick–Slide Motion of Maxwell–Coulomb Damper
Figure 2 illustrates a single-degree-of-freedom system of mass M and stiffness K with a Maxwell–Coulomb (MC) friction damper by connecting the Coulomb damper of equivalent damping with the spring of stiffness in series excited by a harmonic force of amplitude .
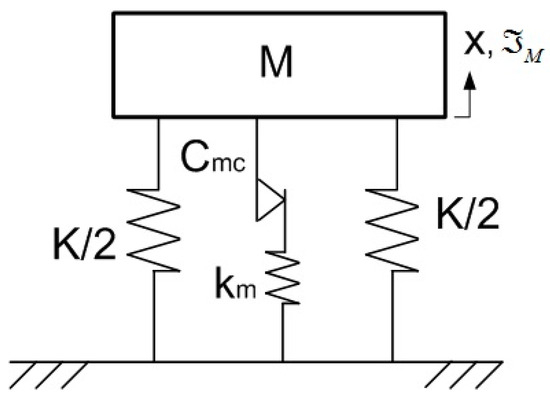
Figure 2.
Modeling of spring–mass by Maxwell–Coulomb damper.
Its motion details are illustrated by the hysteresis loop in Figure 3. Starting from the stick motion in Case A, one can balance the forces acting on the system mass M without the Coulomb element to establish its forward equation of motion (EOM).
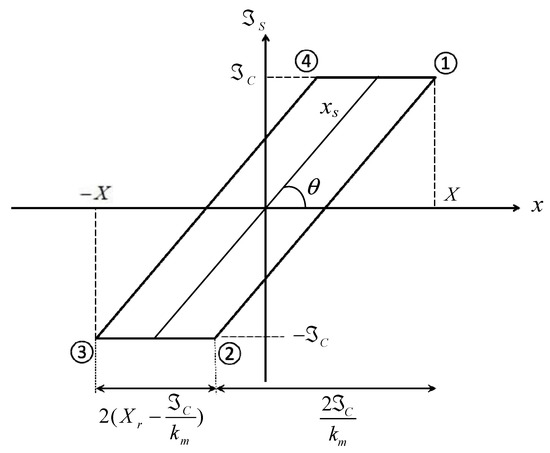
Figure 3.
Hysteresis loop of Maxwell spring and Coulomb damper interaction.
Case A: from 1 to 2 is the stick motion in which MC damper force is balanced as
where is Coulomb damping force amplitude, is friction coefficient, is damper normal force. As is the displacement amplitude, X − x is the time deviation of x from this constant.
At Figure 4, intermediate displacement at stick position is subtraction of half sliding displacement (Figure 3) from x
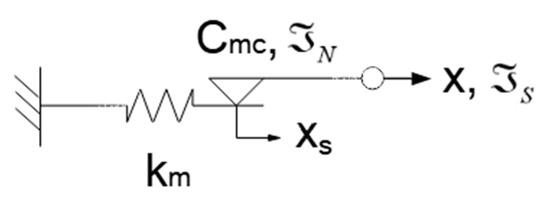
Figure 4.
Force balance of MC damper by intermediate displacement.
Its equation of motion becomes
where is the excitation force applied directly on the system mass. In the numerical ordinary differential equation, one can set
Rewrite Equation (11) as
where , . On the other hand, Coulomb damping is generated by Coulomb element Cmc only in the Maxwell arrangement. In this sliding motion, the forces acting on the system mass M are balanced by neglecting the Maxwell spring element.
Case B: from 2 to 3
in which Coulomb damping factor . Spring deflection is constant while x sliding at Coulomb element
Rewrite Equation (14) as
In the reverse EOM, Case C from 3 to 4 , its damper force becomes
and at stick position is addition of half sliding displacement to x
Substituting into Equation (11) and using Equation (12), we can write
Case D is from 4 to 1 with . Its equation of motion can be established using Equation (16). Meanwhile, spring deflection is constant as forward motion
These four cases from A to D are combined individually and consecutively to construct the hysteresis loop as shown in Figure 3.
As we have to generate , backward-difference approximation for is used. Applying recurrence formula to Equation (13) of case A, we can derive ODE as
Similarly for case B, using recurrence formula, one can obtain
Ultimately, the central difference (CD) form of recurrence equation is
2.3. Resonant Transmissibility Contour Using Energy Dissipation
In the combined model with the four different sets of motion, its energy dissipation per cycle is computed using its hysteresis loop in Figure 3 as
This result was obtained by Brizard et al. [3] also. Equating this to Equation (2), its equivalent viscous damping factor is derived as
Substituting this into Equation (1), we can establish its motion amplitude as
Due to strong coupled motion X in the denominator, its explicit solution is not easy to compute. Analytical solution of Maxwell-viscous Coulomb model was resolved by Wong and Wong [13] after excessive computation. Wisely, Equation (26) can be resolved by setting input frequency at resonant frequency, i.e., as
Solving Equation (27) explicitly using its quadratic solution:
in which , and .
For this equation, singularity may exist at resonant frequency, , where square root term becomes
Substituting back to Equation (28)
Then, its transmissibility becomes
where is Coulomb damping ratio, is Maxwell spring stiffness ratio. Two complementary solutions can be obtained from this equation, namely “minus” and “plus” solution in the denominator. From the “minus” solution of Equation (31), the singular point to avoid is . When singularity occurs, this solution is complemented by the “plus” solution under nonlinear minimum transmissibility condition [11]. Compared with rigid Coulomb damper, this condition is additional. Therefore, the singularity problem is eliminated in this model. The “plus” and “minus” solutions of Equation (31) can be plotted in the following three global zones:
(1) Below the singularity point, , patterns of are very similar. Smaller amplitude is obtained from the “plus” solution as Figure 5.
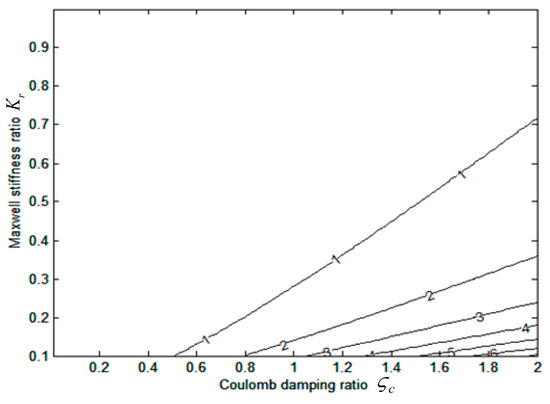
Figure 5.
Contour plot of MC damper model addition solution at global zones of [0, 2.0], [0.1, 1.0].
(2) At the singularity point, , the “plus” solution come into play as complementary solution to bring down the large amplitude effects of singularity.
(3) Above the singularity point, , one notices that the pattern of “minus” solution is reversed. Contours decrease from the left side. For the “plus” solution, contours increase linearly toward the right side as shown in Figure 5.
3. Motion Simulation, Optimal Design and Performance Evaluation
3.1. Stick–Slide Motion Simulation of Turbine Blade
In the analysis of Wang and Chen [5], turbine blade damper was developed with Maxwell–Coulomb (MC) arrangement. Our turbine blade model is simulated using four different cases of stick–slide motion. This allows extensive analyses of this highly nonlinear motion to be uniquely conducted. Its system parameters are as follows: , , and excitation force , at resonant . For the MC damper, the stiffness ratio of its Maxwell spring is ; = 0.69; . Using the CD method, a MATLAB ODE45 solver is programmed to simulate its system responses. From its hysteresis loop, shown in Figure 6, one discovers that it is closely correlated with Figure 3 and the theoretical results. For its displacement by Equation (7), X = 5.8 mm, while the simulation displacement from the figure is 5.7 mm. Thus, the percentage error is only −1.3%. Then, the simulated transmissibility = 0.610. From Equation (31), its denominator varies between to . Here, a simulation factor is implemented in the denominator as . When = 0.53, the percentage error is −1.9%. For the damper force comparison, the simulated = 140N. Meanwhile, the theoretical = 149N, being −5.9% larger. The displacement ratio of stick–slide motions is computed from Figure 3 as = 0.212. The simulated = 0.238, with +12.2% error, and the simulated = 0.238, with +12.2% error. Hence, the simulated motion is fully complied with theoretical cases A to D. Hence, the accuracy of the CD method is fully validated on this blade model.
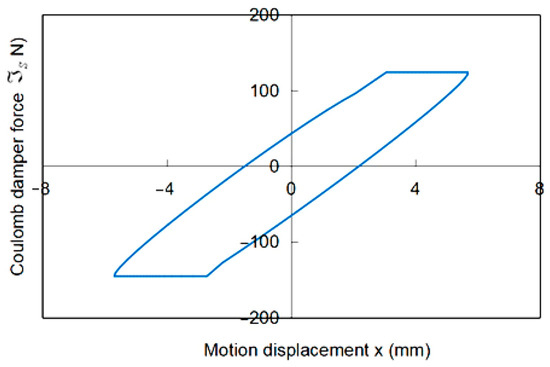
Figure 6.
Hysteresis loop of turbine blade using CD solver.
Meanwhile, its motion response is plotted in Figure 7. It rises rapidly under the restoring force of the Maxwell spring in stick case C. Then, it drops gradually under constant Coulomb force in slide case D. Afterwards, it drops drastically due to the restoring spring force of stick case A. Then, as a result of the Coulomb damping force in slide case B, it rises gradually. On the other hand, the damper force is illustrated in Figure 7. Its form is basically similar to that of the rigid Coulomb damper, alternating between high and low levels. The differences between them can be found in the switching curves and the lengths of the constant levels. It is not the same as the straight line for rigid damper, the curves are inclined due to the Maxwell spring. Moreover, the period length follows the sequential order of the motion displacement.
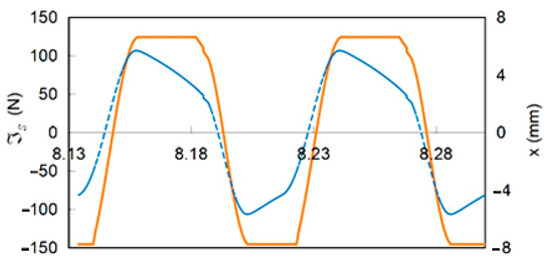
Figure 7.
x ( ) and (
) and ( ) of turbine blade at λ = 1.0.
) of turbine blade at λ = 1.0.
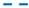 ) and (
) and ( ) of turbine blade at λ = 1.0.
) of turbine blade at λ = 1.0.
For large range simulation, the contour levels are lower than the analytical solution. There is a slight motion profile suppression or offset, as seen in Figure 7. This is caused by the (i) uneven time period of forward and reverse motions (Figure 7); (ii) actual skew-symmetric motion profile of 17% force amplitude ratio; (iii) unbalanced upper and lower loop energy, with up to 12% deviation (Figure 6), due to frictional coupling effect [14]; (iv) approximation in recurrence formulation. Overall, the profiles are closely correlated with the theoretical model (Figure 3).
3.2. Optimal Contour Design by Central Difference Unconstrained Search
Although there is no global optimal solution in the contour plot, one can generate its optimal design curve using unconstrained optimization methods, such as Newton search (NS), Gauss–Newton (GN) or Gradient search (GS). Consider this as unconstrained optimization problem of . Starting from kth design point Xk, second-order Taylor expansion of for an amount of is
in which is the Hessian matrix and is the gradient direction. In the contour plane, the Hessian matrix is defined as
where . Meanwhile, the gradient direction is
A necessary condition for minimization occurs when the direct derivative of equals zero:
From this equation, one can obtain its descent step directly:
Substituting this step into its expansion form, one achieves the search equation
When the data to construct the design path are numerical or experimental, instead of analytical, the central difference form of its gradient direction is used, as
where . Meanwhile, the central difference Hessian is
in which , , and are the gradients at and in the ith direction, defined in Equation (38). is its central difference in jth direction. Thus, in Equation (36) can be determined using Equations (34) and (39). Hence, the central difference Newton search (CDNS) design path can be generated by the search scheme in Equation (37).
Besides the CDNS method, the gradient search method (CDGS) is also used to search the design path. With this method, its descent step is
In addition, the Gauss–Newton method (CDGN) is established by its descent step
The designed turbine blade model is simulated with system parameters , , excitation force at resonant and frictional coefficient . Specifically, its frequency-dependent performance is investigated by frequency-tuning the CD model. Transmissibility curves at refined design ranges of [1.0, 2.0], [0.2, 0.4] are generated in Figure 8. For the rigid Coulomb model, Equation (7) is used, where increases drastically and explodes at . Then, it decreases gradually afterwards. Now, for the MC model, their curves increase rapidly to the resonant peaks. Then, they drop gradually to steady levels. Overall, their levels decrease from (z1) to (z2). Compared with R1, these dampers significantly tune-down the to a flatter curve [1] through the spring ratio and friction damping ratio. As increases 0.2(K1) from to 0.4(K2), resonant frequencies are tuned-up from to , as mentioned by Ricciardelli and Vickery [1].
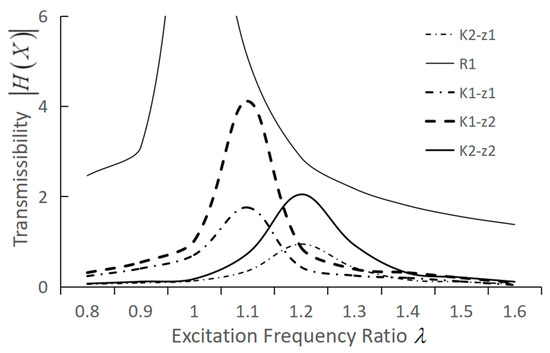
Figure 8.
Frequency-tuned of various Coulomb dampers (Rigid Coulomb R1 and MC model: = 0.2(K1); = 0.4(K2); = 1(z1); = 2(z2)).
Using these performance trends and the maximum amplitude approach, resonant transmissibility contours are generated in the ranges [0, 2.5], [0.1, 0.8], as seen in Figure 9. The design paths of three developed optimal methods are generated and plotted as dotted curves with black squares and circles to compare their applicability. In the lower range of , the first path starts from point A, where = 3.26 and . For the CDNS method, its design curve converges rapidly in three searches to point B, with = 1.21 bounded at = 0.3. The reduction in is 66%. Its increase in is the fastest, from −168 (positive definite) to 0.579 (negative definite). Then, design curve of the CDGS method converges in four searches to B’, with = 0.836. The reduction in is 83%. increases from −253 to −5.63, remaining positive definite. For the CDGN method, the design curve converges vigorously in three searches to B″, when = 1.30. The reduction in is 56%. Its decrease from −253 to −18.8, remaining positive definite. Thus, the fastest increase occurs in the CDNS method. For the comparison in , the reduction percentages are in the following order: CDGN (4.17%); CDNS (16.7%); CDGS (62.5%). As CDNS is situated in the middle of and reduction, it offers the best compensation among these methods. Hence, the CDNS path is established in the upper range of . It converges convexly from C, with = 2.72 at = 0.3. Then, in five steps, it is bounded at D, where = 0.7, with = 0.848. Reductions in and are 9.52% and 68%, respectively. Both cases using the CDNS method illustrate that when sufficient reduction is engaged, reduction can be much enhanced in this Maxwell arrangement. Simultaneously, is lessened mildly in the second path due to the initial position. These paths allow the designs in global ranges to be made up effectively in a few steps.
Figure 9.
Resonant contour plot of in ranges = [0, 2.5] and = [0.1, 0.8].
3.3. Performance Evaluation in Seismic Response Design of Adjacent Single-Story Buildings
In seismic response design [7,8,9], adjacent buildings between a single-story tower (m1) and a single-story podium (m2) are modeled as linear shear types and connected by a viscous damper. Its mass–spring–damper model with an MC damper is 2DOF, as demonstrated in Figure 10. According to the structural parameters of Chen and Wu [9], m1 = 3.63 × 105 kg and . Meanwhile, the damping parameters are given by Bhaskararao and Jangid [7] as , where are their viscous damping ratios, and , where . Assume that and are the mass and frequency ratios between adjacent buildings. Their ratio parameters are
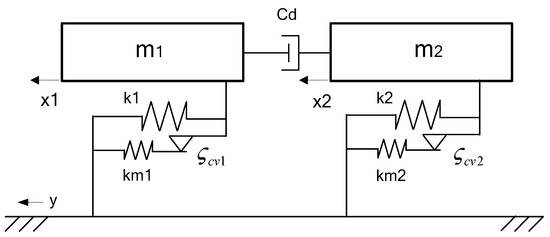
Figure 10.
Seismic response model of adjacent tower and podium subjected to harmonic ground motion.
Let be the viscous damping coefficient of the connection damper. Then, its normalized damping factor is .
Replacing MC dampers (, ) with viscous dampers () forms the 2DOF viscous damper with the CD representation:
Under seismic acceleration , ground excitations become . Numerical solutions are obtained by tuning harmonic excitation frequency . Its seismic responses are recorded at maximum displacement. Moreover, the regular increment of is set for each test. Its is plotted against in Figure 11. Its comparison with the results stated by Bhaskararao and Jangid [7] are displayed in Table 1. From this table, its minimum value is obtained as 1.832, which is 7.5% lower than the steady-state responses. Meanwhile, its , which is 1.6% larger. The discrepancies are due to the resolution of the data interval and numerical approach of CD ODE. Furthermore, for the podium (m2), the minimum value is 4.843, which is 3.9% lower, and its = 0.297, which is 4.8% smaller. In order to correlate the building’s seismic response using the developed MC damper with that of viscous damper, one can find the parametric viscous damping ratio by equating their hysteresis energies using Equation (25).
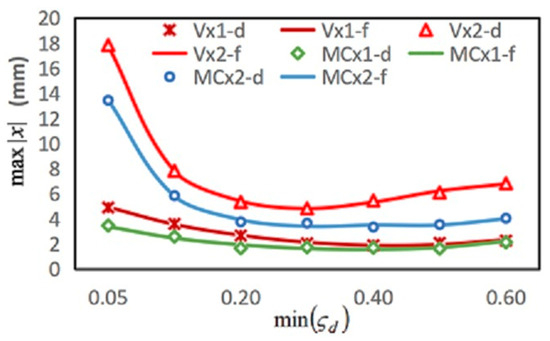
Figure 11.
Comparison of -max|x| by viscous (V) and MC dampers (d—data; f—curve fitted).

Table 1.
Optimal damper parameter comparison between steady-state, viscous, and MC methods.
Here, is the viscous transmissibility from Equation (8). Rearranging into quadratic equation yields
Then, it is solved as
Substituting , where and , in Equations (17) and (18) form the loop motion equations. Then, viscous ODE Equations (39)–(41) are transformed to MC ODE by these equations. Utilizing their solutions, the maximum displacement curves are generated, as shown in Figure 11. Under different resonant frequencies close to their system resonance, damping parameters are generated, as shown in Table 1.
From Table 1, it is interesting to note that max(x) are reduced by 15.3 and 23%. Hence, the improved performance of the MC damper at a lower range is validated. Meanwhile, the min() ratios remain unchanged. Thus, the performance of the connection damper is un-altered and the MC damper can be applied directly to this structure.
4. Experimental Validation and Optimal Design of Prototype Damper
A vibration test is carried out on the prototype damper system to experimentally validate the previous analysis, with and at frequency , a condition that is very close to its resonance. The prototype is of a piston–cylinder type, which is well connected to the adjustable Maxwell spring and Coulomb damping device (CDD) [15]. A linear slide block platform is established for the linear horizontal motion of this system, consisting of slide blocks, a linear guide rail, and a support rail, as shown in Figure 12.

Figure 12.
Linear slide block platform of prototype damper.
Excitation force is transmitted from the shaker to structural system through the shaker spring:
where y is the shaker displacement, is the shaker spring stiffness, and y − x is the shaker–damper relative displacement. An equipment schematic of the prototype test is illustrated in Figure 13. Vibration signals on slide block and shaker are captured by accelerometers. These signals are conditioned at the spectrum analyzer.
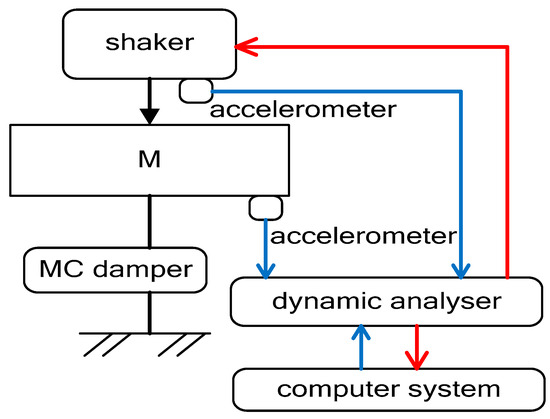
Figure 13.
Equipment schematic of prototype damper test.
A Coulomb damping test is conducted by increasing the angle of the Coulomb damping device (CDD) from 90°, to 180°, to 270° in three coil tests. [1.15, 1.36] increases, as illustrated in Figure 14. This leads to an increase in hysteresis loop energy from 0.0190 J, to 0.0317 J, to 0.0369 J. This trend is consistent with the decrease in , as seen in Figure 5, Figure 9, and Figure 14. The slope angle of its principal axis ranges from 39.9° to 40.5°. Deviations are small, only within 1.8%. Since there is no change in , its slope basically remains the same as in Figure 3. The Coulomb damping ratio of the CDD is calculated by . In case B of forward motion, the coupling ratio [14] between displacement and normal force increases with . This leads to an increase in loop gradient. Similar findings are recorded in case D of reverse motion. However, the gradient becomes saturated at . In the shaking table test of Brizard [3], their gradients increased continuously. Meanwhile, straight bounds on the displacements were generated, indicating high Maxwell spring stiffness in the hydraulic jack.
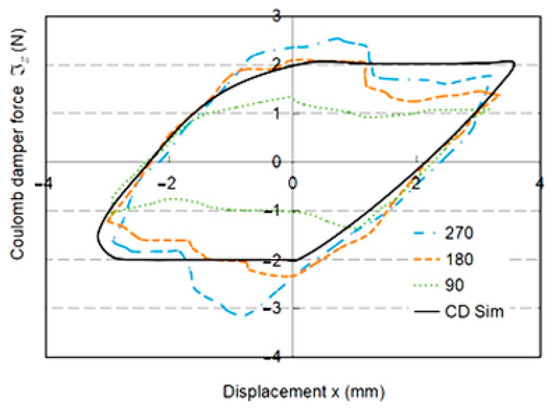
Figure 14.
Experimental loop under variation of = 90°, 180°, and 270° and CD simulation comparison at = 180°.
Using the hysteresis loops in Figure 14, the fastening screw tuning the Coulomb damping angle is related to , with Coulomb angle factor and residual damping force :
In this line fitting of the Coulomb force test, the line slope = 6.81 × 10−3 N/degree and the line constant . Meanwhile, hysteresis loops at medium = 180° from the CD simulation and experiment are compared in the figure, as they represent the common experimental features. From this comparison, their motions are seen to be close to each other. Simulation loop energy 0.0317 J displays a 5.11% deviation from the experimental value. For the Coulomb damping force, is found in the simulation, which is 8.8% deviated from the experimental measurement. Compared to the experimental sliding motions under this force, they are slightly inclined. This is caused by the flexural stiffness of the rubber friction plate inside the CDD.
On the other hand, in the Maxwell spring test, one can decrease the Maxwell spring coil number from 4, to 3, to 2 (which is 7 in K with same helical spring dimensions), i.e., [1.75, 3.50], while keeping the Coulomb device at 90°. It is interesting to note that hysteresis loop energy HKr decreases from 0.0776 J, to 0.0387 J, to 0.0214 J, as shown in Figure 15. This is caused by the well-tightened joint and lessened coupling effect in the CDD. Simultaneously, the slope angle of its principal axis increases from 31.7°, to 37.8°, to 48.5°. From Figure 3, the theoretical slope angle is computed as
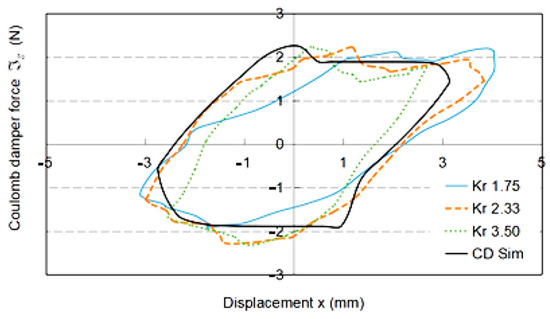
Figure 15.
Experimental loop under variation of = 1.75, 2.33, and 3.50 and CD simulation comparison at = 2.33.
For this spring–mass system, the theoretical are 32.7°, 40.6°, and 52.1°, respectively. Compared with the experimental , their percentage errors are 3.24 to 7.58%. Hence, is validated using Equation (51). The next step is to compare the CD solver with the simulation using the experimental data. From hysteresis plot of three coils test in the figure, one discovers that both loops are well matched. The simulation is 36.5°, with a 3.4% error from the experimental . Meanwhile, HKr = 0.0375J, which is only 3.1% deviated from the experimental result.
Taking even-interval tests of and Maxwell spring coil number, their experimental record is obtained. The corresponding values in are computed using the line fit of Equation (50). Meanwhile, Kr are computed using the coil numbers of Maxwell spring. Inputting this record into our self-developed MATLAB program generates the experimental contour plot shown in Figure 16.
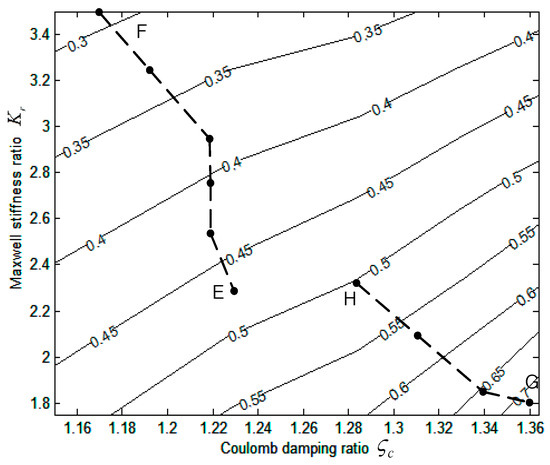
Figure 16.
Experimental contour plot of max in ranges [1.15, 1.36] and [1.75, 3.50].
To check the applicability of this plot in local ranges [1.15, 1.36] and [1.75, 3.50], design paths are established using CDNS. In the lower range of , the first design path starts from E, where = 0.465. A Maxwell three-coil spring is used, with a stiffness ratio of = 2.33. Meanwhile, is turned to 135°, and = 1.23, as obtained by Equation (50). Using the CDNS approach, its design path is shown as the dotted curve with black circles from E to F. It converges from E in five steps to F, with = 0.292 bounded at a two-coil spring, with = 3.50. is minimized to 100°, with = 1.17. Reduction in is 69%. Due to the constant curvature of the contour in separate ranges, the pattern of varies linearly. Meanwhile, increases vigorously from −21.0 to −2.74, indicating that the increase is significant. Hence, the CDNS approach is accurate and effective in these experimental ranges.
For a second design path in the upper range of , as shown by the dotted curve from G to H, it converges from G, where = 0.707 at the four-coil spring, with = 1.80. is at 270°, with = 1.36. It is bounded at H at the third step, with = 0.515, where = 2.33 for the three-coil spring. is minimized to 215°, with = 1.32. Ultimately, is reduced 27%. From the analytical solution given by Equation (31), its contour decreases monotonically from 0.75 to 0.35. In comparison with the experimental contour seen in Figure 16, it is also monotonic, decreasing from 0.65 to 0.40. Hence, the experimental contour is closely correlated.
5. Conclusions
A structural model of a Maxwell–Coulomb friction damper is established using a damping energy approach. ODEs on stick–slide motions are developed using a CD solver. Analytical transmissibility at resonance is derived for a global zone contour design purpose. Motion response on turbine blade vibration isolation is simulated. Its motion parameters X, , , and deviate only −1.3% to +12.2% from the computed results. Frequency-dependent performance is investigated by tuning at its design model. Its curve becomes flatter with resonant frequency being tuned up by . Optimal NS, GS, and GN methods are evaluated on turbine blade contour design paths. Using the CDNS method, designs of the proposed damper can be achieved on its resonant contour plot with a reduction in X of up to 66% in a few search steps. In the seismic response design of adjacent single-story buildings, an equivalent Coulomb damping ratio is implemented. Maximum displacements are reduced significantly from 15 to 23% at lower damping ratios. Experimental validation is carried out with a prototype damper test. Close correlation with its numerical simulations is observed at different loop energies and angles. The contour plot of the resonant transmissibility is validated by an analytical solution. Bounded CDNS paths allow prototype designs based on their experimental contour plot, with a maximum reduction in resonant amplitude of 69% in just three to five search steps.
Author Contributions
Conceptualization, W.-O.W.; methodology, C.-N.W.; software, C.-N.W.; validation, C.-N.W. and W.-O.W.; formal analysis, C.-N.W.; investigation, C.-N.W.; resources, W.-O.W.; data curation, C.-N.W.; writing—original draft preparation, C.-N.W.; writing—review and editing, W.-O.W.; visualization, C.-N.W.; supervision, W.-O.W.; project administration, W.-O.W.; funding acquisition, W.-O.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Research Grant Council of Hong Kong SAR, China, Ref. 15206120.
Data Availability Statement
Research data may be shared upon request.
Acknowledgments
The authors are grateful for the contribution of student assistant Christian Stuff for CD solver programming and Baiyang Shi of UWE for the damper experiment. The authors would like to thank The Hong Kong Polytechnic University for the laboratory support for the experiments in this research.
Conflicts of Interest
The authors declare no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
References
- Ricciardelli, F.; Vickery, B.J. Tuned vibration absorbers with dry friction damping. Earthq. Eng. Struct. Dyn. 1999, 28, 707–723. [Google Scholar] [CrossRef]
- Lee, J.; Berger, E.; Kim, J.H. Feasibility study of a tunable friction damper. J. Sound Vib. 2005, 283, 707–722. [Google Scholar] [CrossRef]
- Brizard, D.; Besset, S.; Jézéquel, L.; Troclet, B. Design and test of a friction damper to reduce engine vibrations on a space launcher. Arch. Appl. Mech. 2013, 83, 799–815. [Google Scholar] [CrossRef]
- Sinha, A.; Trikutam, K.T. Optimal vibration absorber with a friction damper. J. Vib. Acoust. 2018, 140, 021015. [Google Scholar] [CrossRef]
- Wang, J.H.; Chen, W.K. Investigation of the vibration of a blade with friction damper by HBM. J. Eng. Gas Turbines Power 1993, 115, 294–299. [Google Scholar] [CrossRef]
- Hatada, T.; Kobori, T.; Ishida, M.; Niwa, N. Dynamic analysis of structures with Maxwell model. Earthq. Eng. Struct. Dyn. 2000, 29, 159–176. [Google Scholar] [CrossRef]
- Bhaskararao, A.V.; Jangid, R.S. Optimum viscous damper for connecting adjacent SDOF structures for harmonic and stationary white-noise random excitations. Earthq. Eng. Struct. Dyn. 2007, 36, 563–571. [Google Scholar] [CrossRef]
- Patel, C.C.; Jangid, R.S. Dynamic response of adjacent structures connected by friction damper. Earthq. Struct. 2011, 2, 149–169. [Google Scholar] [CrossRef]
- Chen, P.; Wu, X. Investigations on the Dynamic Response of Adjacent Buildings Connected by Viscous Dampers. Buildings 2022, 12, 1480. [Google Scholar] [CrossRef]
- Wu, W.X.; Shua, C.; Wang, C.M. Mesh-free least-squares-based finite difference method for large-amplitude free vibration analysis of arbitrarily shaped thin plates. J. Sound Vib. 2008, 317, 955–974. [Google Scholar] [CrossRef]
- Fung, R.; Chang, H. Dynamic and energetic analyses of a string/slider non-linear coupling system by variable grid finite difference. J. Sound Vib. 2001, 239, 505–514. [Google Scholar] [CrossRef]
- Kheiri, M.; Paidoussis, M.P.; Amabili, M.; Epureanu, B.I. Three-dimensional dynamics of long pipes towed underwater, Part 2 Linear dynamics. Ocean Eng. 2013, 64, 161–173. [Google Scholar] [CrossRef]
- Wong, W.O.; Wong, C.N. Optimal design of Maxwell viscous-Coulomb air damper with a modified fixed point theory. J. Vib. Acoust. 2021, 143, 031002. [Google Scholar] [CrossRef]
- Patel, C.C. Random response analysis of parallel structures coupled with Maxwell damper. ISET J. Earthq. Technol. 2019, 56, 57–75. [Google Scholar]
- Wong, C.N.; Chan, K.T. Identification of cooler tubes with tube-to-baffle impacts. J. Vib. Acoust. 1998, 120, 419–425. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).