Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude
Abstract
1. Introduction
2. Materials and Methods
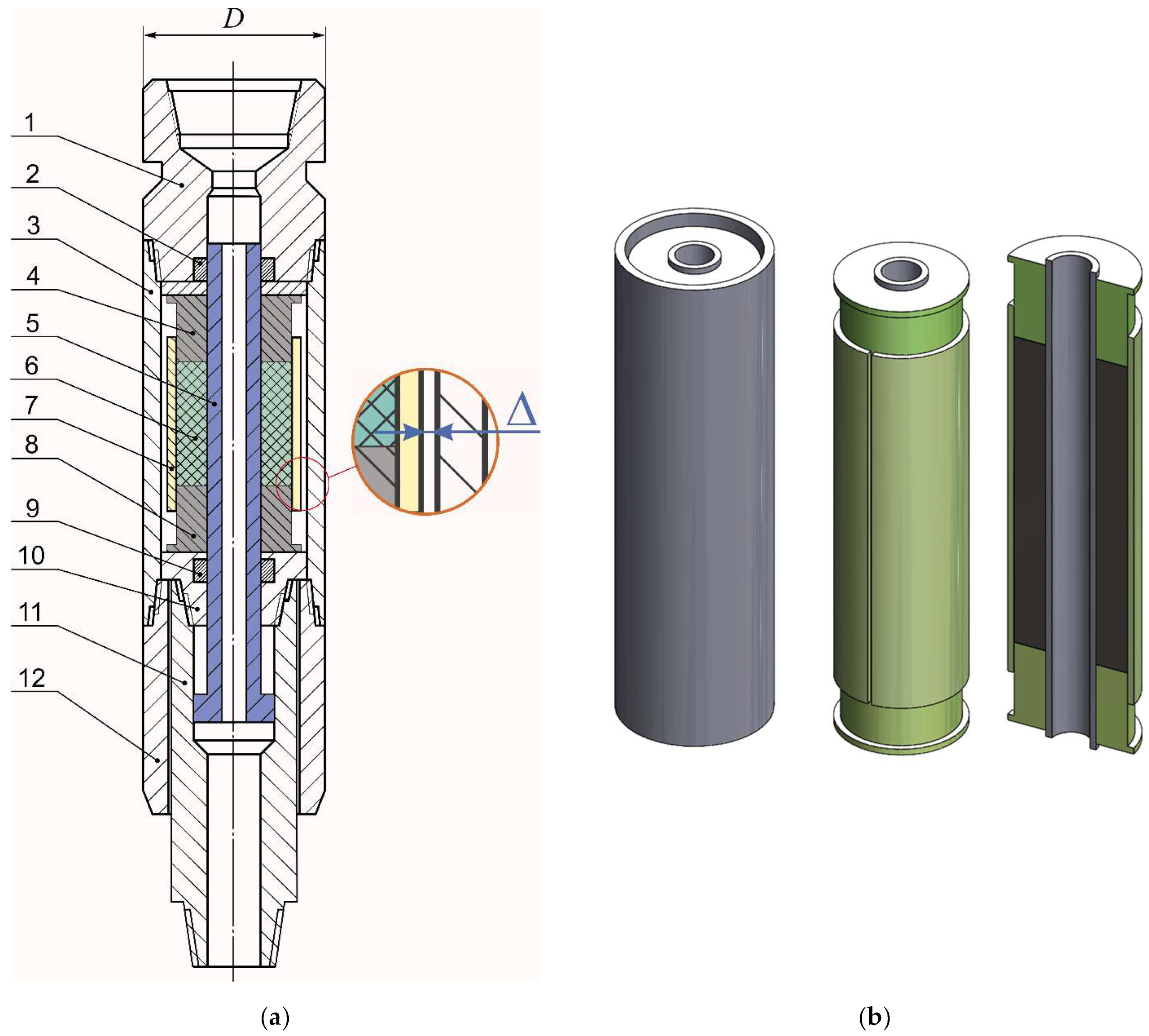
2.1. Design Features of an Adaptive Drilling Shock Absorber with a Shell Elastic Element
2.2. Calculation Scheme of the Shell Elastic Element of a Drilling Shock Absorber
- -
- in sliding zones:
- -
- in adhesion zones:
2.3. Finite Element Model of the Device
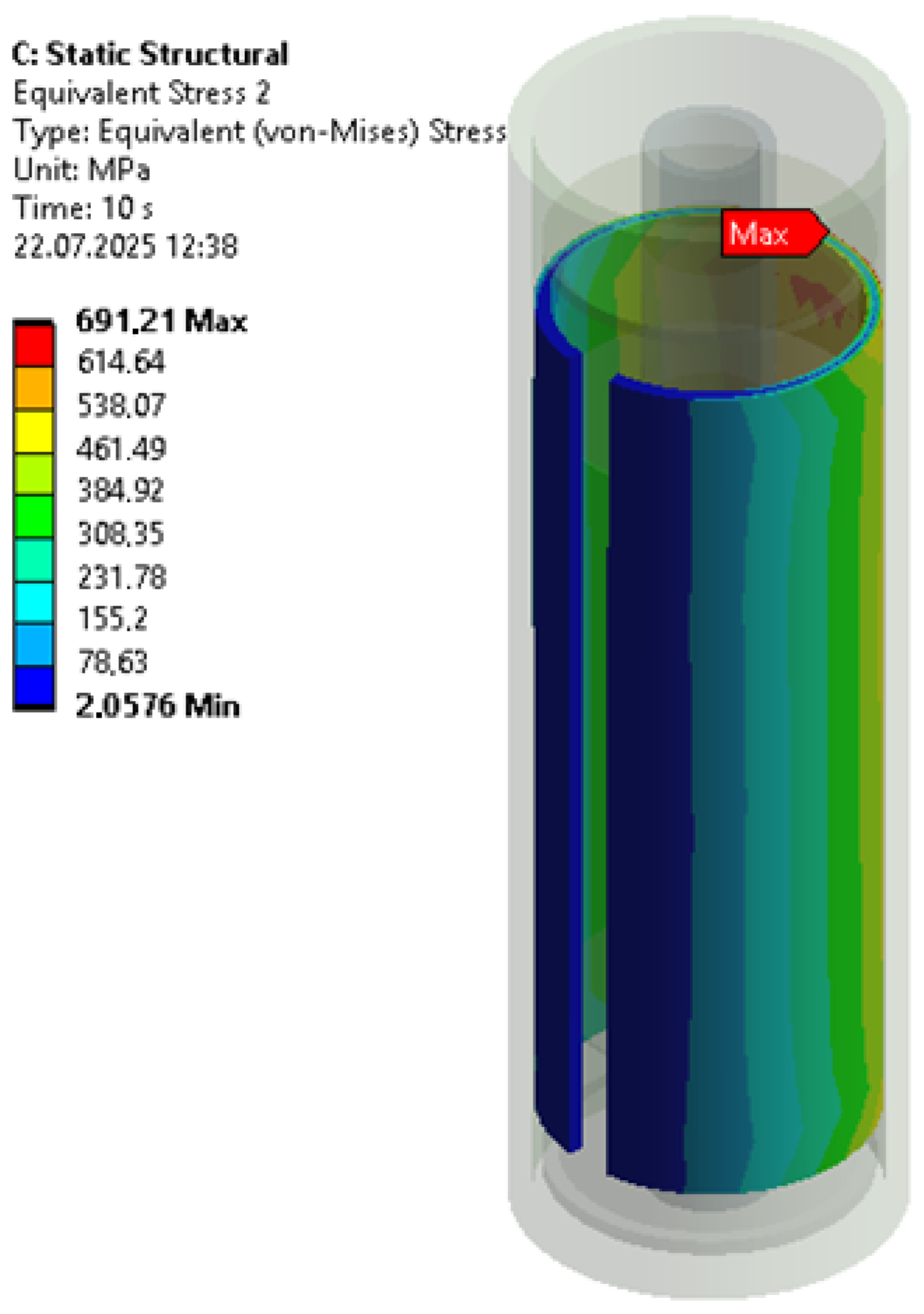
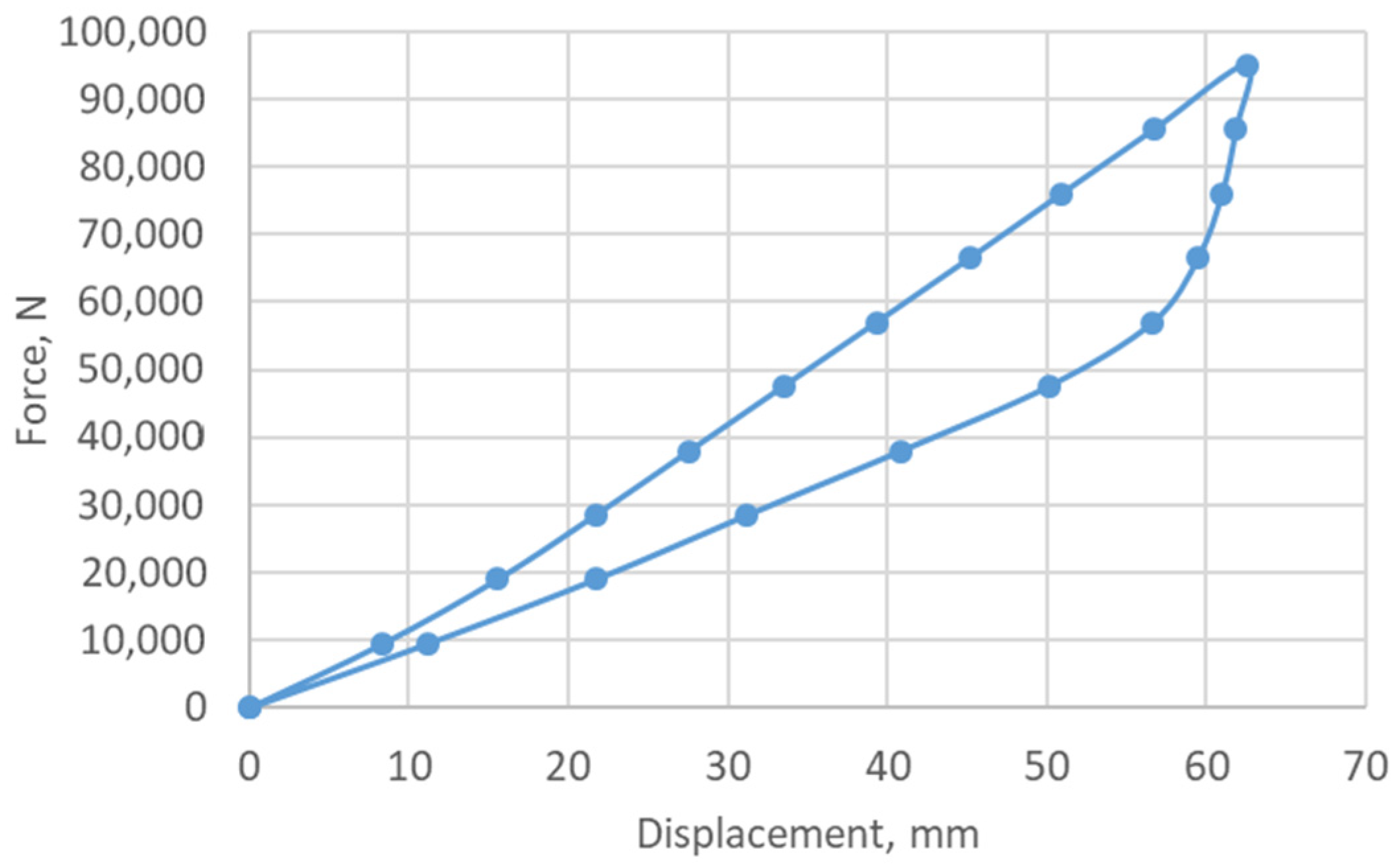
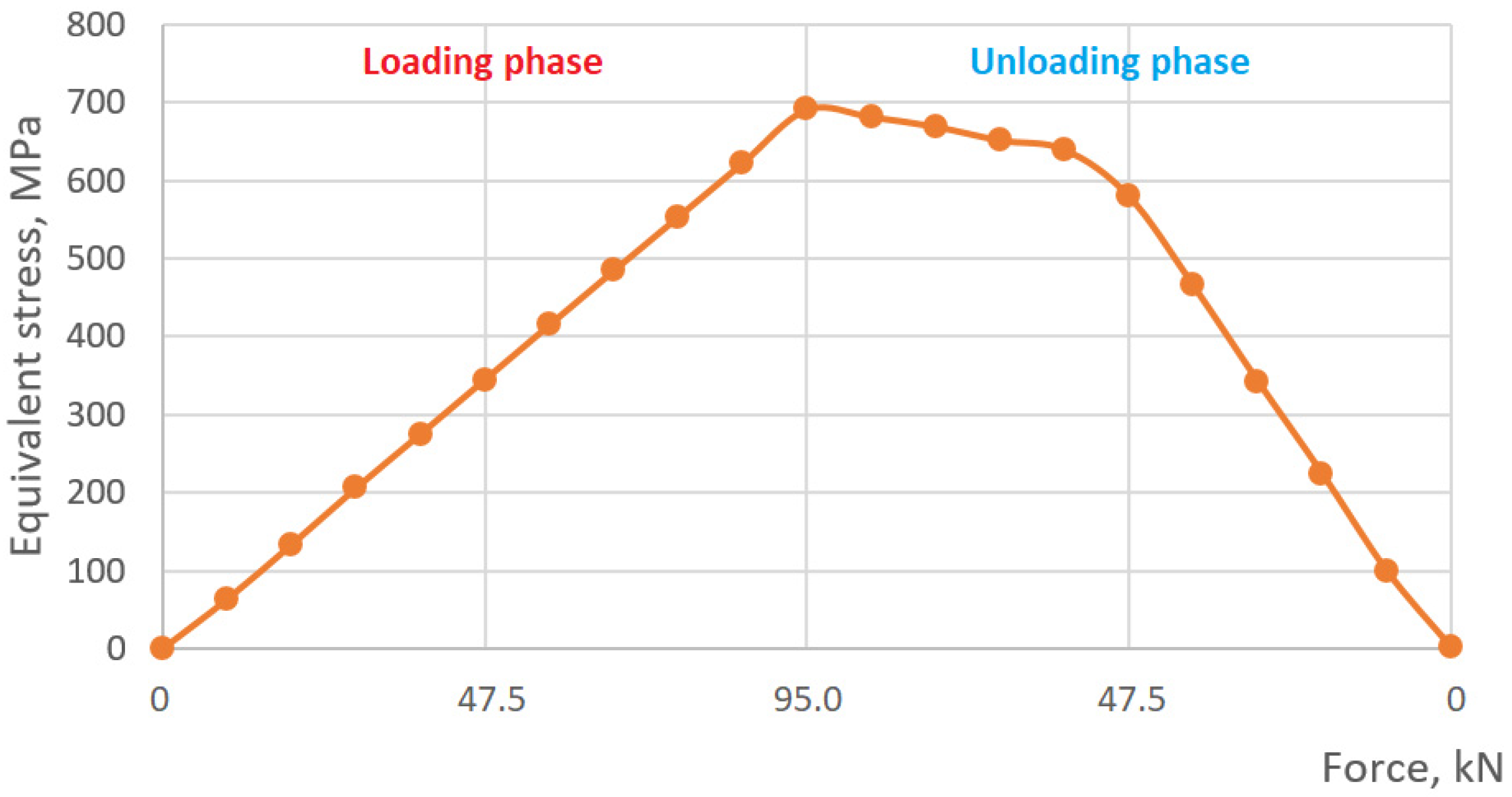
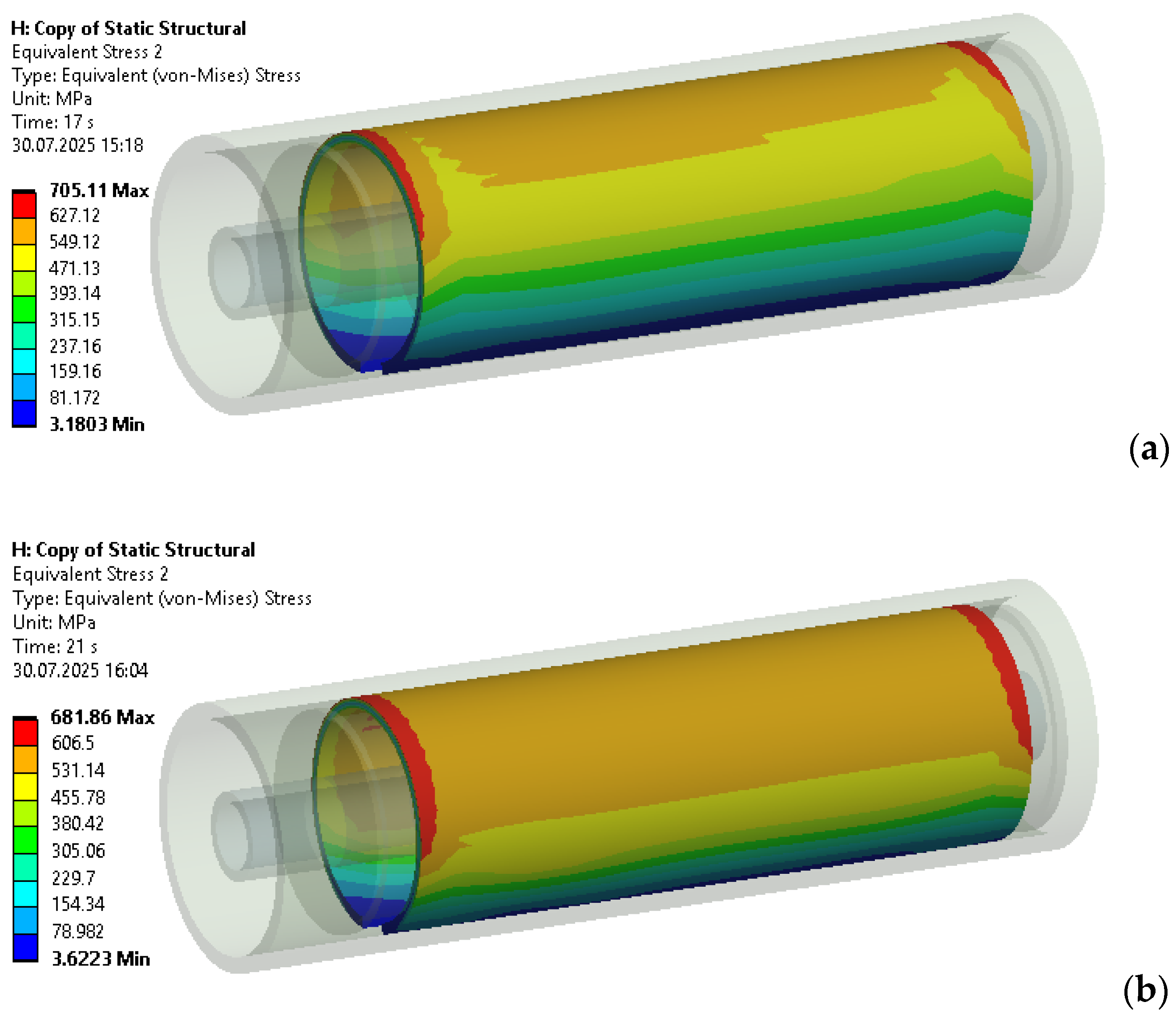
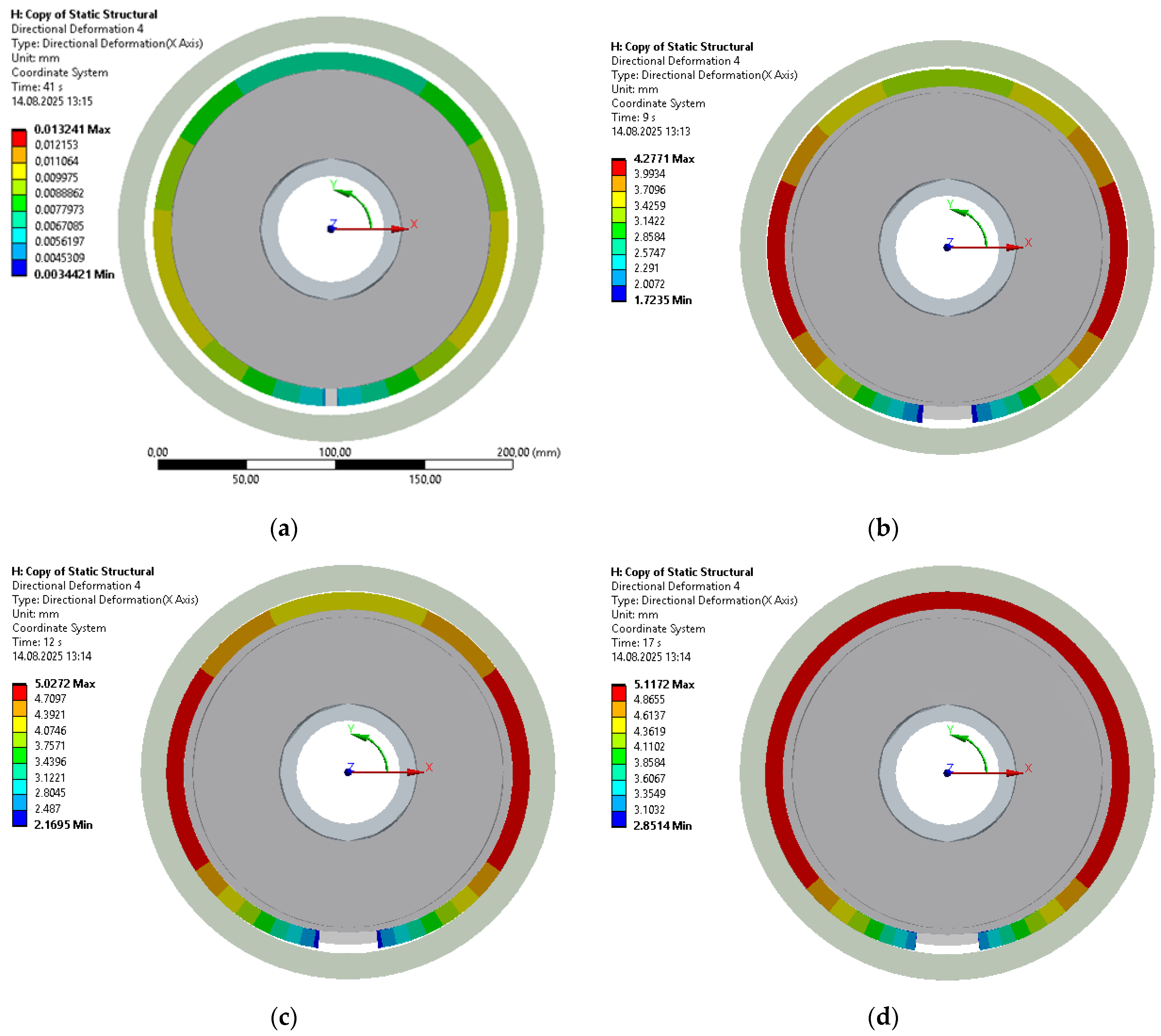
3. Results
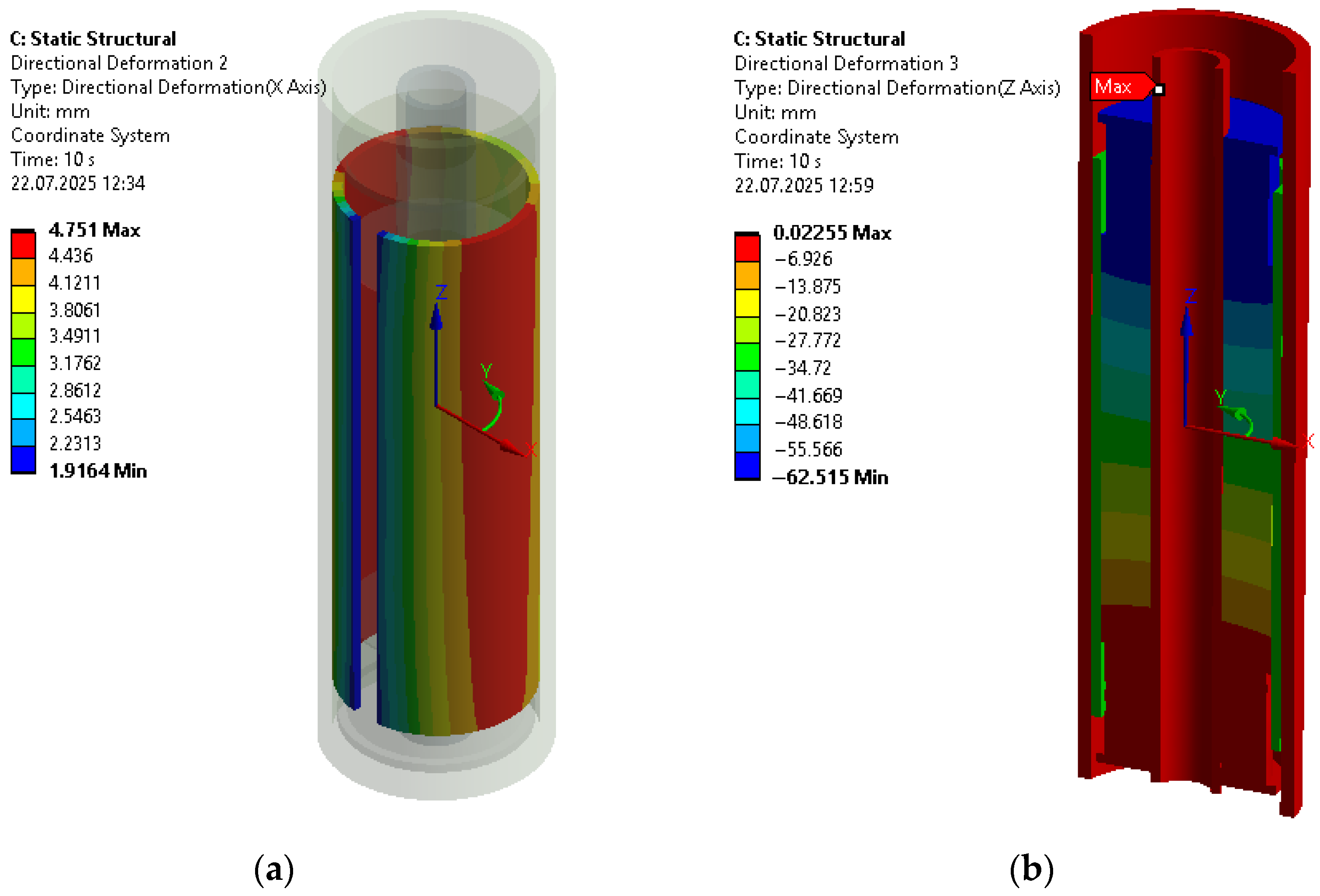
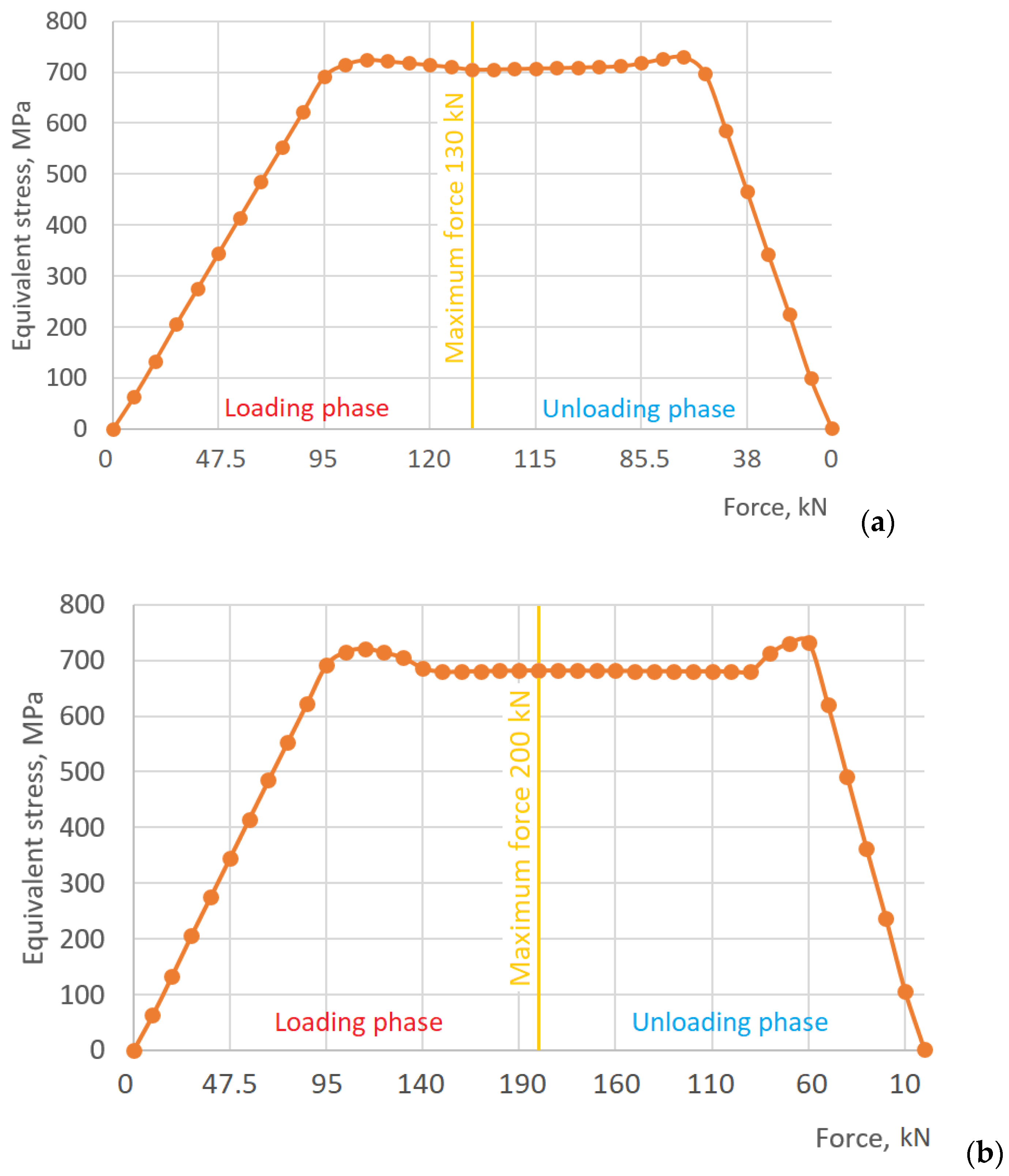
3.1. Operation of the Shock Absorber in Normal Loading Mode (With Unclosed Radial Clearance)
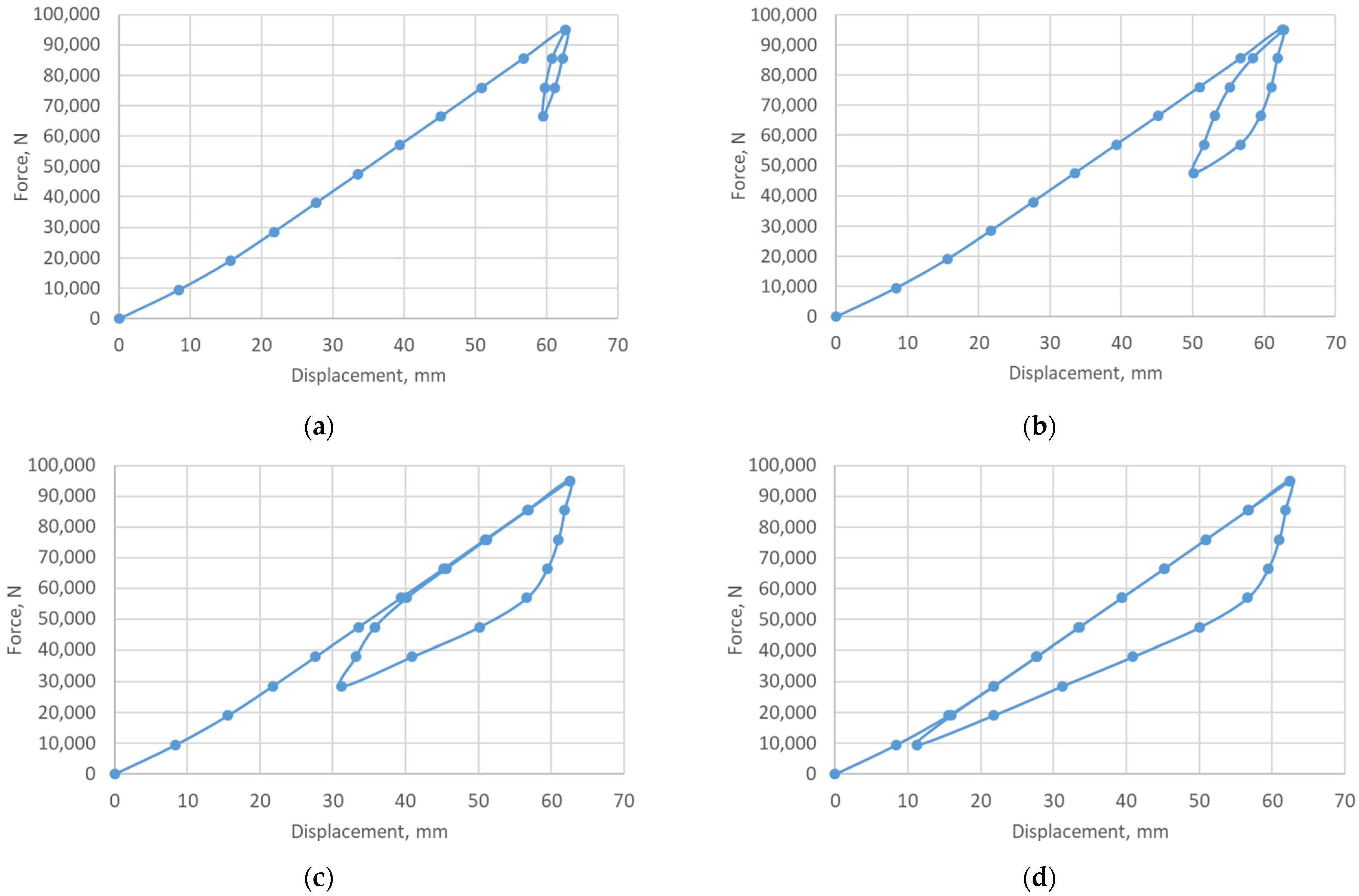
3.2. Adaptive Behavior of the Shock Absorber in Emergency Mode (Radial Clearance Closure)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Zhang, H.; Guan, Z. Dynamic Characteristics of Downhole Bit Load and Analysis of Conversion Efficiency of Drill String Vibration Energy. Energies 2021, 14, 229. [Google Scholar] [CrossRef]
- Cveticanin, L.; Kraljevic, S.; Cverticanin, D. Review on dynamic models of drilling systems applied in oil and gas industry. Acta Mech. 2023, 234, 4427–4442. [Google Scholar] [CrossRef]
- Wang, R.; Liu, X.; Song, G.; Zhou, S. Non-Linear Dynamic Analysis of Drill String System with Fluid-Structure Interaction. Appl. Sci. 2021, 11, 9047. [Google Scholar] [CrossRef]
- Bembenek, M.; Grydzhuk, Y.; Gajdzik, B.; Ropyak, L.; Pashechko, M.; Slabyi, O.; Al-Tanakchi, A.; Pryhorovska, T. An Analytical–Numerical Model for Determining “Drill String–Wellbore” Frictional Interaction Forces. Energies 2024, 17, 301. [Google Scholar] [CrossRef]
- Chen, C.; Bi, C.; Ji, G.; Wang, H.; Huo, Y.; Yu, P. Research on Vibration Reduction, Energy Enhancement, and Speed Increase Methods for Drilling String in Deep Heterogeneous Strata. Processes 2024, 12, 2645. [Google Scholar] [CrossRef]
- Sui, D.; Aadnøy, B.S. Rate of Penetration Estimation with Parameter Correction. Appl. Sci. 2025, 15, 4650. [Google Scholar] [CrossRef]
- Li, J.; Peng, J.; Ge, D.; Zhang, G. Simulation and Experimental Research on a Fluidic Oscillator with a Deflector Structure. Energies 2025, 18, 1336. [Google Scholar] [CrossRef]
- Akl, W.; Alsupie, H.; Sassi, S.; Baz, A.M. Vibration of Periodic Drill-Strings with Local Sources of Resonance. Vibration 2021, 4, 586–601. [Google Scholar] [CrossRef]
- Aarsnes, U.J.F.; van de Wouw, N. Effect of shock subs on self-excited vibrations in drilling systems. J. Pet. Sci. Eng. 2019, 181, 106217. [Google Scholar] [CrossRef]
- Landar, S.; Velychkovych, A.; Mykhailiuk, V. Numerical and analytical models of the mechanism of torque and axial load transmission in a shock absorber for drilling oil, gas and geothermal wells. Eng. Solid Mech. 2024, 12, 207–220. [Google Scholar] [CrossRef]
- Abu Seer, T.; Vahdati, N.; Shiryayev, O. Adaptive Torsional Tuned Vibration Absorber for Rotary Equipment. Vibration 2019, 2, 116–134. [Google Scholar] [CrossRef]
- Velichkovich, A.S. Design features of shell springs for drilling dampers. Chem. Pet. Eng. 2007, 43, 458–461. [Google Scholar] [CrossRef]
- Kulke, V.; Thunich, P.; Schiefer, F.; Ostermeyer, G.-P. A Method for the Design and Optimization of Nonlinear Tuned Damping Concepts to Mitigate Self-Excited Drill String Vibrations Using Multiple Scales Lindstedt-Poincaré. Appl. Sci. 2021, 11, 1559. [Google Scholar] [CrossRef]
- Zribi, F.; Sidhom, L.; Gharib, M. Stick–Slip Suppression in Drill String Systems Using a Novel Adaptive Sliding Mode Control Approach. Vibration 2024, 7, 479–502. [Google Scholar] [CrossRef]
- Al Shekaili, A.; Afebu, K.O.; Liu, Y.; Papatheou, E. Experimental analysis of drillstring vibrations using a small-scale drilling rig. Nonlinear Dyn. 2025, 113, 17491–17518. [Google Scholar] [CrossRef]
- Landar, S.; Velychkovych, A.; Ropyak, L.; Andrusyak, A. A Method for Applying the Use of a Smart 4 Controller for the Assessment of Drill String Bottom-Part Vibrations and Shock Loads. Vibration 2024, 7, 802–828. [Google Scholar] [CrossRef]
- Boukredera, F.S.; Hadjadj, A.; Youcefi, M.R. Drilling vibrations diagnostic through drilling data analyses and visualization in real time application. Earth Sci. Inform. 2021, 14, 1919–1936. [Google Scholar] [CrossRef]
- Ivan, S.; Andrii, V. Analytical Model of Structural Damping in Friction Module of Shell Shock Absorber Connected to Spring. Shock Vib. 2023, 4140583, 17. [Google Scholar] [CrossRef]
- Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Numerical Model for Studying the Properties of a New Friction Damper Developed Based on the Shell with a Helical Cut. Appl. Mech. 2025, 6, 1. [Google Scholar] [CrossRef]
- Donmez, A.; Cigeroglu, E.; Ozgen, G.O. An Improved Quasi-Zero Stiffness Vibration Isolation System Utilizing Dry Friction Damping. Nonlinear Dyn. 2020, 101, 107–121. [Google Scholar] [CrossRef]
- He, S.; Zhang, W.; Li, Z. Application of Dry Friction Contact in Vibration Reduction in Engineering—A Short Review. Coatings 2023, 13, 910. [Google Scholar] [CrossRef]
- Huang, Z.; Tan, J.; Liu, C.; Lu, X. Dynamic characteristics of a segmented supercritical driveline with flexible couplings and dry friction dampers. Symmetry 2021, 13, 281. [Google Scholar] [CrossRef]
- Pesek, L.; Pust, L.; Snabl, P.; Bula, V.; Hajzman, M.; Byrtus, M. Dry-friction damping in vibrating systems, theory and application to the bladed disc assembly. In Nonlinear Structural Dynamics and Damping; Jauregui, J., Ed.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2019; Volume 69. [Google Scholar] [CrossRef]
- Wahad, H.S.; Tudor, A.; Vlase, M.; Cerbu, N.; Subhi, K.A. The effect of friction in coulombian damper. IOP Conf. Ser. Mater. Sci. Eng. 2017, 174, 012021. [Google Scholar] [CrossRef]
- Jaisee, S.; Yue, F.; Hao Ooi, Y. A state-of-the-art review on passive friction dampers and their applications. Eng. Struct. 2021, 235, 112022. [Google Scholar] [CrossRef]
- Melatti, V.; D’Ayala, D. Methodology for the assessment and refinement of friction-based dissipative devices. Eng. Struct. 2021, 229, 111666. [Google Scholar] [CrossRef]
- Gao, S.; Wang, Y. An evaluation method for dry friction damping of ring damper in gas turbine engines under axial vibration. Aerospace 2021, 8, 302. [Google Scholar] [CrossRef]
- Duriagina, Z.A.; Kulyk, V.V.; Filimonov, O.S.; Trostianchyn, A.M.; Sokulska, N.B. The role of stress–strain state of gas turbine engine metal parts in predicting their safe life. Prog. Phys. Met. 2021, 22, 643–677. [Google Scholar] [CrossRef]
- Velichkovich, A.S. Shock Absorber for Oil-Well Sucker-Rod Pumping Unit. Chem. Petrol. Eng. 2005, 41, 544–546. [Google Scholar] [CrossRef]
- Velichkovich, A.S.; Popadyuk, I.I.; Shopa, V.M. Experimental study of shell flexible component for drilling vibration damping devices. Chem. Pet. Eng. 2011, 46, 518–524. [Google Scholar] [CrossRef]
- Al-Rubaii, M.; Al-Shargabi, M.; Al-Shehri, D. A Novel Automated Model for Evaluation of the Efficiency of Hole Cleaning Conditions during Drilling Operations. Appl. Sci. 2023, 13, 6464. [Google Scholar] [CrossRef]
- Panevnik, D.A.; Velichkovich, A.S. Assessment of the stressed state of the casing of the above-bit hydroelevator. Neft. Khozyaystvo Oil Ind. 2017, 1, 70–73. [Google Scholar]
- Song, H.-X.; Zhang, S.-L.; Chen, X.-W.; Wyclif, K.; Guo, J.-X.; Xiong, R.-Y.; Wang, L. Research on the pollution and damage mechanism of drilling fluid on casing during ultra-deep well drilling process. Pet. Sci. 2025, 22, 1234–1251. [Google Scholar] [CrossRef]
- Shatskyi, I.; Makoviichuk, M.; Ropyak, L.; Velychkovych, A. Analytical Model of Deformation of a Functionally Graded Ceramic Coating under Local Load. Ceramics 2023, 6, 1879–1893. [Google Scholar] [CrossRef]
- Ropyak, L.; Shihab, T.; Velychkovych, A.; Dubei, O.; Tutko, T.; Bilinskyi, V. Design of a Two-Layer Al–Al2O3 Coating with an Oxide Layer Formed by the Plasma Electrolytic Oxidation of Al for the Corrosion and Wear Protections of Steel. Prog. Phys. Met. 2023, 24, 319–365. [Google Scholar] [CrossRef]
- Ma, Z.; Zhou, R.; Yang, Q. Recent Advances in Quasi-Zero Stiffness Vibration Isolation Systems: An Overview and Future Possibilities. Machines 2022, 10, 813. [Google Scholar] [CrossRef]
- Sui, G.; Zhang, X.; Hou, S.; Shan, X.; Hou, W.; Li, J. Quasi-Zero Stiffness Isolator Suitable for Low-Frequency Vibration. Machines 2023, 11, 512. [Google Scholar] [CrossRef]
- Karpenko, M.; Ževžikov, P.; Stosiak, M.; Skačkauskas, P.; Borucka, A.; Delembovskyi, M. Vibration Research on Centrifugal Loop Dryer Machines Used in Plastic Recycling Processes. Machines 2024, 12, 29. [Google Scholar] [CrossRef]
- Wriggers, P. Computational Contact Mechanics, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; ISBN 978-3-540-32608-3. [Google Scholar]
- Popov, V.L. Contact Mechanics and Friction: Physical Principles and Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Bedzir, A.A.; Shatskii, I.P.; Shopa, V.M. Nonideal contact in a composite shell structure with a deformable filler. Int. Appl. Mech. 1995, 31, 351–354. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Olejnik, P. Analysis of Dynamic Systems with Various Friction Laws. ASME Appl. Mech. Rev. 2005, 58, 389–411. [Google Scholar] [CrossRef]
- Olukoko, O.A.; Becker, A.A.; Fenner, R.T. A Review of Three Alternative Approaches to Modelling Frictional Contact Problems Using the Boundary Element Method. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1994, 444, 37–51. [Google Scholar]
- Man, K.W.; Aliabadi, M.H.; Rooke, D.P. BEM Frictional Contact Analysis: Modelling Considerations. Eng. Anal. Bound. Elem. 1993, 11, 77–85. [Google Scholar] [CrossRef]
- Shatskii, I.P. Model for Contact of Crack Boundaries in a Bending Plate. J. Math. Sci. 2001, 103, 357–362. [Google Scholar] [CrossRef]
- Dutkiewicz, M.; Velychkovych, A.; Shatskyi, I.; Shopa, V. Efficient Model of the Interaction of Elastomeric Filler with an Open Shell and a Chrome-Plated Shaft in a Dry Friction Damper. Materials 2022, 15, 4671. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.W. Numerical Methods for Elastic Contact Problems. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.W., Eds.; Springer: Boston, MA, USA, 2013. [Google Scholar] [CrossRef]
- Lu, Y.; Arakelian, V. A New Solution to Force Analysis Including Coulomb Friction in Mechanism Joints. Mech. Mach. Theory 2024, 202, 105776. [Google Scholar] [CrossRef]
- Prajapati, D.K.; Prakash, C.; Saxena, K.; Gupta, M.; Mehta, J.S. Prediction of Contact Response Using Boundary Element Method (BEM) for Different Surface Topography. Int. J. Interact. Des. Manuf. 2024, 18, 2725–2732. [Google Scholar] [CrossRef]
- Vashishtha, G.; Chauhan, S.; Singh, R.; Singh, M.; Tejani, G.G. A Review of Numerical Techniques for Frictional Contact Analysis. Lubricants 2025, 13, 18. [Google Scholar] [CrossRef]
- Dovbnya, K.; Shevtsova, N. Studies on the stress state of an orthotropic shell of arbitrary curvature with the through crack under bending loading. Strength Mater. 2014, 46, 345–349. [Google Scholar] [CrossRef]
- Makovijchuk, M.V.; Daliak, T.M.; Shatskij, I.P. Interaction of Contact Crack with Collinear Slit Under Shallow Spherical Shell Bending. Int. Appl. Mech. 2024, 60, 171–178. [Google Scholar] [CrossRef]
- Shatskyi, I.P.; Makoviichuk, M.V.; Shcherbii, A.B. Equilibrium of cracked shell with flexible coating. In Proceedings of the 11th International Conference on Shell Structures: Theory and Applications, SSTA 2017, Gdansk, Poland, 11–13 October 2017; CRC Press: Boca Raton, FL, USA, 2018; Volume 4, pp. 165–168. [Google Scholar] [CrossRef]
- Goryacheva, I.G.; Martynyak, R.M. Contact problems for textured surfaces involving frictional effects. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 707–716. [Google Scholar] [CrossRef]
- Shatskii, I.P. Tension of a plate containing a rectilinear cut with hinged rims. J. Appl. Mech. Tech. Phys. 1989, 30, 828–832. [Google Scholar] [CrossRef]
- Rong, L.; Tie, Z.; Wu, X.J.; Wang, C.H. Crack closure effect on stress intensity factors of an axially and a circumferentially cracked cylindrical shell. Int. J. Fract. 2004, 125, 227–248. [Google Scholar] [CrossRef]
- Shats’kyi, I.P.; Makoviichuk, M.V. Contact Interaction of Crack Lips in Shallow Shells in Bending with Tension. Mater. Sci. 2005, 41, 486–494. [Google Scholar] [CrossRef]
- Yue, F.; Wu, Z. Fracture Mechanical Analysis of Thin-Walled Cylindrical Shells with Cracks. Metals 2021, 11, 592. [Google Scholar] [CrossRef]
- Zhangabay, N.; Ibraimova, U.; Bonopera, M.; Suleimenov, U.; Avramov, K.; Chernobryvko, M.; Utelbayeva, A.; Uspenskyi, B. Finite-Element Modeling of the Dynamic Behavior of a Crack-like Defect in an Internally Pressurized Thin-Walled Steel Cylinder. Appl. Sci. 2024, 14, 1790. [Google Scholar] [CrossRef]
- Laursen, T.A. Computational Contact and Impact Mechanics; Springer: Berlin/Heidelberg, Germany, 2003; ISBN 978-3-642-07685-5. [Google Scholar]
- Lyashenko, I.A.; Filippov, A.E.; Popov, V.L. Friction in Adhesive Contacts: Experiment and Simulation. Machines 2023, 11, 583. [Google Scholar] [CrossRef]
- Zou, X.; Yang, C.; Liu, B. The Contact and Transient Dynamic Analysis of Gear Meshing with ANSYS. Open Access Libr. J. 2020, 7, 1–10. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. Frictionless vs. Frictional Contact in Numerical Wear Predictions of Conformal and Non-conformal Sliding Couplings. Tribol. Lett. 2022, 70, 115. [Google Scholar] [CrossRef]
- Yin, Z.; Hu, Z.; Gao, H.; Lin, G. A FETI B-Differentiable Equation Method for Elastic Frictional Contact Problem with Nonconforming Mesh. Comput. Mech. 2024, 73, 1095–1124. [Google Scholar] [CrossRef]
- Kwon, S.L.; Kim, S.; Ha, D.; Yun, G.J. A Fully Nonlinear Three-Dimensional Dynamic Frictional Contact Analysis Method under Large Deformation with the Area Regularization. Eng. Comput. 2024, 40, 399–421. [Google Scholar] [CrossRef]
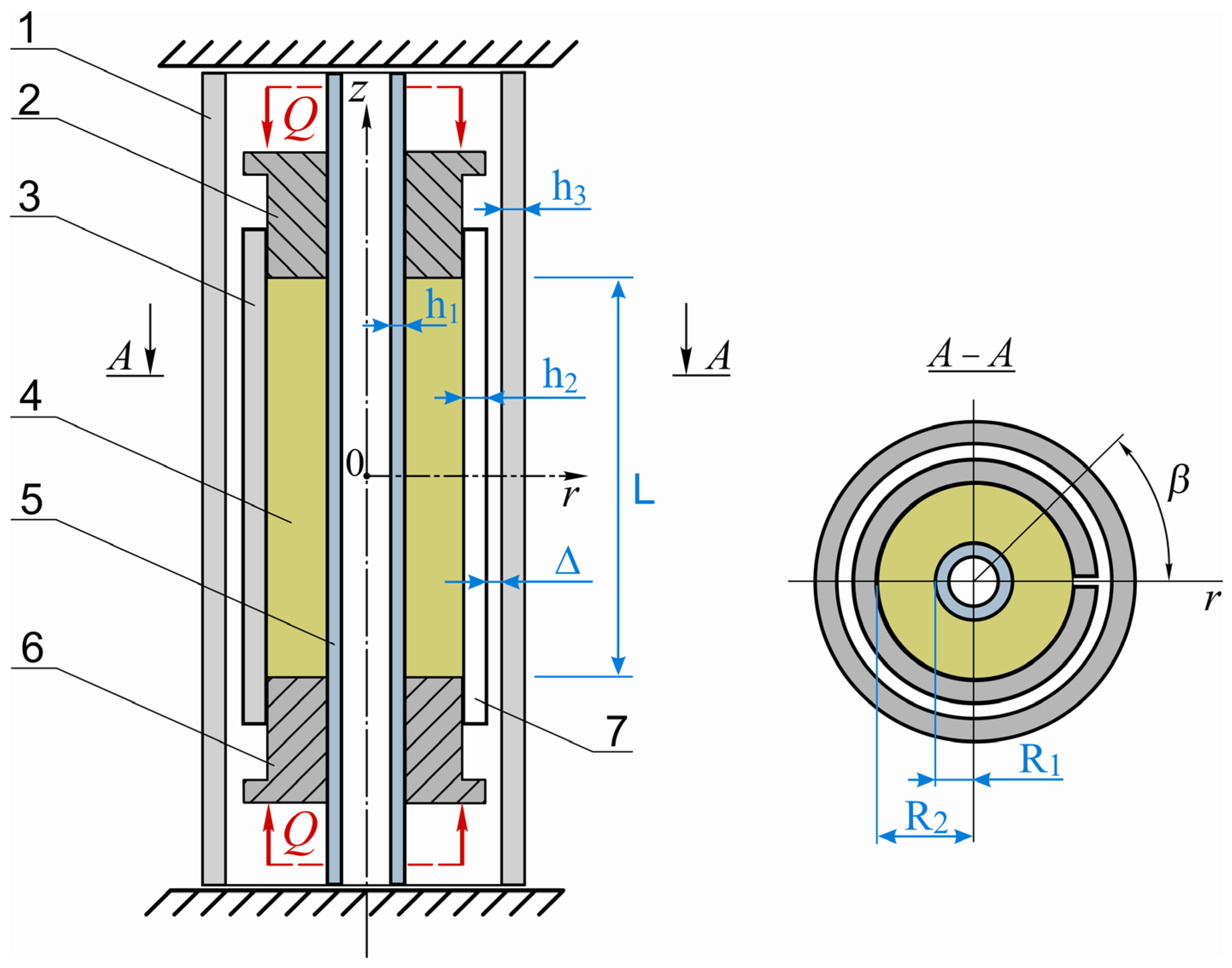



| Shock Absorber Diameter, D, mm | Shaft Thickness, h1, mm | Shaft Radius, R1, mm | Shell Thickness, h2, mm | Shell Radius, R2, mm | Housing Thickness, h3, mm | Clearance Value, , mm | Filler Length, L, mm |
|---|---|---|---|---|---|---|---|
| 240.0 | 10 | 40 | 10 | 90 | 15 | 5 | 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velychkovych, A.; Mykhailiuk, V.; Andrusyak, A. Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude. Vibration 2025, 8, 60. https://doi.org/10.3390/vibration8040060
Velychkovych A, Mykhailiuk V, Andrusyak A. Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude. Vibration. 2025; 8(4):60. https://doi.org/10.3390/vibration8040060
Chicago/Turabian StyleVelychkovych, Andrii, Vasyl Mykhailiuk, and Andriy Andrusyak. 2025. "Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude" Vibration 8, no. 4: 60. https://doi.org/10.3390/vibration8040060
APA StyleVelychkovych, A., Mykhailiuk, V., & Andrusyak, A. (2025). Evaluation of the Adaptive Behavior of a Shell-Type Elastic Element of a Drilling Shock Absorber with Increasing External Load Amplitude. Vibration, 8(4), 60. https://doi.org/10.3390/vibration8040060









