A Time-Domain Solution Method for the Vibration Performance of Viscoelastic Functionally Graded Porous Beams
Abstract
1. Introduction
2. Viscoelastic Functionally Graded Porous Beam
3. Theoretical Formulation
3.1. Basic Equations
3.2. Bernstein Polynomial Method
4. Results and Discussion
4.1. Convergence
4.2. Validation
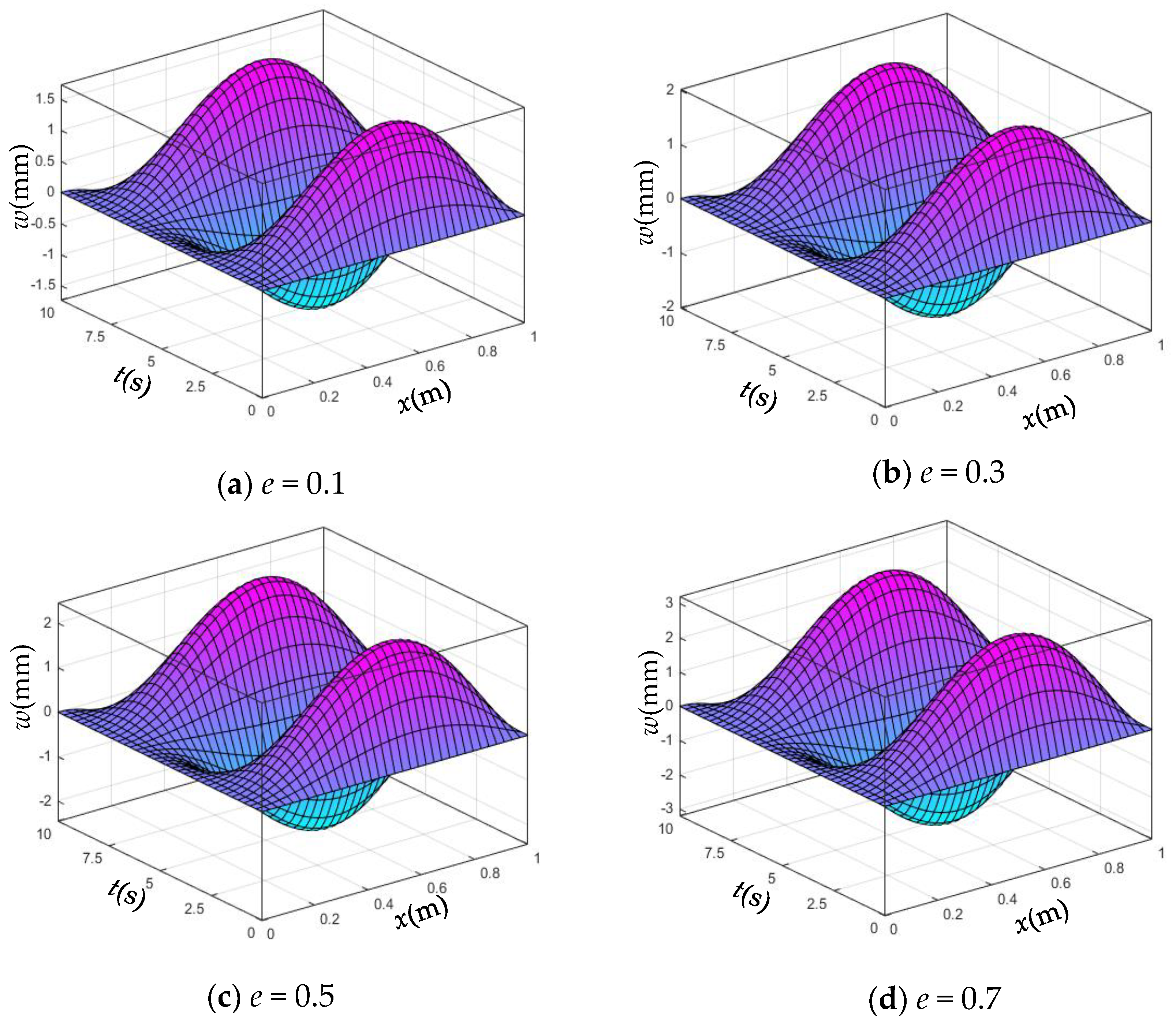
4.3. Parametric Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, H.L.; Yang, J.; Kitipornchai, S. Mechanical analysis of functionally graded porous structures: A review. Int. J. Struct. Stab. Dyn. 2020, 20, 2041015. [Google Scholar] [CrossRef]
- Zhou, K.; Huang, X.C.; Tian, J.J.; Hua, H.X. Vibration and flutter analysis of supersonic porous functionally graded material plates with temperature gradient and resting on elastic foundation. Compos. Struct. 2018, 204, 63–79. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibrations of medium thickness functionally graded plates. Compos. Struct. 2018, 202, 1253–1262. [Google Scholar] [CrossRef]
- Babaei, M.; Kiarasi, F.; Asemi, K.; Hosseini, M. Functionally graded saturated porous structures: A review. J. Comput. Appl. Math. 2022, 53, 297–308. [Google Scholar] [CrossRef]
- Xu, W.T.; Pan, G.J.; Moradi, Z.; Shafiei, N. Nonlinear forced vibration analysis of functionally graded non-uniform cylindrical microbeams applying the semi-analytical solution. Compos. Struct. 2021, 275, 114395. [Google Scholar] [CrossRef]
- Al Rjoub, Y.S.; Hamad, A.G. Free vibration of functionally Euler-Bernoulli and Timoshenko graded porous beams using the transfer matrix method. Ksce. J. Civ. Eng. 2017, 21, 792–806. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and post buckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef]
- Ebrahimi-Nejad, S.; Shaghaghi, G.R.; Miraskari, F. Size-dependent vibration in two-directional functionally graded porous nanobeams under hygro-thermo-mechanical loading. Eur. Phys. J. Plus 2019, 134, 465. [Google Scholar] [CrossRef]
- Noori, A.R.; Aslan, T.A.; Temel, B. Dynamic analysis of functionally graded porous beams using complementary functions method in the Laplace domain. Compos. Struct. 2021, 256, 113094. [Google Scholar] [CrossRef]
- Jędrysiak, J. Theoretical tolerance modelling of dynamics and stability for axially functionally graded (AFG) beams. Materials 2023, 16, 2096. [Google Scholar] [CrossRef]
- Qin, B.; Zhong, R.; Wang, Q.S.; Zhao, X. A Jacobi-Ritz approach for FGP beams with arbitrary boundary conditions based on a higher-order shear deformation theory. Compos. Struct. 2020, 247, 112435. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.N.; Nguyen, T.K.; Vo, T.P. A new two-variable shear deformation theory for bending, free vibration and buckling analysis of functionally graded porous beams. Compos. Struct. 2022, 282, 115095. [Google Scholar] [CrossRef]
- Esen, I. Dynamic response of functional graded Timoshenko beams in a thermal environment subjected to an accelerating load. Eur. J. Mech. A-Solids 2019, 78, 103841. [Google Scholar] [CrossRef]
- Alnujaie, A.; Akbas, S.D.; Eltaher, M.A.; Assie, A.E. Damped forced vibration analysis of layered functionally graded thick beams with porosity. Smart Struct. Syst. 2021, 27, 679–689. [Google Scholar] [CrossRef]
- Wu, J.; Chen, L.; Wu, R.; Chen, X.C. Nonlinear forced vibration of bidirectional functionally graded porous material beam. Shock. Vib. 2021, 2021, 6675125. [Google Scholar] [CrossRef]
- Lei, Y.L.; Gao, K.; Wang, X.W.; Yang, J. Dynamic behaviors of single-and multi-span functionally graded porous beams with flexible boundary constraints. Appl. Math. Model. 2020, 83, 754–776. [Google Scholar] [CrossRef]
- Keleshteri, M.M.; Jelovica, J. Analytical assessment of nonlinear forced vibration of functionally graded porous higher order hinged beams. Compos. Struct. 2022, 298, 115994. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Civalek, Ö. On dynamic instability of magnetically embedded viscoelastic porous FG nanobeam. Int. J. Eng. Sci. 2019, 143, 14–32. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Thai, H.T.; Civalek, Ö. On viscoelastic transient response of magnetically imperfect functionally graded nanobeams. Int. J. Eng. Sci. 2022, 172, 103629. [Google Scholar] [CrossRef]
- Pawlus, D. Dynamic behaviour of three-layered annular plates with viscoelastic core under lateral loads. J. Theor. Appl. Mech. 2015, 53, 775–788. [Google Scholar] [CrossRef][Green Version]
- Zhang, W.; Capilnasiu, A.; Sommer, G.; Holzapfel, G.A.; Nordsletten, D.A. An efficient and accurate method for modeling nonlinear fractional viscoelastic biomaterials. Comput. Methods Appl. Mech. Eng. 2020, 362, 112834. [Google Scholar] [CrossRef]
- Amabili, M.; Balasubramanian, P.; Breslavsky, I. Anisotropic fractional viscoelastic constitutive models for human descending thoracic aortas. J. Mech. Behav. Biomed. Mater. 2019, 99, 186–197. [Google Scholar] [CrossRef]
- Li, X.; Xue, Z.; Tian, X. A modified fractional order generalized bio-thermoelastic theory with temperature-dependent thermal material properties. Int. J. Therm. Sci. 2018, 132, 249–256. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic dynamics of axially FG microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
- Shariati, A.; Jung, D.W.; Mohammad-Sedighi, H.; Zur, K.K.; Habibi, M.; Safa, M. On the vibrations and stability of moving viscoelastic axially functionally graded nanobeams. Materials 2020, 13, 1707. [Google Scholar] [CrossRef] [PubMed]
- Akbaş, Ş.D.; Fageehi, Y.A.; Assie, A.E.; Eltaher, M.A. Dynamic analysis of viscoelastic functionally graded porous thick beams under pulse load. Eng. Comput. 2020, 27, 365–377. [Google Scholar] [CrossRef]
- Lewandowski, R.; Baum, M. Dynamic characteristics of multilayered beams with viscoelastic layers described by the fractional Zener model. Arch. Appl. Mech. 2015, 85, 1793–1814. [Google Scholar] [CrossRef]
- Zheng, G.Z.; Zhang, N.T.; Lv, S.T. The application of fractional derivative viscoelastic models in the finite element method: Taking several common models as examples. Fractal. Fract. 2024, 8, 103. [Google Scholar] [CrossRef]
- Hu, D.; Zhang, J.; Chen, H. Random flutter analysis of a novel binary airfoil with fractional order viscoelastic constitutive relationship. Mech. Syst. Signal. Pr. 2024, 221, 111755. [Google Scholar] [CrossRef]
- Song, P.; Wei, P.; Zhou, X. Vibration of rectangular plate on fractional order viscoelastic foundation subjected to standing and moving loads. Mech. Time-Depend. Mat. 2024, 28, 541–561. [Google Scholar] [CrossRef]
- Loghman, E.; Kamali, A.; Bakhtiari-Nejad, F.; Abbaszadeh, M. Nonlinear free and forced vibrations of fractional modeled viscoelastic FGM micro-beam. Appl. Math. Model. 2021, 92, 297–314. [Google Scholar] [CrossRef]
- Taşkin, M.; Demir, Ö. Effect of porosity distribution on vibration and damping behavior of inhomogeneous curved sandwich beams with fractional derivative viscoelastic core. Eng. Comput. 2023, 40, 538–563. [Google Scholar] [CrossRef]
- Abu-Alshaikh, I.M.; Almbaidin, A.A. Analytical responses of functionally graded beam under moving mass using Caputo and Caputo–Fabrizio fractional derivative models. J. Vib. Control 2020, 26, 1859–1867. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Y.; Dang, R.; Cheng, G.; Xie, J. Shifted Legendre polynomials algorithm used for the numerical analysis of viscoelastic plate with a fractional order model. Math. Comput. Simulat. 2022, 193, 190–203. [Google Scholar] [CrossRef]
- Xu, J.; Chen, Y.D.; Tai, Y.P.; Xu, X.M.; Shi, G.D.; Chen, N. Vibration analysis of complex fractional viscoelastic beam structures by the wave method. Int. J. Mech. Sci. 2020, 167, 105204. [Google Scholar] [CrossRef]


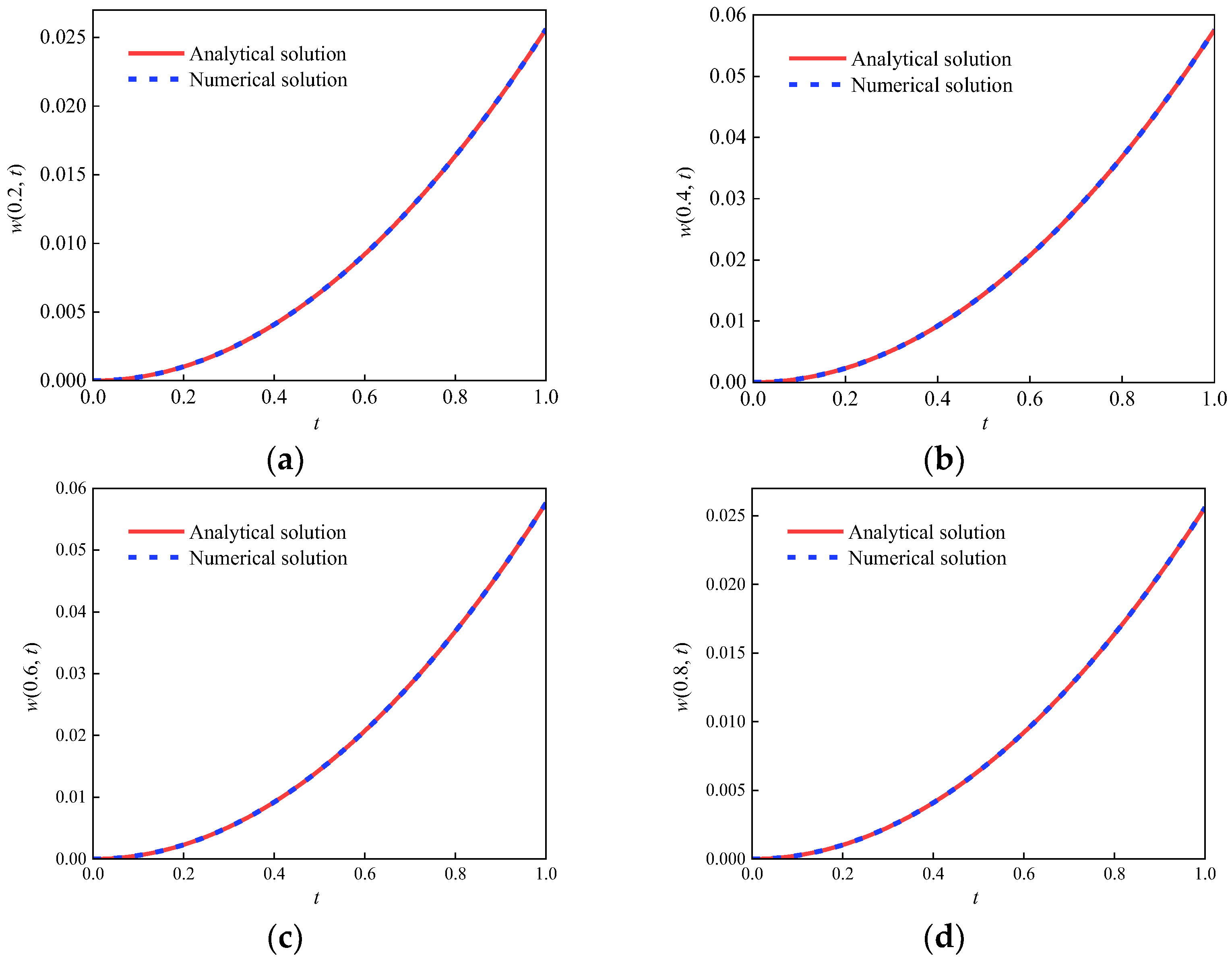







| Boundary Condition | Beam Type | Mid-Span Deflections (mm) | |||||
|---|---|---|---|---|---|---|---|
| N = 6 | N = 7 | N = 8 | N = 9 | N = 10 | N = 11 | ||
| C-H | Type 1 | 2.524 | 2.145 | 2.100 | 2.102 | 2.096 | 2.096 |
| Type 2 | 2.128 | 1.733 | 1.697 | 1.698 | 1.694 | 1.694 | |
| Type 3 | 2.914 | 2.544 | 2.490 | 2.492 | 2.486 | 2.485 | |
| Type 4 | 2.483 | 2.100 | 2.056 | 2.057 | 2.052 | 2.051 | |
| C-F | Type 1 | 22.099 | 22.720 | 22.281 | 22.309 | 22.322 | 22.325 |
| Type 2 | 17.856 | 18.358 | 18.003 | 18.026 | 18.036 | 18.038 | |
| Type 3 | 26.203 | 26.940 | 26.418 | 26.452 | 26.467 | 26.471 | |
| Type 4 | 21.629 | 22.237 | 21.807 | 21.835 | 21.847 | 21.850 | |
| C-C | Type 1 | 0.957 | 0.987 | 0.966 | 0.966 | 0.964 | 0.964 |
| Type 2 | 0.774 | 0.797 | 0.780 | 0.781 | 0.779 | 0.779 | |
| Type 3 | 1.135 | 1.170 | 1.145 | 1.146 | 1.143 | 1.143 | |
| Type 4 | 0.937 | 0.966 | 0.945 | 0.946 | 0.944 | 0.943 | |
| H-H | Type 1 | 4.755 | 4.906 | 4.797 | 4.799 | 4.788 | 4.787 |
| Type 2 | 3.842 | 3.964 | 3.876 | 3.878 | 3.869 | 3.868 | |
| Type 3 | 5.638 | 5.817 | 5.688 | 5.690 | 5.677 | 5.676 | |
| Type 4 | 4.654 | 4.802 | 4.695 | 4.697 | 4.686 | 4.686 | |
| Boundary Condition | Beam Type | Mid-Span Deflections (mm) | ||||
|---|---|---|---|---|---|---|
| M × M = 10 × 10 | M × M = 20 × 20 | M × M = 30 × 30 | M × M = 40 × 40 | M × M = 50 × 50 | ||
| C-H | Type 1 | 2.093 | 2.096 | 2.096 | 2.096 | 2.096 |
| Type 2 | 1.691 | 1.694 | 1.694 | 1.694 | 1.694 | |
| Type 3 | 2.482 | 2.486 | 2.486 | 2.486 | 2.486 | |
| Type 4 | 2.049 | 2.052 | 2.052 | 2.052 | 2.052 | |
| C-F | Type 1 | 22.212 | 22.243 | 22.243 | 22.322 | 22.321 |
| Type 2 | 17.947 | 17.972 | 18.035 | 18.036 | 18.036 | |
| Type 3 | 26.337 | 26.374 | 26.374 | 26.467 | 26.467 | |
| Type 4 | 21.739 | 21.770 | 21.770 | 21.847 | 21.847 | |
| C-C | Type 1 | 0.963 | 0.964 | 0.964 | 0.964 | 0.964 |
| Type 2 | 0.778 | 0.779 | 0.779 | 0.779 | 0.779 | |
| Type 3 | 1.142 | 1.143 | 1.143 | 1.143 | 1.143 | |
| Type 4 | 0.942 | 0.944 | 0.944 | 0.944 | 0.944 | |
| H-H | Type 1 | 4.781 | 4.788 | 4.788 | 4.788 | 4.788 |
| Type 2 | 3.863 | 3.869 | 3.869 | 3.869 | 3.869 | |
| Type 3 | 5.669 | 5.677 | 5.677 | 5.677 | 5.677 | |
| Type 4 | 4.680 | 4.686 | 4.686 | 4.686 | 4.686 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Zeng, T.; Yang, Y.; Wang, X.; Xu, G.; Cheng, S. A Time-Domain Solution Method for the Vibration Performance of Viscoelastic Functionally Graded Porous Beams. Vibration 2025, 8, 28. https://doi.org/10.3390/vibration8020028
Cui Y, Zeng T, Yang Y, Wang X, Xu G, Cheng S. A Time-Domain Solution Method for the Vibration Performance of Viscoelastic Functionally Graded Porous Beams. Vibration. 2025; 8(2):28. https://doi.org/10.3390/vibration8020028
Chicago/Turabian StyleCui, Yuhua, Tao Zeng, Yipeng Yang, Xiaohong Wang, Guodong Xu, and Su Cheng. 2025. "A Time-Domain Solution Method for the Vibration Performance of Viscoelastic Functionally Graded Porous Beams" Vibration 8, no. 2: 28. https://doi.org/10.3390/vibration8020028
APA StyleCui, Y., Zeng, T., Yang, Y., Wang, X., Xu, G., & Cheng, S. (2025). A Time-Domain Solution Method for the Vibration Performance of Viscoelastic Functionally Graded Porous Beams. Vibration, 8(2), 28. https://doi.org/10.3390/vibration8020028






