Experimental Investigation of Ventilation Effects on Combustion Efficiency and Heat Release Rate in Small-Scale Compartment Fires
Abstract
1. Introduction
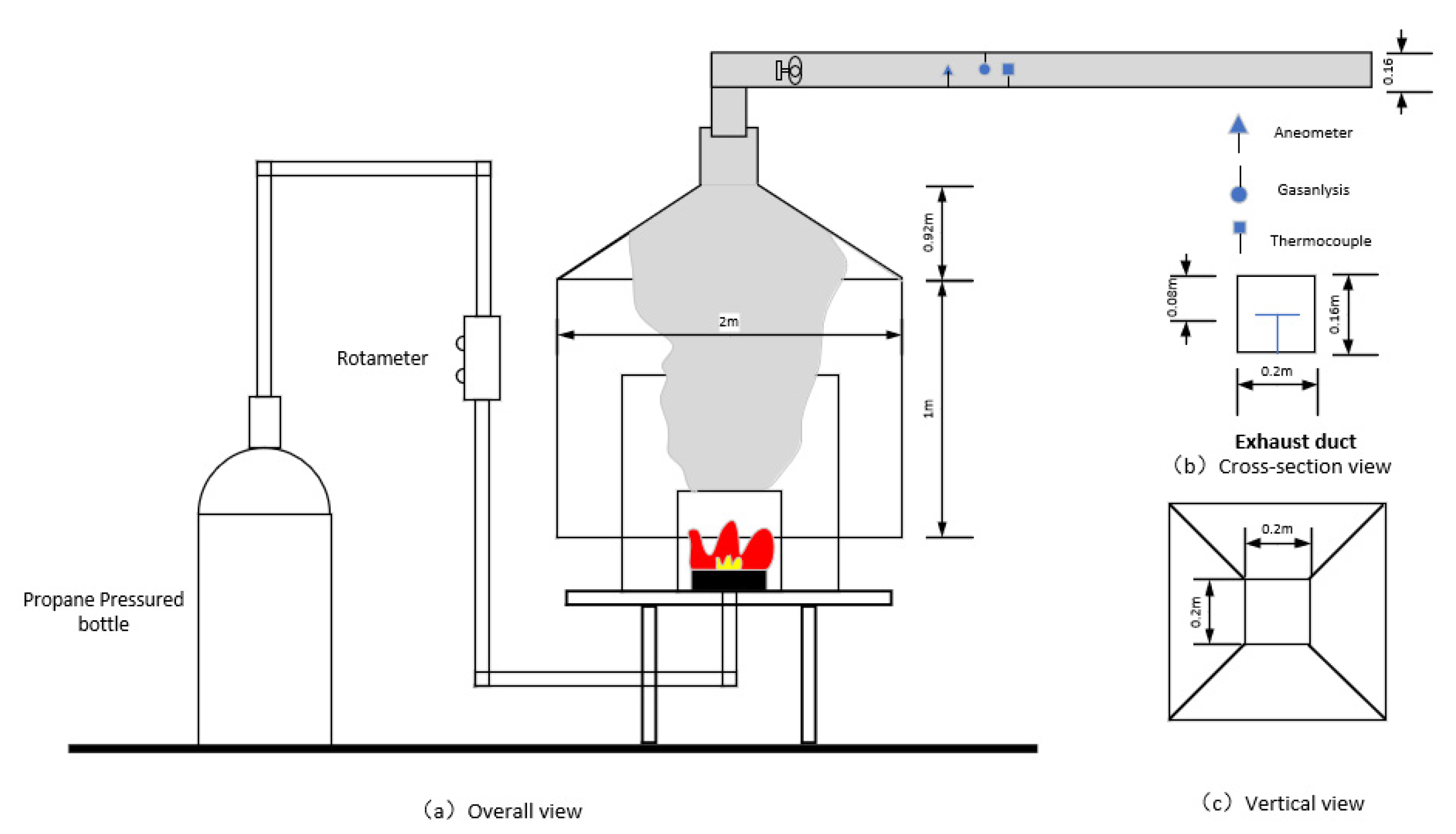
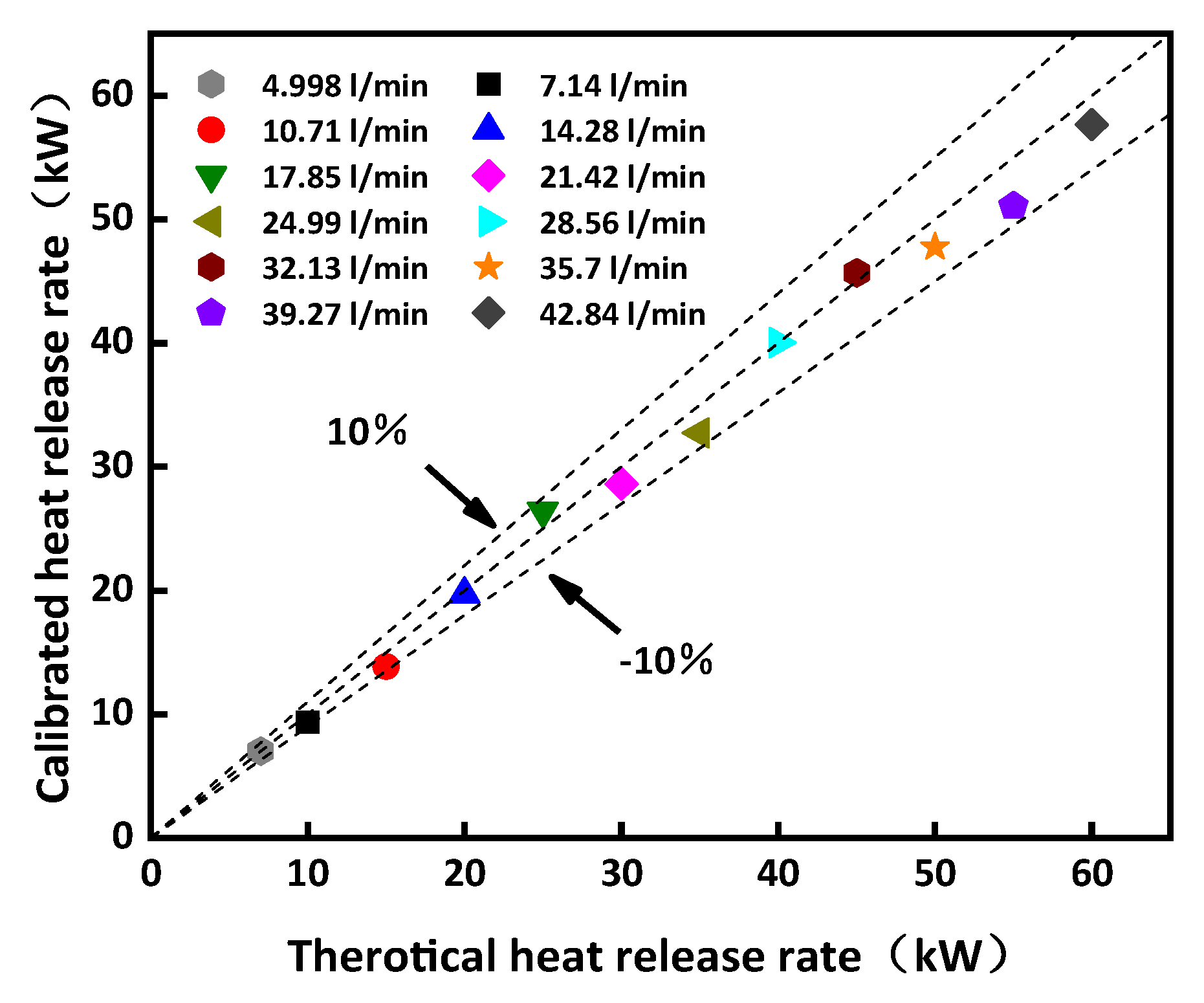
2. Experimental Setup
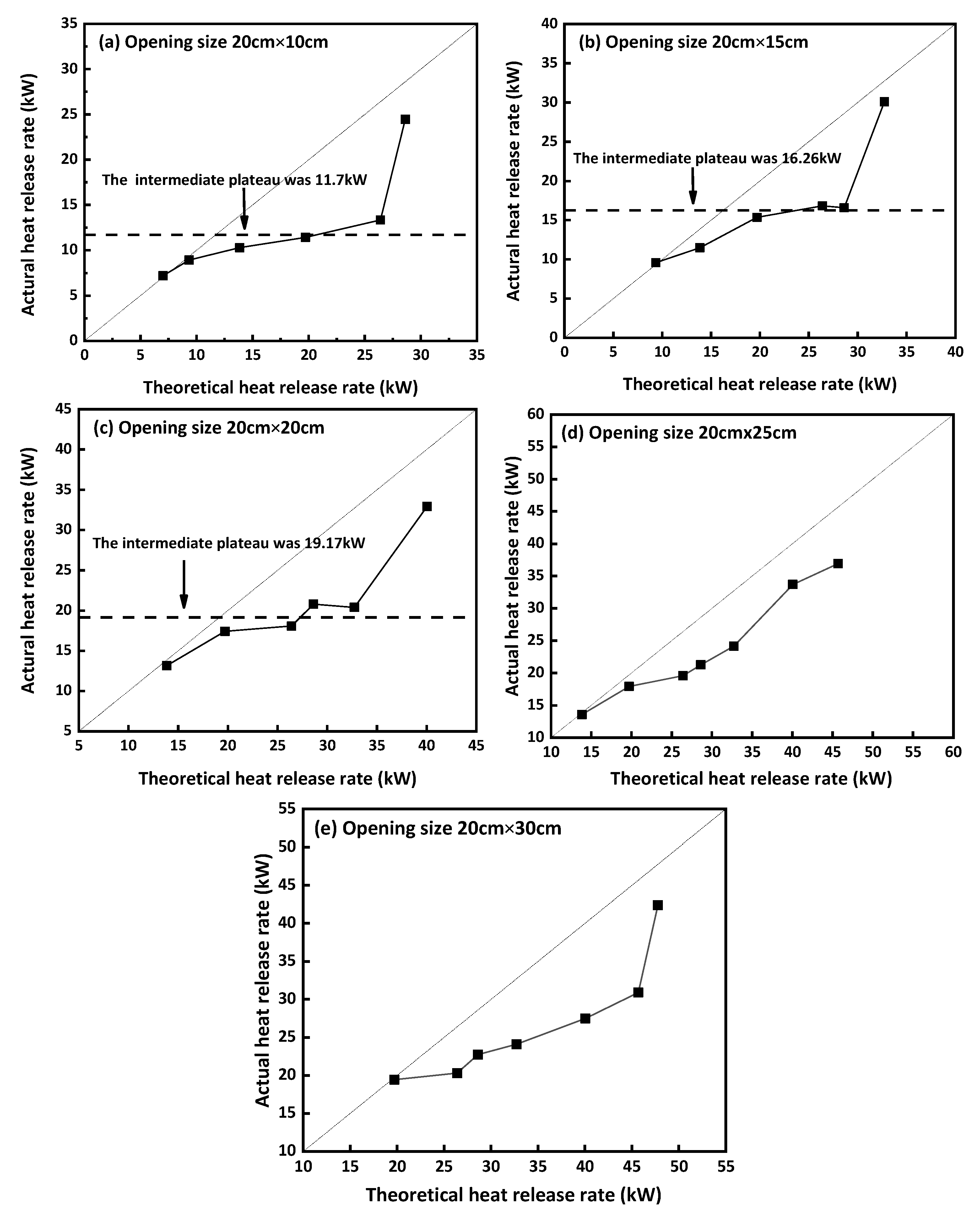
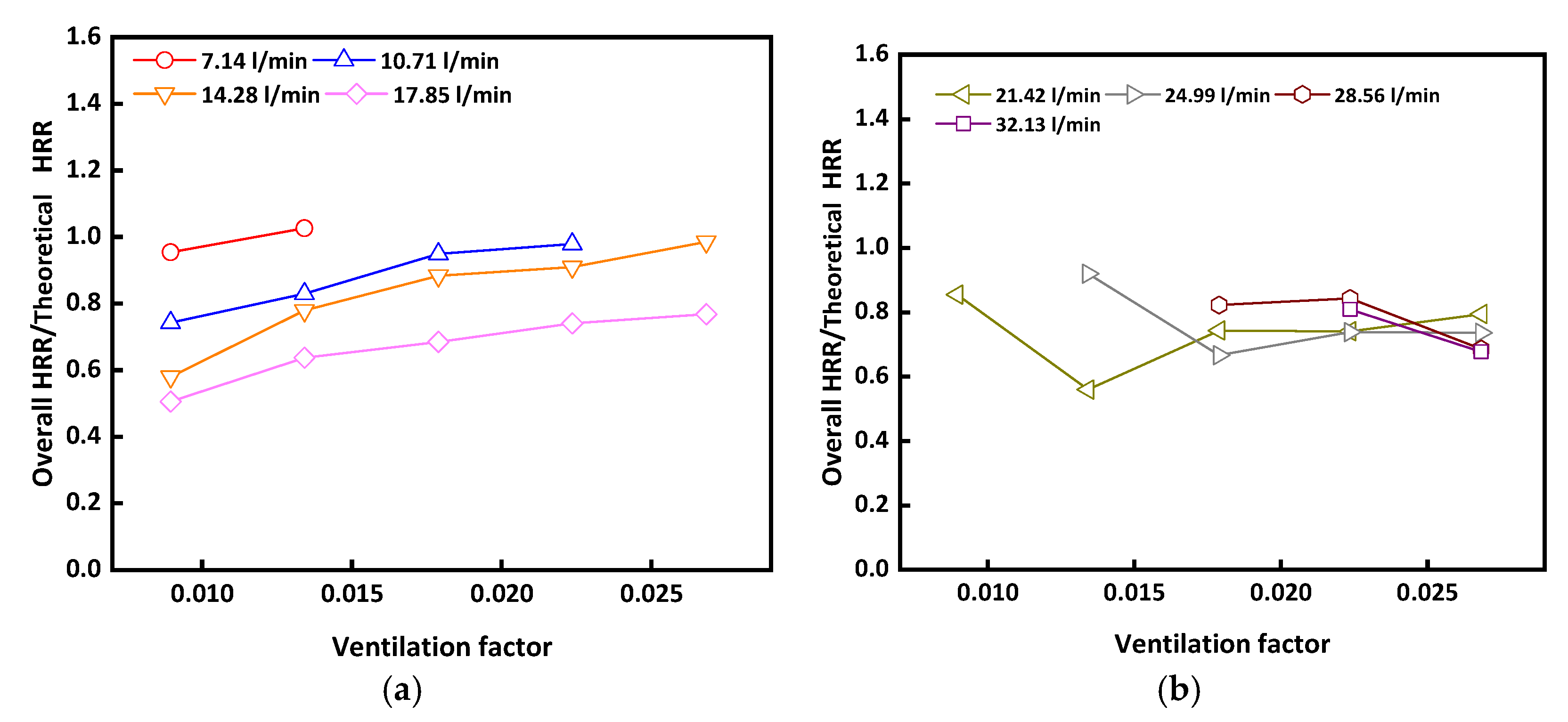
3. Results
Impact of Opening Factor on HRR
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kawagoe, K.; Sekine, T. Estimation of fire temperature rise curves in concrete buildings and its application. Bull. Jpn. Assoc. Fire Sci. Eng. 1963, 13, 1–12. [Google Scholar]
- Kawagoe, K. Fire Behaviour in Rooms; Report 27; Building Research Institute, Ministry of Construction: Tokyo, Japan, 1958.
- Babrauskas, V.; Williamson, R.B. Post-flashover compartment fires: Basis of a theoretical model. Fire Mater. 1978, 2, 39–53. [Google Scholar] [CrossRef]
- Chotzoglou, K.E.; Asimakopoulou, E.K.; Zhang, J.; Delichatsios, M.A. An experimental investigation of burning behaviour of liquid pool fire in corridor-like enclosures. Fire Saf. J. 2019, 108, 102826. [Google Scholar] [CrossRef]
- Thomas, P.H.; Heselden, A.; Law, M. Fully-Developed Compartment Fires: Two Kinds of Behaviour; HM Stationery Office: London, UK, 1967. [Google Scholar]
- Thomas, I.R.; Bennetts, I.D. Fires in enclosures with single ventilation openings—Comparison of long and wide enclosures. Fire Saf. Sci. 2000, 6, 941–952. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Lee, Y.P.; Delichatsios, M.A.; Silcock, G.W.H. Heat fluxes and flame heights in façades from fires in enclosures of varying geometry. Proc. Combust. Inst. 2007, 31, 2521–2528. [Google Scholar] [CrossRef]
- Yamada, T.; Takanashi, K.I.; Yanai, E.; Suzuki, T.; Sekizawa, A.; Sato, H.; Kurioka, H. An experimental study of ejected flames and combustion efficiency. Fire Saf. Sci. 2003, 7, 903–914. [Google Scholar] [CrossRef]
- Huggett, C. Estimation of rate of heat release by means of oxygen consumption measurements. Fire Mater. 1980, 4, 61–65. [Google Scholar] [CrossRef]
- Cai, N.; Chow, W.K. Numerical studies on heat release rate in room fire on liquid fuel under different ventilation factors. Int. J. Chem. Eng. 2012, 2012, 910869. [Google Scholar] [CrossRef]
- Zhao, G.; Beji, T.; Merci, B. Application of FDS to under-ventilated enclosure fires with external flaming. Fire Technol. 2016, 52, 2117–2142. [Google Scholar] [CrossRef]
- Afflard, A.; Koutaiba, E.M.; Asimakopoulou, E.; Kolaitis, D.; Zhang, J.; Lardet, P. Numerical investigation of fire development in a medium scale iso9705 compartment-façade configuration. In Proceedings of the Fire Safety of Facades International Symposium, Paris, France, 25–27 July 2019; pp. 26–27. [Google Scholar]
- Law, M. Fire safety of external building elements. Eng. J. 1978, 15, 59–74. [Google Scholar] [CrossRef]
- Dinenno, P.J.; Society of Fire Protection Engineers; National Fire Protection Association. SFPE Handbook of Fire Protection Engineering; National Fire Protection Association: Quincy, MA, USA, 1995. [Google Scholar]
- Chow, W.K.; Han, S.S. Heat release rate calculation in oxygen consumption calorimetry. Appl. Therm. Eng. 2011, 31, 304–310. [Google Scholar] [CrossRef]
- Rockett, J.A. Fire induced gas flow in an enclosure. Combust. Sci. Technol. 1976, 12, 165–175. [Google Scholar] [CrossRef]
- Karlsson, B.; Quintiere, J. Energy release rates. In Enclosure Fire Dynamics; CRC Press: Boca Raton, FL, USA, 2000; Chapter 3. [Google Scholar]
- Chow, W.K.; Zou, G.W. Correlation equations on fire-induced air flow rates through doorway derived by large eddy simulation. Build. Environ. 2005, 40, 897–906. [Google Scholar] [CrossRef]
- Asimakopoulou, E.K.; Chotzoglou, K.; Kolaitis, D.I.; Founti, M.A. Characteristics of externally venting flames and their effect on the façade: A detailed experimental study. Fire Technol. 2016, 52, 2043–2069. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, T.; Huang, X. Numerical modeling of compartment fires: Ventilation characteristics and limitation of Kawagoe’s law. Fire Technol. 2022, 60, 1245–1268. [Google Scholar] [CrossRef]




| No. | Flow Rate (L/min) | cm) | Theoretical HRR (kW) | Combustion Efficiency | ||
|---|---|---|---|---|---|---|
| I-1 | 14.28 | 40.25 | 20 × 30 | 20.17 | 19.43 | 0.96 |
| I-2 | 17.85 | 25.21 | 20.3 | 0.81 | ||
| I-3 | 21.42 | 30.25 | 22.73 | 0.75 | ||
| I-4 | 24.99 | 35.29 | 24.1 | 0.68 | ||
| I-5 | 28.56 | 40.33 | 27.5 | 0.68 | ||
| I-6 | 32.13 | 45.37 | 30.9 | 0.68 | ||
| I-7 | 35.7 | 50.41 | 42.4 | 0.84 | ||
| II-1 | 10.71 | 33.54 | 20 × 25 | 15.12 | 13.56 | 0.90 |
| II-2 | 14.28 | 20.17 | 17.93 | 0.89 | ||
| II-3 | 17.85 | 25.21 | 19.56 | 0.78 | ||
| II-4 | 21.42 | 30.25 | 21.26 | 0.70 | ||
| II-5 | 24.99 | 35.29 | 24.16 | 0.68 | ||
| II-6 | 28.56 | 40.33 | 33.7 | 0.84 | ||
| II-7 | 32.13 | 45.37 | 36.93 | 0.81 | ||
| III-1 | 10.71 | 26.83 | 20 × 20 | 15.12 | 13.15 | 0.87 |
| III-2 | 14.28 | 20.17 | 17.42 | 0.86 | ||
| III-3 | 17.85 | 25.21 | 18.08 | 0.72 | ||
| III-4 | 21.42 | 30.25 | 20.79 | 0.69 | ||
| III-5 | 24.99 | 35.29 | 20.39 | 0.58 | ||
| III-6 | 28.56 | 40.33 | 32.92 | 0.82 | ||
| IV-1 | 7.14 | 20.12 | 20 × 15 | 10.08 | 9.59 | 0.95 |
| IV-2 | 10.71 | 15.12 | 11.49 | 0.76 | ||
| IV-3 | 14.28 | 20.17 | 15.36 | 0.76 | ||
| IV-4 | 17.85 | 25.21 | 16.83 | 0.67 | ||
| IV-5 | 21.42 | 30.25 | 16.59 | 0.55 | ||
| IV-6 | 24.99 | 35.29 | 30.1 | 0.85 | ||
| V-1 | 5 | 13.42 | 20 × 10 | 7.06 | 7.19 | 1.02 |
| V-2 | 7.14 | 10.08 | 8.92 | 0.88 | ||
| V-3 | 10.71 | 15.12 | 10.29 | 0.68 | ||
| V-4 | 14.28 | 20.17 | 11.43 | 0.57 | ||
| V-5 | 17.85 | 25.21 | 13.35 | 0.53 | ||
| V-6 | 21.42 | 30.25 | 24.45 | 0.81 |
| Researchers | Method | Scale | Fire Stage | ||
|---|---|---|---|---|---|
| Rockett [17] | Experiment | Full scale | All stages | 0.40–0.61 | - |
| Chotzoglou [4] | Experiment ethanol | Small scale | All stages | 0.347–0.516 | 1100 |
| Karlsson & Quintiere [18] | Theoretical | Multi scales | Under-ventilated | 0.50 | 1518 |
| Chow et al. [19] | 3-D simulation | Full scale | Over-ventilated | 0.47/0.44 | |
| Lee et al. [8] | Experiment | Small scale | Under-ventilated | 1500 | |
| Zhao et al. [12] | 3-D simulation | Small scale | Under-ventilated | 0.41 | 1131 |
| Asimakopoulou et al. [20] | 3-D simulation | Small scale | Under-ventilated | 925 | |
| Wang [21] | 3-D simulation | Full scale | Over-ventilated | 0.44 | 1158 |
| Wang [21] | 2-D simulation | Full scale | Over-ventilated | 0.52 | 1220 |
| This work | Experiment | Small scale | Over-ventilated | 0.357–0.436 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Sheng, Y.; Liao, Q.; Yu, Q.; Xiao, Z.; Chen, G.; Wang, H.; Lin, P. Experimental Investigation of Ventilation Effects on Combustion Efficiency and Heat Release Rate in Small-Scale Compartment Fires. Fire 2025, 8, 215. https://doi.org/10.3390/fire8060215
Li W, Sheng Y, Liao Q, Yu Q, Xiao Z, Chen G, Wang H, Lin P. Experimental Investigation of Ventilation Effects on Combustion Efficiency and Heat Release Rate in Small-Scale Compartment Fires. Fire. 2025; 8(6):215. https://doi.org/10.3390/fire8060215
Chicago/Turabian StyleLi, Weiheng, Yong Sheng, Qishuo Liao, Qi Yu, Zhiqiang Xiao, Guo Chen, Hao Wang, and Peng Lin. 2025. "Experimental Investigation of Ventilation Effects on Combustion Efficiency and Heat Release Rate in Small-Scale Compartment Fires" Fire 8, no. 6: 215. https://doi.org/10.3390/fire8060215
APA StyleLi, W., Sheng, Y., Liao, Q., Yu, Q., Xiao, Z., Chen, G., Wang, H., & Lin, P. (2025). Experimental Investigation of Ventilation Effects on Combustion Efficiency and Heat Release Rate in Small-Scale Compartment Fires. Fire, 8(6), 215. https://doi.org/10.3390/fire8060215










