Abstract
The Multi-Mode Model (MMM) is a physics-based anomalous transport model integrated into TRANSP for predicting electron and ion thermal transport, electron and impurity particle transport, and toroidal and poloidal momentum transport. While MMM provides valuable predictive capabilities, its computational cost, although manageable for standard simulations, is too high for real-time control applications. MMMnet, a neural network-based surrogate model, is developed to address this challenge by significantly reducing computation time while maintaining high accuracy. Trained on TRANSP simulations of DIII-D discharges, MMMnet incorporates an updated version of MMM (9.0.10) with enhanced physics, including isotopic effects, plasma shaping via effective magnetic shear, unified correlation lengths for ion-scale modes, and a new physics-based model for the electromagnetic electron temperature gradient mode. A key advancement is MMMnet’s ability to predict all six transport coefficients, providing a comprehensive representation of plasma transport dynamics. MMMnet achieves a two-order-of-magnitude speed improvement while maintaining strong correlation with MMM diffusivities, making it well-suited for real-time tokamak control and scenario optimization.
1. Introduction
Tokamaks require significant control to manage the complex and dynamic nature of plasma behavior and to meet the stringent requirements for achieving and maintaining fusion conditions. This control is crucial, as plasma turbulence strongly influences the transport of heat, particles, and momentum, directly affecting the ability to sustain fusion-relevant conditions. To model and predict plasma turbulence transport, physics-based fluid transport models such as the Multi-Mode Model (MMM) have been developed [1]. A large-scale validation exercise was recently conducted to demonstrate MMM’s capability to accurately predict transport coefficients for heat, particles, and momentum on a discharge timescale. These coefficients are incorporated into transport evolution equations to replicate a wide range of conventional tokamak profiles from EAST, KSTAR, JET, and DIII-D, as well as profiles from the low-aspect-ratio spherical tokamak NSTX [2,3].
However, in control-oriented simulations, achieving both high accuracy and fast computation is crucial for accurately predicting plasma profiles and assessing the performance and stability of plasma operating scenarios. This speed requirement often leads to the use of empirical models, which compromises accuracy. Physics-based models for turbulent transport, such as MMM [1] and TGLF [4], and for heating and current drive, such as NUBEAM [5] and GENRAY [6], along with the pedestal model EPED [7], are generally too computationally intensive for integrated modeling and control applications [8]. To address this challenge, machine learning (ML) techniques are being employed to achieve both accuracy and speed. Neural network-based surrogate models have been developed for MMM [9,10], NUBEAM [11,12,13], GENRAY [14], TGLF, and EPED [15].
This study leverages a neural network-based surrogate model for MMM to achieve a significant reduction in computation time. MMMnet, the so-called neural network-based version of MMM, is trained on TRANSP predictive runs for DIII-D discharges. Building on previous work [10], this version of MMMnet incorporates an updated MMM (9.0.10) with expanded physics [3]. These enhancements introduce isotopic effects, plasma shaping via effective magnetic shear, and impurity dilution. Additional improvements include a unified correlation length for ion-scale modes rotating in both electron and ion directions, finite Larmor radius effects, and faster solvers. Together, these advancements improve the model’s accuracy, consistency, computational speed, and physical realism. These upgrades are crucial for predicting and optimizing high-beta plasmas and advancing reactor concepts such as the Fusion Pilot Plant.
MMM consists of several key components, each addressing different aspects of plasma transport. The Weiland model predicts transport driven by ion temperature gradients (ITGs), trapped electrons (TEs), kinetic ballooning (KB), peeling, and high-mode-number MHD modes, contributing to electron and ion thermal, electron particle, and momentum transport. The recently introduced electromagnetic electron temperature gradient mode (ETGM) includes drift Alfvén dynamics and both electrostatic and electromagnetic ETG modes, specifically addressing electron thermal transport [16]. The microtearing mode (MTM) has been updated to model transport driven by electron temperature gradients in both collisionless and collisional regimes, incorporating magnetic flux surface perturbations and contributing to electron thermal transport [17]. Additionally, the drift-resistive ballooning mode (DRIBM) has been enhanced to account for transport driven by gradients, electron inertial effects, and inductive processes, which contribute to electron and ion thermal transport, as well as electron particle transport [18].
Moreover, a significant enhancement in this MMMnet version is the inclusion of surrogate models for all transport coefficients, including electron and ion thermal diffusivities, toroidal and poloidal momentum transport, and electron and impurity particle diffusivities. This improvement, along with the incorporation of advanced MMM physics, represents a substantial advancement over the previous version [10], which used an older MMM version (7.1) and provided only three transport coefficients. In contrast to previous approaches that used Principal Component Analysis (PCA) for dimensionality reduction, this research retains the original data dimensions to preserve feature integrity. This retention strategy has led to improved correlation between MMM and MMMnet diffusivities compared to prior work. Six separate neural network models have been trained, one for each of the six diffusivities.
This article is organized as follows: Section 2 details the methodology for acquiring training data from TRANSP simulations of 203 DIII-D discharges. Section 3 discusses data preprocessing techniques such as standardization and normalization, which are crucial in ML, as well as the information loss associated with dimensionality reduction. Section 4 describes the architecture and operation of neural networks, emphasizing their ability to model complex functions given sufficient training data and hidden layers. Section 5 outlines the training workflow of MMMnet, detailing data acquisition, preprocessing, model training, hyperparameter tuning, and evaluation to ensure both accuracy and computational efficiency. Section 6 evaluates the performance of MMMnet, highlighting its strong correlation with MMM’s computed diffusivities, efficient performance on testing data, and significantly reduced computation times, while noting some limitations in predicting electron and impurity particle diffusivities. Finally, Section 7 discusses the results and outlines future work aimed at integrating MMMnet into control-oriented codes and improving its accuracy for electron and impurity particle diffusivities.
2. Real-Time Data Acquisition
Neural network surrogate models require large datasets to learn complex dynamic systems with high dimensionality. Machine learning-based surrogate models can be trained on large datasets generated using physics-based simulations (e.g., TRANSP) to reproduce their results with significantly reduced computational cost. TRANSP [19], a widely used code in nearly all tokamak experiments, generates such data in both interpretive and predictive modes.
In interpretive mode, TRANSP inputs experimental data, enforces the transport equations, and produces transport coefficients for consistency. In predictive mode, it uses physics-based transport models like MMM to advance the transport equations forward in time. While MMM’s computation time is manageable for standard simulations, real-time control applications require significantly faster predictions. To integrate MMM’s predictive power into control-oriented modeling codes like COTSIM (Control-Oriented Transport SIMulator), MMMnet has been developed for DIII-D.
The dataset used in this study was obtained from TRANSP simulations of 203 experimental discharges from DIII-D. Anomalous diffusivity values were computed through predictive simulations using the MMM 9.0.10 module, resulting in a total of 377,306 time slices generated from these TRANSP runs. The discharges simulated in this study include DIII-D Ohmic, L-mode, and H-mode plasmas with co- and counter rotations, as well as plasmas with internal transport barriers.
The transport model MMM is combined with the Chang–Hinton neoclassical transport model [20] in TRANSP to describe transport in each discharge. Equilibrium data are obtained from the EFIT reconstruction algorithm. The safety factor (q) profile evolves based on the magnetic diffusion equation, while temperature, density, and momentum profiles evolve according to transport equations. Neutral beam injection heating and current drive are modeled using NUBEAM, whereas electron cyclotron heating and current drive are computed with the toroidal ray tracing code TORAY [21].
In TRANSP, spatially varying plasma properties, commonly referred to as profiles, are represented as discrete radial points evenly distributed along the normalized effective minor radius, , which ranges from 0 at the magnetic axis to 1 at the last closed flux surface. Here, represents the mean effective minor radius defined as , where is the toroidal magnetic flux, is the vacuum toroidal magnetic field at the tokamak’s major radius , and represents the mean effective minor radius at the last closed flux surface.
For this study, each input and output profile consists of 40 radial points, where represents the distance between successive radial points. MMMnet inputs consist of two scalars and eighteen profiles. It is important to provide the neural network with the correct set of input profiles to improve the predictions and facilitate integration with control algorithms. Since MMM is a gradient-based code, the normalized gradients of densities, temperatures, velocities, and safety factors are also considered separate inputs. The normalized gradients used by MMM can be computed as
where is the normalized gradient for a given plasma profile y (where ) and R is the major radius and r is the minor radius of the plasma. Table 1 provides the inputs and outputs of MMMnet, specifying their dimensions and denoting scalars with the superscript s and profiles with gradients with an asterisk.

Table 1.
A list of MMMnet’s inputs and outputs.
The dataset is divided into three categories, i.e., training, validation, and testing. The training set consists of 80% of the overall data, while 10% is assigned to the validation set, and the remaining 10% is assigned to the testing set.
3. Data Preprocessing
In previous work [10], linear PCA was used to reduce the data dimensionality. While PCA is a powerful tool for dimensionality reduction and data visualization, it is sensitive to scaling, and improper handling can lead to the loss of profile variance information. Beyond scaling issues, PCA assumes linear relationships between variables, which may not hold for inherently nonlinear data, such as poloidal momentum diffusivity. In such cases, standard PCA may fail to capture important features, necessitating the use of non-linear PCA for more effective dimensionality reduction [22]. This work uses a discrete nodal representation for profiles, consistent with TRANSP.
To improve neural network performance, all profiles should be scaled consistently. Data scaling is achieved through normalization (scaling profiles to a range, such as ) or standardization (scaling profiles to have zero mean and unit variance), both of which enhance convergence during training. Standardization prevents inputs with larger magnitudes, such as densities, from disproportionately influencing those with smaller magnitudes. Additionally, standardization ensures all inputs have equal initial influence during optimization, helping to prevent bias during backpropagation.
The DIII-D experimental dataset exhibits notable variations across different discharges, indicating that MMMnet was trained on a diverse dataset encompassing a wide range of experimental conditions. The standardization of the input data is performed as
where is the standardized value, is the actual value , n is the total number of inputs, is the mean, and is the standard deviation of the data.
The standardized distribution of input data is shown in Figure 1. Each violin plot provides a visual representation of how individual variables vary across the dataset after standardization, as described in Equation (2), where each quantity is normalized to have zero mean and unit variance. The width of each violin indicates the relative density of data points at different standardized values. These plots are shown separately for the center and edge of the plasma, reflecting potential spatial differences in profile behavior. These distributions demonstrate the diversity and representativeness of the dataset used to train MMMnet. Broad or multimodal shapes—such as those observed in the standardized electron or ion temperatures and toroidal velocity—indicate that these quantities vary significantly across discharges, possibly reflecting multiple operational regimes such as Ohmic, L-mode, and H-mode plasmas, as well as cases with internal transport barriers. Because each variable is standardized, these distributions reflect variation relative to the mean, not absolute physical values. Multimodal distributions suggest clustering of input values around two or more distinct ranges, which could correspond to different classes of discharges. In contrast, narrow distributions—such as for poloidal velocity near the plasma edge—suggest that this variable does not vary substantially across the diverse set of discharges, despite the inclusion of both L-mode and H-mode plasmas. This could reflect its limited role in regime differentiation. Identifying these patterns is important for assessing which inputs are likely to have a stronger influence on transport predictions and where further data expansion may improve model generalization.
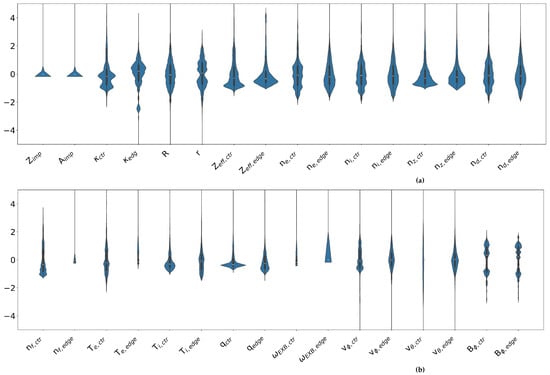
Figure 1.
Violin plots (a) and (b) showing the standardized distribution of the dataset. The horizontal axis represents different quantities, while the vertical axis indicates their range. The subscripts ‘ctr’ and ‘edge’ denote distributions at the center and edge of the DIII-D plasma, respectively.
4. Neural Network Architecture
Neural networks operate by constructing mathematical models that approximate complex functions, inspired by the behavior of the nervous system. These networks can learn a wide range of functions, including nonlinear ones, given sufficient training data and at least one adequately sized hidden layer. MMMnet leverages this capability to efficiently predict MMM outputs while significantly reducing computational cost. To achieve this, the three key data subsets, training, validation, and testing, serve distinct roles. The training dataset optimizes the model’s weights and biases, the validation dataset helps tune hyperparameters and prevent overfitting, and the testing dataset evaluates the model’s performance on unseen data.
The Keras neural network library and sequential model have been used to develop the surrogate model. Although MMMnet refers collectively to the surrogate modeling framework, it is implemented as six separately trained neural networks, each dedicated to predicting one of the six transport coefficients. This design choice was based on comparative testing, which showed that separately trained models yielded better agreement with the original MMM outputs than a single integrated network. Additionally, this approach improves computational efficiency and preserves COTSIM’s modularity. In scenarios where only a subset of transport coefficients is required (e.g., excluding particle transport), invoking only the relevant networks avoids unnecessary computation. Keras (version 3.10.0) is a user-friendly Python (version 3.12.11) library that provides a well-established way to build fully connected networks [23].The network type used in this work is a Multilayer Perceptron (MLP), which consists of fully connected neurons, as illustrated in Figure 2. A neuron is the mathematical function (3) that takes one or more inputs and produces an output. The input layer, or the first layer of the model, must specify the shape of the incoming data. This ensures that the model understands the structure and dimensions of the input data. The input variables are then multiplied by a matrix of weights with m the total number of neurons in the hidden layer (layers of neurons between the input and output layers) and n the number of inputs. The sum of the products of the weights and input variables is added to the bias term. A nonlinear activation function is then applied to the resulting weighted sum, transforming the input. The output of a single neuron can be written as
where is the bias term that allows the neuron to activate even if all inputs are zero. The rectified linear unit (ReLU) is used as an activation function in the hidden layer to introduce non-linearity in the network, i.e.,
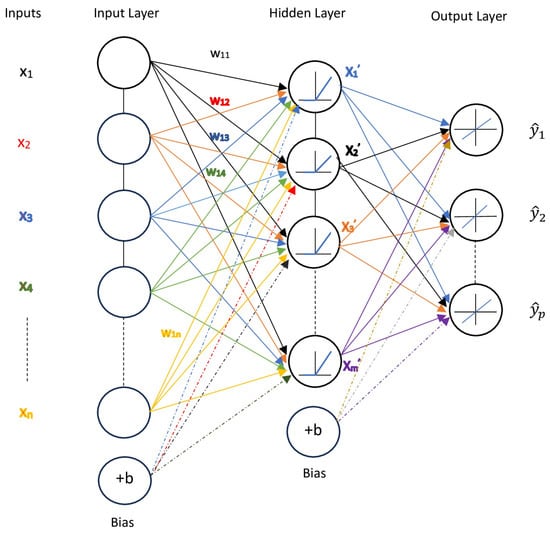
Figure 2.
The neural network architecture used in this study is a Multilayer Perceptron, consisting of fully connected neurons arranged in multiple layers. Each network receives as input a set of scalar and profile quantities, where each profile is defined over 40 radial grid points. The output of each network is a transport coefficient profile, also defined over the same 40-point radial grid. This schematic illustrates the data flow and architecture of one such network.
Neural networks, such as the MLP, are called feedforward networks, where information flows from a set of inputs through a series of hidden units to a set of outputs. Keras takes care of the random initialization of weights and biases. The training or learning algorithm for weights and biases is based on a procedure known as error backpropagation. The backpropagation of errors is a technique used to iteratively adjust the network’s weights to minimize the mean squared error (MSE) between the target values (ground truth) and the corresponding predicted values. The loss function is defined as
where p is the number of samples, is the target value, and is the predicted value. Since the predicted values depend on the network’s weights, the loss function is also a function of these weights. The MSE loss function (5) is particularly suitable for regression problems where the neural network predicts a continuous scalar value.
The model’s performance can be evaluated by observing the loss as a function of epochs (number of full passes through the dataset), as shown in Figure 3. The figure depicts the training and validation loss curves of a neural network over 100 epochs, with the blue line representing the training loss and the orange line representing the validation loss. Training loss measures how well the model fits the training data during each epoch, while validation loss evaluates how well the trained model generalizes to unseen data. Initially, both losses are high, indicating an untrained model, but they decrease rapidly in the early epochs, demonstrating effective learning. After approximately 20 epochs, the losses stabilize and fluctuate at lower values, suggesting that the model has converged. The close alignment of training and validation losses indicates that the model is not overfitting and performs consistently on both datasets, reflecting good generalization to unseen data.
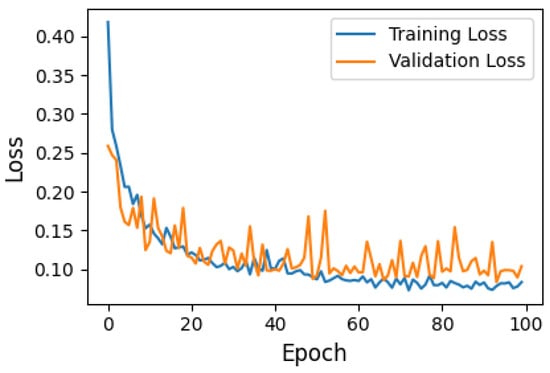
Figure 3.
Training and validation loss curves. The plot shows the loss over epochs for both the training and validation datasets.
A random search was conducted to determine the optimal neural network hyperparameters aimed at balancing model accuracy and computational efficiency. In ML, hyperparameters are configurable parameters that define the learning process of a model. The summary of hyperparameters is shown in Table 2. The performance of the model is evaluated using the MSE as both the loss function and the performance metric. The ReLU activation function was selected for its simplicity and effectiveness in introducing nonlinearity while avoiding the vanishing gradient problem that often affects sigmoid and tanh activations. ReLU also accelerates training due to its computational efficiency. The Adam optimizer was chosen for its adaptive learning rate capabilities, which combine the strengths of Root Mean Square Propagation (RMSProp) and momentum-based methods. This results in faster convergence and greater robustness across a variety of training conditions. These choices were validated through the hyperparameter scan, which confirmed that models using ReLU and Adam consistently outperformed alternatives.

Table 2.
Final neural network hyperparameters.
5. MMMnet Training Workflow and Model Development
The workflow for training MMMnet is illustrated in Figure 4. This process begins with acquiring data from TRANSP simulations of DIII-D discharges, which provide the inputs and outputs for the neural network. The data undergoes standardization to ensure consistent scaling before being split into three subsets: training, validation, and testing. The training set is used to optimize the model’s weights and biases, while the validation set is utilized for hyperparameter tuning and overfitting prevention. The testing dataset serves to evaluate the model’s generalization to unseen data.
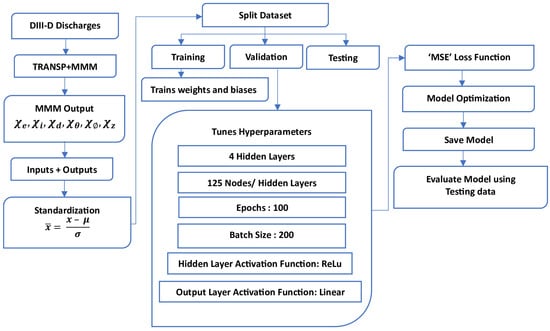
Figure 4.
Schematic of training MMMnet: from data acquisition to training, validation, and evaluation of the model.
The neural network architecture comprises four hidden layers, each with 125 nodes, using a ReLU activation function (4) in the hidden layers and a linear activation function, , in the output layer. Several neural network models were tested, varying the number of hidden layers (ranging from 2 to 6) and the number of nodes per layer (ranging from 64 to 256), using the validation dataset to assess performance. Models with fewer than four hidden layers exhibited noticeably lower accuracy, particularly for momentum and impurity diffusivities. Conversely, increasing the number of layers beyond four yielded marginal improvements in accuracy at the cost of significantly higher training and inference time. The four-layer model with 125 nodes per layer consistently provided the best trade-off between regression performance and speed, as evidenced by the validation loss convergence and the correlation metrics presented in Table 3. In addition, the model is trained over 100 epochs with a batch size of 200, minimizing the MSE loss function. This model was, thus, selected as the optimal configuration for MMMnet. Once training is complete, the model is saved and evaluated on the testing dataset to assess accuracy and computational efficiency.

Table 3.
Correlation analysis between MMM and MMMNet for the training and testing data.
This systematic workflow ensures that MMMnet achieves both high accuracy and reduced computational cost, making it a viable surrogate model for integrating MMM predictions into control-oriented transport modeling.
6. Performance Evaluation and Validation of MMMnet
The performance of MMMnet is assessed through correlation analysis and evaluation on previously unseen testing data, as shown in Figure 5 and Figure 6. The results demonstrate strong agreement between MMMnet’s predictions and the diffusivities computed by MMM, with the correlation coefficients summarized in Table 3. This indicates that MMMnet effectively captures the underlying behavior of MMM rather than simply memorizing the training data. Notably, in Figure 6, peaks in diffusivity are observed at specific radial locations for (a) the toroidal momentum diffusivity, (e) the electron particle diffusivity, and (f) the impurity particle diffusivity. These peaks occur at both large and small gradient values of the plasma profiles. At large gradients, strong instabilities enhance transport, leading to high diffusivity. At small gradients, although instability growth rates are reduced, diffusivity can still be elevated due to the gradient appearing in the denominator of the diffusivity expressions.
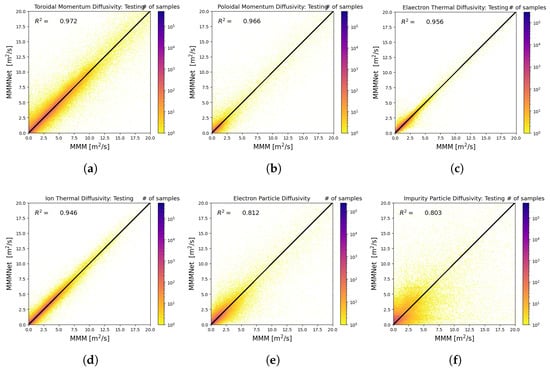
Figure 5.
Comparison of transport coefficients: (a,b) toroidal and poloidal momentum diffusivities, (c,d) electron and ion thermal diffusivities, and (e,f) electron and impurity particle diffusivities. Strong correlations indicate that MMMnet accurately replicates MMM values. Narrow correlation bands suggest low variance, highlighting model precision. The slightly lower accuracy for electron and impurity particle diffusivities is likely due to their complex dynamics.
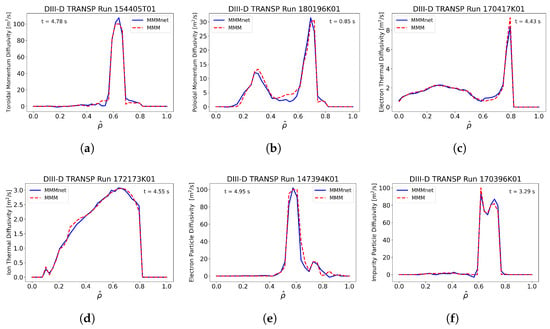
Figure 6.
Evaluation of various DIII-D runs shows MMMnet’s strong performance and predictive accuracy for MMM transport coefficients: (a) toroidal momentum diffusivity (); (b) poloidal momentum diffusivity (); (c) electron thermal diffusivity (); (d) ion thermal diffusivity (); (e) electron particle diffusivity (); (f) impurity particle diffusivity ().
The surrogate model delivers high accuracy while significantly reducing computation time. Specifically, MMMnet delivers precise predictions two orders of magnitude faster than MMM v9.0.1, highlighting its superior computational efficiency. All computational time measurements were obtained on a MacBook Pro (Apple Inc., Cupertino, CA, USA) with a 2.3 GHz 8-Core Intel Core i9 processor and 16 GB RAM. As shown in Table 3, MMMnet predicts transport coefficients with computational times ranging from 0.06 ms to 0.15 ms per inference, demonstrating a substantial speedup compared to MMM while maintaining strong correlation. The narrow correlation bands in Figure 5 suggest low variance in MMMnet’s predictions, further underscoring its reliability.
However, the electron particle and impurity particle diffusivities exhibit slightly lower regression accuracy, likely due to their complex dynamics. Improving accuracy for these transport coefficients may require additional training data or a more sophisticated model architecture. However, increasing model complexity could impact computational efficiency. Despite this, MMMnet’s overall performance confirms its capability as an efficient and accurate surrogate model for MMM.
7. Conclusions
Tokamaks require precise control to manage complex plasma behavior and achieve fusion conditions. This study presents the development of MMMnet, a neural network-based surrogate model for the anomalous transport model MMM, designed to significantly reduce computation time while maintaining high accuracy. Trained on 203 experimental shots from the DIII-D tokamak, MMMnet utilizes a multilayer perceptron architecture. Careful hyperparameter tuning ensured an optimal balance between regression accuracy and computational efficiency.
The results demonstrate that MMMnet effectively replicates MMM-computed transport coefficients, achieving high correlation coefficients while substantially reducing computation time. Specifically, MMMnet predicts diffusivities two orders of magnitude faster than MMM v9.0.1, making it well-suited for integration into control-oriented codes such as COTSIM. This capability enables real-time prediction of temperature, density, and momentum profiles, which is crucial for advanced plasma control.
Going forward, MMMnet is expected to support scenario planning, iterative control design, and real-time applications—including plasma control, estimation, and forecasting—for DIII-D, paving the way for more efficient and predictive tokamak operations.
Author Contributions
K.S.: writing, editing—original draft, data curation, visualization, validation, methodology, and investigation. B.L.: visualization and validation. Z.W. and S.T.P.: conceptualization (support). T.R.: writing, review, editing, conceptualization, and supervision. E.S.: review, funding acquisition, conceptualization, and supervision. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Fusion Energy Sciences (award numbers: DE-SC0010661, DE-SC0013977, and DE-FC02-04ER54698).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
Disclaimer
This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
References
- Rafiq, T.; Kritz, A.H.; Weiland, J.; Pankin, A.Y.; Luo, L. Physics basis of Multi-Mode anomalous transport module. Phys. Plasmas 2013, 20, 032506. [Google Scholar] [CrossRef]
- Rafiq, T.; Wang, Z.; Morosohk, S.; Schuster, E.; Weiland, J.; Choi, W.; Kim, H.T. Validating the Multi-Mode Model’s Ability to Reproduce Diverse Tokamak Scenarios. Plasma 2023, 6, 435–458. [Google Scholar] [CrossRef]
- Rafiq, T.; Wilson, C.; Clauser, C.; Schuster, E.; Weiland, J.; Anderson, J.; Kaye, S.; Pankin, A.; LeBlanc, B.; Bell, R. Predictive modeling of NSTX discharges with the updated Multi-Mode anomalous transport module. Nucl. Fusion 2024, 64, 076024. [Google Scholar] [CrossRef]
- Staebler, G.M.; Kinsey, J.E.; Waltz, R.E. A theory-based transport model with comprehensive physics. Phys. Plasmas 2007, 14, 055909. [Google Scholar] [CrossRef]
- Pankin, A.; McCune, D.; Andre, R.; Bateman, G.; Kritz, A. The tokamak Monte Carlo fast ion module NUBEAM in the National Transport Code Collaboration library. Comput. Phys. Commun. 2004, 159, 157–184. [Google Scholar] [CrossRef]
- Harvey, R.W.; McCoy, M.G. The CQL3D Fokker–Planck Code. In Proceedings of the IAEA Technical Committee Meeting on Advances in Simulation and Modeling of Thermonuclear Plasmas, Montreal, QC, Canada, 15–17 June 1992; pp. 489–526. [Google Scholar]
- Snyder, P.B.; Groebner, R.J.; Leonard, A.W.; Osborne, T.H.; Wilson, H.R. Development and validation of a predictive model for the pedestal height. Phys. Plasmas 2009, 16, 056118. [Google Scholar] [CrossRef]
- Leard, B.R.; Paruchuri, S.T.; Rafiq, T.; Schuster, E. Fast model-based scenario optimization in NSTX-U enabled by analytic gradient computation. Fusion Eng. Des. 2023, 192, 113606. [Google Scholar] [CrossRef]
- Leard, B.; Wang, Z.; Morosohk, S.; Rafiq, T.; Schuster, E. Fast Neural-Network Surrogate Model of the Updated Multi-Mode Anomalous Transport Module for NSTX-U. IEEE Trans. Plasma Sci. 2024, 52, 4126–4132. [Google Scholar] [CrossRef]
- Morosohk, S.; Pajares, A.; Rafiq, T.; Schuster, E. Neural network model of the multi-mode anomalous transport module for accelerated transport simulations. Nucl. Fusion 2021, 61, 106040. [Google Scholar] [CrossRef]
- Boyer, M.; Kaye, S.; Erickson, K. Real-time capable modeling of neutral beam injection on NSTX-U using neural networks. Nucl. Fusion 2019, 59, 056008. [Google Scholar] [CrossRef]
- Morosohk, S.M.; Boyer, M.D.; Schuster, E. Accelerated version of NUBEAM capabilities in DIII-D using neural networks. Fusion Eng. Des. 2021, 163, 112125. [Google Scholar] [CrossRef]
- Wang, Z.; Morosohk, S.; Rafiq, T.; Schuster, E.; Boyer, M.; Choi, W. Neural network model of neutral beam injection in the EAST tokamak to enable fast transport simulations. Fusion Eng. Des. 2023, 191, 113514. [Google Scholar] [CrossRef]
- Wallace, G.; Bai, Z.; Sadre, R.; Perciano, T.; Bertelli, N.; Shiraiwa, S.; Bethel, E.; Wright, J. Towards fast and accurate predictions of radio frequency power deposition and current profile via data-driven modelling: Applications to lower hybrid current drive. J. Plasma Phys. 2022, 88, 895880401. [Google Scholar] [CrossRef]
- Meneghini, O.; Smith, S.; Snyder, P.; Staebler, G.; Candy, J.; Belli, E.; Lao, L.; Kostuk, M.; Luce, T.; Luda, T.; et al. Self-consistent core-pedestal transport simulations with neural network accelerated models. Nucl. Fusion 2017, 57, 086034. [Google Scholar] [CrossRef]
- Rafiq, T.; Wilson, C.; Luo, L.; Weiland, J.; Schuster, E.; Pankin, A.Y.; Guttenfelder, W.; Kaye, S. Electron temperature gradient driven transport model for tokamak plasmas. Phys. Plasmas 2022, 29, 092503. [Google Scholar] [CrossRef]
- Rafiq, T.; Weiland, J.; Kritz, A.H.; Luo, L.; Pankin, A.Y. Microtearing modes in tokamak discharges. Phys. Plasmas 2016, 23, 062507. [Google Scholar] [CrossRef]
- Rafiq, T.; Bateman, G.; Kritz, A.H.; Pankin, A.Y. Development of drift-resistive-inertial ballooning transport model for tokamak edge plasmas. Phys. Plasmas 2010, 17, 082511. [Google Scholar] [CrossRef]
- Pankin, A.; Breslau, J.; Gorelenkova, M.; Andre, R.; Grierson, B.; Sachdev, J.; Goliyad, M.; Perumpilly, G. TRANSP integrated modeling code for interpretive and predictive analysis of tokamak plasmas. arXiv 2024, arXiv:2406.07781. [Google Scholar] [CrossRef]
- Chang, C.S.; Hinton, F.L. Effect of impurity particles on the finite-aspect ratio neoclassical ion thermal conductivity in a tokamak. Phys. Fluids 1986, 29, 3314–3316. [Google Scholar] [CrossRef]
- Kritz, A.; Hsuan, H.; Goldfinger, R.; Batchelor, D. Ray Tracing Study of Electron Cyclotron Heating in Toroidal Geometry. In Heating in Toroidal Plasmas 1982; Gormezano, C., Leotta, G., Sindoni, E., Eds.; Elsevier: Amsterdam, The Netherlands, 1982; pp. 707–723. [Google Scholar] [CrossRef]
- Mori, Y.; Kuroda, M.; Makino, N. Nonlinear Principal Component Analysis and Its Applications; Springer: Singapore, 2016. [Google Scholar]
- Pang, B.; Nijkamp, E.; Wu, Y.N. Deep Learning With TensorFlow: A Review. J. Educ. Behav. Stat. 2020, 45, 227–248. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).