A Theoretical Study of the Ionization States and Electrical Conductivity of Tantalum Plasma
Abstract
1. Introduction
2. Methods
2.1. Ionized Species
2.2. Nonideal Saha Equations
2.3. Electrical Conductivity
3. Results and Discussion
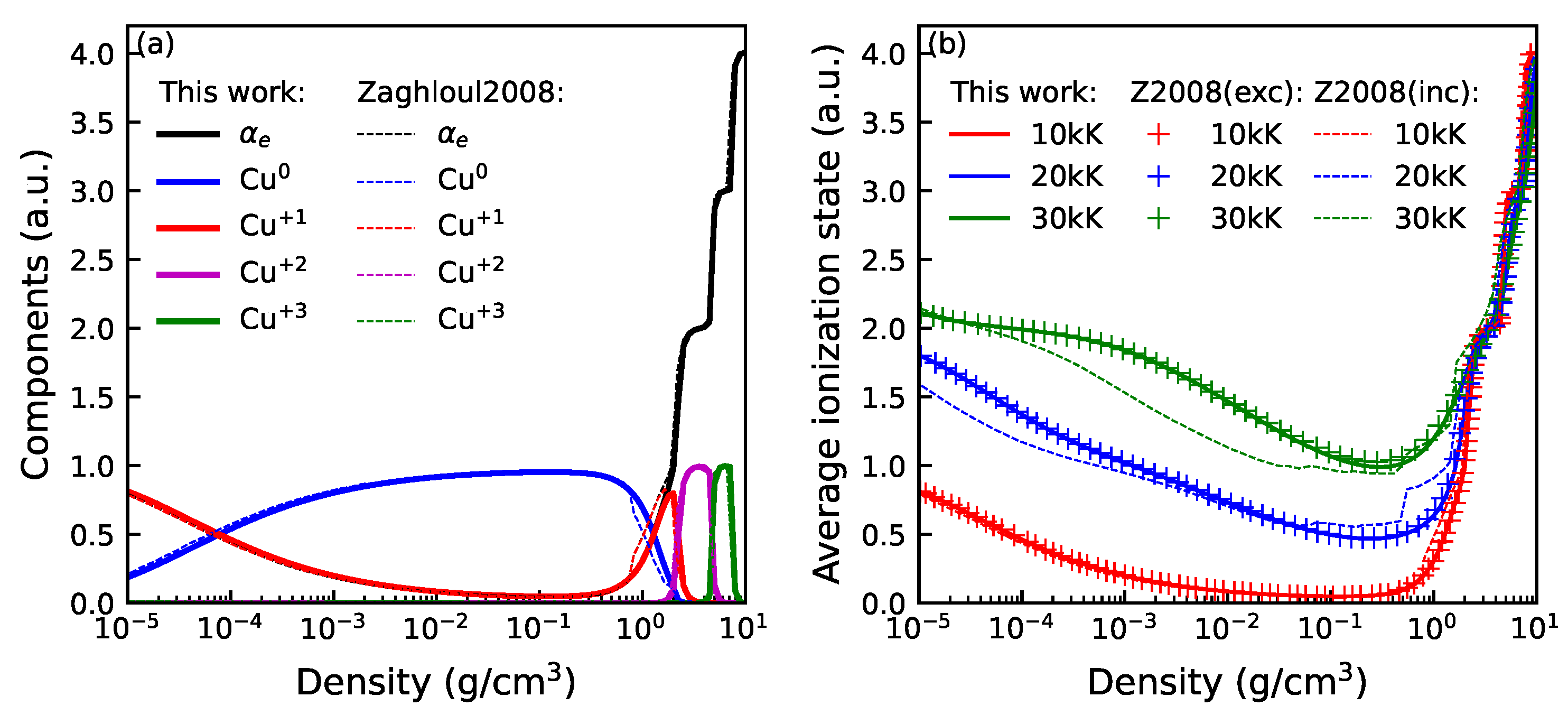
3.1. Validation of Saha Equation Solver
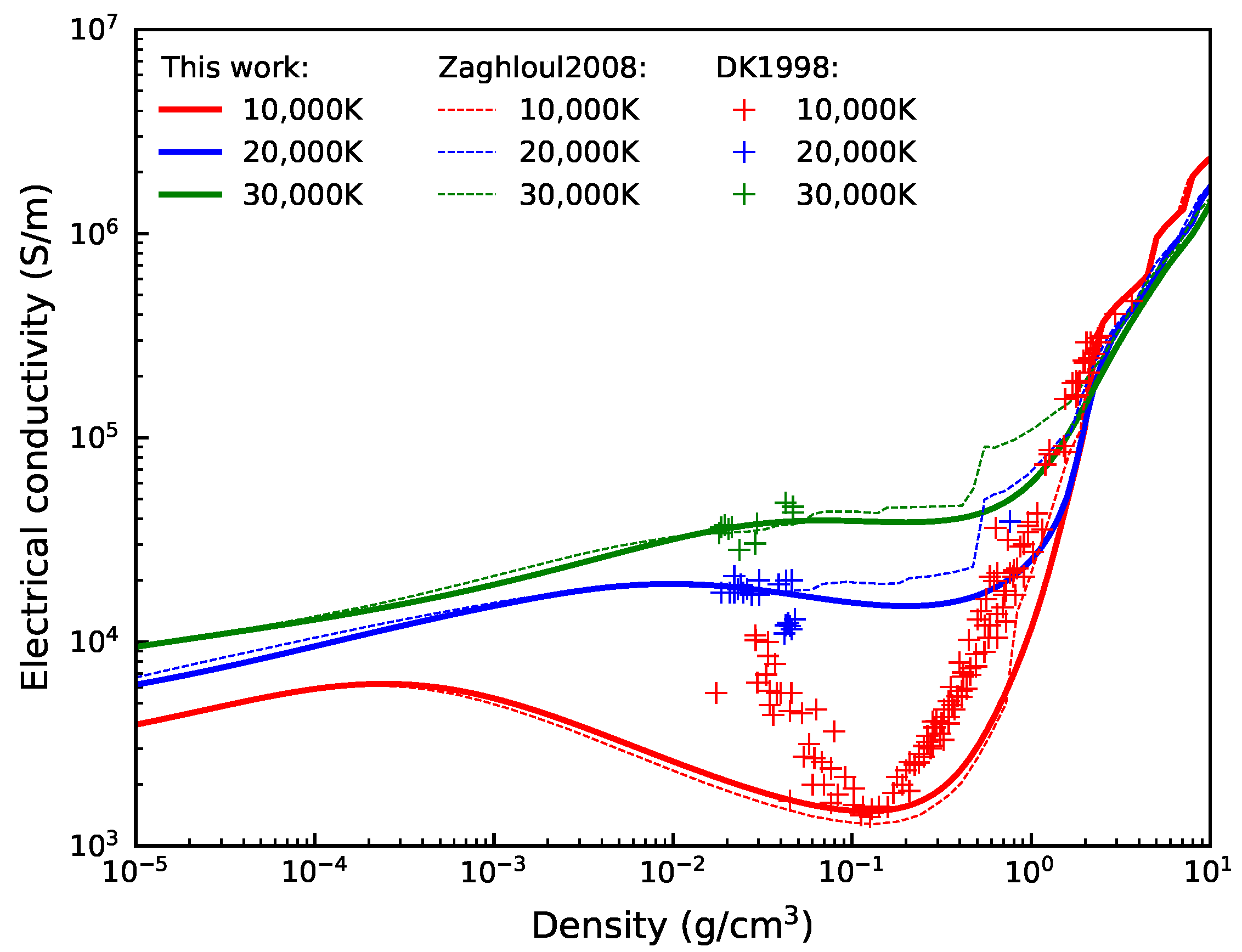
3.2. Validation of Electrical Conductivity Calculation
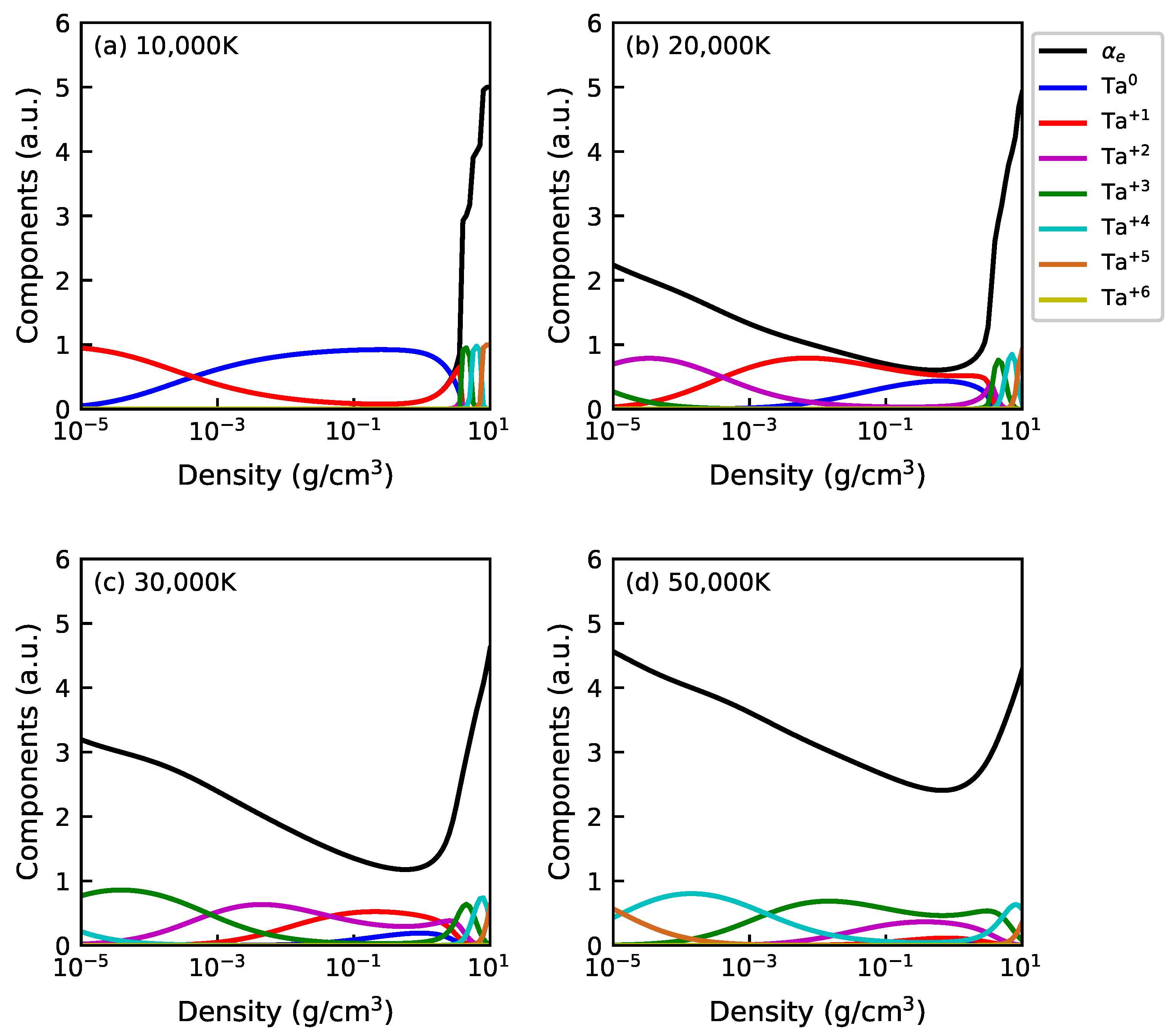
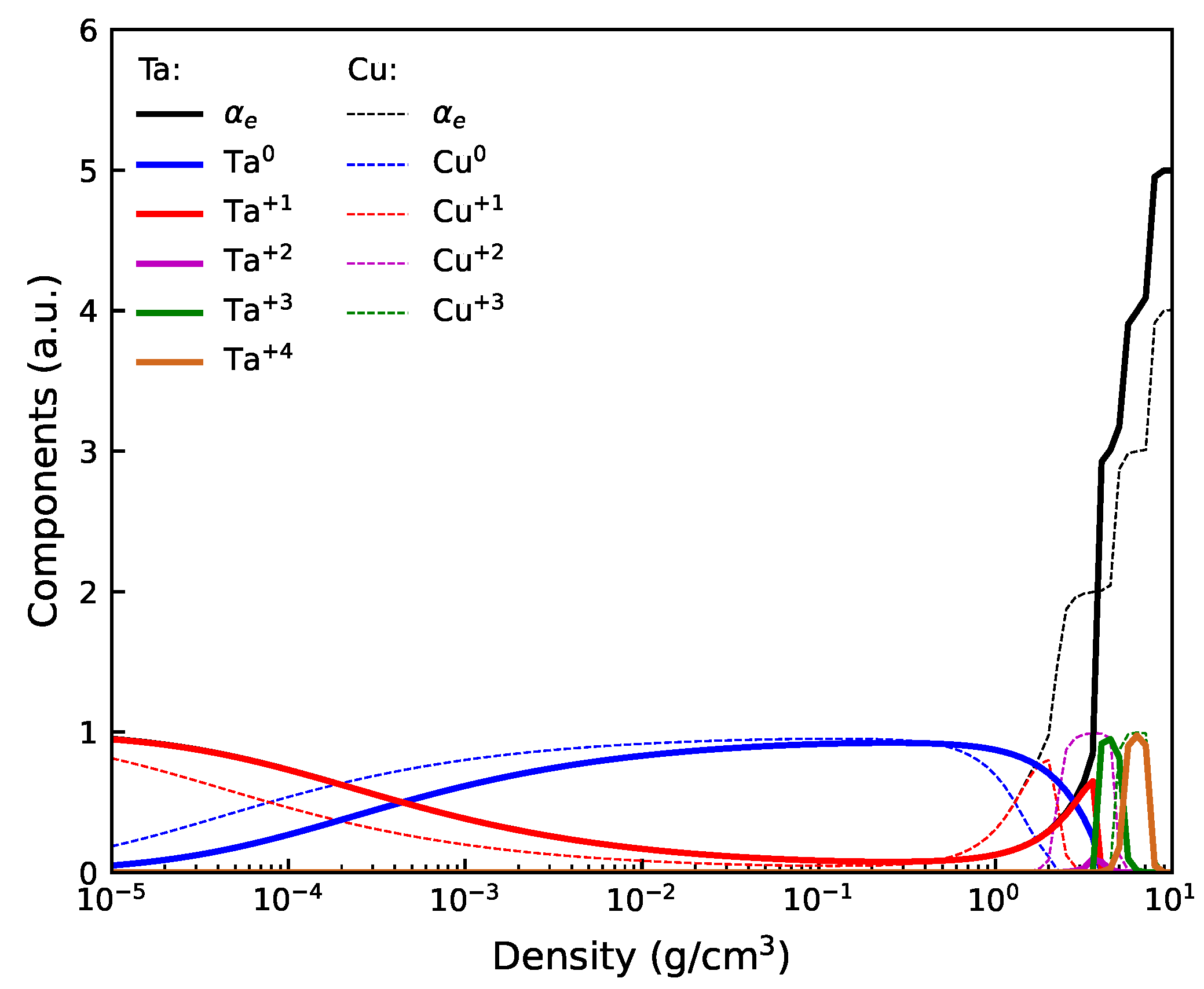
3.3. Ionization States of Tantalum Plasmas
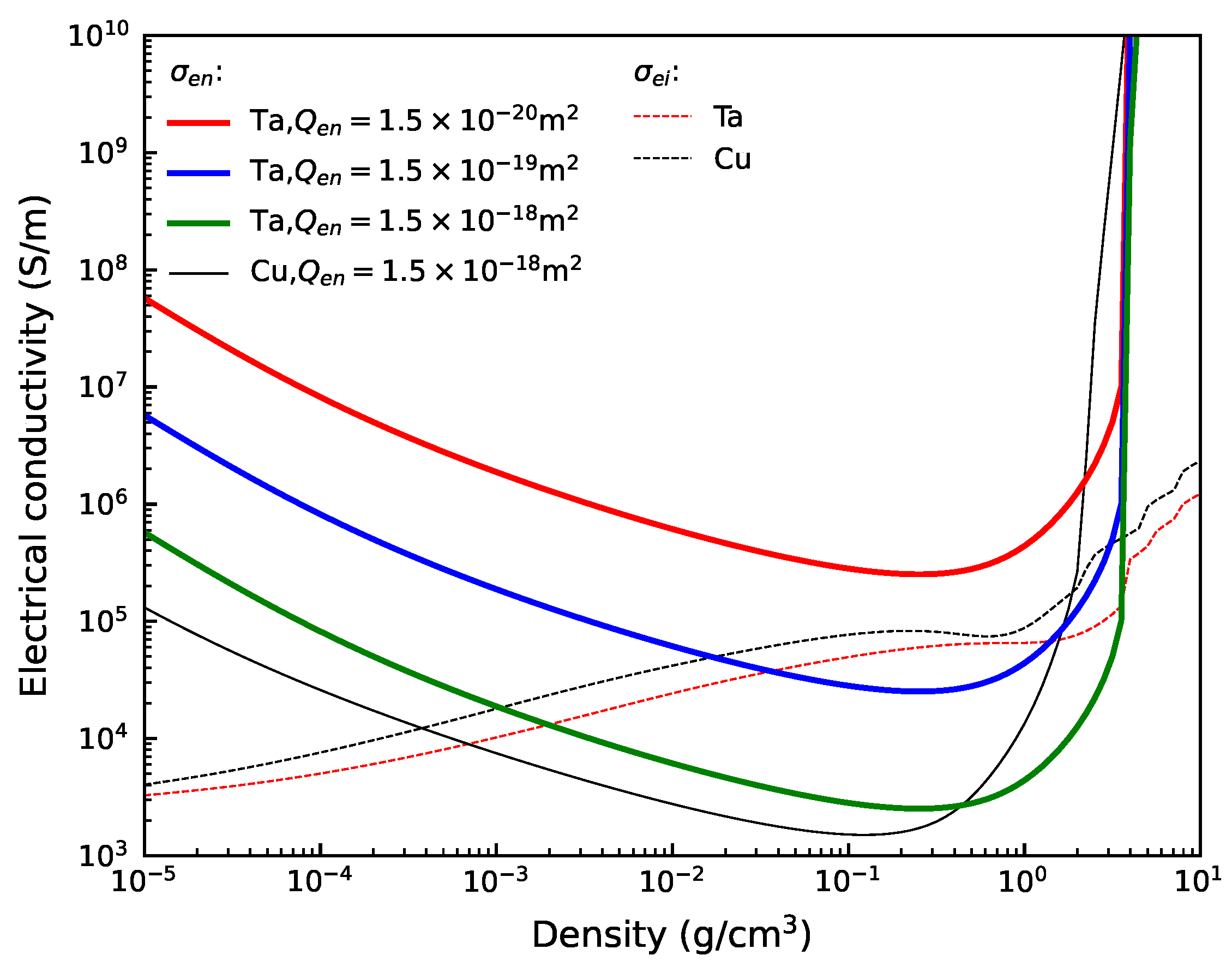
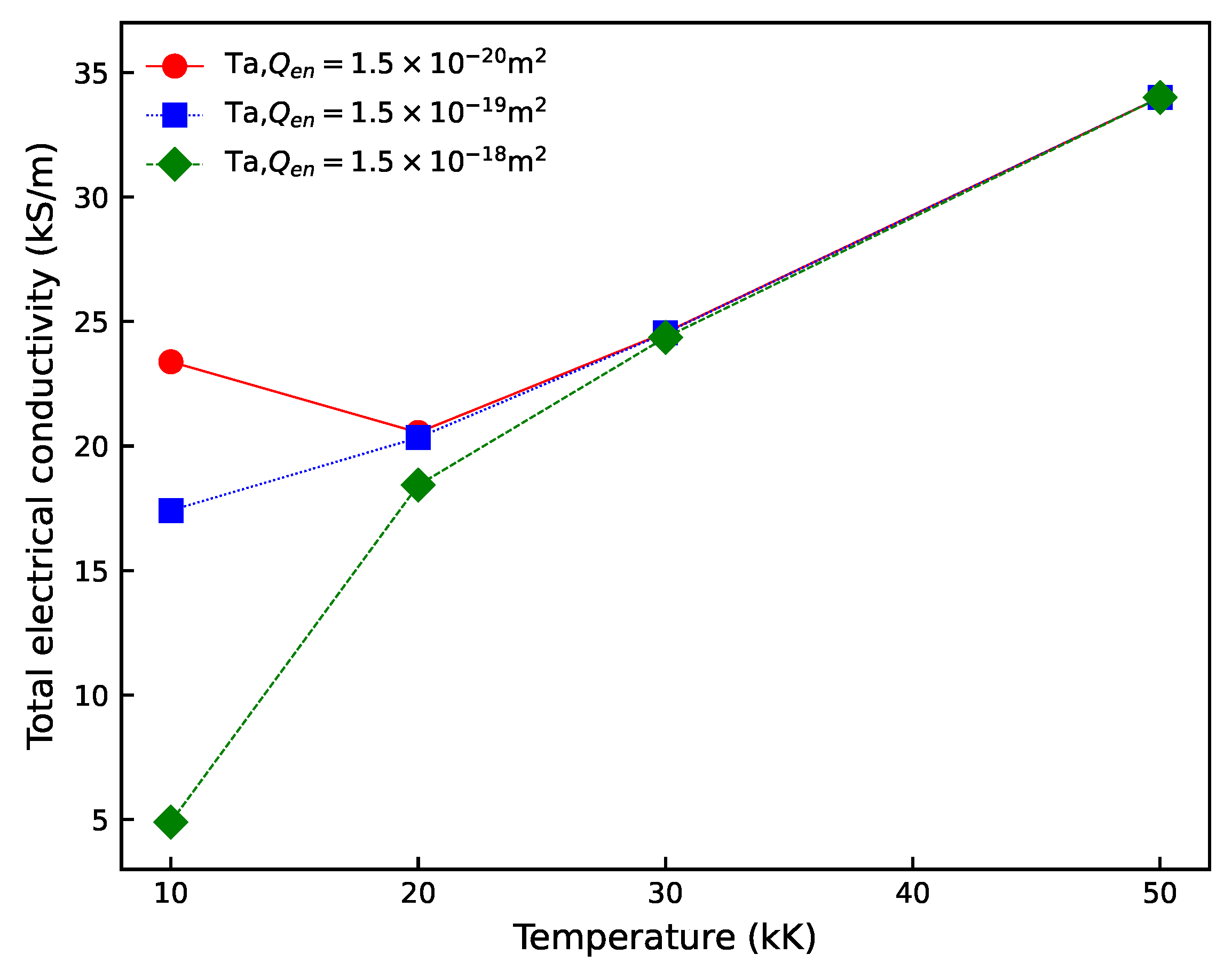
3.4. Electrical Conductivity of Tantalum Plasmas
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bayu-Aji, L.B.; Engwall, A.M.; Bae, J.H.; Baker, A.A.; Beckham, J.L.; Shin, S.J.; Lepro Chavez, X.; McCall, S.K.; Moody, J.D.; Kucheyev, S.O. Sputtered Au-Ta films with tunable electrical resistivity. J. Phys. D Appl. Phys. 2021, 54, 075303. [Google Scholar] [CrossRef]
- Frederick, C.A.; Forsman, A.C.; Hund, J.F.; Eddinger, S.A. Fabrication of Ta2O5 aerogel targets for radiation transport experiments using thin film fabrication and laser processing. Fusion Sci. Technol. 2009, 55, 499–504. [Google Scholar] [CrossRef]
- Baker, A.A.; Engwall, A.M.; Bayu-Aji, L.B.; Bae, J.H.; Shin, S.J.; Moody, J.D.; Kucheyev, S.O. Tantalum suboxide films with tunable composition and electrical resistivity deposited by reactive magnetron sputtering. Coatings 2022, 12, 917. [Google Scholar] [CrossRef]
- Bhandarkar, S.; Baumann, T.; Alfonso, N.; Thomas, C.; Baker, K.; Moore, A.; Larson, C.; Bennett, D.; Sain, J.; Nikroo, A. Fabrication of low-density foam liners in hohlraums for NIF targets. Fusion Sci. Technol. 2018, 73, 194–209. [Google Scholar] [CrossRef]
- Berger, R.L.; Arrighi, W.; Chapman, T.; Dimits, A.; Banks, J.W.; Brunner, S. The competing effects of wave amplitude and collisions on multi-ion species suppression of stimulated Brillouin scattering in inertial confinement fusion hohlraums. Phys. Plasmas 2023, 30, 042715. [Google Scholar] [CrossRef]
- Zhernokletov, M.V.; Simakov, G.V.; Sutulov, Y.N.; Trunin, R.F. Expansion isentropes of aluminum, iron, molybdenum, lead, and tantalum. High Temp. 1995, 33, 40–43. [Google Scholar]
- Miljacic, L.; Demers, S.; Hong, Q.J.; van de Walle, A. Equation of state of solid, liquid and gaseous tantalum from first principles. Calphad 2015, 51, 133–143. [Google Scholar] [CrossRef]
- DeSilva, A.W.; Vunni, G.B. Electrical conductivity of dense Al, Ti, Fe, Cu, Mo, Ta, and W plasmas. Phys. Rev. E 2011, 83, 037402. [Google Scholar] [CrossRef]
- Apfelbaum, E.M. The pressure, internal energy, and conductivity of tantalum plasma. Contrib. Plasma Phys. 2017, 57, 479–485. [Google Scholar] [CrossRef]
- Harris, G.M.; Roberts, J.E.; Trulio, J.G. Equilibrium properties of a partially ionized plasma. Phys. Rev. 1960, 119, 1832–1841. [Google Scholar] [CrossRef]
- Zaghloul, M.R. Reduced formulation and efficient algorithm for the determination of equilibrium composition and partition functions of ideal and nonideal complex plasma mixtures. Phys. Rev. E 2004, 69, 026702. [Google Scholar] [CrossRef]
- Zaghloul, M.R. A simple theoretical approach to calculate the electrical conductivity of nonideal copper plasma. Phys. Plasmas 2008, 15, 042705. [Google Scholar] [CrossRef]
- Wang, W.Z.; Rong, M.Z.; Yan, J.D.; Murphy, A.B.; Spencer, J.W. Thermophysical properties of nitrogen plasmas under thermal equilibrium and non-equilibrium conditions. Phys. Plasmas 2011, 18, 113502. [Google Scholar] [CrossRef]
- Das, M. Transition energies and polarizabilities of hydrogen like ions in plasma. Phys. Plasmas 2012, 19, 092707. [Google Scholar] [CrossRef]
- Ecker, G.; Kröll, W. Lowering of the ionization energy for a plasma in thermodynamic equilibrium. Phys. Fluids 1963, 6, 62–69. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D., Jr. Lowering of ionization potentials in plasmas. Astrophys. J. 1966, 144, 1203–1211. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; Team, N.A. NIST Atomic Spectra Database. 2024. Available online: https://physics.nist.gov/asd (accessed on 10 April 2025).
- Trayner, C.; Glowacki, M.H. A new technique for the solution of the Saha equation. J. Sci. Comput. 1995, 10, 139–149. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, I. Calculation of ionization balance and electrical conductivity in nonideal aluminum plasma. Phys. Rev. E 2003, 68, 056410. [Google Scholar] [CrossRef]
- Fu, Z.; Jia, L.; Sun, X.; Chen, Q. Electrical conductivity of warm dense tungsten. High Eenergy Density Phys. 2013, 9, 781–786. [Google Scholar] [CrossRef]
- Desjarlais, M.P. Practical improvements to the Lee-More conductivity near the metal-insulator transition. Contrib. Plasma Phys. 2001, 41, 267–270. [Google Scholar] [CrossRef]
- Spitzer, L., Jr.; Härm, R. Transport phenomena in a completely ionized gas. Phys. Rev. 1953, 89, 977–981. [Google Scholar] [CrossRef]
- Zollweg, R.J.; Liebermann, R.W. Electrical conductivity of nonideal plasmas. J. Appl. Phys. 1987, 62, 3621–3627. [Google Scholar] [CrossRef]
- Zaghloul, M.R. On the calculation of the electrical conductivity of hot dense nonideal plasmas. Plasma Phys. Rep. 2020, 46, 574–586. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, I. Electrical conductivities of nonideal iron and nickel plasmas. Contrib. Plasma Phys. 2007, 47, 173–176. [Google Scholar] [CrossRef]
- DeSilva, A.W.; Katsourous, J.D. Electrical conductivity of dense copper and aluminum plasmas. Phys. Rev. E 1998, 57, 5945–5951. [Google Scholar] [CrossRef]
- Kim, K.; Jang, S. System modeling and simulation of flyer acceleration and explosive detonation in exploding foil initiator. AIP Adv. 2023, 13, 065329. [Google Scholar] [CrossRef]
- Limpouch, J.; Tikhonchuk, V.; Renner, O.; Agarwal, S.; Burian, T.; Cervenka, J.; Dostal, J.; Dudzak, R.; Ettel, D.; Gintrand, A.; et al. Laser interaction with undercritical foams of different spatial structures. Matter Radiat. Extrem. 2025, 10, 017402. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y.C. Absorption coefficient of aluminum near the critical point and the consequences on high-power nanosecond laser ablation. Appl. Phys. Lett. 2006, 89, 111902. [Google Scholar] [CrossRef]
- Lee, Y.T.; More, R.M. An electron conductivity model for dense plasmas. Phys. Fluids 1984, 27, 1273–1286. [Google Scholar] [CrossRef]
- Spaeth, M.L.; Manes, K.R.; Kalantar, D.H.; Miller, P.E.; Heebner, J.E.; Bliss, E.S.; Spec, D.R.; Parham, T.G.; Whitman, P.K.; Wegner, P.J.; et al. Description of the NIF laser. Fusion Sci. Technol. 2016, 69, 25–145. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhang, Q.; Feng, Q.; Yu, Z.; Mai, J.; Zhang, H.; Huang, L.; Huang, C.; Li, M. A Theoretical Study of the Ionization States and Electrical Conductivity of Tantalum Plasma. Plasma 2025, 8, 16. https://doi.org/10.3390/plasma8020016
Chen S, Zhang Q, Feng Q, Yu Z, Mai J, Zhang H, Huang L, Huang C, Li M. A Theoretical Study of the Ionization States and Electrical Conductivity of Tantalum Plasma. Plasma. 2025; 8(2):16. https://doi.org/10.3390/plasma8020016
Chicago/Turabian StyleChen, Shi, Qishuo Zhang, Qianyi Feng, Ziyue Yu, Jingyi Mai, Hongping Zhang, Lili Huang, Chengjin Huang, and Mu Li. 2025. "A Theoretical Study of the Ionization States and Electrical Conductivity of Tantalum Plasma" Plasma 8, no. 2: 16. https://doi.org/10.3390/plasma8020016
APA StyleChen, S., Zhang, Q., Feng, Q., Yu, Z., Mai, J., Zhang, H., Huang, L., Huang, C., & Li, M. (2025). A Theoretical Study of the Ionization States and Electrical Conductivity of Tantalum Plasma. Plasma, 8(2), 16. https://doi.org/10.3390/plasma8020016






