Strong, Weak and Merging Lines in Atomic Spectra
Abstract
1. Introduction
2. Estimation of the Maximal Line Strength
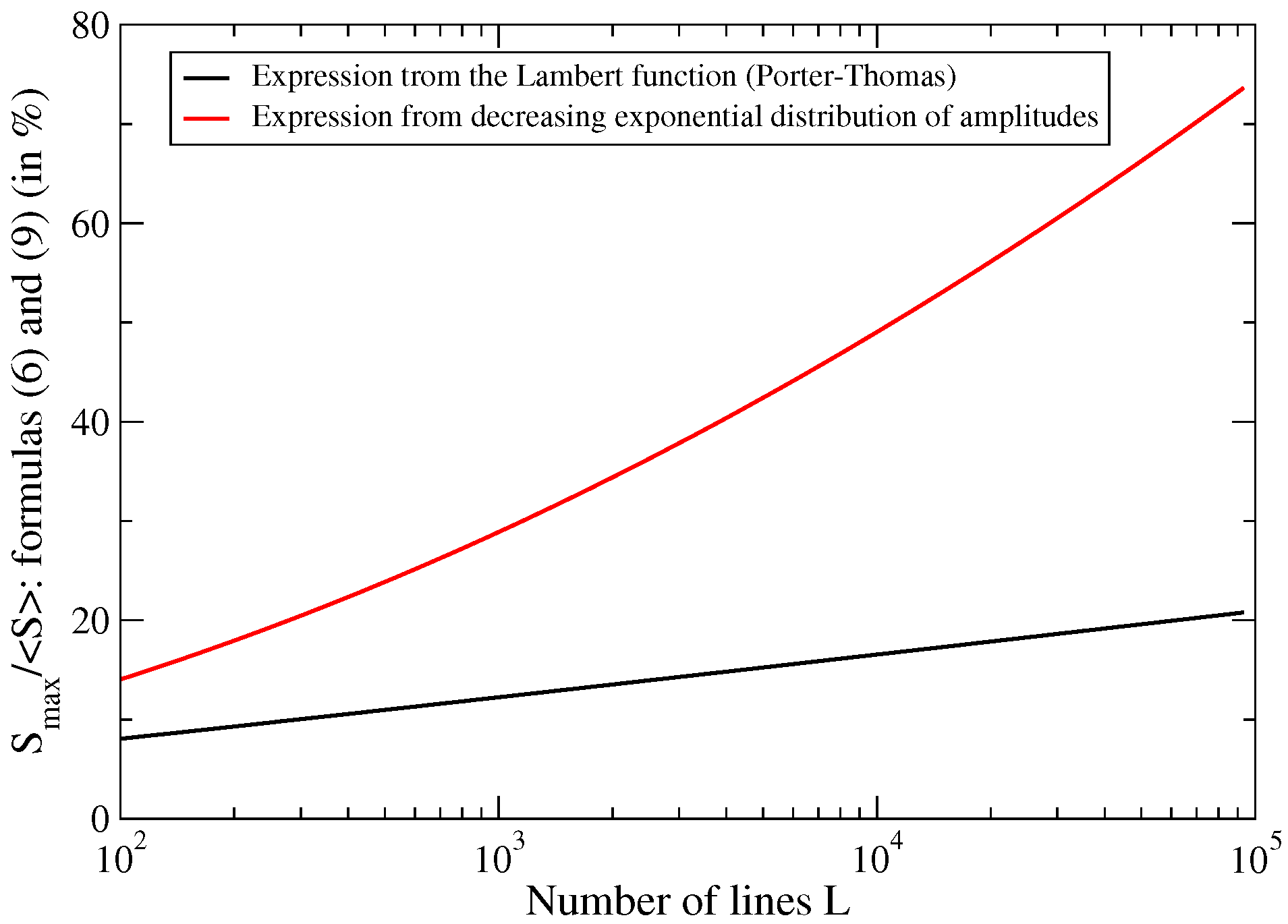
2.1. Porter–Thomas Distribution
2.2. Decreasing Exponential Distribution for the Line Amplitudes
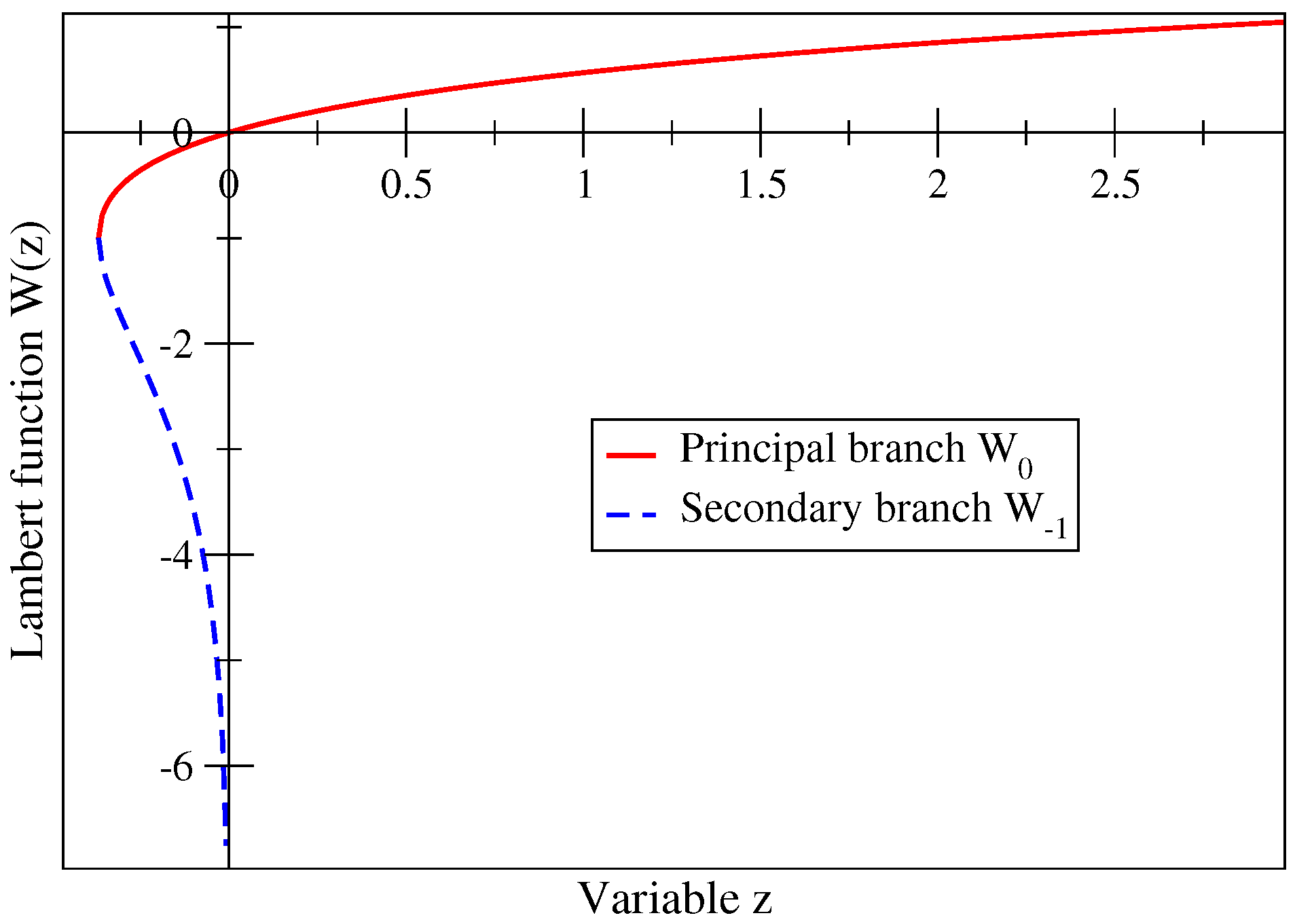
2.3. Maximal Strength Associated with Learner’s Rule
3. On the Number of Strong and Weak Lines
3.1. Porter–Thomas Law
3.2. Decreasing Exponential Distribution of the Amplitudes
3.3. Imposing a Number of Lines and Searching for the Threshold
4. Merging Lines Together: Band Models
4.1. Non-Overlapping Model
4.1.1. Lorentzian Shape
4.1.2. Gaussian (Doppler) Shape
4.2. Overlapping Models
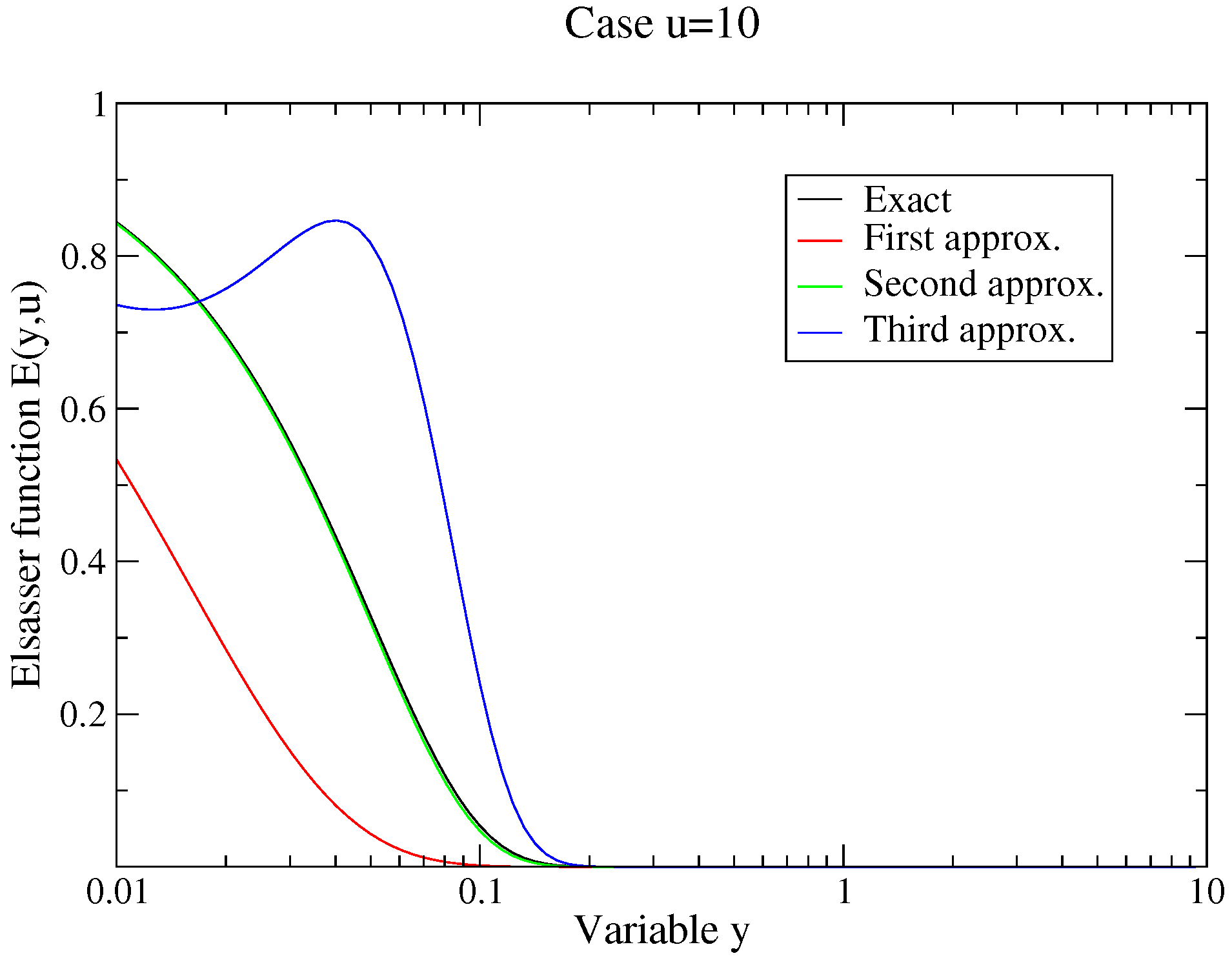
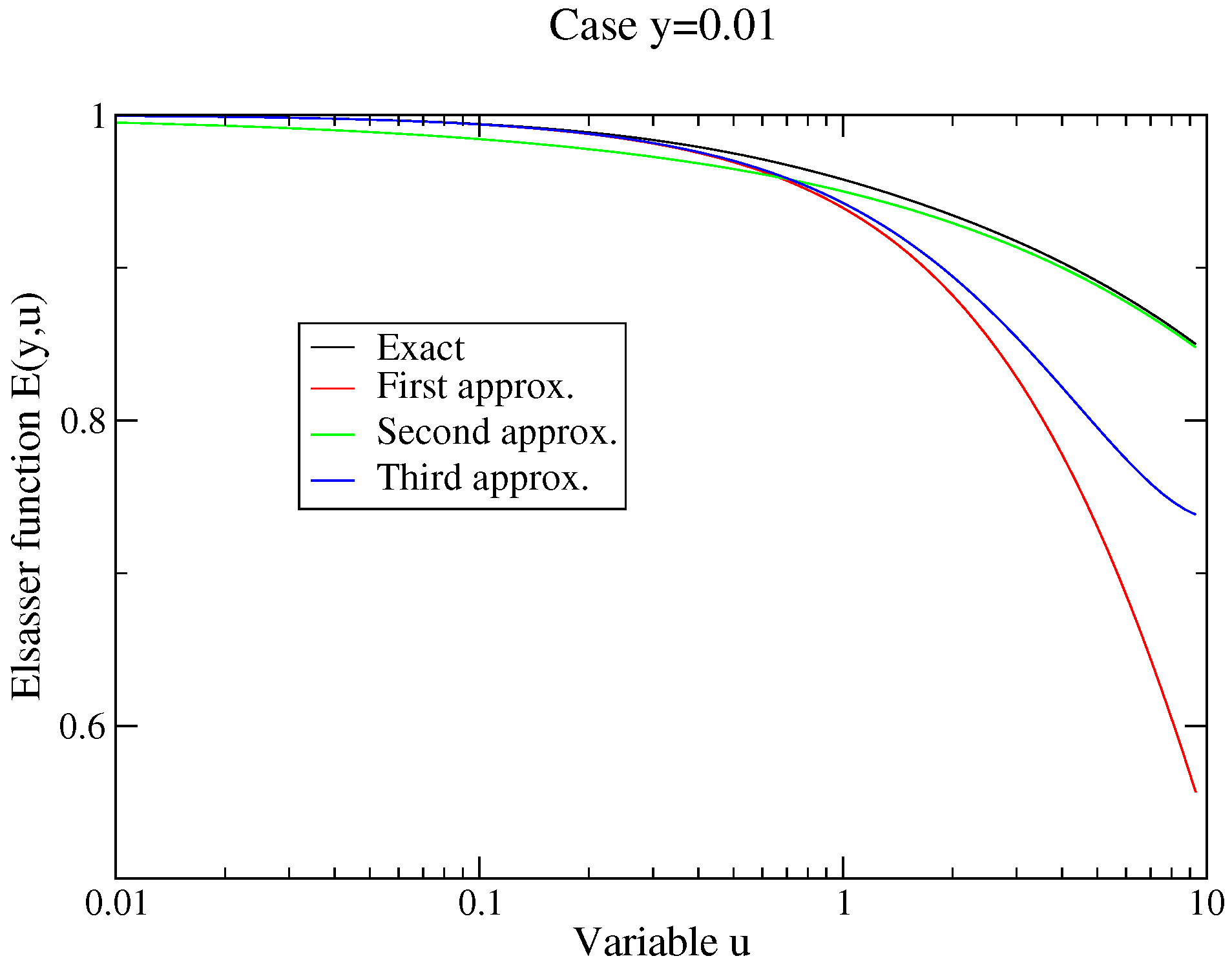
4.2.1. The Elsasser Model
4.2.2. The Mayer–Goody Model
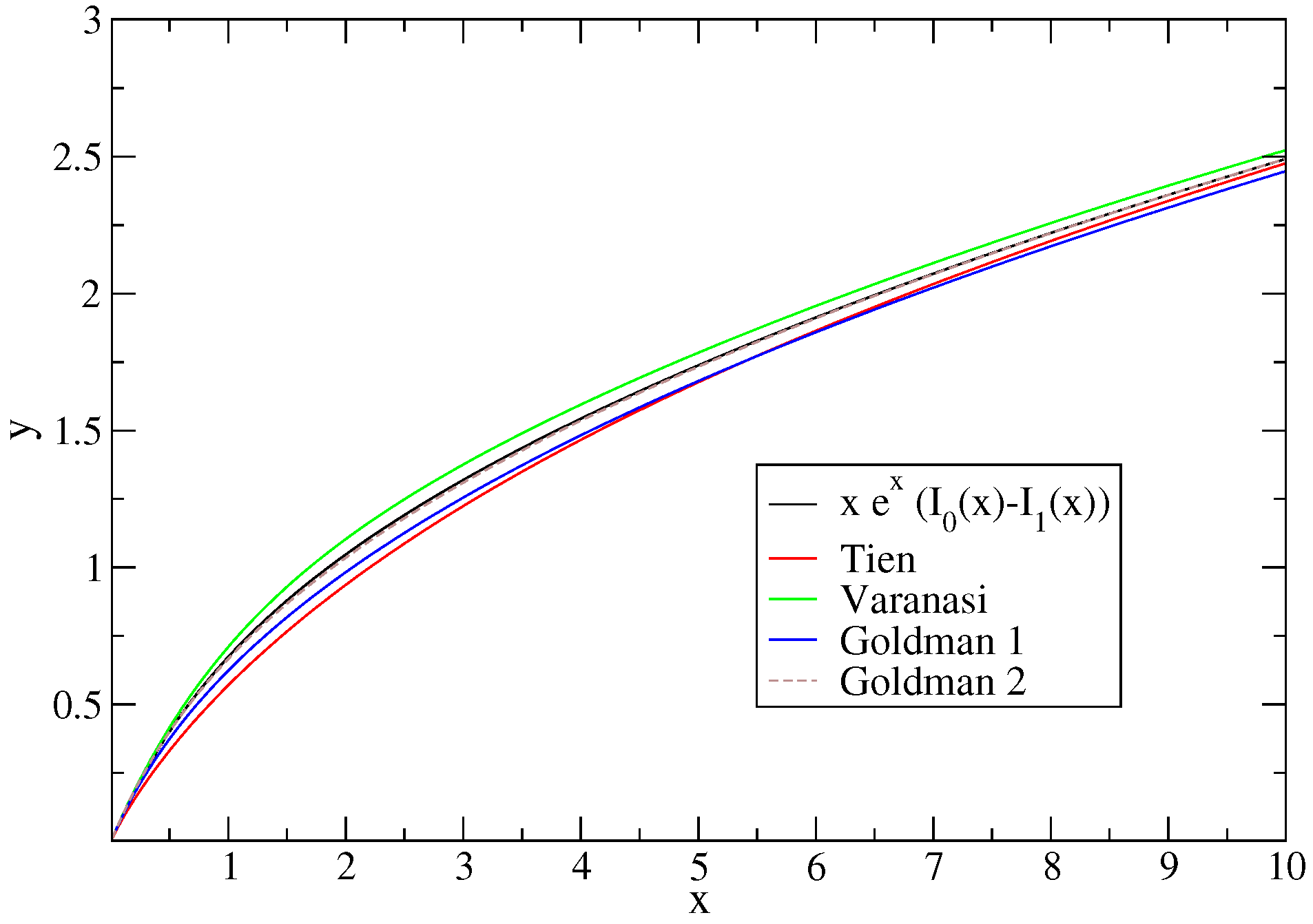
4.3. Equivalent Width of a Lorentz Line
4.4. General Considerations About the Merging of Lines (Blanketing)
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GOE | Gaussian Orthogonal Ensemble |
| LTE | Local Thermodynamic Equilibrium |
| MUTA | Mixed Unresolved Transition Arrays |
| RTA | Resolved Transition Arrays |
| UTA | Unresolved Transition Arrays |
| SOSA | Spin–Orbit–Split Arrays |
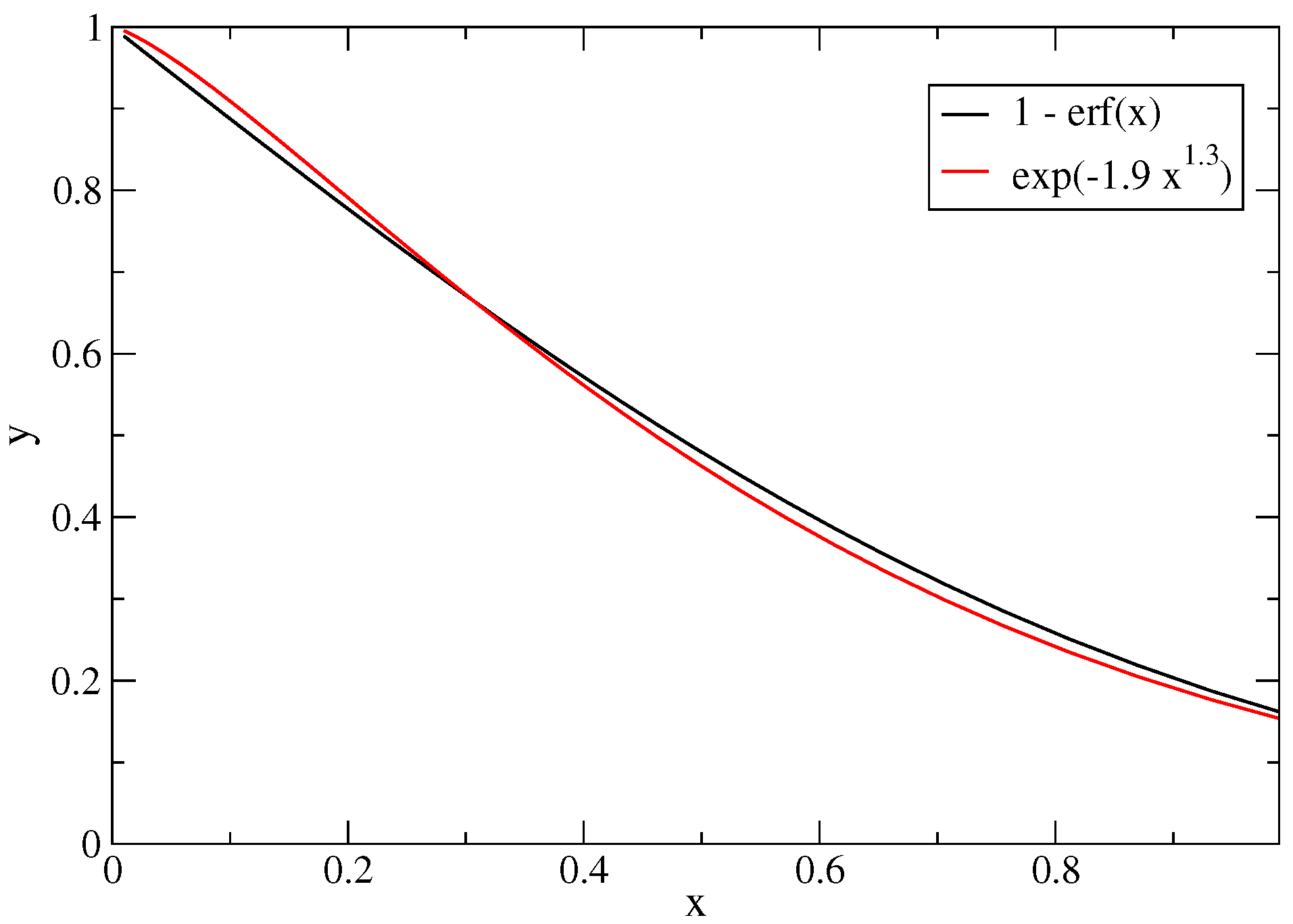
Appendix A. On the Computation of the Error Function
Appendix B. The Chernhoff Bound
Appendix C. The Gini Coefficient: Applicable to Atomic Spectra?
References
- Moszkowski, S.A. Some Statistical Properties of Level and Line Distributions in Atomic Spectra; Rand Corporation Research Memorandum RM-2610-AEC; RAND: Santa Monica, CA, USA, 1960. [Google Scholar]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distributions of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C. Level and line statistics in atomic spectra. J. Phys. B At. Mol. Phys. 1987, 20, 1659–1677. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Klapisch, M. Transition arrays in the spectra of ionized atoms. Adv. At. Mol. Phys. 1988, 23, 131–195. [Google Scholar]
- Rose, S.J. Calculations of the radiative opacity of laser-produced plasmas. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 1667–1681. [Google Scholar] [CrossRef]
- Gaffney, J.A.; Rose, S.J. The effect of unresolved transition arrays on plasma opacity calculations. High Energy Density Phys. 2011, 7, 240–246. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Bauche, J.; Bauche-Arnoult, C. Effect of third-and fourth-order moments on the modeling of unresolved transition arrays. High Energy Density Phys. 2009, 5, 294–301. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST ASD Team. NIST Atomic Spectra Database, Version 5.10; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2024. [Google Scholar] [CrossRef]
- Kato, D.; Murakami, I.; Tanaka, M.; Banerjee, S.; Gaigalas, G.; Radžiūtė, L.; Rynkun, P. Japan-Lithuania Opacity Database for Kilonova. 2021. Available online: http://dpc.nifs.ac.jp/DB/Opacity-Database/ (accessed on 27 April 2025).
- Ryabchikova, T.; Piskunov, N.; Kurucz, R.L.; Stempels, H.C.; Heiter, U.; Pakhomov, Y.; Barklem, P.S. A major upgrade of the VALD database. Phys. Scr. 2015, 90, 054005. [Google Scholar]
- Pain, J.-C.; Ralchenko, Y. Benford’s law in atomic spectra and opacity databases. J. Quant. Spectrosc. Radiat. Transf. 2024, 322, 109010. [Google Scholar] [CrossRef]
- Fontes, C.J.; Fryer, C.L.; Wollaeger, R.T.; Mumpower, M.R.; Sprouse, T.M. Actinide opacities for modelling the spectra and light curves of kilonovae Get access Arrow. Mon. Not. Roy. Astron. Soc. 2023, 519, 2862–2878. [Google Scholar] [CrossRef]
- Pain, J.-C.; Croset, P. Ideas and tools for error detection in opacity databases. Atoms 2023, 11, 27. [Google Scholar] [CrossRef]
- Elsasser, W.M. Mean absorption and equivalent absorption coefficient of a band spectrum. Phys. Rev. 1938, 54, 126–129. [Google Scholar] [CrossRef]
- Benedict, W.S.; Herman, R.; Moore, G.E.; Silverman, S. The strengths, widths, and shapes of infrared lines: I. General considerations. Can. J. Phys. 1956, 34, 830–849. [Google Scholar] [CrossRef]
- Bykov, G.A.; Hien, P.Z. Calculation of parameters of experimental spectra of resonance absorption of gamma quanta in crystals. Soviet Phys. JETP 1963, 16, 646. [Google Scholar]
- Porter, C.E.; Thomas, R.G. Fluctuations of nuclear reaction widths. Phys. Rev. 1956, 104, 483–491. [Google Scholar] [CrossRef]
- Porter, C.E. Statistical Theories of Spectra: Fluctuations; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Bauche, J.; Bauche-Arnoult, C. Statistical properties of atomic spectra. Comp. Phys. Rep. 1990, 12, 3–28. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Wyart, J.-F.; Fournier, K.B. Effects of the exchange Slater integrals on the shapes of transition arrays. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 57–70. [Google Scholar] [CrossRef]
- Rosenzweig, N.; Porter, C.E. “Repulsion of energy levels” in complex atomic spectra. Phys. Rev. 1960, 120, 1698–1714. [Google Scholar] [CrossRef]
- Camarda, H.S.; Georgopulos, P.D. Statistical behavior of atomic energy levels: Agreement with Random-Matrix Theory. Phys. Rev. Lett. 1983, 50, 492–495. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Gribakina, A.A.; Gribakin, G.F. Statistics of electromagnetic transitions as a signature of chaos in many-electron atoms. Phys. Rev. A 1998, 58, 230–237. [Google Scholar] [CrossRef]
- Bogomolny, E.; Sieber, M. Eigenfunction distribution for the Rosenzweig-Porter model. Phys. Rev. E 2018, 98, 032139. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Wyart, J.-F. Intensity distribution in atomic transition arrays. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 41–47. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Peyrusse, O. Atomic Properties in Hot Plasmas: From Levels to Superconfigurations; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Wilson, B.G.; Rogers, F.; Iglesias, C. Random-matrix method for the simulation of large atomic E1 transition arrays. Phys. Rev. A 1998, 37, 2695–2697. [Google Scholar] [CrossRef] [PubMed]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Kendall, M.G.; Stuart, A. Advanced Theory of Statistics; Hafner: New York, NY, USA, 1969; Volume 1. [Google Scholar]
- Corless, R.M.; Gonnand, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Caillol, J.M. Some applications of the Lambert W function to classical statistical mechanics. J. Phys. A Math. Gen. 2003, 36, 10431. [Google Scholar] [CrossRef]
- Veberič, D. Lambert W function for applications in physics. Comput. Phys. Commun. 2012, 183, 2622–2628. [Google Scholar] [CrossRef]
- Comtet, L. Inversion de yα ey et y logα y au moyen des nombres de Stirling. C. R. Acad. Sci. Paris (In French). 1970, 270, 1085–1088. [Google Scholar]
- Jeffrey, D.J.; Corless, R.M.; Hare, D.E.G.; Knuth, D.E. On the inversion of yα ey in terms of associated Stirling numbers. C. R. Acad. Sci. Paris 1995, 320, 1449–1452. [Google Scholar]
- Hassani, M. Approximation of the Lambert W function. Rgmia Res. Rep. Collect. 2005, 8, 12. [Google Scholar]
- Comtet, L. Advanced Combinatorics; D. Reidel Publishing Company: Berlin/Heidelberg, Germany, 1974. [Google Scholar]
- Mitrinović, D.S.; Mitrinović, R.S. Tableaux qui fournissent des polynômes de Stirling. Publ. Fac. Electrotech. Univ. Belgrade Ser. Math. Phys. 1960, 34, 1–23. [Google Scholar]
- Karanicoloff, C. Sur une représentation des nombres de Stirling dans une forme explicite. Publ. Fac. Electrotech. Univ. Belgrade Ser. Math. Phys. 1961, 67, 9–10. (In French) [Google Scholar]
- Fritsch, F.N.; Shafer, R.E.; Crowley, W.P. Solution of the transcendental equation wew = x. Commun. ACM 1973, 16, 123–124. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C. Scars of symmetries in complex atomic spectra. Phys. Rev. Lett. 1992, 69, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Bauche, J.; Bauche-Arnoult, C.; Wyart, J.-F.; Duffy, P.; Klapisch, M. Simulation of atomic transition arrays for opacity calculations. Phys. Rev. A 1991, 44, 5707–5714. [Google Scholar] [CrossRef] [PubMed]
- Dufty, P.; Klapisch, M.; Bauche, J.; Bauche-Arnoult, C. Monte Carlo simulation of complex spectra for opacity calculations. Phys. Rev. A 1991, 44, 5715–5724. [Google Scholar]
- Bauche, J.; Bauche-Arnoult, C. Recent progress in the global description of atomic transitions. Phys. Scr. T 1996, 65, 99–103. [Google Scholar] [CrossRef]
- Gilleron, F.; Bauche, J.; Bauche-Arnoult, C. A Statistical approach for simulating detailed-line spectra. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 3057–3074. [Google Scholar] [CrossRef]
- Gumbel, E.J. Les valeurs extrêmes des distributions statistiques. Ann. L’Institut Henri Poincaré 1935, 5, 115–158. (In French) [Google Scholar]
- Gumbel, E.J.; Lieblein, J. Statistical Theory of Extreme Values and Some Practical Applications: A Series of Lectures; US Government Printing Office: Washington, DC, USA, 1954; Volume 33. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; New York Chichester; Columbia University Press: West Sussex, UK, 1958. [Google Scholar]
- Learner, R.C.M. A simple (and unexpected) experimental law relating to the number of weak line in a complex spectrum. J. Phys. B Atom. Mol. Phys. 1982, 15, L891–L895. [Google Scholar] [CrossRef]
- Pain, J.-C. Regularities and symmetries in atomic structure and spectra. High Energy Density Phys. 2013, 9, 392–401. [Google Scholar] [CrossRef][Green Version]
- Pain, J.-C.; Croset, P. Checking the reliability of opacity databases. Eur. Phys. J. D 2023, 77, 60. [Google Scholar] [CrossRef]
- Porcherot, Q.; Pain, J.-C.; Gilleron, F.; Blenski, T. A consistent approach for mixed detailed and statistical calculation of opacities in hot plasmas. High Energy Density Phys. 2011, 7, 234–239. [Google Scholar] [CrossRef]
- Mazevet, S.; Abdallah, J. Mixed UTA and detailed line treatment for mid-Z opacity and spectral calculations. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3419–3429. [Google Scholar] [CrossRef]
- Robert, E. (Unpublished). Available online: https://fr.wikipedia.org/wiki/Fonction_d%27erreur (accessed on 27 April 2025).
- Carlitz, L. The inverse of the error function. Pacific J. Math. 1963, 13, 459–470. [Google Scholar] [CrossRef][Green Version]
- Blair, J.M.; Edwards, C.A.; Johnson, J.H. Rational Chebyshev approximations for the inverse of the error function. Math. Comp. 1976, 30, 827–830. [Google Scholar] [CrossRef]
- Poppe, G.P.M.; Wijers, C.M.J. More efficient computation of the complex error function. Assoc. Comput. Mach. 1990, 16, 38–46. [Google Scholar] [CrossRef]
- Whitman, R.I. Effects of Three Transmission Models in the Rotational Water-Vapor Band on Radiance Calculations and Constituent Inferences; National Aeronautics and Space Administration Report 6112; NASA: Washington, DC, USA, 1971. [Google Scholar]
- Burn, J.W.; Uplinger, W.G. The Determination of Atmospheric Temperature Profiles from Planetary Limb Radiance Profiles; National Aeronautics and Space Administration Report 71606130; NASA: Washington, DC, USA, 1970. [Google Scholar]
- Ladenburg, R.; Fritz, R. Über selektive Absorption. Ann. Phys. 1923, 347, 181–209. [Google Scholar] [CrossRef]
- Reiche, F. Total absorption and overlapping effect due to two spectral lines of equal width and strength. J. Opt. Soc. Am. 1956, 46, 590–597. [Google Scholar] [CrossRef]
- Nossal, R.; Weiss, G.H. Analysis of a generalized Ladenburg-Reiche integral. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 763–770. [Google Scholar] [CrossRef]
- Maass, F.; Martin, P.; Olivares, J. Analytic approximation to Bessel function J0(x). Comput. Appl. Math. 2020, 39, 222. [Google Scholar] [CrossRef]
- Mayer, H. Methods of Opacity Calculations; Los Alamos Report LA 647; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1947. [Google Scholar]
- Poirier, M. Analytical description of absorption profiles in warm dense plasmas: Discussion of the non-overlapping-line limit. High Energy Density Phys. 2013, 9, 618–625. [Google Scholar] [CrossRef]
- Kaplan, L.D.; Eggers, D.F. Intensity and line-width of the 15-micron CO2 band, determined by a curve-of-growth method. J. Chem. Phys. 1956, 25, 876–883. [Google Scholar] [CrossRef]
- Seitz, W.S.; Lundholm, D.V. Elsasser model for band absorption; series representation of a useful integral. J. Opt. Soc. Am. 1964, 54, 315–318. [Google Scholar] [CrossRef]
- Kiselev, K.A. Analytical calculation of the Elsasser integral. J. Appl. Spectrosc. 1973, 19, 1488–1491. [Google Scholar] [CrossRef]
- Arfken, G. Modified Bessel functions, Iν(x) and Kν(x). In Mathematical Methods for Physicists, 3rd ed.; Academic Press: Orlando, FL, USA, 1985; pp. 610–616. [Google Scholar]
- Goody, R.M.; Yung, Y.L. The Elsasser Function. In Atmospheric Radiation: Theoretical Basis, 2nd ed.; Oxford Academic: New York, NY, USA, 1989. [Google Scholar]
- Kaplan, L.D. Regions of validity of various absorption-coefficient approximations. J. Meteorol. 1953, 10, 100–104. [Google Scholar] [CrossRef]
- Plass, G.N. Regions of validity of various absorption-coefficient approximations. J. Atmos. Sci. 1954, 11, 163–164. [Google Scholar] [CrossRef]
- Wark, D.Q.; Wolk, M. An extension of a table of absorption for Elsasser bands. Mon. Weather Rev. 1960, 88, 249–250. [Google Scholar] [CrossRef]
- Zachor, A.S. Absorptance and radiative transfer by a regular band. J. Quant. Spectrosc. Radial. Transf. 1967, 7, 857–870. [Google Scholar] [CrossRef]
- Goody, R.M. A statistical model for water-vapor absorption. Quart. J. Roy. Meteorol. Soc. 1952, 78, 165–169. [Google Scholar] [CrossRef]
- Plass, G.N. Useful representations for measurements of spectral band absorption. J. Opt. Soc. Am. 1960, 50, 868–875. [Google Scholar] [CrossRef]
- Vardya, M.S. Simplified description of the line absorption coefficient in blanketing effect computation. J. Quant. Spectrosc. Radiat. Transf. 1966, 6, 539–548. [Google Scholar] [CrossRef]
- Sakai, H.; Stauffer, F.R. Equivalent width due to two overlapping lines. J. Opt. Soc. Am. 1964, 54, 759–762. [Google Scholar] [CrossRef]
- Hirono, M.; Suda, T. Band absorption by the spectral lines with a super-Lorentz line shape. J. Phys. Soc. Jpn. 1983, 52, 1157–1163. [Google Scholar] [CrossRef]
- Berk, A. Voigt equivalent widths and spectral-bin single-line transmittances: Exact expansions and the MODTRAN 5 implementation. J. Quant. Spectrosc. Radiat. Transf. 2013, 118, 102–120. [Google Scholar] [CrossRef]
- Tien, C.L. A simple approximate formula for radiation from a line with resonance contours. J. Quant. Spectrosc. Radiat. Transf. 1966, 6, 893–894. [Google Scholar] [CrossRef]
- Goldman, A. On simple approximations to the equivalent width of a Lorentz line. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 829–831. [Google Scholar] [CrossRef]
- Martin, P.; Olivares, J.; Sotomayor, A. Precise analytic approximation for the modified Bessel function I1(x). Rev. Mex. Fis. 2017, 63, 130–133. [Google Scholar]
- Olivares, J.; Martin, P.; Valero, E. A simple approximation for the modified Bessel function of zero order I0(x). J. Phys. Conf. Ser. 2018, 1043, 012003. [Google Scholar] [CrossRef]
- Abdallah, J., Jr.; Kilcrease, D.P.; Magee, N.H.; Mazevet, S.; Hakel, P.; Sherrill, M.E. Spectral line strength binning method for opacity calculations. High Energy Density Phys. 2007, 3, 309–313. [Google Scholar] [CrossRef]
- Colgan, J.; Abdallah, J.; Faenov, A.; Pikuz, T.A.; Skobelev, I.Y. MUTA calculations of a laser-produced Mg hollow atom spectrum. Phys. Scr. 2008, 78, 015302. [Google Scholar] [CrossRef]
- Deprince, J.; Carvajal Gallego, H.; Ben Nasr, S.; Maison, L.; Pain, J.-C.; Palmeri, P.; Quinet, P. Radiative and opacity data obtained from large-scale atomic structure calculations and from statistical simulations for the spectral analysis of kilonovae in their photospheric and nebular phases: The sample case of Er III. Eur. Phys. J. D 2024, 78, 105. [Google Scholar] [CrossRef]
- Eakin, R.T. Interference in transmission spectra of overlapping Lorentzian lines. J. Quant. Spectrosc. Radiat. Transf. 1988, 39, 225–236. [Google Scholar] [CrossRef]
- Rosenkranz, W. Interference coefficients for overlapping oxygen lines in air. J. Quant. Spectrosc. Radiat. Transf. 1988, 39, 281–297. [Google Scholar] [CrossRef]
- Dickson, L.E. Divisibility and Primality. In History of the Theory of Numbers; Dover: New York, NY, USA, 2005; Volume 1, p. 13. [Google Scholar]
- Eakin, R.T. A combinatorial partition of Mersenne numbers arising from spectroscopy. J. Number Theory 2012, 132, 2166–2183. [Google Scholar] [CrossRef][Green Version]
- Irons, F.E. The escape factor in plasma spectroscopy–I. The escape factor defined and evaluated. J. Quant. Spectrosc. Radiat. Transf. 1979, 22, 1–20. [Google Scholar] [CrossRef]
- Griem, H.R. Stark broadening of higher hydrogen and hydrogen-like lines by electrons and ions. Astrophys. J. Lett. 1960, 132, 883–893. [Google Scholar] [CrossRef]
- Basor, E.L.; Tracy, C.A.; Widom, H. Asymptotics of level-spacing distributions for random matrices. Phys. Rev. Lett. 1992, 69, 5–8. [Google Scholar] [CrossRef]
- Majumdar, S.N.; Nadal, C.; Scardicchio, A.; Vivo, P. Index distribution of Gaussian random matrices. Phys. Rev. Lett. 2009, 103, 220603. [Google Scholar] [CrossRef]
- Pain, J.-C. Random-matrix theory for complex atomic spectra. Chin. J. Phys. 2012, 50, 523–532. [Google Scholar]
- Schöpf, H.M.; Supancic, P.H. On Bürmann’s theorem and its application to problems of linear and nonlinear heat transfer and diffusion. Math. J. 2014, 16, 1–44. [Google Scholar] [CrossRef][Green Version]
- Chernoff, H. A Measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Huber, M. Halving the bounds for the Markov, Chebyshev, and Chernoff inequalities using smoothing. Am. Math. Mon. 2019, 126, 915–927. [Google Scholar] [CrossRef]
- Hoeffding, W. Probability inequalities for sums of bounded random variables. J. Am. Stat. Assoc. 1963, 58, 13–30. [Google Scholar] [CrossRef]
- Bernstein, S.N. On certain modifications of Chebyshev’s inequality. Dokl. Akad. Nauk SSSR 1937, 17, 275–277. [Google Scholar]
- Gini, C. Variabilità e mutabilità (1912). In Memorie di Metodologica Statistica; Pizetti, E., Salvemini, T., Eds.; Libreria Eredi Virgilio Veschi: Rome, Italy, 1955. (In Italian) [Google Scholar]
- Gini, C. Measurement of inequality of incomes. Econ. J. 1921, 31, 124–126. [Google Scholar] [CrossRef]
- Abraham, R.G.; van den Bergh, S.; Nair, P. A new approach to galaxy morphology. I. Analysis of the Sloan Digital Sky Survey Early Data Release. Astrophys. J. Lett. 2003, 588, 218–229. [Google Scholar] [CrossRef]
- Lotz, J.M.; Madau, P.; Giavalisco, M.; Primack, J.; Ferguson, H.C. The rest-frame far-ultraviolet morphologies of star-forming galaxies at z ≈ 1.5 and 4. Astrophys. J. Lett. 2006, 636, 592–609. [Google Scholar] [CrossRef]
- Florian, M.K.; Gladders, M.D.; Li, N.; Sharo, K. The Gini Coefficient as a tool for image family identification in strong lensing systems with multiple images. Astrophys. J. Lett. 2016, 816, L23. [Google Scholar] [CrossRef]
- Sen, A. On Economic Inequality, 2nd ed.; Oxford University Press: Oxford, UK, 1977. [Google Scholar]
- Dorfman, R. A Formula for the Gini Coefficient. Rev. Econ. Stat. 1979, 61, 146–149. [Google Scholar] [CrossRef]

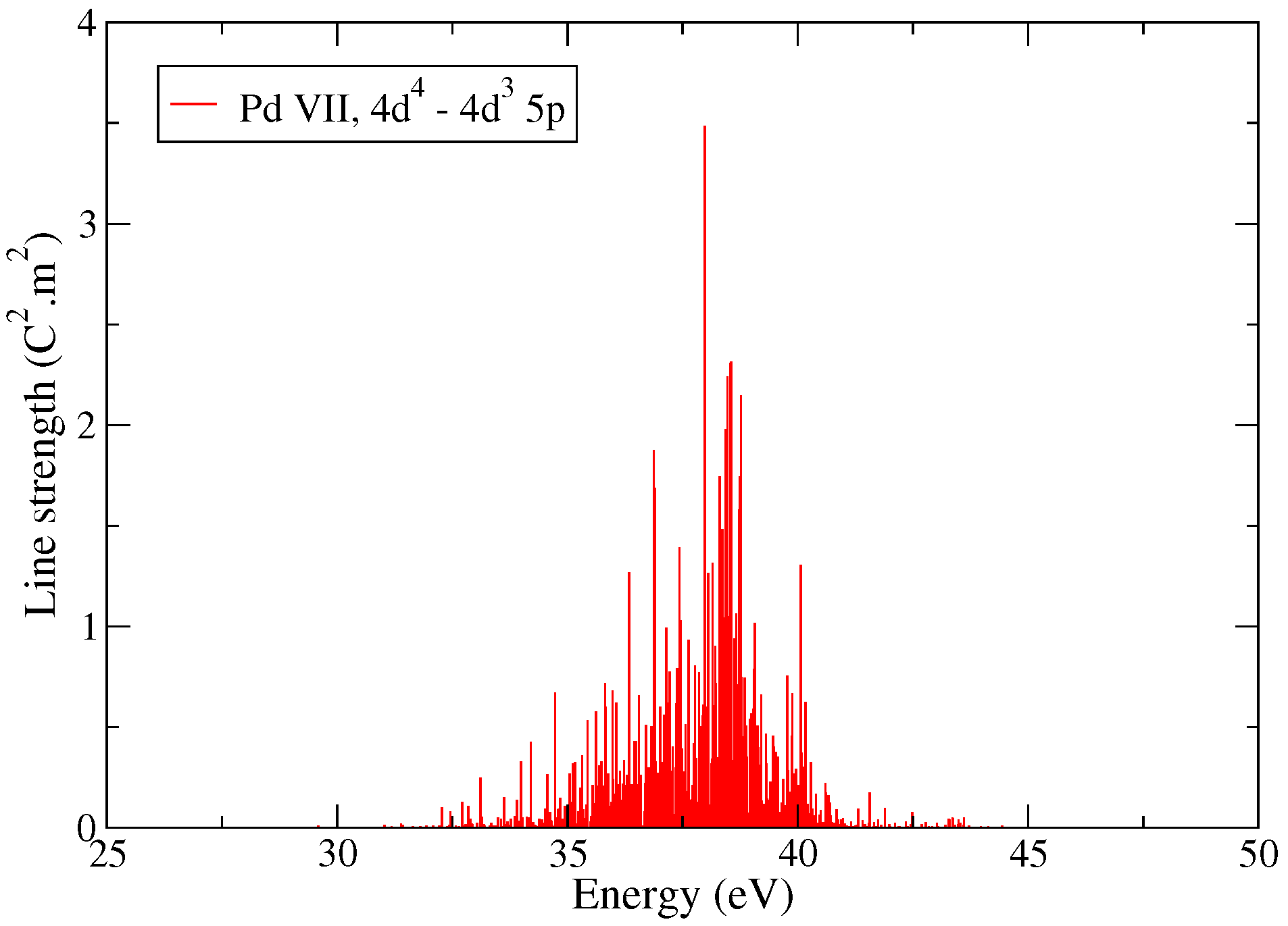
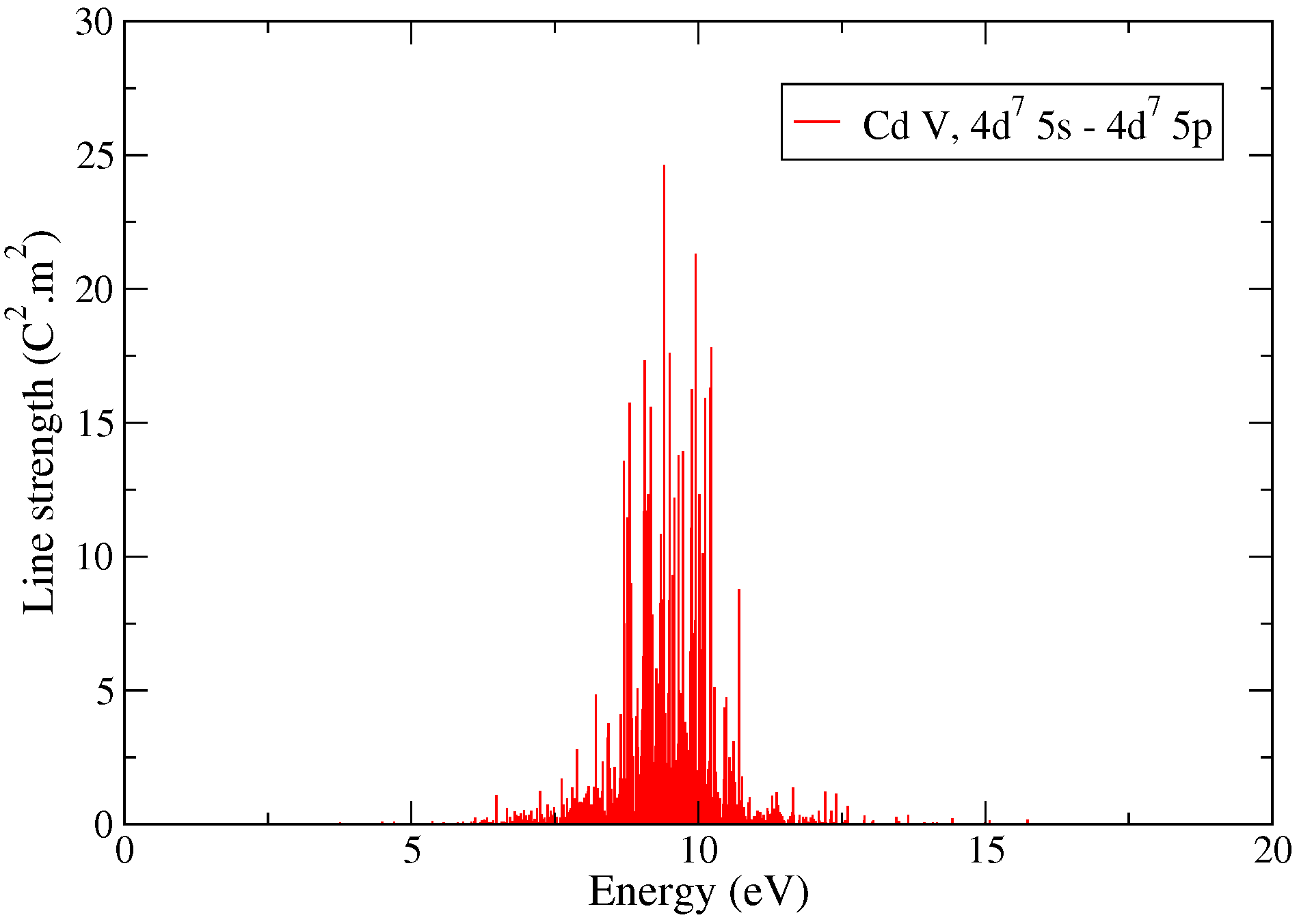





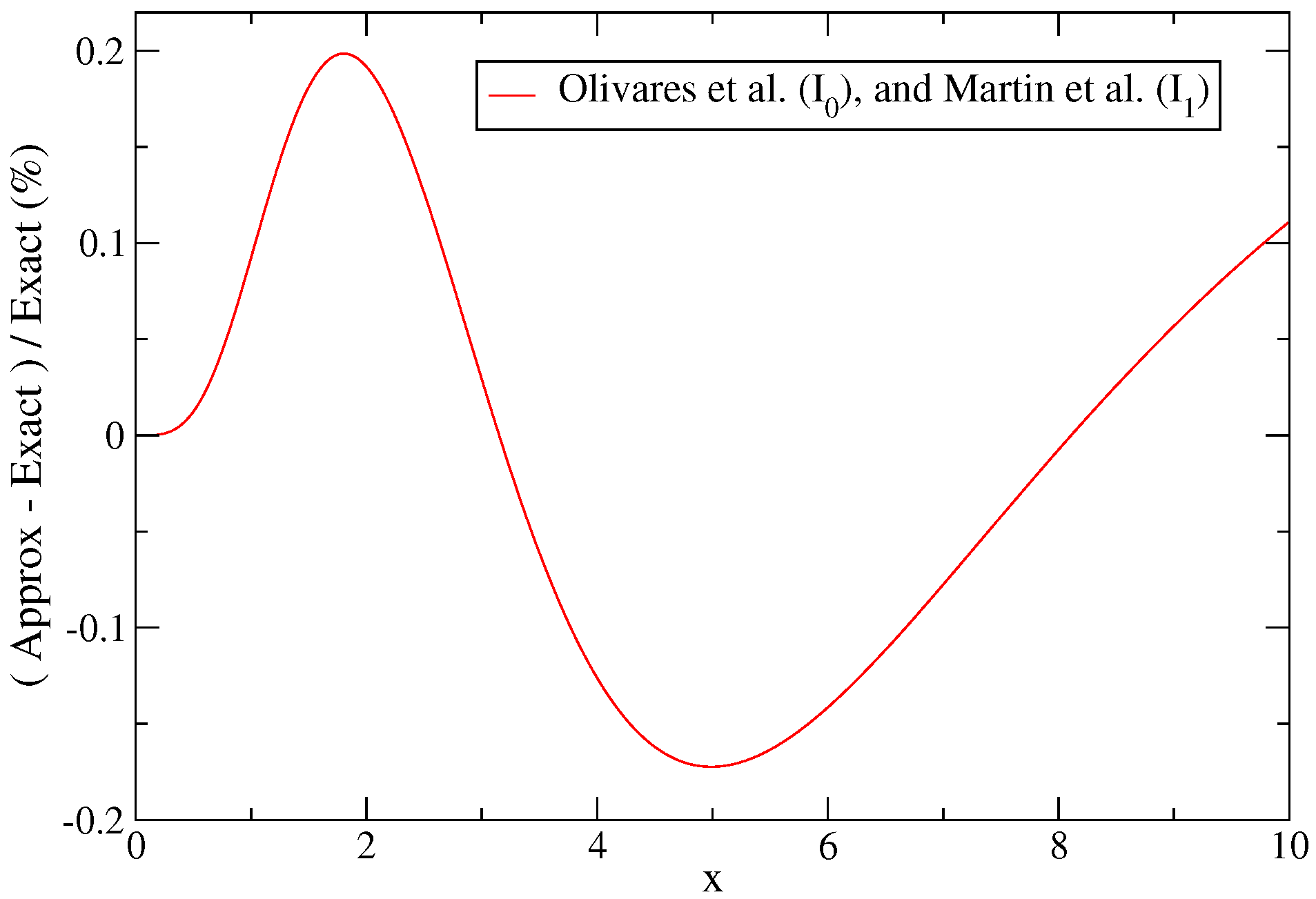
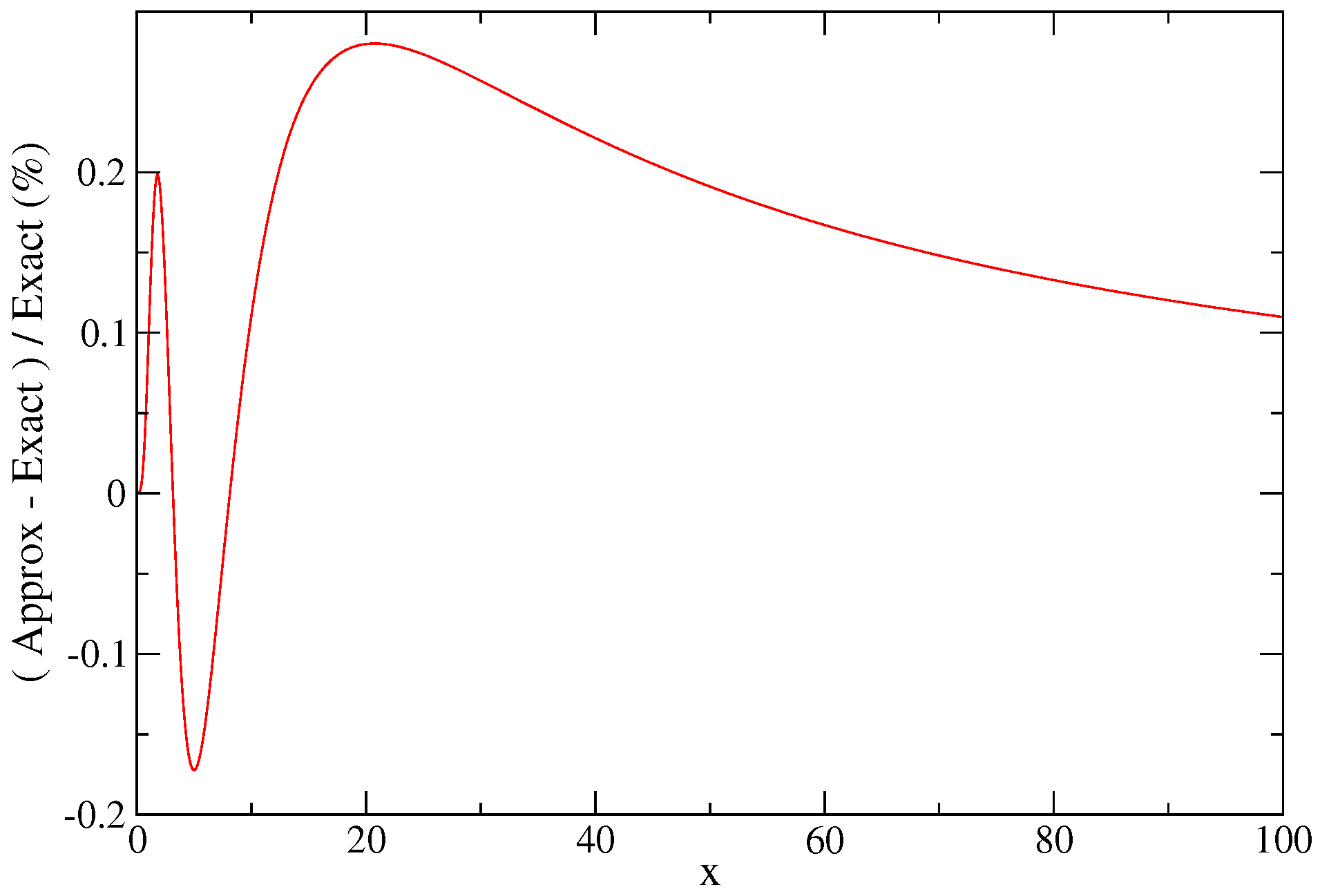
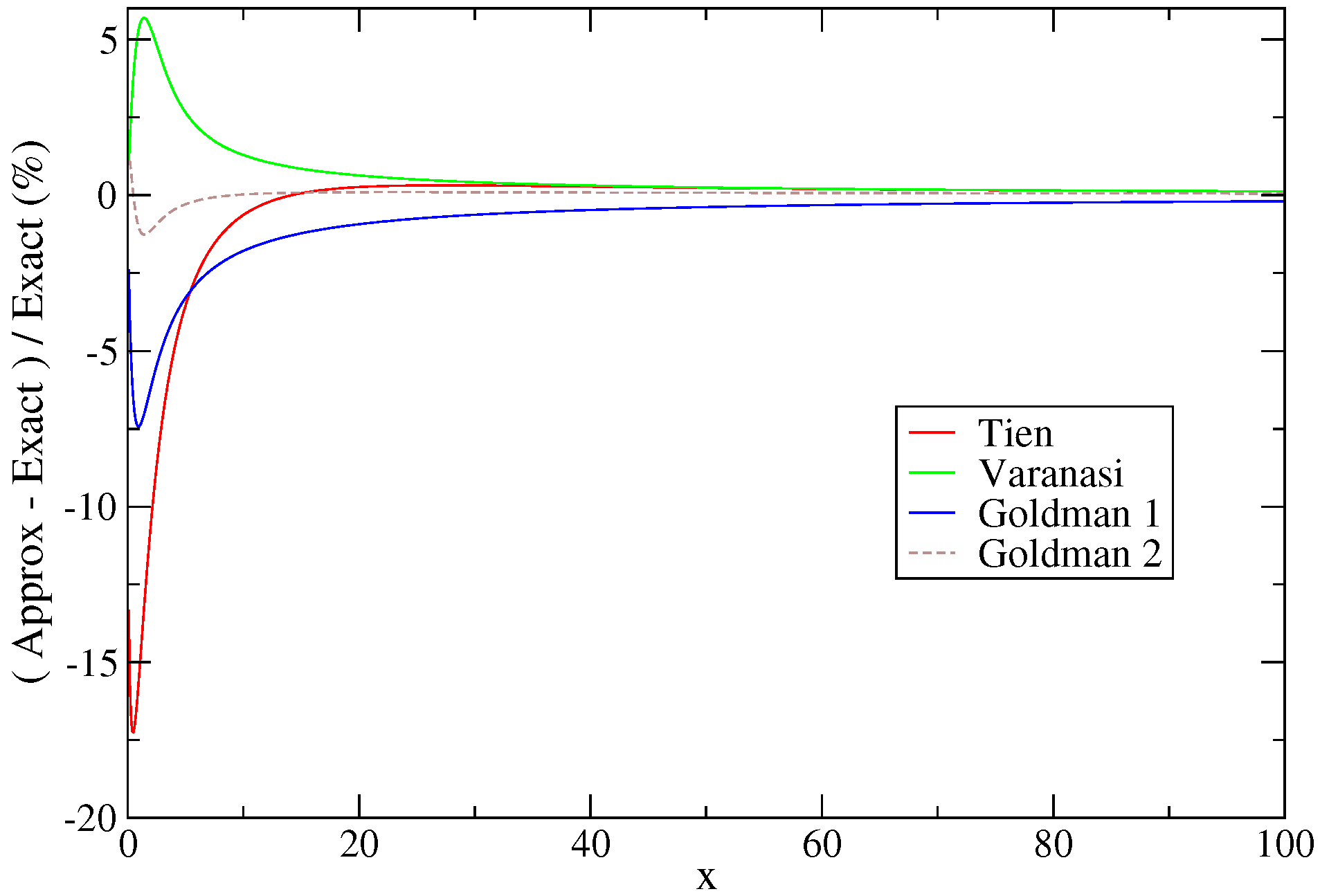
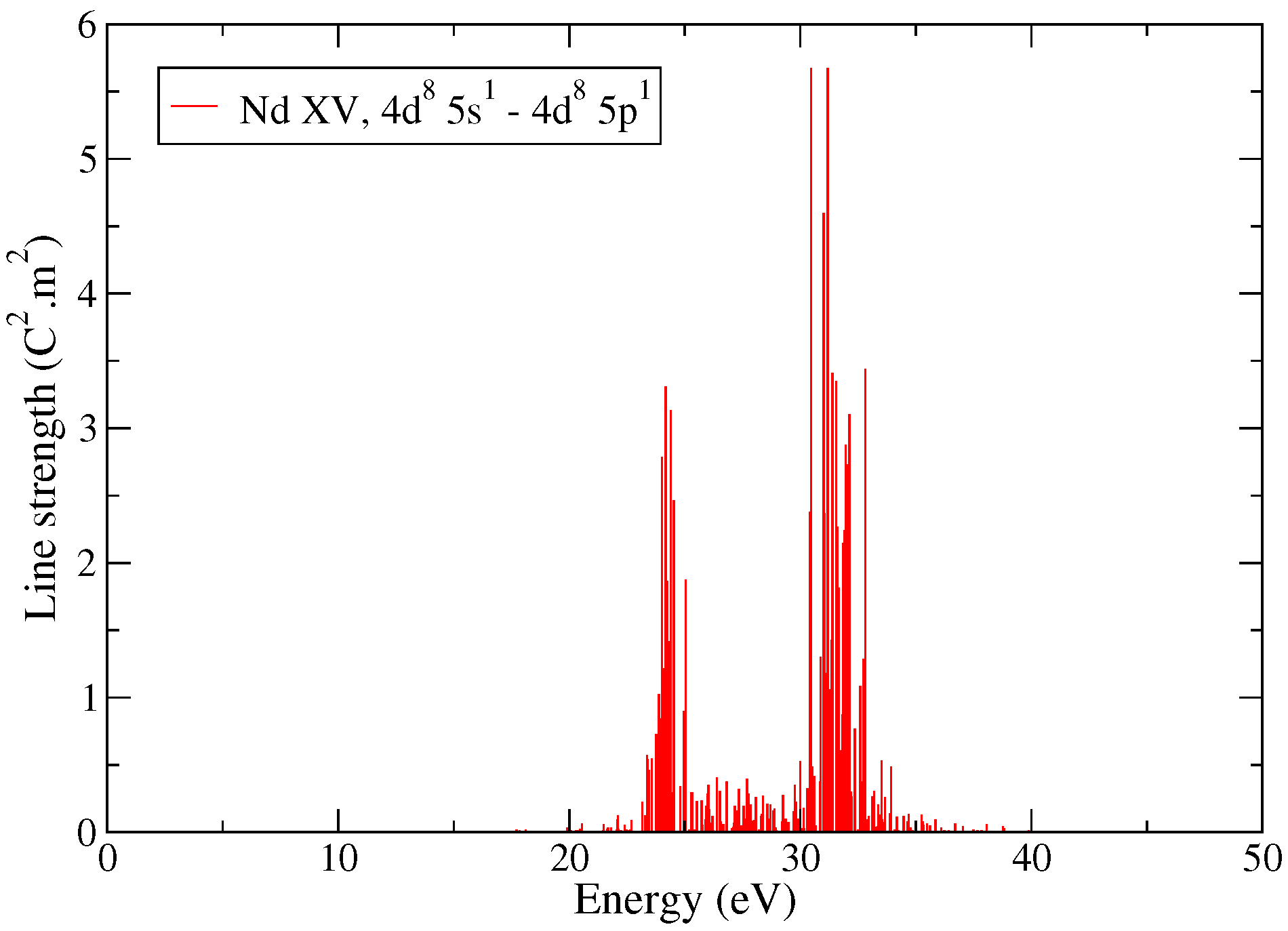
| Transition Array | LS | jj | jℓ | IC |
|---|---|---|---|---|
| d4 − d3 p | 637 | 859 | 1718 (p) − 1053 (d) | 1718 |
| d5 − d4 f | 1903 | 2471 | 3286 (d) − 5470 (f) | 5470 |
| d5 − d4 p | 1150 | 1572 | 3245 (p) − 1925 (d) | 3245 |
| d9 f − d8 f2 | 1331 | 1602 | 2780 (d) − 2727 (f) | 3590 |
| p3 d2 − p2 d3 | 6129 | 6915 | 13,611 (p) − 12,128 (d) | 18,237 |
| p3 − p2 d | 46 | 56 | 71 (p) − 97 (d) | 97 |
| Pd VII | Cd V | |
|---|---|---|
| 4d4 − 4d3 5p | 4d7 5s − 4d7 5p | |
| Total number of lines | 1718 | 2082 |
| Variance in the amplitudes v | 1.7161 | 24.2064 |
| Exact maximal strength | 53 | 1050 |
| Approximate (Formula (6)) | 22.73 | 329.27 |
| Approximate (Formula (8)) | 22.53 | 326.55 |
| Approximate (Formula (9)) | 56.88 | 840.68 |
| 4d4 | 4d3 5p | |
|---|---|---|
| (4d, 4d) | 73,800 | 76,300 |
| (4d, 4d) | 50,500 | 52,700 |
| (4d, 5p) | 30,323 | |
| (4d, 5p) | 10,000 | |
| (4d, 5p) | 8020 | |
| 2200 | 2390 | |
| 5784 |
| No. lines | No. lines | No. lines | |
|---|---|---|---|
| Exact | Formula (13) | Formula (17) | |
| 0.003 | 781 | 1460.33 | 1314.87 |
| 0.01 | 524 | 1253.99 | 1054.35 |
| 0.03 | 311 | 934.66 | 737.49 |
| 0.06 | 185 | 683.32 | 519.56 |
| 0.3 | 20 | 100.73 | 118.48 |
| 0.5 | 14 | 25.15 | 54.41 |
| 0.6 | 5 | 12.87 | 39.14 |
| 0.8 | 1 | 3.46 | 21.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pain, J.-C. Strong, Weak and Merging Lines in Atomic Spectra. Plasma 2025, 8, 17. https://doi.org/10.3390/plasma8020017
Pain J-C. Strong, Weak and Merging Lines in Atomic Spectra. Plasma. 2025; 8(2):17. https://doi.org/10.3390/plasma8020017
Chicago/Turabian StylePain, Jean-Christophe. 2025. "Strong, Weak and Merging Lines in Atomic Spectra" Plasma 8, no. 2: 17. https://doi.org/10.3390/plasma8020017
APA StylePain, J.-C. (2025). Strong, Weak and Merging Lines in Atomic Spectra. Plasma, 8(2), 17. https://doi.org/10.3390/plasma8020017