Plasma-Assisted Abatement of Per- and Polyfluoroalkyl Substances (PFAS): Thermodynamic Analysis and Validation in Gliding Arc Discharge

Abstract

Per- and polyfluoroalkyl substances (PFAS) are a group of synthetic organofluorine surfactants that are resistant to typical methods of degradation. Thermal techniques along with other novel, less energy-intensive techniques are currently being investigated for the treatment of PFAS-contaminated matrices. Non-equilibrium plasma is one technique that has shown promise for the treatment of PFAS-contaminated water. To better tailor non-equilibrium plasma systems for this application, knowledge of the energy required for mineralization, and in turn the roles that plasma reactive species and heat can play in this process, would be useful. In this study, fundamental thermodynamic equations were used to estimate the enthalpies of reaction (480 kJ/mol) and formation (−4640 kJ/mol) of perfluorooctanoic acid (PFOA, a long-chain legacy PFAS) in water. This enthalpy of reaction estimate indicates that plasma reactive species alone cannot catalyze the reaction; because the reaction is endothermic, energy input (e.g., heat) is required. The estimated enthalpies were used with HSC Chemistry software to produce a model of PFOA defluorination in a 100 mg/L aqueous solution as a function of enthalpy. The model indicated that as enthalpy of the reaction system increased, higher PFOA defluorination, and thus a higher extent of mineralization, was achieved. The model results were validated using experimental results from the gliding arc plasmatron (GAP) treatment of PFOA or PFOS-contaminated water using argon and air, separately, as the plasma gas. It was demonstrated that PFOA and PFOS mineralization in both types of plasma required more energy than predicted by thermodynamics, which was anticipated as the model did not take kinetics into account. However, the observed trends were similar to that of the model, especially when argon was used as the plasma gas. Overall, it was demonstrated that while energy input (e.g., heat) was required for the non-equilibrium plasma degradation of PFOA in water, a lower energy barrier was present with plasma treatment compared to conventional thermal treatments, and therefore mineralization was improved. Plasma reactive species, such as hydroxyl radicals ($\cdot \mathrm{OH}$) and/or hydrated electrons (e⁻_(aq)), though unable to accelerate an endothermic reaction alone, likely served as catalysts for PFOA mineralization, helping to lower the energy barrier. In this study, the activation energies (E_a) for these species to react with the alpha C–F bond in PFOA were estimated to be roughly 1 eV for hydroxyl radicals and 2 eV for hydrated electrons.

1. Introduction

1.1. Per- and Polyfluoroalkyl Substances’ (PFAS) Contamination in the Environment

Per- and polyfluoroalkyl substances (PFAS) are a diverse class of synthetic organofluorine compounds that have garnered attention as contaminants of emerging concern due to their widespread use, persistent nature, and potential for bioaccumulation and toxicity. First produced in the United States in the 1940s and 1950s, PFAS are water and oil repellent, thermally stable surfactants, which has made them useful in a variety of industrial and consumer products, such as paints, firefighting foams, cookware, food packaging, and more [1]. These unique physical and chemical properties also make some PFAS resistant to degradation, which has led to their ubiquitous accumulation in organisms and the environment. As the accumulative nature of PFAS has become apparent, so has their toxicity. Research has shown that some PFAS are linked to reproductive, developmental, immunological, hepatological, and carcinogenic health effects [1,2].

Due to the risks associated with PFAS, a plethora of efforts have been made to determine viable techniques for their degradation. Although difficult to achieve, complete mineralization (conversion to carbon oxides and HF) is the optimal goal of these techniques because PFAS are known to transform into recalcitrant by-products of concern. Thermal techniques, including incineration [3,4], thermal desorption [5,6], pyrolysis and gasification [4,7,8,9,10], smoldering combustion [11], and hydrothermal liquefaction [12,13], have been investigated and in some cases applied for PFAS treatment in various matrices (e.g., water, soil, and spent filter materials, among others) [14]. While effective, these techniques can be energy-intensive. For example, the incineration of PFAS-contaminated matrices typically uses temperatures of 900 °C or greater [3,4]. Further, these techniques may create harmful by-products. The United States Department of Defense placed a halt on the use of incineration as a destruction and disposal method for PFAS-contaminated matrices as of April 2022, which is speculated to be in part linked to the lack of data surrounding the nature of the by-products formed by this treatment [15,16]. Other novel and less energy-intensive techniques, including but not limited to non-equilibrium plasma treatment [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35], supercritical water oxidation (SCWO) [36,37], sonochemical treatment [38,39,40], and electrochemical oxidation/reduction [41,42,43,44,45,46], are also being investigated for this application.

1.2. The Promising Potential of Non-Equilibrium Plasma for the Treatment of PFAS-Contaminated Water

Non-equilibrium plasma is a partially ionized gas that is not in thermodynamic equilibrium because the temperature of the electrons is much hotter than that of the rest of the gas. This plasma generates a reactive environment that can include heat, UV photons, free radicals, free electrons, ions, and/or neutral or excited atoms and molecules [47]. The type of reactive environment created can be controlled by the type of discharge applied, the gas used to create this discharge, and the matrix to which it is applied. This selectivity that non-equilibrium plasma provides makes it a versatile technology that is useful for a variety of applications, including PFAS treatment.

Currently, most investigations using non-equilibrium plasma for PFAS treatment have focused on PFAS-contaminated water matrices. An assortment of discharges with differing reactor configurations has been studied for this application. Several groups have tested reactors that use pulsed streamer discharge over the liquid surface with various carrier gases, such as argon [21,26] and air [26]. Groups have also tested dielectric barrier discharge (DBD) reactors, both submerged [17] and over the liquid surface [26], using helium, argon [26], and air [17] as carrier gases. Plasma jets [31], corona discharges (typically pulsed) [26,29], and plasma gas in bubbles [20,32] have also been tested. One group tested submerged gliding arc plasmatron (GAP) discharge using air, nitrogen, and oxygen as carrier gases [30]; an updated version of the reactor used by Lewis et al., with air as the carrier gas, was also used in this study. While the non-equilibrium plasma treatment techniques tested to date are promising, complete mineralization of PFAS is not always achieved, and their associated energy costs are still relatively high for large-scale water treatment.

To better tailor non-equilibrium plasma systems for PFAS-contaminated water treatment, it would be useful to know the amount of energy required for mineralization to occur. This knowledge would help researchers to enhance their understanding of the roles that plasma reactive species and energy input (e.g., heat) can play in PFAS mineralization in their treatment systems. In this work, perfluorooctanoic acid (PFOA) mineralization in water was studied through a thermodynamic lens to determine the minimum amount of energy this process requires. PFOA was investigated in this study because, along with perfluorooctanesulfonic acid (PFOS), it has been the focus of most PFAS treatment research to date due to its widespread historical use and regulatory scrutiny. Thermodynamic studies of PFAS to date have included a calorimetry study of polytetrafluoroethylene (PTFE) [48], as well as modeling thermochemical properties of a variety of PFAS [46,49,50,51,52,53]. To our knowledge, four computational studies relating to thermodynamics have been conducted investigating PFOA. Blotevogel et al., 2023 employed the highest-level coupled cluster theory to study the stability of PFOA during thermal decomposition. The temperature required and potential pathways to achieve 99% destruction of PFOA during incineration were explored [52]. However, the requirements for the complete mineralization of PFOA were not explored. The thermodynamic stability of various isomers of PFOA were studied by Rayne and Forest in 2010 using Hartree-Fock and density functional theory (DFT) calculations, and by Hidalgo et al. in 2015 using DFT calculations. These studies focused on the free energy associated with these compounds, but did not explore their mineralization [50,51]. Baggioli et al., 2018 and Bentel et al., 2019 used DFT calculations to estimate bond dissociation energies (BDE) for various bonds in PFOA in an aqueous medium, which are used in the calculations in this study [46,53].

To begin this study, the reaction enthalpy (${\mathsf{\Delta }\mathrm{H}}_{\mathrm{RXN}}^{\circ }$) of PFOA mineralization in water, without the reactive species or additional oxidizing agent present, and the enthalpy of formation of PFOA (${\mathsf{\Delta }\mathrm{H}}_{\mathrm{F}}^{\circ }$) were estimated. These estimates were used to produce a model of PFOA defluorination as a function of enthalpy. This model was then validated using experiments in which PFOA and PFOS-contaminated water were treated in a laboratory-scale GAP liquid treatment system. Importantly, gliding arc discharge was chosen for this study because, in contrast to the other discharges tested for PFAS-contaminated water treatment, it combines the characteristics of thermal and non-equilibrium plasma systems. The advantages of gliding arc include high power density associated with thermal systems, as well as the selectivity associated with non-equilibrium systems. Further, while the temperature of the gas in the gliding arc discharge was relatively low when compared to thermal plasma systems (300–1000 K versus 3000–5000 K), it was elevated compared to strictly non-equilibrium plasma systems [54]. Energy input (e.g., heat), it will be demonstrated, is an important factor for PFAS mineralization, which also influenced the choice to use gliding arc discharge in this study.

To close, a preliminary kinetic analysis was conducted to estimate the activation energy (E_a) for hydroxyl radicals ($\cdot \mathrm{OH}$) and hydrated electrons (e⁻_(aq)), two reactive species often associated with PFAS degradation in non-equilibrium plasma treatment systems and advanced oxidation processes in general, to separately react with the alpha C–F bond in PFOA. Ultimately, this work will show that, while the reactive species plasma generates can serve as catalysts for PFOA mineralization, energy (e.g., heat) is also required to accelerate the reaction.

2. Materials and Methods

2.1. Thermodynamic Modeling

2.1.1. Enthalpy of PFOA Mineralization in Water

The mineralization reaction that is the focus of this study is shown below in Reaction 1:

$${\mathrm{C}}_8{\mathrm{HF}}_{15}{\mathrm{O}}_2\left(\mathrm{PFOA},\mathrm{aq}\right){+7\mathrm{H}}_2\mathrm{O}\left(\mathrm{l}\right)\to 15\mathrm{HF}\left(\mathrm{aq}\right)+7\mathrm{CO}\left(\mathrm{g}\right){+\mathrm{CO}}_2\left(\mathrm{g}\right)$$

(Reaction 1)

The enthalpy of this reaction was estimated using Equation (1) along with localized bond dissociation energies (BDEs) for covalent bonds in non-ionic solutions. The applicable BDEs are shown in

Table 1. (a) Bonds broken and (b) bonds formed during PFOA mineralization in water. These were used with Equation (1) to estimate the enthalpy of this reaction.

(a)
Type	Number of Bonds	BDE (kJ/mol)
O–H (in H2O)	14	497.32 [57]
C=O	1	799 [56]
C–O	1	464.0056 [55]
O–H (in PFOA)	1	475.79 [53]
C–F (1)	3	492.50 [46]
C–F (2)	2	453.13 [46]
C–F (3)	2	446.77 [46]
C–F (4)	2	447.73 [46]
C–F (5)	2	448.78 [46]
C–F (6)	2	452.12 [46]
C–F (7)	2	449.07 [46]
C–C (1)	1	383.6728 [55]
C–C (2)	1	371.1208 [55]
C–C (3)	1	371.9576 [55]
C–C (4)	1	372.3760 [55]
C–C (5)	1	376.9784 [55]
C–C (6)	1	349.7824 [55]
C–C (7)	1	371.5392 [55]
		= 18,171 kJ/mol
(b)
Type	Number of Bonds	BDE (kJ/mol)
C≡O	7	1076.63 [57]
C=O (in CO2)	2	804.42 [57]
H–F	15	569.68 [57]
		= 17,690.44 kJ/mol

. For reference, the mineralization reaction showing chemical structures is depicted in Figure 1. The bonds in the chemical structure of PFOA are numbered to reflect the BDEs in Table 1. The BDEs for C–F bonds in PFOA were taken from Bentel et al., 2019 [46]; these values were converted from kcal/mol to kJ/mol. The BDE for the O–H bond in PFOA was taken from Baggioli et al., 2018 [53]; an average of the various estimates the manuscript provides for this BDE was used. The BDEs for C–C bonds and the C–O bond in PFOA were estimated using The National Renewable Energy Laboratory’s ALFABET BDE estimator tool, which, like Bentel et al., 2019 and Baggioli et al., 2018, uses density functional theory (DFT) to estimate the BDE [55]. Density functional theory calculations for BDEs are based on the electronic structure of a molecule, which is why BDEs for the same kind of bond (e.g., C–F) vary based on the position of the bond in the molecule. The BDE for the C=O bond in PFOA was taken from Kildahl 1995 [56]; to the best of our knowledge, a DFT calculation for this bond is not available in the literature. The BDEs for all bonds in H₂O, HF, CO, and CO₂ were taken from the table of bond dissociation energies in polyatomic molecules in the CRC Handbook of Chemistry and Physics [57]. While the BDEs in Table 1 are presented with the precision with which they were shown in their various sources, our final estimate of the enthalpy of the reaction was rounded to reflect the inherent lack of precision when using this calculation method.

$${\mathsf{\Delta }\mathrm{H}}_{\mathrm{RXN}}^{\circ }=\sum {\mathrm{BDE}}_{\left(\mathrm{bonds}\mathrm{broken}\right)}-\sum {\mathrm{BDE}}_{\left(\mathrm{bonds}\mathrm{formed}\right)}$$

(1)

2.1.2. Enthalpy of Formation of PFOA

The estimated mineralization reaction enthalpy (~480 kJ/mol) and the standard enthalpies of formation of H₂O(l), HF(aq), CO(g), and CO₂(g), shown in

Table 2. Standard enthalpies of formation for species involved in PFOA mineralization reaction. Values are for the given phases at 298 K.

Compound	Phase	$\mathbf{Standard}\mathbf{Enthalpy}\mathbf{of}\mathbf{Formation}({\mathsf{\Delta }\mathbf{H}}_{\mathbf{F}}^{\circ }$, kJ/mol)
H2O	l	−285.8 [59]
HF	aq	−332.6 [59]
CO	g	−110.5 [59]
CO2	g	−393.5 [59]

, were used in Equation (2) to estimate the enthalpy of formation (${\mathsf{\Delta }\mathrm{H}}_{\mathrm{F}}^{\circ }$) of PFOA. As with our enthalpy of reaction estimate, our final estimate of the enthalpy of the formation of PFOA was rounded to reflect the inherent lack of precision when using this calculation method.

$$\begin{gathered} {\mathsf{\Delta }\mathrm{H}}_{\mathrm{RXN}}^{\circ }=\sum ∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{{}_{\left(\mathrm{products}\right)}}_{}-\sum ∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{{}_{\left(\mathrm{reactants}\right)}}_{}{}_{} \\ {\mathsf{\Delta }\mathrm{H}}_{\mathrm{RXN}}^{\circ }=[∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{HF}\right)}+∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{CO}\right)}+∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{{(\mathrm{CO}}_2)}]-[∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{PFOA}\right)}+∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{{(\mathrm{H}}_2\mathrm{O})}{]}_{} \\ \therefore ∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{PFOA}\right)}=[∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{HF}\right)}+∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{\left(\mathrm{CO}\right)}+∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{{(\mathrm{CO}}_2)}]-∆{\mathrm{H}}_{\mathrm{F}}^{\circ }{}_{{(\mathrm{H}}_2\mathrm{O})}{-\mathsf{\Delta }\mathrm{H}}_{\mathrm{RXN}}^{\circ } \end{gathered}$$

(2)

2.1.3. Thermodynamic Model of PFOA Mineralization in Water

Using the estimated enthalpy of formation of PFOA (~−4640 kJ/mol), the composition of the mineralization reaction system as a function of temperature was modeled with HSC Chemistry software (version 6.1), Outotec, Pori, Finland [59]. The user feeds this software the desired substances in the reaction system and their input amounts. The system could be assessed over a range of temperatures or pressures, also provided by the user. The software then uses the enthalpy (H), standard molar entropy (S°), and specific heat (C_p) of the substances in the system to conduct stepwise calculations using the Gibbs energy minimization method over the range of temperatures or pressures provided. The number of calculation steps may be specified by the user; the default is 21 steps, which was used in this work. Model results can be viewed in various forms, but for the purpose of this work, (1) the equilibrium composition of the reaction system as a function of temperature and (2) enthalpy of the reaction system as a function of temperature were chosen.

The software’s database contained the required thermochemical data for all components of the reaction system aside from PFOA. PFOA was manually added to the database as a new chemical species, and its estimated enthalpy of formation was entered. To produce the model, this software requires two other thermochemical properties of PFOA that, to our knowledge, are not currently available in the literature: standard molar entropy (S°) and specific heat (C_p). The software’s database contains these data for aqueous octanoic acid (C₈H₁₆O₂), which has a similar chemical structure to PFOA, but without a perfluorinated alkyl chain, as depicted in Figure 2. Standard molar entropy and specific heat values for octanoic acid, 350 and 700 J/mol$·$K, respectively, were entered as estimates for PFOA. It was assumed that these values remained constant over the temperature range analyzed.

The equilibrium pressure was set to 1 bar and the temperature varied from 25 to 250 °C. The raw material inputs were 55.5 mol H₂O and 0.242 mmol PFOA, which amounted to 1 L of a 100 mg/L PFOA solution. While not environmentally relevant, this concentration was used to mimic the elevated concentrations often used in laboratory studies of non-equilibrium plasma treatment technologies for PFAS-contaminated water [18,29,30,32]. Solutions of 100 mg/L PFOA or PFOS were also used to assess our GAP liquid treatment system, as described later in this paper. For reference, a study conducted by Quiñones and Snyder in 2009 found that PFOA concentrations in a variety of drinking water sources in the United States ranged from <5 to 30 ng/L [60]. Elevated concentrations are often used in laboratory studies on PFAS treatment methods due to the limitations of analytical methods available for PFAS compounds and their by-products. For example, a fluoride analysis is needed to determine defluorination of the parent compound, which is often used as a metric to represent PFAS mineralization. The use of a fluoride ion-selective electrode (ISE) is a robust method for a fluoride analysis, but the limit of quantification is typically around 0.5 mg/L [61].

The data output by the model was given in moles of each compound in the reaction system (PFOA, H₂O, HF, CO, and CO₂) as a function of temperature (°C), and separately, enthalpy of the reaction system (kJ/L) as a function of temperature (°C). These results were processed in Microsoft Excel (Version 16.72) to convert the data to percent PFOA defluorination (%) as a function of the reaction system enthalpy (kJ/L) for ease of interpretation in relation to our experimental data and data available from other research on the non-equilibrium plasma treatment of PFAS-contaminated water. The percent of PFOA defluorination (%) was calculated at each enthalpy value using the data output by the model and Equation (3).

$$\mathrm{Percent}\mathrm{PFOA}\mathrm{Defluorination}(\%)=\frac{\mathrm{HF}\left(\mathrm{mol}\right)}{{\mathrm{PFOA}}_{\mathrm{Initial}}\left(\mathrm{mol}\right)\times \frac{15\mathrm{mol}\mathrm{HF}}{1\mathrm{mol}\mathrm{PFOA}}}$$

(3)

2.2. Experimental Validation of Thermodynamic Model Using GAP Liquid Treatment System

To assess the model and estimated thermochemical properties of PFOA, the model results were compared to experimental results from the treatment of 100 mg/L PFOA and PFOS solutions in our GAP liquid treatment system.

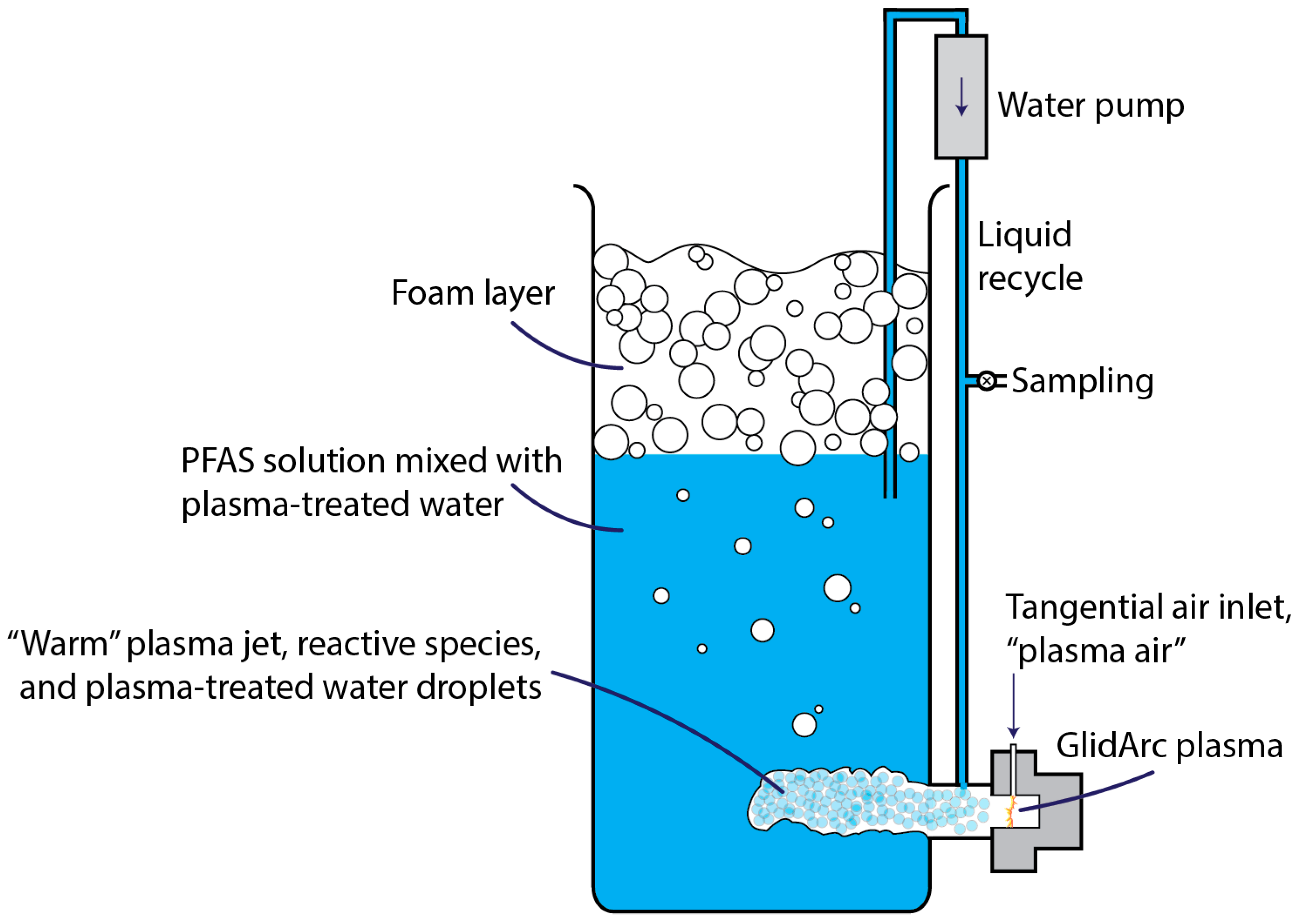
2.2.1. GAP Liquid Treatment System

A schematic of the GAP liquid treatment system is shown in Figure 3. An earlier version of this system is described in detail in Lewis et al., 2020 [30]. The updates made to this system were as follows:

• Liquid was now continuously recycled from the top of the reactor (near the air–water interface) to just above the plasmatron;
• Samples were taken from the recycle line;
• Atomization air was removed;
• Recycle through the plasmatron was removed.

2.2.2. PFOA and PFOS GAP Treatment Experiments

The solutions were prepared by adding 100 mg of PFOA (CAS 335-67-1, 96% purity, manufactured by Sigma-Aldrich, St. Louis, MO, USA) or PFOS (PFOSK was used, CAS 2795-39-3, 98% purity, manufactured by Sigma-Aldrich, St. Louis, MO, USA) to 1 L of distilled water in a polypropylene volumetric flask. To dissolve the PFOA or PFOS, the solutions were placed on a stirring hot plate for 2 h.

Four experiments were conducted with varying parent compounds (PFOA or PFOS) and plasma gas (argon or air), as outlined in

Table 3. Varied conditions for experiments treating PFOA and PFOS in the GAP liquid treatment system.

Parent Compound	Plasma Gas	Plasma Power (W)
PFOA	Argon	180
PFOS	Argon	180
PFOA	Air	350
PFOS	Air	375

below. Plasma power, also shown in Table 3, varied between experiments due to differences in the breakdown voltage between argon and air. Plasma power refers to the average power on the gliding arc. This was calculated by multiplying the supplied current, which was held constant over the course of an experiment, by the average voltage of the arc, which was measured using a multimeter. Plasma gas was set to 40 L/min in each experiment. Each run was 60 min. Samples (10 mL) were taken from the sampling port every 10 min beginning at time 0 (before the system was powered).

2.2.3. GAP Energy Input Calculations

To compare the results across GAP experiments despite differences in plasma power, the energy input from plasma discharge was calculated at each time point using Equation (4).

$$\mathrm{Energy}\mathrm{Input}(\mathrm{kJ}/\mathrm{L})=\frac{\mathrm{Plasma}\mathrm{Power}\left(\mathrm{kW}\right)\times \mathrm{Time}\left(\mathrm{s}\right)}{\mathrm{Initial}\mathrm{Volume}\left(\mathrm{L}\right)}$$

(4)

2.2.4. Fluoride Analysis via Ion-Selective Electrode

The fluoride analysis was conducted using an ion-selective electrode (ORION^TM Ionplus Sure-Flow Solid State Combination Fluoride Electrode, Thermo Fisher Scientific, Waltham, MA, USA). The calibration ranged from 0.5 mg/L to 5 mg/L, which encompassed the range of fluoride production in these experiments. The fluoride electrode filling solution used was manufactured by Thermo Fisher Scientific. Standards (0.5, 1.0, and 5.0 mg/L) manufactured by LabChem (Zelienople, PA, USA) were used for calibration. As recommended by the electrode manufacturer, the samples were diluted with equal volume TISAB II, manufactured by LabChem, prior to analysis. All measurements were taken at room temperature.

It should be noted that a fluoride analysis alone cannot provide a comprehensive picture of the fate of PFAS during treatment, and other analytical techniques, such as targeted PFAS analysis, suspect screening, and total organic fluorine (TOF) analysis, are needed to complement these results. However, the fluoride analysis is useful in that it can be conducted more quickly and inexpensively than these other techniques. Further, as discussed in Lewis et al., 2020, the fluorine mass balance for this system during PFOA treatment suggested that the compound mineralized rather than breaking down into other quantifiable PFAS compounds, which makes fluoride a valuable measurement for assessing this system’s performance while treating this compound [30]. Our recent findings, to be published, showed a similar trend for PFOS treatment in this system.

2.3. Data Analysis and Graphing

The thermodynamic model and experimental results were graphed using MATLAB version 9.13.0.2126072, The MathWorks Inc., Natick, MA, USA (R2022b Update 3) [62].

2.4. Preliminary Kinetic Analysis

Studies to date on non-equilibrium plasma systems for the treatment of PFAS-contaminated water emphasize the importance of investigating the role that different reactive species play in the degradation mechanism. Specifically, scavengers are often used to evaluate the influence that hydroxyl radicals (^•OH) and electrons (e⁻) have on PFAS degradation in these systems [18,21]. In this study, the Sabo method was used to estimate the activation energy for hydroxyl radicals (^•OH) and hydrated electrons (e⁻_(aq)), separately, to react with the alpha C–F bond in PFOA, which was labelled C–F (7) in Figure 1 and Table 1 [63]. The alpha bond was chosen for these calculations because studies suggest that this position has a high reactivity due to its proximity to the carboxyl head group, which shows the inductive effect [46,64,65].

2.4.1. Hydroxyl Radical Activation Energy

The defluorination of the C($\mathsf{\alpha }$)–F bond in PFOA by a hydroxyl radical is shown below in Reaction 2. The formula used to estimate the activation energy of this process is shown in Equation (5). The applicable BDEs are shown in Table 4. The value used for the free energy associated with the ionization of HF ($∆{\mathrm{G}}_{a,HF}^{°}$) was 9.2 kJ/mol, taken from Ando and Hynes 1999 [66].

$$\cdot {\mathrm{OH}+\mathrm{C}}_8{\mathrm{HF}}_{15}{\mathrm{O}}_2\left(\mathrm{PFOA}\right)\to {\mathrm{HF}+\mathrm{C}}_8{\mathrm{HF}}_{14}{\mathrm{O}}_3$$

(Reaction 2)

$${\mathrm{E}}_{\mathrm{a}}=\sum {\mathrm{BDE}}_{\left(\mathrm{bonds}\mathrm{broken}\right)}-(0.84\times \sum {\mathrm{BDE}}_{\left(\mathrm{bonds}\mathrm{formed}\right)})-(0.84\times ∆{\mathrm{G}}_{a,HF}^{°})$$

(5)

2.4.2. Hydrated Electron Activation Energy

The defluorination of the C($\mathsf{\alpha }$)–F bond in PFOA by a hydrated electron is shown below in Reaction 3. The formula used to estimate the activation energy of this process is shown in Equation (6). The C($\mathsf{\alpha }$)–F bond energy presented in Table 4 was used in this calculation as well. The value used for the electron affinity of fluorine was 328 kJ/mol, taken from Myers 1990 [67].

$${\mathrm{e}}^{-}{}_{\left(\mathrm{aq}\right)}{+\mathrm{C}}_8{\mathrm{HF}}_{15}{\mathrm{O}}_2\left(\mathrm{PFOA}\right)\to {\mathrm{F}}^{-}+\cdot {\mathrm{C}}_8{\mathrm{HF}}_{14}{\mathrm{O}}_2$$

(Reaction 3)

$${\mathrm{E}}_{\mathrm{a}}=\sum {\mathrm{BDE}}_{\left(\mathrm{bonds}\mathrm{broken}\right)}-({0.84\times \mathrm{e}}^{-}\mathrm{affinity}\mathrm{for}\mathrm{F})$$

(6)

Table 4. (a) Bonds broken and (b) bonds formed when PFOA defluorination is initiated by a hydroxyl radical. These BDE values were used with Equation (5) to estimate the activation energy of this reaction.

	(a)
Type	Number of Bonds	BDE (kJ/mol)
$\cdot$O–H	1	425.76 [68]
C($\mathsf{\alpha }$)–F	1	449.07 [46]
	(b)
Type	Number of Bonds	BDE (kJ/mol)
H–F	1	565 [56]
C–O	1	358 [56]

Table 4. (a) Bonds broken and (b) bonds formed when PFOA defluorination is initiated by a hydroxyl radical. These BDE values were used with Equation (5) to estimate the activation energy of this reaction.

	(a)
Type	Number of Bonds	BDE (kJ/mol)
$\cdot$O–H	1	425.76 [68]
C($\mathsf{\alpha }$)–F	1	449.07 [46]
	(b)
Type	Number of Bonds	BDE (kJ/mol)
H–F	1	565 [56]
C–O	1	358 [56]

3. Results and Discussion

3.1. Enthalpy Calculations

The estimated enthalpy of PFOA mineralization in water (Reaction 1) was ~480 kJ/mol (5 eV), meaning that the reaction is slightly endothermic. In terms of plasma treatment, the acceleration of an exothermic reaction (e.g., oxidation of hydrocarbons) requires only plasma reactive species to be catalyzed. An endothermic reaction, however, requires for its acceleration not only plasma reactive species, but also some energy input. Thus, from our estimation, it was determined that energy (e.g., heat) is required to accelerate PFOA mineralization in plasma treatment systems.

We acknowledge that the method used to calculate the enthalpy of the mineralization reaction, and in turn the enthalpy of the formation of PFOA, resulted in rough estimates of these thermochemical properties. The implications of this on our modeling work are discussed in the following section, especially in relation to our estimate for the enthalpy of the formation of PFOA, which was ~−4640 kJ/mol (−48 eV). More robust efforts, such as calorimetry experiments, are required to determine precise values for these thermochemical properties.

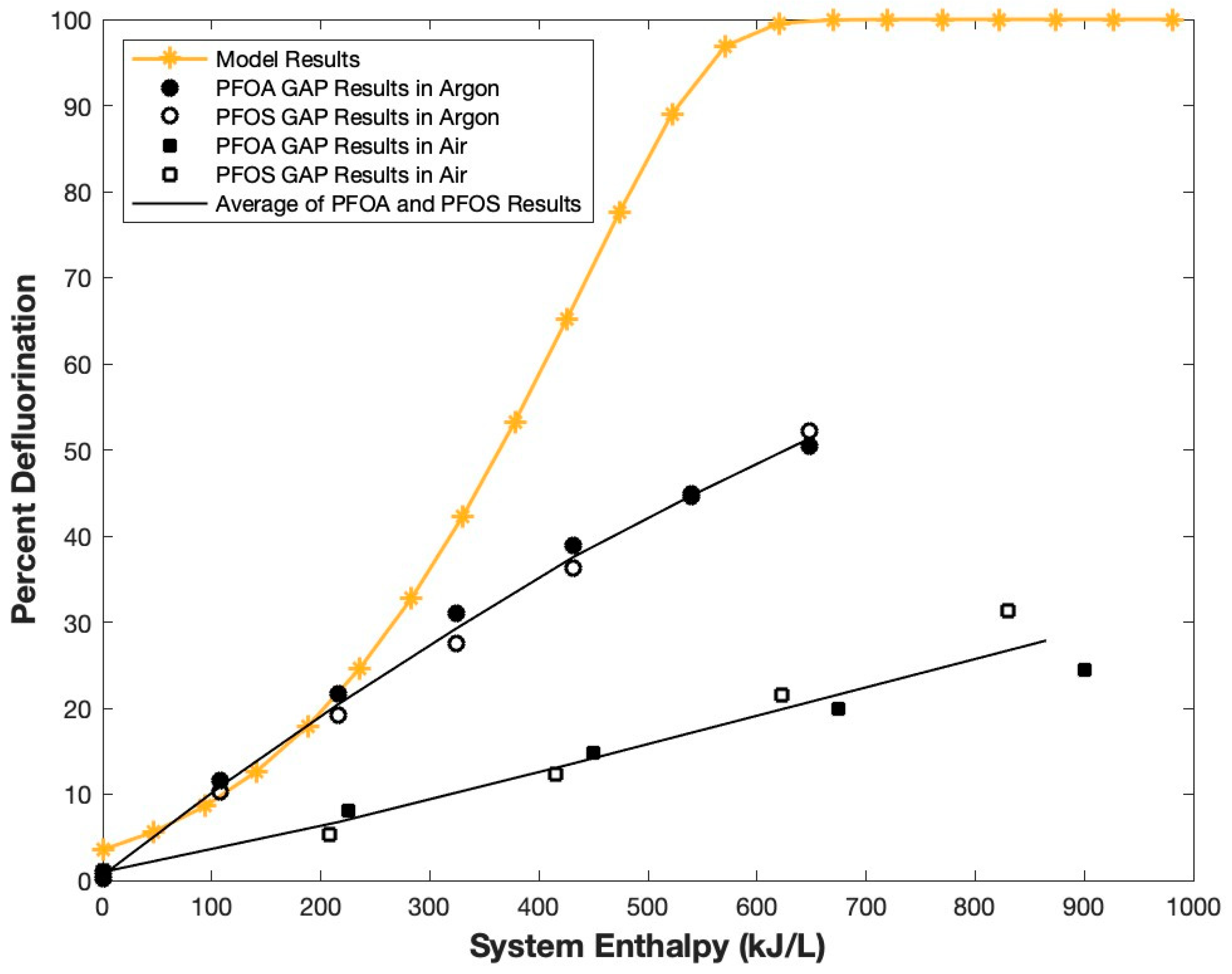
3.2. Thermodynamic Model of PFOA Mineralization in Water and Experimental Validation Using GAP Liquid Treatment System

The modeled PFOA defluorination results as a function of reaction system enthalpy are shown in Figure 4. These results predict that significant PFOA mineralization can be achieved at an enthalpy of around 700 kJ/L. A few factors should be considered when assessing the accuracy of this model. Foremost, the model is dependent on the value given for the PFOA enthalpy of formation, which in this case is a rough estimate. To illustrate the uncertainty in our thermodynamics calculations and in turn our model results, calculations were also conducted using average BDEs for all bonds in PFOA, taken from Kildahl 1995 [56]. The use of these BDEs resulted in an estimated PFOA enthalpy of formation of −4730 kJ/mol, which flattened the slope of the defluorination trend predicted by the model. In this case, it was predicted that a reaction system enthalpy of around 1800 kJ/L is required to achieve significant PFOA mineralization. The results shown in this manuscript used DFT-calculated PFOA BDEs from various sources [46,53,55], which we concluded would produce more reliable results due to their specificity. However, due to the uncertainty associated with the calculations used, the selection of BDEs heavily influences results.

Further, the standard molar entropy and specific heat values used for PFOA, which are the values associated with octanoic acid, are likely underestimates, as these thermochemical properties typically increase with mass. This relationship could be seen for select shorter-chain perfluoroalkyl compounds in Snitsiriwat et al., 2022; generally, as alkyl chains become fluorinated, standard molar entropy and specific heat values increase [49]. This relationship could also be seen when comparing other hydrocarbons and their perfluorinated counterparts for which these thermochemical properties are known. For example, the standard molar entropy values for C₆H₆ and C₆F₆ are 173.26 and 280.79 J/mol$·$K, respectively, while the specific heat values are 136.06 and 221.58 J/mol$·$K, respectively [69,70].

Because we predicted that the standard molar entropy and specific heat values used for PFOA in the model are underestimates, the impact that increasing these properties has on model results was explored. To the best of our knowledge, there is no sufficient data on the thermochemical properties of perfluoroalkyl carboxylic acids (PFCAs) to determine if there is a specific trend between the standard molar entropy and specific heat of these compounds and their hydrocarbon counterparts (e.g., to create a plot of standard molar entropies of PFCAs vs. those of hydrocarbons of the same chain length), which then might be used to estimate these properties for PFOA. However, by comparing the standard molar entropy and specific heat of CF₃COOH, calculated via DFT in Snitsiriwat et al., 2022 [49], with those of CH₃COOH, it can be estimated that these properties differ by a factor of 1.2–1.4. This range was used as a rough conversion factor when assessing how increasing these properties impacts the model results. It was found that, as these properties increase, the slope of the defluorination trend predicted by the model flattens. Thus, in using the standard molar entropy and specific heat of octanoic acid in the model, the amount of energy required for complete PFOA mineralization in this system is likely underestimated. In future studies, modeling of the mineralization of hydrocarbons and their perfluorinated counterparts (e.g., C₆H₆ and C₆F₆, or C₇H₁₆ and C₇F₁₆) should be conducted to enhance our understanding of the implications of the assumptions regarding standard molar entropy and specific heat values made here.

Also shown in Figure 4 are the PFOA and PFOS defluorination results from the experimental validation conducted in the GAP liquid treatment system, using either argon or air as the plasma gas. For these results, the calculated energy input from the plasma discharge was used to represent system enthalpy. PFOS was included here because, though structurally different from PFOA, it was expected to follow a similar trend, as confirmed by the results.

Both the model and experimental results demonstrated a direct relationship between system enthalpy and PFOA defluorination. This relationship was apparent in the results from the PFOS experiments as well. This relationship has been demonstrated experimentally by several other groups studying the treatment of PFAS-contaminated water using advanced oxidation processes. For example, Pinkard et al., 2021, who explored the supercritical water oxidation of PFOS, demonstrated an increase in PFOS defluorination with the increasing reactor temperature, and thus increasing system enthalpy [36]. Kulkarni et al., 2022 demonstrated that the increased reactor temperature and power supplied, which would both cause an increase in system enthalpy, resulted in higher levels of degradation for a variety of PFAS compounds (including PFOA) during treatment in a sonolysis reactor, though mineralization products were not quantified in this study [71]. Stratton et al., 2017 demonstrated increased levels of both PFOA degradation and defluorination with increased plasma discharge power, and thus system enthalpy, in their pulsed streamer (with laminar jet and bubbling) plasma reactor [21].

Based on the model results and the corresponding temperature data from the model, the relevant temperature requirement for the plasma–water surface area, where most of the mineralization process is hypothesized to occur, is about 195 °C. This temperature is lower than those seen in thermal treatment processes of PFAS-contaminated matrices. For example, the incineration of PFAS-contaminated matrices is typically conducted at temperatures greater than 900 °C [3,4]. Thermal desorption has been shown to be effective at removing PFAS from contaminated matrices at temperatures between 350 and 400 °C [6]. Smoldering combustion also uses temperatures exceeding 900 °C [11]. Further, in each of these techniques requiring high temperatures, full mineralization, to the best of our knowledge, has not been demonstrated. Importantly, the thermodynamic calculations conducted here predict the minimum energy and temperature required for PFOA mineralization to occur and do not consider the mechanism or transition products. Consideration of these details would require a more detailed kinetic analysis. However, in experiments conducted in our GAP liquid treatment system, it was observed that during non-equilibrium plasma treatment, the system behaves more closely to what was predicted by fundamental thermodynamics, which demonstrates that mineralization is possible with a smaller energy barrier than that seen in thermal treatment.

It is important to note that the reaction system studied in the model is not directly comparable to that used in our GAP experiments, nor to those in PFAS treatment systems studied in the literature or utilized on a larger scale. The model falls short in that it does not consider elements likely to be present that may influence the reaction, such as reactive species, which are present in non-equilibrium plasma systems and other advanced oxidation processes. The model also does not consider transformation products in the reaction system. Further, the model does not consider several properties of PFAS that would likely impact the efficiency of their mineralization, including their surfactant properties, their tendency to adsorb to interfaces, and that they would be present in an anionic form at any relevant pH. However, the model provides theoretical confirmation that enthalpy and PFOA defluorination are directly related, as well as an estimate of the amount of energy required, from a thermodynamic standpoint, to mineralize PFOA, which can be useful when assessing treatment techniques.

3.3. Preliminary Kinetic Analysis

It was estimated that the activation energies for hydroxyl radicals (^•OH) and hydrated electrons (e⁻_(aq)), separately, to react with the alpha C–F in PFOA are roughly 1 eV and 2 eV, respectively. Though not yet investigated in our GAP system, studies suggest that gliding arc discharges in argon typically create a more electron-rich reactive environment, while those in air create a more hydroxyl radical-rich environment [72,73]. Thus, our GAP experimental results suggest that the activation energy for electrons to initiate PFOA defluorination may actually be lower than that for hydroxyl radicals. However, the trend might also suggest that the energy required to produce electrons in argon is lower than that required to produce hydroxyl radicals in air.

These activation energies are indicative of the important role that supplied energy (e.g., heat) plays in PFAS degradation in these systems. While these reactive species may be present during non-equilibrium plasma treatment, for them to react with PFAS, the activation energy, at minimum, must be supplied. Pinkard et al. also highlighted the importance of heat in meeting activation energy requirements during SCWO of PFOS-contaminated water, which, like non-equilibrium plasma, uses oxidative radicals to degrade PFAS. As mentioned previously, this group demonstrated that increased temperature led to increased PFAS mineralization in their system [36].

It should be noted that this kinetic analysis is limited in its scope. Foremost, the method used provides only a rough estimate of activation energy; more robust analyses such as kinetics-focused experiments along with the application of the Arrhenius equation are required to determine precise values. Further, it was assumed that these reactive species result in the complete dissociation of the alpha C–F bond in PFOA, which, while supported by our experimental results and the fluorine mass balance in Lewis et al., 2020 [30], may not necessarily be the case. Also, some studies suggest that hydroxyl radicals will not react with PFOA under typical advanced oxidation conditions [74,75]. Further explorations of the intermediates that may form and confirmation of which reactive species partake in the reaction are necessary.

4. Conclusions

In this work, PFOA mineralization in water was assessed from a fundamental thermodynamic standpoint. To begin, the enthalpy of this mineralization reaction and the enthalpy of the formation of PFOA were estimated using thermodynamic calculations. PFOA mineralization in water as a function of system enthalpy was then modeled with HSC Chemistry software. The thermodynamic calculations and model were validated by experiments in a gliding arc plasmatron (GAP) batch reactor. Finally, a preliminary kinetic analysis of PFOA mineralization by plasma reactive species often associated with PFAS mineralization in plasma treatment systems (specifically ^•OH and e⁻_(aq)) was conducted. The major conclusions drawn from this work are as follows:

• The estimated enthalpy of PFOA mineralization in water (Equation (1)) is 480 kJ/mol, making the reaction endothermic. Thus, plasma reactive species alone cannot accelerate the reaction, and energy input (e.g., heat) is required for PFOA mineralization in plasma treatment systems;
• The estimated enthalpy of the formation of PFOA is −4640 kJ/mol;
• Though energy is required, PFOA mineralization is possible with a lower energy barrier than that seen in thermal treatment, likely in part due to catalysis by plasma reactive species such as ^•OH and e⁻_(aq). This is validated by the GAP experiments presented here as well as other cited publications;
• The activation energies for ^•OH and e⁻_(aq), separately, to react with the alpha C–F bond in PFOA are estimated to be around 1 eV and 2 eV, respectively.