Size-Independent Flexure Test Technique for the Mechanical Properties of Geocomposites Reinforced by Unidirectional Fibers
Abstract
:1. Introduction
2. Theory of Size-Independent Flexure-Test Technique
2.1. Modulus of Elasticity
2.2. Strength
2.3. Displacement Rate
3. Experiments
4. Results and Discussion
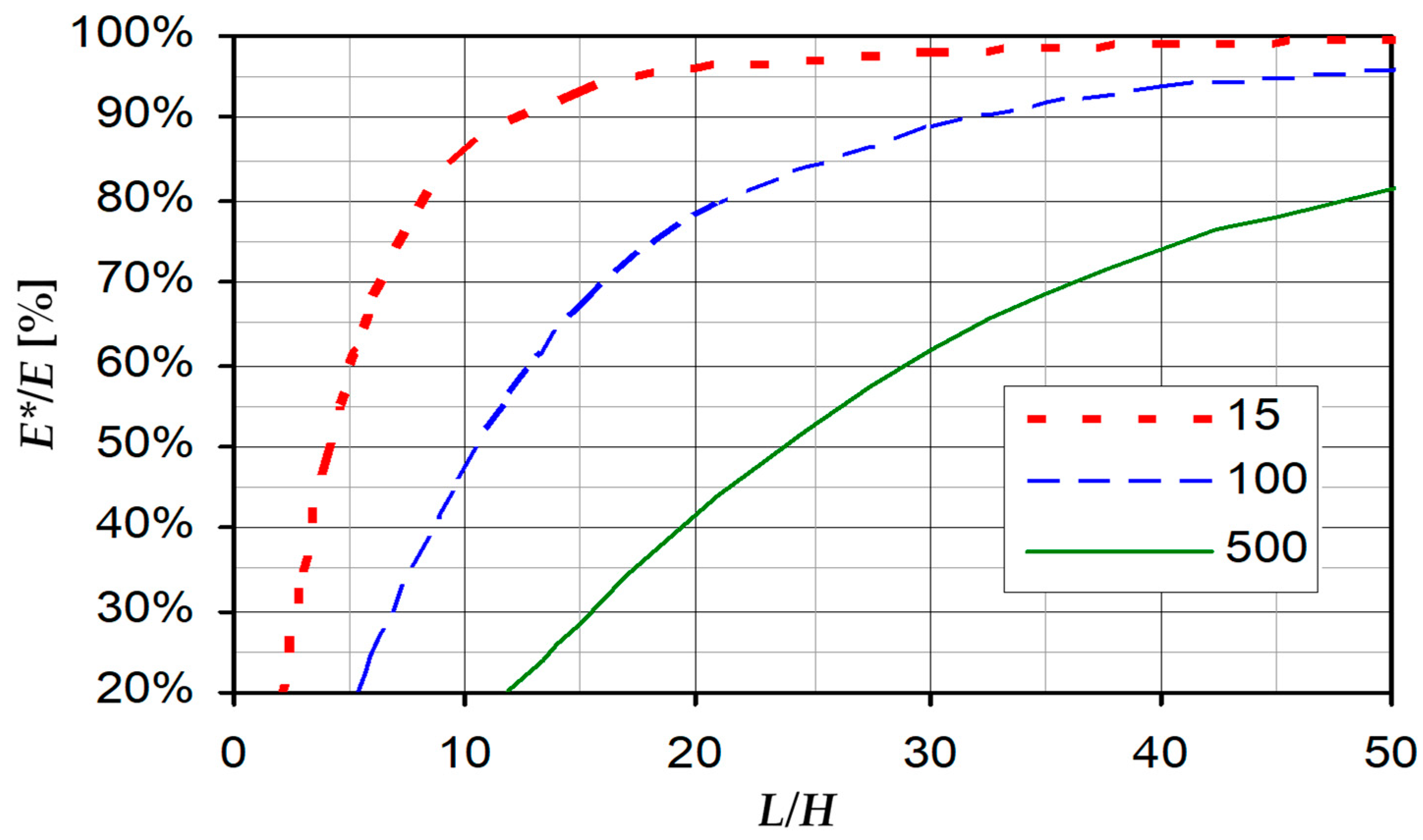
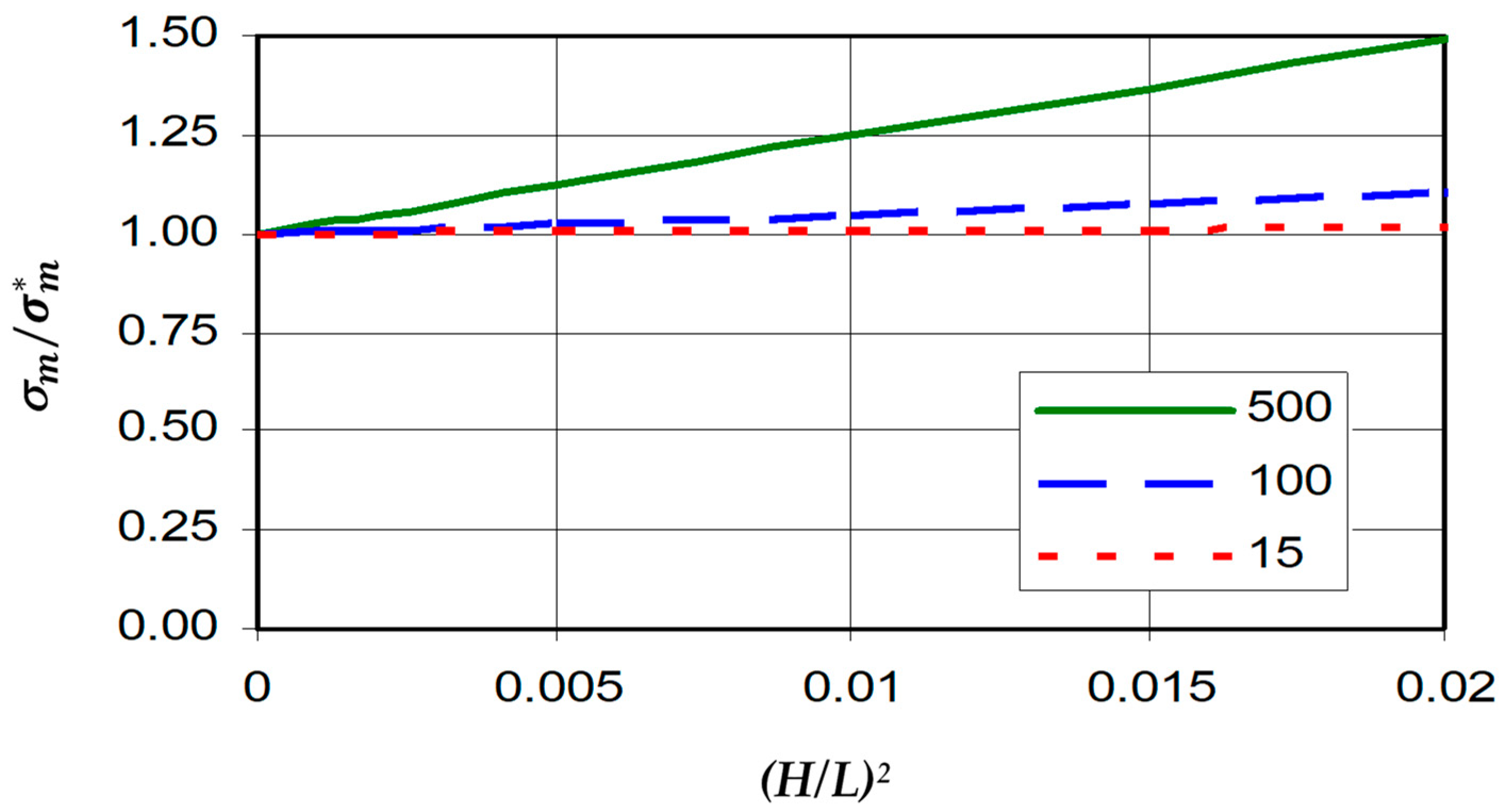
4.1. Compliance with Theory
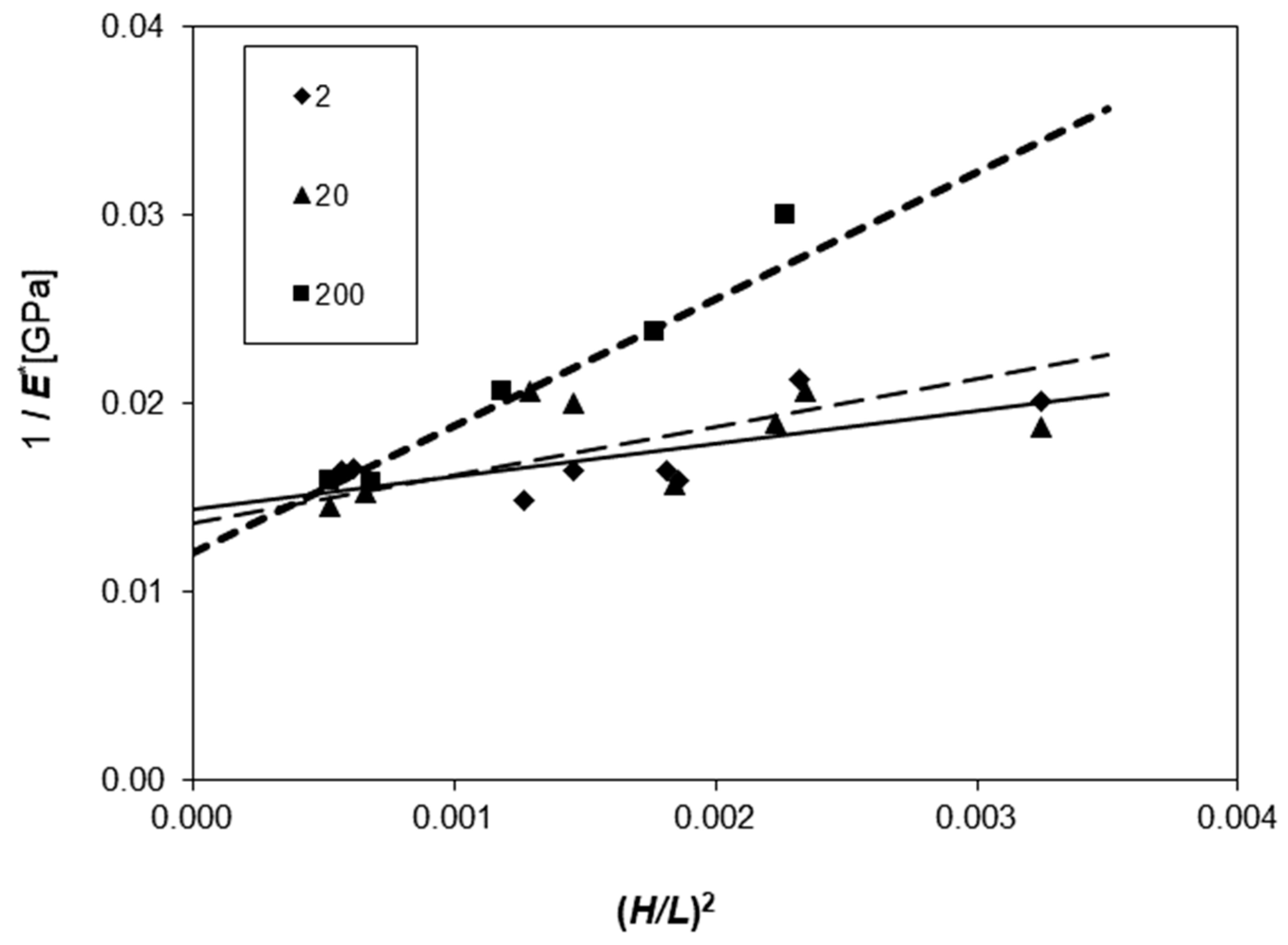
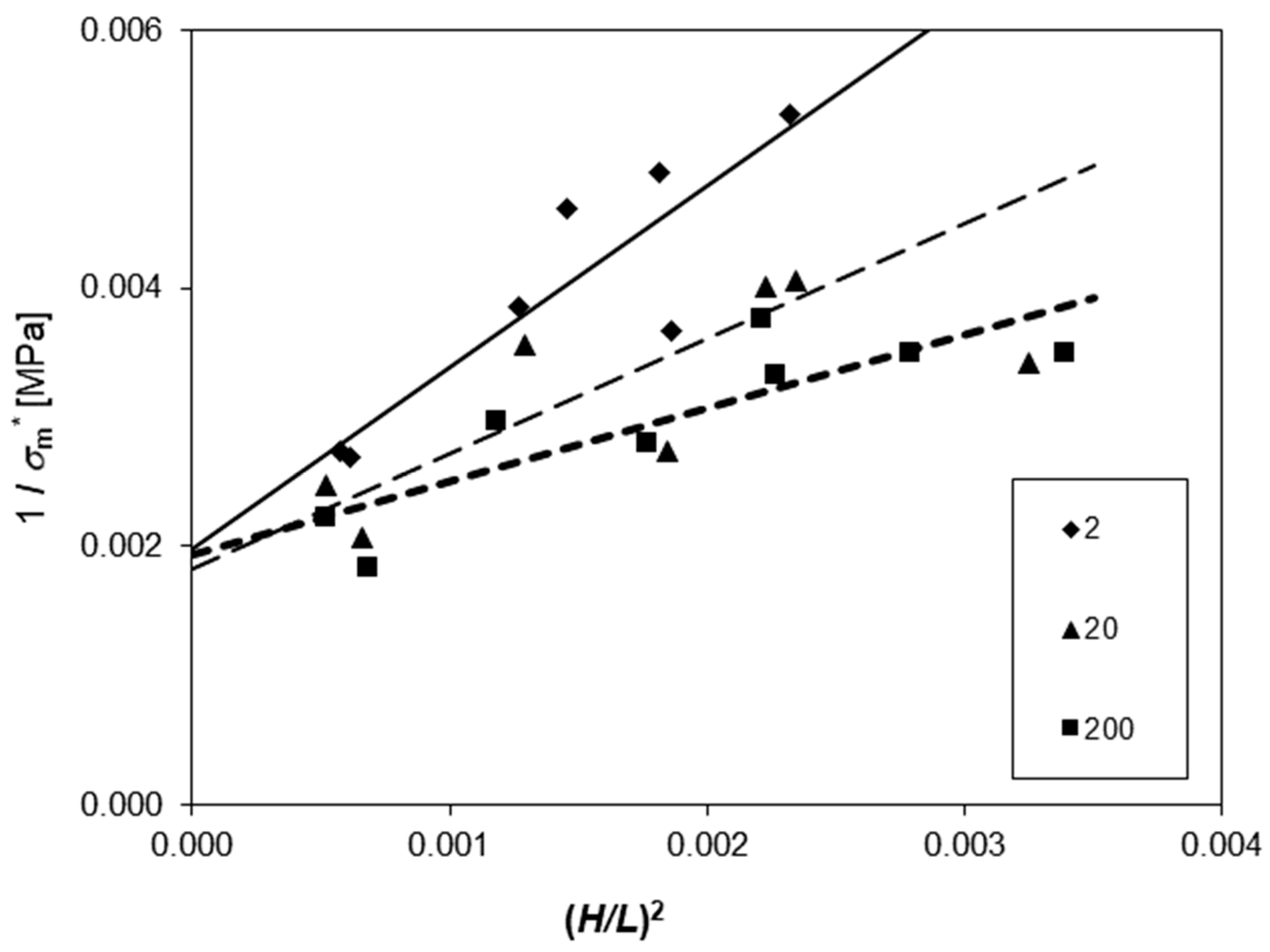
4.2. Displacement Rate
4.3. Unidirectional and Woven Fabrics
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davidovits, J. Chemistry of Geopolymeric systems, terminology. In Proceedings of the 2nd International Conference on Geopolymere, Sain-Quentin, France, 30 June—2 July 1999; pp. 9–22. [Google Scholar]
- Davidovits, J.; Sawyer, J.L. Early High-Strength Mineral Polymer. U.S. Patent 4,509,985, 9 April 1985. [Google Scholar]
- Davidovits, J. GEOPOLYMERS: Inorganic Polymeric New Materials. J. Therm. Anal. 1991, 37, 1633–1656. [Google Scholar] [CrossRef]
- Davidovits, J. Geopolymer—Fiber composites. In Geopolymer Chemistry & Applications; Joseph, D., Ed.; Geopolymer Institute: Saint-Quentin, France, 2008. [Google Scholar]
- Davidovits, N.; Davidovics, M.; Davidovits, J. Ceramic-ceramic composite material and production method. Composites 1991, 22, 4888311. [Google Scholar] [CrossRef]
- Davidovits, J. 30 Years of Successes and Failures in Geopolymer Applications—Market Trends and Potential breakthroughs. In Proceedings of the Geopolymer 2002 Conference, Melbourne, Australia, 28–29 October 2022; pp. 1–16. Available online: https://www.geopolymer.org/wp-content/uploads/30YearsGEOP.pdf (accessed on 15 July 2023).
- Davidovits, J. Geopolymer chemistry and sustainable Development—The Poly(sialate) terminologys: A very useful and simple model for the promotion and understanding of green-chemistry. In Proceedings of the Geopolymer 2005 World Congress, Saint-Quentin, France, 29 June–1 July 2005; Geopolymer Institute: Saint-Quentin, France, 2005; pp. 9–16. [Google Scholar]
- Lyon, R.E.; Balaguru, P.N.; Foden, A.; Sorathia, U.; Davidovits, J.; Davidovics, M. Fire resistant alumosilicate cemposites. Fire Mater. 1997, 21, 67–73. [Google Scholar] [CrossRef]
- Duxson, P.; Fernández-Jiménez, A.; Provis, J.; Lukey, G.; Palomo, A.; van Deventer, J. Geopolymer technology: The current state of the art. J. Mater. Sci. 2007, 42, 2917–2933. [Google Scholar] [CrossRef]
- Papakonstantinou, C.G.; Balaguru, P.; Lyon, R.E. Comparative study of high temperature composites. Compos. Part B Eng. 2001, 32, 637–649. [Google Scholar] [CrossRef]
- Papakonstantinou, C.G.; Balaguru, P.N. Use of Geopolymer Matrix for High Temperature Resistant Hybrid Laminates and Sandwich Panels. In Proceedings of the Geopolymer 2005 World Congress, Saint-Quentin, France, 29 June–1 July 2005; Geopolymer Institute: Saint-Quentin, France, 2005; pp. 201–207. Available online: http://books.google.com.vn/books?id=wIFo7L_zO8AC&pg=PA201&lpg=PA201&dq=Use+of+geopolymer+matrix+for+high+temperature+resistant+hybrid+laminates+and+sandwich+panels,+Geopolymer,+Green+Chemistry+and+Sustainable+Development+Solutions&source=bl&ots=Fk-tmE9Tb_ (accessed on 10 August 2023).
- Sheppar, L.M. Geopolymer Composites: A Ceramics Alternative to Polymer Matrices. In Proceedings of the The 105th Annual Meeting and Exposition of the American Ceramic Society, Nashville, TN, USA, 27–30 April 2003; Available online: http://composite.about.com/library/weekly/aa030529.htm (accessed on 10 August 2023).
- Bortnovsky, O.; Bezucha, P.; Dedeček, J.; Sobalík, Z.; Vodičková, V.; Kroisová, D.; Roubíček, P.; Urbanová, M. Properties of Phosphorus-Containing Geopolymer Matrix and Fiber-Reinforced Composite. Mech. Prop. Perform. Eng. Ceram. Compos. IV 2009, 283–299. [Google Scholar] [CrossRef]
- Bell, J.L.; Comrie, D.C.; Gordon, M.; Kriven, W.M. Graphite Fiber Reinforced Geopolymer Molds for Near Net Shape Casting of Molten Diferrous Silicide. In Proceedings of the GGC 2005: International Workshop On Geopolymers And Geopolymer Concrete, Perth, Australia, 28–29 September 2005; Curtin University of Technology: Bentley, WA, Australia, 2005. [Google Scholar]
- American Society for Testing & Materials. Standard Test Method for Flexural Properties of Continuous Fiber-Reinforced Advanced Ceramic Composites; ASTM: West Conshohocken, PA, USA, 2013; Volume 15. [Google Scholar]
- DIN V ENV 658-3:1993-02; Advanced Technical Ceramics—Mechanical Properties of Ceramic Composites at Room Temperature—Part 3: Determination of Flexural Strength. The European Committee for Standardisation: Bruxelles, Belgium, 1993.
- BS IN ISO 14125:1998; Fiber-Reinforced Plastic Composites—Determination of Flexural Properties. British Standard Institute: London, UK, 2003.
- Geopolymer Institute. Geopolymer Camp. Geopolymer Cement and Geopolymer Concrete—Geopolymer Institute. 2009. Available online: http://www.geopolymer.org/camp (accessed on 10 August 2023).
- EN ISO 14130; Plastic Composites Reinforced with Fibers—Determination of Effective Interlaminar Shear Strength by Short Beam Method. The International Organization for Standardization: London, UK, 1997.
- EN 13706-2; Reinforced Plastics Composites—Specifications for Pultruded Profiles—Method of Test and General Requirements. European Standard: Pilsen, Czech Republic, 2002.
- Tarnopolsky, Y.M.; Roze, A.V.; Polyakov, V.A. Shear effects in flexure of oriented glass-fiber laminates. Mech. Polim. 1965, 2, 38–46. (In Russian) [Google Scholar]
- Tarnopolsky, Y.M.; Roze, A.V. Specialties of Calculation of Reinforced Plastics Details; Zinatne Press: Riga, Latvia, 1969. (In Russian) [Google Scholar]
- Tarnopolsky, Y.M.; Kincis, T.Y. Static Test Methods for Composites (Translated from the Third, Revised and Supplemented Soviet Edition under the Editorship of George Lubin); Van Nostrand Reinhold Company: New York, NY, USA, 1985; pp. 285–298. [Google Scholar]
- Pernica, D.; Reis, P.; Ferreira, J.; Louda, P. Effect of test conditions on the bending strength of a geopolymer-reinforced composite. J. Mater. Sci. 2010, 45, 744–749. [Google Scholar] [CrossRef]
- Xiem, N.T.; Kroisová, D.; Louda, P.; Hung, T.D.; Rozek, Z. Effects of temperature and plasma treatment onmechanical properties of ceramic fibres. J. Achiev. Mater. Manuf. Eng. 2009, 37, 526–531. [Google Scholar]



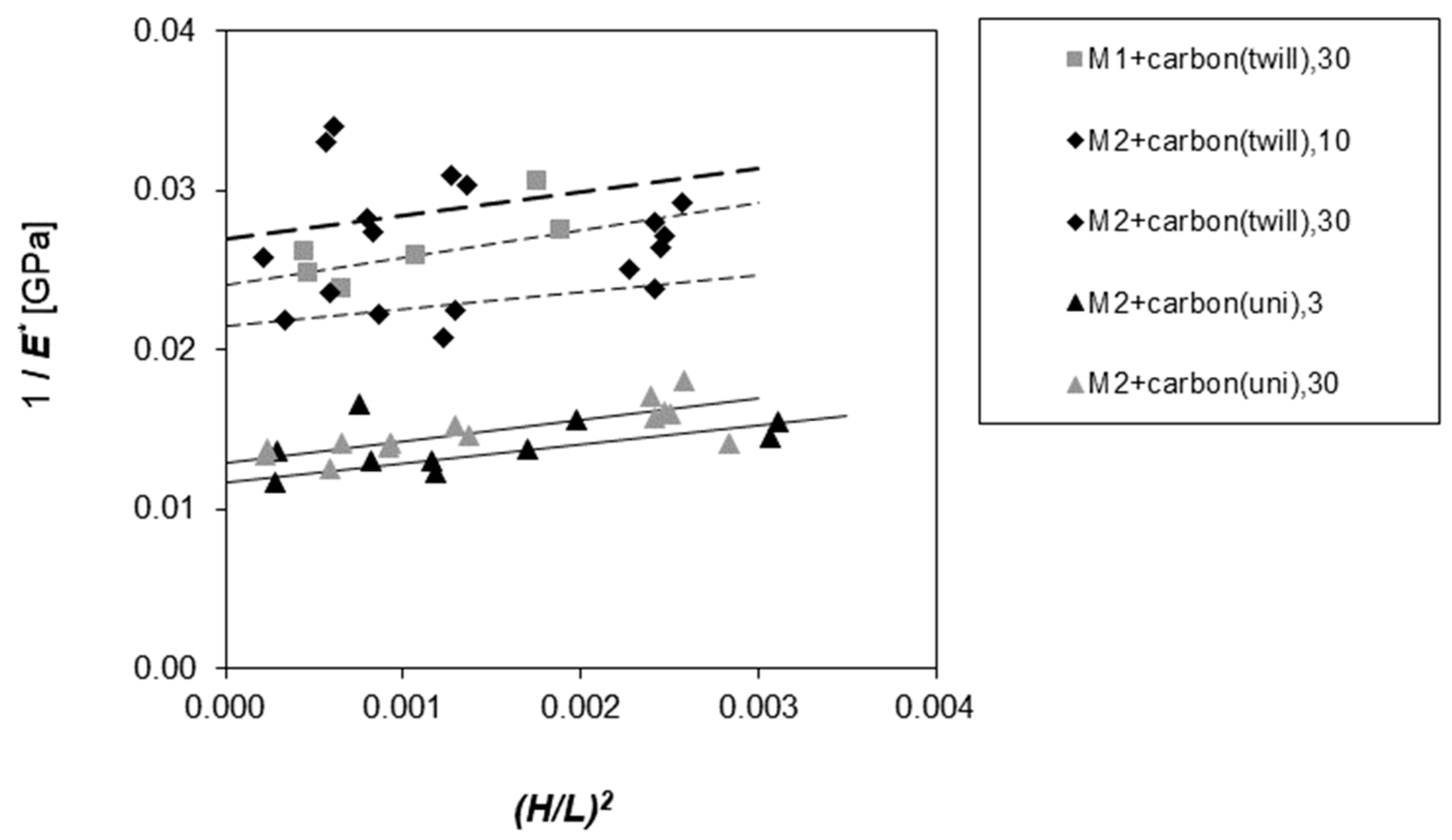
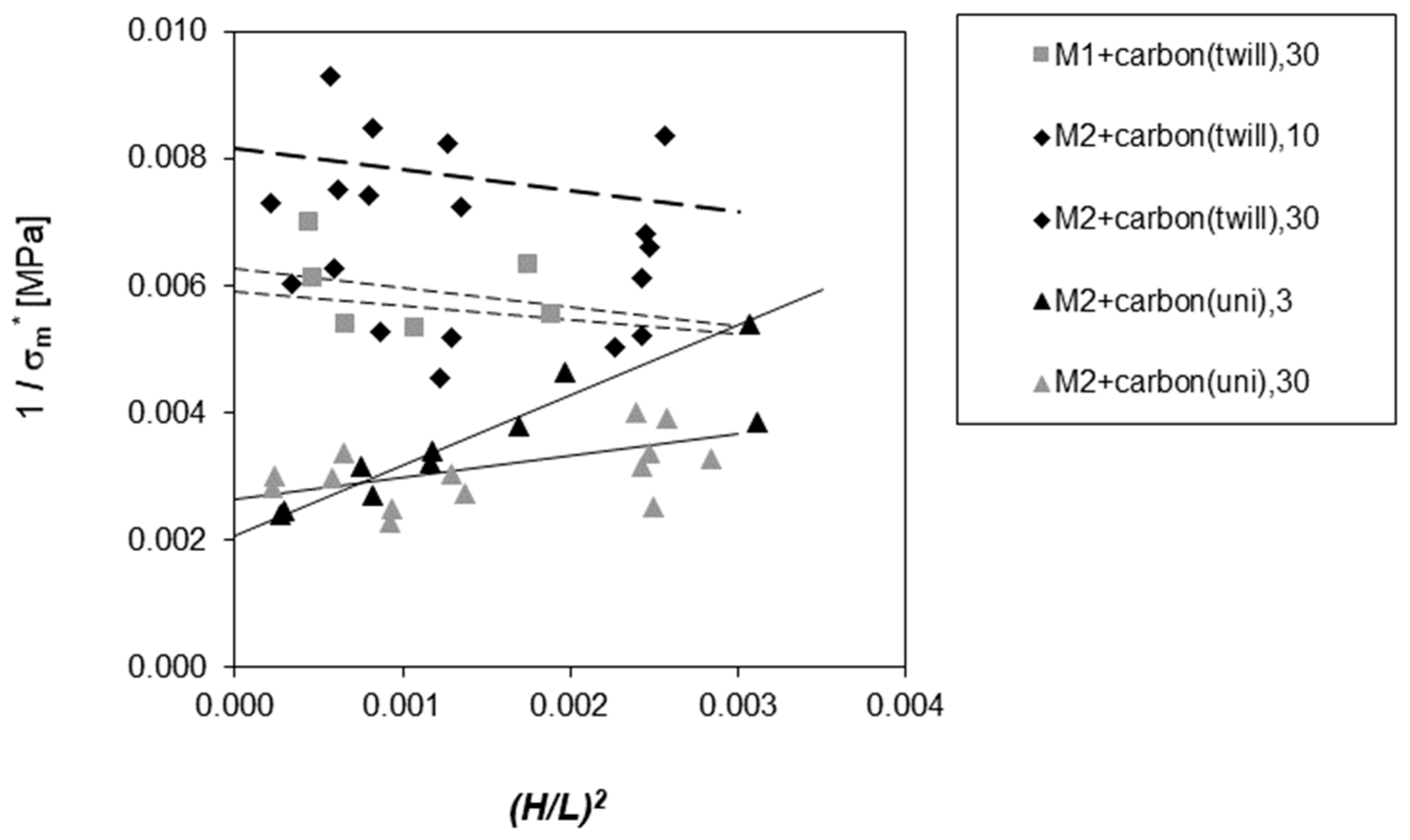


| Matrix | Laboratory | Flexural Modulus | Shear Modulus | Flexural Strength | |||
|---|---|---|---|---|---|---|---|
| E [GPa] | G [GPa] | E/G | σm[MPa] | ||||
| M2 | VUANCH | 109 ± 32 | ±29% | 0.76 | 143 | 631 ± 75 | ±12% |
| M2 | TUL | 111 ± 14 | ±13% | 0.73 | 152 | 571 ± 75 | ±13% |
| M1 | VUANCH | 96 ± 26 | ±27% | 0.35 | 278 | 316 ± 18 | ±6% |
| M1 | TUL | 128 ± 21 | ±17% | 0.33 | 392 | 323 ± 18 | ±5% |
| Matrix | Fiber | Flexural Modulus | Shear Modulus | Flexural Strength | Slope | Product | ||
|---|---|---|---|---|---|---|---|---|
| E [GPa] | G [GPa] | E/G | σm [MPa] | T [MPa] | P | ∏ | ||
| M1 | basalt | 58.1 ± 3.1 | 0.45 | 129 | 400 ± 29 | 3.27 | 0.18 | 1.06 |
| carbon | 179.5 ± 24.9 | 0.47 | 380 | 672 ± 68 | 2.95 | 0.28 | 1.66 | |
| E-glass | 61.1 ± 11.6 | 0.16 | 388 | 145 ± 14 | 0.94 | 0.42 | 2.53 | |
| M2 | basalt | 61.0 ± 4.0 | 0.50 | 122 | 306 ± 28 | 1.16 | 0.08 | 0.46 |
| carbon | 138.5 ± 10.7 | 0.81 | 171 | 649 ± 75 | 1.58 | 0.08 | 0.42 | |
| E-glass | 65.0 ± 5.2 | 0.46 | 142 | 276 ± 50 | 1.19 | 0.12 | 0.61 | |
| Speed | Flexural Modulus | Shear Module | Flexural Strength | Reciprocal Slope |
|---|---|---|---|---|
| [mm/min] | E [GPa] | G [GPa] | σm [MPa] | T [MPa] |
| 2 | 69.7 ± 6.5 | 0.7 | 505.2 ± 129.7 | 0.7 |
| 20 | 73.3 ± 10.2 | 0.5 | 546.0 ± 145.2 | 1.1 |
| 200 | 83.4 ± 6.3 | 0.2 | 518.1 ± 78.6 | 1.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran Doan, H.; Kroisova, D.; Bortnovsky, O. Size-Independent Flexure Test Technique for the Mechanical Properties of Geocomposites Reinforced by Unidirectional Fibers. Ceramics 2023, 6, 2053-2069. https://doi.org/10.3390/ceramics6040126
Tran Doan H, Kroisova D, Bortnovsky O. Size-Independent Flexure Test Technique for the Mechanical Properties of Geocomposites Reinforced by Unidirectional Fibers. Ceramics. 2023; 6(4):2053-2069. https://doi.org/10.3390/ceramics6040126
Chicago/Turabian StyleTran Doan, Hung, Dora Kroisova, and Oleg Bortnovsky. 2023. "Size-Independent Flexure Test Technique for the Mechanical Properties of Geocomposites Reinforced by Unidirectional Fibers" Ceramics 6, no. 4: 2053-2069. https://doi.org/10.3390/ceramics6040126
APA StyleTran Doan, H., Kroisova, D., & Bortnovsky, O. (2023). Size-Independent Flexure Test Technique for the Mechanical Properties of Geocomposites Reinforced by Unidirectional Fibers. Ceramics, 6(4), 2053-2069. https://doi.org/10.3390/ceramics6040126









