Thermoresponsive Effects in Droplet Size Distribution, Chemical Composition, and Antibacterial Effectivity in a Palmarosa (Cymbopogon martini) O/W Nanoemulsion
Abstract
1. Introduction
2. Materials and Methods
- (1)
- Analyse the thermoresponsive droplet size behaviour for a stable one-year 5% O/W NE of Palmarosa under heating and cooling cycles ranging from 10 °C to 50 °C.
- (2)
- Determine whether, under thermal cycles, there exists a hysteresis process for the characteristic and average diameters in the droplet size distribution.
- (3)
- Compare whether an NE exposed to repeated thermal cycles of heating and cooling in the range of 10 °C to 50 °C exhibits changes in its chemical composition.
- (4)
- Compare whether an NE exposed to repeated thermal cycles of heating and cooling in the range of 10 °C to 50 °C has altered antibacterial effectiveness.
2.1. Materials
2.1.1. Essential Oils, Surfactant, and Continuous Phase
2.1.2. Bacterial Strains
2.2. Methods
2.2.1. Nanoemulsion Preparation
Initial Preparation of the Emulsion
Ultrasonication Method
2.2.2. Composition Characterisation
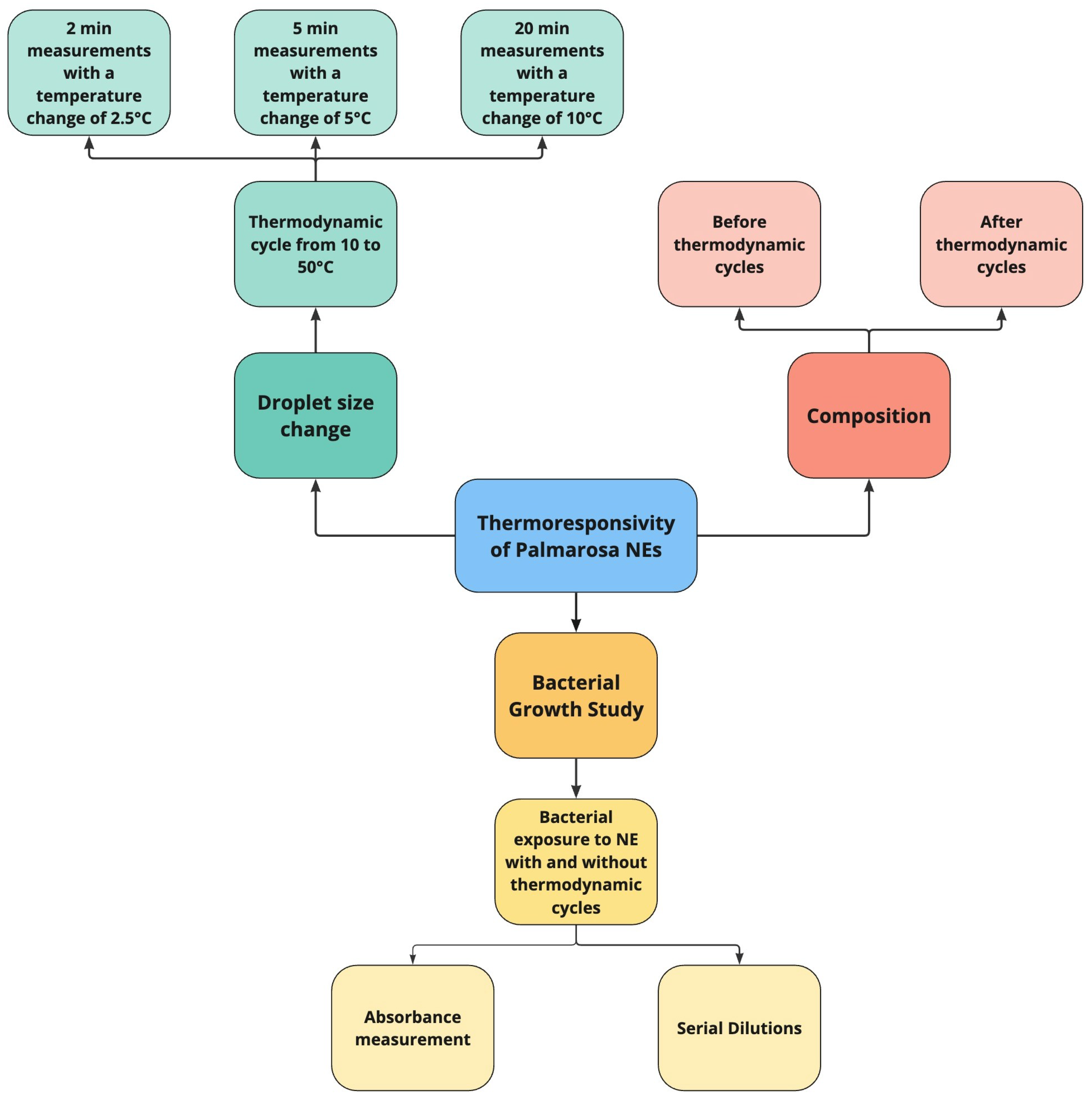
2.3. Droplet Size Thermoresponsivity and Hysteresis
2.3.1. Dynamic Light Scattering and Thermoresponsivity Tests
2.3.2. Polydispersity
2.3.3. Hysteresis Analysis
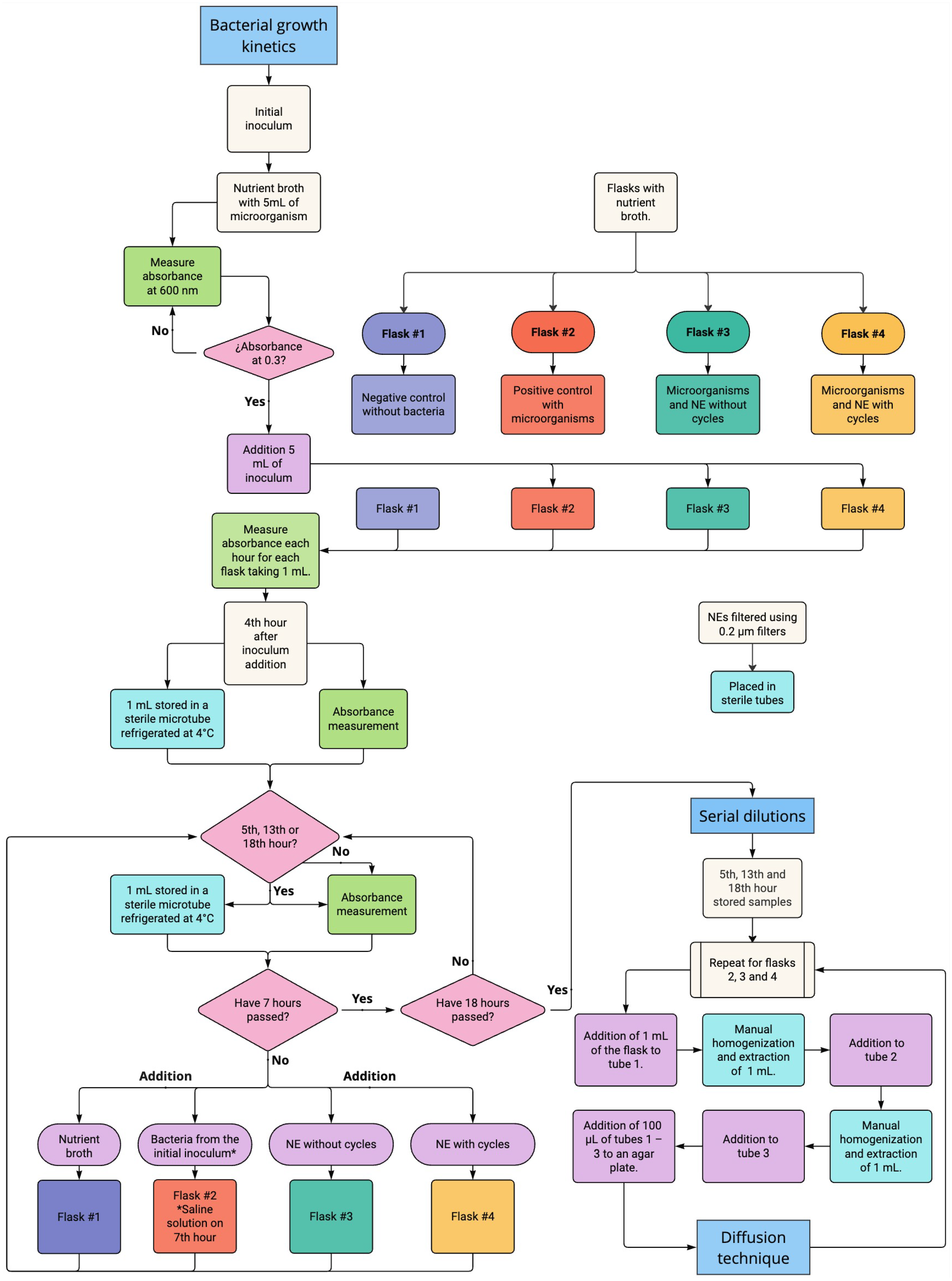
2.4. Bacterial Growth Kinetics and Serial Dilutions
2.4.1. Method of Optical Density Measurement During Growing
2.4.2. Method of Spread Plate in Serial Dilutions
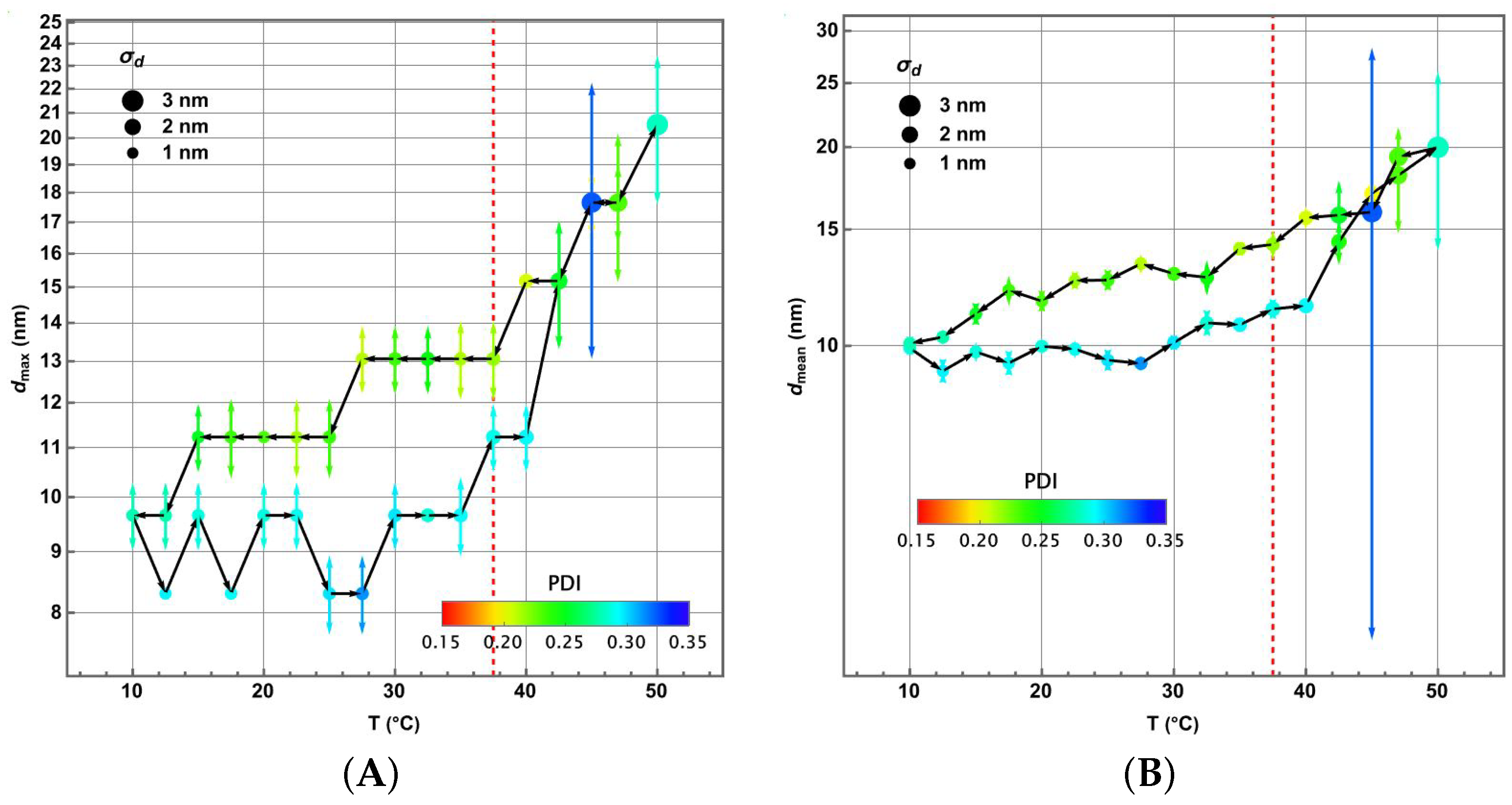
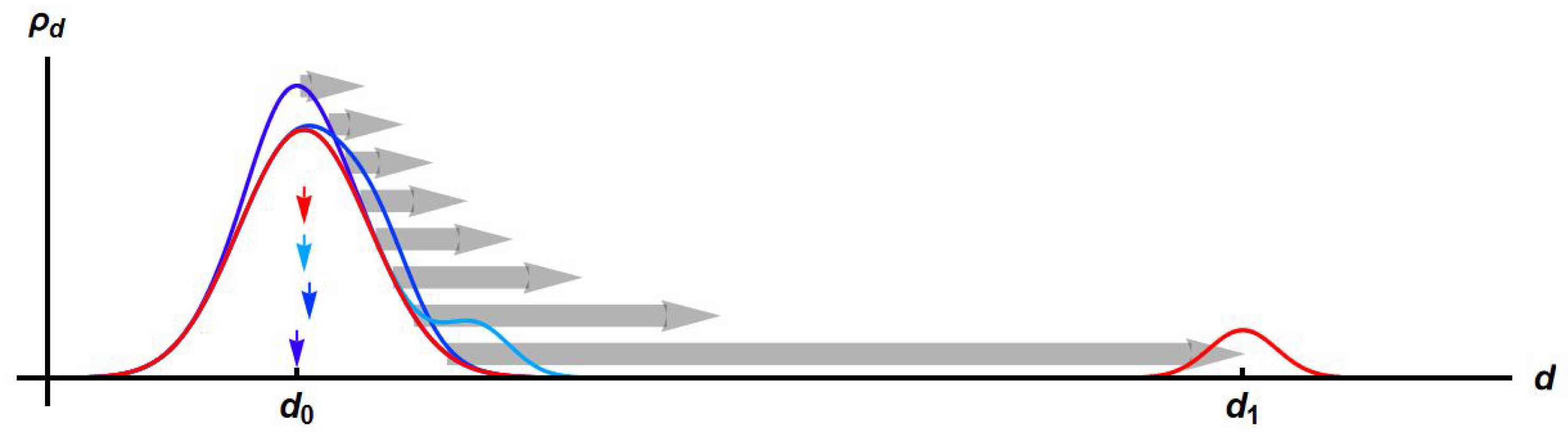
3. Effect of Temperature on Physical Properties
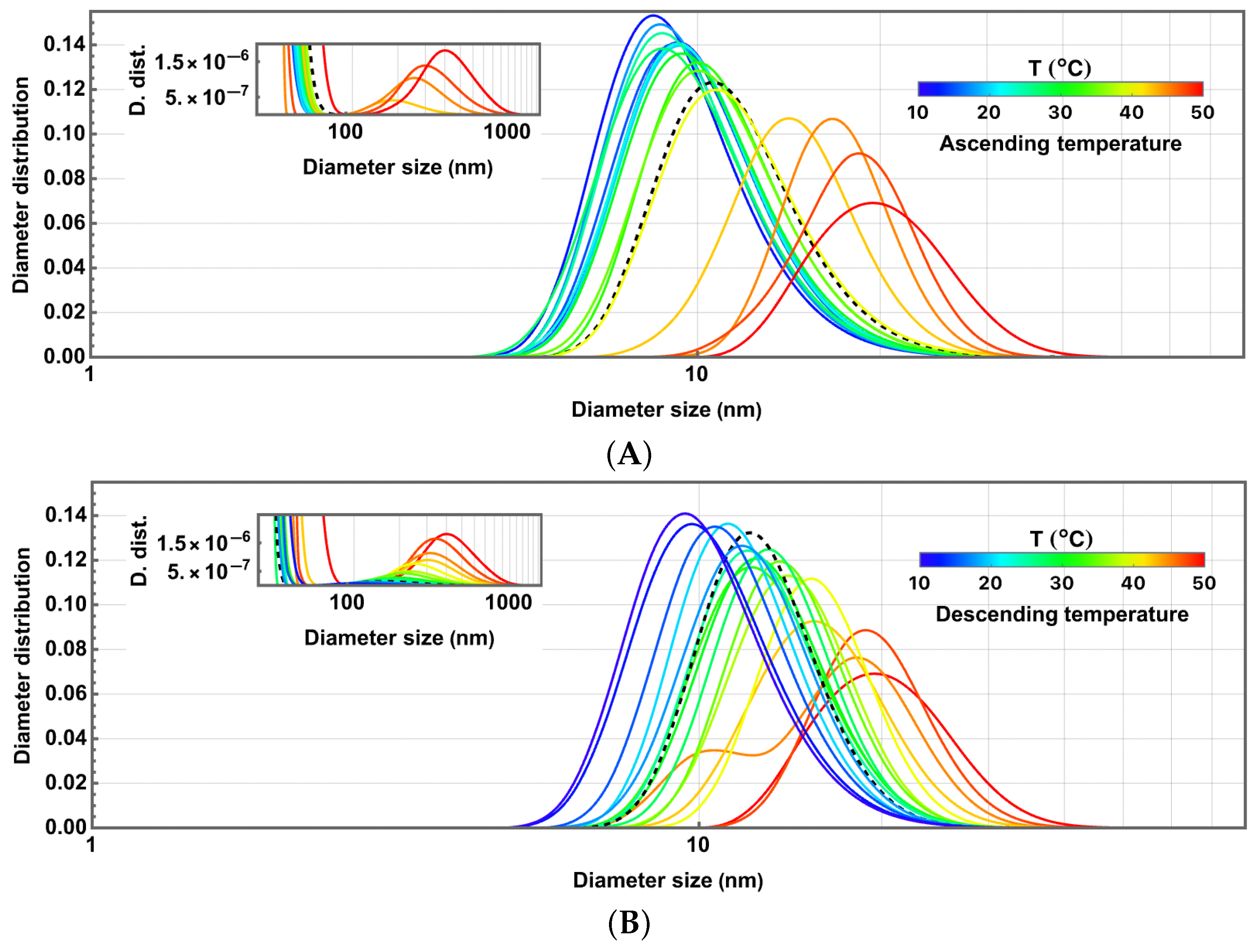
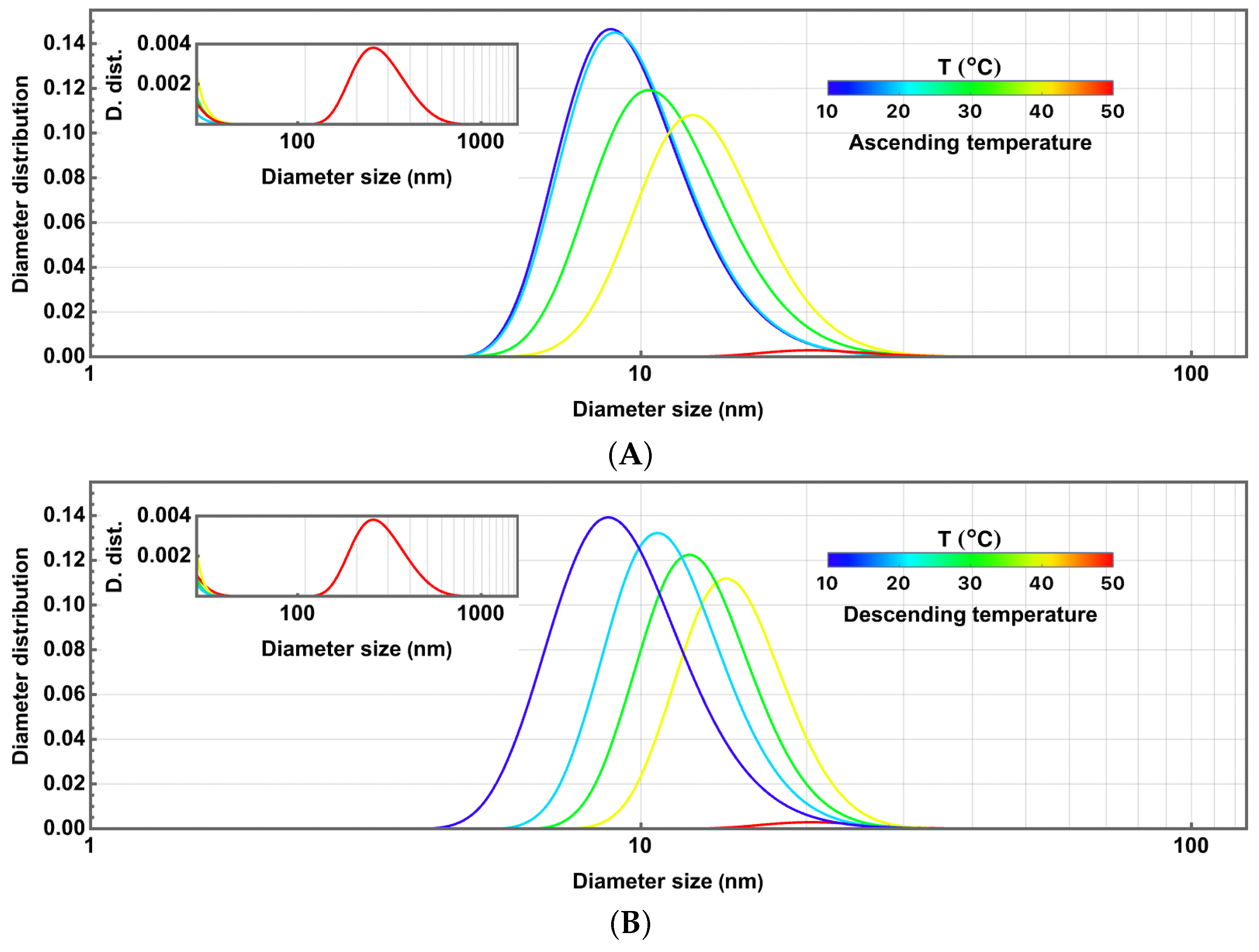
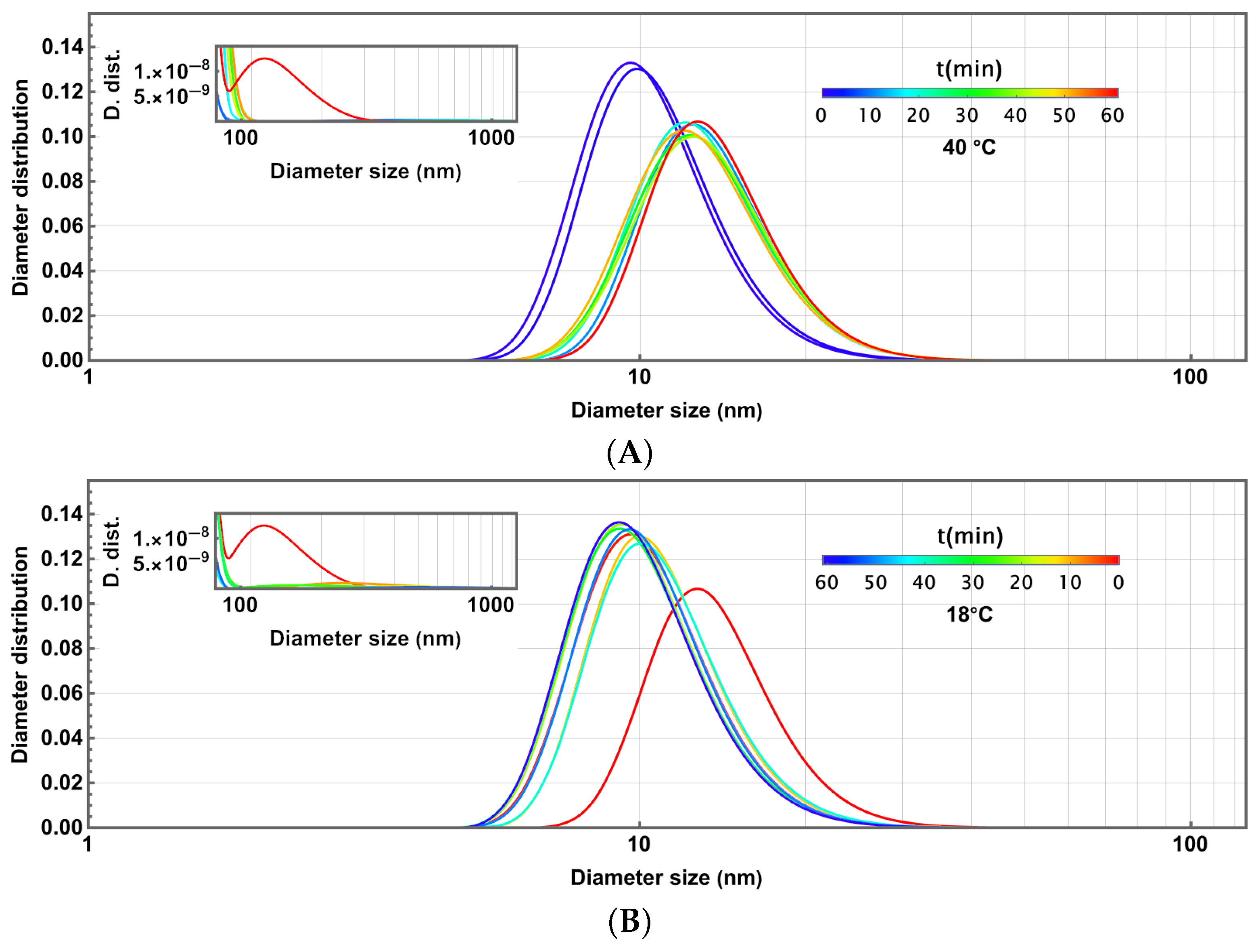
3.1. Initial Thermoresponsive Droplet Size Analysis
3.2. Thermoresponsivity and Fast Changes in Temperature
3.3. Dynamical Thermoresponsivity Under Maintained Changes in Temperature
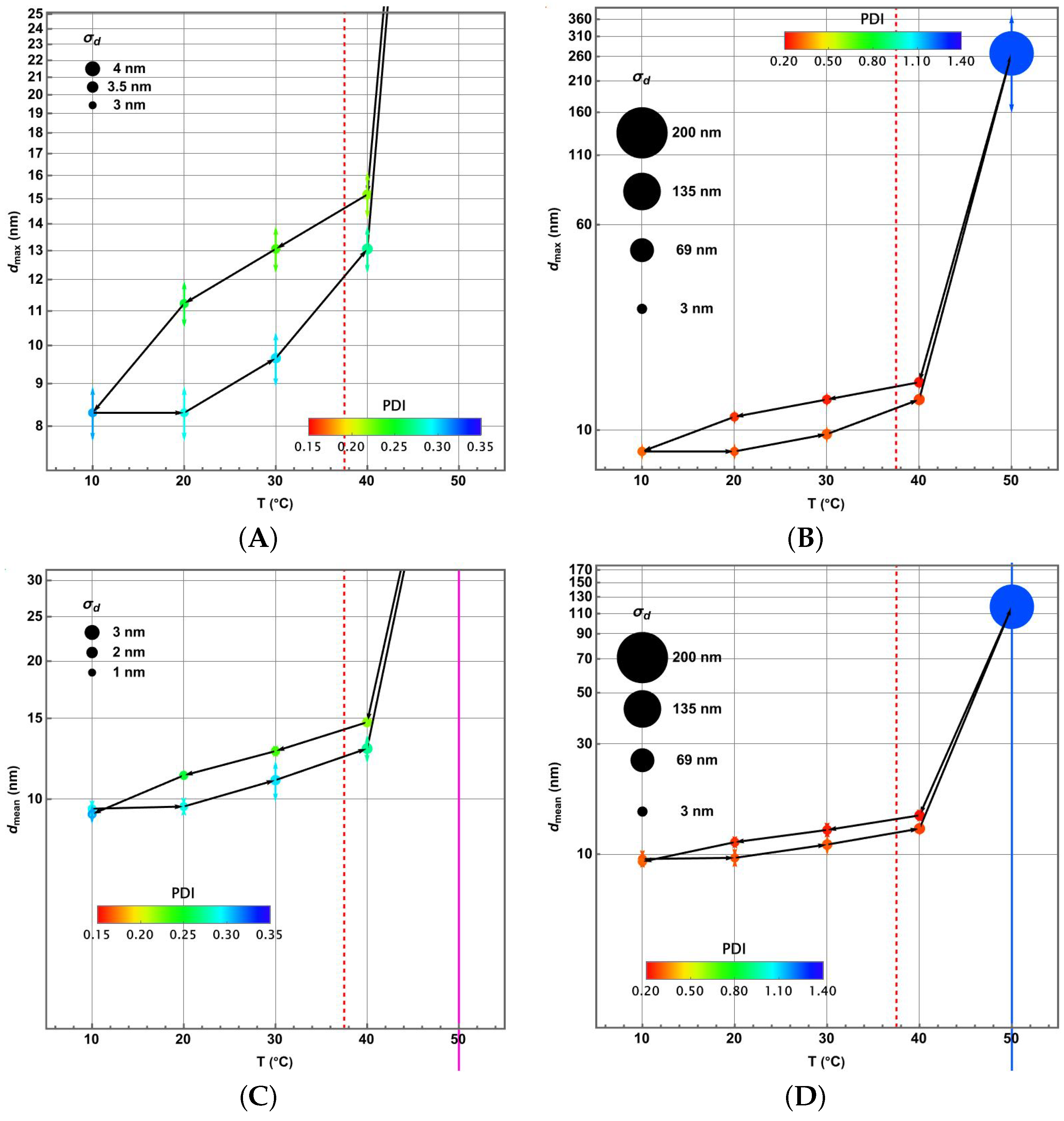
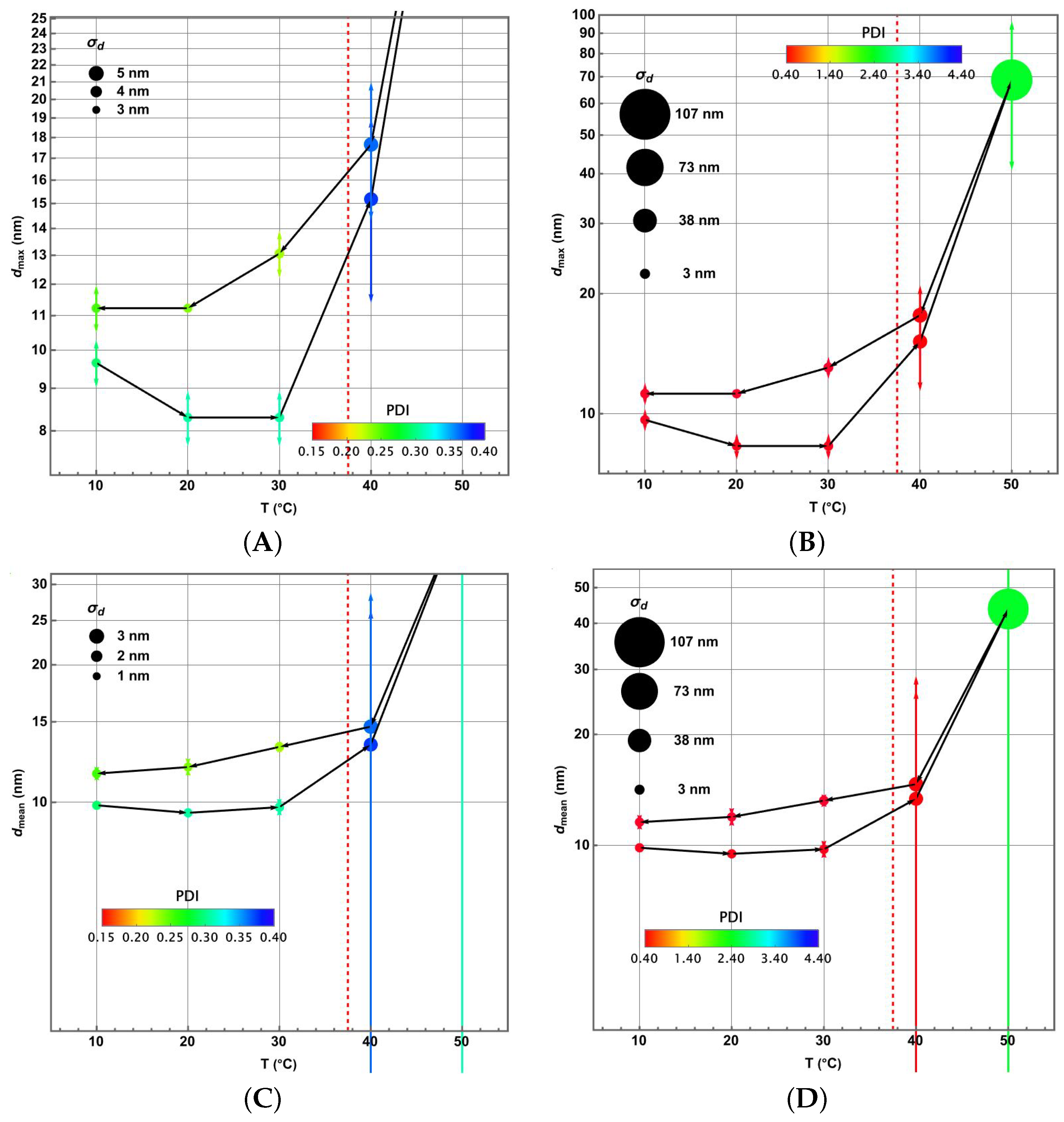
3.4. Piecewise Hysteresis Diagrams for Droplet Sizes
3.5. Dynamical Process Observed on Droplet Sizes Under a Maintained Raising or Lowering of Temperature
3.6. Some Remarks About Polydispersity Through the Heating and Cooling Cycles
3.7. Statistical Analysis of Meaningful Differences in Physical Parameters Characterising Droplet Size Distributions
3.8. Discussion: Droplet Size Thermoresponsivity
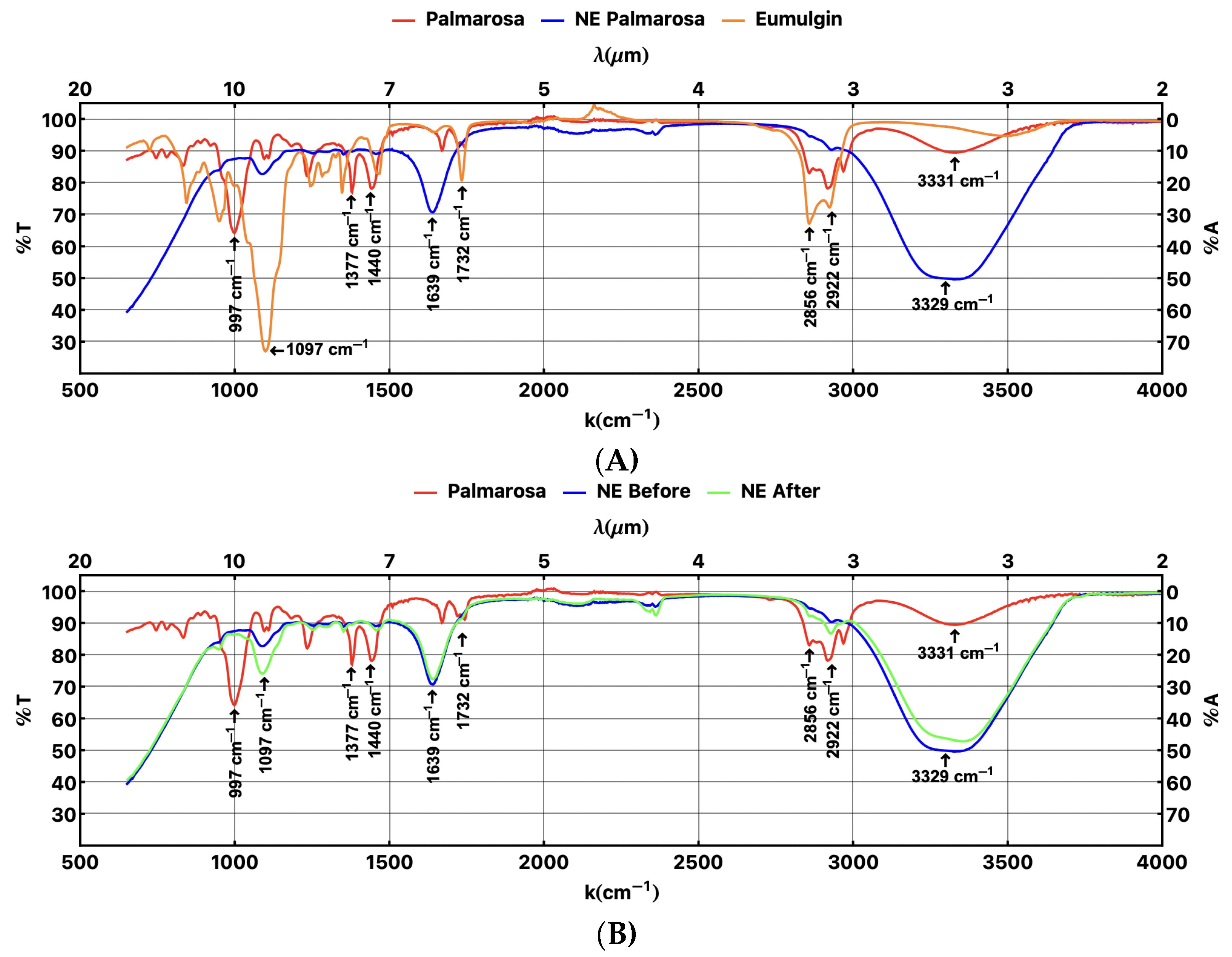
4. Comparative Chemical Composition
4.1. Initial Composition Analysis
4.2. Effect of Thermal Cycles on Composition of NEs
4.3. Discussion: Comparative Composition Spectrum
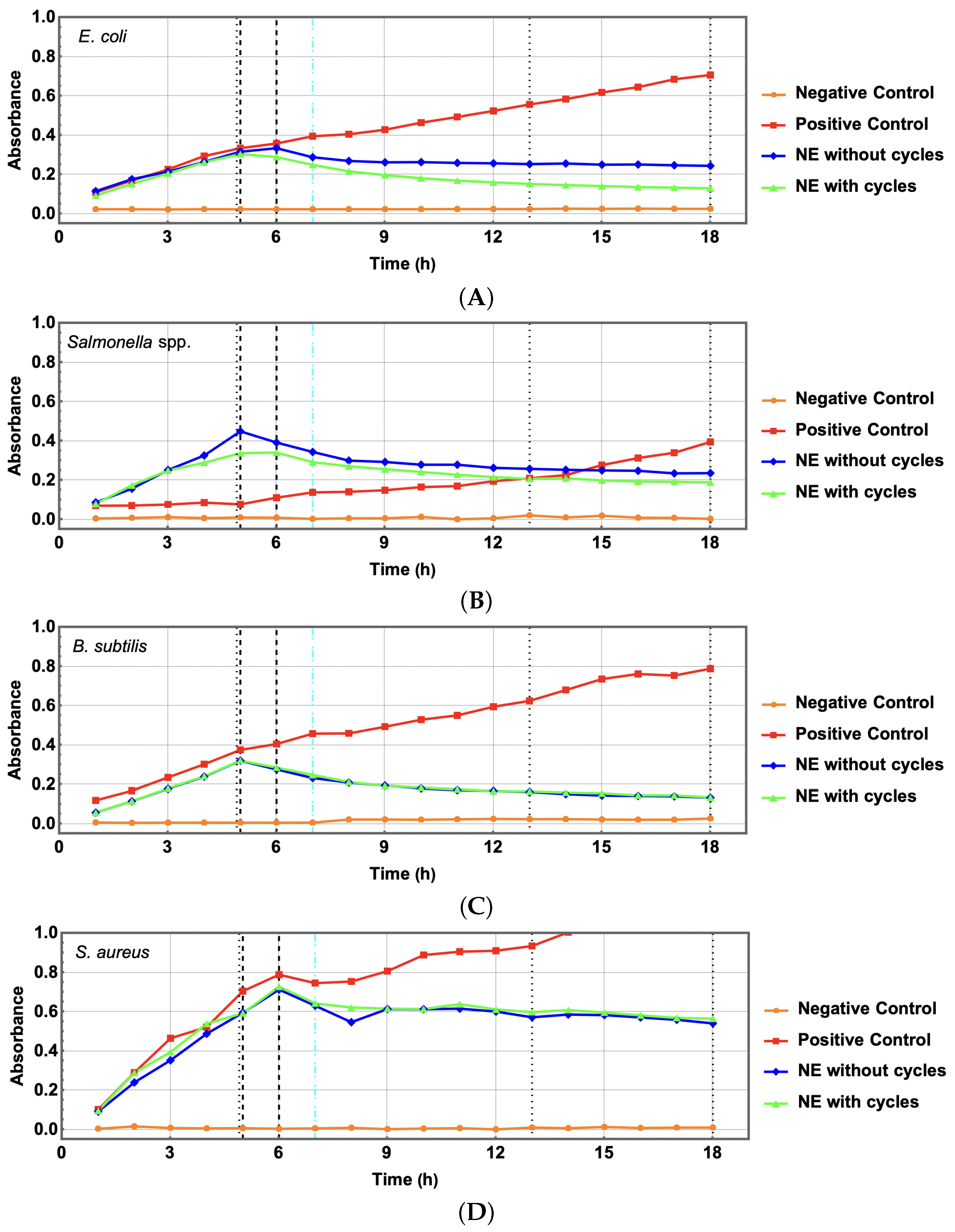
5. Preservation of Antibacterial Features
5.1. Comparative Antibacterial Effectiveness: Bacterial Growth Kinetics
5.2. Statistical Analysis of Meaningful Differences in OD for NE Treatments
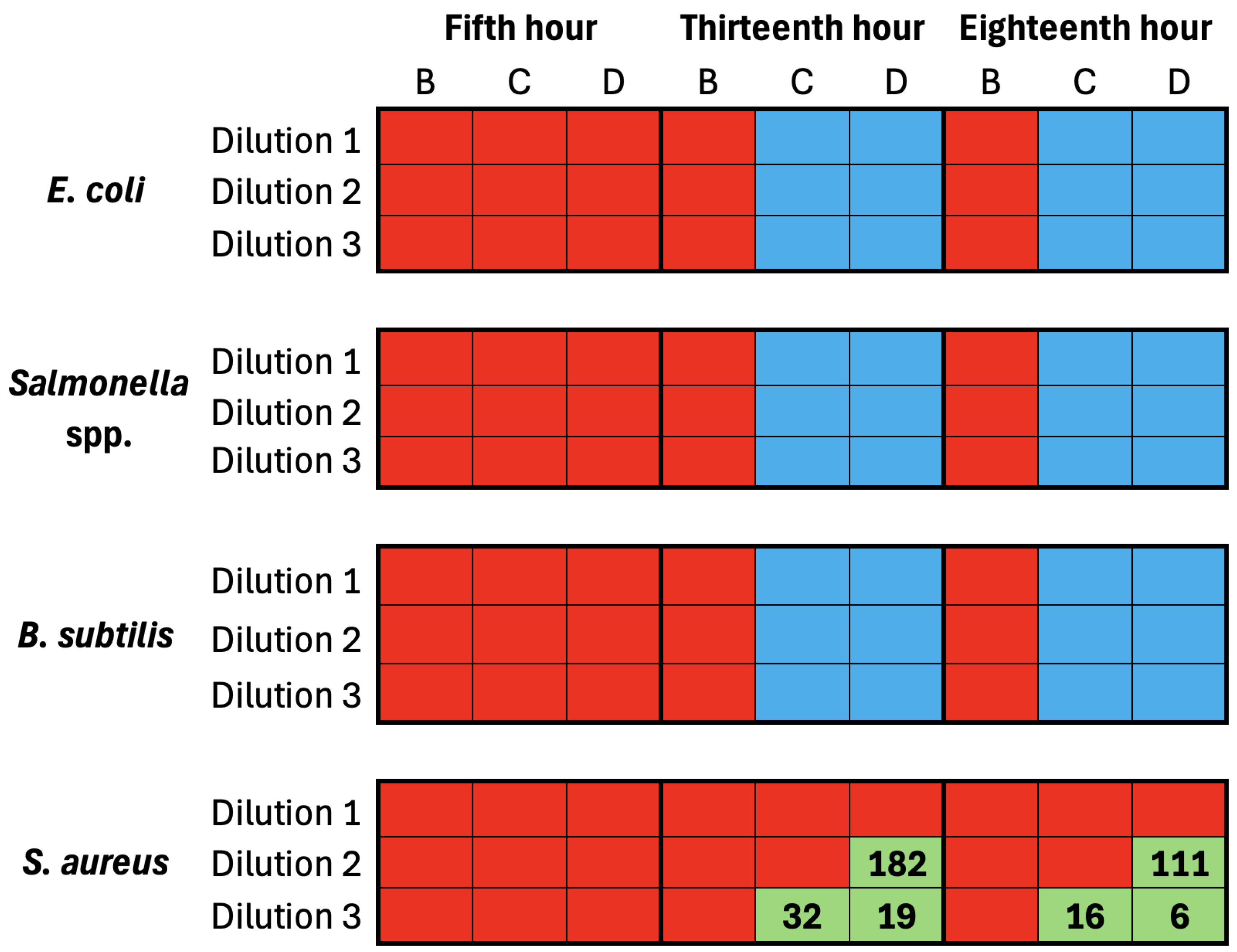
5.3. Comparative Antibacterial Effectiveness: Bacterial Colonies’ Counting
5.4. Discussion: Conserved Antibacterial Features
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AFM | Atomic Force Microscopy |
| ATR | Attenuated Total Reflectance |
| CFUs | Uncountable Colony-forming Units |
| CPI | Catastrophic Phase Inversion |
| DLS | Dynamic Light Scattering |
| EOs | Essential Oils |
| NEs | Nanoemulsions |
| OD | Optical Density |
| O/W | Oil in Water |
| PDI | Polydispersity Index |
| SP | Spread-Plate |
| TPI | Transitional Phase Inversion |
| WHO | World Health Organization |
| W/O | Water in Oil |
Appendix A. Processed OD Values in the Study of Bacterial Kinetics
| Measure | Time (min) | Ascending Temperature T (°C) | Descending Temperature T (°C) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 50 | 40 | 30 | 20 | 10 | ||
| Max. (nm) | 2 | 9.65 ± 0.64 | 9.65 ± 0.64 | 9.65 ± 0.64 | 11.20 ± 0.74 | 20.50 ± 2.93 | 15.20 ± 0.00 | 13.10 ± 0.86 | 11.20 ± 0.00 | 9.65 ± 0.64 |
| 5 | 8.30 ± 0.64 | 8.30 ± 0.64 | 9.65 ± 0.74 | 13.10 ± 0.86 | 267.00 ± 109.00 | 15.20 ± 1.00 | 13.10 ± 0.86 | 11.20 ± 0.74 | 8.30 ± 0.64 | |
| 20 | 9.65 ± 0.64 | 8.30 ± 0.64 | 8.30 ± 0.64 | 15.20 ± 3.79 | 68.70 ± 27.90 | 17.70 ± 3.35 | 13.10 ± 0.86 | 11.20 ± 0.00 | 11.20 ± 0.74 | |
| (nm) | 2 | 9.92 ± 0.22 | 9.99 ± 0.28 | 10.10 ± 0.19 | 11.50 ± 0.37 | 20.00 ± 6.05 | 15.60 ± 0.62 | 12.90 ± 0.43 | 11.70 ± 0.10 | 10.10 ± 0.21 |
| 5 | 9.53 ± 0.04 | 9.64 ± 0.01 | 11.00 ± 1.17 | 12.90 ± 0.96 | 118.00 ± 16,500.00 | 14.70 ± 0.45 | 12.70 ± 0.23 | 11.30 ± 0.35 | 9.27 ± 0.48 | |
| 20 | 9.85 ± 0.30 | 9.48 ± 0.32 | 9.76 ± 0.03 | 13.40 ± 13.00 | 43.80 ± 1730.00 | 14.60 ± 14.20 | 13.20 ± 0.24 | 11.90 ± 0.02 | 11.60 ± 0.13 | |
| (nm) | 2 | 2.84 | 2.87 | 3.01 | 3.38 | 5.62 | 3.21 | 3.02 | 2.71 | 2.81 |
| 5 | 2.78 | 2.78 | 3.29 | 3.52 | 148.00 | 3.23 | 2.97 | 2.87 | 2.87 | |
| 20 | 2.89 | 2.90 | 2.98 | 5.02 | 107.00 | 5.33 | 3.07 | 2.88 | 2.93 | |
| PDI | 2 | 0.29 | 0.29 | 0.30 | 0.29 | 0.28 | 0.21 | 0.23 | 0.23 | 0.28 |
| 5 | 0.29 | 0.29 | 0.30 | 0.27 | 1.26 | 0.22 | 0.23 | 0.25 | 0.31 | |
| 20 | 0.29 | 0.31 | 0.31 | 0.38 | 2.45 | 0.36 | 0.23 | 0.24 | 0.25 | |
Appendix B. Diagrammatic Description for the SP and the Serial Dilution Methods Followed in the Antibacterial Study
Appendix C. Processed OD Values in the Study of Bacterial Kinetics
| Bacteria | E. coli | Salmonella spp. | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hour | A | B | C | D | A | B | C | D | |
| 1 | 0.023 | 0.109 | 0.115 | 0.093 | 0.005 | 0.070 | 0.087 | 0.080 | |
| 2 | 0.023 | 0.169 | 0.176 | 0.152 | 0.008 | 0.071 | 0.157 | 0.174 | |
| 3 | 0.022 | 0.226 | 0.214 | 0.205 | 0.012 | 0.076 | 0.252 | 0.250 | |
| 4 | 0.023 | 0.294 | 0.264 | 0.262 | 0.007 | 0.086 | 0.326 | 0.289 | |
| 5 | 0.023 | 0.334 | 0.316 | 0.304 | 0.010 | 0.077 | 0.449 | 0.338 | |
| 6 | 0.023 | 0.358 | 0.334 | 0.289 | 0.009 | 0.111 | 0.392 | 0.341 | |
| 7 | 0.023 | 0.395 | 0.288 | 0.249 | 0.003 | 0.138 | 0.344 | 0.292 | |
| 8 | 0.023 | 0.405 | 0.269 | 0.216 | 0.006 | 0.141 | 0.300 | 0.271 | |
| 9 | 0.023 | 0.428 | 0.262 | 0.197 | 0.006 | 0.149 | 0.293 | 0.256 | |
| 10 | 0.023 | 0.464 | 0.263 | 0.181 | 0.013 | 0.165 | 0.279 | 0.242 | |
| 11 | 0.024 | 0.493 | 0.259 | 0.169 | 0.001 | 0.170 | 0.279 | 0.228 | |
| 12 | 0.024 | 0.524 | 0.257 | 0.160 | 0.006 | 0.195 | 0.263 | 0.216 | |
| 13 | 0.024 | 0.557 | 0.253 | 0.152 | 0.021 | 0.210 | 0.258 | 0.207 | |
| 14 | 0.026 | 0.584 | 0.256 | 0.146 | 0.010 | 0.226 | 0.253 | 0.210 | |
| 15 | 0.025 | 0.618 | 0.250 | 0.141 | 0.019 | 0.277 | 0.250 | 0.199 | |
| 16 | 0.026 | 0.645 | 0.251 | 0.136 | 0.009 | 0.313 | 0.248 | 0.193 | |
| 17 | 0.025 | 0.685 | 0.247 | 0.133 | 0.008 | 0.340 | 0.235 | 0.192 | |
| 18 | 0.025 | 0.707 | 0.244 | 0.130 | 0.003 | 0.395 | 0.236 | 0.189 | |
| Bacteria | B. subtilis | S. aureus | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hour | A | B | C | D | A | B | C | D | |
| 1 | 0.007 | 0.119 | 0.057 | 0.057 | 0.004 | 0.102 | 0.092 | 0.096 | |
| 2 | 0.005 | 0.168 | 0.115 | 0.115 | 0.016 | 0.290 | 0.240 | 0.289 | |
| 3 | 0.006 | 0.235 | 0.178 | 0.180 | 0.008 | 0.465 | 0.353 | 0.395 | |
| 4 | 0.006 | 0.302 | 0.239 | 0.241 | 0.006 | 0.522 | 0.488 | 0.539 | |
| 5 | 0.006 | 0.375 | 0.320 | 0.321 | 0.007 | 0.705 | 0.595 | 0.593 | |
| 6 | 0.006 | 0.405 | 0.276 | 0.285 | 0.004 | 0.789 | 0.713 | 0.728 | |
| 7 | 0.006 | 0.458 | 0.232 | 0.248 | 0.006 | 0.746 | 0.631 | 0.643 | |
| 8 | 0.022 | 0.459 | 0.209 | 0.212 | 0.009 | 0.754 | 0.547 | 0.622 | |
| 9 | 0.022 | 0.493 | 0.194 | 0.193 | 0.002 | 0.807 | 0.614 | 0.616 | |
| 10 | 0.021 | 0.529 | 0.180 | 0.184 | 0.005 | 0.889 | 0.613 | 0.614 | |
| 11 | 0.023 | 0.551 | 0.171 | 0.175 | 0.007 | 0.906 | 0.616 | 0.639 | |
| 12 | 0.025 | 0.595 | 0.167 | 0.166 | 0.001 | 0.911 | 0.601 | 0.612 | |
| 13 | 0.024 | 0.625 | 0.162 | 0.165 | 0.010 | 0.935 | 0.572 | 0.598 | |
| 14 | 0.024 | 0.680 | 0.151 | 0.159 | 0.007 | 1.005 | 0.586 | 0.609 | |
| 15 | 0.022 | 0.736 | 0.144 | 0.155 | 0.013 | 1.050 | 0.583 | 0.596 | |
| 16 | 0.021 | 0.762 | 0.142 | 0.145 | 0.008 | 1.090 | 0.571 | 0.582 | |
| 17 | 0.021 | 0.754 | 0.140 | 0.145 | 0.010 | 1.104 | 0.559 | 0.569 | |
| 18 | 0.027 | 0.789 | 0.133 | 0.134 | 0.010 | 1.165 | 0.541 | 0.565 | |
Appendix D. Agar Plates of the Spread-Plate Diffusion Process

Appendix E. Two-Factor ANOVA Test with Tukey’s Post-Test for the Physical Parameters’ Analysis and for Bacterial Growth and Inhibition by NEs
| Physical Parameter | Factor | ANOVA Test p-Value | Tukey’s Post-Test Mean Differences Found |
|---|---|---|---|
| Max. | Waiting time | 0.403 | None |
| Temperature | 0.109 | None | |
| Waiting time | 0.402 | None | |
| Temperature | 0.039 | 1–5, 2–5, 3–5, 5–9 | |
| Waiting time | 0.381 | None | |
| Temperature | 0.009 | 1–5, 2–5, 3–5, 4–5, 5–6, 5–7, 5–8, 5–9 | |
| PDI | Waiting time | 0.305 | None |
| Temperature | 0.034 | 5–6, 5–7, 5–8, 5–9 |
| Bacteria | Factor | ANOVA Test p-Value | Tukey’s Post-Test Mean Differences Found |
|---|---|---|---|
| E. coli | NE | 1–2 | |
| Hour | 0.001 | 6–9, …, 6–18, 7–18 | |
| Salmonella spp. | NE | 1–2 | |
| Hour | 6–10, 7–10, 8–10, 10–14 | ||
| B. subtilis | NE | 1–2 | |
| Hour | All pairs | ||
| S. aureus | NE | 1–2 | |
| Hour | 6–7, …, 6–18, 7–16, …, 7–18, 9–18, 10–18, 11–17, 11–18, 12–18 |
References
- Mason, G.; Wilking, J.; Meleson, K.; Chang, C.; Graves, S. Nanoemulsions: Formation, structure, and physical properties. J. Phys. Condens. Matter 2006, 18, R635. [Google Scholar] [CrossRef]
- Ozogul, Y.; Karsli, G.T.; Durmuş, M.; Yazgan, H.; Oztop, H.M.; McClements, D.J.; Ozogul, F. Recent developments in industrial applications of nanoemulsions. Adv. Colloid Interface Sci. 2022, 304, 102685. [Google Scholar] [CrossRef]
- Weisany, W.; Yousefi, S.; Tahir, N.A.-R.; Golestanehzadeh, N.; McClements, D.J.; Adhikari, B.; Ghasemlou, M. Targeted delivery and controlled released of essential oils using nanoencapsulation: A review. Adv. Colloid Interface Sci. 2022, 303, 102655. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, C.; Wang, H.; Chen, C.; Teng, H.; Xiao, J.; Chen, L. Emulsion and its application in the food field: An update review. eFood 2023, 4, e102. [Google Scholar] [CrossRef]
- Krishnamoorthy, R.; Athinarayanan, J.; Periasamy, V.S.; Adisa, A.R.; Al-Shuniaber, M.A.; Gassem, M.A.; Alshatwi, A.A. Antimicrobial activity of nanoemulsion on drug-resistant bacterial pathogens. Microb. Pathog. 2018, 120, 85–96. [Google Scholar] [CrossRef]
- Dey, D.; Chowdhury, S.; Sen, R. Insight into recent advances on nanotechnology-mediated removal of antibiotic resistant bacteria and genes. J. Water Process. Eng. 2023, 52, 103535. [Google Scholar] [CrossRef]
- Mba, I.E.; Nweze, E.I. Nanoparticles as therapeutic options for treating multidrug-resistant bacteria: Research progress, challenges, and prospects. World J. Microbiol. Biotechnol. 2021, 37, 108. [Google Scholar] [CrossRef]
- Nazzaro, F.; Fratianni, F.; Martino, L.D.; Coppola, R.; Feo, V.D. Effect of Essential Oils on Pathogenic Bacteria. Pharmaceuticals 2013, 6, 1451–1474. [Google Scholar] [CrossRef]
- Rodrigue, K.C.T.; Djouhou, M.C.; Koudoro, Y.A.; Dahouenon-Ahoussi, E.; Avlessi, F.; Koko, C.; Sohounhloue, D.; Simal-Gandara, J. Essential oils as natural antioxidants for the control of food preservation. Food Chem. Adv. 2023, 2, 100312. [Google Scholar] [CrossRef]
- Santamarta, S.; Aldavero, A.C.; Ángeles Rojo, M. Antibacterial Properties of Cymbopogon martinii Essential Oil Against Bacillus subtillis Food Industry Pathogen. Proceedings 2020, 66, 1. [Google Scholar] [CrossRef]
- Castro, J.C.; Pante, G.C.; de Souza, D.S.; Pires, T.Y.; Miyoshi, J.H.; Garcia, F.P.; Nakamura, C.V.; Mulati, A.C.N.; Mossini, S.A.G.; Junior, M.M.; et al. Molecular inclusion of Cymbopogon martinii essential oil with β-cyclodextrin as a strategy to stabilize and increase its bioactivity. Food Hydrocoll. Health 2022, 2, 100066. [Google Scholar] [CrossRef]
- Wei, S.M.; Zhao, X.; Yu, J.; Yin, S.J.; Liu, M.J.; Bo, R.N.; Li, J.G. Characterization of tea tree oil nanoemulsion and its acute and subchronic toxicity. Regul. Toxicol. Pharmacol. 2021, 124, 104999. [Google Scholar] [CrossRef]
- Qi, J.; Gong, M.; Zhang, R.; Song, Y.; Liu, Q.; Zhou, H.; Wang, J.; Mei, Y. Evaluation of the antibacterial effect of tea tree oil on Enterococcus faecalis and biofilm in vitro. J. Ethnopharmacol. 2021, 281, 114566. [Google Scholar] [CrossRef] [PubMed]
- Lira, M.H.P.D.; de Andrade Júnior, F.P.; Moraes, G.F.Q.; da Silva Macena, G.; de Oliveira Pereira, F.; Lima, I.O. Antimicrobial activity of geraniol: An integrative review. J. Essent. Oil Res. 2020, 32, 187–197. [Google Scholar] [CrossRef]
- Aljabri, N.M.; Shi, N.; Cavazos, A. Nanoemulsion: An emerging technology for oilfield applications between limitations and potentials. J. Pet. Sci. Eng. 2022, 208, 109306. [Google Scholar] [CrossRef]
- McClements, D.J. Advances in edible nanoemulsions: Digestion, bioavailability, and potential toxicity. Prog. Lipid Res. 2021, 81, 101081. [Google Scholar] [CrossRef]
- Czerniel, J.; Gostyńska, A.; Jańczak, J.; Stawny, M. A critical review of the novelties in the development of intravenous nanoemulsions. Eur. J. Pharm. Biopharm. 2023, 191, 36–56. [Google Scholar] [CrossRef]
- Cox, S.D.; Mann, C.M.; Markham, J.L.; Gustafson, J.E.; Warmington, J.R.; Wyllie, S.G. Determining the Antimicrobial Actions of Tea Tree Oil. Mol. J. Synth. Chem. Nat. Prod. Chem. 2001, 6, 87. [Google Scholar] [CrossRef]
- Maurya, A.; Singh, V.K.; Das, S.; Prasad, J.; Kedia, A.; Upadhyay, N.; Dubey, N.K.; Dwivedy, A.K. Essential Oil Nanoemulsion as Eco-Friendly and Safe Preservative: Bioefficacy Against Microbial Food Deterioration and Toxin Secretion, Mode of Action, and Future Opportunities. Front. Microbiol. 2021, 12, 751062. [Google Scholar] [CrossRef]
- Gupta, S.; Chavhan, S.; Sawant, K.K. Self-nanoemulsifying drug delivery system for adefovir dipivoxil: Design, characterization, in vitro and ex vivo evaluation. Colloids Surfaces Physicochem. Eng. Asp. 2011, 392, 145–155. [Google Scholar] [CrossRef]
- Mushtaq, A.; Wani, S.M.; Malik, A.R.; Gull, A.; Ramniwas, S.; Nayik, G.A.; Ercisli, S.; Marc, R.A.; Ullah, R.; Bari, A. Recent insights into Nanoemulsions: Their preparation, properties and applications. Food Chem. X 2023, 18, 100684. [Google Scholar] [CrossRef]
- Ashaolu, T.J. Nanoemulsions for health, food, and cosmetics: A review. Environ. Chem. Lett. 2021, 19, 3381–3395. [Google Scholar] [CrossRef] [PubMed]
- Sneha, K.; Kumar, A. Nanoemulsions: Techniques for the preparation and the recent advances in their food applications. Innov. Food Sci. Emerg. Technol. 2022, 76, 102914. [Google Scholar] [CrossRef]
- Choi, S.J.; McClements, D.J. Nanoemulsions as delivery systems for lipophilic nutraceuticals: Strategies for improving their formulation, stability, functionality and bioavailability. Food Sci. Biotechnol. 2020, 29, 149–168. [Google Scholar] [CrossRef] [PubMed]
- Gauthier, G.; Capron, I. Pickering nanoemulsions: An overview of manufacturing processes, formulations, and applications. JCIS Open 2021, 4, 100036. [Google Scholar] [CrossRef]
- Jafari, S.; McClements, D. Nanoemulsions: Formulation, Applications, and Characterization; Elsevier Science: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Kumar, M.; Bishnoi, R.S.; Shukla, A.K.; Jain, C.P. Techniques for Formulation of Nanoemulsion Drug Delivery System: A Review. Prev. Nutr. Food Sci. 2019, 24, 225–234. [Google Scholar] [CrossRef]
- Sánchez-Gaitán, E.; González-López, V.; Delgado, F. Polydispersity and composition stability in a long-term follow-up of palmarosa (Cymbopogon martini) and tea tree (Melaleuca alternifolia) O/W nanoemulsions for antibacterial use. Colloids Interfaces 2025, 9, 5. [Google Scholar] [CrossRef]
- Carson, C.F.; Hammer, K.A.; Riley, T.V. Melaleuca alternifolia (Tea Tree) Oil: A Review of Antimicrobial and Other Medicinal Properties. Clin. Microbiol. Rev. 2006, 19, 50. [Google Scholar] [CrossRef]
- Sanchez-Gaitan, E.J.; Rivero-Aranda, R.; Gonzalez-Lopez, V.; Delgado, F. Thermoresponsive test for a O/W Palmarosa Nanoemulsion: Dropletsize DLS, chemical composition FTIR and antibacterial test. Mendeley Data 2025. [Google Scholar] [CrossRef]
- FDA Center for Drug Evaluation and Research. Inactive Ingredient Search for Approved Drug Products; U.S. Food & Drug Administration: Silver Spring, MD, USA, 2023.
- Trefalt, G.; Szilágyi, I.; Borkovec, M. Schulze-Hardy rule revisited. Colloid Polym. Sci. 2020, 298, 961–967. [Google Scholar] [CrossRef]
- Schulze, H. Schwefelarsen in wässriger Lösung. J. Prakt. Chem. 1882, 25, 431–452. [Google Scholar] [CrossRef]
- Hardy, W.B.; Neville, F.H. A preliminary investigation of the conditions which determine the stability of irreversible hydrosols. Proc. R. Soc. Lond. 1900, 66, 110–125. [Google Scholar] [CrossRef]
- Gupta, A.; Eral, H.B.; Hatton, T.A.; Doyle, P.S. Nanoemulsions: Formation, properties and applications. Soft Matter 2016, 12, 2826–2841. [Google Scholar] [CrossRef] [PubMed]
- Yi, L.; Wang, C.; van Vuren, T.; Lohse, D.; Risso, F.; Toschi, F.; Sun, C. Physical mechanisms for droplet size and effective viscosity asymmetries in turbulent emulsions. J. Fluid Mech. 2022, 951. [Google Scholar] [CrossRef]
- Gupta, A.; Eral, H.B.; Hatton, T.A.; Doyle, P.S. Controlling and predicting droplet size of nanoemulsions: Scaling relations with experimental validation. Soft Matter 2016, 12, 1452–1458. [Google Scholar] [CrossRef]
- Beal, J.; Farny, N.G.; Haddock-Angelli, T.; Selvarajah, V.; Baldwin, G.S.; Buckley-Taylor, R.; Gershater, M.; Kiga, D.; Marken, J.; Sanchania, V.; et al. Robust estimation of bacterial cell count from optical density. Commun. Biol. 2020, 3, 512. [Google Scholar] [CrossRef]
- Mira, P.; Yeh, P.; Hall, B.G. Estimating microbial population data from optical density. PLoS ONE 2022, 17, e0276040. [Google Scholar] [CrossRef]
- Reynolds, J. Serial Dilution Protocols. Am. Soc. Microbiol. 2005, 2005, 1–7. [Google Scholar]
- Sanders, E.R. Aseptic Laboratory Techniques: Plating Methods. J. Vis. Exp. 2012, 63, e3064. [Google Scholar] [CrossRef]
- Kumar, N.; Verma, A.; Mandal, A. Formation, characteristics and oil industry applications of nanoemulsions: A review. J. Pet. Sci. Eng. 2021, 206, 109042. [Google Scholar] [CrossRef]
- Tukey, J.W. Comparing Individual Means in the Analysis of Variance. Biometrics 1949, 5, 99–114. [Google Scholar] [CrossRef]
- Scarlett, B. (Ed.) Spectroscopy. In Particle Characterization: Light Scattering Methods; Springer: Dordrecht, The Netherlands, 2002; pp. 223–288. [Google Scholar] [CrossRef]
- Ross Hallett, F. Scattering and Particle Sizing Applications. In Encyclopedia of Spectroscopy and Spectrometry, 2nd ed.; Lindon, J.C., Ed.; Academic Press: Oxford, UK, 1999; pp. 2488–2494. [Google Scholar] [CrossRef]
- Malvern Instruments Ltd. Zetasizer Nano User Manual; Malvern Instruments Ltd.: Worcestershire, UK, 2013. [Google Scholar]
- Goddeeris, C.; Cuppo, F.; Reynaers, H.; Bouwman, W.; Van den Mooter, G. Light scattering measurements on microemulsions: Estimation of droplet sizes. Int. J. Pharm. 2006, 312, 187–195. [Google Scholar] [CrossRef]
- Gupta, A.; Narsimhan, V.; Hatton, T.A.; Doyle, P.S. Kinetics of the Change in Droplet Size During Nanoemulsion Formation. Langmuir 2016, 32, 11551–11559. [Google Scholar] [CrossRef]
- Peng, F.; Ke, Y.; Lu, S.; Zhao, Y.; Hu, X.; Deng, Q. Anion amphiphilic random copolymers and their performance as stabilizers for O/W nanoemulsions. RSC Adv. 2019, 9, 14692–14700. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, A.E.; Duarte, J.L.; Cruz, R.A.; da Conceição, E.C.; Carvalho, J.C.; Fernandes, C.P. Utilization of dynamic light scattering to evaluate Pterodon emarginatus oleoresin-based nanoemulsion formation by non-heating and solvent-free method. Rev. Bras. Farmacogn. 2017, 27, 401–406. [Google Scholar] [CrossRef]
- Ee, S.L.; Duan, X.; Liew, J.; Nguyen, Q.D. Droplet size and stability of nano-emulsions produced by the temperature phase inversion method. Chem. Eng. J. 2008, 140, 626–631. [Google Scholar] [CrossRef]
- Marinković, J.; Bošković, M.; Tasić, G.; Vasilijević, B.; Marković, D.; Marković, T.; Nikolić, B. Cymbopogon martinii essential oil nanoemulsions: Physico-chemical characterization, antibacterial and antibiofilm potential against Enterococcus faecalis. Ind. Crop. Prod. 2022, 187, 115478. [Google Scholar] [CrossRef]
- Zhou, S.; Rao, Y.; Li, J.; Huang, Q.; Rao, X. Staphylococcus aureus small-colony variants: Formation, infection, and treatment. Microbiol. Res. 2022, 260, 127040. [Google Scholar] [CrossRef]
- Baron, S. Medical Microbiology, 4th ed.; University of Texas Medical Branch at Galveston: Galveston, TX, USA, 1996. [Google Scholar]
- Errington, J.; van der Aart, L.T. Microbe Profile: Bacillus subtilis: Model organism for cellular development, and industrial workhorse. Microbiology 2020, 166, 425–427. [Google Scholar] [CrossRef]
- Riley, M. Size Limits of Very Small Microorganisms: Proceedings of a Workshop; National Academies Press: Washington, DC, USA, 1999. [Google Scholar]
- Drepper, F.; Biernat, J.; Kaniyappan, S.; Meyer, H.E.; Mandelkow, E.M.; Warscheid, B.; Mandelkow, E. A Combinatorial Native MS and LC-MS/MS Approach Reveals High Intrinsic Phosphorylation of Human Tau but Minimal Levels of Other Key Modifications. J. Biol. Chem. 2020, 295, 18213–18225. [Google Scholar] [CrossRef]
- Parastan, R.; Kargar, M.; Solhjoo, K.; Kafilzadeh, F. Staphylococcus aureus biofilms: Structures, antibiotic resistance, inhibition, and vaccines. Gene Rep. 2020, 20, 100739. [Google Scholar] [CrossRef]



| EO | Time | Max. (nm) | (nm) | (nm) | PDI | Range | (mV) |
|---|---|---|---|---|---|---|---|
| Palmarosa | 1 year | 8.82 | 9.94 | 3.00 | 0.30 | 15.717 | −1.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Gaitán, E.; Rivero-Aranda, R.; González-López, V.; Delgado, F. Thermoresponsive Effects in Droplet Size Distribution, Chemical Composition, and Antibacterial Effectivity in a Palmarosa (Cymbopogon martini) O/W Nanoemulsion. Colloids Interfaces 2025, 9, 47. https://doi.org/10.3390/colloids9040047
Sánchez-Gaitán E, Rivero-Aranda R, González-López V, Delgado F. Thermoresponsive Effects in Droplet Size Distribution, Chemical Composition, and Antibacterial Effectivity in a Palmarosa (Cymbopogon martini) O/W Nanoemulsion. Colloids and Interfaces. 2025; 9(4):47. https://doi.org/10.3390/colloids9040047
Chicago/Turabian StyleSánchez-Gaitán, Erick, Ramón Rivero-Aranda, Vianney González-López, and Francisco Delgado. 2025. "Thermoresponsive Effects in Droplet Size Distribution, Chemical Composition, and Antibacterial Effectivity in a Palmarosa (Cymbopogon martini) O/W Nanoemulsion" Colloids and Interfaces 9, no. 4: 47. https://doi.org/10.3390/colloids9040047
APA StyleSánchez-Gaitán, E., Rivero-Aranda, R., González-López, V., & Delgado, F. (2025). Thermoresponsive Effects in Droplet Size Distribution, Chemical Composition, and Antibacterial Effectivity in a Palmarosa (Cymbopogon martini) O/W Nanoemulsion. Colloids and Interfaces, 9(4), 47. https://doi.org/10.3390/colloids9040047










