Characterization of Multimodal Silicas Using TG/DTG/DTA, Q-TG, and DSC Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation
2.2. Textural Characteristics
2.3. Thermal Analysis
2.4. Quasi-Isothermal Desorption of Water
2.5. DSC Investigations
2.6. Scanning Electron Microscopy
3. Results and Discussion
3.1. Structural Analysis
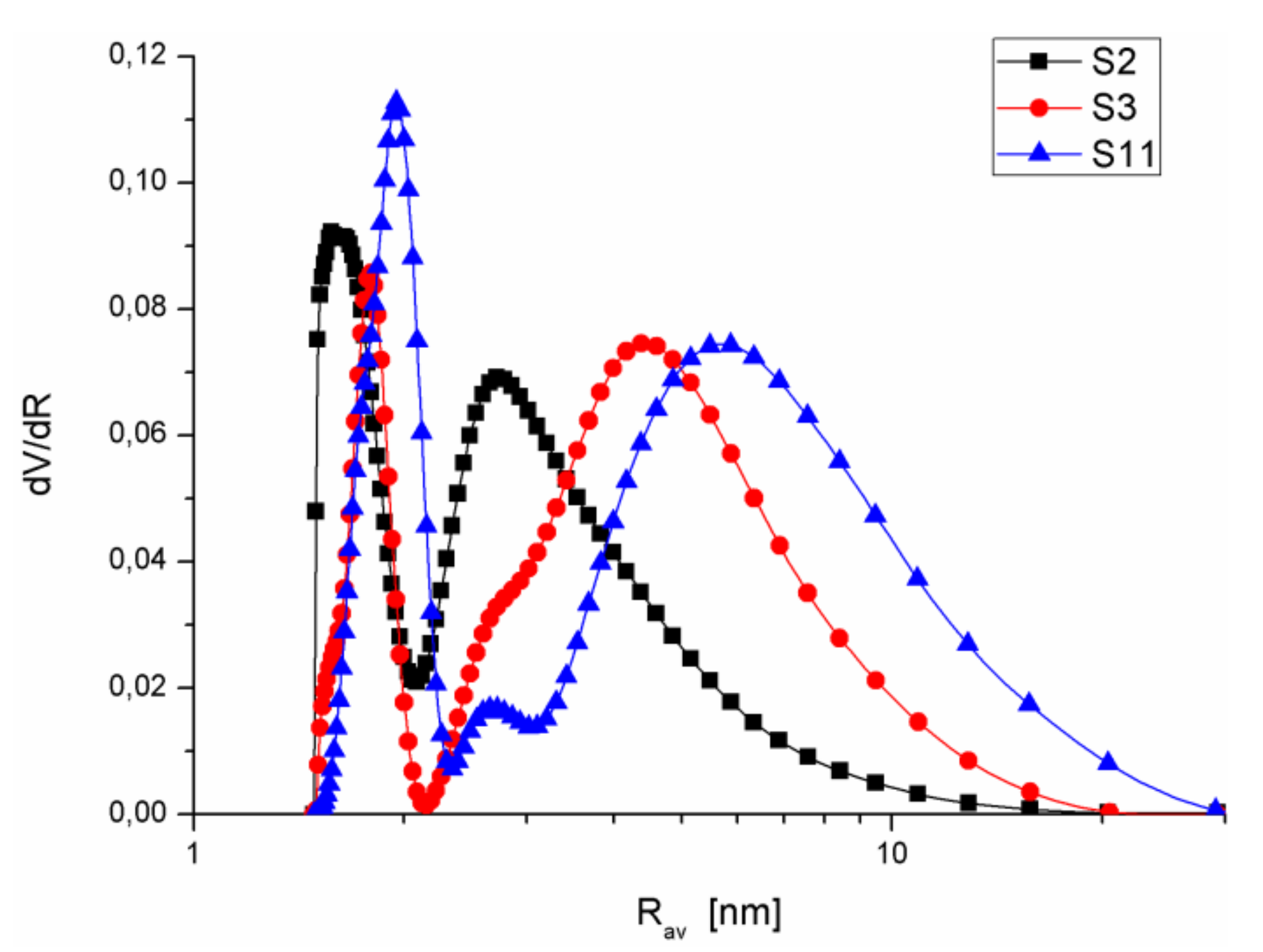
3.2. Thermoporometry DSC
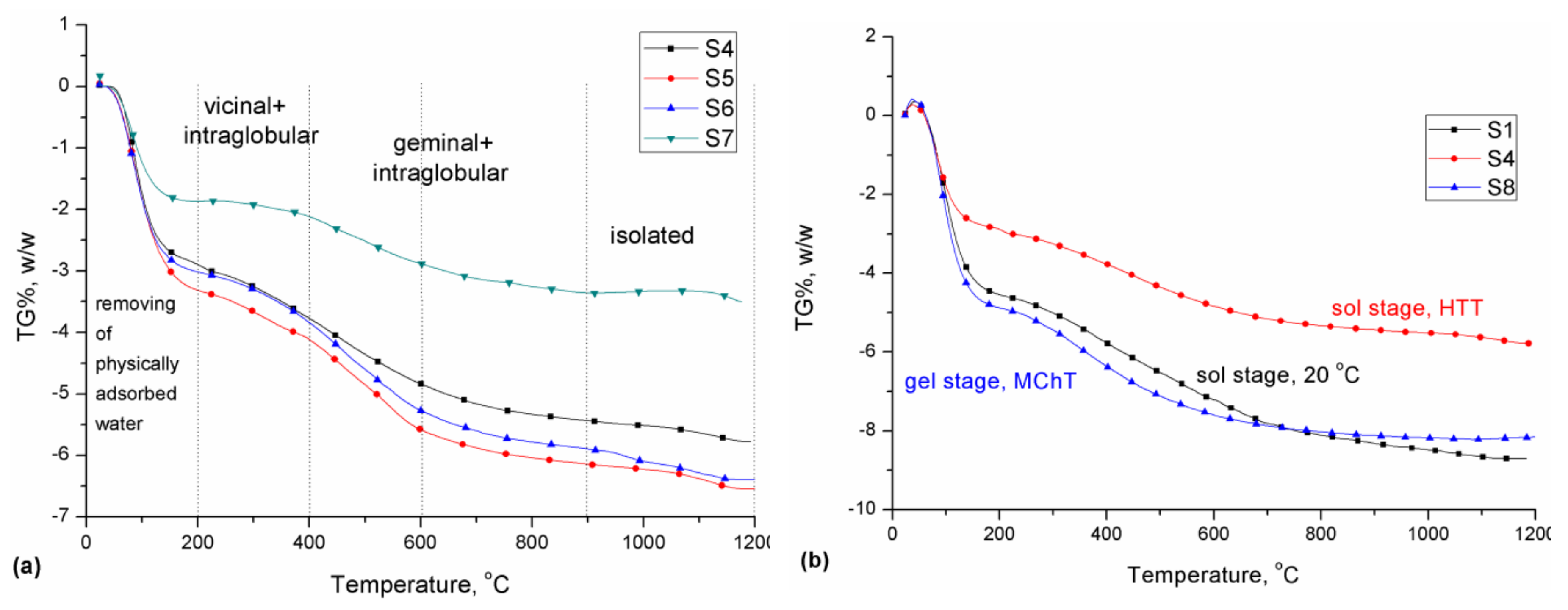
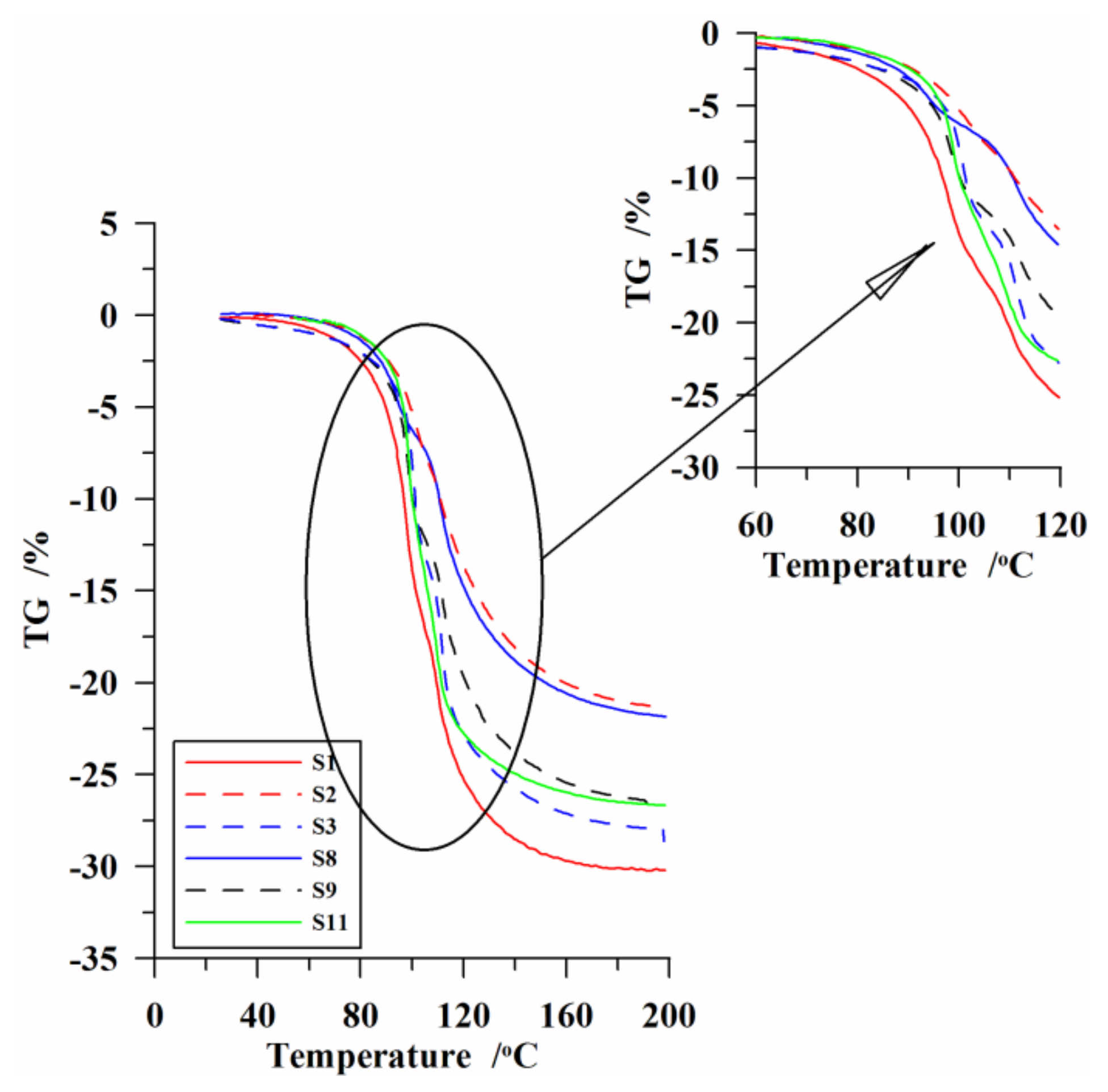
3.3. Thermal Analysis
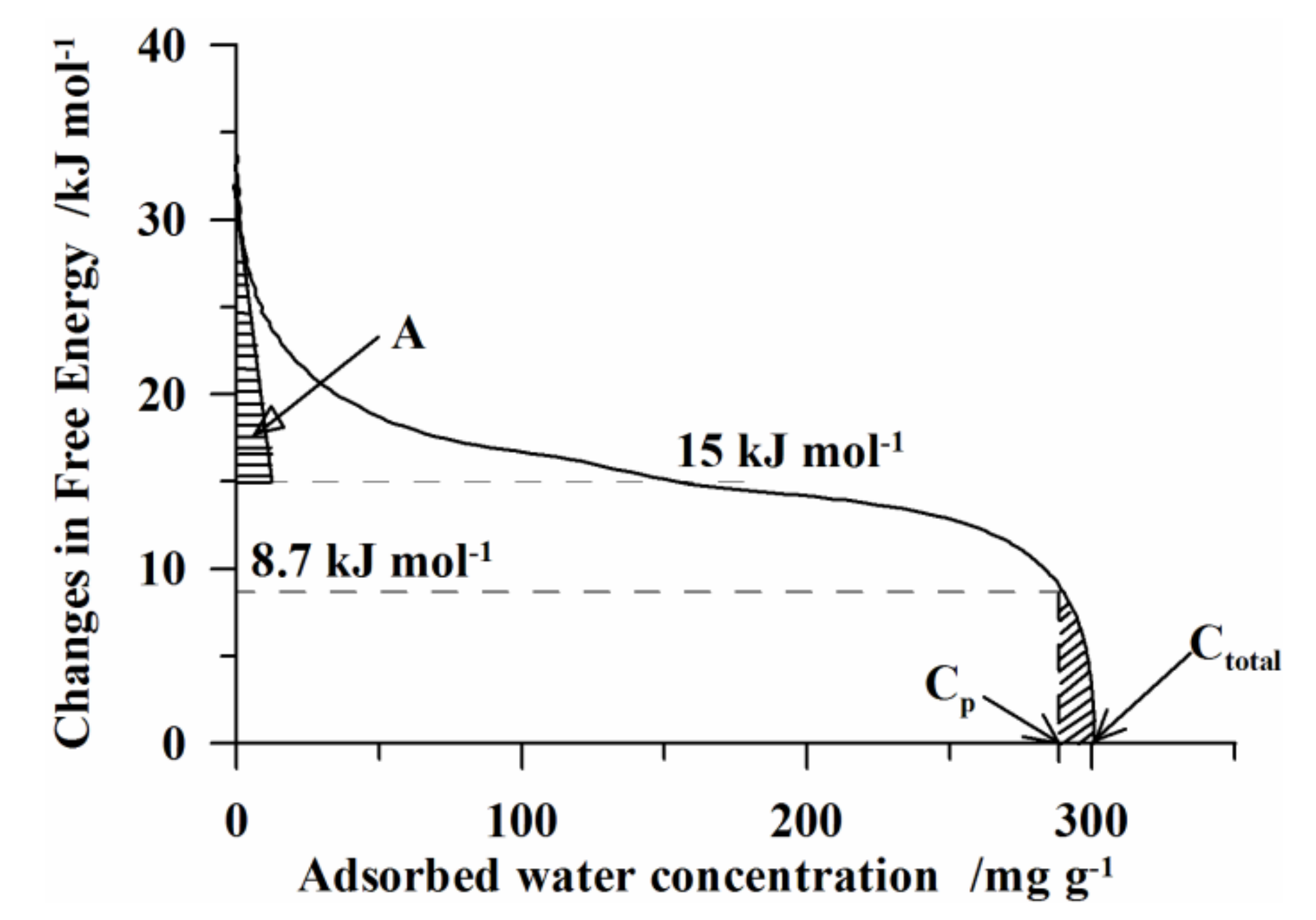
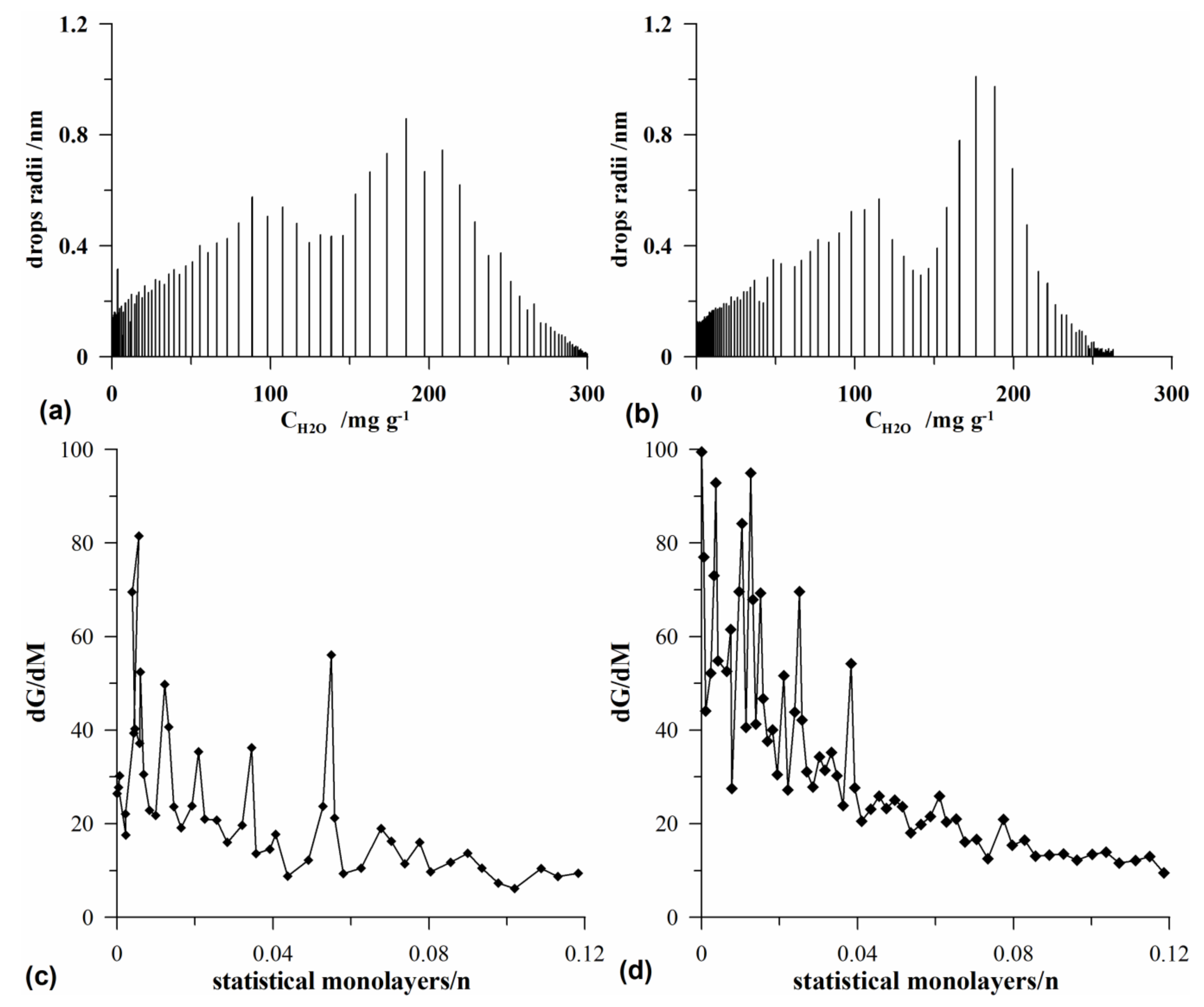
3.4. Quasi-Isothermal Analysis
3.5. SEM
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Unger, K.K. Porous Silica; Elsevier: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Bergna, H.E. The Colloid Chemistry of Silica; Advances in Chemistry, American Chemical Society: Washington, DC, USA, 1994. [Google Scholar]
- Kuang, D.; Brezesinski, T.; Smarsly, B. Hierarchical Porous Silica Materials with a Trimodal Pore System Using Surfactant Templates. J. Am. Chem. Soc. 2004, 126, 10534–10535. [Google Scholar] [CrossRef] [PubMed]
- Fujita, S.; Nakano, H.; Ishii, M.; Nakamura, H.; Inagaki, S. Preparation of hierarchical porous silica and its optical property. Microporous Microporous Mater. 2006, 96, 205–209. [Google Scholar] [CrossRef]
- Khalameida, S.V.; Sydorchuk, V.V.; Skubiszewska-Zięba, J. One-step free-template preparation of silica with hierarchical; porous structure. In Proceedings of the IEEE 7th International Conference on Nanomaterials: Applications and Properties, Odessa, Ukraine, 10–15 September 2017; pp. 1–4, ISBN 978-1-5386-2810-2. [Google Scholar]
- Snyder, L.R.; Ward, J.W. The surface structure of porous silica. J. Phys. Chem. 1966, 70, 3941–3952. [Google Scholar] [CrossRef]
- Zhuravlev, L.T. Structurally bound water and surface characterization of amorphous silica. Pure Appl. Chem. 1989, 61, 1969–1976. [Google Scholar] [CrossRef]
- Sydorchuk, V.; Khalameida, S.; Zazhigalov, V.; Skubiszewska-Zięba, J.; Leboda, R.; Wieczorek-Ciurowa, K. Influence of mechanochemical activation in various media on structure of porous and non-porous silicas. Appl. Surf. Sci. 2010, 257, 446–450. [Google Scholar] [CrossRef]
- Skubiszewska-Zięba, J.; Khalameida, S.; Sydorchuk, V. Comparison of surface properties of silica xero- and hydrogels hydrothermally modified using mechanochemical, microwave and classical methods. Colloids Surf. A 2016, 504, 139–153. [Google Scholar] [CrossRef]
- Charmas, B.; Skubiszewska-Zięba, J. Application of differential scanning calorimetry to study porous structure of hydrothermally modified silicas. J. Therm. Anal. Calorim. 2017, 129, 23–32. [Google Scholar] [CrossRef]
- Turov, V.V.; Leboda, R.; Skubiszewska-Zięba, J.; Charmas, B. Application of quasi-isothermal thermogravimetry for estimation of some properties of hydration layers in mesoporous adsorbents. Colloids Surf. A 2001, 181, 1–9. [Google Scholar] [CrossRef]
- Skubiszewska-Zięba, J.; Charmas, B.; Leboda, R.; Tertykh, V.A.; Yanishpolskii, V.V. Complex investigations of structural and thermal properties of silica-titania adsorbents. J. Therm. Anal. Calorim. 2012, 108, 1085–1092. [Google Scholar] [CrossRef]
- Farias, R.F.; Airoldi, C. Thermogravimetry as a reliable tool to estimate the density of silanols on a silica gel surface. J. Therm. Anal. 1998, 53, 751–756. [Google Scholar] [CrossRef]
- Burneau, A.; Lepage, J.; Maurice, G. Porous silica—Water interactions. I. Structural and dimensional changes induced by water adsorption. J. Non-Cryst. Solids 1997, 217, 1–10. [Google Scholar] [CrossRef]
- Skubiszewska-Zięba, J. The impact of microwave energy on the results of silica gel hydrothermal modification. Adsorption 2010, 16, 485–493. [Google Scholar] [CrossRef]
- Nawrocki, J. The silanol group and its role in liquid chromatography. J. Chromatogr. A 1997, 779, 29–71. [Google Scholar] [CrossRef]
- Dugas, V.; Checalier, Y. Surface hydroxylation and silane grafting on fumes and thermal silica. J. Colloid Interface Sci. 2003, 264, 354–361. [Google Scholar] [CrossRef]
- Alessi, A.; Agnello, S.; Buscarino, G.; Gelardi, F.M. Raman and IR investigation of silica nanoparticles structure. J. Non-Cryst. Solids 2013, 362, 20–24. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity, 2nd ed.; Academic Press: London, UK, 1982. [Google Scholar]
- Gun’ko, V.M. Composite materials: Textural characteristics. Appl. Surf. Sci. 2014, 307, 444–454. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Mikhalovsky, S.V. Evaluation of slitlike porosity of carbon adsorbents. Carbon 2004, 42, 843–849. [Google Scholar] [CrossRef]
- Charmas, B.; Skubiszewska-Zięba, J.; Waniak-Nowicka, H. Thermal and calorimetric investigations of titania–silica composites. Adsorpt. Sci. Technol. 2017, 35, 706–713. [Google Scholar] [CrossRef]
- Gun’ko, V.M.; Do, D.D. Pore structure of carbon adsorbents was characterized using the regularization procedure. Colloids Surf. A 2001, 19, 71–83. [Google Scholar] [CrossRef]
- Zhuravlev, L.T. The surface chemistry of amorphous silica. Zhuravlev model. Colloids Surf. A. 2000, 173, 1–38. [Google Scholar] [CrossRef]
- Linsen, B.G. Physical and Chemical Aspects of Adsorbents and Catalysis; Academic Press: London, UK, 1970. [Google Scholar]
- Charmas, B. TG and DSC studies of bone tissue. Effects of osteoporosis. Thermochim. Acta 2013, 573, 73–81. [Google Scholar] [CrossRef]
- Charmas, B. Adsorption and Calorimetric Studies of Properties of Hydrothermally Modified Carbosils. J. Therm. Anal. Calorim. 2014, 115, 1395–1405. [Google Scholar] [CrossRef]
- Gunko, V.M.; Turov, V.V. Nuclear Magnetic Resonance Studies of Interfacial Phenomena; Taylor & Francis: San Diego, CA, USA, 2013. [Google Scholar]
- Brun, M.; Lallemand, A.; Quinson, J.; Eyraud, C. A new method for the simultaneous determination of the size and the shape of pores. Thermochim. Acta 1977, 21, 59–88. [Google Scholar] [CrossRef]
- Landry, M.R. Thermoporometry by differential scanning calorimetry: Experimental considerations and applications. Thermochim. Acta 2005, 433, 27–50. [Google Scholar] [CrossRef]
- Rouquerol, J.; Baron, G.; Denoyel, R.; Giesche, H.; Groen, J.; Klobes, P.; Levitz, P.; Neimark, A.V.; Rigby, S.; Skudas, R.; et al. Recommendations for the Characterization of Porous Solids. Pure Appl. Chem. 1994, 66, 1739–1758. [Google Scholar] [CrossRef]
- Leboda, R.; Charmas, B.; Sidorchuk, V.V. Physico-Chemical and Technological Aspects of Hydrothermal Modification of Complex Sorbents and Catalysts. I. Modification of Porous and Crystalline Structures. Adsorpt. Sci. Technol. 1997, 15, 189–214. [Google Scholar] [CrossRef]
- Khalameida, S.; Sydorchuk, V.; Zazhigalov, V.; Wieczorek-Ciurowa, K.; Skubiszewska-Zięba, J.; Charmas, B. The Interaction between Barium and Titanium Oxides under Mechanochemical, Hydrothermal and Microwave Treatments and Properties of Prepared Products. Adv. Sci. Eng. Med. 2017, 9, 235–246. [Google Scholar] [CrossRef]
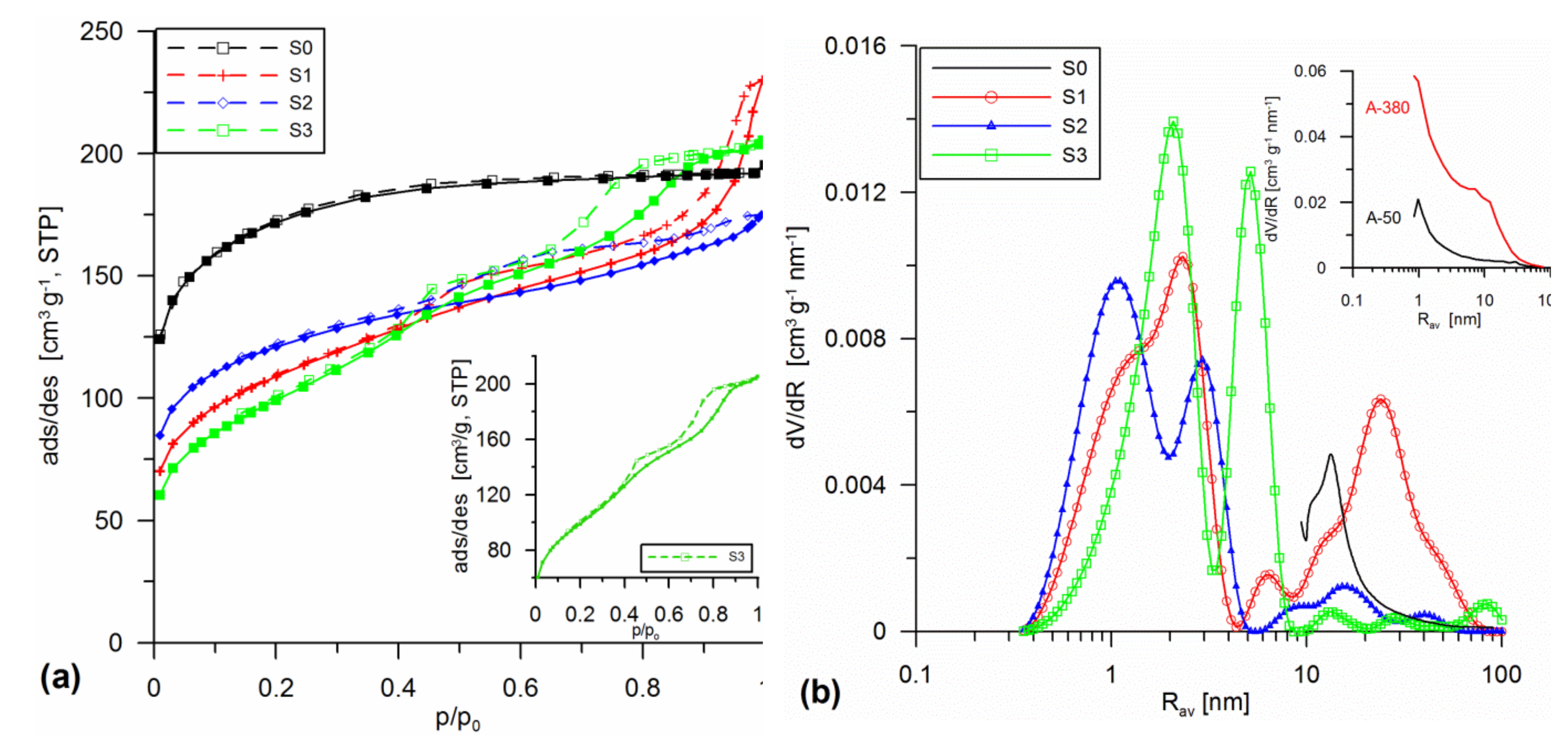
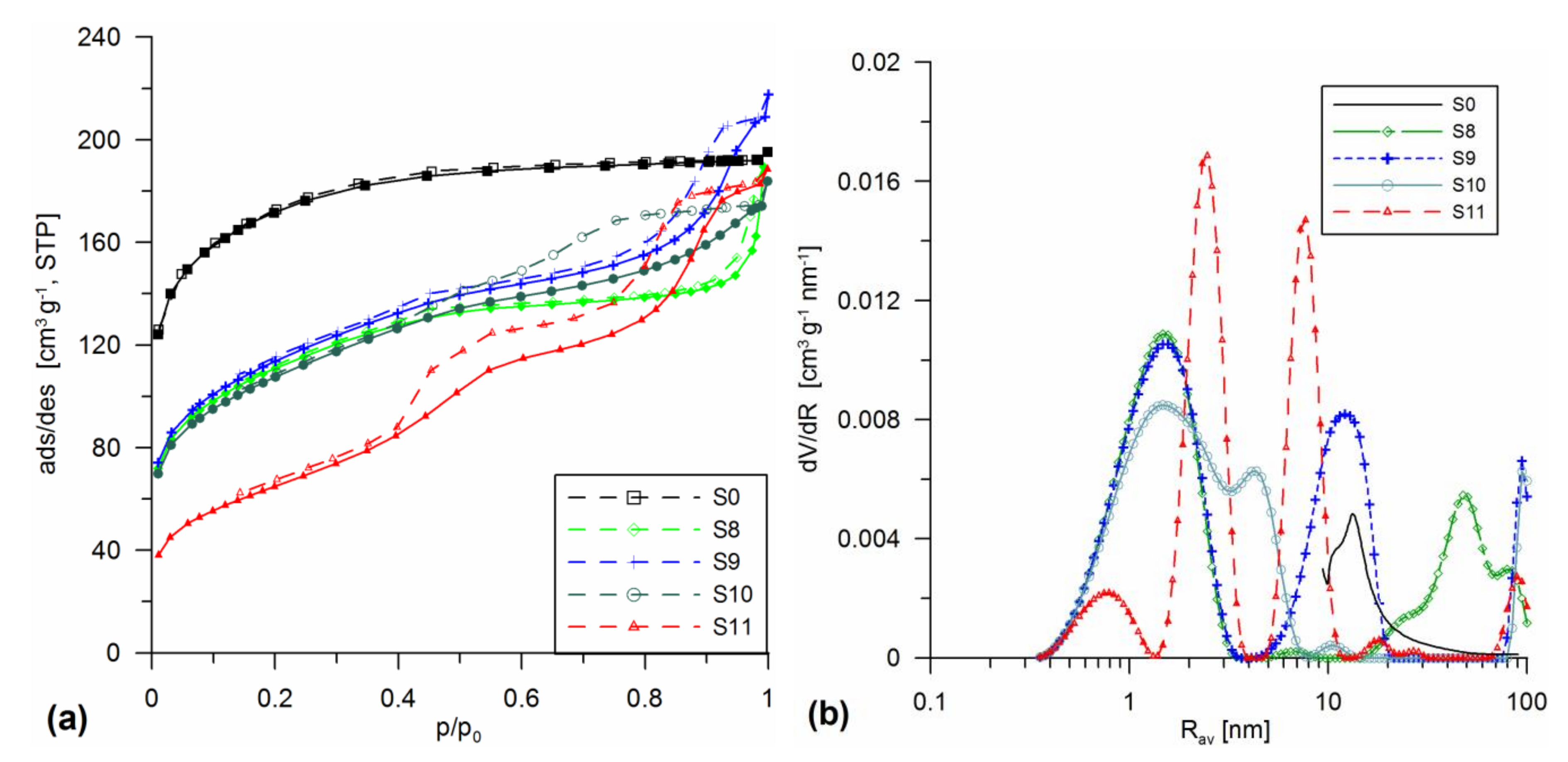
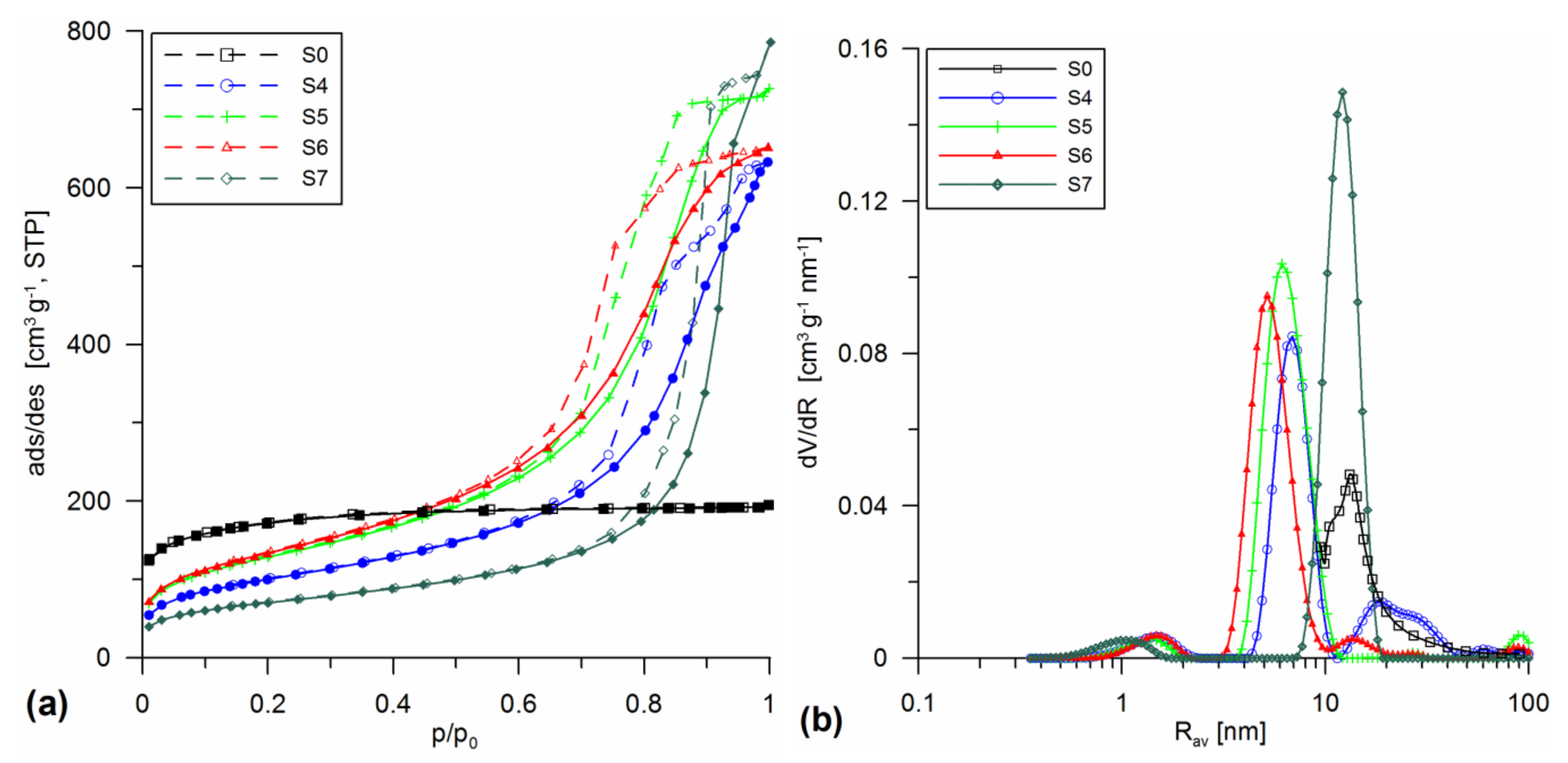


| Sample | Procedure | SBET | Smicro/%Smicro | Smeso/%Smeso | Smacro/%Smacro | Vmicro/%Vmicro | Vmeso/%Vmeso | Vmacro/%Vmacro | Vp | Rav | Rdom (N2) | Rdom (DSC) | Δw |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0 | SiO2 initial, sol gel 20 °C | 607 | - | - | - | 0.13 | - | - | 0.31 | - | 13.2 | - | - |
| addition in the sol stage 20 °C | |||||||||||||
| S1 | SiO2 + 30% A-50 sol 20 | 385.1 | 170.3 44.2 | 211.9 55 | 2.9 0.7 | 0.06 16.8 | 0.249 70 | 0.047 13.2 | 0.356 | 1.85 | 2.3; 6.3; 24.3 | 1.7;2.6; 6 | 0.11 |
| S2 | SiO2 + 10% A-50 + 10% A-380 sol 20 | 431.6 | 253.2 58.7 | 178.2 41.3 | 0.3 0.1 | 0.092 34 | 0.174 64.4 | 0.005 1.7 | 0.271 | 1.25 | 1.1; 3 | 1.5; 2.9 | 0.07 |
| S3 | SiO2 + 20% SiO2-MChT sol 20 | 355.0 | 82.2 23.1 | 272.5 76.8 | 0.4 0.1 | 0.028 8.9 | 0.282 88.6 | 0.008 2.5 | 0.318 | 1.8 | 2.1; 5.2 | 1.8; 4.6 | 0.17 |
| Addition in the Sol/Gel Stage at 200 °C under HTT | |||||||||||||
| S4 | SiO2 + 30% A-50 sol HTT 200 | 363.9 | 25.9 7.0 | 332.8 91.4 | 5.2 1.4 | 0.011 1.1 | 0.887 90.6 | 0.082 8.4 | 0.98 | 5.4 | 1.5; 7; 18 | - | 0.15 |
| S5 | SiO2 + 20% A-380 sol HTT 200 | 466.8 | 30.5 6.5 | 435.4 93.3 | 0.9 0.2 | 0.012 1.1 | 1.083 96.3 | 0.029 2.6 | 1.124 | 4.8 | 1.5; 6 | - | 0.14 |
| S6 | SiO2 + 10% A-50 + 10% A-380 sol HTT 200 | 486.7 | 15.7 3.2 | 470.4 96.6 | 0.6 0.1 | 0.007 0.7 | 0.986 97.7 | 0.017 1.7 | 1.01 | 4.15 | 1.5; 5 | - | 0.15 |
| S7 | SiO2 + 20% SiO2-MChT sol HTT 200 | 255.2 | 70.6 27.6 | 184.6 72.4 | 0 0 | 0.036 2.9 | 1.18 97.1 | 0 0 | 1.216 | 10 | 1; 12 | - | -0.02 |
| Milling at 300 or 500 rpm, Addition on the Wet Gel Stage | |||||||||||||
| S8 | SiO2 gel + 30% A-50 MChT 300 | 395.4 | 187.2 43.7 | 204.7 51.8 | 3.5 0.9 | 0.065 22.2 | 0.151 51.7 | 0.076 26.1 | 0.292 | 1.55 | 1.5; 6; 50 | 1.2;2.6; 5.7 | 0.14 |
| S9 | SiO2 gel + 20% A-380 MChT 300 | 405.0 | 182 44.9 | 222.5 54.9 | 0.5 0.1 | 0.064 19 | 0.252 74.9 | 0.021 6.1 | 0.337 | 1.65 | 1.5; 12 | 1.5;1.8; 4.7 | 0.13 |
| S10 | SiO2 gel + 10% A-50 + 20% A-380 MChT 300 | 383.0 | 166.7 43.5 | 216 56.4 | 0.4 0.1 | 0.059 20.7 | 0.209 73.4 | 0.017 6.0 | 0.285 | 1.5 | 1.5; 4.2 | - | 0.14 |
| S11 | SiO2 gel + 20% SiO2-MChT MChT 500 | 234.2 | 76.9 32.8 | 157 67 | 0.3 0.1 | 0.026 8.9 | 0.253 86.8 | 0.013 4.4 | 0.292 | 2.5 | 0.8; 2.5; 7.7 | 2; 2.7; 6 | 0.06 |
| Cooling Stage | |||
|---|---|---|---|
| Tonset | Tend | Tmin | ΔH |
| 4.31 | 2.9 | 3.9 | −171.99 |
| −7.50 | −8.2 | −7.8 | −172.02 |
| −31.11 | −34.8 | −33.2 | −171.91 |
| −37.93 | −41.2 | −39.7 | −172.04 |
| Heating Stage | |||
| Tonset | Tend | Tmax | ΔH |
| −29.24 | −24.2 | −26.8 | 130.75 |
| 4.82 | 5.6 | 5.2 | 131.28 |
| 0.10 | 4.4 | 3.3 | 131.2 |
| Sample | ΔHcooling J g−1 | ΔHheating J g−1 |
|---|---|---|
| S1 | 172.1 | 130.7 |
| S2 | 145.1 | 73.4 |
| S3 | 301 | 183.2 |
| S8 | 270.5 | 253.2 |
| S9 | 224.3 | 147.3 |
| S11 | 305.5 | 198.1 |
| Sample | Temperature Range of Mass Loss, °C | ||||
|---|---|---|---|---|---|
| 200–400 | 400–600 | 600–900 | 900–1200 | 200–1200 | |
| OH Groups Content, υOH mmol g−1 σOH OH nm−2 | |||||
| Vicinal + Intraglobular | Geminal + Intraglobular | Geminal + Intraglobular | Isolated | Total | |
| S1 | 1.41(2.19) | 1.68(2.61) | 1.31(2.04) | 0.45(0.70) | 4.84(7.54) |
| S2 | 2.05(2.85) | 1.85(2.58) | 0.73(1.02) | 0.01(0.01) | 4.64(6.45) |
| S3 | 0.25(0.42) | 0.85(1.44) | 0.52(0.88) | 0.20(0.33) | 1.82(3.08) |
| S4 | 1.04(1.72) | 1.24(2.04) | 0.67(1.11) | 0.40(0.65) | 3.35(5.52) |
| S5 | 0.89(1.15) | 1.71(2.20) | 0.63(0.81) | 0.47(0.60) | 3.70(4.76) |
| S6 | 0.94(1.16) | 1.65(2.03) | 0.72(0.89) | 0.57(0.70) | 3.88(4.78) |
| S7 | 0.25(0.60) | 0.88(2.07) | 0.54(1.26) | 0.20(0.48) | 1.87(4.41) |
| S8 | 1.74(2.64) | 1.45(2.19) | 0.60(0.91) | 0.06(0.09) | 3.84(5.83) |
| S9 | 2.15(3.18) | 1.63(2.41) | 0.66(0.98) | 0.24(0.36) | 4.68(6.93) |
| S10 | 1.23(1.93) | 1.76(2.76) | 0.87(1.36) | 0.16(0.24) | 4.02(6.29) |
| S11 | 1.55(3.98) | 1.39(3.56) | 0.70(1.80) | 0.17(0.44) | 3.82(9.78) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charmas, B.; Kucio, K.; Sydorchuk, V.; Khalameida, S.; Zięzio, M.; Nowicka, A. Characterization of Multimodal Silicas Using TG/DTG/DTA, Q-TG, and DSC Methods. Colloids Interfaces 2019, 3, 6. https://doi.org/10.3390/colloids3010006
Charmas B, Kucio K, Sydorchuk V, Khalameida S, Zięzio M, Nowicka A. Characterization of Multimodal Silicas Using TG/DTG/DTA, Q-TG, and DSC Methods. Colloids and Interfaces. 2019; 3(1):6. https://doi.org/10.3390/colloids3010006
Chicago/Turabian StyleCharmas, Barbara, Karolina Kucio, Volodymyr Sydorchuk, Svitlana Khalameida, Magdalena Zięzio, and Aldona Nowicka. 2019. "Characterization of Multimodal Silicas Using TG/DTG/DTA, Q-TG, and DSC Methods" Colloids and Interfaces 3, no. 1: 6. https://doi.org/10.3390/colloids3010006
APA StyleCharmas, B., Kucio, K., Sydorchuk, V., Khalameida, S., Zięzio, M., & Nowicka, A. (2019). Characterization of Multimodal Silicas Using TG/DTG/DTA, Q-TG, and DSC Methods. Colloids and Interfaces, 3(1), 6. https://doi.org/10.3390/colloids3010006





