Microscopic Characterization of Pb_10−xCu_x(PO₄)₆O by ³¹P and ⁶³/⁶⁵Cu NMR Measurements

Abstract

The report of the first room-temperature, ambient-pressure superconductivity in copper-doped lead apatite Pb_10−xCu_x(PO₄)₆O has attracted lots of attention. However, subsequent studies revealed the presence of numerous impurity phases in the polycrystalline sample, and the sharp superconducting-like transition is not due to a superconducting transition but most likely due to a reduction in resistivity caused by the first-order structural phase transition of Cu₂S at around 385 K from the β phase at high temperature to the γ phase at low temperature. Before now, only bulk measurements have been performed on a Pb_10−xCu_x(PO₄)₆O powder sample, which could be affected by the impurity phases, masking the intrinsic properties of Pb_10−xCu_x(PO₄)₆O. In this study, ³¹P and ^63/65Cu nuclear magnetic resonance (NMR) measurements have been performed on a Pb_10−xCu_x(PO₄)₆O powder sample to investigate its physical properties from a microscopic point of view. Our NMR data evidence the non-magnetic insulating nature of Pb_10−xCu_x(PO₄)₆O without any trace of electron correlation effects. Furthermore, the ^63/65Cu NMR results suggest that no copper or very little copper is substituted for Pb in Pb₁₀(PO₄)₆O prepared by sintering Pb₂SO₅ and Cu₃P.

1. Introduction

Recently, copper-doped lead apatite Pb_10−xCu_x(PO₄)₆O has been proposed as a candidate room-temperature and ambient-pressure superconductor from resistivity and levitation measurements [1,2,3], which has stimulated a lot of experimental and theoretical studies on this material. However, the resistivity is not actually zero but around 2 × 10⁻³ Ωcm at the temperature just below the claimed superconducting transition temperature [3], making the claim doubtful. Experimentally, impurity phases have been reported to be unavoidable from the solid-state reaction methods [2,4,5,6]. Subsequent studies indicate that the sharp superconducting-like transition is most likely due to a reduction in resistivity caused by the first-order structural phase transition of Cu₂S at around 385 K, from the high temperature β phase to the γ phase at a low temperature, and Pb_10−xCu_x(PO₄)₆O shows an insulating behavior [7,8]. It has also been suggested that the original reported diamagnetic behavior and levitation experiments may arise from either diamagnetism or small ferromagnetic impurities [9,10,11], but not due to superconductivity.

Even though the parent compound Pb₁₀(PO₄)₆O was considered to be an insulator, theoretical studies based on density functional theory (DFT) calculations suggest that Cu doping will create flat bands and induce insulator–metal transition, leading to a metallic state in Cu-substituted Pb₁₀(PO₄)₆O [12,13,14,15,16,17,18,19,20]. However, an ab initio calculation study based on strong-coupling Migdal–Eliashberg theory indicates that the electron–phonon coupling strength is insufficient to overcome the Coulomb repulsion between electron pairs and thus does not support high-temperature superconductivity in Pb₉Cu(PO₄)₆O via the conventional electron–phonon Migdal–Eliashberg mechanism [21]. Even neglecting Coulomb repulsion of the electron pairs, a superconducting transition temperature was suggested to be less than 2 K assuming a phonon-mediated superconducting mechanism [21]. Thus, if high-temperature superconductivity were possible in this system, the mechanism of superconductivity would be unconventional beyond the BCS theory. In fact, recent self-consistent many-body perturbation theory predicts strong spin fluctuations in Pb_10−xCu_x(PO₄)₆O [22]. Furthermore, antiferromagnetic fluctuations for the undoped material were suggested by a fluctuation exchange calculation study, which also suggests ferromagnetic fluctuations at a very low electron doping level [23]. On the contrary, another theoretical study suggests that orbital and spin fluctuations are weak, not enough to support superconductivity at high temperatures [24]. Experimentally, a logarithmic temperature dependence of resistivity ρ ∝ ln(1/T) in a wide temperature range of 10–300 K has been observed and was ascribed to the strong correlation effect in this system [25]. However, due to the multiphases in the compounds, the results of bulk measurements usually contain contributions from all the phases, and it may not be easy to distinguish and separate each contribution. Thus, the nature of the magnetic fluctuations of Pb_10−xCu_x(PO₄)₆O is still an open question.

Nuclear magnetic resonance (NMR) is a powerful technique to investigate static spin susceptibility and low-energy spin excitations from a microscopic point of view. The temperature dependence of the nuclear spin–lattice relaxation rate (1/T₁) reflects the wave vector q-summed dynamical susceptibility. On the other hand, NMR spectrum measurements, in particular, the NMR shift K, give us information on static magnetic susceptibility. Thus, from the temperature dependence of 1/T₁ and K, one can microscopically obtain valuable insights into the electronic and magnetic properties. Here, we performed ³¹P and ^63/65Cu NMR on a Pb_10−xCu_x(PO₄)₆O powder sample to reveal its intrinsic physical properties. ³¹P NMR results indicate that Pb_10−xCu_x(PO₄)₆O is a non-magnetic insulator without any obvious magnetic fluctuations. ^63/65Cu NMR results reveal that no copper or very little copper substitutes for Pb in Pb₁₀(PO₄)₆O prepared using the solid-state reaction of Pb₂SO₅ and Cu₃P.

2. Materials and Methods

2.1. Material Preparation

The Pb_10−xCu_x(PO₄)₆O powder sample was prepared using a solid-state reaction of Pb₂SO₅ and Cu₃P [6]. The uniformly mixed pellets of Pb₂SO₅ and Cu₃P were sealed in a high-vacuum quartz tube and raised to a temperature of 925 °C at a rate of 1.5 °C/min, held for 20 h, and then cooled in a furnace to obtain the target product Pb_10−xCu_x(PO₄)₆O. Aside from the main phase Pb_10−xCu_x(PO₄)₆O with x to be determined, copper metal and Cu₂S have been found to be impurity phases from the X-ray diffraction measurements [6].

2.2. Nuclear Magnetic Resonance

NMR measurements of ³¹P (I = ${\displaystyle \frac{1}{2}}$, ${\displaystyle \frac{{\mathrm{{\rm Y}}}_{\mathrm{N}}}{2\mathrm{\pi }}}$ = 17.2356 MHz/T), ⁶³Cu (I = ${\displaystyle \frac{3}{2}}$, ${\displaystyle \frac{{\mathrm{{\rm Y}}}_{\mathrm{N}}}{2\mathrm{\pi }}}$ = 11.285 MHz/T), and ⁶⁵Cu (I = ${\displaystyle \frac{3}{2}}$, ${\displaystyle \frac{{\mathrm{{\rm Y}}}_{\mathrm{N}}}{2\mathrm{\pi }}}$ = 12.089 MHz/T) nuclei were conducted using a laboratory-built, phase-coherent spin-echo pulse spectrometer. A high-homogeneity magnetic field was generated by a custom-built magnet from Oxford Instruments. The power amplifiers from JEOL Ltd. (Tokyo, Japan) were used to generate adjustable radio frequency pulses to excite the nuclear-spin system, while the pulse generator and the NMR probe were lab-built. The ³¹P, ⁶³Cu, and ⁶⁵Cu NMR spectra were obtained by Fourier transform of the Hahn spin-echo signals at magnetic fields μ₀H of 7.3685 T, 7.3685 T, and 6.8784 T, respectively. To avoid the ^63/65Cu NMR contribution of an NMR coil, a silver coil was used. The 1/T₁ was measured with a saturation recovery method. 1/T₁ at each temperature was determined by fitting the nuclear magnetization M versus time t using the exponential function 1 − M(t)/M(∞) = $e^{{-\left({\displaystyle \frac{t}{T_1}}\right)}^{\beta }}$, where M(t) and M(∞) are the nuclear magnetization at time t after the saturation and the equilibrium nuclear magnetization at t → ∞, respectively. Here, β is the stretching exponent. A fit with β < 1 indicates a distribution of relaxation rates. For ³¹P NMR, the recovery curves were fit with a nearly temperature-independent value of β~0.65. On the other hand, single exponential behaviors of the nuclear recovery curves were found for the ^63/65Cu NMR measurements. The nuclear spin–spin relaxation rate 1/T₂ for ³¹P at each temperature was determined by fitting the decay curve of nuclear magnetization M measured at 2τ using the exponential function M(2τ) = M(0) $e^{{-\left({\displaystyle \frac{2\tau }{T_2}}\right)}^{{\beta }^{\prime }}}$, where τ is the time interval between the first π/2 pulse and the second π pulse, M(2τ) is the nuclear magnetization for pulse separation τ, M(0) is a fitting parameter corresponding to the nuclear magnetization at time τ = 0, and β′ is the stretching exponent. β′ was found to be around 1.5 and nearly temperature-independent.

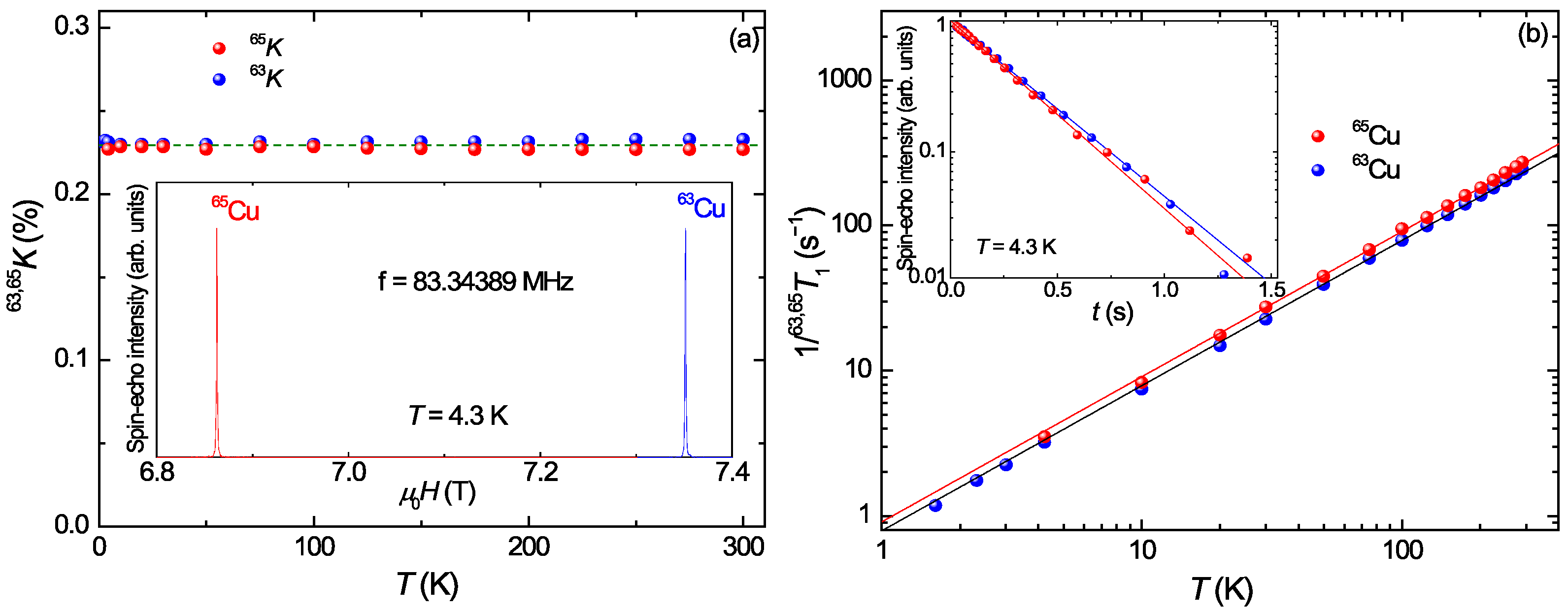
3. Results and Discussion

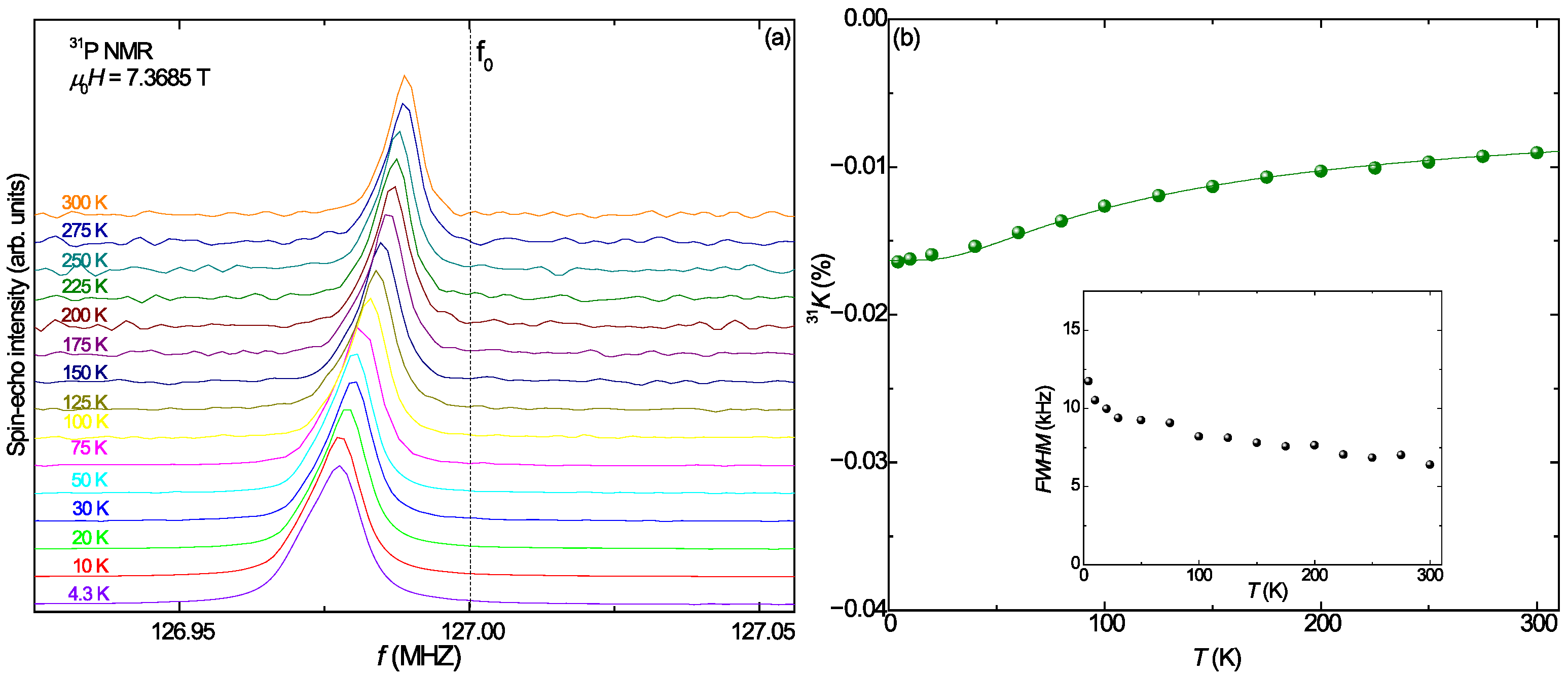
3.1. ³¹P NMR Spectra

Figure 1a shows the temperature dependence of the ³¹P NMR spectra of Pb_10−xCu_x(PO₄)₆O measured under μ₀H = 7.3685 T. The Larmor frequency f₀ is also shown in the figure. The observed spectra are relatively sharp, whose full width at half maximum (FWHM) is 6.41 kHz (= 3.72 Oe) at 300 K and increases slightly with decreasing temperature, as shown in the inset in Figure 1b. The peak position of the ³¹P NMR spectra shifts very little as temperature decreases. The temperature dependence of NMR shift for ³¹P, ³¹K, determined by the peak position, is shown in Figure 1b, where ³¹K decreases slightly as the temperature lowers from −0.009(1)% at room temperature to −0.016(1)% at 4.2 K. Since the NMR shift is related to static magnetic susceptibility (χ), the small negative ³¹K could be due to the diamagnetism observed in the magnetic susceptibility of this material [6]. It is noted that, although the magnetic susceptibility shows an increase at low temperatures, we did not observe such a change in ³¹K corresponding to the increase in χ at low temperatures [6,11]. Thus, we conclude that the increase in magnetic susceptibility at low temperatures is not intrinsic but extrinsic, coming from impurity phases.

As we will show below, almost no Pb atoms are replaced by Cu atoms in our powder sample Pb_10−xCu_x(PO₄)₆O (that is, x~0). The small magnitude of ³¹K suggests no obvious magnetism in our sample and a non-magnetic semiconducting ground state of Pb_10-xCu_x(PO₄)₆O with x~0, where ³¹K is expected to be temperature-independent. The small temperature dependence of ³¹K, therefore, could originate from carriers due to thermal excitation. In semiconductors, the NMR shift is known to be proportional to T^1/2*exp(−∆/2k_BT), where ∆ is the magnitude of the energy gap between the top of the valence band and the bottom of the conduction band [26]. However, the temperature dependence of ³¹K could not be reproduced by this formula. Instead, we found that the temperature dependence of ³¹K can be reproduced by a simple thermal activation form of ³¹K = K₀ + A × exp(−∆/k_BT) with K₀ = −0.0163%, A = 0.0105%, and ∆/k_B = 110 K, as shown by the solid curve in Figure 1b. Here, K₀ is the temperature-independent part of ³¹K, which originates from diamagnetism. At present, we do not have any clear idea of how to explain the temperature dependence of ³¹K. However, similar temperature dependence of the NMR shift has been observed in several semiconductors, such as PbTe [27], and topological insulators (Bi,Sb)(Te,Se,S) [28,29], where the thermal activation behavior is considered to originate from the thermally excited carriers. It is noted that the magnitude of ∆~110(5) K (=9.5 meV) is much smaller than the band gap (200–500 meV) between the valence and conduction bands reported from the temperature dependence of resistivity measurements [11,30]. Thus, the small activation energy may suggest the existence of an impurity band between the valence and conduction bands.

3.2. Nuclear Spin–Lattice Relaxation Rate 1/³¹T₁ and Nuclear Spin–Spin Relaxation Rate 1/³¹T₂

We also carried out measurements of the nuclear spin–lattice relaxation rate 1/T₁ of ³¹P NMR to derive further information on the physical properties of Pb_10−xCu_x(PO₄)₆O. The inset in Figure 2a shows typical recovery curves at 100 and 300 K, where the solid curves are the fits when using the stretched exponential function with 1/T₁ = 0.05 (1/s) and β = 0.63(4), and 1/T₁ = 0.02 (1/s) and β = 0.66(2) for T = 100 K and 300 K, respectively. The temperature dependence of the estimated 1/T₁ is shown in Figure 2a, where 1/T₁ decreases gradually from 300 K to ~50 K and then becomes nearly independent of temperature at low temperatures. The relatively small values of 1/T₁ suggest a non-magnetic insulating ground state without any obvious magnetic fluctuations in Pb_10−xCu_x(PO₄)₆O, consistent with ³¹K data shown above.

In semiconductors, the temperature dependence of 1/T₁ is expected to be 1/T₁~T²*exp(−∆/2k_BT) [26]. However, the experimental data cannot be reproduced by the formula at all. Instead, similar to the case of ³¹K, we found that the 1/T₁ data between ~60 K and 300 K can be roughly reproduced by the simple thermal activation form of 1/T₁ = A′ × exp(−∆/k_BT) with A′ = 0.07 (1/s) and ∆/k_B = 110(20) K, as shown by the solid curve in Figure 2a. Below ~60 K, 1/³¹T₁ deviates from the fitting; although we do not know the origin, it is most likely due to a small quantity of impurities, which may produce a small increase in FWHM at low temperatures, as observed.

As shown above, our NMR spectra and 1/T₁ measurements of ³¹P indicate that the system has a non-magnetic insulating ground state without any phase transitions below 300 K. We did not find any trace of phase transitions either in the temperature dependence of the ³¹P spin–spin relaxation rate 1/³¹T₂ shown in Figure 2b, where 1/³¹T₂ increases slightly and smoothly with a decreasing temperature, evidencing no phase transition below 300 K.

Several theoretical studies indicate that the dominant contribution to the flat bands in Pb_10−xCu_x(PO₄)₆O is from Cu d-electrons [12,13,14,15,16,17,18,19,20]. Therefore, since magnetic fluctuations, if they exist, are expected to originate from the Cu d electrons, NMR measurements on Cu sites are very important. Thus, we carried out ^63/65Cu NMR measurements on the Pb_10−xCu_x(PO₄)₆O powder sample. We observed very sharp ^63/65Cu NMR lines, as shown in the inset of Figure 3a. We examined the observed ^63/65NMR lines from the temperature dependencies of NMR shifts (Figure 3a) and 1/T₁ (Figure 3b) measurements. The observed NMR shift of K~0.23% and 1/T₁ data (1/T₁T = 0.79 (1/sK) for ⁶³Cu and 1/T₁T = 0.91 (1/sK) for ⁶⁵Cu) are the same as those in Cu metals [31]. Therefore, we conclude that the observed Cu signals are from Cu metals, not from Cu ions in Pb_10-xCu_x(PO₄)₆O if any Cu atoms exist. We also tried to search for any other ^63/65Cu NMR signal; however, no other NMR signal was detected. Thus, our NMR results suggest that no copper or only very little copper substitutes for Pb in our Pb_10−xCu_x(PO₄)₆O powder sample, which was synthesized by sintering Pb₂SO₅ and Cu₃P.

It is worth mentioning that we do not observe any ^63/65Cu NMR signals from Cu₃P in our powder sample. This is consistent with no observation of any trace of ³¹P NMR signals from a metallic Cu₃P in which K = 0.012% and 1/T₁T = 0.21 (1/sK) for ³¹P NMR were reported [32]. Thus, we consider that most starting materials of Cu₃P reacted in forming Cu metal or Cu₂S. This conclusion is supported by the fact that a lot of copper metal was observed in the sample studied here [6], and by the observation of other copper compounds in the sample prepared by similar preparation methods [33,34]. Actually, recent studies based on DFT suggest that, since the substitutional formation energy is large, Cu substitution is highly thermodynamically disfavored and the incorporation of Cu at the Pb sites proves to be extremely difficult [18]. Here, our NMR measurements revealed that almost no Pb atoms are replaced by Cu atoms in our Pb_10−xCu_x(PO₄)₆O powder sample (that is, x~0), consistent with the theoretical prediction [18]. It is also noted that no ^63/65Cu NMR signals from Cu₂S were detected in our measurements, suggesting that not much Cu₂S is present in our powder sample. Quite recently, single crystals of Pb_10−xCu_x(PO₄)₆O have been successfully synthesized via the traveling solvent floating zone growth method [35]. The measurements on the single crystals confirmed the non-magnetic insulating state of Pb_10−xCu_x(PO₄)₆O. In the single crystals, EDS measurements indicate that there are Cu atoms in the single crystal, but x was found to be around 0.5 on average with a very large distribution of copper content between 0.1 and ~1 throughout the sample. As described above, no observation of magnetic fluctuations has been found in our Pb_10−xCu_x(PO₄)₆O powder sample with x~0, and this is most likely due to the lack of Cu substitution. Therefore, it is interesting to perform NMR measurements on single crystals to see whether magnetic fluctuations exist or not, even though x is distributed.

4. Conclusions

In summary, we have performed ³¹P and ^63/65Cu NMR measurements on a Pb_10−xCu_x(PO₄)₆O powder sample prepared by sintering Pb₂SO₅ and Cu₃P. From the results of ^63/65Cu NMR measurements, we have concluded that most starting materials of Cu₃P react in forming Cu metal or Cu₂S and that the value of x in our Pb_10−xCu_x(PO₄)₆O is close to 0, showing that almost no Pb atoms are replaced by Cu atoms with this sample preparation method. From ³¹P NMR measurements, the non-magnetic insulating state has been revealed for Pb_10−xCu_x(PO₄)₆O with x~0. Thus, we consider that most previous experimental studies on Pb_10−xCu_x(PO₄)₆O powder samples might only have measured Pb₁₀(PO₄)₆O or one with very little copper doping. Further studies are urgently required to shed light on the intrinsic physical properties of Cu-substituted Pb_10−xCu_x(PO₄)₆O.