The Effects of Fiber Concentration, Orientation, and Aspect Ratio on the Frontal Polymerization of Short Carbon-Fiber-Reinforced Composites: A Numerical Study
Abstract
1. Introduction
2. Theory
3. Determination of FP Cure Kinetics Reaction Parameters

4. Simulation Model
5. Model Validation
6. Results and Discussion
- All short carbon fibers are assumed to have a constant diameter (based on manufacturer datasheets), and their lengths are varied systematically to achieve specific aspect ratios ranging from 50 to 500. Fibers are modeled as straight, rigid rods with no curvature, waviness, or tapering, ensuring uniform geometry across simulations.
- Fibers are distributed within the matrix domain using a randomly aligned, non-overlapping algorithm that does not account for physical agglomeration or clustering effects commonly observed in real composite manufacturing. Each fiber acts independently, with no interaction or contact with neighboring fibers.
- This study assumes in-plane (2D) fiber alignment at defined angles (e.g., 0°, 15°, 30°) to enable controlled evaluation of orientation effects. This assumption is relevant to processes with partial fiber alignment.
| Variations in Fiber Concentration (Vf) Analyzed When Aspect Ratio Is 100 and Orientation Angle Is 0° | Variations in Fiber Orientation (FO) Analyzed When Fiber Volume Is 20% and the Aspect Ratio Is 50 | Variations in Aspect Ratio (AR) Analyzed When Fiber Volume Is 20% and Orientation Angle Is 0° |
|---|---|---|
| 10% | 0° | 50 |
| 20% | 15° | 100 |
| 30% | 30° | 200 |
| 45° | 300 | |
| 60° | 400 | |
| 75° | 500 |
6.1. Effect of Fiber Concentrations
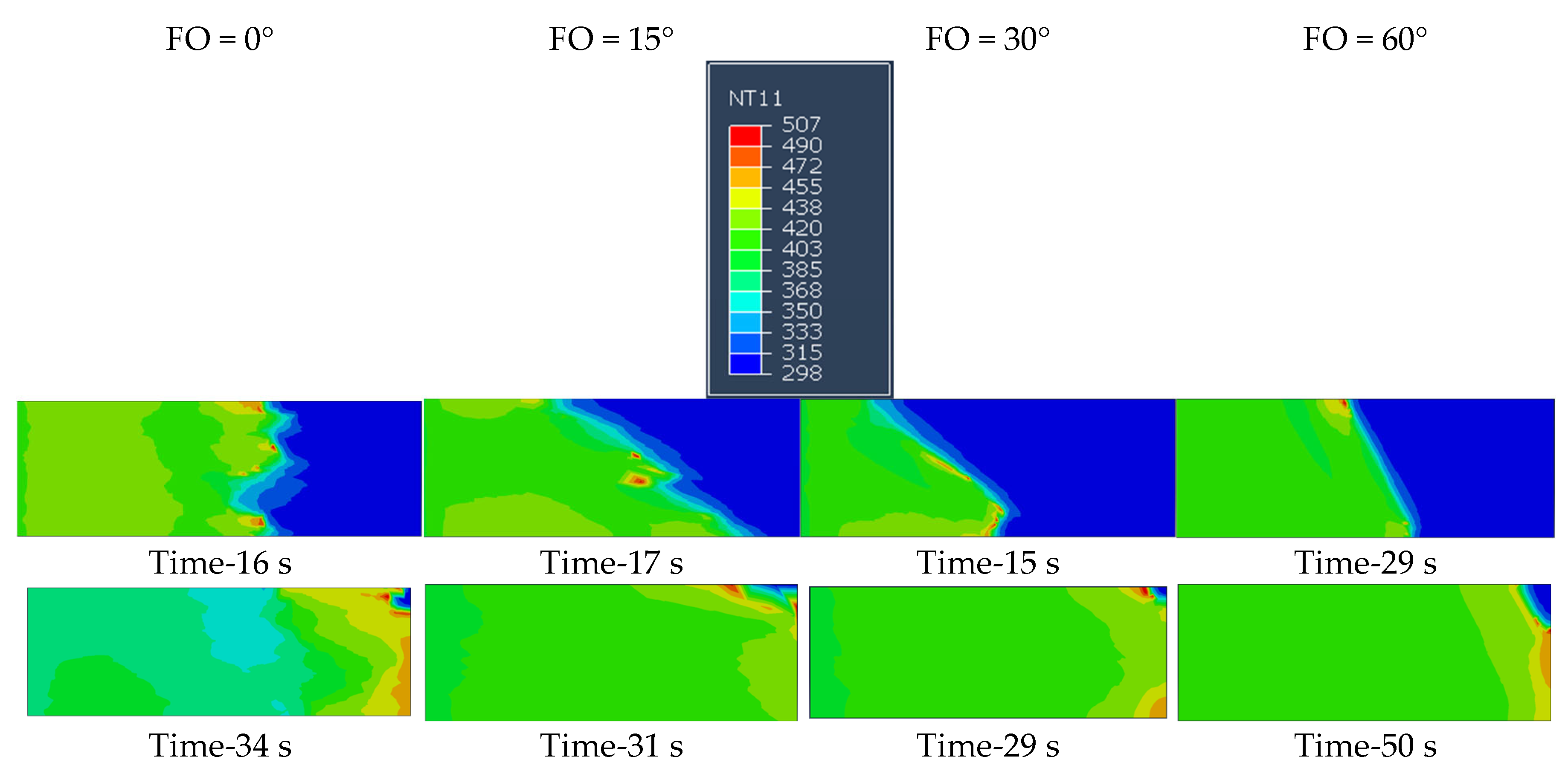
6.2. Effect of Fiber Orientation
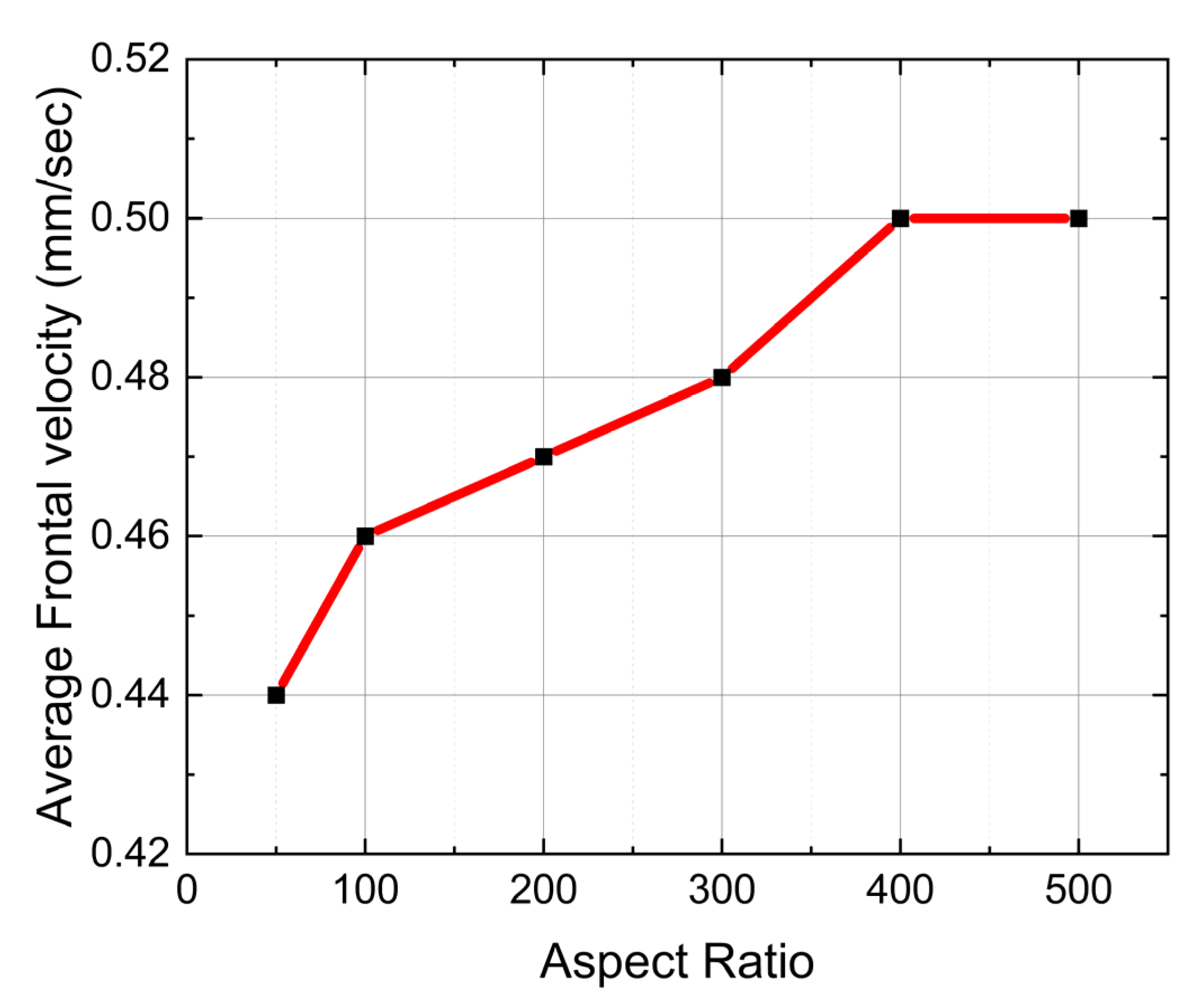
6.3. Effect of Aspect Ratio
7. Conclusions
- The fiber concentrations in terms of volume fraction significantly influence the degree of cure, reaction temperature distribution, and velocity in frontal polymerization of short SCF/Ep composites. The cure time is reduced from 40 s to 28 s as the SCF volume percentage increases from 10% to 30%.
- The orientation of the short fibers also significantly affects the curing dynamics, with specific angles facilitating better heat transfer and resulting in faster polymerization. The highest (0.52 mm/s) and lowest (0.25 mm/s) frontal velocity is observed for fiber orientations of 30 degrees and 75 degrees, respectively. The curing reaction also follows the path of fiber orientation.
- The fiber aspect ratio shows some influence on polymerization time and reaction temperature distribution in low fiber aspect ratios (50–400), but the frontal velocity remains the same above a fiber aspect ratio of 400.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suslick, B.A.; Hemmer, J.; Groce, B.R.; Stawiasz, K.J.; Geubelle, P.H.; Malucelli, G.; Mariani, A.; Moore, J.S.; Pojman, J.A.; Sottos, N.R. Frontal Polymerizations: From Chemical Perspectives to Macroscopic Properties and Applications. Chem. Rev. 2023, 123, 3237–3298. [Google Scholar] [CrossRef] [PubMed]
- Robertson, I.D.; Yourdkhani, M.; Centellas, P.J.; Aw, J.E.; Ivanoff, D.G.; Goli, E.; Lloyd, E.M.; Dean, L.M.; Sottos, N.R.; Geubelle, P.H.; et al. Rapid Energy-Efficient Manufacturing of Polymers and Composites Via Frontal Polymerization. Nature 2018, 557, 223. [Google Scholar] [CrossRef] [PubMed]
- Esposito, G.; Tandon, G.; Abbott, A.; Butcher, D.; Koerner, H. Frontal polymerization for UV- and thermally initiated EPON 826 resin. Polym. Eng. Sci. 2024, 64, 4760–4773. [Google Scholar] [CrossRef]
- Bomze, D.; Knaack, P.; Koch, T.; Jin, H.; Liska, R. Radical induced cationic frontal polymerization as a versatile tool for epoxy curing and composite production. J. Polym. Sci. Part Polym. Chem. 2016, 54, 3751–3759. [Google Scholar] [CrossRef]
- Gary, D.P.; Ngo, D.; Bui, A.; Pojman, J.A. Charge transfer complexes as dual thermal/photo initiators for free-radical frontal polymerization. J. Polym. Sci. 2022, 60, 1624–1630. [Google Scholar] [CrossRef]
- Groce, B.R.; Ferguson, M.M.; Pojman, J.A. Thermally initiated cationic frontal polymerization of epoxies and vinyl ethers through a lone onium salt. J. Polym. Sci. 2023, 61, 3149–3158. [Google Scholar] [CrossRef]
- Staal, J.; Smit, E.; Caglar, B.; Michaud, V. Thermal management in radical induced cationic frontal polymerisation for optimised processing of fibre reinforced polymers. Compos. Sci. Technol. 2023, 237, 110009. [Google Scholar] [CrossRef]
- Topkaya, T.; Gao, Y.; Geubelle, P. Frontal Polymerization in Short-Fiber-Reinforced Thermoset Composites. ACS Appl. Polym. Mater. 2022, 4, 6880–6886. [Google Scholar] [CrossRef]
- Abasi, F.O.; Aabass, R.U. Thermo-mechanical behavior of epoxy composite reinforced by carbon and Kevlar fiber. MATEC Web Conf. 2018, 225, 01022. [Google Scholar] [CrossRef]
- Pokharel, A.; Falua, K.J.; Babaei-Ghazvini, A.; Acharya, B. Biobased Polymer Composites: A Review. J. Compos. Sci. 2022, 6, 255. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Xian, G. Hygrothermal effects on high VF pultruded unidirectional carbon/epoxy composites: Moisture uptake. Compos. Part B Eng. 2009, 40, 41–49. [Google Scholar] [CrossRef]
- Ramírez-Herrera, C.A.; Cruz-Cruz, I.; Jiménez-Cedeño, I.H.; Martínez-Romero, O.; Elías-Zúñiga, A. Influence of the Epoxy Resin Process Parameters on the Mechanical Properties of Produced Bidirectional [±45°] Carbon/Epoxy Woven Composites. Polymers 2021, 13, 1273. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Zhang, J.; Cao, M.; Wang, M.; Gu, B.; Sun, B. A Mesoscale Study of Thermal Expansion Behaviors of Epoxy Resin and Carbon Fiber/Epoxy Unidirectional Composites Based on Periodic Temperature and Displacement Boundary Conditions. Polym. Test. 2016, 55, 44–60. [Google Scholar] [CrossRef]
- Goli, E.; Robertson, I.D.; Agarwal, H.; Pruitt, E.L.; Grolman, J.M.; Geubelle, P.H.; Moore, J.S. Frontal Polymerization Accelerated by Continuous Conductive Elements. J. Appl. Polym. Sci. 2019, 136, 47418. [Google Scholar] [CrossRef]
- Elenchezhian, M.; Enos, R.; Martin, N.; Sen, S.; Zhang, D.; Pantelelis, N. Cure process modeling and characterization of composites using in-situ dielectric and fiber otpic sensor monitoring. In Proceedings of the Composites and Advance Materials Expo (CAMX) 2022, Anaheim, CA, USA, 17–20 October 2022. [Google Scholar]
- Kumar, A.; Gao, Y.; Geubelle, P.H. Analytical Estimates of Front Velocity in the Frontal Polymerization of Thermoset Polymers and Composites. J. Polym. Sci. 2021, 59, 1109. [Google Scholar] [CrossRef]
- Wang, Y. Modeling the through-thickness frontal polymerization of unidirectional carbon fiber thermoset composites: Effect of microstructures. J. Appl. Polym. Sci. 2022, 139, e52735. [Google Scholar] [CrossRef]
- Feng, Q.; Li, F.; Yan, Q.-Z.; Zhu, Y.-C.; Ge, C.-C. Frontal Polymerization Synthesis and Drug Delivery Behavior of Thermo-Responsive Poly(N-Isopropylacrylamide) Hydrogel. Colloid Polym. Sci. 2010, 288, 915. [Google Scholar] [CrossRef]
- Goli, E.; Gai, T.; Geubelle, P.H. Impact of Boundary Heat Losses on Frontal Polymerization. J. Phys. Chem. B 2020, 124, 6404. [Google Scholar] [CrossRef]
- Sharifi, A.M.; Kwon, D.-J.; Shah, S.Z.H.; Lee, J. Modeling of frontal polymerization of carbon fiber and dicyclopentadiene woven composites with stochastic material uncertainty. Compos. Struct. 2023, 326, 117582. [Google Scholar] [CrossRef]
- Vyas, S.; Zhang, X.; Goli, E.; Geubelle, P.H. Frontal Vs. Bulk Polymerization of Fiber-Reinforced Polymer-Matrix Composites. Compos. Sci. Technol. 2020, 198, 108303. [Google Scholar] [CrossRef]
- Gao, Y.; Rodriguez Koett, L.E.; Hemmer, J.; Gai, T.; Parikh, N.A.; Sottos, N.R.; Geubelle, P.H. Frontal Polymerization of Thin Layers on a Thermally Insulating Substrate. ACS Appl. Polym. Mater. 2022, 4, 4919. [Google Scholar] [CrossRef]
- Aktas, A.; Krishnan, L.; Kandola, B.; Boyd, S.; Shenoi, R. A cure modelling study of an unsaturated polyester resin system for the simulation of curing of fibre-reinforced composites during the vacuum infusion process. J. Compos. Mater. 2015, 49, 2529–2540. [Google Scholar] [CrossRef]
- Cui, H.-W.; Jiu, J.; Nagao, S.; Sugahara, T.; Suganuma, K.; Uchida, H. Using Ozawa method to study the curing kinetics of electrically conductive adhesives. J. Therm. Anal. Calorim. 2014, 117, 1365–1373. [Google Scholar] [CrossRef]
- Cui, H.-W.; Suganuma, K.; Uchida, H. Using the Ozawa Method to Study the Thermally Initiated Curing Kinetics of Vinyl Ester Resin. RSC Adv. 2015, 5, 2677–2683. [Google Scholar] [CrossRef]
- Yang, G.; Yuan, Z.; Yang, Z.; Zhang, M. Nonisothermal curing kinetics of a novel polymer containing phenylsilylene and propargyl–hexafluorobisphenol a units. J. Appl. Polym. Sci. 2013, 127, 3178–3185. [Google Scholar] [CrossRef]
- Qiao, Y.; Xing, A.; Gao, C.; Yuan, P.; He, Z.; Lv, J.; Li, S.; Xue, P.; Niu, S.; Li, X. A study on cure kinetics and time-temperature-transformation cure diagram of epoxy/cyanate ester co-curing system. Polymer 2025, 324, 128230. [Google Scholar] [CrossRef]
- Puhurcuoğlu, N.; Arman, Y. Parameter estimation of epoxy resin cure kinetics by dynamics DSC data. Polym. Adv. Technol. 2024, 35, e6498. [Google Scholar] [CrossRef]
- Um, M.-K.; Daniel, I.M.; Hwang, B.-S. A study of cure kinetics by the use of dynamic differential scanning calorimetry. Compos. Sci. Technol. 2002, 62, 29–40. [Google Scholar] [CrossRef]
- Patham, B. Multiphysics simulations of cure residual stresses and springback in a thermoset resin using a viscoelastic model with cure-temperature-time superposition. J. Appl. Polym. Sci. 2013, 129, 983–998. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Liu, Y. Construction of improved isothermal TTT cure diagram based on an epoxy–amine thermoset. J. Appl. Polym. Sci. 2019, 136, 47279. [Google Scholar] [CrossRef]
- D’Mello, R.J.; Maiarù, M.; Waas, A.M. Effect of the curing process on the transverse tensile strength of fiber-reinforced polymer matrix lamina using micromechanics computations. Integrating Mater. Manuf. Innov. 2015, 4, 119–136. [Google Scholar] [CrossRef]
- Xiao, H.; He, Q.; Duan, Y.; Wang, J.; Yao, Q.; Ming, Y.; Zhang, C.; Zhu, Y. Low-temperature 3D printing and curing process of continuous fiber-reinforced thermosetting polymer composites. Polym. Compos. 2023, 44, 2322–2330. [Google Scholar] [CrossRef]
- Greenfeld, I.; Shneider, M.; Kaestner, A.; Wagner, H.D. Stiffness modeling of thermoset polymer fibers. J. Polym. Sci. 2024, 62, 2780–2796. [Google Scholar] [CrossRef]
- Tarafdar, A.; Jia, C.; Hu, W.; Hosein, I.D.; Fu, K.; Wang, Y. Three-dimensional modeling of frontal polymerization for rapid, efficient, and uniform thermoset composites manufacturing. Compos. Part B Eng. 2023, 266, 111029. [Google Scholar] [CrossRef]
- Tiani, R.; Pojman, J.A.; Rongy, L. Critical Role of Layer Thickness in Frontal Polymerization. J. Phys. Chem. B 2022, 126, 3607. [Google Scholar] [CrossRef]
- Ziaee, M.; Naseri, I.; Johnson, J.W.; Franklin, K.A.; Yourdkhani, M. Frontal Polymerization and Three-Dimensional Printing of Thermoset Polymers with Tunable Thermomechanical Properties. ACS Appl. Polym. Mater. 2023, 5, 1715–1724. [Google Scholar] [CrossRef]
- Vyas, S.; Goli, E.; Zhang, X.; Geubelle, P.H. Manufacturing of Unidirectional Glass-Fiber-Reinforced Composites Via Frontal Polymerization: A Numerical Study. Compos. Sci. Technol. 2019, 184, 107832. [Google Scholar] [CrossRef]
- Yi, X.; Li, S.; Wen, P.; Yan, S. Numerical Simulation of Polyacrylamide Hydrogel Prepared via Thermally Initiated Frontal Polymerization. Polymers 2024, 16, 873. [Google Scholar] [CrossRef]
- Shams, A.T.; Papon, E.A.; Shinde, P.S.; Bara, J.; Haque, A. Degree of Cure, Microstructures, and Properties of Carbon/Epoxy Composites Processed via Frontal Polymerization. Polymers 2024, 16, 1493. [Google Scholar] [CrossRef]
- Du, S.; Guo, Z.-S.; Zhang, B.; Wu, Z. Cure kinetics of epoxy resin used for advanced composites. Polym. Int. 2004, 53, 1343–1347. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, X. Autocatalytic curing kinetics of thermosetting polymers: A new model based on temperature dependent reaction orders. Polymer 2010, 51, 3814–3820. [Google Scholar] [CrossRef]
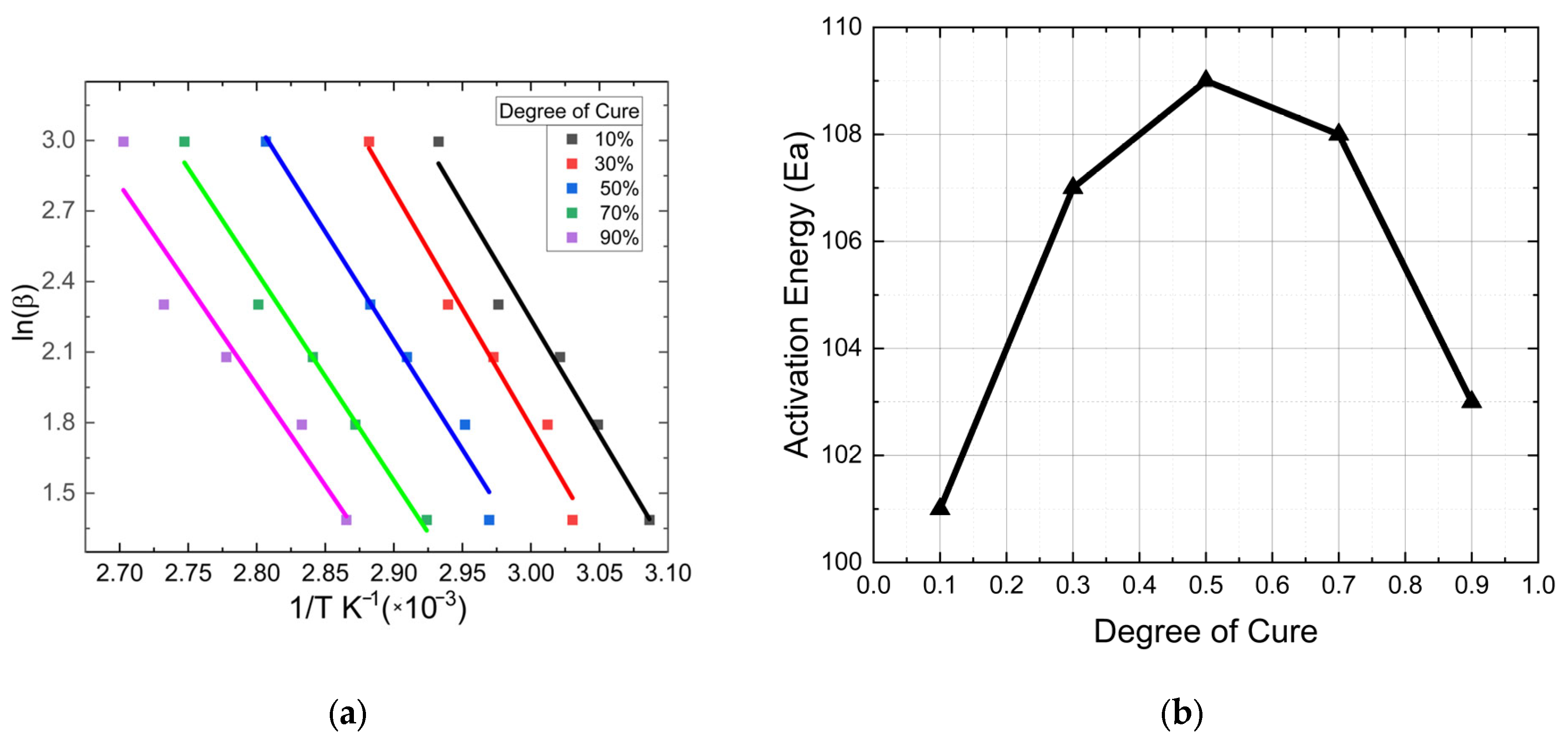




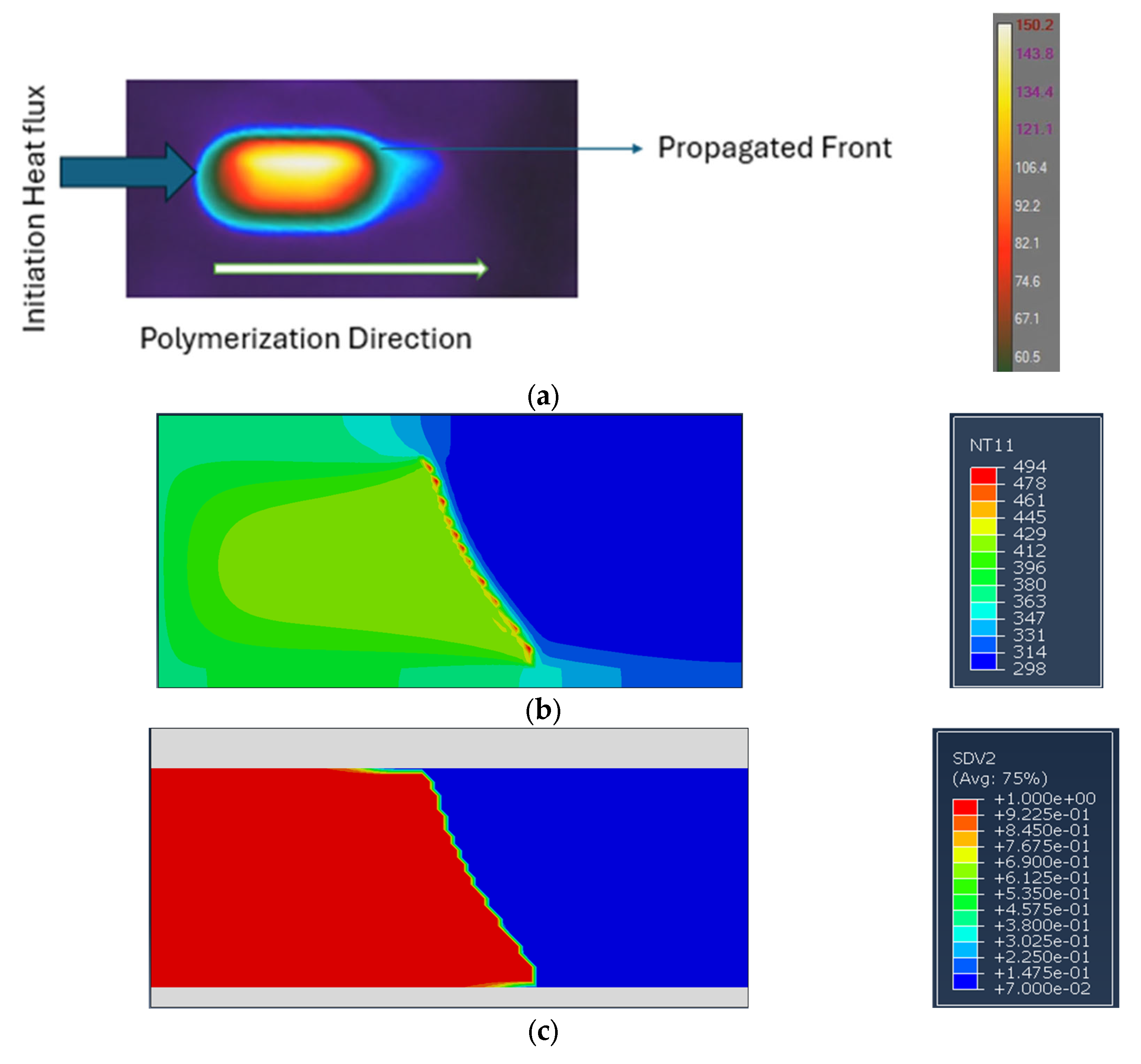

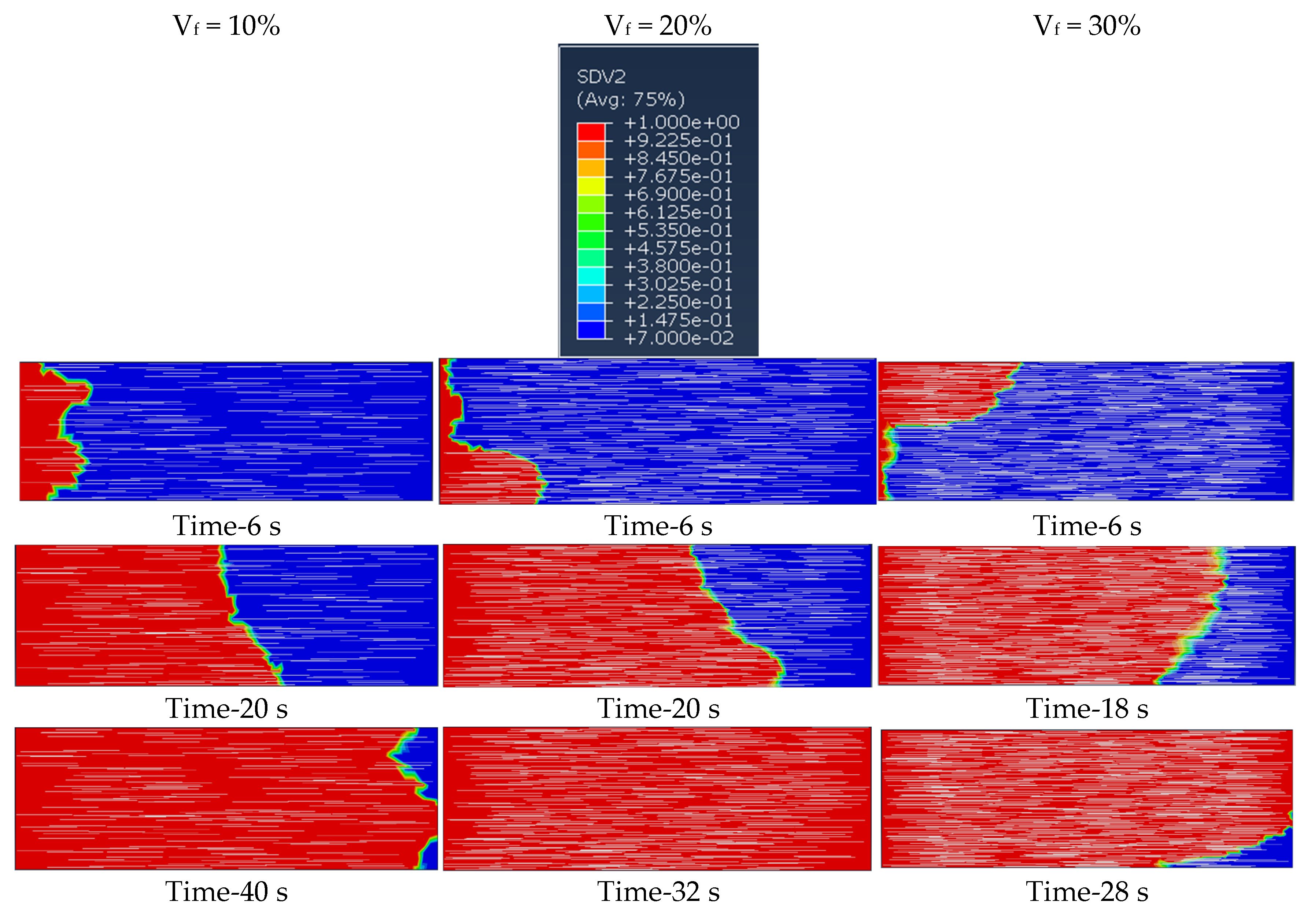


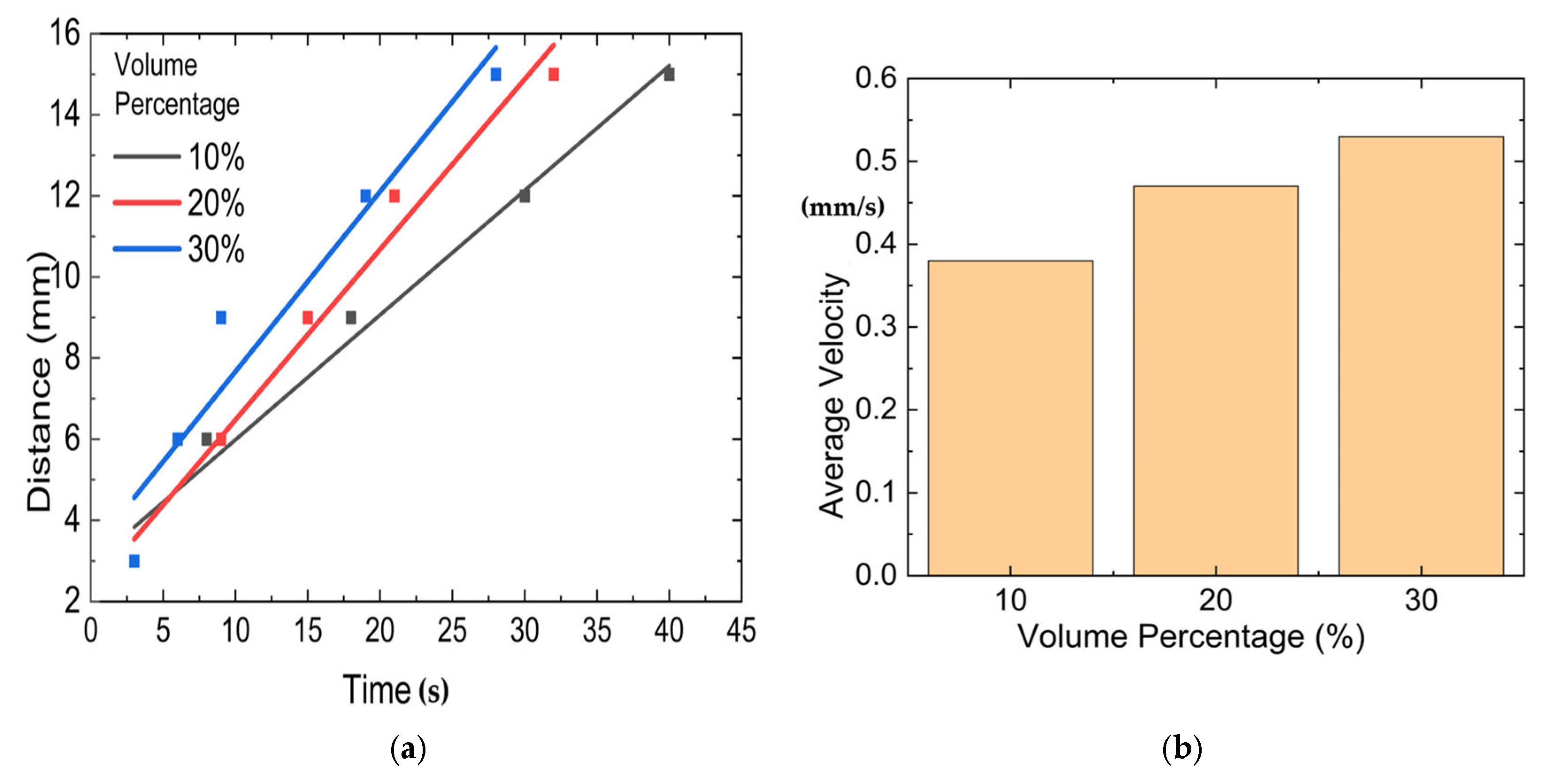



| Heating Rate | m + n | m − n | m | n | ln A |
|---|---|---|---|---|---|
| 5 | 2.81 | 1.08 | 1.96 | 0.74 | 31.017 |
| 10 | 2.79 | 1.04 | 1.94 | 0.79 | 30.914 |
| 15 | 2.75 | 0.98 | 1.85 | 0.87 | 30.896 |
| 20 | 2.73 | 0.97 | 1.81 | 0.89 | 30.873 |
| Average | 2.76 | 1.02 | 1.89 | 0.87 | 30.895 |
| Material | Density (ρ) kg/m3 | Thermal Conductivity, k (W/m·K) | Specific Heat Cp (J/kg·K) | Total Enthalpy of Reaction Hr (J/g) |
|---|---|---|---|---|
| Epoxy (Epon-828) | 1200 | 0.2 | 1750 | 410 |
| Glass | 2230 | 1.14 | 800 | - |
| Carbon Fiber | 1760 | 10.45 | 795 | - |
| Fiber Orientation Angle | 0° | 15° | 30° | 45° | 60° | 75° |
|---|---|---|---|---|---|---|
| Average Velocity (mm/s) | 0.44 | 0.48 | 0.52 | 0.37 | 0.30 | 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shams, A.T.; Papon, E.A.; Haque, A. The Effects of Fiber Concentration, Orientation, and Aspect Ratio on the Frontal Polymerization of Short Carbon-Fiber-Reinforced Composites: A Numerical Study. J. Compos. Sci. 2025, 9, 307. https://doi.org/10.3390/jcs9060307
Shams AT, Papon EA, Haque A. The Effects of Fiber Concentration, Orientation, and Aspect Ratio on the Frontal Polymerization of Short Carbon-Fiber-Reinforced Composites: A Numerical Study. Journal of Composites Science. 2025; 9(6):307. https://doi.org/10.3390/jcs9060307
Chicago/Turabian StyleShams, Aurpon Tahsin, Easir Arafat Papon, and Anwarul Haque. 2025. "The Effects of Fiber Concentration, Orientation, and Aspect Ratio on the Frontal Polymerization of Short Carbon-Fiber-Reinforced Composites: A Numerical Study" Journal of Composites Science 9, no. 6: 307. https://doi.org/10.3390/jcs9060307
APA StyleShams, A. T., Papon, E. A., & Haque, A. (2025). The Effects of Fiber Concentration, Orientation, and Aspect Ratio on the Frontal Polymerization of Short Carbon-Fiber-Reinforced Composites: A Numerical Study. Journal of Composites Science, 9(6), 307. https://doi.org/10.3390/jcs9060307






