Parametric Optimization of Dry Sliding Wear Attributes for AlMg1SiCu Hybrid MMCs: A Comparative Study of GRA and Entropy-VIKOR Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of Composites
Design of Experiments
2.2. MCDM/MADM Techniques
2.2.1. Grey Relational Analysis (GRA)
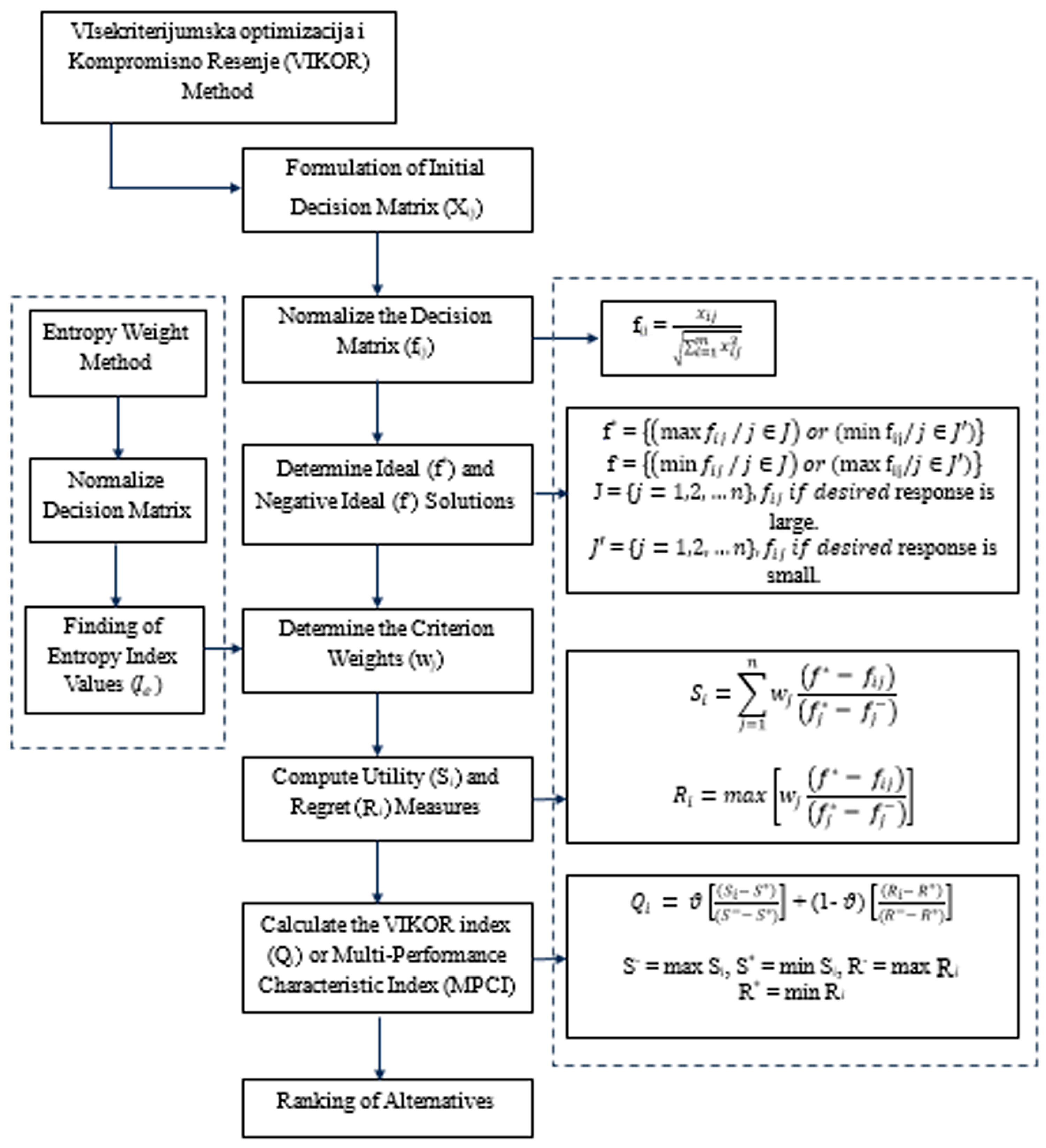
2.2.2. VIKOR Analysis
3. Results and Discussion
3.1. Grey Analysis
3.1.1. Taguchi Analysis
3.1.2. Analysis of Variance (ANOVA)
3.2. Entropy-VIKOR Analysis
Response Surface Methodology (RSM)
3.3. Comparison of Grey and Entropy-VIKOR Approaches
3.4. Morphologies of Worn-Out Surfaces
4. Conclusions
- The ultrasonic stir-casting process effectively overcomes the limitations of conventional methods by enhancing particle dispersion, reducing porosity, and improving matrix-reinforcement bonding, leading to superior wear resistance properties;
- The grey analysis identified the optimal process parameters for minimizing the multi-responses of wear features, at 10 wt.% reinforcement content, 50 N load, 2.5 m/s sliding velocity, and 750 m sliding distance;
- ANOVA and signal-to-noise (S/N) ratio results indicate that reinforcement content is the most influential factor, while sliding velocity has the least impact on the multi-response value of the GRG;
- A multi-order regression model for the VIKOR index (Qi) demonstrated high accuracy, with a variance of 0.0216, a coefficient of determination (R2) value of 99.60%, and an adjusted R2 of 99.14%;
- Entropy-weighted VIKOR analysis combined with response surface methodology (RSM) offers greater insights and higher accuracy than Taguchi grey relational analysis;
- Morphological studies revealed that wear mechanisms are predominantly driven by plowing, abrasion, and adhesion;
- The combination of GRA and entropy-VIKOR provides a robust, data-driven approach for multi-criteria optimization, reducing subjective bias and ensuring balanced performance evaluation, making it ideal for complex composite systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RF | Reinforcement Content (wt.%) |
| N | Normal Load |
| v | Sliding Velocity |
| SD | Sliding Distance |
| OA | Orthogonal Array |
| GRC | Grey Relational Coefficient |
| GRG | Grey Relational Grade |
| Ie | Entropy Index |
| Si | Utility Measure |
| Ri | Regret Measure |
| Qi | VIKOR Index |
References
- Singh, J.; Chauhan, A. A review of microstructure, mechanical properties and wear behavior of hybrid aluminium matrix composites fabricated via stir casting route. Sadhana 2019, 44, 16. [Google Scholar] [CrossRef]
- Krstic, J.; Jovanovic, J.; Gajevic, S.; Miladinovic, S.; Vaxevanidis, N.M.; Kiss, I.; Stojanovic, B. Application of Metal Matrix Nanocomposites in Engineering. Adv. Eng. Lett. 2024, 3, 180–190. [Google Scholar] [CrossRef]
- Kumar, S.; Singh, R.; Hashmi, M.S.J. Metal matrix composite: A methodological review. Adv. Mater. Process. Technol. 2020, 6, 13–24. [Google Scholar] [CrossRef]
- Ramanathan, A.; Krishnan, P.K.; Muraliraja, R. A review on the production of metal matrix composites through stir casting–Furnace design, properties, challenges, and research opportunities. J. Manuf. Process. 2019, 42, 213–245. [Google Scholar] [CrossRef]
- Singh, L.; Singh, B.; Saxena, K.K. Manufacturing techniques for metal matrix composites (MMC): An overview. Adv. Mater. Process. Technol. 2020, 6, 441–457. [Google Scholar] [CrossRef]
- Ravishankar, B.; Nayak, S.K.; Kader, M.A. Hybrid composites for automotive applications—A review. J. Reinf. Plast. Compos. 2019, 38, 835–845. [Google Scholar] [CrossRef]
- Aynalem, G.F. Processing methods and mechanical properties of aluminium matrix composites. Adv. Mater. Sci. Eng. 2020, 2020, 3765791. [Google Scholar] [CrossRef]
- Samal, P.; Vundavilli, P.R.; Meher, A.; Mahapatra, M.M. Recent progress in aluminum metal matrix composites: A review on processing, mechanical and wear properties. J. Manuf. Process. 2020, 59, 131–152. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, W.; Li, G.; Guan, F.; Yu, Y.; Fan, Z. Microstructure and mechanical properties of SiCnp/Al6082 aluminum matrix composites prepared by squeeze casting combined with stir casting. J. Mater. Process. Technol. 2020, 283, 116699. [Google Scholar] [CrossRef]
- Surya, M.S.; Prasanthi, G. Effect of silicon carbide weight percentage and number of layers on microstructural and mechanical properties of Al7075/SiC functionally graded material. Silicon 2022, 14, 1339–1348. [Google Scholar] [CrossRef]
- Sakthivelu, S.; Sethusundaram, P.P.; Ravichandran, M.; Meignanamoorthy, M. Experimental investigation and analysis of properties and dry sliding wear behavior of Al-Fe-Si alloy matrix composites. Silicon 2021, 13, 1285–1294. [Google Scholar] [CrossRef]
- Manikandan, R.; Arjunan, T.V. Mechanical and tribological behaviors of aluminium hybrid composites reinforced by CDA-B4C. Mater. Res. Express 2020, 7, 016584. [Google Scholar] [CrossRef]
- Vithal, D.N.; Krishna, B.B.; Krishna, G.M. Microstructure, mechanical properties and fracture mechanisms of ZrB2 ceramic reinforced A7075 composites fabricated by stir casting. Mater. Today Commun. 2020, 25, 101289. [Google Scholar] [CrossRef]
- Dey, D.; Bhowmik, A.; Biswas, A. Effect of SiC content on mechanical and tribological properties of Al2024-SiC composites. Silicon 2022, 14, 1–11. [Google Scholar] [CrossRef]
- Jojith, R.; Radhika, N. Investigation of mechanical and tribological behavior of heat-treated functionally graded Al-7Si/B4C composite. Silicon 2020, 12, 2073–2085. [Google Scholar] [CrossRef]
- Gowrishankar, T.P.; Manjunatha, L.H.; Sangmesh, B. Mechanical and Wear behavior of Al6061 reinforced with Graphite and TiC Hybrid MMCs. Mater. Res. Innov. 2020, 24, 179–185. [Google Scholar] [CrossRef]
- Jayakumar, E.; Praveen, A.P.; Rajan, T.P.D.; Pai, B.C. Studies on tribological characteristics of centrifugally cast SiCp-reinforced functionally graded A319 aluminium matrix composites. Trans. Indian Inst. Met. 2018, 71, 2741–2748. [Google Scholar] [CrossRef]
- David Raja Selvam, J.; Dinaharan, I.; Rai, R.S.; Mashinini, P.M. Dry sliding wear behavior of in-situ fabricated TiC particulate reinforced AA6061 aluminium alloy. Tribol.-Mater. Surf. Interfaces 2019, 13, 1–11. [Google Scholar] [CrossRef]
- Prasad Reddy, A.; Vamsi Krishna, P.; Rao, R.N. Two-body abrasive wear behavior of AA6061-2SiC-2Gr hybrid nanocomposite fabricated through ultrasonically assisted stir casting. J. Compos. Mater. 2019, 53, 2165–2180. [Google Scholar] [CrossRef]
- Bharti, S.; Ghetiya, N.D.; Patel, K.M. Micro-hardness and wear behavior of AA2014/Al2O3 surface composite produced by friction stir processing. SN Appl. Sci. 2020, 2, 1760. [Google Scholar] [CrossRef]
- Kumar, J.; Singh, D.; Kalsi, N.S.; Sharma, S.; Mia, M.; Singh, J.; Rao, K.V. Investigation on the mechanical, tribological, morphological and machinability behavior of stir-casted Al/SiC/Mo reinforced MMCs. J. Mater. Res. Technol. 2021, 12, 930–946. [Google Scholar] [CrossRef]
- Prasad Reddy, A.; Vamsi Krishna, P.; Rao, R.N. Tribological behavior of Al6061–2SiC-xGr hybrid metal matrix nanocomposites fabricated through ultrasonically assisted stir casting technique. Silicon 2019, 11, 2853–2871. [Google Scholar] [CrossRef]
- Aherwar, A.; Ahirwar, A.; Pathak, V.K. Dry sliding tribological characteristics evaluation and prediction of TiB2-CDA/Al6061 hybrid composites exercising machine learning methods. Sci. Rep. 2025, 15, 16710. [Google Scholar] [CrossRef]
- Kumaraswamy, J.; Bharath, L.; Anil, K.C.; Geetha, T.M.; Nagesh, R. Results in mechanical properties and wear behaviour of AA6061-Si3N4 composites. Results Surf. Interfaces 2025, 18, 100376. [Google Scholar] [CrossRef]
- Udaya Prakash, J.; Jebarose Juliyana, S.; Saleem, M.; Moorthy, T.V. Optimisation of dry sliding wear parameters of aluminium matrix composites (356/B4C) using Taguchi technique. Int. J. Ambient. Energy 2021, 42, 140–142. [Google Scholar] [CrossRef]
- Mohanavel, V.; Ravichandran, M. Optimization of parameters to improve the properties of AA7178/Si3N4 composites employing Taguchi approach. Silicon 2022, 14, 1381–1394. [Google Scholar] [CrossRef]
- Reddy, P.V.; Prasad, P.R.; Krishnudu, D.M.; Goud, E.V. An investigation on mechanical and wear characteristics of Al 6063/TiC metal matrix composites using RSM. J. Bio-Tribo-Corros. 2019, 5, 90. [Google Scholar] [CrossRef]
- Surya, M.S.; Prasanthi, G.; Gugulothu, S.K. Investigation of mechanical and wear behaviour of Al7075/SiC composites using response surface methodology. Silicon 2021, 13, 2369–2379. [Google Scholar] [CrossRef]
- Kumar, M. Mechanical and sliding wear performance of AA356-Al2O3/SiC/graphite alloy composite materials: Parametric and ranking optimization using Taguchi DOE and hybrid AHP-GRA method. Silicon 2021, 13, 2461–2477. [Google Scholar] [CrossRef]
- Raju, S.S.; Rao, G.S.; Samantra, C. Wear behavioral assessment of Al-CSAp-MMCs using a grey-fuzzy approach. Measurement 2019, 140, 254–268. [Google Scholar] [CrossRef]
- Ahamad, N.; Mohammad, A.; Sadasivuni, K.K.; Gupta, P. Wear, optimization, and surface analysis of Al-Al2O3-TiO2 hybrid metal matrix composites. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 93–102. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, M.; Pandey, B. Investigations on mechanical and sliding wear performance of AA7075-SiC/marble dust/graphite hybrid alloy composites using hybrid ENTROPY-VIKOR method. Silicon 2022, 14, 2051–2065. [Google Scholar] [CrossRef]
- Dhilip, J.D.J.; Ganesan, K.P.; Sivalingam, V. Machinability studies and optimization of process parameters in wire electrical discharge machining of aluminum hybrid composites by the VIKOR method. J. Mater. Eng. Perform. 2024, 33, 5547–5562. [Google Scholar] [CrossRef]
- ASTM G99; Standard Test Method for Wear Testing with a Pin-on-Disk Apparatus. ASTM International: West Conshohocken, PA, USA, 2017.
- Ch, M.R.; Prasad, K.D.; Subbaiah, K.V. Application of integrated entropy-COPRAS and ANN approaches for maximizing wire EDM machinability attributes of Al6082-T6/GNP/TiB2 composites. Eng. Res. Express 2024, 6, 035535. [Google Scholar] [CrossRef]
- Soni, S.; Gohil, P. Optimization of reinforcement ratio and stirring speed on mechanical properties of Al-TiB2-B4C hybrid composite using Taguchi–grey relational analysis. Mater. Res. Express 2024, 11, 126510. [Google Scholar] [CrossRef]

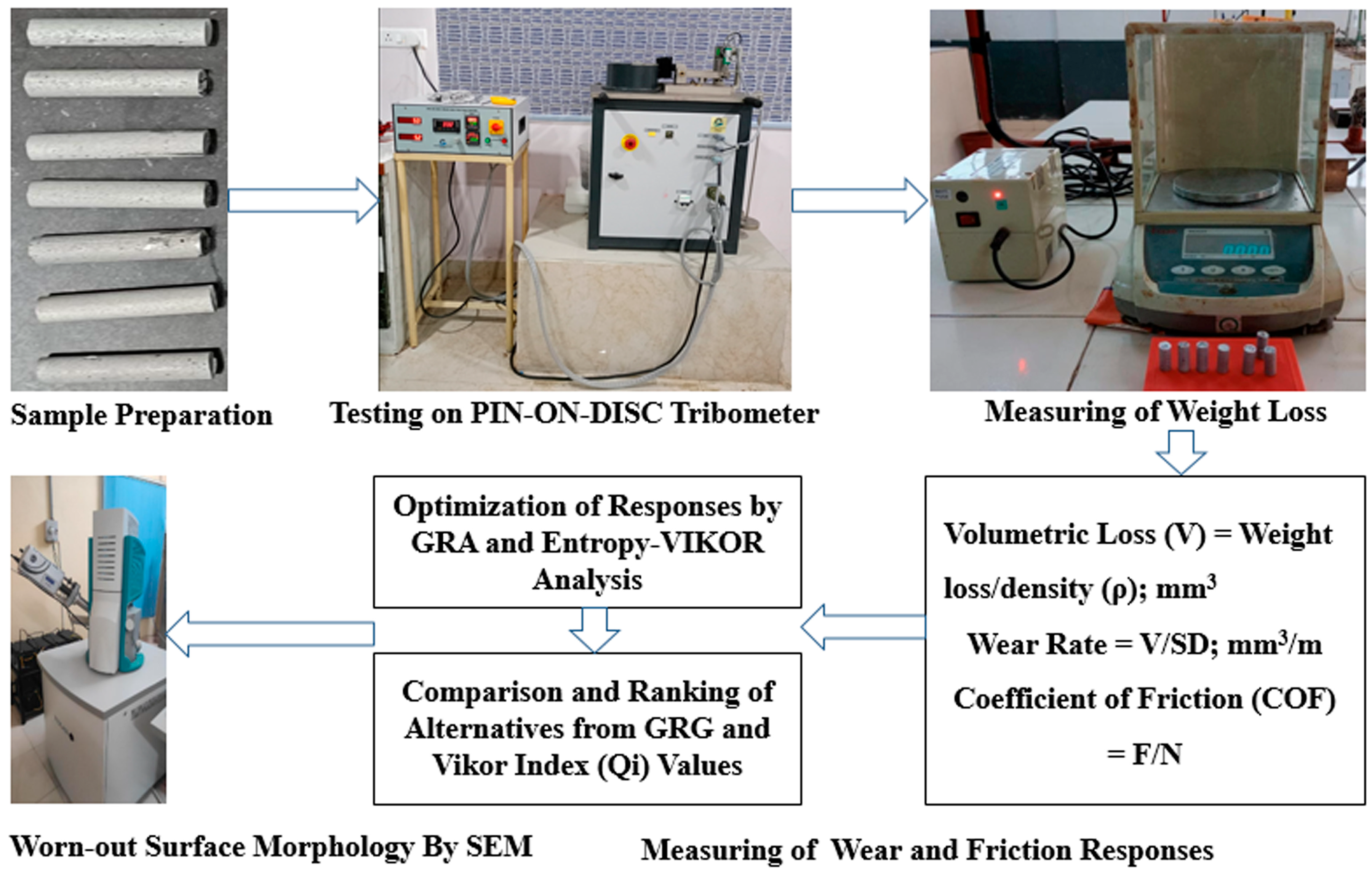






| Parameter | Level 1 | Level 2 | Level 3 |
|---|---|---|---|
| Reinforcement Content, wt.% | 2 | 6 | 10 |
| Normal Load (FN), N | 10 | 30 | 50 |
| Sliding Velocity (v), m/s | 1 | 1.75 | 2.5 |
| Sliding Distance (SD), m | 300 | 525 | 750 |
| S. No. | RF Wt.% | N | v | SD |
|---|---|---|---|---|
| 1 | 2 | 10 | 1 | 300 |
| 2 | 2 | 10 | 1.75 | 525 |
| 3 | 2 | 10 | 2.5 | 750 |
| 4 | 2 | 30 | 1 | 525 |
| 5 | 2 | 30 | 1.75 | 750 |
| 6 | 2 | 30 | 2.5 | 300 |
| 7 | 2 | 50 | 1 | 750 |
| 8 | 2 | 50 | 1.75 | 300 |
| 9 | 2 | 50 | 2.5 | 525 |
| 10 | 6 | 10 | 1 | 525 |
| 11 | 6 | 10 | 1.75 | 750 |
| 12 | 6 | 10 | 2.5 | 300 |
| 13 | 6 | 30 | 1 | 750 |
| 14 | 6 | 30 | 1.75 | 300 |
| 15 | 6 | 30 | 2.5 | 525 |
| 16 | 6 | 50 | 1 | 300 |
| 17 | 6 | 50 | 1.75 | 525 |
| 18 | 6 | 50 | 2.5 | 750 |
| 19 | 10 | 10 | 1 | 750 |
| 20 | 10 | 10 | 1.75 | 300 |
| 21 | 10 | 10 | 2.5 | 525 |
| 22 | 10 | 30 | 1 | 300 |
| 23 | 10 | 30 | 1.75 | 525 |
| 24 | 10 | 30 | 2.5 | 750 |
| 25 | 10 | 50 | 1 | 525 |
| 26 | 10 | 50 | 1.75 | 750 |
| 27 | 10 | 50 | 2.5 | 300 |
| S. No. | V, mm3 | WR, mm3/m | COF |
|---|---|---|---|
| 1 | 9.4347 | 0.0314 | 0.4583 |
| 2 | 7.9917 | 0.0152 | 0.5251 |
| 3 | 6.5118 | 0.0087 | 0.5918 |
| 4 | 6.8448 | 0.013 | 0.4984 |
| 5 | 5.3648 | 0.0072 | 0.5206 |
| 6 | 5.6608 | 0.0189 | 0.4995 |
| 7 | 4.2548 | 0.0057 | 0.5064 |
| 8 | 4.5138 | 0.015 | 0.4937 |
| 9 | 3.0709 | 0.0058 | 0.507 |
| 10 | 6.3289 | 0.0121 | 0.3169 |
| 11 | 4.8938 | 0.0065 | 0.3837 |
| 12 | 5.1882 | 0.0173 | 0.3202 |
| 13 | 3.7532 | 0.005 | 0.4513 |
| 14 | 4.0475 | 0.0135 | 0.4301 |
| 15 | 2.5757 | 0.0049 | 0.4523 |
| 16 | 2.9069 | 0.0097 | 0.4521 |
| 17 | 1.4718 | 0.0028 | 0.4654 |
| 18 | 0.0736 | 0.0001 | 0.4788 |
| 19 | 3.2794 | 0.0044 | 0.1756 |
| 20 | 3.5709 | 0.0119 | 0.112 |
| 21 | 2.1134 | 0.004 | 0.1788 |
| 22 | 2.4413 | 0.0081 | 0.3607 |
| 23 | 0.9838 | 0.0019 | 0.383 |
| 24 | 0.4373 | 0.0006 | 0.4052 |
| 25 | 0.1458 | 0.0003 | 0.4238 |
| 26 | 1.5668 | 0.0021 | 0.4371 |
| 27 | 1.2753 | 0.0043 | 0.4244 |
| S. No. | Normalization (Nij) | Loss Function (∆) | ||||
|---|---|---|---|---|---|---|
| V | WR | COF | V | WR | COF | |
| 1 | 0.0000 | 0.0000 | 0.2782 | 1.0000 | 1.0000 | 0.7218 |
| 2 | 0.1541 | 0.5176 | 0.1390 | 0.8459 | 0.4824 | 0.8610 |
| 3 | 0.3122 | 0.7252 | 0.0000 | 0.6878 | 0.2748 | 1.0000 |
| 4 | 0.2767 | 0.5879 | 0.1947 | 0.7233 | 0.4121 | 0.8053 |
| 5 | 0.4348 | 0.7732 | 0.1484 | 0.5652 | 0.2268 | 0.8516 |
| 6 | 0.4031 | 0.3994 | 0.1924 | 0.5969 | 0.6006 | 0.8076 |
| 7 | 0.5533 | 0.8211 | 0.1780 | 0.4467 | 0.1789 | 0.8220 |
| 8 | 0.5257 | 0.5240 | 0.2045 | 0.4743 | 0.4760 | 0.7955 |
| 9 | 0.6798 | 0.8179 | 0.1767 | 0.3202 | 0.1821 | 0.8233 |
| 10 | 0.3318 | 0.6166 | 0.5729 | 0.6682 | 0.3834 | 0.4271 |
| 11 | 0.4851 | 0.7955 | 0.4337 | 0.5149 | 0.2045 | 0.5663 |
| 12 | 0.4536 | 0.4505 | 0.5661 | 0.5464 | 0.5495 | 0.4339 |
| 13 | 0.6069 | 0.8435 | 0.2928 | 0.3931 | 0.1565 | 0.7072 |
| 14 | 0.5755 | 0.5719 | 0.3370 | 0.4245 | 0.4281 | 0.6630 |
| 15 | 0.7327 | 0.8466 | 0.2907 | 0.2673 | 0.1534 | 0.7093 |
| 16 | 0.6973 | 0.6933 | 0.2912 | 0.3027 | 0.3067 | 0.7088 |
| 17 | 0.8506 | 0.9137 | 0.2634 | 0.1494 | 0.0863 | 0.7366 |
| 18 | 1.0000 | 1.0000 | 0.2355 | 0.0000 | 0.0000 | 0.7645 |
| 19 | 0.6575 | 0.8626 | 0.8674 | 0.3425 | 0.1374 | 0.1326 |
| 20 | 0.6264 | 0.6230 | 1.0000 | 0.3736 | 0.3770 | 0.0000 |
| 21 | 0.7821 | 0.8754 | 0.8608 | 0.2179 | 0.1246 | 0.1392 |
| 22 | 0.7471 | 0.7444 | 0.4817 | 0.2529 | 0.2556 | 0.5183 |
| 23 | 0.9028 | 0.9425 | 0.4352 | 0.0972 | 0.0575 | 0.5648 |
| 24 | 0.9611 | 0.9840 | 0.3889 | 0.0389 | 0.0160 | 0.6111 |
| 25 | 0.9923 | 0.9936 | 0.3501 | 0.0077 | 0.0064 | 0.6499 |
| 26 | 0.8405 | 0.9361 | 0.3224 | 0.1595 | 0.0639 | 0.6776 |
| 27 | 0.8716 | 0.8658 | 0.3489 | 0.1284 | 0.1342 | 0.6511 |
| S. No. | Grey Relational Coefficients (GRC) | GRG | ||
|---|---|---|---|---|
| V | WR | COF | ||
| 1 | 0.3333 | 0.3333 | 0.4092 | 0.3586 |
| 2 | 0.3715 | 0.5089 | 0.3674 | 0.4159 |
| 3 | 0.4210 | 0.6454 | 0.3333 | 0.4666 |
| 4 | 0.4087 | 0.5482 | 0.3830 | 0.4466 |
| 5 | 0.4694 | 0.6879 | 0.3699 | 0.5091 |
| 6 | 0.4558 | 0.4543 | 0.3824 | 0.4308 |
| 7 | 0.5282 | 0.7365 | 0.3782 | 0.5476 |
| 8 | 0.5132 | 0.5123 | 0.3859 | 0.4705 |
| 9 | 0.6096 | 0.7330 | 0.3779 | 0.5735 |
| 10 | 0.4280 | 0.5660 | 0.5393 | 0.5111 |
| 11 | 0.4927 | 0.7098 | 0.4689 | 0.5571 |
| 12 | 0.4778 | 0.4764 | 0.5354 | 0.4965 |
| 13 | 0.5599 | 0.7616 | 0.4142 | 0.5785 |
| 14 | 0.5408 | 0.5387 | 0.4299 | 0.5032 |
| 15 | 0.6516 | 0.7653 | 0.4135 | 0.6101 |
| 16 | 0.6229 | 0.6198 | 0.4136 | 0.5521 |
| 17 | 0.7700 | 0.8529 | 0.4043 | 0.6757 |
| 18 | 1.0000 | 1.0000 | 0.3954 | 0.7985 |
| 19 | 0.5935 | 0.7845 | 0.7904 | 0.7228 |
| 20 | 0.5723 | 0.5701 | 1.0000 | 0.7142 |
| 21 | 0.6965 | 0.8005 | 0.7822 | 0.7597 |
| 22 | 0.6641 | 0.6617 | 0.4910 | 0.6056 |
| 23 | 0.8372 | 0.8968 | 0.4696 | 0.7345 |
| 24 | 0.9279 | 0.9690 | 0.4500 | 0.7823 |
| 25 | 0.9848 | 0.9874 | 0.4348 | 0.8023 |
| 26 | 0.7581 | 0.8867 | 0.4246 | 0.6898 |
| 27 | 0.7957 | 0.7884 | 0.4344 | 0.6728 |
| Level | RF wt.% | N | v | SD |
|---|---|---|---|---|
| 1 | −6.660 | −5.364 | −5.108 | −5.633 |
| 2 | −4.725 | −4.929 | −4.813 | −4.440 |
| 3 | −2.876 | −3.968 | −4.339 | −4.187 |
| ∆ | 3.784 | 1.396 | 0.769 | 1.446 |
| Rank | 1 | 3 | 4 | 2 |
| Source | DF | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 14 | 0.400360 | 0.028597 | 13.39 | 0.000 |
| Linear | 4 | 0.370782 | 0.092695 | 43.39 | 0.000 |
| RF wt.% | 1 | 0.284962 | 0.284962 | 133.40 | 0.000 |
| N | 1 | 0.033826 | 0.033826 | 15.83 | 0.002 |
| v | 1 | 0.012044 | 0.012044 | 5.64 | 0.035 |
| SD | 1 | 0.039950 | 0.039950 | 18.70 | 0.001 |
| Square | 4 | 0.010369 | 0.002592 | 1.21 | 0.355 |
| RF wt.% × RF wt.% | 1 | 0.000351 | 0.000351 | 0.16 | 0.693 |
| N × N | 1 | 0.002729 | 0.002729 | 1.28 | 0.280 |
| V × v | 1 | 0.000574 | 0.000574 | 0.27 | 0.614 |
| SD × SD | 1 | 0.006716 | 0.006716 | 3.14 | 0.102 |
| Square | 4 | 0.010369 | 0.002592 | 1.21 | 0.355 |
| 2-way Interaction | 6 | 0.019209 | 0.003202 | 1.50 | 0.259 |
| RF wt.% × N | 1 | 0.015013 | 0.015013 | 7.03 | 0.021 |
| RF wt.% × v | 1 | 0.000498 | 0.000498 | 0.23 | 0.638 |
| RF wt.% × SD | 1 | 0.000367 | 0.000367 | 0.17 | 0.686 |
| N × v | 1 | 0.000069 | 0.000069 | 0.03 | 0.861 |
| N × SD | 1 | 0.002624 | 0.002624 | 1.23 | 0.289 |
| v × SD | 1 | 0.003930 | 0.003930 | 1.84 | 0.200 |
| Error | 12 | 0.025634 | 0.002136 | ||
| Total | 26 | 0.425995 |
| S. No. | Normalization (fij) | Entropy Indices (Ie) | ||||
|---|---|---|---|---|---|---|
| V | WR | COF | V | WR | COF | |
| 1 | 0.4103 | 0.5506 | 0.2045 | −0.22184 | −0.27162 | −0.13037 |
| 2 | 0.3476 | 0.2665 | 0.2343 | −0.20108 | −0.17935 | −0.14302 |
| 3 | 0.2832 | 0.1525 | 0.2641 | −0.17709 | −0.12372 | −0.1549 |
| 4 | 0.2977 | 0.2279 | 0.2224 | −0.18275 | −0.16221 | −0.13806 |
| 5 | 0.2333 | 0.1262 | 0.2323 | −0.15622 | −0.1083 | −0.14219 |
| 6 | 0.2462 | 0.3314 | 0.2229 | −0.16182 | −0.20513 | −0.13827 |
| 7 | 0.1850 | 0.0999 | 0.2260 | −0.13369 | −0.09152 | −0.13956 |
| 8 | 0.1963 | 0.2630 | 0.2203 | −0.13918 | −0.17785 | −0.13717 |
| 9 | 0.1336 | 0.1017 | 0.2262 | −0.10643 | −0.09269 | −0.13967 |
| 10 | 0.2752 | 0.2122 | 0.1414 | −0.1739 | −0.15475 | −0.10054 |
| 11 | 0.2128 | 0.1140 | 0.1712 | −0.14697 | −0.10066 | −0.11521 |
| 12 | 0.2256 | 0.3033 | 0.1429 | −0.1528 | −0.19441 | −0.10129 |
| 13 | 0.1632 | 0.0877 | 0.2014 | −0.1226 | −0.08312 | −0.12899 |
| 14 | 0.1760 | 0.2367 | 0.1919 | −0.12918 | −0.16624 | −0.12477 |
| 15 | 0.1120 | 0.0859 | 0.2018 | −0.09377 | −0.08189 | −0.12919 |
| 16 | 0.1264 | 0.1701 | 0.2017 | −0.10233 | −0.13336 | −0.12915 |
| 17 | 0.0640 | 0.0491 | 0.2077 | −0.06176 | −0.0536 | −0.13175 |
| 18 | 0.0032 | 0.0018 | 0.2136 | −0.00528 | −0.00336 | −0.13434 |
| 19 | 0.1426 | 0.0772 | 0.0784 | −0.11152 | −0.07559 | −0.06492 |
| 20 | 0.1553 | 0.2087 | 0.0500 | −0.11841 | −0.15305 | −0.04588 |
| 21 | 0.0919 | 0.0701 | 0.0798 | −0.08109 | −0.07037 | −0.06582 |
| 22 | 0.1062 | 0.1420 | 0.1609 | −0.09017 | −0.1177 | −0.11028 |
| 23 | 0.0428 | 0.0333 | 0.1709 | −0.04522 | −0.03957 | −0.11506 |
| 24 | 0.0190 | 0.0105 | 0.1808 | −0.02362 | −0.0155 | −0.1197 |
| 25 | 0.0063 | 0.0053 | 0.1891 | −0.00947 | −0.00865 | −0.1235 |
| 26 | 0.0681 | 0.0368 | 0.1950 | −0.06477 | −0.04282 | −0.12618 |
| 27 | 0.0555 | 0.0754 | 0.1894 | −0.05533 | −0.0743 | −0.12362 |
| S. No. | Utility Measure (Si) | Regret Measure (Ri) | VIKOR Index (Qi) |
|---|---|---|---|
| 1 | 0.9797 | 0.5380 | 1.0000 |
| 2 | 0.6513 | 0.3293 | 0.6127 |
| 3 | 0.4881 | 0.2678 | 0.4628 |
| 4 | 0.5618 | 0.2816 | 0.5164 |
| 5 | 0.4039 | 0.2201 | 0.3693 |
| 6 | 0.6141 | 0.3231 | 0.5864 |
| 7 | 0.3298 | 0.1739 | 0.2828 |
| 8 | 0.4985 | 0.2561 | 0.4566 |
| 9 | 0.2823 | 0.1247 | 0.2077 |
| 10 | 0.4974 | 0.2602 | 0.4601 |
| 11 | 0.3515 | 0.2005 | 0.3213 |
| 12 | 0.5398 | 0.2956 | 0.5186 |
| 13 | 0.2885 | 0.1530 | 0.2395 |
| 14 | 0.4437 | 0.2303 | 0.4010 |
| 15 | 0.2380 | 0.1041 | 0.1630 |
| 16 | 0.3343 | 0.1650 | 0.2763 |
| 17 | 0.1580 | 0.0582 | 0.0737 |
| 18 | 0.0554 | 0.0555 | 0.0156 |
| 19 | 0.2168 | 0.1333 | 0.1810 |
| 20 | 0.3482 | 0.2028 | 0.3218 |
| 21 | 0.1619 | 0.0848 | 0.1025 |
| 22 | 0.2736 | 0.1375 | 0.2158 |
| 23 | 0.1097 | 0.0410 | 0.0303 |
| 24 | 0.0680 | 0.0444 | 0.0112 |
| 25 | 0.0536 | 0.0472 | 0.0062 |
| 26 | 0.1456 | 0.0621 | 0.0709 |
| 27 | 0.1694 | 0.0721 | 0.0938 |
| Source | DF | Adj SS | Adj MS | F | p |
|---|---|---|---|---|---|
| Model | 14 | 1.41262 | 0.100902 | 214.67 | 0.000 |
| Linear | 4 | 1.27336 | 0.318339 | 677.26 | 0.000 |
| RF wt.% | 1 | 0.66550 | 0.665495 | 1415.84 | 0.000 |
| N | 1 | 0.34650 | 0.346502 | 737.18 | 0.000 |
| v | 1 | 0.05740 | 0.057396 | 122.11 | 0.000 |
| SD | 1 | 0.20396 | 0.203962 | 433.93 | 0.000 |
| Square | 4 | 0.04992 | 0.012480 | 26.55 | 0.000 |
| RF wt.% × RF wt.% | 1 | 0.00645 | 0.006446 | 13.71 | 0.003 |
| N × N | 1 | 0.00294 | 0.002938 | 6.25 | 0.028 |
| v × v | 1 | 0.00001 | 0.000011 | 0.02 | 0.881 |
| SD × SD | 1 | 0.04053 | 0.040526 | 86.22 | 0.000 |
| 2-way Interaction | 6 | 0.08935 | 0.014891 | 31.68 | 0.000 |
| RF wt.% × N | 1 | 0.04039 | 0.040390 | 85.93 | 0.000 |
| RF wt.% × v | 1 | 0.00522 | 0.005220 | 11.11 | 0.006 |
| RF wt.% × SD | 1 | 0.02069 | 0.020695 | 44.03 | 0.000 |
| N × v | 1 | 0.00254 | 0.002538 | 5.40 | 0.039 |
| N × SD | 1 | 0.00976 | 0.009759 | 20.76 | 0.001 |
| v × SD | 1 | 0.00079 | 0.000785 | 1.67 | 0.221 |
| Error | 12 | 0.00564 | 0.000470 | ||
| Total | 26 | 1.41826 |
| S. No. | Ranking | ||||
|---|---|---|---|---|---|
| Grey Analysis | Entropy-VIKOR Analysis | S. No. | Grey Analysis | Entropy-VIKOR Analysis | |
| 1 | 27 | 27 | 15 | 11 | 9 |
| 2 | 26 | 26 | 16 | 16 | 14 |
| 3 | 23 | 22 | 17 | 9 | 6 |
| 4 | 24 | 23 | 18 | 2 | 3 |
| 5 | 19 | 18 | 19 | 6 | 10 |
| 6 | 25 | 25 | 20 | 7 | 17 |
| 7 | 17 | 15 | 21 | 4 | 8 |
| 8 | 22 | 20 | 22 | 12 | 12 |
| 9 | 14 | 11 | 23 | 5 | 4 |
| 10 | 18 | 21 | 24 | 3 | 2 |
| 11 | 15 | 16 | 25 | 1 | 1 |
| 12 | 21 | 24 | 26 | 8 | 5 |
| 13 | 13 | 13 | 27 | 10 | 7 |
| 14 | 20 | 19 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Badi, K.P.; Putti, S.R.; Chapa, M.R.; Cheepu, M. Parametric Optimization of Dry Sliding Wear Attributes for AlMg1SiCu Hybrid MMCs: A Comparative Study of GRA and Entropy-VIKOR Methods. J. Compos. Sci. 2025, 9, 297. https://doi.org/10.3390/jcs9060297
Badi KP, Putti SR, Chapa MR, Cheepu M. Parametric Optimization of Dry Sliding Wear Attributes for AlMg1SiCu Hybrid MMCs: A Comparative Study of GRA and Entropy-VIKOR Methods. Journal of Composites Science. 2025; 9(6):297. https://doi.org/10.3390/jcs9060297
Chicago/Turabian StyleBadi, Krishna Prafulla, Srinivasa Rao Putti, Maheswara Rao Chapa, and Muralimohan Cheepu. 2025. "Parametric Optimization of Dry Sliding Wear Attributes for AlMg1SiCu Hybrid MMCs: A Comparative Study of GRA and Entropy-VIKOR Methods" Journal of Composites Science 9, no. 6: 297. https://doi.org/10.3390/jcs9060297
APA StyleBadi, K. P., Putti, S. R., Chapa, M. R., & Cheepu, M. (2025). Parametric Optimization of Dry Sliding Wear Attributes for AlMg1SiCu Hybrid MMCs: A Comparative Study of GRA and Entropy-VIKOR Methods. Journal of Composites Science, 9(6), 297. https://doi.org/10.3390/jcs9060297







