Abstract
Elastic moduli are important mechanical properties that describe a material’s stiffness and its deformation under elastic loading. In addition to experimental techniques, computational homogenization is commonly used for composite materials to calculate their elastic moduli. This research employs a deep learning algorithm, specifically a Feedforward Neural Network (FNN), to predict the longitudinal and transverse Young’s modulus, shear modulus, and Poisson’s ratio of various unidirectional (UD) composites. The predictions are based on several features, including the names of the composites, Young’s moduli and Poisson’s ratios of the fibers and matrices, and the fiber volume fraction. Initially, 20 different UD composites were selected from the existing literature. ANSYS-19 Material Designer was then utilized to calculate the elastic moduli of these materials while varying the fiber volume fraction from 0.2 to 0.7. This process generated a dataset of 1948 samples, with 80% of the data allocated for training the FNN model and the remaining 20% used to evaluate performance metrics of the test data. These metrics include mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and R2 score. The results indicate that, with optimized hyperparameters, the FNN model can accurately predict the elastic moduli, demonstrating its effectiveness as a tool for calculating the elastic properties of UD composites.
1. Introduction
Over the past few decades, composite materials have drawn significant attention in multiple industries, including aerospace, naval, automotive, building and construction, and so on, due to their better mechanical performance. These advantages include mechanical strength, lightweight, corrosion resistance, and the ability to withstand harsh environments compared to conventional or single-constituent materials [1]. In recent times, various types of composite materials have become available. However, based on the fiber reinforcement type, composite materials are classified into unidirectional composites and woven or multidirectional composites. Particularly in unidirectional composites, fibers are aligned in one direction, mainly benefiting them by effectively absorbing loads and offering maximum strength and stiffness [2,3,4]. Unidirectional composites can be fabricated using various manufacturing methods, including conventional techniques such as injection molding, compression molding, vacuum-assisted resin transfer molding (VARTM), and advanced methods such as 3D printing [2,5]. While 3D printing is more advanced and offers advantageous features like sustainability and environmental friendliness, conventional methods consistently deliver superior mechanical performance. For example, this research compared conventionally fabricated carbon fiber-reinforced thermoplastic composites with 3D-printed composites and found that conventionally fabricated composites provided significantly better mechanical properties (strength: 1500 MPa, stiffness: 135 GPa) than 3D-printed composites (strength: 986 MPa, stiffness: 64 GPa) [5].
Various theoretical models have previously been proposed and developed to compute the elastic moduli of unidirectional composites, such as the Rule of Mixture (ROM), Modified Rule of Mixture (MROM), Halpin–Tsai model, Chamis model, Mori–Tanaka model (M-T), self-consistent model (S-C), and Bridging model (BM) [6]. ROM is the first theoretical simplified model that enables the calculation of elastic moduli (E11, υ12, E22, G12) by considering an equal amount of experienced strain on both fiber and matrix. Later, the ROM is modified into MROM, incorporating fiber length and orientations into the calculation; the modified theory enables the prediction of the elastic moduli (E22, G12), which was unattainable by ROM [6,7]. The Halpin–Tsai model is another well-known semi-empirical approach proposed for calculating the elastic moduli, specifically the transverse modulus (E22), within a suitable volume fraction range of 0.25 to 0.55 without unnecessary complexity [8]. The Halpin–Tsai model also considers the fiber aspect ratio, inter-fiber spacing, and fiber end gap in the transverse modulus of discontinuous fiber composites [9]. However, compared to other theoretical models and experimental results, it may exhibit negligible deviations in predicting the transverse modulus (E22) [9,10]. Another model, called the self-consistent model, is widely adopted in micromechanics to predict elastic moduli. This model primarily estimates elastic properties by considering inclusions, where a single particle inclusion is embedded in the effective medium [11,12]. Similarly, the Mori–Tanaka model (M-T) is also well-known for predicting elastic moduli [13,14,15]. The main benefit of this model is that it can consider the multiple filler ratios, fiber length distributions, and orientation of composites in the model [14]. Furthermore, it can also be used to compute the composite’s thermal expansion coefficient. For example, this study calculates the thermal expansion coefficient of composites employing the M-T model and found that the M-T model can predict the moduli in an identical manner compared to other theoretical models [13]. However, the M-T model may cause some difficulties, particularly where nonlinear analyses or time dependence are required to consider in composite materials [16]. The Bridging model is another popular micromechanics approach used to predict the transverse modulus (E22), as well as in-plane and out-plane shear modulus (G12, G23) of unidirectional composites [17]. This model is particularly convenient for micromechanical modeling since it can compute the elastic moduli by correlating the average stress states in the constituent fibers and matrix through the bridging matrix [18]. However, in recent times, the Bridging model has also been employed to predict the strength of an interface crack containing unidirectional composites. The investigations found that the Bridging model can predict the transverse moduli even in the presence of an interface crack. In addition, in comparison to experimental outcomes, the Bridging model showed good agreement for predicting off-axis tensile strength [19]. Similarly, the Chamis model has also been effectively used to predict the elastic properties of unidirectional composites [20]. This model enables the calculation of all independent effective properties, including E11, E22, υ12, G12, and G23. Notably, in this model, E11 and υ12 are calculated in the same formula as ROM, while the other moduli’s volume fraction (Vf) is replaced by its square root [6]. The Chamis model has also been further developed into the parallel-series model to compute moduli under more complex conditions, such as fiber undulations [21]. Overall, compared to other theoretical models, the Chamis model may provide better accuracy in its predictions [17].
In computational mechanics, Representative Volume Element (RVE) generation through the finite element method (FEM) is the most straightforward technique for computing the mechanical properties of composite materials, facilitating understanding of the materials’ behavior from the micro to macro scale [22]. Previously, significant research and extensive investigations have been conducted on RVE to enhance the accuracy of numerical outcomes compared to theoretical and experimental results [23]. During numerical investigations, factors such as fiber volume fraction, fiber diameter, fiber shape, fiber aspect ratio, and fiber overlapping may significantly influence the moduli of unidirectional composites [22,24,25]. Focusing on fiber volume fractions, substantial research has been conducted. Increasing volume fractions may increase the RVE size, which impacts the elastic moduli and damage initiation strength [26]. In some previous investigations, both real experiments and FEM analyses have suggested that the optimal fiber volume fraction ranges between 0.1 and 0.7 [1,27,28], since excessive volume fractions may lead to losing ductility in final components. In terms of fiber shape in RVEs, a comparison between hexagonal and square RVEs employing ANSYS and theoretical methods has been conducted in this study to calculate the thermal conductivity of a unidirectional composite. The outcomes suggest that while other moduli are unaffected by fiber shape, the hexagonal array aligns more closely with the Hashin model than the ROM and Chawla models [29].
Micro-voids are a type of defect often observed during composite manufacturing or throughout their service life [30]. In RVE generations, micro-voids can significantly influence the elastic modulus. This research considers two types of voids: inter-fiber voids and matrix voids. The investigation found that in RVE composites, void content ranging from 1% to 5% may reduce the elastic moduli, particularly affecting transverse strength [31]. Later on, a similar approach considering different types of micro-voids (circular, elliptical, and arbitrary) in RVEs, along with additional factors such as thermal residual stress, is explored in this research. The investigation found that different voids can influence the properties of the RVE. However, these voids are primarily responsible for creating premature cracks around them in the composites [32]. In addition to the effect of micro-voids, recent research has also emphasized the influence of interface defects and uncertainties on the homogenized elastic and thermal properties of periodic fiber-reinforced composites [33]. The study utilized stochastic finite element methods (SFEMs) and Monte Carlo simulations to analyze how uncertainties propagate during homogenization. Furthermore, Artificial Neural Networks (ANNs) were employed to optimize the fitting of response polynomials that relate input uncertainties—such as defect size and quantity—to the effective material properties. The findings indicated that interface defects significantly impact both the homogenized elastic moduli and thermal conductivity.
In recent times, ML has been extensively used as an important tool to predict the mechanical properties of composites, the effect of manufacturing processes, and to identify damage and structural health monitoring [34]. For instance, three different ML models, namely, Linear, Ensemble, and ANN models, are trained to predict the transverse modulus of UD composite. It was found that the Ensemble model can predict the modulus with an R2 score of 1 [35]. Another study based on computer-generated microstructures of UD and the corresponding FE analyses suggested that the Machine Learning Algorithm can be an effective tool to predict the elastic moduli with less time and effort. Though the example is presented based on finite element data, it is suggested that the same can be applied based on experiments too [36]. A mean absolute percentage error (MAPE) is used to calculate the error for effective elastic properties of UD composites using the Convolution Neural Network (CNN) model. The fiber volume fraction is varied, and for each fiber volume fraction, elastic properties are predicted, and the error is calculated [37]. Despite the low error percentage (>3%), the problem in the study is that each volume fraction is studied separately, whereas it could be studied together to calculate the elastic properties. Recent research optimized the backpropagation neural network model to accurately predict the elastic properties of three different UD composites: basalt fiber, carbon fiber, and glass fiber with epoxy. The error percentage is less than 2%; however, the study’s main limitation is that the variety of fiber is limited to only three [38].
In summary, there is a lack of literature considering a wide range of fiber and matrix variations to predict the elastic properties of various UD composites combined using ML models. The present study addresses this issue and considers 20 different fiber and matrix combinations of various glass fibers, carbon fibers, natural fibers, etc., to predict the elastic properties of UD using a feedforward deep neural network model. The presentation of the research article is as follows: Section 2 describes the mechanical properties found in the literature, along with numerical setup and validation. Next, in Section 3, the FNN architecture is defined with the data collection strategy for the present study. Finally, Section 4 proposes an optimized FNN model after statistical evaluation.
2. Materials and Methods
2.1. Materials
To predict the elastic moduli of unidirectional composites, various materials have been selected. The fibers include both isotropic and orthotropic types, while the matrices used in this research are isotropic. The selected fibers include polymeric, carbon, glass, and natural fibers. Table 1 and Table 2 present the material properties of all the fibers and matrices. Please note that in Table 1, several epoxy matrices with different elastic moduli are shown. Epoxy matrices from different literature sources differ in formulation and curing processes, leading to variation in reported elastic moduli. The exact modulus used for simulation in each composite material is taken directly from its corresponding reference, as indicated.

Table 1.
Material properties of unidirectional fibers and matrices (Isotropic).

Table 2.
Material properties of unidirectional fibers and matrices (Orthotropic).
2.2. Numerical Setup and Validation
The present study employs the ANSYS Material Designer module to calculate the elastic moduli of 20 different combinations of fibers and matrices of a fiber volume fraction ranging from 0.2 to 0.7, providing sufficient data for the Artificial Neural Network (ANN) model analyzed later in this research. One of the module’s primary advantages is its ability to automatically generate the Randomized Volume Element (RVE) for UD composites once the user inputs the mechanical properties of the fiber and matrix, along with the fiber diameter and volume fraction. In addition, the geometry type, which is rectangular for the UD composite, must be selected. Following this, the meshing of the element is performed using a block and conformal meshing approach, which is recommended for UD composites [51]. Additionally, a mesh convergence study was conducted to determine the optimal element size for this research, focusing on a glass fiber and epoxy matrix with a fiber volume fraction of 0.5, as detailed in Table 3. The table indicates that variations in the maximum element size do not impact the elastic modulus. However, a slight change is observed in the shear modulus when the element size is decreased from 3 µm to 2 µm. Beyond this point, further reductions in mesh size do not yield any noticeable changes. Therefore, a mesh size of 2 µm has been selected for the numerical calculations in this study. Figure 1a displays a Scanning Electron Micrograph (SEM) of the interface of a unidirectional composite with square-shaped fibers [52]. In Figure 1b, a unidirectional composite RVE is shown. Similarly, in Figure 1c, a meshed unidirectional composite RVE is presented. Since the RVE is designed to represent a repeating structure, periodicity is in composites. Therefore, a periodic boundary condition is applied to avoid any boundary effects. Figure 2a illustrates a schematic representation of the periodic boundary condition applied to the RVE [53], while Figure 2b illustrates the step-by-step setup for calculating the elastic moduli in the ANSYS Material Design Module.

Table 3.
Mesh convergence study.
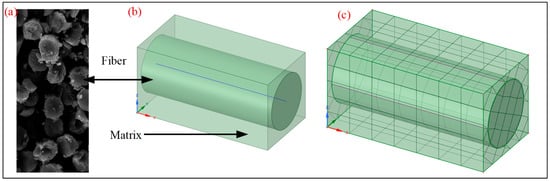
Figure 1.
(a) SEM interface of a unidirectional composite, (b) RVE of a unidirectional composite, (c) block and conformal meshed RVE.
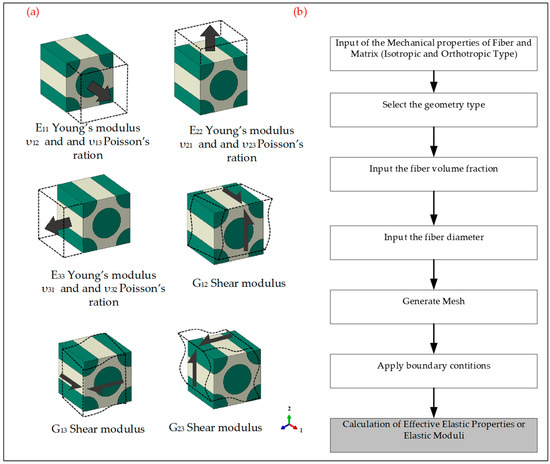
Figure 2.
(a) ANSYS Material Designer setup to calculate the elastic moduli, (b) periodic boundary conditions applied to RVE.
To ensure the reliability of our research and simulations, we conducted a numerical, experimental, and theoretical comparison with the findings from the literature [6]. The numerical validation against the experimental results is presented in Table 4. The material properties of the carbon fiber and the epoxy matrix were obtained from the same source. Overall, the ANSYS Design Module demonstrated good agreement with the experimental results, especially for the transverse elastic moduli (E22 = E33) and Poisson’s ratio (ν12), with deviations remaining minimal (between 0% and 1.67%). The longitudinal modulus (E11) showed a low deviation of 1.59% at a fiber volume fraction (Vf) of 0.5 but a slightly higher deviation of 6.57% at Vf = 0.6. The shear moduli (G12, G31, G23) were also reasonably predicted, although a higher deviation, reaching up to 13.5%, was noted at higher fiber content. In summary, these results indicate that ANSYS provides reliable predictions for the elastic properties of unidirectional composites, with minor variations considered acceptable for numerical simulations. Lastly, for ν12, due to the lack of experimental data, we used the well-known micromechanical model M-T for comparison.

Table 4.
Experimental and numerical elastic modulus of carbon–epoxy unidirectional composite.
3. FNN Architecture and Data Collection Strategy
The Feedforward Neural Network, or in short “FNN”, is a subcategory of the ANN where data are fed as input, processed through one or more hidden layers, and propagated to the output. As the name suggests, data flow only in one direction, and feedback from the output does not reconnect or loop back through the layers to the input. These layers are made up of neurons, which are the building blocks of neural networks, and are connected to each other through synaptic weights. The weighted sum of the input data is processed through an activation function, generating an output that is then sent as input to the connected neurons [54]. To capture the complex behavior and pattern of the datasets, the neural network utilizes a learning algorithm that adjusts the synaptic weights based on the calculated error between the predicted and actual outputs.
The type of error function or cost function depends on the specific task, for instance, cross-entropy for classification or mean squared error (MSE) for regression. The most common learning algorithm for FNNs is backpropagation combined with gradient descent (such as Adam) [55]. During training, the model iterates through the data multiple times, each iteration called an epoch, in which the weights are updated to minimize the cost function. Based on the number of hidden layers, an FNN can be further categorized as a shallow neural network (with one hidden layer) or a deep FNN (with two or more hidden layers) [56], as shown in Figure 3.
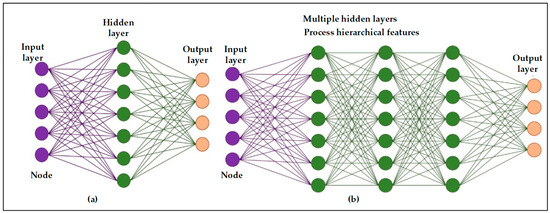
Figure 3.
Neural network: (a) shallow neural network with a single hidden layer, (b) deep neural network with multiple hidden layers [56].
To improve the learning capability of neural network models, hyperparameters are configured before the training process begins. These hyperparameters have a significant effect on the learning process, with some being adopted by default within the training model, while others require explicit implementation. A set of hyperparameters used for FNN models is shown in Table 5, along with the ranges studied for the current research.

Table 5.
Hyperparameters for FNN.
The present research utilizes a dataset of 1948 samples to predict the effective elastic properties of unidirectional composite materials, namely, elastic moduli E11 and E22 = E3, Shear moduli G12 = G31 and G23, and Poisson’s ratios υ23 and υ12 = υ13. All of them are used as a target variable and excluded from the dataset while training. In contrast, the name of the composites, Young’s moduli and Poisson’s ratio of fiber and matrix, along with the fiber volume fraction, are utilized as input variables for the training. Since the names of the composites represent categorical data, a one-hot encoding is required to transform them to numerical data [57]. The fiber volume fraction ranges from 0.2 to 0.7, with an average of 98 data points collected within this range for each composite, resulting in a total dataset of 1948 samples. The training data and test data ratio is 80:20.
4. Evaluation of FNN Model
After tuning the hyperparameters, it was found that the relu activation function in the hidden layers and a linear activation in the output layer, combined with the AdamW optimizer, performed best with a hidden layer architecture of 33/16/8/4/1. The optimal batch size was 32, and the number of epochs was 400. Notably, these parameters yielded the highest accuracy in terms of MAE, MSE, RMSE, and R2 score, which are the core evaluation metrics for predictive analysis. As previously discussed, an adaptive learning rate was maintained, as it proved suitable for the present predictions. The results of the optimized parameters are summarized in Table 6.

Table 6.
Optimized parameters.
To examine the performance of the FNN model, at first, MAE is utilized, which describes the average magnitude of errors between the predicted and actual values of a dataset. The expression is given as follows [58]:
where is the actual value, is the predicted value, and n is the total number of observations. MAE is a non-negative value, and if the value is 0, then it suggests that no error is found. A value closer to 0 indicates the predicted values are closer to actual values and the prediction is fairly accurate.
For the case of E11 prediction, it is found that the value of MAE is 0.09, which suggests that the FNN model can predict the elastic moduli of composite materials with high accuracy, as shown in Table 6. It is important to note that the calculated elastic moduli of different composite materials vary from 3.69 GPa to 190.42 GPa, representing a good variation in magnitude. Despite that, the predictions made by the FNN model are excellent. Similar to E11 prediction, E22 = E23, G12 = G31, and G23 also suggest a very good accuracy with MAE values of 0.0177, 0.0263, and 0.0368, respectively, despite having large magnitude variations, to be exact, 1.7848 GPa to 170.74 GPa for E22 = E23, 0.55 GPa to 70 GPa for G12 = G31, and 0.53 GPa to 69.18 GPa for G23. However, in the case of Poisson’s ratio, the model outperforms all other predictions and represents an excellent accuracy, with a value of 0.0002 for V12 = V13 and 0.0023 for V23. This exceptional observation is mainly due to the fact that the Poisson’s ratio variation is relatively small and ranges between 0.2 and 0.45, which helps the FNN model to predict the values with negligible error.
MSE is another statistical parameter that defines the predictive accuracy while penalizing the large errors. The formula to calculate the MSE is as follows [58]:
Similar to the previous observation, the values of MSE for all cases suggest an excellent accuracy, as shown in Table 7. Notably, for the present observation, MAE values are higher than the MSE values, suggesting that the errors are less than 1 in magnitude for most cases, which leads to this outcome. A similar observation can be found in the literature [58]. Furthermore, RMSE values, which are the root square of MSE, scale the error back to the original unit, which is widely used as an evaluation matrix alongside MAE and MSE [58]. The values of RMSE for test data, as shown in Table 7, suggest that the FNN can predict the elastic moduli with high accuracy. Finally, the coefficient of determination, which is denoted as an R2 score, can range from 0 to 1, where 0 represents that the model completely fails to capture any variance during testing and 1 suggests that the model can explain the variance with full perfection. The R2 score is formulated as follows [59]:

Table 7.
The results of the evaluation metrics.
For the present elastic moduli predictions, it is found that the optimized FNN model in the target variables can capture the variance with full perfection, as shown in Table 7.
Next, the results are plotted for training loss and validation loss over a number of epochs during the elastic moduli training and testing, as shown in Figure 4. Training loss represents the learning capability of the model based on the loss function (MSE) with the increment of the epoch numbers, while validation loss calculates the MSE on the unseen data or test data. As shown in the figure, it is apparent that the model starts with high MSE for training and validation loss, and just after running a few epochs (5 to 10), the MSE values significantly drop and start to converge. It also suggests that during the training, the model learns very quickly and improves its performance over time (number of epochs). The same is true for the unseen data, as the model performs well, and the validation loss also starts to decrease sharply. It might seem that 400 epochs are a little more than the required number of epochs for the present training and testing. However, it sometimes takes a high number of epochs to converge fully with the least MSE values for training loss and validation loss.
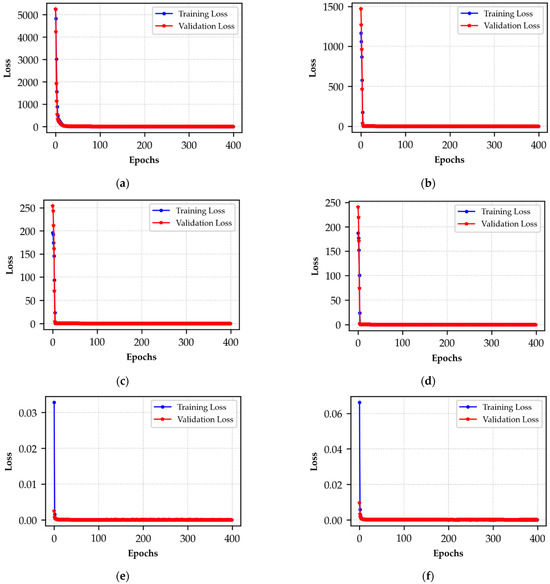
Figure 4.
Training loss and validation loss vs. epochs: (a) E11, (b) E22 = E23, (c) G12 = G31, (d) G23, (e) V12 = V13, (f) V23.
Finally, the results are plotted based on the predicted data vs. actual data to visualize the accuracy of the predicted data during training and testing for all elastic properties, as shown in Figure 5. This figure apparently helps to identify whether the optimized FNN model is overfitting, underfitting, or generalizing well to unseen data. In case the model had overfitted, the model would align well with the perfect fit line during training; however, it would fail to follow the trend during testing. In contrast, underfitting would suggest that, both during training and testing, the model’s prediction is scattered and away from the perfect line. However, for the present case, both during training and testing, predicted values vs. actual values closely follow the perfect fit for all elastic properties. This suggests that the model performs well on seen and unseen data, and it can accurately predict Young’s moduli [E11, and E22 = E23], shear moduli [G12 = G31, and G23], and Poisson’s ratios [V12 = V13 and V23].
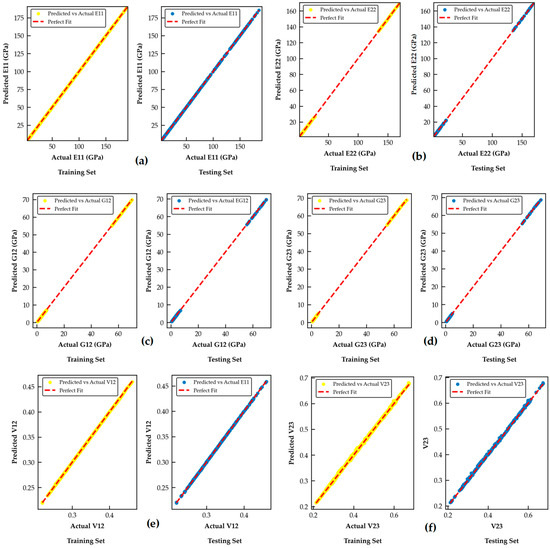
Figure 5.
Predicted data vs. actual data during training and testing: (a) E11, (b) E22 = E23, (c) G12 = G31, (d) G23, (e) V12 = V13, (f) V23.
5. Limitations
While the developed Feedforward Neural Network (FNN) model demonstrates excellent predictive performance for the elastic properties of unidirectional (UD) composite materials, several limitations must be acknowledged.
First, the mechanical parameters were determined based on numerical simulations at the microscale using Representative Volume Elements (RVEs) within ANSYS Material Designer. These RVEs represent idealized conditions and do not account for large-scale manufacturing defects, such as voids, resin-rich zones, fiber misalignments, or interface debonding. Consequently, while the model effectively captures the stiffness properties in a controlled microstructural context, applying these results directly to larger-scale structures may lead to discrepancies due to real-world imperfections.
Second, the model considers only three input parameters: Young’s moduli and Poisson’s ratios of the fiber and matrix, as well as the fiber volume fraction. It does not include strength properties essential for analyzing failure and damage tolerance. Additionally, the study solely focuses on unidirectional fiber orientations and does not address layup configurations like cross-ply, angle-ply, or woven fiber arrangements. This limitation restricts the model’s applicability to more complex laminate designs.
Third, although a diverse range of composite materials—including glass, carbon, natural, and polymeric fibers—was considered, they were grouped into a single dataset. This approach introduces variability that may obscure subtle trends specific to each fiber–matrix composite material. While this grouping is intended to improve the model’s generalizability, it may compromise accuracy for particular composites, e.g., unidirectional metal matrix composite. Future iterations of the model could benefit from subgroup classification or hierarchical modeling.
Fourth, while the input dataset includes the bulk properties of the matrix and fiber, it does not consider curing and manufacturing conditions (such as temperature, pressure, and resin infiltration quality), which are known to significantly impact the mechanical behavior of composites. The omission of these factors stems from inconsistent reporting across literature sources, but it limits the model’s ability to reflect processing-related variability.
Lastly, the model is trained exclusively on elastic properties. It does not account for time-dependent behaviors (such as viscoelasticity or creep), environmental degradation, or the impact of aging. Incorporating these effects would require more complex data collection and model structures, potentially involving hybrid experimental–numerical approaches and multi-scale modeling.
These limitations outline the model’s current applicability boundaries and suggest directions for further research to enhance its physical realism and practical usability in composite design and certification.
6. Conclusions
This study implemented and evaluated an FNN model to predict the elastic properties of twenty different unidirectional composite materials. The optimized FNN model, employing a ReLU activation function in the hidden layers, a linear activation in the output layer, and the AdamW optimizer with an architecture of 33/16/8/4/1, exhibited excellent predictive performance across various evaluation metrics, including MAE, MSE, RMSE, and R2. Notably, the model achieved high accuracy in predicting Young’s moduli (E11, E22 = E23), shear moduli (G12 = G31, G23), and Poisson’s ratios (V12 = V13, V23), despite the dataset covering a wide range of magnitudes. The evaluation metrics confirm the model’s robustness, as indicated by low MAE, MSE, and RMSE values and an R2 score of 1 for all predicted properties. Convergence analysis of training and validation loss over multiple epochs further validated the model’s learning capability, demonstrating an efficient optimization process. Additionally, the comparison between predicted and actual values indicates that the model generalizes well, showing no signs of overfitting or underfitting.
Overall, the results suggest that the FNN model is an efficient tool for predicting the elastic moduli of UD composite materials. This study demonstrated that if trained with the required dataset, it can generalize to unknown UD composites with minimal input details. Future research will focus on developing a comprehensive database to optimize the model for tailoring UD composite properties to specific requirements.
Author Contributions
Conceptualization, S.B.R. and M.M.R.; methodology, S.B.R. and M.M.R.; software, S.B.R., M.M.R., J.S. and G.V.; validation, M.M.R., J.S., G.V. and S.B.R.; formal analysis, S.B.R., M.M.R. and J.S.; investigation, S.B.R. and M.M.R.; resources, S.B.R. and M.M.R.; data curation, S.B.R. and M.M.R. and J.S.; writing—original draft preparation, S.B.R., J.S. and M.M.R.; writing—review and editing, S.B.R., M.M.R. and J.S.; visualization, S.B.R. and M.M.R.; supervision, S.B.R. and G.V.; project administration, S.B.R. and G.V.; funding acquisition, S.B.R. and G.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rayhan, S.B.; Rahman, M.M. Modeling Elastic Properties of Unidirectional Composite Materials Using Ansys Material Designer. Procedia Struct. Integr. 2020, 28, 1892–1900. [Google Scholar] [CrossRef]
- Sayam, A.; Rahman, A.N.M.M.; Rahman, M.S.; Smriti, S.A.; Ahmed, F.; Rabbi, M.F.; Hossain, M.; Faruque, M.O. A Review on Carbon Fiber-Reinforced Hierarchical Composites: Mechanical Performance, Manufacturing Process, Structural Applications and Allied Challenges; Springer Nature: Singapore, 2022; Volume 32, ISBN 0123456789. [Google Scholar]
- Abramovich, H. Introduction to Composite Materials; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; ISBN 9780081004296. [Google Scholar]
- Koyanagi, J.; Hatta, H.; Kotani, M.; Kawada, H. A Comprehensive Model for Determining Tensile Strengths of Various Unidirectional Composites. J. Compos. Mater. 2009, 43, 1901–1914. [Google Scholar] [CrossRef]
- Blok, L.G.; Longana, M.L.; Yu, H.; Woods, B.K.S. An Investigation into 3D Printing of Fibre Reinforced Thermoplastic Composites. Addit. Manuf. 2018, 22, 176–186. [Google Scholar] [CrossRef]
- Younes, R.; Hallal, A.; Fardoun, F.; Chehade, F.H. Comparative Review Study on Elastic Properties Modeling for Unidirectional Composite Materials; INTECH Open Access Publisher: London, UK, 2012. [Google Scholar]
- Andre, N.G.; Ishak, Z.A.M. Predicting the Tensile Modulus of Randomly Oriented Nonwoven Kenaf/Epoxy Composites. Procedia Chem. 2016, 19, 419–425. [Google Scholar] [CrossRef]
- Zhou, D.; Tong, X.; Liu, H.; Lv, S.; Srivatsan, T.S.; Gao, X. A Modified Halpin-Tsai Model for Predicting the Elastic Modulus of Composite Materials. AIP Adv. 2024, 14, 015157. [Google Scholar] [CrossRef]
- Fu, S.Y.; Hu, X.; Yue, C.Y. A New Model for the Transverse Modulus of Unidirectional Fiber Composites. J. Mater. Sci. 1998, 33, 4953–4960. [Google Scholar] [CrossRef]
- Chandekar, H.; Chaudhari, V.V.; Waigaonkar, S. Theoretical Models for Stiffness Prediction of Short Fibre Composites. Mater. Today Proc. 2022, 57, 711–714. [Google Scholar] [CrossRef]
- Raju, B.; Hiremath, S.R.; Roy Mahapatra, D. A Review of Micromechanics Based Models for Effective Elastic Properties of Reinforced Polymer Matrix Composites. Compos. Struct. 2018, 204, 607–619. [Google Scholar] [CrossRef]
- Yanase, K.; Ju, J.W. Effective Elastic Moduli of Spherical Particle Reinforced Composites Containing Imperfect Interfaces. Int. J. Damage Mech. 2012, 21, 97–127. [Google Scholar] [CrossRef]
- Lu, P. Further Studies on Mori-Tanaka Models for Thermal Expansion Coefficients of Composites. Polymer 2013, 54, 1691–1699. [Google Scholar] [CrossRef]
- Lee, D. Local Anisotropy Analysis Based on the Mori-Tanaka Model for Multiphase Composites with Fiber Length and Orientation Distributions. Compos. Part B Eng. 2018, 148, 227–234. [Google Scholar] [CrossRef]
- Abaimov, S.G.; Khudyakova, A.A.; Lomov, S.V. On the Closed FORM Expression of the Mori-Tanaka Theory Prediction for the Engineering Constants of a Unidirectional Fiber-Reinforced Ply. Compos. Struct. 2016, 142, 1–6. [Google Scholar] [CrossRef]
- Valentová, S.; Šejnoha, M.; Vorel, J. Comparing Mori-Tanaka Method and First-Order Homogenization Scheme in the Viscoelastic Modeling of Unidirectional Fibrous Composites. Acta Polytech. CTU Proc. 2020, 26, 133–138. [Google Scholar] [CrossRef]
- Rezasefat, M.; Mostafavi, Y.; Ma, D.; Manes, A. A Hybrid Micro-Macro Mechanical Damage Model to Consider the Influence of Resin-Rich Zones on the Transverse Tensile Behaviour of Unidirectional Composites. Compos. Struct. 2023, 308, 116714. [Google Scholar] [CrossRef]
- Huang, Z.M. Simulation of the Mechanical Properties of Fibrous Composites by the Bridging Micromechanics Model. Compos. Part A Appl. Sci. Manuf. 2001, 32, 143–172. [Google Scholar] [CrossRef]
- Mao, R.S.; Huang, Z.M.; Wang, Z.W. Predicting Strength of a Unidirectional Composite Containing Interface Crack. Compos. Sci. Technol. 2021, 207, 108665. [Google Scholar] [CrossRef]
- Potluri, R.; Diwakar, V.; Venkatesh, K.; Srinivasa Reddy, B. Analytical Model Application for Prediction of Mechanical Properties of Natural Fiber Reinforced Composites. Mater. Today Proc. 2018, 5, 5809–5818. [Google Scholar] [CrossRef]
- Udhayaraman, R.; Mulay, S.S. Multi-Scale Approach Based Constitutive Modelling of Plain Woven Textile Composites. Mech. Mater. 2017, 112, 172–192. [Google Scholar] [CrossRef]
- Balasubramani, N.K.; Zhang, B.; Chowdhury, N.T.; Mukkavilli, A.; Suter, M.; Pearce, G.M. Micro-Mechanical Analysis on Random RVE Size and Shape in Multiscale Finite Element Modelling of Unidirectional FRP Composites. Compos. Struct. 2022, 282, 115081. [Google Scholar] [CrossRef]
- Wan, L.; Ismail, Y.; Sheng, Y.; Ye, J.; Yang, D. A Review on Micromechanical Modelling of Progressive Failure in Unidirectional Fibre-Reinforced Composites. Compos. Part C Open Access 2023, 10, 100348. [Google Scholar] [CrossRef]
- Yao, Y.; Zhong, Y.; Su, Z.; Muhammad, R.; Wang, D.; Li, Y.; Li, S.; Sun, G. Micromechanical Analyses of Unidirectional (UD) Discontinuous Flax Fiber Reinforced Composites. Compos. Sci. Technol. 2024, 258, 110893. [Google Scholar] [CrossRef]
- Maragoni, L.; Carraro, P.A.; Quaresimin, M. Development, Validation and Analysis of an Efficient Micro-Scale Representative Volume Element for Unidirectional Composites. Compos. Part A Appl. Sci. Manuf. 2018, 110, 268–283. [Google Scholar] [CrossRef]
- Alhaddad, W.; He, M.; Halabi, Y.; Almajhali, K.Y.M. Influence of Fiber Volume Fraction on the Predictability of UD FRP Ply Behavior: A Validated Micromechanical Virtual Testing Approach. Materials 2024, 17, 4736. [Google Scholar] [CrossRef] [PubMed]
- Shah Mohammadi, M.; Komeili, M.; Phillion, A.B.; Milani, A.S. Toward Better Understanding of the Effect of Fiber Distribution on Effective Elastic Properties of Unidirectional Composite Yarns. Comput. Struct. 2016, 163, 29–40. [Google Scholar] [CrossRef]
- Bahmani, A.; Li, G.; Willett, T.L.; Montesano, J. Three-Dimensional Microscopic Assessment of Randomly Distributed Representative Volume Elements for High Fiber Volume Fraction Unidirectional Composites. Compos. Struct. 2018, 192, 153–164. [Google Scholar] [CrossRef]
- Devireddy, S.B.R.; Biswas, S. Effect of Fiber Geometry and Representative Volume Element on Elastic and Thermal Properties of Unidirectional Fiber-Reinforced Composites. J. Compos. 2014, 2014, 629175. [Google Scholar] [CrossRef]
- Hyde, A.; He, J.; Cui, X.; Lua, J.; Liu, L. Effects of Microvoids on Strength of Unidirectional Fiber-Reinforced Composite Materials. Compos. Part B Eng. 2020, 187, 107844. [Google Scholar] [CrossRef]
- Ashouri Vajari, D.; González, C.; Llorca, J.; Legarth, B.N. A Numerical Study of the Influence of Microvoids in the Transverse Mechanical Response of Unidirectional Composites. Compos. Sci. Technol. 2014, 97, 46–54. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, P.; Fei, Q.; Guo, F. Computational Evaluation of the Effects of Void on the Transverse Tensile Strengths of Unidirectional Composites Considering Thermal Residual Stress. Compos. Struct. 2019, 227, 111287. [Google Scholar] [CrossRef]
- Kamiński, M. Probabilistic Entropy and Relative Entropy for the Effective Characteristics of the Fiber-Reinforced Composites with Stochastic Interface Defects. Comput. Methods Appl. Mech. Eng. 2024, 432, 117308. [Google Scholar] [CrossRef]
- Loh, J.Y.Y.; Yeoh, K.M.; Raju, K.; Pham, V.N.H.; Tan, V.B.C.; Tay, T.E. A Review of Machine Learning for Progressive Damage Modelling of Fiber-Reinforced Composites; Springer: Dordrecht, The Netherlands, 2024; Volume 31, ISBN 1044302410. [Google Scholar]
- Huang, H.; Hadigheh, S.A.; Aghabalaei Baghaei, K. Influences of Fibre Shape on the Transverse Modulus of Unidirectional Fibre Reinforced Composites Using Finite Element and Machine Learning Methods. Compos. Struct. 2023, 312, 116872. [Google Scholar] [CrossRef]
- Pathan, M.V.; Ponnusami, S.A.; Pathan, J.; Pitisongsawat, R.; Erice, B.; Petrinic, N.; Tagarielli, V.L. Predictions of the Mechanical Properties of Unidirectional Fibre Composites by Supervised Machine Learning. Sci. Rep. 2019, 9, 13964. [Google Scholar] [CrossRef]
- Chang, H.-S.; Huang, J.-H.; Tsai, J.-L. Predicting Mechanical Properties of Unidirectional Composites Using Machine Learning. Multiscale Sci. Eng. 2022, 4, 202–210. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, X.; Gao, Y.; Zhu, R.; Chen, Y.; Liu, T. A Novel Framework to Predict Transversal and Shear Parameters of Unidirectional Composites by Combining Experimental, Numerical and Machine Learning Methods. Polym. Compos. 2025, 1–12. [Google Scholar] [CrossRef]
- Karadeniz, Z.H.; Kumlutas, D. A Numerical Study on the Coefficients of Thermal Expansion of Fiber Reinforced Composite Materials. Compos. Struct. 2007, 78, 1–10. [Google Scholar] [CrossRef]
- Rahman, M.M.; Sultana, J. Design and Optimization of Natural Fiber Reinforced Hybrid Composite RVE: A Finite Element Analysis. In Proceedings of the 2023 International Conference on Engineering, Science and Advanced Technology (ICESAT), Mosul, Iraq, 21–22 June 2023; pp. 204–209. [Google Scholar] [CrossRef]
- Yun, J.-H.; Jeon, Y.-J.; Kang, M.-S. Prediction of Elastic Properties Using Micromechanics of Polypropylene Composites Mixed with Ultrahigh-Molecular-Weight Polyethylene Fibers. Molecules 2022, 27, 5752. [Google Scholar] [CrossRef]
- Mali, R.; Pise, U. Modeling Elastic Properties of Biocomposites Using Various Analytical Models and Ansys Material Designer. Mater. Today Proc. 2023, 72, 1372–1378. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. A Virtual Framework for Prediction of Full-Field Elastic Response of Unidirectional Composites. Comput. Mater. Sci. 2013, 70, 82–99. [Google Scholar] [CrossRef]
- Maligno, A.R.; Warrior, N.A.; Long, A.C. Effects of Interphase Material Properties in Unidirectional Fibre Reinforced Composites. Compos. Sci. Technol. 2010, 70, 36–44. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, B.; Tang, Z.; Qi, G. Stress Transfer Analysis of Unidirectional Composites with Randomly Distributed Fibers Using Finite Element Method. Compos. Part B Eng. 2015, 69, 278–285. [Google Scholar] [CrossRef]
- Bulsara, V.N.; Talreja, R.; Qu, J. Damage Initiation under Transverse Loading of Unidirectional Composites with Arbitrarily Distributed Fibers. Compos. Sci. Technol. 1999, 59, 673–682. [Google Scholar] [CrossRef]
- Chen, J.; Wan, L.; Ismail, Y.; Hou, P.; Ye, J.; Yang, D. Micromechanical Analysis of UD CFRP Composite Lamina under Multiaxial Loading with Different Loading Paths. Compos. Struct. 2021, 269, 114024. [Google Scholar] [CrossRef]
- Tang, Z.; Guo, L.; Li, Z.; Huang, K.; Zheng, T.; Sun, R. A Comparative Study of Void Characteristics on the Mechanical Response of Unidirectional Composites. Mech. Mater. 2022, 174, 104456. [Google Scholar] [CrossRef]
- Li, N.; Chen, P.H.; Ling, X. A Microscopic Elasto-Plastic Damage Model for Characterizing Transverse Responses of Unidirectional Fiber-Reinforced Polymer Composites. Thin-Walled Struct. 2020, 154, 106828. [Google Scholar] [CrossRef]
- Fu, C.; Wang, X. Prediction of the Cohesive Strength for Simulating Composite Delamination by a Micro-Mechanical Model Based on Random RVE. Compos. Struct. 2021, 262, 113343. [Google Scholar] [CrossRef]
- Canonsburg, A.D. Material Designer User’s Guide; ANSYS: Canonsburg, PA, USA, 2024. [Google Scholar]
- Wang, N.; Li, Z.; Peng, Y.; Jiang, Z.; Li, H. Micro–Macro Coupling Study on the Mechanical Properties of Continuous Fiber-Reinforced Composites. Polymers 2024, 16, 2995. [Google Scholar] [CrossRef] [PubMed]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS Plugin Tool for Periodic RVE Homogenisation. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]
- Sazlı, M.H. A Brief Review of Feed-Forward Neural Networks. Commun. Fac. Sci. Univ. Ankara Ser. A2–A3 Phys. Sci. Eng. 2006, 50, 11–17. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Han, D.; Kwon, S. Application of Machine Learning Method of Data-driven Deep Learning Model to Predict Well Production Rate in the Shale Gas Reservoirs. Energies 2021, 14, 3629. [Google Scholar] [CrossRef]
- Rayhan, S.B.; Rahman, M.M.; Sultana, J.; Szávai, S.; Varga, G. Finite Element and Machine Learning-Based Prediction of Buckling Strength in Additively Manufactured Lattice Stiffened Panels. Metals 2025, 15, 81. [Google Scholar] [CrossRef]
- Hooshmand, M.J.; Sakib-Uz-Zaman, C.; Khondoker, M.A.H. Machine Learning Algorithms for Predicting Mechanical Stiffness of Lattice Structure-Based Polymer Foam. Materials 2023, 16, 7173. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Mu, Z.; Ge, X. Machine Learning-Based Prediction of Elastic Buckling Coefficients on Diagonally Stiffened Plate Subjected to Shear, Bending, and Compression. Sustainability 2023, 15, 7815. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).