Abstract
The present work aims to carry out free vibration and buckling analysis of functionally graded hybrid reinforced laminated composite plates under thermal conditions. Finite element-based solutions are presented within the framework of recently proposed higher-order zigzag theory. Different variations of concentration of graphene platelets and fibers within the plate across its thickness are considered. First, the plate polymer is assumed to be reinforced using graphene platelets and then with fibers. The multiscale material properties of hybrid reinforced plates are obtained using the Halpin–Tsai micromechanical model. The nature of the distribution of graphene platelets and fibers across the thickness of the plate widely governs the free vibration behavior of functionally graded hybrid reinforced composite plates. The number of layers and shape factors also affect the free vibration behavior of functionally graded hybrid reinforced composite plates.
1. Introduction
Laminated composites are layered structures and are made up of orthotropic materials. Because of their excellent properties, such as lesser self-weight, higher strength, resistance towards corrosion, etc., laminated structures are used widely in aerospace, aeronautics, marine, naval, automobile, and civil engineering structures [1]. Reinforcing components are widely introduced within the composites to enhance their strength. Carbon fibers, carbon nanotubes (CNTs), graphene, silicon oxide, nanoparticles, etc., are some of the widely used reinforcing materials. When more than one reinforcing materials are introduced within the matrix, the resulting component is called a hybrid reinforced composite [2].
By employing hybrid materials, the properties of the laminate can be affected by controlling the amount of concentration of the reinforcing materials within the matrix [3]. Recently, CNTs are gaining popularity for enhancing the stiffness of the matrix. CNTs possess Young’s modulus up to 1 TPa. However, problems associated with the manufacturing of CNTs limit their use as a reinforcing material [4]. Therefore, researchers have incorporated two different types of reinforcing materials to enhance the strength and stiffness of the laminates [5]. Liew et al. [6] presented a detailed review of the mechanical behavior of functionally graded CNT-reinforced composites. A detailed review of the behavior of functionally graded CNT-reinforced composites was presented by Zhang et al. [7]. Soni et al. [8] presented a detailed review of studying the mechanical behavior of CNT-reinforced composite structures. Garg et al. [9] presented a detailed review of the use of CNTs for enhancing the mechanical properties of the engineered structures. A detailed review of the use of physics-informed machine learning approaches for predicting the behavior of laminated composites was presented by Khalid et al. [10]. A detailed review of the available literature on quantifying the behavior of CNT-reinforced nanostructures was presented by Garg et al. [11].
For studying the behavior of laminated composites, the theories available in the literature can be classified into two broader categories, namely, equivalent single layer theory (ESL) and layerwise theories (LWT). ESL theories are simplified models for the analysis of laminated composite plates and shells with the aim of approximately treating a multi-layered composite as one homogenized layer representing its mechanical behavior. The intention of these theories is to reduce the complexity of modeling each individual layer with regard to catching the general structural response and making it fit for engineering applications where computational efficiency is required. The classical lamination theory (CLT) assumes that the plane section remains plane and normal to the mid-plane after deformations. However, this theory neglects the transverse shear deformation effects.
The first-order shear deformation theory (FSDT), also called the Reissner–Mindlin plate theory, takes into account transverse shear deformation effects. Mandal et al. [12] employed FSDT to study the dynamic behavior of laminated plates with cutouts. Bourada et al. [13] employed Navier method-based FSDT to quantify the buckling behavior of rectangular laminates. Lu et al. [14] studied the dynamic behavior of elliptical porous cylindrical shells by using the Jacobi polynomials Ritz method. Saiah et al. [15] predicted free vibration behavior of functionally graded graphene-reinforced composites. Wang and Zhang [16] carried out free vibration analysis of graphene-reinforced porous doubly-curved shells by using a semi-analytical method. Using the Jacobi–Ritz boundary element method, Gao et al. [17] predicted the vibro-acoustic response of conical shell structures. Gwak et al. [18] proposed improved FSDT for predicting the behavior of layered structures within the framework of finite element-based FSDT. Using the Lekhnitskii smeared stiffener approach, Liu et al. [19] studied the buckling response of stiffened functionally graded graphene-reinforced layered cylindrical shell structures. Saood et al. [20] predicted the vibration behavior of sectorial plates under forced conditions by employing FSDT. However, FSDT uses a shear correction factor to compensate for the non-uniform distribution of transverse shear stresses through the thickness. The shear correction factor is necessary because the theory assumes a constant transverse shear strain across the thickness, which is not physically accurate. Determining an appropriate shear correction factor is challenging, and using incorrect values can lead to errors in shear stress predictions. This is especially problematic for laminates with varying layer thicknesses or material properties [21]. For thick laminates, FSDT may underpredict or overpredict transverse shear stresses, leading to inaccuracies in the stress distribution and overall structural response [22].
Higher-order shear deformation theory (HSDT) expands the in-plane displacement field as higher-order variations with respect to the thickness coordinates of the plate, thereby predicting the more accurate distribution of the transverse shear stresses across the thickness of the laminate. Fan and Wang [23,24] predicted the dynamic behavior of cracked hybrid laminated plates under a non-linear range. Shen et al. [25] studied the buckling behavior of CNT-reinforced laminated plates under thermal conditions by employing a two-step perturbation technique. By employing HSDT, Belkacem et al. [26] studied the buckling behavior of hybrid laminated composite plates. Wang et al. [27] employed a perturbation technique for studying the free vibration behavior of initially stressed functionally graded CNT-reinforced hybrid composite plates under thermal conditions. Using quasi-3D SDT, Jafari and Kiani [28] predicted the free vibration behavior of functionally graded graphene-reinforced composite plates. Chen et al. [29] employed the Galerkin method for quantifying the buckling behavior of CNT-reinforced plates under thermal conditions. Garg et al. [30] studied the bending and free vibration response of hybrid reinforced laminated composite beams by using HSDT. Belarbi et al. [31] employed parabolic shear deformation theory to predict the mechanical behavior of CNT-reinforced beams. Wu and Xu [32] presented strong and weak formulations within HSDT for predicting the bending behavior of functionally graded beams.
Although HSDT improves the prediction of transverse shear stresses compared to FSDT, it does not completely eliminate errors in through-thickness stress predictions. The determination of stresses is still private with respect to the assumed displacement field; in addition, their accurate determination may require post-processing in certain cases [33]. Incorporation of HSDT into FEA requires special elements that can support higher-order displacement fields [34]. It is more challenging to develop these elements and ensure that they are stable and accurate. The selection of higher-order terms in the displacement field determines the accuracy of the HSDT model [35]. If the selected higher-order terms are inadequate to represent the actual behavior of displacements, the results obtained may not be appreciably better than FSDT [36].
One of the advanced modeling approaches used to analyze laminated composite plates and shells is layer-wise theory. Contrary to ESL theories, which model the whole laminate as a homogenized single layer, layer-wise theories take into consideration the variation of displacement and stresses in each layer. It provides a more detailed and precise model of the mechanical behavior in complex laminates when through-thickness stress distribution becomes important. Garg et al. [37] compared the free vibration response of symmetric and unsymmetric functionally graded CNT-reinforced composite beams by employing HOZT. Chiker et al. [38] studied the free vibration response of hybrid laminated plates with functionally graded CNT-reinforced laminates using LWT. Garg et al. [39] predicted fundamental frequencies of functionally graded CNT-reinforced beams under thermal conditions.
The different concentrations of the fibers and CNTs within each layer are taken, giving rise to an overall functionally graded structure across its thickness. From the detailed review, it can be seen that the free vibration and buckling behavior of functionally graded hybrid reinforced laminated composite plates under thermal conditions have not been explored. In the present work, an attempt has been made to predict the free vibration and buckling behavior of functionally graded hybrid reinforced laminated composite plate, which is carried out using recently proposed finite element-based HOZT.
2. Mathematical Formulation
The hybrid reinforced laminated composite plate is assumed to comprise several layers in which the concentration of GPLs and fibers varies regularly. Thus, the continuous variation of the GPs and fibers along the thickness are called functionally graded hybrid reinforced laminated composite (FGHRLC) plates. Consider a FGHRLC plate with dimensions along the X- and Y-axis, respectively, with thickness equal to units. The plate lies in the X-Y plane with the thickness along the Z-axis (Figure 1). Shape factors, i.e., and govern the content of GPL and fibers gradient along the thickness direction of the plate. The volume fraction of the GPLs and fibers for the k-th layer can be worked out as
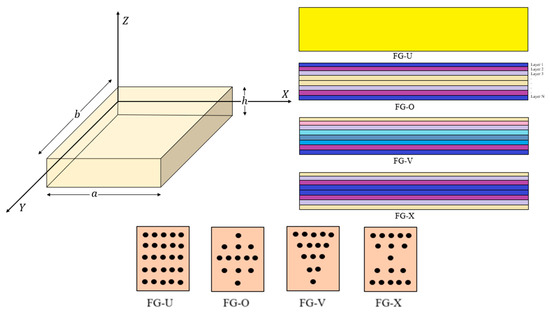
Figure 1.
Schematic of plate and functionally graded hybrid reinforced laminated composite plate.
Uniform distribution of fibers and CNTs (FG-U): The fibers and CNTs are distributed uniformly across the thickness of the plate.
O-distribution of fibers and CNTs (FG-O): The fibers and CNTs are distributed in such a way that at the top and bottom surfaces of the plate, the distribution is minimum, with maximum at the middle axis of the plate.
X-distribution of fibers and CNTs (FG-X): The fibers and CNTs are distributed in such a way that at the top and bottom surfaces of the plate, the distribution is maximum, with minimum at the middle axis of the plate.
V-distribution of fibers and CNTs (FG-V): The fibers and CNTs are distributed in such a way that at the top surface of the plate, the distribution is maximum, with minimum at the bottom surface of the plate.
where denotes the number of layers, and represents the total volume fraction of the GPLs and fibers, respectively. The value of the can be obtained as
where and denotes the mass densities of GPLs and matrix, respectively. is the weight fraction of GPLs in the layer.
At first, the GPLs are embedded in the matrix followed by adding the fibers. Therefore, the effective material property of GPL-reinforced polymer in the framework of the Halpin–Tsai micromechanical model can be expressed as
where is the effective Young’s modulus at temperature of GPL-reinforced polymer, , , , can be determined as
where , , and are the average length, width, and thickness of GPLs, respectively. and are the Young’s modulus of GPL and matrix at temperature (T), respectively. The values for the shear modulus, density, Poisson’s ratio, and thermal expansion coefficient can be worked out as
The fibers are added to the GPL-reinforced composite to obtain a hybrid-reinforced composite. The effective Young’s modulus, shear modulus, density, Poisson’s ratio, and thermal expansion coefficient for hybrid reinforced composite can be obtained as
Polymethylmethacrylate (PMMA) is a versatile polymer often used as a matrix material in graphene and carbon nanotube (CNT)-reinforced hybrid composites due to its excellent optical clarity, lightweight nature, and good mechanical properties. However, its use comes with specific requirements and restrictions. Effective interfacial bonding between PMMA and reinforcements is critical to ensure efficient load transfer and improved composite performance, which often necessitates surface functionalization of graphene and CNTs. The processing of PMMA-based composites must be conducted at moderate temperatures (below 200 °C) to prevent thermal degradation. Homogeneous dispersion of graphene and CNTs is also vital, requiring techniques like sonication or solution blending to avoid filler agglomeration that could act as stress concentrators. Furthermore, the filler content must be optimized (typically 0.5–5 wt%) to achieve a balance between property enhancement and processability. PMMA’s susceptibility to UV degradation limits its outdoor applications unless UV stabilizers are added, and its low glass transition temperature (~105 °C) restricts its use in high-temperature environments. Additionally, the thermal expansion mismatch between PMMA and reinforcements can induce residual stresses, impacting the composite’s structural integrity. Despite these restrictions, PMMA remains a promising matrix for hybrid composites, particularly in applications requiring transparency, lightweight properties, and moderate mechanical performance enhancements.
For temperature-dependent properties of matrix (PMMA), the density and Poisson’s ratio of the matrix are assumed to be independent of the temperature, while the thermal expansion coefficient and Young’s modulus are taken as temperature-dependent and are adopted from the work of Dat et al. [40] as
where is the rise or fall in temperature from the room temperature T = 300 K.
Plate Kinematics
The in-plane and transverse displacement fields can be stated as [41]
where , and are the mid-plane displacement of any point lying on the mid-plane. , , , and are the higher-order unknowns. and are the unit functions. , , , and are the slopes of the -th and -th layer for the upper and lower layers, respectively. The stress–strain relationship can be stated as
Imposing transverse shear stress-free conditions at the top and bottom surfaces of the plate along with the continuity along the interfaces and applying additional conditions , at the top of the plate, and , at the bottom of the plate, the unknowns, ,, , , , , ,…,, , , ,…,, , , ,…,, , , ,…, can be stated as
where the terms , , , , ,, , and denotes the constants and , , , and are coefficients depending on the material properties of the layer.
The strain vector can be expressed as
Avoiding the issues in handling C1 continuity conditions, the derivative terms can be expressed as
Using nine-noded quadratic element with 7-degrees of freedom per node, the displacement vector can be expressed as
where and are the shape functions and displacement vectors associated with the node.
Using Equation (16), Equation (14) can be expressed as
where is the strain–displacement matrix in Cartesian coordinates.
With the help of Hamilton’s principle, the equation of motion is stated as (without considering work done by external forces and damping)
In the above equation, represents kinetic energy, which is calculated as
where stands for the density of the material and , and are the derivatives of , and , respectively.
in Equation (18) represents potential energy which is expressed as
or
The dynamic equations for a system given by Hamilton’s principle are
In the above equation , , , and represents global mass matrix, nodal acceleration vector of system, reduced global stiffness matrix, and unknown nodal vector, respectively. The frequency can be evaluated using
At any point within the plate, displacement due to free vibration can be written as
or
where the matrix is similar to that contains terms in form of and the unit step function.
The consistent elemental mass matrix for an element can be stated as
where is the mass density of the ith layer and is the shape function matrix and the matrix is
The elemental stiffness, mass, and load matrix are assembled to form corresponding global matrices by taking into account the behavior of all the elements. Finally, the free vibration problem is solved as an eigenvalue problem.
Splitting the strains in Equation (16) in linear and non-linear range and can be stated as
where
and
or
and the elements contained in , and are function of unit step function and thickness coordinate and is the strain–displacement relationship in Cartesian coordinates.
With the matrix in the above equation, the geometric stiffness matrix can be derived and may be written as
where is the in-plane stress components of the kth layer can be written as
The total potential energy of the plate under hygrothermal and transverse load may can be written as
where is the plate’s strain energy and is the energy due to external loading.
or
where .
Or
where .
Now, calculating the elemental potential energy by combining Equations (34) and (36)–(38) as
where is the geometric stiffness matrix.
By minimizing the Equation (39) with respect to , we get
where is the buckling load factor.
3. Results and Discussion
The present section deals with the free vibration and buckling behavior of functionally graded hybrid reinforced laminated composite plates under thermal conditions. Since no results are available in the literature, the present results are therefore validated with those obtained for the free vibration analysis of FG-CNT reinforced composite plates under thermal conditions. The validation results are presented in Table 1. The present results are compared with those obtained by Lei et al. [42] and Zhu et al. [43] using FSDT and are found to be in agreement.

Table 1.
Validation of non-dimensional natural frequency for FG-CNT reinforced composite plate with simply supported end conditions.
Table 2 shows the variation of critical buckling temperature (in K) and frequencies (in Hz) for the simply supported (SSSS) functionally graded hybrid reinforced laminated composite plate under thermal conditions with and . As the temperature T increases from 300 to 400, both the frequencies (F) and the critical buckling load (B) generally decrease across all FG distributions and material compositions. This reduction in frequencies and critical buckling load with rising temperature is typical due to thermal softening, where the material’s stiffness diminishes, leading to reduced resistance to deformation.

Table 2.
Variation of frequencies (in Hz) and critical buckling temperature (in K) for SSSS functionally graded hybrid reinforced laminated composite plate under thermal conditions with and .
With an increase in the volume fraction of fiber Vf, there is a notable increase in both frequency (F) and critical buckling load (B) values across all FG distributions and temperatures. A higher fiber volume fraction enhances the plate’s stiffness and stability, resulting in improved resistance to buckling and increased vibrational frequencies. Increasing Mg from 0.01 to 0.05 appears to positively impact both the critical buckling load (B) and frequencies (F), though the magnitude of this impact varies. Higher graphene platelet content increases the material’s load-carrying capacity and stability, likely due to the reinforcing effect of graphene, which provides better mechanical properties.
Different FG distributions (X, U, O, and V) exhibit distinct effects on the frequencies and buckling loads. Generally, FG-X and FG-O show higher frequency and buckling load values, whereas FG-U and FG-V are slightly lower. This suggests that the specific arrangement of reinforcement material influences the composite’s mechanical behavior, where certain distributions lead to more efficient reinforcement dispersion.
Figure 2 shows the variation of critical buckling temperature for the SSSS plate with different values of and for FG-X plate. As the temperature increases (from Figure 2a at 300 K to Figure 2e at 400 K), the critical buckling temperature generally decreases for all values of Sf and Sg. This decreasing trend with temperature indicates thermal softening effects, where the material’s stiffness reduces with higher thermal exposure, leading to a lower critical buckling threshold. At each temperature level, the critical buckling temperature increases with an increase in Sf from 0 to 0.5. A higher Sf value, which corresponds to a more concentrated fiber distribution, enhances the plate’s stiffness and stability, leading to higher critical buckling temperatures. Within each line corresponding to a specific Sf, the critical buckling temperature also increases as Sg increases from 0 to 0.5. A higher Sg value implies a greater distribution concentration of graphene platelets, which reinforces the plate’s structural integrity and stability, thereby increasing its resistance to buckling under thermal loads. With an increase in temperature of 25 K, about 15% increase in critical buckling temperature is observed in all of the cases.
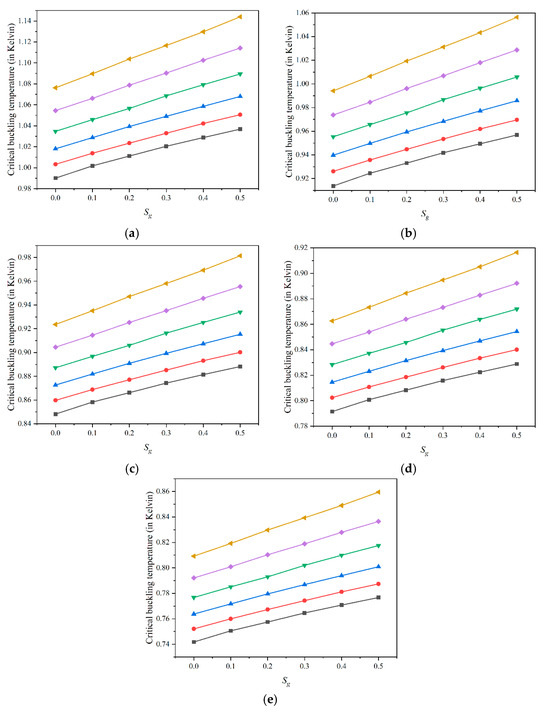
Figure 2.
Variation of critical buckling temperature for FG-X plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
Figure 3 shows the variation of critical buckling temperature for the SSSS plate with different values of and for the FG-V plate. From T at 300 K to 400 K, there is a general decline in the critical buckling temperature as the temperature increases. This behavior, similar to previous observations, is due to thermal softening, where the material’s stiffness is reduced at elevated temperatures, lowering the critical buckling threshold. For each subfigure, the critical buckling temperature decreases as Sf increases from 0 to 0.5. A lower Sf value (closer to zero) results in a higher critical buckling temperature, indicating that the distribution of fibers becomes less effective in enhancing thermal stability as Sf increases. This trend suggests that a more concentrated fiber distribution (lower Sf) enhances the plate’s resistance to buckling under thermal loads. For each value of Sf, the critical buckling temperature decreases as Sg increases from 0 to 0.5. A higher Sg value (more dispersed graphene platelets) reduces the critical buckling temperature, which implies that a more concentrated distribution of graphene platelets (lower Sg) is more beneficial for enhancing the plate’s thermal stability. The highest critical buckling temperatures are observed with the lowest values of both Sf and Sg, showing that more concentrated distributions of fibers and graphene platelets improve the thermal stability of the FG-V plate. Conversely, the lowest critical buckling temperatures are observed with higher Sf and Sg values, where both fibers and graphene platelets are more dispersed, resulting in a less stable structure under thermal loads. At lower values of , the decrease of about 8% in the values of the critical buckling temperature was observed, whereas at higher values, a change of about 15–20% was observed. Thus, the higher values of greatly affects the buckling behavior of the plate.
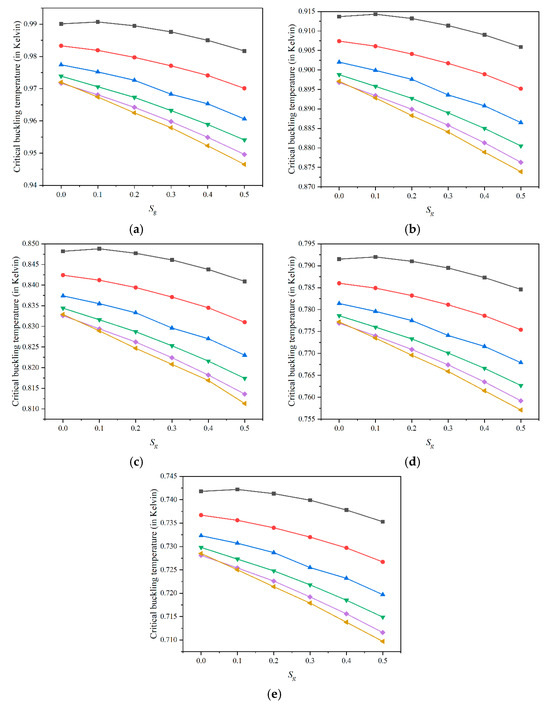
Figure 3.
Variation of critical buckling temperature for FG-V plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
Figure 4 shows the variation of critical buckling temperature for the SSSS plate with different values of and for FG-O plate. Increasing temperatures from 300 K to 400 K, the critical buckling temperature decreases. This trend aligns with the phenomenon of thermal softening, where the composite plate’s stiffness is reduced at higher temperatures, lowering the critical buckling temperature. For each subfigure at each temperature level, the critical buckling temperature decreases as Sf increases from 0 to 0.5. A lower Sf value, where fibers are more concentrated, results in a higher critical buckling temperature, suggesting that concentrated fiber distribution enhances the plate’s thermal stability and resistance to buckling. Similarly, within each line for a given Sf, the critical buckling temperature decreases as Sg increases from 0 to 0.5. This decrease in critical buckling temperature with higher Sg values indicates that a more concentrated distribution of graphene platelets (lower Sg) contributes positively to the plate’s structural stability under thermal loading conditions. The highest critical buckling temperatures are achieved when both Sf and Sg are at their lowest values, showing that concentrated distributions of fibers and graphene platelets maximize thermal stability. The lowest critical buckling temperatures are observed at higher values of Sf and Sg, where the distributions are more dispersed, indicating reduced stability under elevated temperatures. A decrease of about 17% in the values of critical buckling temperature was observed for all values of .
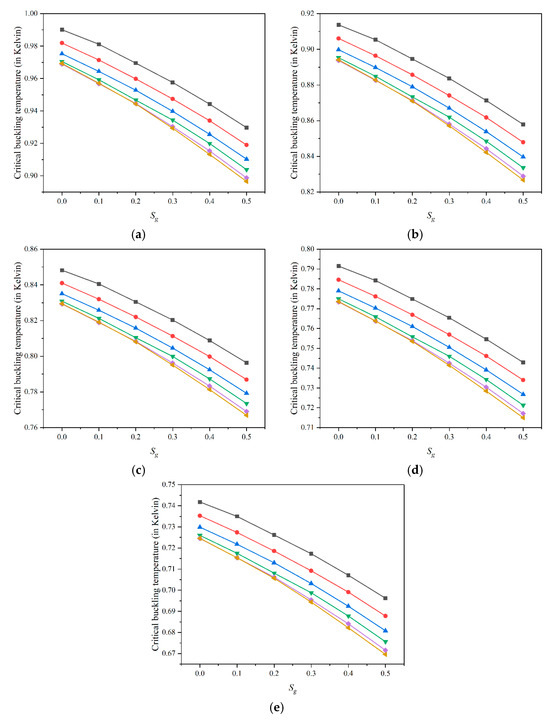
Figure 4.
Variation of critical buckling temperature for FG-O plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
Figure 5 shows the variation of fundamental frequency for the SSSS plate with different values of and for FG-X plate. With the increase in temperature, the fundamental frequency generally decreases. The reduction in frequency with rising temperature indicates thermal softening, where increased temperature lowers the stiffness of the material, resulting in a decrease in the plate’s natural frequency. the fundamental frequency increases as Sf increases from 0 to 0.5. Higher Sf values, corresponding to a more concentrated distribution of fibers, enhance the plate’s stiffness, leading to an increase in the fundamental frequency. This indicates that a higher concentration of fibers improves vibrational stability. Within each line representing a specific Sf value, the fundamental frequency also increases with an increase in Sg from 0 to 0.5. Higher Sg values contribute positively to the structural stiffness, resulting in an increased frequency (about 16%). This demonstrates that a higher concentration of graphene platelets improves the vibrational characteristics of the FG-X plate. The highest fundamental frequencies are observed when both Sf and Sg are at their maximum values, suggesting that concentrated distributions of fibers and graphene platelets significantly enhance the plate’s vibrational stability. The lowest frequencies occur at the lowest values of Sf and Sg, where reinforcement concentrations are minimal, resulting in a less stiff and more flexible structure.
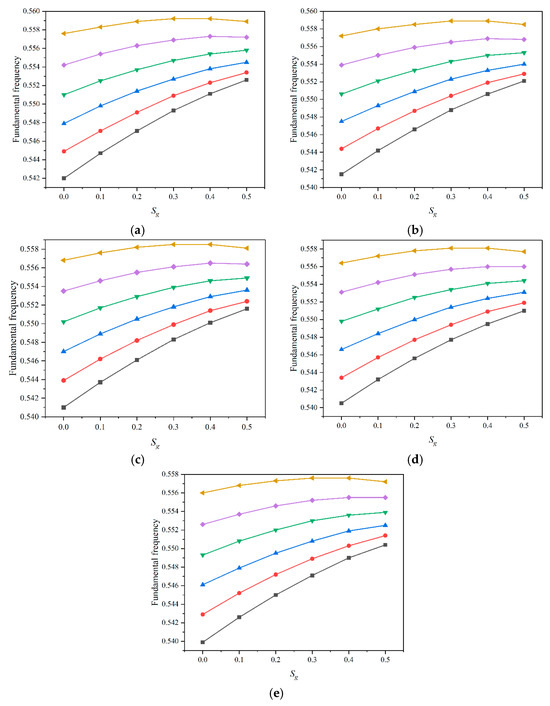
Figure 5.
Variation of fundamental frequency for FG-X plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
Figure 6 shows the variation of fundamental frequency for the SSSS plate with different values of and for the FG-V plate. As the temperature increases from 300 K to 400 K, the fundamental frequency decreases. This reduction with temperature increase is due to thermal softening, where the material’s stiffness diminishes at elevated temperatures, leading to a decrease in the fundamental frequency of the plate. For each case, the fundamental frequency decreases as Sf increases from 0 to 0.5. Lower values of Sf result in higher frequencies, suggesting that concentrated fiber distributions increase the stiffness of the plate and therefore its fundamental frequency. Within each line for a specific Sf value, the fundamental frequency also decreases as Sg increases from 0 to 0.5. A lower Sg value contributes positively to the plate’s stiffness, resulting in a higher frequency. This indicates that concentrated distributions of graphene platelets enhance the vibrational properties of the FG-V plate. The highest fundamental frequencies are observed when both Sf and Sg are at their minimum values (0), showing that concentrated distributions of both fibers and graphene platelets maximize the plate’s vibrational stability. The lowest fundamental frequencies are noted at the highest values of Sf and Sg, where reinforcement is more dispersed, indicating reduced structural stiffness and vibrational resistance. For lower values of , the percentage change in the values of the fundamental frequency is only about 5%, whereas at higher values, the percentage change is more than 18%.
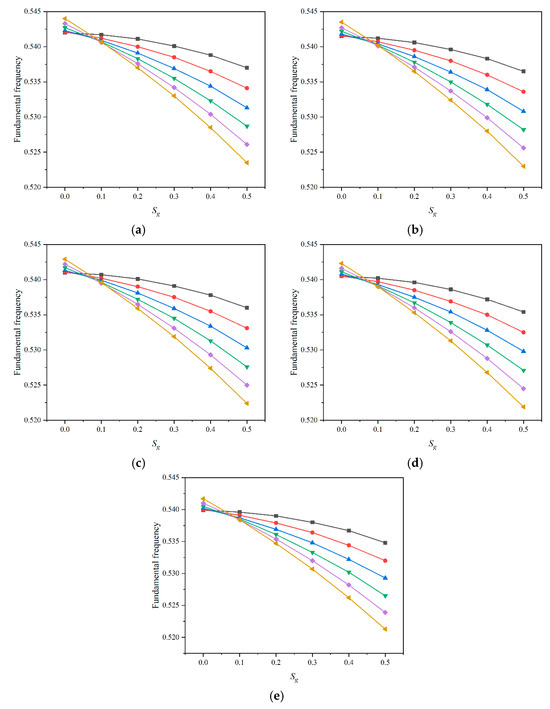
Figure 6.
Variation of fundamental frequency for FG-V plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
Figure 7 shows the variation of fundamental frequency for the SSSS plate with different values of and for FG-O plate. The fundamental frequency decreases as temperature increases. In each case, as Sf increases from 0 to 0.5, the fundamental frequency decreases. Lower values of Sf result in higher frequencies, suggesting that a concentrated distribution of fibers enhances the stiffness and stability of the plate, thereby increasing the fundamental frequency. Within each line corresponding to a specific Sf value, the fundamental frequency decreases as Sg increases from 0 to 0.5. Lower Sg values are associated with higher fundamental frequencies, indicating that a more concentrated distribution of graphene platelets also contributes to increased stiffness and vibrational stability. The highest fundamental frequencies are observed when both Sf and Sg are at their minimum values, highlighting those concentrated distributions of fibers and graphene platelets enhance the plate’s stiffness and fundamental frequency. Conversely, the lowest frequencies are found when both Sf and Sg are at their maximum values, indicating reduced vibrational stability due to a more dispersed distribution of reinforcements.
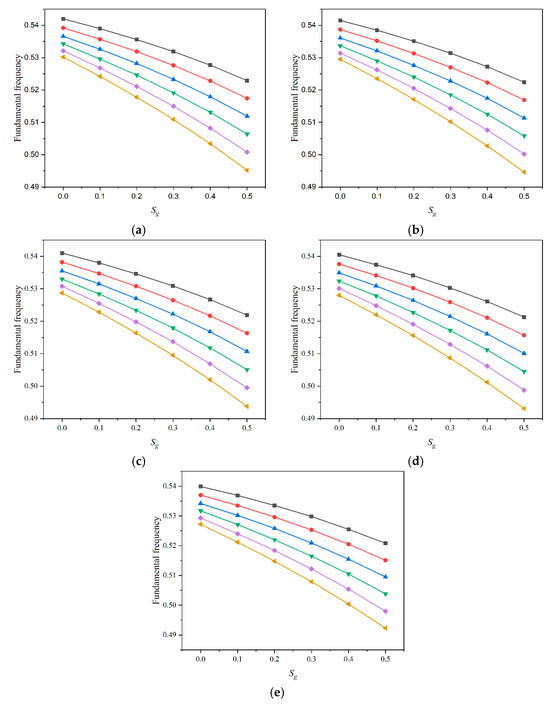
Figure 7.
Variation of fundamental frequency for FG-O plate with different values of  0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
 0,
0,  0.1,
0.1,  0.2,
0.2,  0.3,
0.3,  0.4, and
0.4, and  0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
0.5 at (a) 300 K, (b) 325 K, (c) 350 K, (d) 375 K, and (e) 400 K with and .
4. Conclusions
The present work deals with the free vibration and buckling analysis of functionally graded hybrid reinforced laminated plates under thermal conditions using HOZT. The following important points are noted down:
- Higher temperatures reduce both frequency and critical buckling load due to thermal softening;
- Increasing fiber volume fraction (Vf) and graphene platelet weight fraction (Mg) enhances the plate’s stability and vibrational resistance;
- Different FG distributions have varied impacts on the composite’s performance, with FG-X and FG-O showing slightly better structural stability under thermal loads;
- For the FG-X plate, the higher values of Sf and Sg lead to higher critical buckling temperatures, reflecting the reinforcing effect of fiber and graphene platelet distributions;
- For the FG-V and FG-O plates, the higher Sf and Sg values (more dispersed fiber and graphene platelet distributions) reduce the critical buckling temperature, indicating lower thermal stability;
- For the FG-X plate, the higher values of Sf and Sg lead to an increase in fundamental frequency, indicating that concentrated distributions of fibers and graphene platelets improve the vibrational performance of the plate;
- For the FG-V and FG-O plates, the higher values of Sf and Sg (dispersed distributions of fibers and graphene platelets) result in lower fundamental frequencies, indicating reduced vibrational stability.
Author Contributions
Conceptualization, A.G. and V.S.; methodology, R.G., A.G., V.S. and L.L.; software, R.G.; validation, R.G. and A.G.; formal analysis, R.G.; investigation, R.G.; data curation, R.G., A.G., V.S. and L.L.; writing—original draft preparation, R.G.; writing—review and editing, A.G., V.S. and L.L., visualization, R.G.; supervision, A.G. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the National Natural Science Foundation of China (Grant No. 52175095), and the Young Top-notch Talent Cultivation Program of Hubei Province of China.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Beber, V.C.; Fernandes, P.H.E.; Nagel, C.; Arnaut, K. Integrated Analytical and Finite Element-Based Modelling, Manufacturing, and Characterisation of Vacuum-Infused Thermoplastic Composite Laminates Cured at Room Temperature. J. Compos. Sci. 2024, 8, 545. [Google Scholar] [CrossRef]
- Panico, M.; Cozzolino, E.; Papa, I.; Taha, I.; Lopresto, V. An Investigation of the Mechanical Properties of Flax/Basalt Epoxy Hybrid Composites from a Sustainability Perspective. Polymers 2024, 16, 2839. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, K.; Hamza, M.H.; Morales, M.A.; Henry, T.C.; Hall, A.; Chattopadhyay, A. Electromagnetic Interference Shielding Analysis of Hybrid Buckypaper-Reinforced Polymer Matrix Composites: A Quantum Tunneling-Informed Equivalent Circuit Approach. Appl. Sci. 2024, 14, 8960. [Google Scholar] [CrossRef]
- Vargas-Lara, F.; Douglas, J.F. Confronting the Complexity of CNT Materials. Soft Matter 2015, 11, 4888–4898. [Google Scholar] [CrossRef] [PubMed]
- Kardooni, M.R.; Shishesaz, M.; Mosalmani, R. Three-Dimensional Thermo-Mechanical Elastic Analysis of Functionally Graded Five Layers Composite Sandwich Plate on Winkler Foundations. J. Compos. Sci. 2022, 6, 372. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical Analysis of Functionally Graded Carbon Nanotube Reinforced Composites: A Review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, C.; Li, H.; Pang, F.; Zou, T.; Wang, H.; Wang, N. Analysis of Functionally Graded Carbon Nanotubereinforced Composite Structures: A Review. Nanotechnol. Rev. 2020, 9, 1408–1426. [Google Scholar] [CrossRef]
- Soni, S.K.; Thomas, B.; Swain, A.; Roy, T. Functionally Graded Carbon Nanotubes Reinforced Composite Structures: An Extensive Review. Compos. Struct. 2022, 299, 116075. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D.; Belarbi, M.-O.; Zenkour, A.M.; Sahoo, R. Estimation of Carbon Nanotubes and Their Applications as Reinforcing Composite Materials–an Engineering Review. Compos. Struct. 2021, 272, 114234. [Google Scholar] [CrossRef]
- Khalid, S.; Yazdani, M.H.; Azad, M.M.; Elahi, M.U.; Raouf, I.; Kim, H.S. Advancements in Physics-Informed Neural Networks for Laminated Composites: A Comprehensive Review. Mathematics 2024, 13, 17. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D.; Zenkour, A.M.; Belarbi, M.-O.; Houari, M.-S.-A. A Review of Available Theories and Methodologies for the Analysis of Nano Isotropic, Nano Functionally Graded, and CNT Reinforced Nanocomposite Structures. Arch. Comput. Methods Eng. 2022, 29, 2237–2270. [Google Scholar] [CrossRef]
- Mandal, A.; Haldar, S.; Ray, C. Dynamic Analysis of Laminated Composite Skew Plates with Cut-Out. Struct. Eng. Mech. 2018, 68, 639–646. [Google Scholar] [CrossRef]
- Bourada, M.; Bouadi, A.; Bousahla, A.A.; Senouci, A.; Bourada, F.; Tounsi, A.; Mahmoud, S. Buckling Behavior of Rectangular Plates under Uniaxial and Biaxial Compression. Struct. Eng. Mech. 2019, 70, 113–123. [Google Scholar] [CrossRef]
- Lu, J.; Yang, Q.; Meng, Z.; Yang, K.; Xu, W.; Chiu, C. Dynamic Analysis of Functionally Graded Porous (FGP) Elliptic Cylindrical Shell Based on Jacobi Polynomials Ritz Method. J. Compos. Sci. 2023, 7, 344. [Google Scholar] [CrossRef]
- Saiah, B.; Bachene, M.; Guemana, M.; Chiker, Y.; Attaf, B. On the Free Vibration Behavior of Nanocomposite Laminated Plates Contained Piece-Wise Functionally Graded Graphene-Reinforced Composite Plies. Eng. Struct. 2022, 253, 113784. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, K. Free Vibration of Graphene Nanoplatelet-Reinforced Porous Double-Curved Shells of Revolution with a General Radius of Curvature Based on a Semi-Analytical Method. Mathematics 2024, 12, 3060. [Google Scholar] [CrossRef]
- Gao, C.; Zheng, J.; Pang, F.; Xu, J.; Li, H.; Yan, J. Prediction of Time Domain Vibro-Acoustic Response of Conical Shells Using Jacobi–Ritz Boundary Element Method. Acoustics 2024, 6, 523–540. [Google Scholar] [CrossRef]
- Gwak, Y.; Nguyen, S.-N.; Kim, J.-S.; Park, H.; Lee, J.; Han, J.-W. Improved Finite Element Thermomechanical Analysis of Laminated Composite and Sandwich Plates Using the New Enhanced First-Order Shear Deformation Theory. Mathematics 2024, 12, 963. [Google Scholar] [CrossRef]
- Liu, Z.; Tornabene, F.; Dimitri, R.; Babaei, M. Numerical Study of the Buckling Response of Stiffened FG Graphene-Reinforced Multilayer Composite Cylindrical Panels. Processes 2024, 12, 430. [Google Scholar] [CrossRef]
- Saood, A.; Khan, Z.A.; Parvez, M.T.; Khan, A.H. On the Large Amplitude Forced Vibration Analysis of Composite Sectorial Plates. J. Compos. Sci. 2021, 5, 83. [Google Scholar] [CrossRef]
- Thomas, B.; Roy, T. Vibration and Damping Analysis of Functionally Graded Carbon Nanotubes Reinforced Hybrid Composite Shell Structures. J. Vib. Control 2017, 23, 1711–1738. [Google Scholar] [CrossRef]
- Pai, P.F. A New Look at Shear Correction Factors and Warping Functions of Anisotropic Laminates. Int. J. Solids Struct. 1995, 32, 2295–2313. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, H. Nonlinear Dynamics of Matrix-Cracked Hybrid Laminated Plates Containing Carbon Nanotube-Reinforced Composite Layers Resting on Elastic Foundations. Nonlinear Dyn. 2016, 84, 1181–1199. [Google Scholar] [CrossRef]
- Fan, Y.; Wang, H. Nonlinear Bending and Postbuckling Analysis of Matrix Cracked Hybrid Laminated Plates Containing Carbon Nanotube Reinforced Composite Layers in Thermal Environments. Compos. Part B Eng. 2016, 86, 1–16. [Google Scholar] [CrossRef]
- Shen, H.-S.; Xiang, Y.; Lin, F.; Hui, D. Buckling and Postbuckling of Functionally Graded Graphene-Reinforced Composite Laminated Plates in Thermal Environments. Compos. Part B Eng. 2017, 119, 67–78. [Google Scholar] [CrossRef]
- Belkacem, A.; Tahar, H.D.; Abderrezak, R.; Amine, B.M.; Mohamed, Z.; Boussad, A. Mechanical Buckling Analysis of Hybrid Laminated Composite Plates under Different Boundary Conditions. Struct. Eng. Mech. 2018, 66, 761–769. [Google Scholar] [CrossRef]
- Wang, H.; Chen, C.-S.; Hsu, C.-Y.; Chen, W.-R. Vibration and Stability of Initially Stressed Functionally Graded Carbon Nanotube-Reinforced Hybrid Composite Plates in Thermal Environments. Mech. Based Des. Struct. Mach. 2022, 50, 1298–1313. [Google Scholar] [CrossRef]
- Jafari, P.; Kiani, Y. Free Vibration of Functionally Graded Graphene Platelet Reinforced Plates: A Quasi 3D Shear and Normal Deformable Plate Model. Compos. Struct. 2021, 275, 114409. [Google Scholar] [CrossRef]
- Chen, C.-S.; Wang, H.; Chen, T.-J.; Chen, W.-R. Parametric Instability of Functionally Graded Carbon Nanotube-Reinforced Hybrid Composite Plates in Thermal Environments. Int. J. Mech. Mater. Des. 2021, 17, 171–186. [Google Scholar] [CrossRef]
- Garg, A.; Mukhopadhyay, T.; Chalak, H.D.; Belarbi, M.-O.; Li, L.; Sahoo, R. Multiscale Bending and Free Vibration Analyses of Functionally Graded Graphene Platelet/Fiber Composite Beams. Steel Compos. Struct. 2022, 44, 707–720. [Google Scholar] [CrossRef]
- Belarbi, M.-O.; Salami, S.J.; Garg, A.; Daikh, A.-A.; Houari, M.-S.-A.; Dimitri, R.; Tornabene, F. Mechanical Behavior Analysis of FG-CNT-Reinforced Polymer Composite Beams via a Hyperbolic Shear Deformation Theory. Contin. Mech. Thermodyn. 2023, 35, 497–520. [Google Scholar] [CrossRef]
- Wu, C.-P.; Xu, Z.-R. Strong and Weak Formulations of a Mixed Higher-Order Shear Deformation Theory for the Static Analysis of Functionally Graded Beams under Thermo-Mechanical Loads. J. Compos. Sci. 2020, 4, 158. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M. Effect of Curvilinear Reinforcing Fibers on the Linear Static Behavior of Soft-Core Sandwich Structures. J. Compos. Sci. 2018, 2, 14. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D. A Review on Analysis of Laminated Composite and Sandwich Structures under Hygrothermal Conditions. Thin-Walled Struct. 2019, 142, 205–226. [Google Scholar] [CrossRef]
- Chen, C.-S.; Fung, C.-P.; Yang, J.-G. Assessment of Plate Theories for Initially Stressed Hybrid Laminated Plates. Compos. Struct. 2009, 88, 195–201. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.; Xie, Z.; Peng, L. Stability Analysis of Curved Beams Based on First-Order Shear Deformation Theory and Moving Least-Squares Approximation. Buildings 2024, 14, 3887. [Google Scholar] [CrossRef]
- Garg, A.; Chalak, H.D.; Zenkour, A.M.; Belarbi, M.-O.; Sahoo, R. Bending and Free Vibration Analysis of Symmetric and Unsymmetric Functionally Graded CNT Reinforced Sandwich Beams Containing Softcore. Thin-Walled Struct. 2022, 170, 108626. [Google Scholar] [CrossRef]
- Chiker, Y.; Bachene, M.; Bouaziz, S.; Guemana, M.; Ben Amar, M.; Haddar, M. Free Vibration Analysis of Hybrid Laminated Plates Containing Multilayer Functionally Graded Carbon Nanotube-Reinforced Composite Plies Using a Layer-Wise Formulation. Arch. Appl. Mech. 2021, 91, 463–485. [Google Scholar] [CrossRef]
- Chalak, H.D.; Zenkour, A.M.; Garg, A. Free Vibration and Modal Stress Analysis of FG-CNTRC Beams under Hygrothermal Conditions Using Zigzag Theory. Mech. Based Des. Struct. Mach. 2021, 51, 4709–4730. [Google Scholar] [CrossRef]
- Dat, N.D.; Quan, T.Q.; Mahesh, V.; Duc, N.D. Analytical Solutions for Nonlinear Magneto-Electro-Elastic Vibration of Smart Sandwich Plate with Carbon Nanotube Reinforced Nanocomposite Core in Hygrothermal Environment. Int. J. Mech. Sci. 2020, 186, 105906. [Google Scholar] [CrossRef]
- Garg, A.; Belarbi, M.O.; Chalak, H.D.; Li, L.; Sharma, A.; Avcar, M.; Sharma, N.; Paruthi, S.; Gulia, R. Buckling and Free Vibration Analysis of Bio-Inspired Laminated Sandwich Plates with Helicoidal/Bouligand Face Sheets Containing Softcore. Ocean Eng. 2023, 270, 113684. [Google Scholar] [CrossRef]
- Lei, Z.X.; Liew, K.M.; Yu, J.L. Free Vibration Analysis of Functionally Graded Carbon Nanotube-Reinforced Composite Plates Using the Element-Free Kp-Ritz Method in Thermal Environment. Compos. Struct. 2013, 106, 128–138. [Google Scholar] [CrossRef]
- Zhu, P.; Lei, Z.X.; Liew, K.M. Static and Free Vibration Analyses of Carbon Nanotube-Reinforced Composite Plates Using Finite Element Method with First Order Shear Deformation Plate Theory. Compos. Struct. 2012, 94, 1450–1460. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).