Numerical Analysis of the Cyclic Behavior of Reinforced Concrete Columns Incorporating Rubber
Abstract
1. Introduction
2. Finite Element Modeling
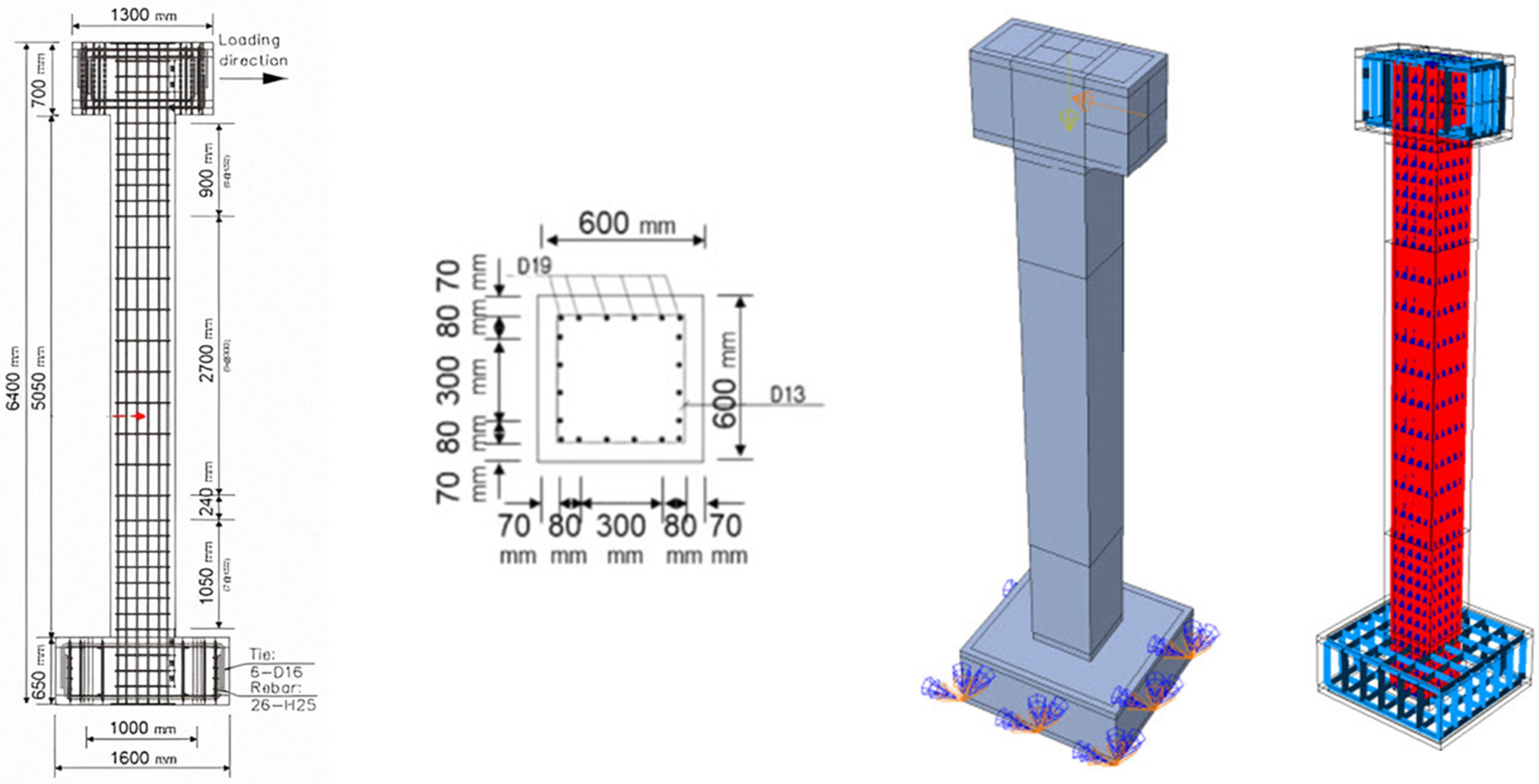
2.1. Model Geometry
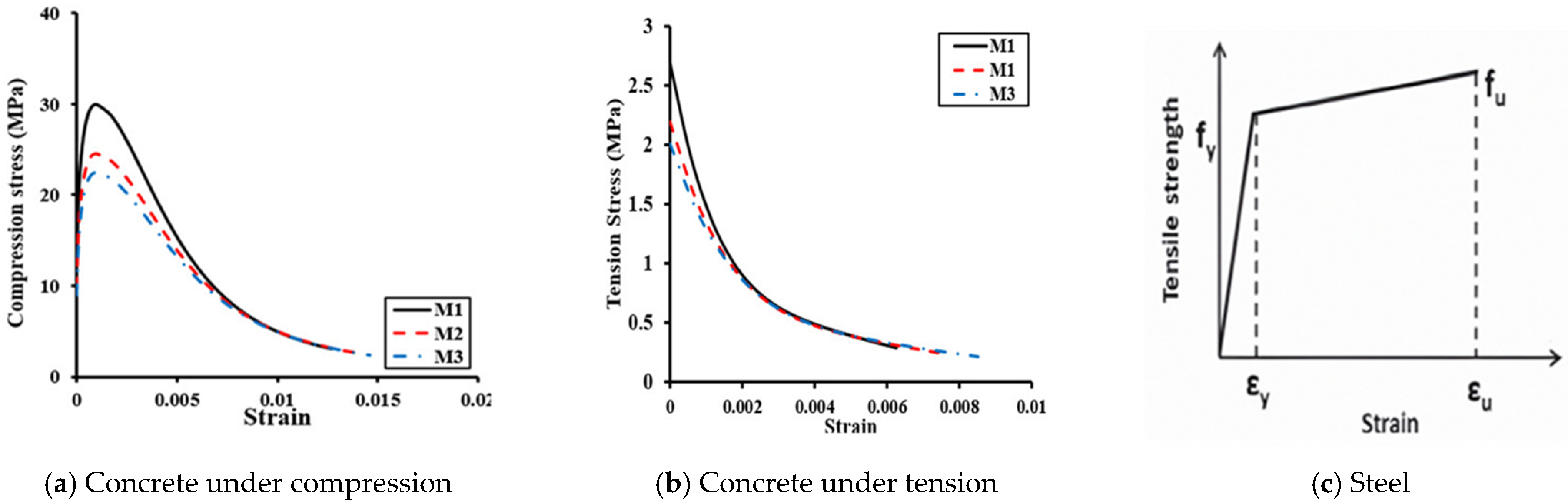
2.2. Material and Element Modeling
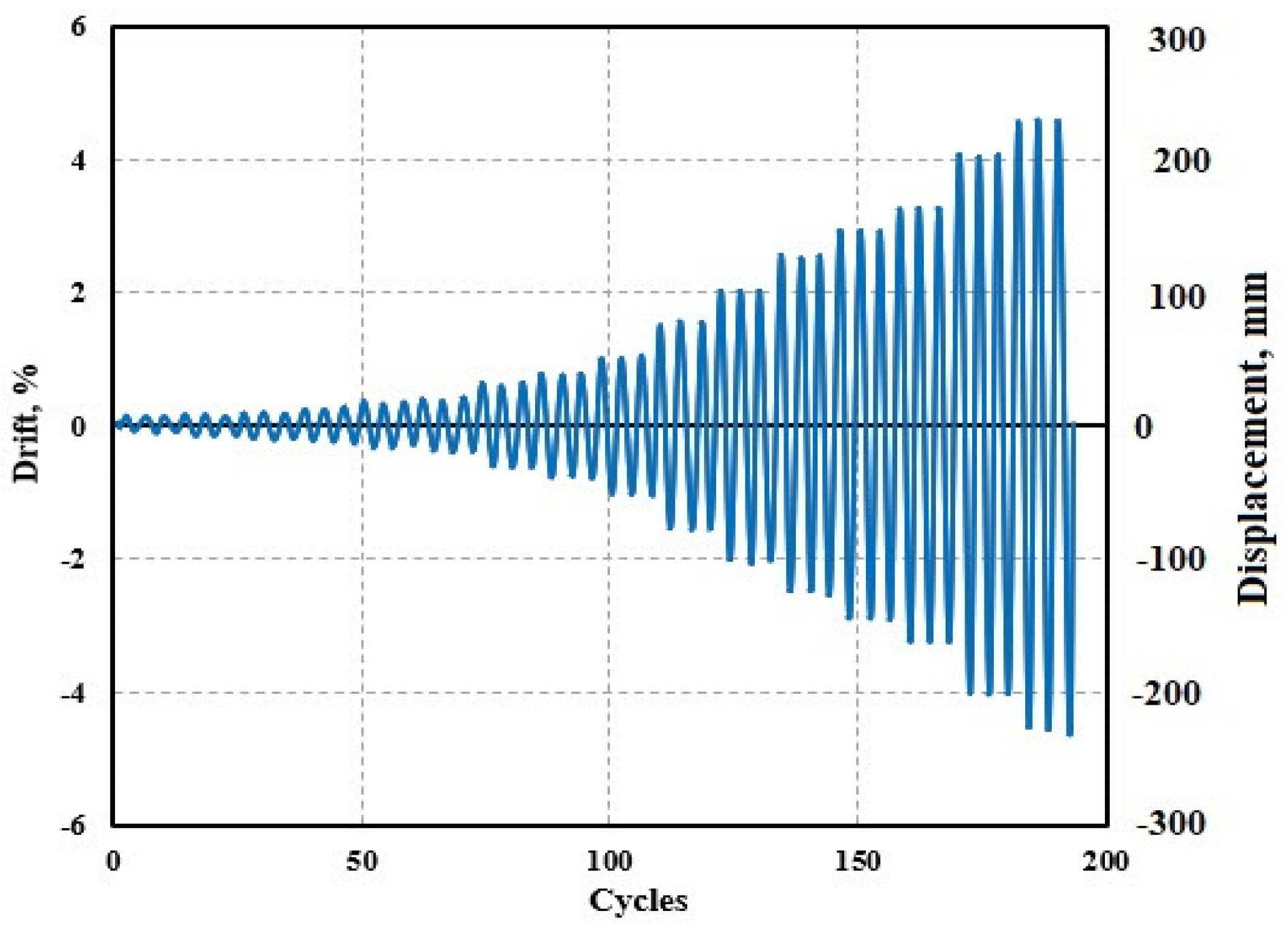
2.3. Loading and Boundary Conditions
3. Results and Discussion
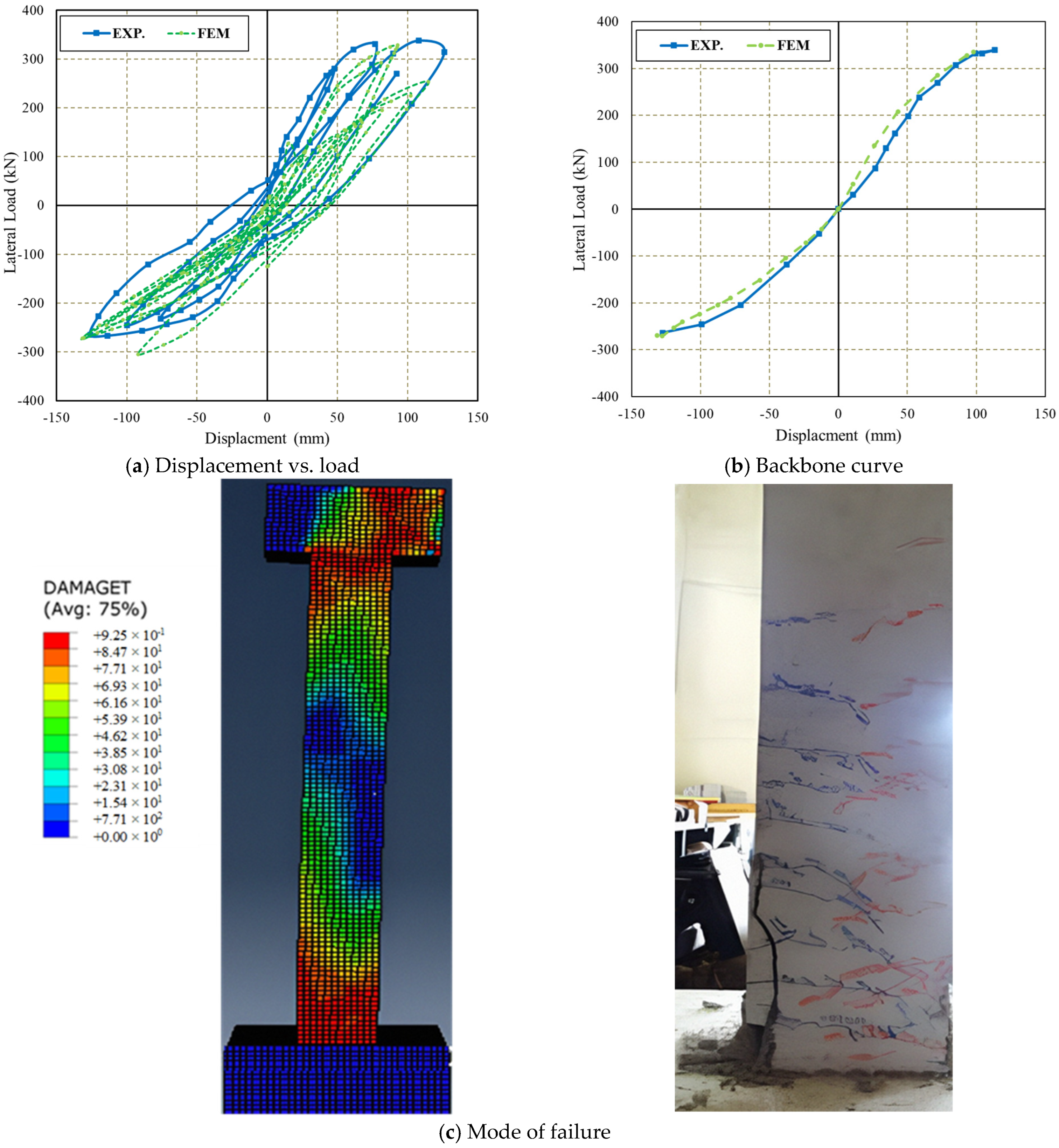
3.1. FE Verification
3.2. Behavior of RRC Columns Under Cyclic Loading
3.2.1. Backbone Curves and Hysterical Behavior
3.2.2. Displacement Ductility
3.2.3. Equivalent Viscous Damping Ratio
4. Conclusions
- The proposed finite element model can precisely predict the behavior of RRC columns under cyclic loads in terms of lateral load–lateral displacement curves.
- Rubberized reinforced concrete columns with 10% and 15% fine aggregate replacement exhibited significantly improved lateral displacement compared to columns without CR.
- RRC columns with 10% and 15% fine aggregate replacement showed small reductions in lateral loads compared to the non-CR columns.
- In circular columns with a height of 1.5 m, replacing 10% and 15% of the fine aggregates with CR resulted in an increase in displacement ductility of 47.8% and 89.04%, respectively.
- Square rubberized reinforced concrete columns with a height of 1.5 m showed a higher incremental lateral displacement, displacement ductility, and damping ratio than circular and rectangular columns of the same height.
- Rubberized reinforced concrete columns performed better in terms of lateral displacement, displacement ductility, and damping ratio when 15% CR was utilized to replace fine aggregates in RC columns. However, there was a minor drop in lateral load capacity.
- Using crumb rubber in reinforced concrete columns can delay earthquake damage and reduce its severity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gagg, C.R. Cement and concrete as an engineering material: An historic appraisal and case study analysis. Eng. Fail. Anal. 2014, 40, 114–140. [Google Scholar] [CrossRef]
- Formela, K. Sustainable development of waste tires recycling technologies–recent advances, challenges and future trends. Adv. Ind. Eng. Polym. Res. 2021, 4, 209–222. [Google Scholar] [CrossRef]
- Ahmad, I.; Iqbal, M.; Abbas, A.; Badrashi, Y.I.; Jamal, A.; Ullah, S.; Yosri, A.M.; Hamad, M. Enhancement of Confinement in Scaled RC Columns using Steel Fibers Extracted from Scrap Tyres. Materials 2022, 15, 3219. [Google Scholar] [CrossRef]
- Pitilakis, K.; Karapetrou, S.; Tsagdi, K. Numerical investigation of the seismic response of RC buildings on soil replaced with rubber–sand mixtures. Soil Dyn. Earthq. Eng. 2015, 79, 237–252. [Google Scholar] [CrossRef]
- Oikonomou, N.; Mavridou, S. The use of waste tyre rubber in civil engineering works. In Sustainability of Construction Materials; Elsevier: Amsterdam, The Netherlands, 2009; pp. 213–238. [Google Scholar]
- Chen, M.; Si, H.; Fan, X.; Xuan, Y.; Zhang, M. Dynamic compressive behavior of recycled tire steel fiber reinforced concrete. Constr. Build. Mater. 2022, 316, 125896. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y. Experimental study of seismic behavior of partially corrosion-damaged reinforced concrete columns strengthened with FRP composites with large deformability. Constr. Build Mater. 2018, 191, 1071–1081. [Google Scholar] [CrossRef]
- Atahan, A.O.; Sevim, U.K. Testing and comparison of concrete barriers containing shredded waste tire chips. Mater. Lett. 2008, 62, 3754–3757. [Google Scholar] [CrossRef]
- Razvi, S.W.N.; Shaikh, M. Effect of confinement on behavior of short concrete column. Procedia Manuf. 2018, 20, 563–570. [Google Scholar] [CrossRef]
- Hassanli, R.; Youssf, O.; Mills, J.E. Seismic Performance of Precast Posttensioned Segmental FRP Confined and Unconfined Crumb Rubber Concrete Columns. J. Compos. Constr. 2017, 21, 04017006. [Google Scholar] [CrossRef]
- Elghazouli, A.Y.; Bompa, D.V.; Xu, B.; Ruiz-Teran, A.M.; Staffor, P.J. Performance of rubberised reinforced concrete members under cyclic loading. Eng. Struct. 2018, 166, 526–545. [Google Scholar] [CrossRef]
- Moustafa, A.; Gheni, A.; ElGawady, M.A. Shaking-Table Testing of High Energy–Dissipating Rubberized Concrete Columns. J. Bridg. Eng. 2017, 22, 04017042. [Google Scholar] [CrossRef]
- Najim, K.B.; Hall, M.R. Mechanical and dynamic properties of self-compacting crumb rubber modified concrete. Constr. Build Mater. 2012, 27, 521–530. [Google Scholar] [CrossRef]
- Youssf, O.; Hassanli, R.; Mills, J.E. Mechanical performance of FRP-confined and unconfined crumb rubber concrete containing high rubber content. J. Build. Eng. 2017, 11, 115–126. [Google Scholar] [CrossRef]
- Son, K.S.; Hajirasouliha, I.; Pilakoutas, K. Strength and deformability of waste tyre rubber-filled reinforced concrete columns. Constr. Build. Mater. 2011, 25, 218–226. [Google Scholar] [CrossRef]
- Xue, J.; Shinozuka, M. Rubberized concrete: A green structural material with enhanced energy dissipation capability. Constr. Build. Mater. 2013, 42, 196–204. [Google Scholar] [CrossRef]
- Egyptian Code Committee. Egyptian Code for Design and Construction of Concrete Structures; ECP 203-2020; Housing and Building National Research Center, HBRC: Cairo, Egypt, 2020.
- Ahmed, M.; Mohamed, H.-A.; Hassan, H.; Zaghlal, M. Rubberized reinforced concrete columns under axial and cyclic loading. Fract. Struct. Integr. 2024, 18, 286–309. [Google Scholar] [CrossRef]
- Xie, J.-H.; Guo, Y.-C.; Liu, L.-S.; Xie, Z.-H. Compressive and flexural behaviors of a new steel-fiber-reinforced recycled aggregate concrete with crumb rubber. Constr. Build Mater. 2015, 79, 263–272. [Google Scholar] [CrossRef]
- Nawar, M.T.; Eisa, A.S.; Elshazli, M.T.; Ibrahim, Y.E.; El-Zohairy, A. Numerical Analysis of Rubberized Steel Fiber Reinforced Concrete Beams Subjected to Static and Blast Loadings. Infrastructures 2024, 9, 52. [Google Scholar] [CrossRef]
- ACI. Guide for Testing Reinforced Concrete Structural Elements Under Slowly Applied Simulated Seismic Loads; ACI 374; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Shin, D.-H.; Kim, H.-J. Cyclic response of rectangular RC columns retrofitted by hybrid FRP sheets. Structures 2020, 28, 697–712. [Google Scholar] [CrossRef]
- Li, Q.; Niu, D.T.; Xiao, Q.H.; Guan, X.; Chen, S.-j. Experimental study on seismic behaviors of concrete columns confned by corroded stirrups and lateral strength prediction. Constr Build Mater. 2018, 162, 704–713. [Google Scholar] [CrossRef]
- Luo, X.; Cheng, J.; Xiang, P.; Long, H. Seismic behavior of corroded reinforced concrete column joints under low-cyclic repeated loading. Arch. Civ. Mech. Eng. 2020, 20, 40. [Google Scholar] [CrossRef]
- ElGawady, M.; Endeshaw, M.; McLean, D.; Sack, R. Retrofitting of Rectangular Columns with Deficient Lap Splices. J. Compos. Constr. 2010, 14, 22–35. [Google Scholar] [CrossRef]
- Mahat, M.; Acharya, M.; Acharya, M.; Mashal, M. Use of Waste Tires as Transverse Reinforcement and External Confinement in Concrete Columns Subjected to Axial Loads and cyclic loads. Sustainability 2023, 15, 11620. [Google Scholar] [CrossRef]
- Priestley, M.; Calvi, G.; Kowalsky, M. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Chopra, A.K. Dynamics of Structures; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Gulkan, P.; Sozen, M.A. Inelastic responses of reinforced concrete structures to earthquake motions. J. Am. Concr. Inst. 1974, 7112, 604–610. [Google Scholar]
- Midorikawa, M.; Hiraishi, H.; Okawa, I.; Iiba, M.; Teshigawara, M.; Isoda, H. Development of seismic performance evaluation procedures in Building Code of Japan. In Proceedings of the 12th World Conference on Earthquake Engineering, Silverstream, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Sipos, T.K.; Jelec, K.; Milicevic, I. Seismic performance of rubberized concrete in structural applications. In Proceedings of the 2nd Croatian Conference on Earthquake Engineering—2CroCEE 2023, Zagreb, Croatia, 22–24 March 2023. [Google Scholar]







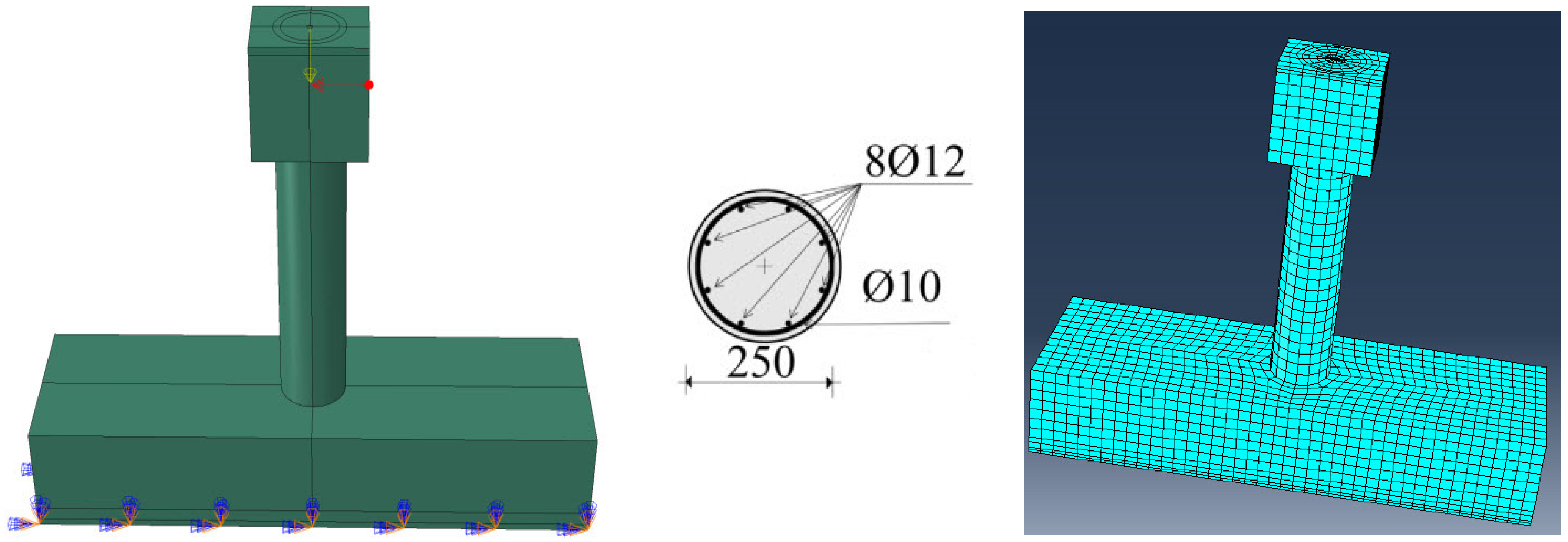

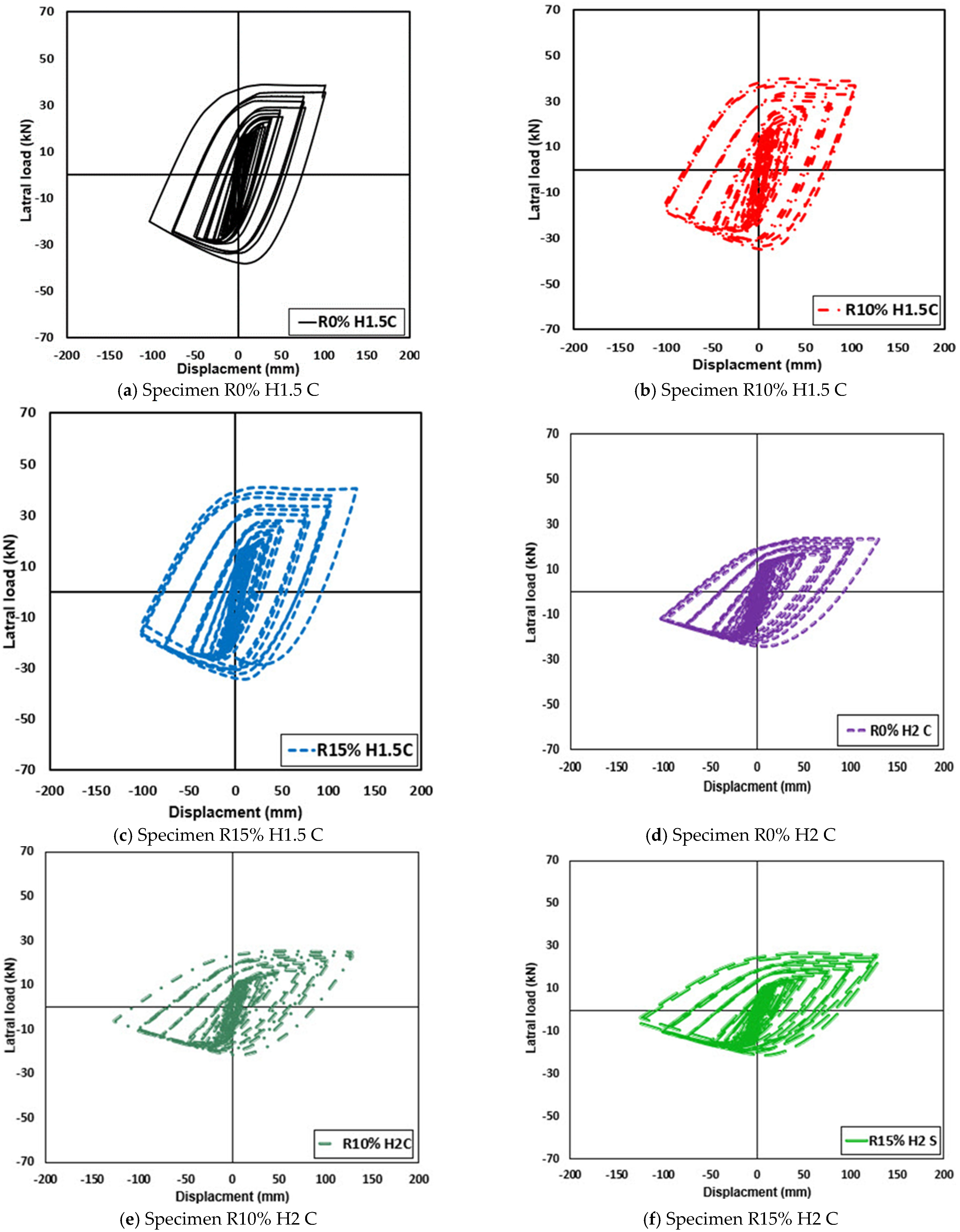


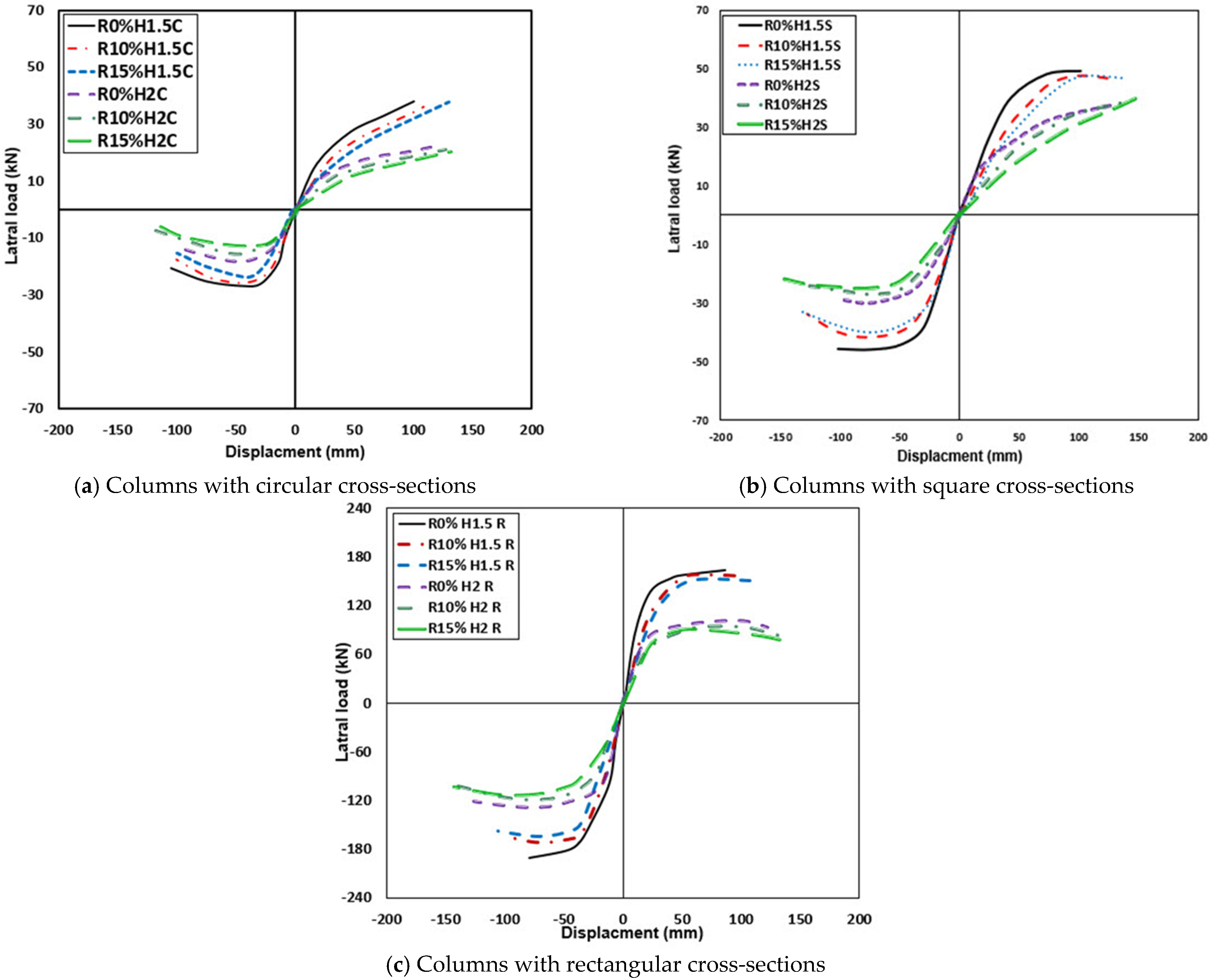
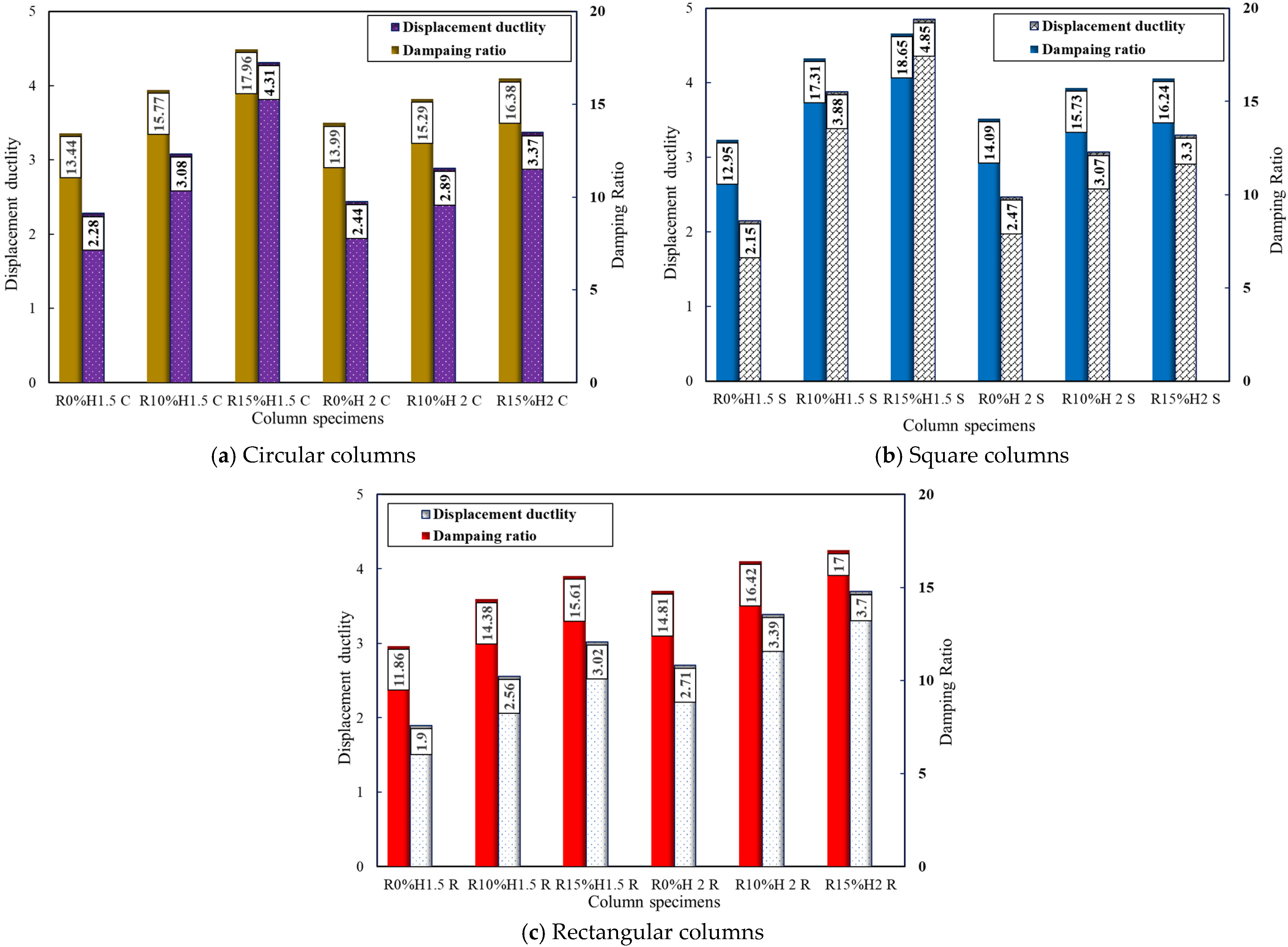

| Group No. | Column Label | Boundary Conditions Hinged–Hinged (Braced) (K = 1) | Longitudinal Reinforcement | Applied Axial Load (kN) |
|---|---|---|---|---|
| 1 | R0% H1.5 C | (λ) = 6 | As = 6ϕ12 | 165 |
| R10% H1.5 C | (λ) = 6 | As = 6ϕ12 | 165 | |
| R15% H1.5 C | (λ) = 6 | As = 6ϕ12 | 165 | |
| R0% H2 C | (λ) = 8 | As = 6ϕ12 | 155 | |
| R10% H2 C | (λ) = 8 | As = 6ϕ12 | 155 | |
| R15% H2 C | (λ) = 8 | As = 6ϕ12 | 155 | |
| 2 | R0% H1.5 S | (λ) = 6 | As = 6ϕ12 | 190 |
| R10% H1.5 S | (λ) = 6 | As = 6ϕ12 | 190 | |
| R15% H1.5 S | (λ) = 6 | As = 6ϕ12 | 190 | |
| R0% H2 S | (λ) = 8 | As = 6ϕ12 | 170 | |
| R10% H2 S | (λ) = 8 | As = 6ϕ12 | 170 | |
| R15% H2 S | (λ) = 8 | As = 6ϕ12 | 170 | |
| 3 | R0% H1.5 R | (λ) = 5 | As = 10ϕ16 | 710 |
| R10% H1.5 R | (λ) = 5 | As = 10ϕ16 | 710 | |
| R15% H1.5 R | (λ) = 5 | As = 10ϕ16 | 710 | |
| R0% H2 R | (λ) = 6.67 | As = 10ϕ16 | 650 | |
| R10% H2 R | (λ) = 6.67 | As = 10ϕ16 | 650 | |
| R15% H2 R | (λ) = 6.67 | As = 10ϕ16 | 650 |
| Concrete Mix | Compressive Strength Fcu (MPa) | Tensile Strength Ftu (MPa) | Young’s Modulus E (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| M1 (R0%) | 30 | 2.64 | 26,884 | 0.2 |
| M2 (R10%) | 24.5 | 2.15 | 24,723 | 0.2 |
| M3 (R15%) | 22.05 | 1.94 | 24,041 | 0.2 |
| Steel Type | Ultimate Strength (MPa) | Yield Strength (MPa) | Elastic Models E (MPa) | Poisson’s Ratio |
|---|---|---|---|---|
| Main reinforcement (Φ 12 and 16 mm) | 640 | 420 | 200,000 | 0.3 |
| Stirrups (Φ 8 mm) | 420 | 280 | 200,000 | 0.3 |
| Group No. | Column Label | Lateral Load (kN) | (mm) | (mm) | ||
|---|---|---|---|---|---|---|
| 1 | R0% H1.5 C | 38.04 | 44.01 | 100.4 | 2.28 | 13.44 |
| R10% H1.5 C | 36.21 | 35 | 118.08 | 3.088 | 15.77 | |
| R15% H1.5 C | 35.4 | 30 | 129.3 | 4.31 | 17.96 | |
| R0% H2 C | 22.6 | 50.4 | 123 | 2.44 | 13.99 | |
| R10% H2 C | 21.2 | 44 | 127.4 | 2.89 | 15.29 | |
| R15% H2 C | 20.3 | 39.02 | 131.68 | 3.37 | 16.38 | |
| 2 | R0% H1.5 S | 49.3 | 47 | 101.15 | 2.15 | 12.95 |
| R10% H1.5 S | 46.7 | 33 | 128 | 3.88 | 17.31 | |
| R15% H1.5 S | 46.2 | 28 | 136 | 4.85 | 18.65 | |
| R0% H2 S | 38.29 | 53 | 131.29 | 2.47 | 14.09 | |
| R10% H2 S | 37.05 | 46 | 141.6 | 3.07 | 15.73 | |
| R15% H2 S | 36.02 | 44.4 | 146.3 | 3.3 | 16.24 | |
| 3 | R0% H1.5 R | 164.38 | 46.1 | 87.5 | 1.9 | 11.86 |
| R10% H1.5 R | 156.07 | 40 | 102.56 | 2.56 | 14.38 | |
| R15% H1.5 R | 151.01 | 35.8 | 108.24 | 3.02 | 15.61 | |
| R0% H2 R | 92.4 | 45.2 | 122.37 | 2.71 | 14.81 | |
| R10% H2 R | 79.4 | 41.05 | 139.4 | 3.39 | 16.42 | |
| R15% H2 R | 74.7 | 38.3 | 142.2 | 3.7 | 17.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.A.M.; Mohamed, H.A.; Hassan, H.; El-Zohairy, A.; Emara, M. Numerical Analysis of the Cyclic Behavior of Reinforced Concrete Columns Incorporating Rubber. J. Compos. Sci. 2025, 9, 95. https://doi.org/10.3390/jcs9030095
Ahmed MAM, Mohamed HA, Hassan H, El-Zohairy A, Emara M. Numerical Analysis of the Cyclic Behavior of Reinforced Concrete Columns Incorporating Rubber. Journal of Composites Science. 2025; 9(3):95. https://doi.org/10.3390/jcs9030095
Chicago/Turabian StyleAhmed, Mohammed A. M., Heba A. Mohamed, Hilal Hassan, Ayman El-Zohairy, and Mohamed Emara. 2025. "Numerical Analysis of the Cyclic Behavior of Reinforced Concrete Columns Incorporating Rubber" Journal of Composites Science 9, no. 3: 95. https://doi.org/10.3390/jcs9030095
APA StyleAhmed, M. A. M., Mohamed, H. A., Hassan, H., El-Zohairy, A., & Emara, M. (2025). Numerical Analysis of the Cyclic Behavior of Reinforced Concrete Columns Incorporating Rubber. Journal of Composites Science, 9(3), 95. https://doi.org/10.3390/jcs9030095








