A Theoretical Investigation of the Structural, Electronic and Mechanical Properties of Pristine and Nitrogen-Terminated Carbon Nanoribbons Composed of 4–5–6–8-Membered Rings
Abstract
:1. Introduction
2. Computational Methods
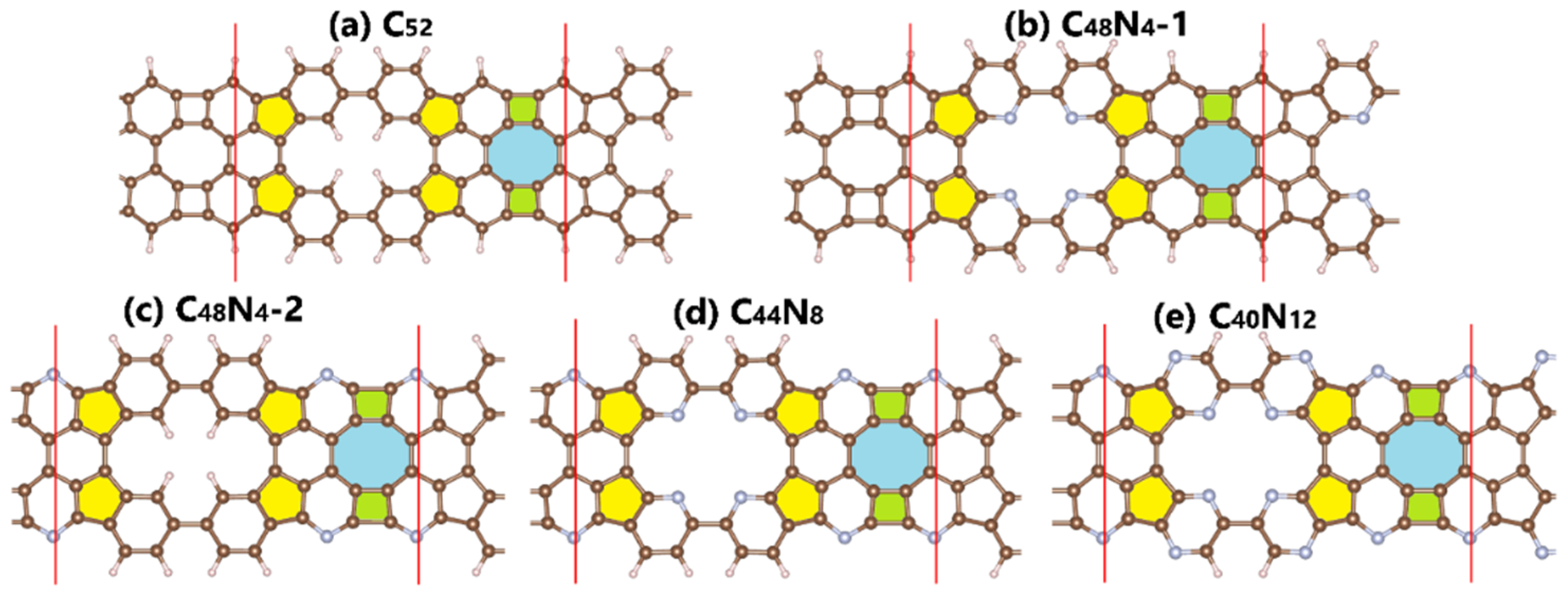
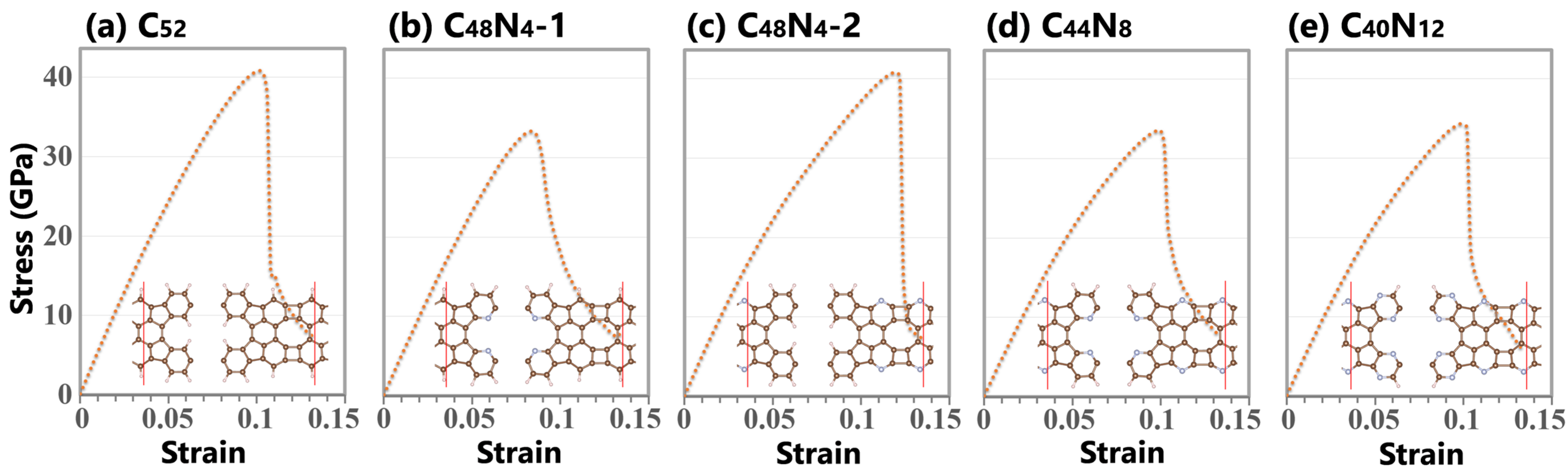
3. Results and Discussions
4. Concluding Remarks
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ge, M.; Sattler, K. Observation of fullerene cones. Chem. Phys. Lett. 1994, 220, 192–196. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejčí, O.; Dimosthenous, S.; Kachel, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene network: A nonbenzenoid carbon allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef] [PubMed]
- Brunetto, G.; Autreto, P.A.S.; Machado, L.D.; Santos, B.I.; dos Santos, R.P.B.; Galvão, D.S. Nonzero Gap Two-Dimensional Carbon Allotrope from Porous Graphene. J. Phys. Chem. C 2012, 116, 12810–12813. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.-Q.; Li, H.-D.; Wang, J.-T. Prediction of a new two-dimensional metallic carbon allotrope. Phys. Chem. Chem. Phys. 2013, 15, 2024–2030. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, X.-F.; Zhang, X.; Zhu, Q.; Dong, H.; Zhao, M.; Oganov, A.R. Phagraphene: A Low-Energy Graphene Allotrope Composed of 5–6–7 Carbon Rings with Distorted Dirac Cones. Nano Lett. 2015, 15, 6182–6186. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef] [Green Version]
- Mortazavi, B.; Shojaei, F.; Zhuang, X. A novel two-dimensional C36 fullerene network; an isotropic, auxetic semiconductor with low thermal conductivity and remarkable stiffness. Mater. Today Nano 2023, 21, 100280. [Google Scholar] [CrossRef]
- Hou, L.; Cui, X.; Guan, B.; Wang, S.; Li, R.; Liu, Y.; Zhu, D.; Zheng, J. Synthesis of a monolayer fullerene network. Nature 2022, 606, 507–510. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Wu, C.; Pan, Q.; Jin, Y.; Lyu, R.; Martinez, V.; Huang, S.; Wu, J.; Wayment, L.J.; Clark, N.A.; et al. Synthesis of γ-graphyne using dynamic covalent chemistry. Nat. Synth. 2022, 1, 449–454. [Google Scholar] [CrossRef]
- Tong, Z.; Pecchia, A.; Yam, C.; Dumitrică, T.; Frauenheim, T. Phononic Thermal Transport along Graphene Grain Boundaries: A Hidden Vulnerability. Adv. Sci. 2021, 8, e2101624. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.; Pecchia, A.; Yam, C.; Dumitrică, T.; Frauenheim, T. Ultrahigh Electron Thermal Conductivity in T-Graphene, Biphenylene, and Net-Graphene. Adv. Energy Mater. 2022, 12, 2200657. [Google Scholar] [CrossRef]
- Kang, F.; Sun, L.; Gao, W.; Sun, Q.; Xu, W. On-Surface Synthesis of a Carbon Nanoribbon Composed of 4–5–6–8-Membered Rings. ACS Nano 2023, 17, 8717–8722. [Google Scholar] [CrossRef]
- Algara-Siller, G.; Severin, N.; Chong, S.Y.; Björkman, T.; Palgrave, R.G.; Laybourn, A.; Antonietti, M.; Khimyak, Y.Z.; Krasheninnikov, A.V.; Rabe, J.P.; et al. Triazine-based graphitic carbon nitride: A two-dimensional semiconductor. Angew. Chem. Int. Ed. 2014, 53, 7450–7455. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Jeon, I.-Y.; Jung, S.-M.; Choi, H.-J.; Seo, J.-M.; Bae, S.-Y.; Sohn, S.-D.; et al. Nitrogenated holey two-dimensional structures. Nat. Commun. 2015, 6, 6486. [Google Scholar] [CrossRef] [Green Version]
- Zeng, J.; Chen, Z.; Zhao, X.; Yu, W.; Wu, S.; Lu, J.; Loh, K.P.; Wu, J. From All-Triazine C3N3 Framework to Nitrogen-Doped Carbon Nanotubes: Efficient and Durable Trifunctional Electrocatalysts. ACS Appl. Nano Mater. 2019, 2, 7969–7977. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Choi, H.-J.; Seo, J.-M.; Jung, S.-M.; Kim, D.; Li, F.; Lah, M.S.; et al. Two-dimensional polyaniline (C 3 N) from carbonized organic single crystals in solid state. Proc. Natl. Acad. Sci. USA 2016, 113, 7414–7419. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Vahidzadeh, E.; Thakur, U.K.; Kar, P.; Alam, K.M.; Goswami, A.; Mahdi, N.; Cui, K.; Bernard, G.M.; Michaelis, V.K.; et al. C3N5: A Low Bandgap Semiconductor Containing an Azo-Linked Carbon Nitride Framework for Photocatalytic, Photovoltaic and Adsorbent Applications. J. Am. Chem. Soc. 2019, 141, 5415–5436. [Google Scholar] [CrossRef] [PubMed]
- Bahari, Y.; Mortazavi, B.; Rajabpour, A.; Zhuang, X.; Rabczuk, T. Application of two-dimensional materials as anodes for rechargeable metal-ion batteries: A comprehensive perspective from density functional theory simulations. Energy Storage Mater. 2020, 35, 203–282. [Google Scholar] [CrossRef]
- Shi, Y.-B.; Lv, S.-H.; Shao, Z.-F.; Dong, H.-K.; Cao, S.; Qian, P. A first-principles study of 1D and 2D C60 nanostructures: Strain effects on band alignments and carrier mobility. J. Physics Condens. Matter 2023, 35, 225701. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.-B.; Chen, Y.-Y.; Wang, H.; Cao, S.; Zhu, Y.-X.; Chu, M.-F.; Shao, Z.-F.; Dong, H.-K.; Qian, P. Investigation of the mechanical and transport properties of InGeX3 (X = S, Se and Te) monolayers using density functional theory and machine learning. Phys. Chem. Chem. Phys. 2023, 25, 13864–13876. [Google Scholar] [CrossRef] [PubMed]
- Izadifar, M.; Ukrainczyk, N.; Koenders, E. Silicate Dissolution Mechanism from Metakaolinite Using Density Functional Theory. Nanomaterials 2023, 13, 1196. [Google Scholar] [CrossRef]
- Izadifar, M.; Valencia, N.C.; Xiao, P.; Ukrainczyk, N.; Koenders, E. 3D Off-Lattice Coarse-Grained Monte Carlo Simulations for Nucleation of Alkaline Aluminosilicate Gels. Materials 2023, 16, 1863. [Google Scholar] [CrossRef]
- Aldakheel, F.; Satari, R.; Wriggers, P. Feed-Forward Neural Networks for Failure Mechanics Problems. Appl. Sci. 2021, 11, 6483. [Google Scholar] [CrossRef]
- Aldakheel, F.; Kandekar, C.; Bensmann, B.; Dal, H.; Hanke-Rauschenbach, R. Electro-chemo-mechanical induced fracture modeling in proton exchange membrane water electrolysis for sustainable hydrogen production. Comput. Methods Appl. Mech. Eng. 2022, 400, 115580. [Google Scholar] [CrossRef]
- Aldakheel, F.; Elsayed, E.S.; Zohdi, T.I.; Wriggers, P. Efficient multiscale modeling of heterogeneous materials using deep neural networks. Comput. Mech. 2023, 72, 155–171. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Shishkin, M.; Kresse, G. Self-consistentGWcalculations for semiconductors and insulators. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 75, 235102. [Google Scholar] [CrossRef]
- Mortazavi, B.; Zhuang, X.; Rabczuk, T.; Shapeev, A.V. Atomistic Modeling of the Mechanical Properties: The Rise of Machine Learning Interatomic Potentials. Mater. Horizons 2023, 10, 1956–1968. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Podryabinkin, E.V.; Roche, S.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. Machine-Learning Interatomic Potentials Enable First-Principles Multiscale Modeling of Lattice Thermal Conductivity in Graphene/Borophene Heterostructures. Mater. Horizons 2020, 7, 2359–2367. [Google Scholar] [CrossRef]
- Ghorbani, K.; Mirchi, P.; Arabha, S.; Rajabpour, A.; Volz, S. Lattice Thermal Conductivity and Young’s Modulus of XN4 (X = Be, Mg and Pt) 2D Materials Using Machine Learning Interatomic Potentials. Phys. Chem. Chem. Phys. 2023, 25, 12923–12933. [Google Scholar] [CrossRef]
- Arabha, S.; Aghbolagh, Z.S.; Ghorbani, K.; Hatam-Lee, M.; Rajabpour, A. Recent Advances in Lattice Thermal Conductivity Calculation Using Machine-Learning Interatomic Potentials. J. Appl. Phys. 2021, 130, 210903. [Google Scholar] [CrossRef]
- Mortazavi, B.; Silani, M.; Podryabinkin, E.V.; Rabczuk, T.; Zhuang, X.; Shapeev, A.V. First-Principles Multiscale Modeling of Mechanical Properties in Graphene/Borophene Heterostructures Empowered by Machine-Learning Interatomic Potentials. Adv. Mater. 2021, 33, 2102807. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mortazavi, B. A Theoretical Investigation of the Structural, Electronic and Mechanical Properties of Pristine and Nitrogen-Terminated Carbon Nanoribbons Composed of 4–5–6–8-Membered Rings. J. Compos. Sci. 2023, 7, 269. https://doi.org/10.3390/jcs7070269
Mortazavi B. A Theoretical Investigation of the Structural, Electronic and Mechanical Properties of Pristine and Nitrogen-Terminated Carbon Nanoribbons Composed of 4–5–6–8-Membered Rings. Journal of Composites Science. 2023; 7(7):269. https://doi.org/10.3390/jcs7070269
Chicago/Turabian StyleMortazavi, Bohayra. 2023. "A Theoretical Investigation of the Structural, Electronic and Mechanical Properties of Pristine and Nitrogen-Terminated Carbon Nanoribbons Composed of 4–5–6–8-Membered Rings" Journal of Composites Science 7, no. 7: 269. https://doi.org/10.3390/jcs7070269





