Abstract
Fiber-reinforced polymer (FRP) composites do not only possess superior mechanical properties, but can also be easy to tailor, install, and maintain. As such, FRPs offer novel and attractive solutions to facilitate strengthening and/or retrofitting of aging, weakened, and upgraded structures. Despite the availability of general code provisions, the design and analysis of FRP-strengthened concrete structures is both tedious and complex—especially in scenarios associated with unique loading conditions. As such, designers often leverage advanced finite element (FE) simulation as a mean to understand and predict the performance of FRP-strengthened structures. In order to narrow this knowledge gap, this paper details suitable strategy for developing and carrying out advanced FE simulations on FRP-strengthened concrete structures. The paper also covers techniques related to simulating adhesives (bonding agents), material constitutive properties and plasticity (cracking/crushing of concrete, yielding of steel reinforcement, and delamination of FRP laminates), as well as different material types of FRP (CFRP, GFRP, and their hybrid combinations), and FRP strengthening systems (sheets, plates, NSM, and rods) under various loading conditions including ambient, earthquake, and fire. The principles, thumb rules, and findings of this work can be of interest to researchers, practitioners, and students.
1. Introduction and Background
Fiber reinforced polymers (FRPs) composites comprise of continuous fibers with load bearing capabilities embedded in binder (i.e., polymer matrix that protects the fibers and facilitates transferring tensile and shear stresses to-and-between these fibers) []. FRPs, which are resistant to chemical corrosion and have low weight-to-high modulus and strength ratios, were initially developed as alternatives to metals often used in aerospace and automotive industries [,]. With recent advancements in manufacturing and materials sciences, FRPs have emerged as an attractive alternative for strengthening and retrofitting of structures, most notably those made from concrete, steel, and masonry [,].
In such applications, FRP systems are externally bonded by means of adhesives to the sides and/or soffit of load bearing structural members (i.e., beams, girders, etc.). The installation of FRP systems provide the structural members with additional stiffness through confinement effect []. Overall, there are two types of FRP strengthening systems: the first type utilizes FRP plates and/or sheets while the second type employs near-surface mounted (NSM) bars or plates. In the first case, FRP plates or sheets can be applied to grinded external surfaces, while in the second case (NSM), FRP rods/strips are installed into pre-cut grooves via epoxy adhesives. Both of these systems have been shown to have comparable performance, with the second having a much improved resistance to weathering and harsh weathering conditions [,].
In all cases, the contribution of an FRP strengthening system to the overall sectional capacity of strengthened members heavily relies upon the presence of an adequate adhesive/bonding agent. This has not only been well-documented over the last few years, but has been also noted in a number of codal provisions including the American Concrete Institute (ACI) 440.2R [], International Federation for Structural Concrete (FIB) [], and Japanese code []. As such, FRP-strengthened structures are commonly labeled under “bond critical” as they rely on the bond action developed at the interface, or FRP and external layers, or grooves. In other words, an FRP system may continue to fully contribute as long as the adhesive layer is properly maintained [,].
Given that both the FRP system and adhesive have limited strain reserve and can only be used within certain environmental conditions—as opposed to metals—then accounting for such factors become critical in the design and analysis of FRP-strengthened structures. This is due to the fact that debonding could potentially occur at low levels of axial strains of FRP, thus externally bonded systems often do not exploit the full tensile strength of FRP and may in fact lead to premature failure [,]. This discussion infers the complex nature of modeling FRP strengthening systems at working conditions and especially under harsh loading conditions, such as cyclic and fire loading.
While the open literature contains a number of attempts that managed to model FRP-strengthened concrete structures, there does not seem to be a uniform understanding on which researchers agree upon when modeling such structures. For example, an early work carried out by Kachlakev et al. [] did not account for the presence of a bonding agent and assumed that the FRP system is perfectly bonded to strengthened concrete beams. This crude assumption indeed simplifies the simulation process and hence continued to be applied till the present day [,]. This assumption overestimates the contribution of the FRP system and is incapable of accurately predicting debonding of FRP system from adjacent concrete surfaces. One should also note that this assumption was common in the era where FE simulation packages did not offer compatible elements and simulation solutions that can model adhesion and bonding mechanisms, and the required tremendous computational resources.
With the advent rise of computational intelligence, FE software offer unique solutions that can accommodate varying levels of simulation complexities through time and resource-efficient solvers [,,,,,]. This opened new opportunities for researchers and designers and allowed them to carry out realistic and improved modeling of FRP-strengthened concrete structures in which due consideration will be given to specifics related to adhesive/bonding agent as well as various failure mechanisms, including FRP debonding. As a result, recent studies employed modern simulation techniques to realize realistic modeling of FRP-related phenomenon [,,,,,].
In one study, Bui et al. [] presented a numerical and 3D FE models of FRP-strengthened Reinforced Concrete Beams (RC beams) using ANSYS environment. This study examined design methods for hybrid FRP-steel beams and examined the ultimate moment capacity, load-deflection response, crack width, and ductility in these beams. Bui et al. [] specifically investigated reinforcement ratio, concrete compressive strength, layout of reinforcement, and the length of FRP bars on the mechanical performance of RC reinforced hybrid beams. Kim and Aboutaha [] developed a similar 3D FE model to examine how the addition of CFRP composites to enhance the flexural capacity and ductility of the beams. These researchers simulated the internal reinforcement and concrete, together with bond, using a smeared relationship with good accuracy. Shrestha et al. [] explored the adequacy of strengthening of RC beam-column connections. These researchers managed to successfully capture the overall behavior of RC specimens and noted difficulties in modeling the failure mechanisms.
In a recent work, Lu et al. [] proposed a fine-meshed meso-scale FE model that can be used to simulate the debonding phenomenon at the FRP-concrete interface in FRP-bonded joints. The outcome of this study achieved good correlation when compared to measured experiments. Similarly, Chen et al. [] explored a variety of modeling assumptions to simplify the complexity commonly associated with the FRP-concrete interface in shear bonded FRP-strengthened RC beams. In this study, Chen et al. used contact elements were to simulate the bond between internal steel reinforcement (flexure bars and stirrups) and concrete as well as between the FRP and concrete interfaces. The authors [,,] also developed a series of 3D nonlinear FE models that incorporate springs and cohesive elements to trace the debonding of FRP plates as well as NSM-strengthened systems. In these studies, spring elements were used to simulate the bond-slip action between the FRP NSM bars and the surrounding resin or mortar surfaces. The success of these studies is the motivation behind this work.
The aim of this paper is to develop a systematic approach that can be viewed as a guide to properly model FRP-strengthened concrete structures. This paper lays out the different simulation techniques that can be applied, with varying complexities, and showcases their use in practical case studies. Hence, a number of 3D FE models were developed while taking into account realistic material constitutive laws for concrete in tension (cracking) and compression, steel yielding, and the FRP and adhesive orthotropic material properties. Furthermore, proper material models to trace the bond-slip action between the steel bars and surrounding concrete surfaces, as well as bond-slip between the FRP plates/sheets or NSM reinforcement and adjacent concrete interfaces are also considered in the developed FE models. This work showcases three environments and loading conditions, namely, ambient, earthquake, and fire, and hence is applicable to most loading conditions one might experience in practical scenarios.
2. Finite Element Model Development Strategies
In general, modeling FRP-strengthened concrete structures requires the development of a proper FE model. Such a model can be developed using freely available or commercial simulation packages. The majority of these packages share similar features with few differences with regard to solvers, element types, material constitutive properties, etc., hence it is a matter of the designer’s/practitioner’s preference to select a simulation package. In this work, we will showcase, as an example, the use of ANSYS and ABAQUS finite element simulation software, since this simulation environment have be extensively tested and validated in modeling FRP-strengthened structures by the authors [,,], as well as by other researchers [,,,,,,,,,,].
2.1. Considerations for Element Types
A typical FE model requires accommodation of concrete, steel reinforcement, FRP system type (plate, sheet, NSM), and loading/boundary support conditions (see Figure 1). Each of these components needs to be appropriately modeled to reflect the unique characteristics associated with each of them. From this perspective, concrete is often modeled using a 3D brick (designated as SOLID65 in ANSYS and C3D8 in ABAQUS) elements—an element specifically developed to simulate rock-like materials. This cubic element is defined by eight nodes, each having three degrees of freedom at each node; translations in the nodal x, y, and z directions and has 2 × 2 × 2 integration scheme. This element type adopts the William and Warnke’s [] mathematical material model and hence is capable of modeling cracking (in three orthogonal directions), crushing, plastic deformation, and creep. It should be noted that to exhibit the nonlinear behavior of concrete, concrete damaged plasticity (CDP) or concrete smeared crack models should be implemented when defining concrete material in ABAQUS.
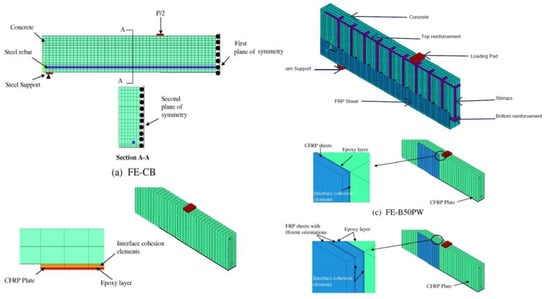
Figure 1.
Typical finite element (FE) models developed in ANSYS for fiber-reinforced polymer (FRP)-strengthened Reinforced Concrete Beams (RC beams) showing different components.
The brick concrete element accommodates defining steel reinforcement by means of smeared or discrete rebars and hence can be used to model concretes with or without reinforcing rebars [,]. There are additional optional concrete-based material parameters that can be used to finetune element’s behavior, such as concrete shear transfer coefficients, tensile stress, and compressive strength. The shear transfer coefficients represent the degree of cracking (i.e., loss of shear transfer) simulated by this element. For example, in order to simulate concrete with smooth crack development, a small shear transfer coefficient can be input (close to 0.0). On the other hand, a larger transfer coefficient with a value close to unity represents a rough crack.
Steel as well as FRP rebars (often used in NSM applications) are modeled using spar/link (designated as LINK8 in ANSYS and T3D2 in ABAQUS) elements. The spar two nodal uniaxial bar-like element has three degrees of freedom at each node. These degrees of freedom include translations in the nodal x, y, and z directions. Such reinforcing elements are capable of simulating common nonlinear effects such as plasticity, creep, swelling, stress stiffening, and large deflection. The link element is usually defined by its cross-sectional area and can accommodate pre-stressing effects (i.e., input of initial strain level).
FRP sheets and/or plates can be modeled using shell (designated as SHELL99 in ANSYS and S4 in ABAQUS) elements, since this element considers orthotropic material properties. The element has the capability to input material properties in a local coordinate system, where the primary axis can be aligned parallel to the main FRP fibers [,]. This element can also be used to model different varying layers (where the first layer can consist of adhesive and following layers can consist of FRP sheets, etc.). The shell elements usually have six translations and rotations degrees of freedom at each node.
Solid brick elements in general (designated as SOLID45 or SOLID185 in ANSYS and C3D8 in ABAQUS) can be used for the 3D modeling of loading/end supports and, in some instances, have been also shown to be appropriate to model FRP plates as well as bonding agents []. Such elements are defined by eight nodes having three translations degrees of freedom at each node. Similar to concrete brick elements, these elements can also simulate nonlinear effects such as plasticity, creep, swelling, stress stiffening etc.
As discussed earlier, the bond interface of steel/FRP rebars-concrete is an important component to be accounted for. This bond-slip behavior can be simulated using spring (designated as COMBIN14 in ANSYS) elements. The spring elements have longitudinal stretching/compressing capabilities and, hence, have three degrees of translations freedom at each node []. In ABAQUS, the bond interface of steel/FRP rebars-concrete is defined by assigning an embedded region constraint with the concrete as the host region and the steel/FRP bars as embedded region. Similarly, the bond behavior between the FRP system and adjacent concrete surfaces is also of importance as this will govern the mode of failure and prediction of debonding surface. This interface FRP/concrete interface can be modeled using contact elements. One such element is the cohesive (designated as INTER205 in ANSYS and COH3D8 in ABAQUS) element []. The cohesive element is a 3D eight-node zero-thickness linear interface element, with the capability to simulate bonded interfaces and any associated delamination that could occur between them. Such elements require the nodes of both surfaces to coincide. Then, this element traces normal stresses and slippage between these interfaces arising from bending or shear actions. Separation between two adjacent surfaces is represented by increasing the displacement between the nodes, within the interface element itself.
2.2. Considerations for Material Parameters
2.2.1. Concrete
Concrete is often simulated using a built-in concrete model. As discussed above, this material model was derived by Williams and Warnke []. Williams and Warnke’s model accounts for the nonlinear behavior of concrete material in response to cracking in tension, crushing in compression, and any plasticity development in internal reinforcement []. In the first case and before the initiation of the first crack, the behavior of concrete can be assumed to be linear elastic. Afterwards, and with the occurrence of cracks, concrete softens and turns nonlinear. To account for this plasticity effect, a multi-nonlinear stress-strain curve is often defined in the concrete material model []. Such stress-strain curves can be plotted following a number of formulae, such as the model from Hognestad et al. [], presented below.
where, fc = concrete compressive stress in MPa corresponding to a specified strain value εc, = concrete compressive strength in MPa.
ANSYS and other finite element software also accommodate finetuning the nonlinear tensile (cracking) behavior of concrete. The tensile behavior of concrete is modeled in a tri-linear manner. The first portion of the tensile stress-strain curve starts as linear elastic up to the concrete tensile (rupture) strength ft. Once the value of the tensile strength of concrete is reached, stress relaxation is simulated with a steep drop of 40% of ft and then followed by linear descending curve up to a strain value of 6εt, where εt is the concrete strain value at ft as shown in Figure 2 [,,]. From this view, the tensile strength of concrete ft is computed as per Equation (4). Knowing this value, as well as modulus property of concrete, then the strain at this particular tensile strength can be estimated in addition to that at failure. Other properties of concrete include Poisson’s ratio, which can vary between 0.18–0.22 [].
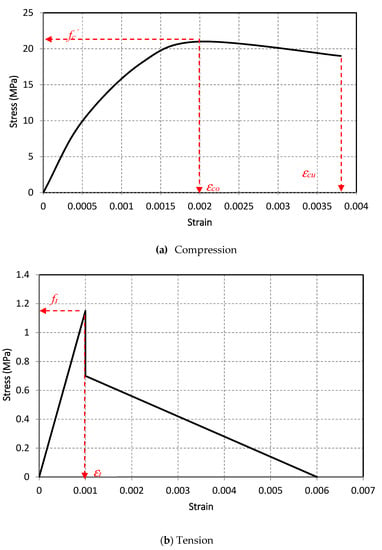
Figure 2.
Typical stress-strain model of concrete used in ANSYS: (a) Compression; (b) Tension.
2.2.2. Steel Reinforcement
The nonlinear response of steel reinforcement material is oftentimes presumed to be linear elastic-perfectly plastic, and in some cases may account for strain hardening effects. In general, steel reinforcement can be assumed to have a Poisson’s ratio of 0.28–0.3 and an elastic modulus of 200–210 GPa. Plasticity in steel reinforcement follows the Von-Misses failure criterion to define yielding of steel. Another property to steel reinforcement includes bond-slip action at the steel rebars/surrounding concrete interface. This longitudinal bond-slip can be taken into account using the spring elements discussed above. These elements require defining a longitudinal stiffness (k). This longitudinal stiffness can be calculated from the secant of the following equation as proposed by Nie et al. []:
where, p is the horizontal distance between the tension steel reinforcement bars in (mm), dr the diameter of the mentioned reinforcements in (mm), Nr the number of reinforcements bars and L1 and L2 is the lengths of two adjacent reinforcement link elements in (mm).
In some cases, accounting for bond-slip action could be complex, and hence prove troublesome. In such scenario, a designer might option to employ a perfect bond between the reinforcement and concrete []. Achieving such perfect bond assumption, both the nodes of steel and adjacent concrete elements are merged together. One should keep in mind that the above assumption is valid in traditional beams given that dowel action of flexural reinforcement is only dominant in deep beams and beams with large sized reinforcement.
It is worth noting that the elastic properties of steel can also be used to model rigid/loading supports. Such supports can come in handy to reduce stress concentration around these highly stressed locations and facilitate smoother convergence, especially in narrow and shallow RC beams [].
2.2.3. FRP and Adhesive
Since FRPs are elastic materials, the mechanical properties of FRP laminates are taken as orthotropic and elastic with a sudden drop to zero once reaching the ultimate strength/strain []. On the other hand, the bonding interface between FRP and concrete can be simply modeled to represent that there is a perfect bond between these components, and can also be modeled using commonly accepted bond-slip models with varying complexities such as those proposed by CEB-FIP model [] or Lu et al. [] which are listed below:
CEP-FIP model (1993) []:
where, is the bond stress at a given slip (s) in (MPa), is the maximum bond stress in (MPa), s is the relative slip at a given shear stress in (mm), and su is the ultimate slip at in (mm).
One should note that CEP provisions stipulates that the maximum possible bond stress achieved is governed by the reinforcement bar type as well as quality and strength of the surrounding concrete. The same provisions recommend using values of and 0.6 mm to substitute the su, for the steel reinforcement and the values of su for the GFRP and CFRP materials can be assumed to roughly be 20.25 MPa, 10.1 MPa, 0.42 mm, 0.33 mm, respectively.
Lu et al. model (2005) []:
The bond-slip of FRP plates/sheets can be modeled via a variety of bond-slip models. One such model was developed by Lu et al. [] and this model is presented in the following expressions and can be seen in Figure 3:
where, is maximum local bond stress in MPa, S is slip between concrete and FRP in mm, is , is width ratio, is a factor depends on interfacial fracture energy, bond strength, interfacial fracture energy, width of FRP sheets in mm, width of concrete section in mm, and is concrete tensile strength in MPa.
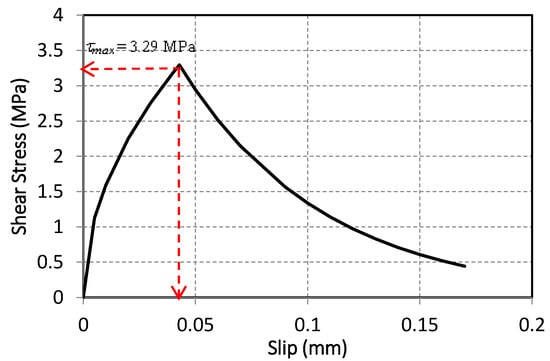
Figure 3.
Typical interfacial stress-slip model used in ANSYS and ABAQUS.
Nabaka et al. (2001) []:
A similar model to that of Lu et al. [] can also be employed. This model was proposed in an earlier study by Nakaba et al. []. The bond strength value for this model is obtained using Equation (13):
where,
s is the slip between the concrete and CFRP interfaces.
While the above models are suitable for FRP sheets/plates, the bond between NSM-FRP rebars and concrete (or filling materials) can be modeled using a different approach. In this approach, interface (or contact) elements can be placed along the perimeter of the longitudinal direction of the NSM groove. The implemented interface elements are then treated via an exponential form of the cohesive zone model. This model starts with an increasing segment up to the ultimate shear stress (τmax) value. This τmax corresponds to a slip (su) value. Beyond this point, a softening response is registered until the ultimate attained slip (assumed to equal to four times the slip corresponding to the ultimate shear stress) is reached. For transparency, τmax for round deformed FRP bars can be evaluated using the following expression proposed by Hassan and Rizkalla [].
where fct is the concrete tensile strength in MPa, μ the coefficient of friction. A value of μ = 1 is used as proposed by De Lorenzis and Teng [] and G1 is a constant taken as 1.0.
2.3. Considerations for Boundary Conditions and Loadings
The majority of RC beams can be grouped under simply supported, cantilever, or continuous conditions. Hence, the developed FE model needs to incorporate realistic boundary conditions to accurately represent the experimental setup. In most loading scenarios, RC beams can be modeled in symmetry. This can be realized by restraining the beam with rollers along the axis of symmetry. At least, one plane of symmetry can be found and the displacement perpendicular to this plane of symmetry needs to be constrained to zero.
2.3.1. Monotonic and Cyclic Loading
Applied loading at ambient conditions comprise of monotonic and cyclic loadings. While the first is often used for most scenarios to represent day-to-day loading conditions, the latter is often used to simulate earthquake events and/or fatigue conditions. Both types of loadings can be applied via force-controlled or displacement control options. For example, a designer can input a series of loads in uniform (or dispersed) increments (i.e., 5 kN, 10 kN etc.)—see Figure 4. Past experiences have shown that a good practice would be to apply smaller magnitudes of loads up until reaching the cracking limit of concrete material, and in some cases up to the yielding point of steel reinforcement. Beyond these points, larger magnitude of loads can be applied. The magnitude of applied forces/displacements can then be reduced upon reaching the ultimate stage where failure is expected. This enables the designer to capture the exact load bearing capacity and failure mechanism of the modeled FRP-strengthened beam.
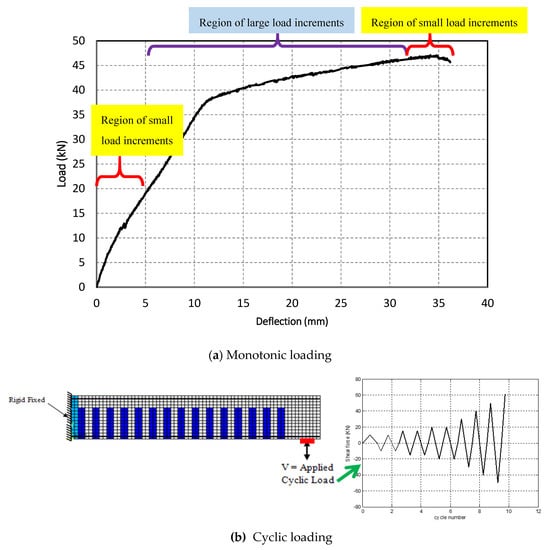
Figure 4.
Consideration for applied loading in ANSYS and ABAQUS: (a) Monotonic loading; (b) Cyclic loading.
These loading are then applied onto a line or group of nodes (and could also be applied onto their respective area). To neutralize any stress concentration effects, the loadings can be applied at rigid supports such as those shown in Figure 1. Similar to applying a monotonic loading, a cyclic loading history can also be applied (say at the free end of the cantilever beam). Cyclic loads are broken down into a series of positive (upward) and negative (downward) load steps and sub-steps. Using this method allows the stiffness matrix of the FE model to be re-adjusted before proceeding to the next incremental load step in order to reflect the nonlinear changes in the model’s structural stiffness.
2.3.2. Fire Loading
For the thermal-structural transient fire analysis, a two-stage procedure is usually followed. In the first stage, a thermal analysis is carried out and this analysis requires the use of thermal elements and associated thermal properties for concrete, steel, and FRP reinforcement. The thermal elements of interest include cubic (designated as SOLID70 in ANSYS) elements capable of modeling concrete material as well as FRP/adhesive/insulation material (with nodal temperature as a degree of freedom), 3D uniaxial 2-node conduction bar often used to model steel/FRP rebars (designated as LINK33 in ANSYS), and a 3D thermal surface (designated as SURF152 in ANSYS) element that can be used to simulate radiation and convection effects.
Under fire conditions, both the thermal and mechanical properties vary with rise in temperature and thus, this variation needs to be incorporated into the FE model. Fortunately, Eurocode 2 [] provides such properties for various concrete types and steel reinforcement. However, the temperature-dependent material properties for FRP, as well as commonly used insulation materials, can be found from the open literature [,,,,]. The material properties needed to properly carry out a heat transfer analysis include the thermal conductivity, specific heat and density.
In the first stage, the designer may option to simulate heat transfer from the fire source to the FRP-strengthened beam (i.e., via convection and radiation) or, for simplicity, may simply apply a nodal temperature versus time (i.e., ASTM E119, ISO 834 etc.) scenario is often applied to the bottom and side surfaces of a beam or depending on the fire incident []. Here, the thermal boundary conditions can be applied via a combination of convection and radiation heat flux. The convective heat transfer coefficient (h) at the fire exposed surface can be assumed to be 25 W/m2K for standard fire conditions and in the range of 40–50 W/m2K for hydrocarbon fires []. The value of the same coefficient is 4 W/m2K the unexposed cold surfaces. Heat transfer via radiation requires the input of emissivity (ε) and Stefan-Boltzman radiation (σ) coefficientS with values of 0.7–0.9 and 5.669 × 10−8 W/m2K4, respectively [,].
The outcome of the thermal analysis is often evaluated by examining the temperature history and temperature gradients between the key locations of the model. The key locations of interest may include the rebar, FRP/concrete interface, and mid-depth of the beam. Then, the resulting nodal temperatures are used as input effects into the second stage of analysis.
In this stage, a structural stress analysis is carried out taking nodal temperatures obtained in the thermal analysis into account to trace the effect of temperature rise on degrading the mechanical properties (strength, modulus) of the different components of the FRP-strengthened beams. A key point to remember is that FRP-strengthened beams are often mechanically loaded with a constant (fixed) magnitude of loading that represents a percentage of its capacity (30–60%). The element types often selected to carry out the stress analysis are those compatible with their thermal counterparts.
2.4. Considerations for Failure Criteria and Convergence Limits
As discussed above, the highly nonlinear response of FRP-strengthened beams requires dividing the applied loading into a series of load steps and sub-steps. The nonlinear change in the structural stiffness is simulated by adjusting the stiffness matrix at the end of each load sub-step using Newton-Raphson equilibrium iterations. The onset of debonding often initiates a large disturbance to the FE simulation and a major difficulty to the solution algorithm. Hence, the designer might option to utilize the automatic time stepping option to predict and to control load step sizes in different sizes. Thus, convergence of the solution can be achieved using the program default force convergence value of 0.005, however may turn difficult to obtain due to materials nonlinearity and large deformations. In order to obtain convergence of the equilibrium iterations, the force convergence tolerance limit value can be increased to (0.05–0.2) to achieve convergence of the solution [].
In all cases, the following assumptions are often followed when simulating FRP-strengthened structures. These assumptions are adopted from best practices suggested by ACI 440.2R-17 standard [] and Fib provisions []:
- Yielding of steel reinforcement in tension is followed by concrete crushing when strain in the top compression fibers exceeds 0.003.
- Shear/tension delamination of the concrete cover may occur once the filling layer or substrate cannot sustain the forces induced in the reinforcing steel/cfrp rebars.
- Debonding of the FRP systems from the concrete substrate (delamination of plates/sheets or NSM bar pull-out).
These failure modes can be predicted by examining the deformed shape, strain, and stress levels in the concrete, FRP bars, and adhesive along their interfaces as shown in Figure 5.
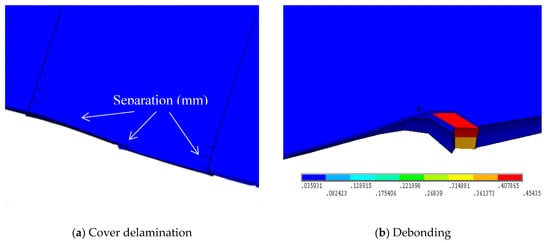
Figure 5.
Comparison between the failure modes of the experimental and FE models developed in ANSYS: (a) Cover delamination; (b) Debonding.
2.5. Considerations for Post-Processing of Results
In order to examine the validity and predictability of a FE model, the FE and experimental results are to be compared. In the case of monotonic or cyclic loading, the mid-span deflection as predicted from the FE analysis and measured in tests are compared throughout the loading history to check if predictions match test observations []. An additional comparison can also be carried out to evaluate hysteresis response and energy dissipation. In all cases, the authors also recommend comparing cracking response and stress/strain distributions as measured in the laboratory tests against that obtained in FE simulations. It should be noted that the above can also be carried out in the case of fire analysis. Additional checks should also be considered to verify predicted temperature rise (with exposure time) against that measured in fire tests, as well as comparing mid-span deflection (and rate of deflection) against codal provisions listed in fire testing standards (i.e., ASTM E119 and ISO834).
3. Challenges, and Future Research Needs
The above literature review indicates that FRPs have great potential for continual integration into civil engineering applications. These materials have superior properties, and thus can be employed in a variety of constructions. Unfortunately, properly modeling the behavior and response of FRP composites is challenging [,] and may hinder designers of utilizing these systems to their full potential. This section aims at highlighting few of these limitations, associated challenges, and required future research needs.
The topics related to FRP in which there is a lack of sufficient experimental data are mainly related to external strengthening of RC beams with FRP laminates bonded with different types of anchorage systems.
The challenges associated with FE modeling are mainly related to the simulation of debonding between the FRP laminates and concrete surfaces. This is due to the lack of data on the coefficient of friction and appropriate range of values for the contact stiffness. Other challenges are associated in the modeling of strengthened RC structures under elevated temperatures. This is due to the several assumptions made due to the limited data on the thermal and mechanical properties of FRP laminates. Moreover, the modeling of FRP splay anchors is another challenge due to the complicated geometry and lack of knowledge on the bond between the anchor and concrete surfaces and between the anchor and FRP laminates.
Future experimental and numerical research studies on FRP-strengthened RC beams are still needed in areas that are not clear or in need of further development to examine and validate performance. The following is a summary of the needed topics:
- Experimental and numerical studies on the thermal and mechanical response of FRP-strengthened beams under cold and hot temperatures.
- Experimental and numerical studies on the creep-rupture behavior and endurance times of FRP-strengthened RC beams.
- Modeling the effects of high concrete strength on the shear and flexural performance of FRP-strengthened beams.
- Experimental and numerical studies on the effects of lightweight concrete on the shear and flexural performance of FRP-strengthened beams.
- Experimental and numerical studies on the long-term deflection behavior of flexural members strengthened with different types of FRP systems.
- Modeling the performance of externally strengthened RC beams anchored with FRP splay anchors under static, cyclic, and fire loadings.
4. Summary and Conclusions
FRP strengthening systems present effective solutions to rehabilitate aging and trauma-weakened concrete structures. However, the integration of these systems can be hindered by our minute capability of properly modeling their behavior. This paper presents effective strategies and guidelines to allow proper simulation of FRP-strengthened structures. The outcomes of this work can be summarized in the following points:
- FRP materials offer unique solutions to aging and new structures that exceed those constructed by traditional materials.
- Developing appropriate modeling techniques is warranted given that the performance of FRP-strengthened concrete structures is complicated and complex.
- There is a need for development of appropriate and validated FE models since they provide more economical solutions than testing. It is beneficial in design oriented parametric studies and could be used in lieu of tests in the laboratory.
Author Contributions
Conceptualization, M.Z.N. and R.A.H.; methodology, J.A.A.; software, M.Z.N. and R.A.H.; validation, M.Z.N., R.A.H. and J.A.A.; resources, M.Z.N., J.A.A., and R.A.H.; writing—original draft preparation, M.Z.N., R.A.H., and J.A.A.; writing—review and editing, M.Z.N., R.A.H., and J.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rasheed, H.A. Strengthening Design of Reinforced Concrete with FRP, 1st ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Hollaway, L.C. A review of the present and future utilisation of FRP composites in the civil infrastructure with reference to their important in-service properties. Constr. Build. Mater. 2010, 24, 2419–2445. [Google Scholar] [CrossRef]
- Naser, M.Z.; Hawileh, R.A.; Abdalla, J.A. Fiber-reinforced polymer composites in strengthening reinforced concrete structures: A critical review. Eng. Struct. 2019, 198, 109542. [Google Scholar] [CrossRef]
- Oliveira, D.V.; Basilio, I.; Loureņo, P.B. Experimental behavior of FRP strengthened masonry arches. J. Compos. Constr. 2010, 14, 312–322. [Google Scholar] [CrossRef]
- Czaderski, C.; Meier, U. EBR Strengthening Technique for Concrete, Long-Term Behaviour and Historical Survey. Polymers 2018, 10, 77. [Google Scholar] [CrossRef] [PubMed]
- Hawileh, R.; Abdalla, J.A.; Naser, M.Z.; Tanarslan, M. Finite element modeling of shear deficient RC beams strengthened with NSM CFRP rods under cyclic loading. ACI Spec. Publ. 2015, 301, 1–18. [Google Scholar]
- Firmo, J.P.; Correia, J.R. Fire behaviour of thermally insulated RC beams strengthened with NSM-CFRP strips: Experimental study. Compos. Part B Eng. 2015, 76, 112–121. [Google Scholar] [CrossRef]
- Zhu, H.; Wu, G.; Zhang, L.; Zhang, J.; Hui, D. Experimental study on the fire resistance of RC beams strengthened with near-surface-mounted high-Tg BFRP bars. Compos. Part B Eng. 2014, 60, 680–687. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440. 2R-17); American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- International Federation for Structural Concrete. FRP Reinforcement in RC Structures; Technical Report; International Federation for Structural Concrete: Lausanne, France, 2007. [Google Scholar]
- Sonobe, Y.; Mochizuki, S.; Matsuzaki, Y.; Shimizu, A. Guidelines for Structural Design of FRP Reinforced Concrete Building Structures. In Rilem Proceedings; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Yuan, C.; Chen, W.; Pham, T.M.; Hao, H. Bond behaviour between hybrid fiber reinforced polymer sheets and concrete. Constr. Build. Mater. 2019, 210, 93–110. [Google Scholar] [CrossRef]
- Naser, M.; Hawileh, R.; Abdalla, J.A.; Al-Tamimi, A. Bond behavior of CFRP cured laminates: Experimental and numerical investigation. J. Eng. Mater. Technol. Trans. ASME 2012, 134, 021002. [Google Scholar] [CrossRef]
- Mosallam, A.; Allam, K.; Salama, M. Analytical and numerical modeling of RC beam-column joints retrofitted with FRP laminates and hybrid composite connectors. Compos. Struct. 2019, 214, 486–503. [Google Scholar] [CrossRef]
- Chellapandian, M.; Prakash, S.S.; Sharma, A. Experimental and finite element studies on the flexural behavior of reinforced concrete elements strengthened with hybrid FRP technique. Compos. Struct. 2019, 208, 466–478. [Google Scholar] [CrossRef]
- Kachlakev, D.; Niller, T.; Yim, S.; Chansawat, K.; Potisuk, T. Finite Element Modeling of Reinforced Concrete Structures Strengthened with FRP Laminates; California Polytechnic State University: San Lius Obispo, CA, USA; Oregon State University: Corvallis, OR, USA, 2001. [Google Scholar]
- Hawileh, R.A.; Abdalla, J.A.; Tanarslan, M.H.; Naser, M.Z. Modeling of nonlinear cyclic response of shear-deficient RC T-beams strengthened with side bonded CFRP fabric strips. Comput. Concr. 2011, 8, 193–206. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Mahmood, M.S. Finite element modeling of reinforced concrete beams strengthened with FRP laminates. Eur. J. Sci. Res. 2009, 30, 526–541. [Google Scholar]
- Shahverdi, M.; Mohammadi, S. Fracture analysis of FRP composites using a meshless finite point collocation method. In Proceedings of the Fourth International Conference on FRP Composites in Civil Engineering (CICE2008), Zurich, Switzerland, 22–24 July 2008. [Google Scholar]
- Lu, X.Z.; Ye, L.P.; Teng, J.G.; Jiang, J.J. Meso-scale finite element model for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 564–575. [Google Scholar] [CrossRef]
- Kadhim, M.M.A.; Jawdhari, A.R.; Altaee, M.J.; Adheem, A.H. Finite element modelling and parametric analysis of FRP strengthened RC beams under impact load. J. Build. Eng. 2020, 32, 101526. [Google Scholar] [CrossRef]
- Bouziadi, F.; Boulekbache, B.; Haddi, A.; Hamrat, M.; Djelal, C. Finite element modeling of creep behavior of FRP-externally strengthened reinforced concrete beams. Eng. Struct. 2020, 204, 109908. [Google Scholar] [CrossRef]
- Godat, A.; Challal, O.; Obaidat, Y. Non-linear finite-element investigation of the parameters affecting externally-bonded FRP flexural-strengthened RC beams. Results Eng. 2020, 8, 100168. [Google Scholar] [CrossRef]
- Nie, X.F.; Zhang, S.S.; Chen, G.M.; Yu, T. Strengthening of RC beams with rectangular web openings using externally bonded FRP: Numerical simulation. Compos. Struct. 2020, 248, 112552. [Google Scholar] [CrossRef]
- Hawileh, R.A. Nonlinear finite element modeling of RC beams strengthened with NSM FRP rods. Constr. Build. Mater. 2012, 27, 461–471. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Bhatt, P.P. A numerical approach for modeling response of fiber reinforced polymer strengthened concrete slabs exposed to fire. Compos. Struct. 2018, 187, 226–240. [Google Scholar] [CrossRef]
- Dal Lago, B.; Taylor, S.E.; Deegan, P.; Ferrara, L.; Sonebi, M.; Crosset, P.; Pattarini, A. Full-scale testing and numerical analysis of a precast fibre reinforced self-compacting concrete slab pre-stressed with basalt fibre reinforced polymer bars. Compos. Part B Eng. 2017, 128, 120–133. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Naser, M.Z.; Abdalla, J.A. Finite element simulation of reinforced concrete beams externally strengthened with short-length CFRP plates. Compos. Part B Eng. 2013, 45, 1722–1730. [Google Scholar] [CrossRef]
- Chen, G.M.; Teng, J.G.; Chen, J.F.; Xiao, Q.G. Finite element modeling of debonding failures in FRP-strengthened RC beams: A dynamic approach. Comput. Struct. 2015, 158, 167–183. [Google Scholar] [CrossRef]
- Bui, L.V.H.; Stitmannaithum, B.; Ueda, T. Mechanical performances of concrete beams with hybrid usage of steel and FRP tension reinforcement. Comput. Concr. 2017, 20, 391–407. [Google Scholar]
- Kim, S.; Aboutaha, R.S. Finite element analysis of carbon fiber-reinforced polymer (CFRP) strengthened reinforced concrete beams. Comput. Concr. 2004, 1, 401–416. [Google Scholar] [CrossRef]
- Shrestha, R.; Smith, S.T.; Samali, B. Finite element modelling of FRP-strengthened RC beam-column connections with ANSYS. Comput. Concr. 2013, 11, 1–20. [Google Scholar] [CrossRef]
- Lu, X.Z.; Teng, J.G.; Ye, L.P.; Jiang, J.J. Bond-slip models for FRP sheets/plates bonded to concrete. Eng. Struct. 2005, 27, 920–937. [Google Scholar] [CrossRef]
- Chen, G.M.; Chen, J.F.; Teng, J.G. On the finite element modelling of RC beams shear-strengthened with FRP. Constr. Build. Mater. 2012, 32, 13–26. [Google Scholar] [CrossRef]
- Sakar, G.; Hawileh, R.A.; Naser, M.Z.; Abdalla, J.A.; Tanarslan, M. Nonlinear behavior of shear deficient RC beams strengthened with near surface mounted glass fiber reinforcement under cyclic loading. Mater. Des. 2014, 61, 16–25. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Musto, H.A.; Abdalla, J.A.; Naser, M.Z. Finite element modeling of reinforced concrete beams externally strengthened in flexure with side-bonded FRP laminates. Compos. Part B Eng. 2019, 173, 106952. [Google Scholar] [CrossRef]
- Liu, Y.; Zwingmann, B.; Schlaich, M. Nonlinear progressive damage analysis of notched or bolted fibre-reinforced polymer (FRP) laminates based on a three-dimensional strain failure criterion. Polymers 2014, 6, 949–976. [Google Scholar] [CrossRef]
- Ameli, M.; Ronagh, H.R.; Dux, P.F. Behavior of FRP strengthened reinforced concrete beams under torsion. J. Compos. Constr. 2007, 11, 384–390. [Google Scholar] [CrossRef]
- Mahini, S.S.; Ronagh, H.R. Numerical modelling of FRP strengthened RC beam-column joints. Struct. Eng. Mech. 2009, 32, 649–665. [Google Scholar] [CrossRef]
- Hassan, N.Z.; Sherif, A.G.; Zamarawy, A.H. Finite element analysis of reinforced concrete beams with opening strengthened using FRP. Ain Shams Eng. J. 2017, 8, 531–537. [Google Scholar] [CrossRef]
- El-Kashif, K.F.O.; Adly, A.K.; Abdalla, H.A. Finite element modeling of RC shear walls strengthened with CFRP subjected to cyclic loading. Alexandria Eng. J. 2019, 58, 189–205. [Google Scholar] [CrossRef]
- Zeng, J.; Guo, Y.; Li, L.; Chen, W. Behavior and Three-Dimensional Finite Element Modeling of Circular Concrete Columns Partially Wrapped with FRP Strips. Polymers 2018, 10, 253. [Google Scholar] [CrossRef]
- Yu, H.; Bai, Y.L.; Dai, J.G.; Gao, W.Y. Finite element modeling for debonding of FRP-to-concrete interfaces subjected to mixed-mode loading. Polymers 2017, 9, 438. [Google Scholar] [CrossRef]
- Gribniak, V.; Misiūnaitė, I.; Rimkus, A.; Sokolov, A.; Šapalas, A. Deformations of FRP–Concrete Composite Beam: Experiment and Numerical Analysis. Appl. Sci. 2019, 9, 5164. [Google Scholar] [CrossRef]
- Willam, K.; Warnke, E. Constitutive model for the triaxial behavior of concrete. Proc. Intl. Assoc. Bridge Structl. Engrs. 1975, 19, 1–30. [Google Scholar]
- Lazzari, B.M.; Filho, A.C.; Lazzari, P.M.; Pacheco, A.R. Using the element-embedded rebar model in ansys to analyze reinforced concrete beams. Comput. Concr. 2017, 19, 347–356. [Google Scholar] [CrossRef]
- Al-Azzawi, A.A.; Abdul Al-Aziz, B.M. Behavior of reinforced lightweight aggregate concrete hollow-core slabs. Comput. Concr. 2018, 21, 117–126. [Google Scholar]
- Hawileh, R.A. Finite element modeling of reinforced concrete beams with a hybrid combination of steel and aramid reinforcement. Mater. Des. 2015, 65, 831–839. [Google Scholar] [CrossRef]
- Dahmani, L.; Khennane, A.; Kaci, S. Crack identification in reinforced concrete beams using ANSYS software. Strength Mater. 2010, 42, 232–240. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Taylor, S.E. Finite-Element Investigation of the Structural Behavior of Basalt Fiber Reinforced Polymer (BFRP)-Reinforced Self-Compacting Concrete (SCC) Decks Slabs in Thompson Bridge. Polymers 2018, 10, 678. [Google Scholar] [CrossRef]
- Hognestad, E.; Hanson, N.W.; McHenry, D. Concrete Stress Distribution in Ultimate Strength Design. ACI J. Proc. 1955, 52, 455–480. [Google Scholar]
- Hawileh, R.A.; El-Maaddawy, T.A.; Naser, M.Z. Nonlinear finite element modeling of concrete deep beams with openings strengthened with externally-bonded composites. Mater. Des. 2012, 42, 378–387. [Google Scholar] [CrossRef]
- Naser, M.Z. Behavior of RC Beams Strengthened with CFRP Laminates Under Fire-A Finite Element Simulation. Master’s Thesis, American University of Sharjah, Sharjah, UAE, 2011. [Google Scholar]
- Nie, J.; Fan, J.; Cai, C.S. Stiffness and deflection of steel-concrete composite beams under negative bending. J. Struct. Eng. 2004, 130, 1842–1851. [Google Scholar] [CrossRef]
- Obaidat, Y.T.; Heyden, S.; Dahlblom, O. The effect of CFRP and CFRP/concrete interface models when modelling retrofitted RC beams with FEM. Compos. Struct. 2010, 92, 1391–1398. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Naser, M.; Zaidan, W.; Rasheed, H.A. Modeling of insulated CFRP-strengthened reinforced concrete T-beam exposed to fire. Eng. Struct. 2009, 31, 3072–3079. [Google Scholar] [CrossRef]
- Martinelli, E.; Napoli, A.; Nunziata, B.; Realfonzo, R. RC Beams Strengthened with Mechanically Fastened Composites: Experimental Results and Numerical Modeling. Polymers 2014, 6, 613–633. [Google Scholar] [CrossRef]
- Comite Euro-International Du Beton. CEB-FIP Model Code 1990: Design Code; Default Book Series; Thomas Telford Ltd.: London, UK, 1993. [Google Scholar]
- Nakaba, K.; Kanakubo, T.; Furuta, T.; Yoshizawa, H. Bond behavior between fiber-reinforced polymer laminates and concrete. ACI Struct. J. 2001, 98, 359–367. [Google Scholar]
- Hassan, T.K.; Rizkalla, S.H. Bond mechanism of near-surface-mounted fiber-reinforced polymer bars for flexural strengthening of concrete structures. ACI Struct. J. 2004, 101, 830–839. [Google Scholar]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part. B Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- CEN. Design of Concrete Structures—Part 1–2: General Rules—Structural Fire Design (EN 1992-1-2); CEN: Brussels, Belgium, 2004. [Google Scholar]
- Bisby, L. Fire Behaviour of Fibre-Reinforced Polymer (FRP) Reinforced or Confined Concrete. Ph.D. Thesis, Queen’s University, Kingston, ON, Canada, 2003. [Google Scholar]
- Naser, M.Z. Properties and material models for modern construction materials at elevated temperatures. Comput. Mater. Sci. 2019, 160, 16–29. [Google Scholar] [CrossRef]
- Yu, B.; Kodur, V. Effect of temperature on strength and stiffness properties of near-surface mounted FRP reinforcement. Compos. Part. B Eng. 2014, 58, 510–517. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Bhatt, P.P.; Naser, M.Z. High temperature properties of fiber reinforced polymers and fire insulation for fire resistance modeling of strengthened concrete structures. Compos. Part. B Eng. 2019, 175, 107104. [Google Scholar] [CrossRef]
- Kodur, V.K.R.; Shakya, A.M. Effect of temperature on thermal properties of spray applied fire resistive materials. Fire Saf. J. 2013, 61, 314–323. [Google Scholar] [CrossRef]
- Džolev, I.M.; Cvetkovska, M.J.; Lađinović, D.; Radonjanin, V.S. Numerical analysis on the behaviour of reinforced concrete frame structures in fire. Comput. Concr. 2018, 21, 637–647. [Google Scholar]
- Wang, Y.; Dong, Y.L.; Zhou, G.C. Nonlinear numerical modeling of two-way reinforced concrete slabs subjected to fire. Comput. Struct. 2013, 119, 23–36. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Kodur, V.K.R. Performance of reinforced concrete slabs under hydrocarbon fire exposure. Tunn. Undergr. Sp. Technol. 2018, 77, 177–187. [Google Scholar] [CrossRef]
- CEN. Eurocode 1. Actions on Structures–Part 1–2: General Actions–Actions on Structures Exposed to Fire (EN 1991-1-2); BSI: London, UK, 2002. [Google Scholar]
- Kohnke, P.C. ANSYS Theory Reference; ANSYS Technology Drive: Canonsburg, PA, USA, 2013. [Google Scholar]
- Federation International Du Béton. Externally Bonded FRP Reinforcement for RC Structures: Technical Report on the Design and Use of Externally Bonded Fibre Reinforced Polymer Reinforcement (FRP EBR) for Reinforced Concrete Structures; International Federation for Structural Concrete: Lausanne, Switzerland, 2001. [Google Scholar]
- Gawil, B.; Wu, H.-C.; Elarbi, A. Modeling the Behavior of CFRP Strengthened Concrete Beams and Columns at Different Temperatures. Fibers 2020, 8, 10. [Google Scholar] [CrossRef]
- Müzel, S.D.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the Finite Element Method in the Analysis of Composite Materials: A Review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).