Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures
Abstract
1. Introduction
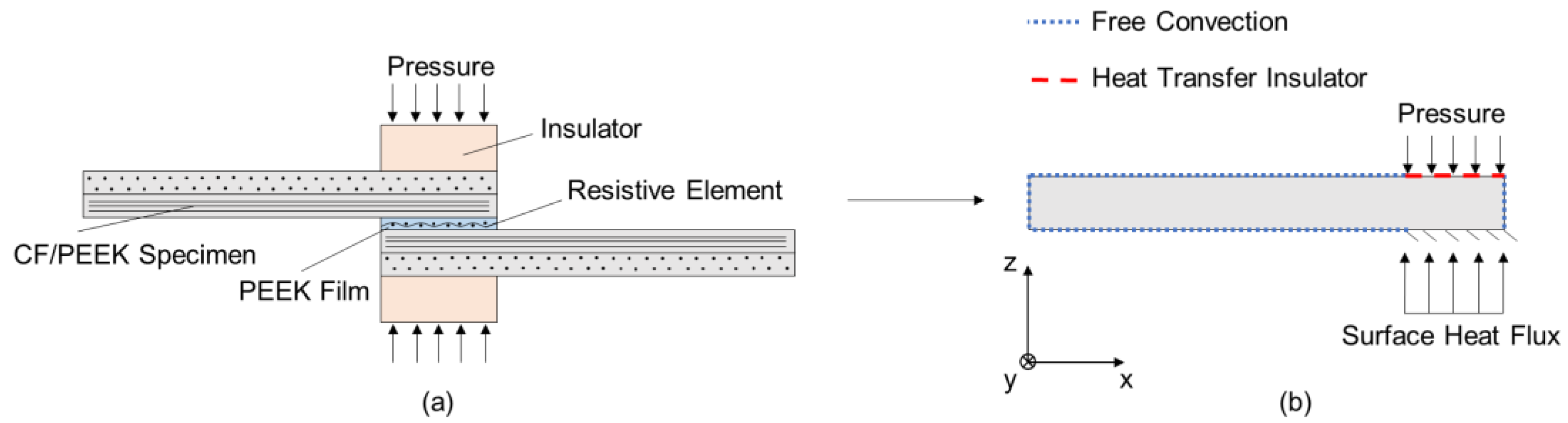
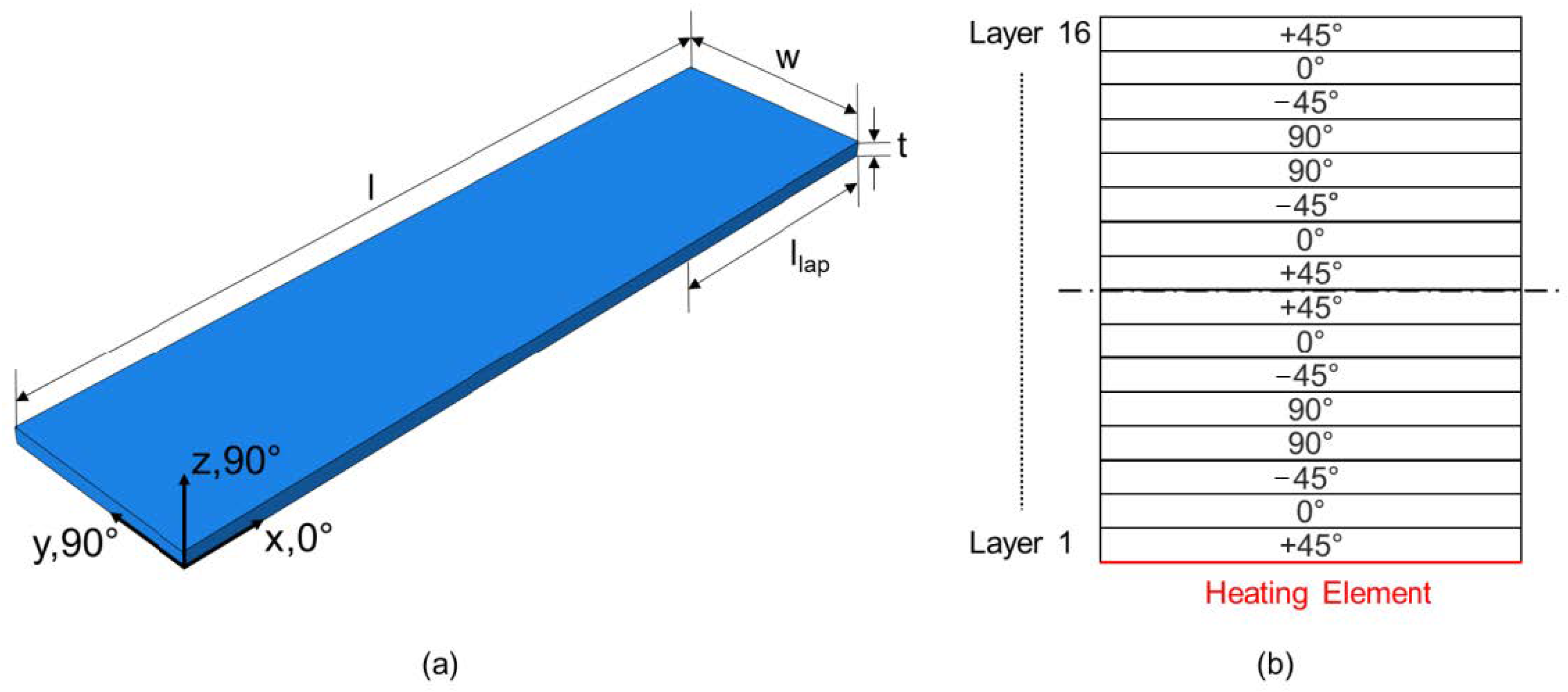
2. Materials and Methods
3. Results
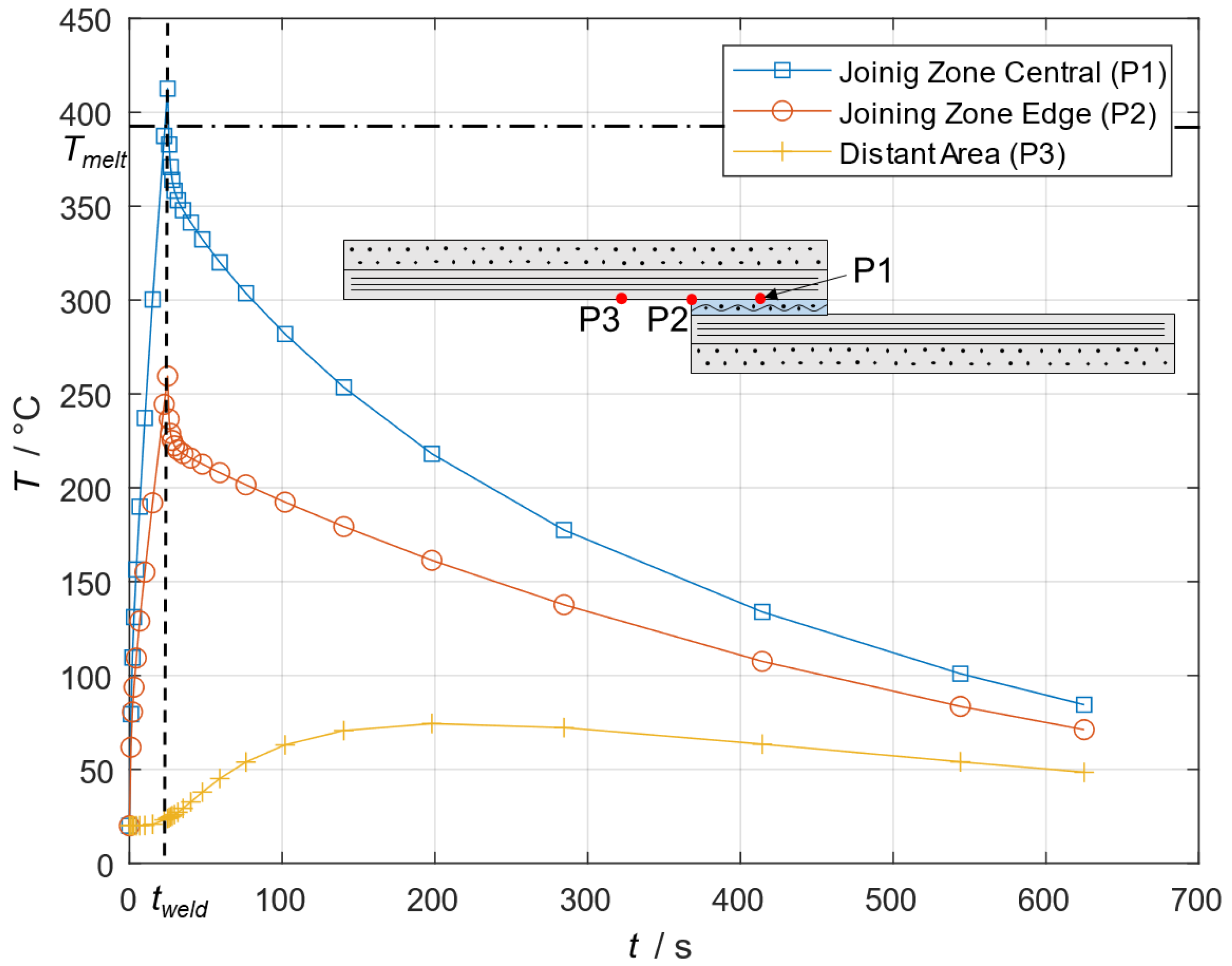
3.1. Welding Simulation
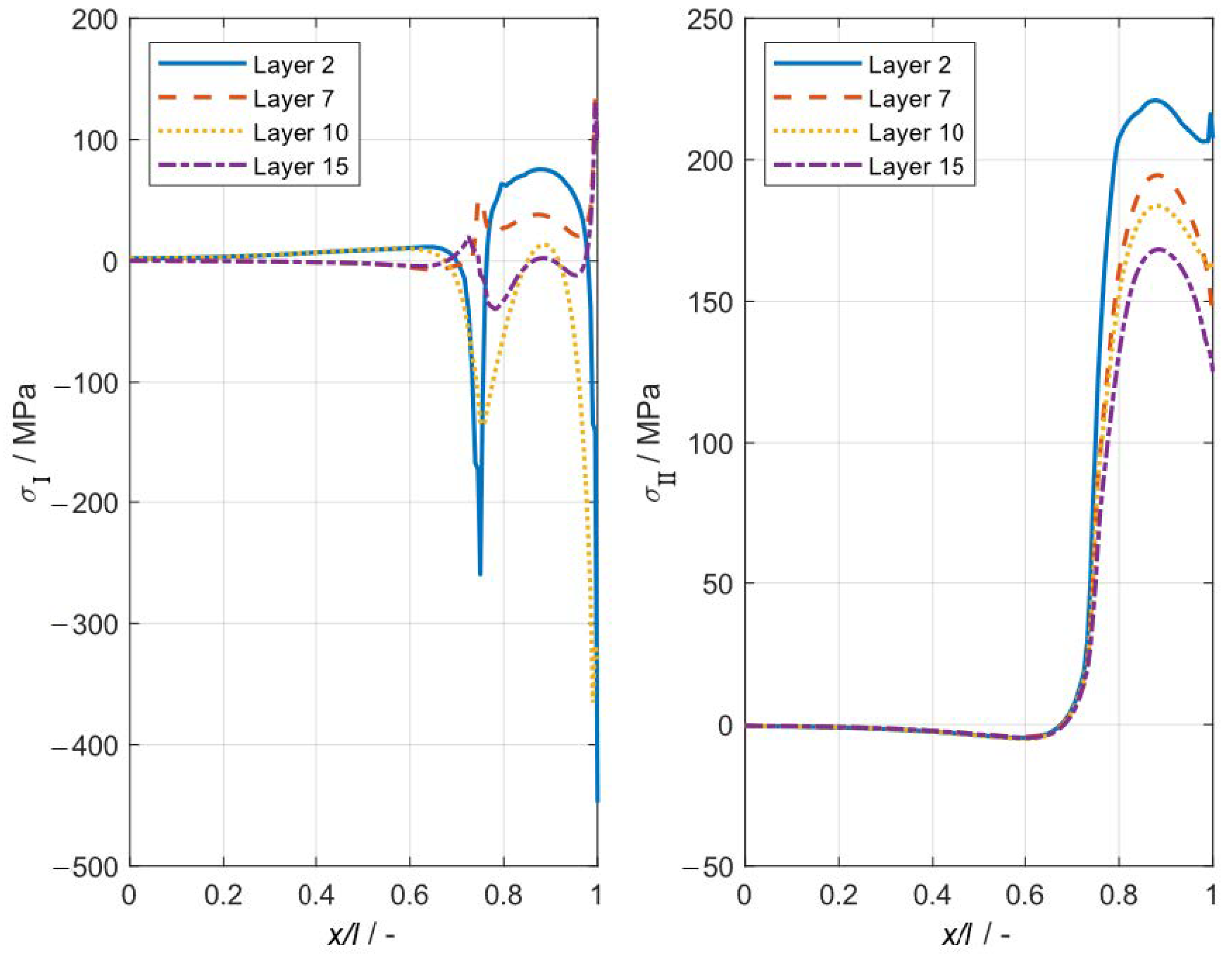
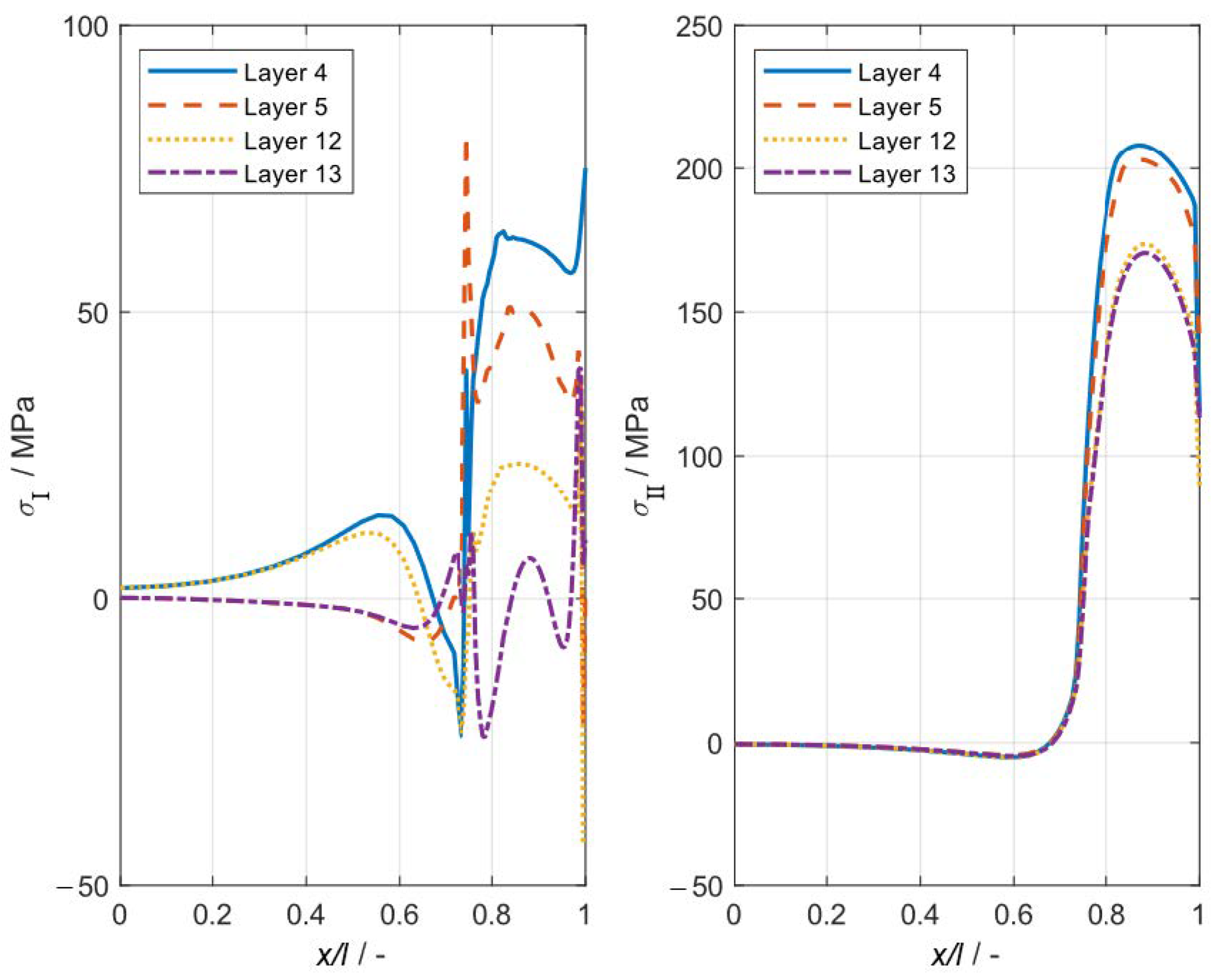
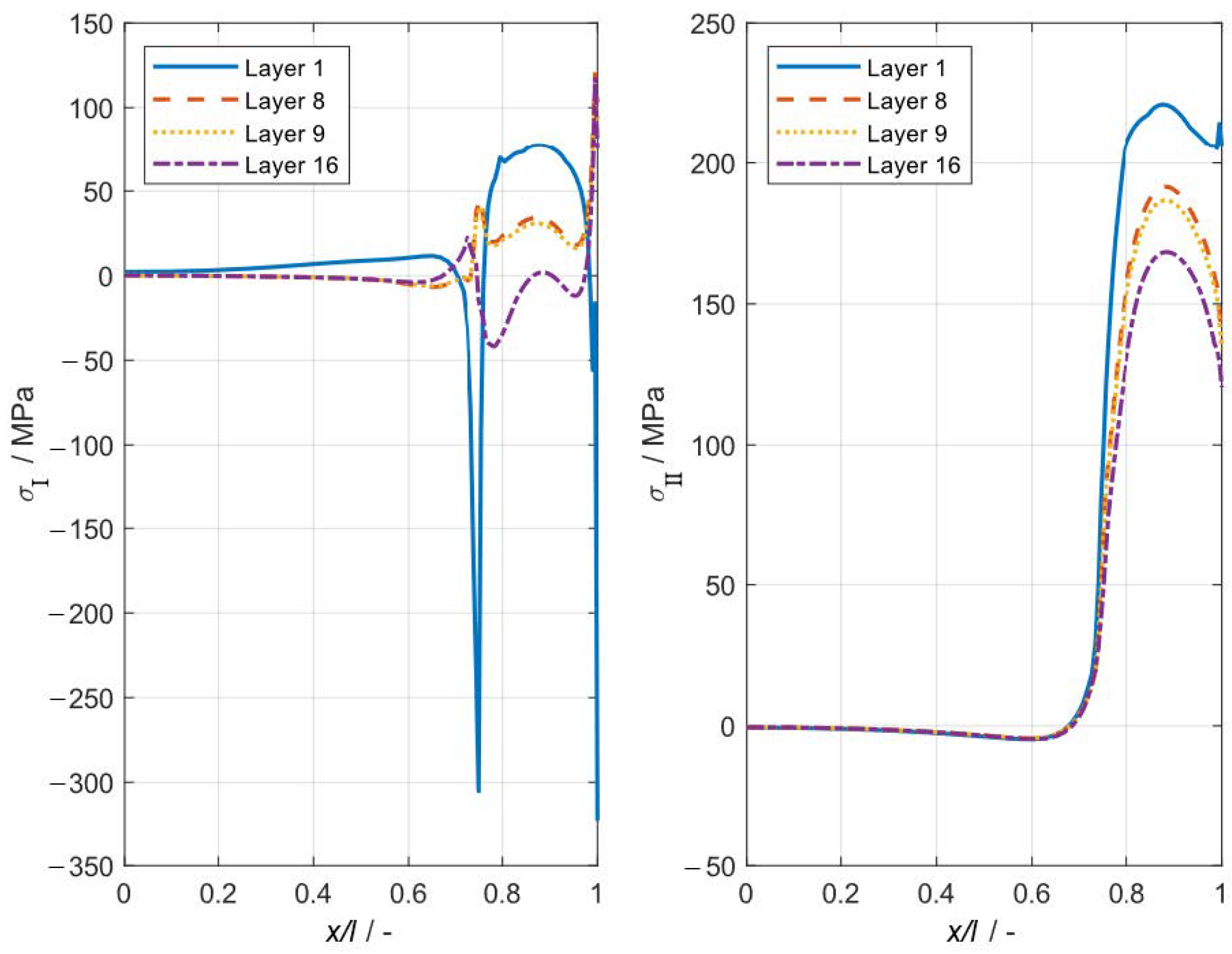
3.2. Residual Stress Analysis
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cogswell, F.N. Thermoplastic Aromatic Polymer Composites: A Study of the Structure, Processing and Properties of Carbon Fibre Reinforced Polyetheretherketone and Related Materials; Butterworth-Heinemann: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, R.; Ai, S.; He, R.; Pei, Y.; Fang, D. Load distribution in threads of porous metal–ceramic functionally graded composite joints subjected to thermomechanical loading. Compos. Struct. 2015, 134, 680–688. [Google Scholar] [CrossRef]
- Lionetto, F.; Pappadà, S.; Buccoliero, G.; Maffezzoli, A. Finite element modeling of continuous induction welding of thermoplastic matrix composites. Mater. Des. 2017, 120, 212–221. [Google Scholar] [CrossRef]
- Gouin O’Shaughnessey, P.; Dubé, M.; Fernandez Villegas, I. Modeling and experimental investigation of induction welding of thermoplastic composites and comparison with other welding processes. J. Compos. Mater. 2016, 50, 2895–2910. [Google Scholar] [CrossRef]
- Sooriyapiragasam, S.K.; Hopmann, C. Modeling of the heating process during the laser transmission welding of thermoplastics and calculation of the resulting stress distribution. Weld World 2016, 60, 777–791. [Google Scholar] [CrossRef]
- Cosson, B.; Deléglise, M.; Knapp, W. Numerical analysis of thermoplastic composites laser welding using ray tracing method. Compos. Part B Eng. 2015, 68, 85–91. [Google Scholar] [CrossRef]
- Zhao, T.; Palardy, G.; Villegas, I.F.; Rans, C.; Martinez, M.; Benedictus, R. Mechanical behaviour of thermoplastic composites spot-welded and mechanically fastened joints: A preliminary comparison. Compos. Part B Eng. 2017, 112, 224–234. [Google Scholar] [CrossRef]
- Lionetto, F.; Dell’Anna, R.; Montagna, F.; Maffezzoli, A. Modeling of continuous ultrasonic impregnation and consolidation of thermoplastic matrix composites. Compos. Part A Appl. Sci. Manuf. 2016, 82, 119–129. [Google Scholar] [CrossRef]
- Stavrov, D.; Bersee, H.E.N. Resistance welding of thermoplastic composites-an overview. Compos. Part A Appl. Sci. Manuf. 2005, 36, 39–54. [Google Scholar] [CrossRef]
- Shi, H.; Villegas, I.F.; Bersee, H.E.N. Strength and failure modes in resistance welded thermoplastic composite joints: Effect of fibre–matrix adhesion and fibre orientation. Compos. Part A Appl. Sci. Manuf. 2013, 55, 1–10. [Google Scholar] [CrossRef]
- Shi, H.; Villegas, I.F.; Octeau, M.-A.; Bersee, H.E.N.; Yousefpour, A. Continuous resistance welding of thermoplastic composites: Modelling of heat generation and heat transfer. Compos. Part A Appl. Sci. Manuf. 2015, 70, 16–26. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Residual stresses in thermoplastic composites—A study of the literature—Part I: Formation of residual stresses. Compos. Part A Appl. Sci. Manuf. 2006, 37, 1847–1857. [Google Scholar] [CrossRef]
- Parlevliet, P.P.; Bersee, H.E.N.; Beukers, A. Residual stresses in thermoplastic composites—A study of the literature. Part III: Effects of thermal residual stresses. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1581–1596. [Google Scholar] [CrossRef]
- Zhou, W.; Zhou, H.; Zhang, R.; Pei, Y.; Fang, D. Measuring residual stress and its influence on properties of porous ZrO2/(ZrO2+Ni) ceramics. Mater. Sci. Eng. A 2015, 622, 82–90. [Google Scholar] [CrossRef][Green Version]
- Jeyakodi, G.K. Finite Element Simulation of the In—Situ AFP Process for Thermoplastic Composites Using Abaqus. Master’s Thesis, Faculty of Aerospace Engineering, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Shi, H.; Villegas, I.F.; Bersee, H.E.N. An investigation on the strain distribution of resistance welded thermoplastic composite joints. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar] [CrossRef]


| Elastic Properties | Thermal Properties | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Young’s Modulus | Shear Modulus | Poisson’s Ratio | Thermal Conductivity Coefficient | Thermal Expansion coefficient | Specific Heat Capacity | |||||
| [MPa] | [MPa] | [MPa] | [MPa] | [-] | [-] | |||||
| 130,000 | 10,300 | 6000 | 4800 | 0.32 | 0.35 | 3.5 | 0.42 | 1.5 × 10−7 | 2.82 × 10−5 | 800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagel, L.; Herwig, A.; Schmidt, C.; Horst, P. Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures. J. Compos. Sci. 2021, 5, 45. https://doi.org/10.3390/jcs5020045
Nagel L, Herwig A, Schmidt C, Horst P. Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures. Journal of Composites Science. 2021; 5(2):45. https://doi.org/10.3390/jcs5020045
Chicago/Turabian StyleNagel, Lukas, Alexander Herwig, Carsten Schmidt, and Peter Horst. 2021. "Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures" Journal of Composites Science 5, no. 2: 45. https://doi.org/10.3390/jcs5020045
APA StyleNagel, L., Herwig, A., Schmidt, C., & Horst, P. (2021). Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures. Journal of Composites Science, 5(2), 45. https://doi.org/10.3390/jcs5020045






