Sheet Metal Profiles with Variable Height: Numerical Analyses on Flexible Roller Beading
Abstract
:1. Introduction
2. Materials and Methods
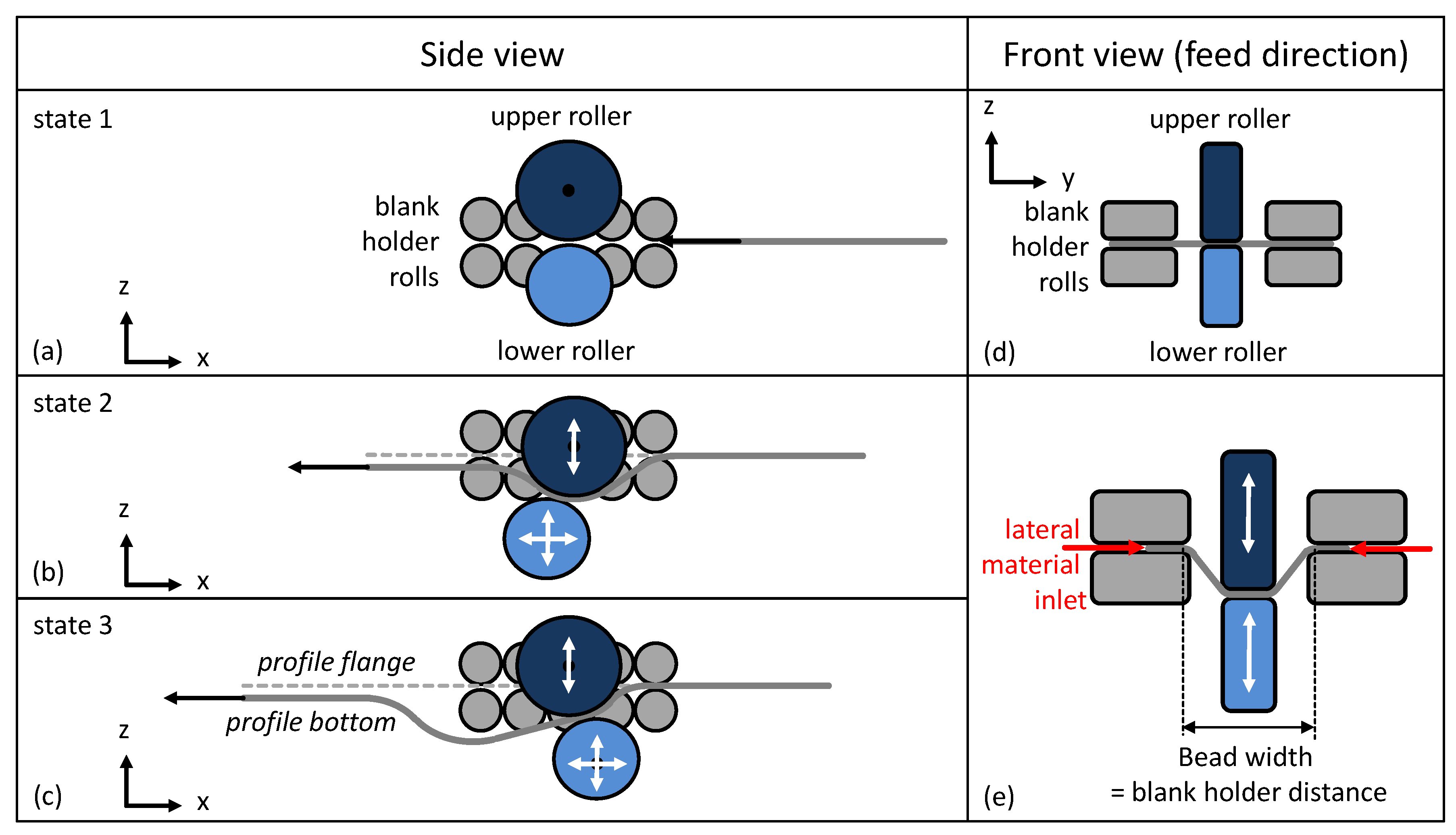
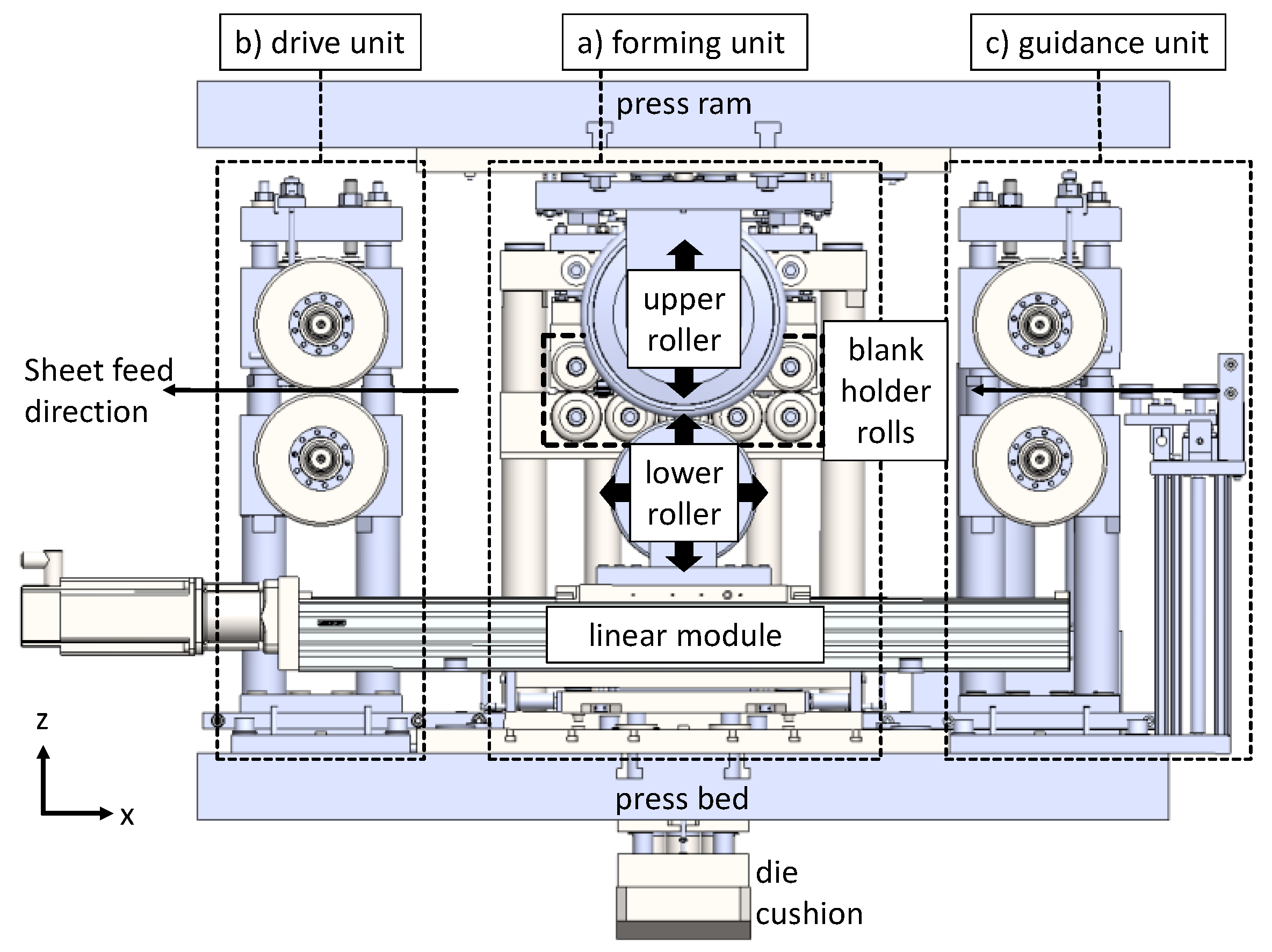
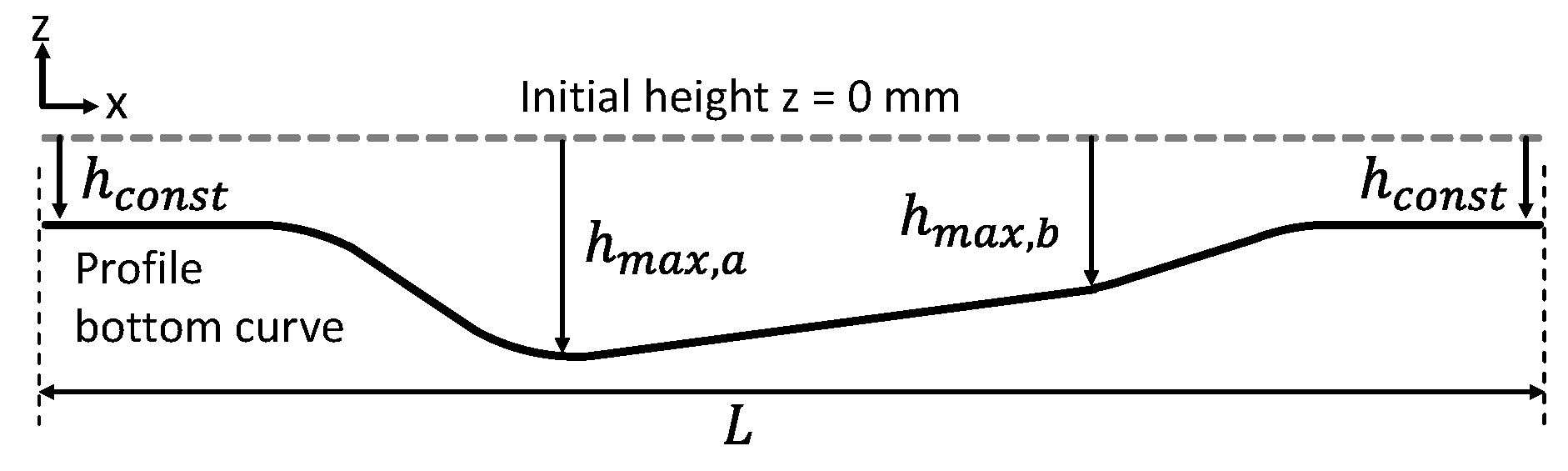
2.1. Flexible Roller Beading
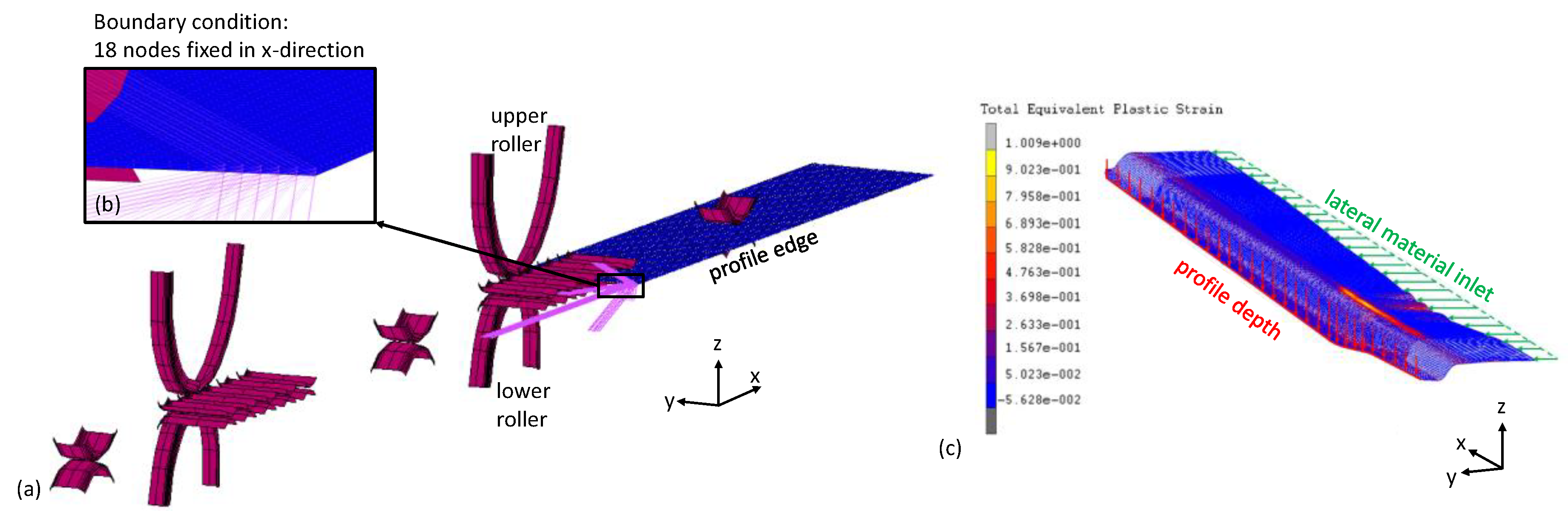
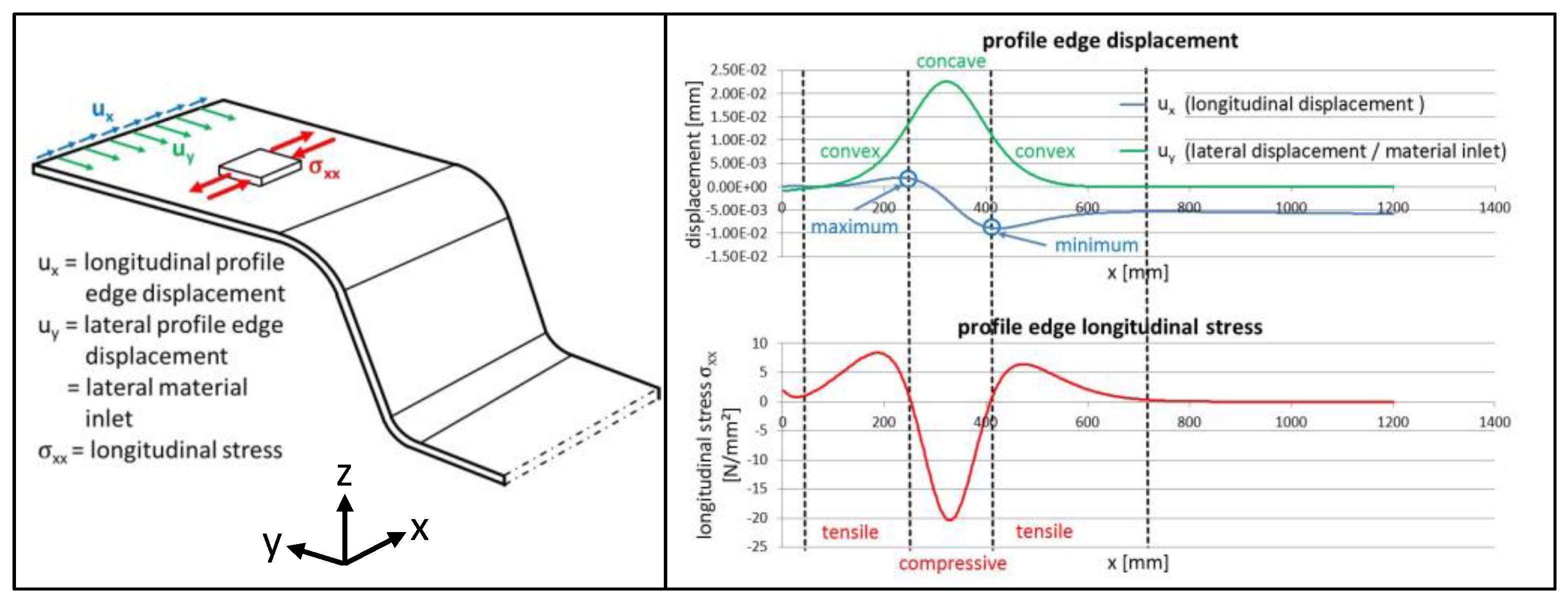
2.2. FE Model for Flexible Roller Beading
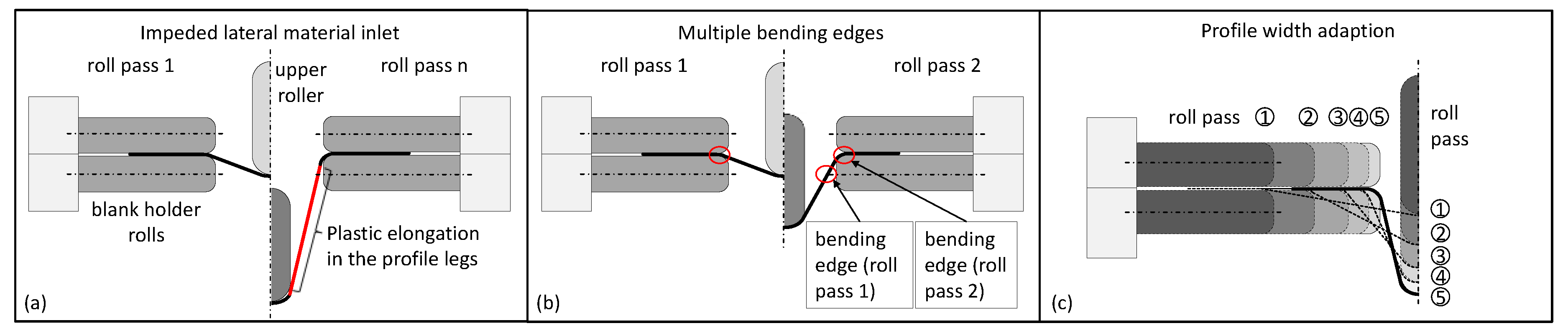
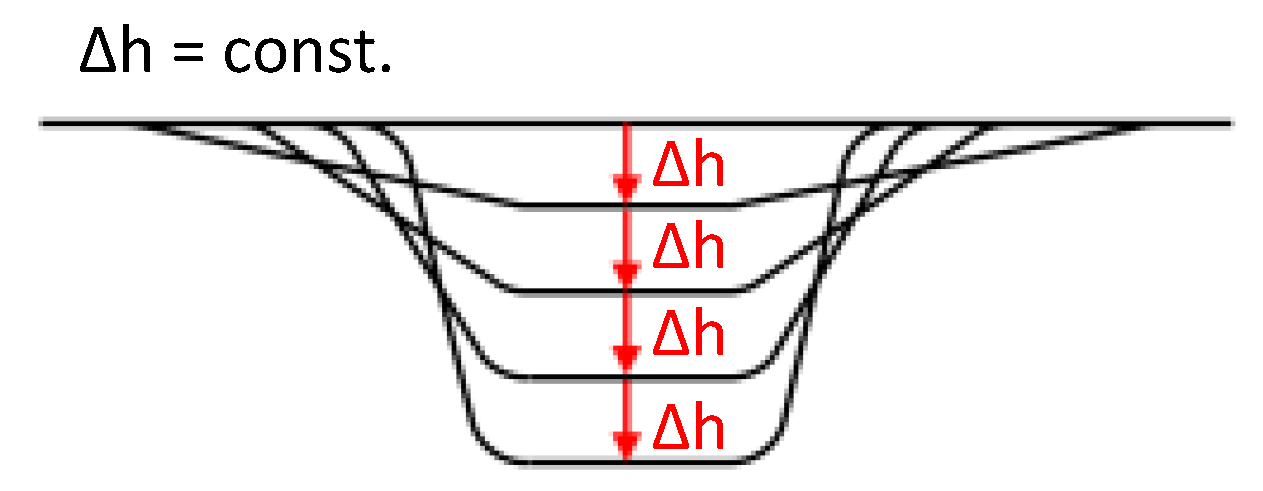
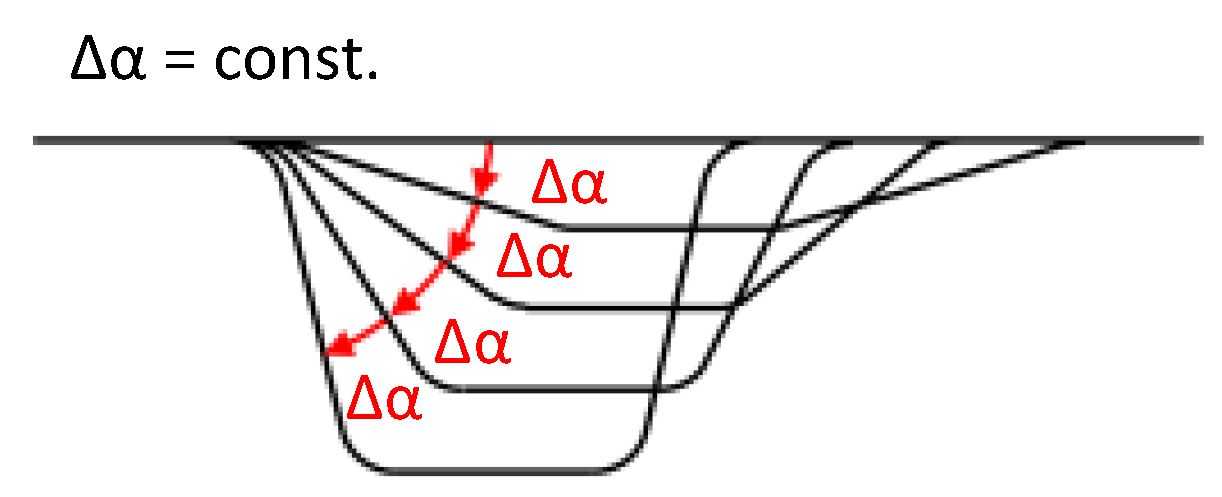
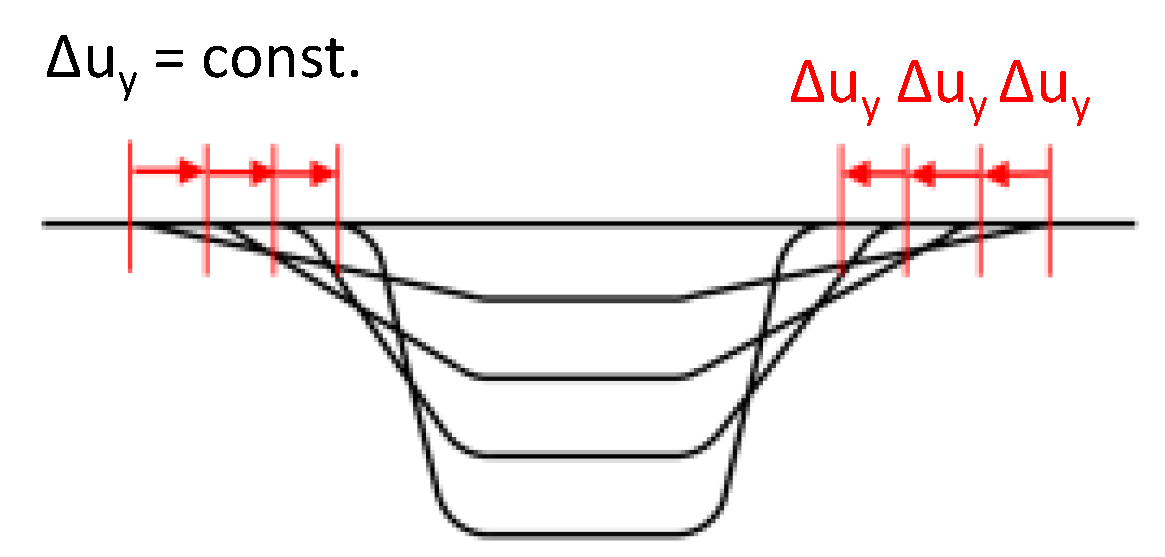
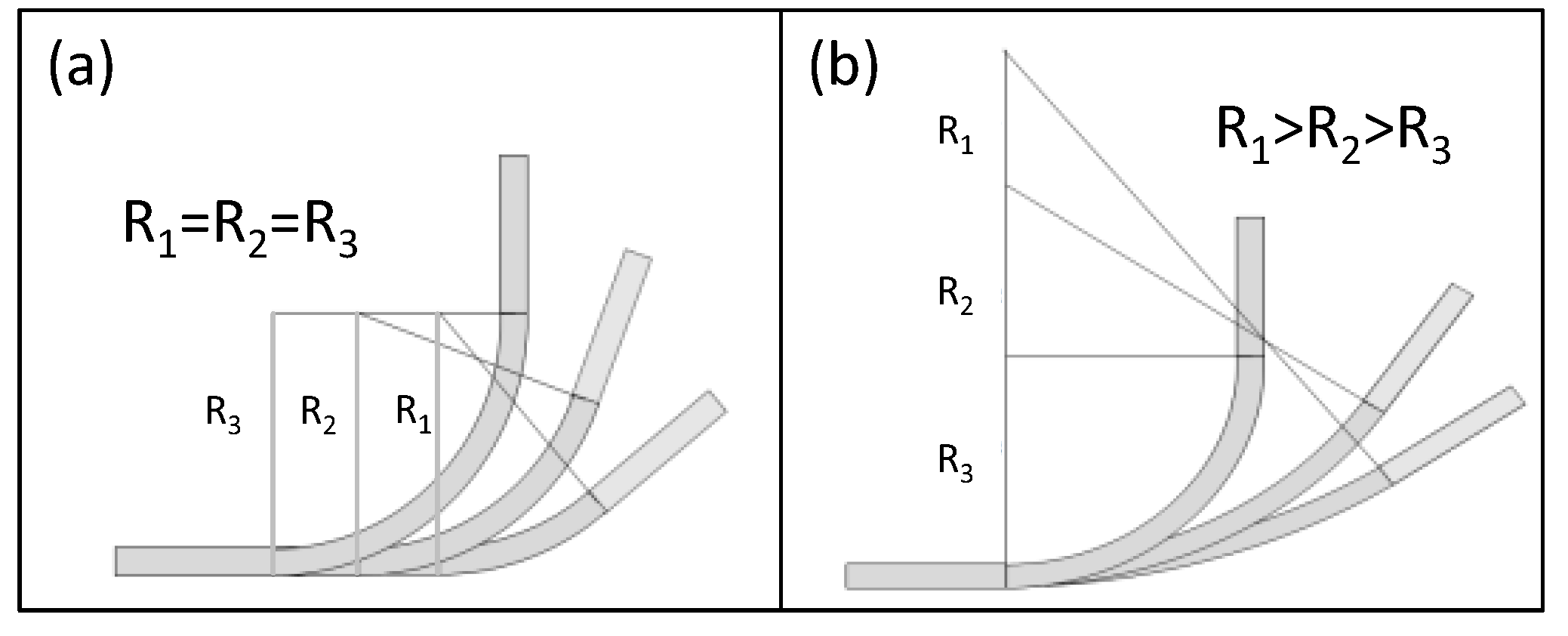
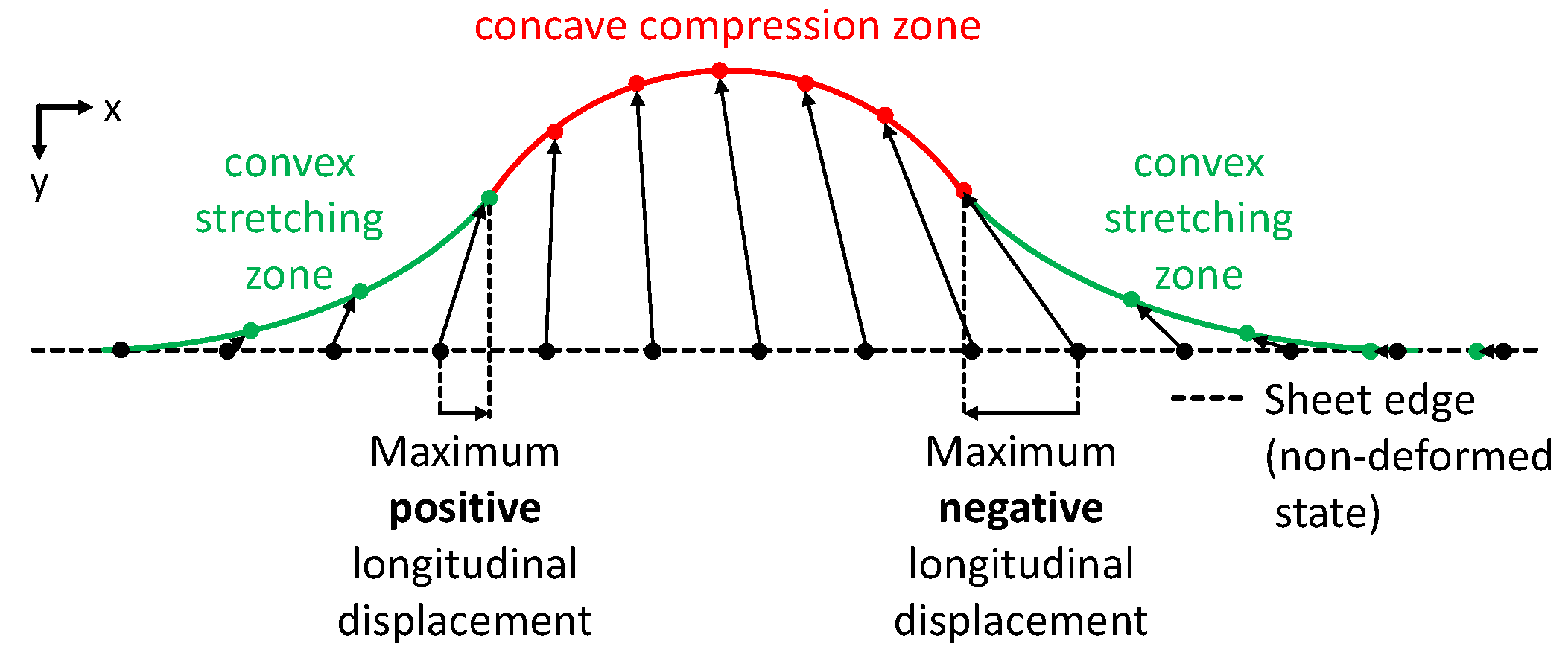
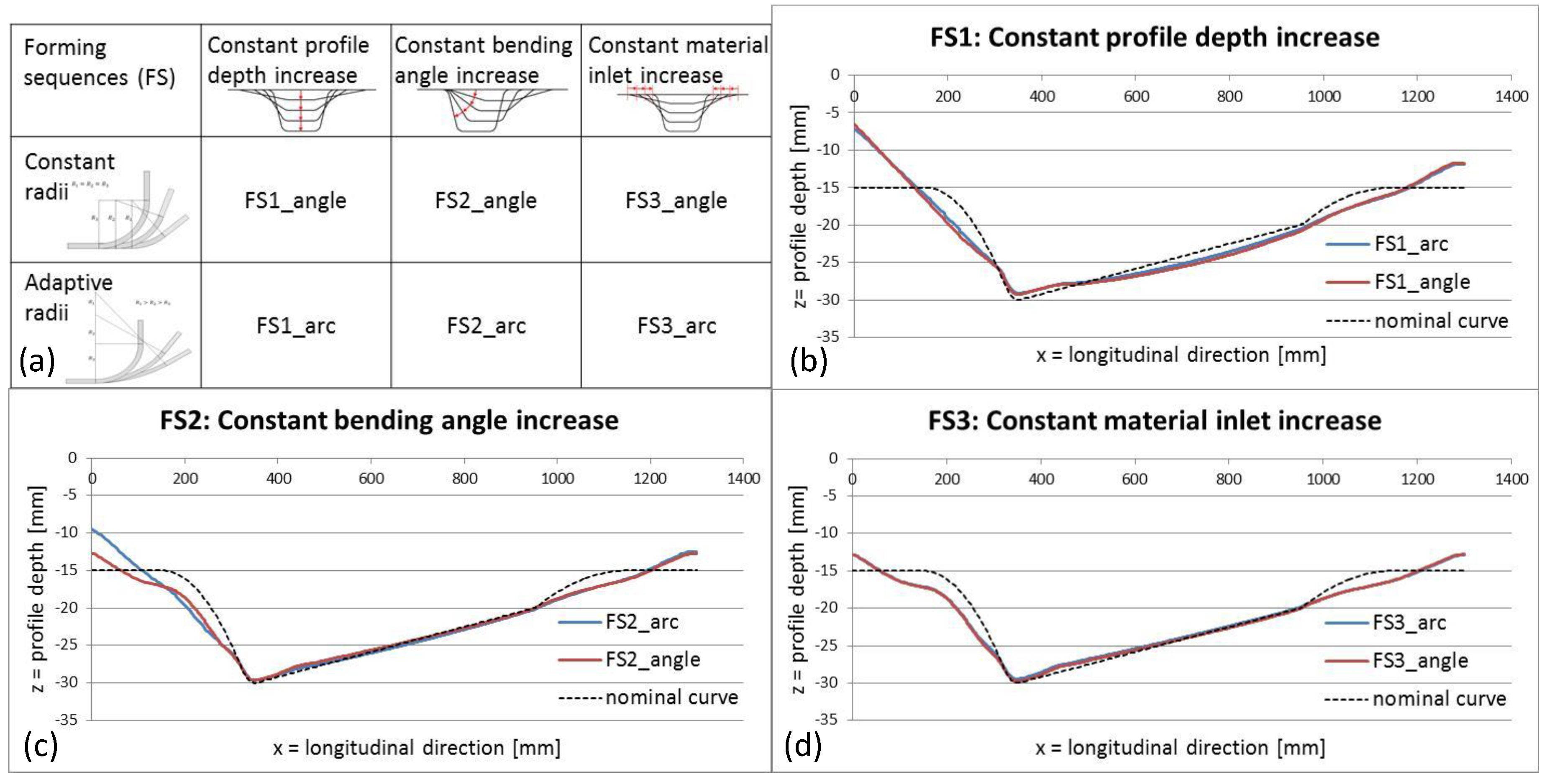
2.3. Principles of Forming Sequence Design
3. Results and Discussion
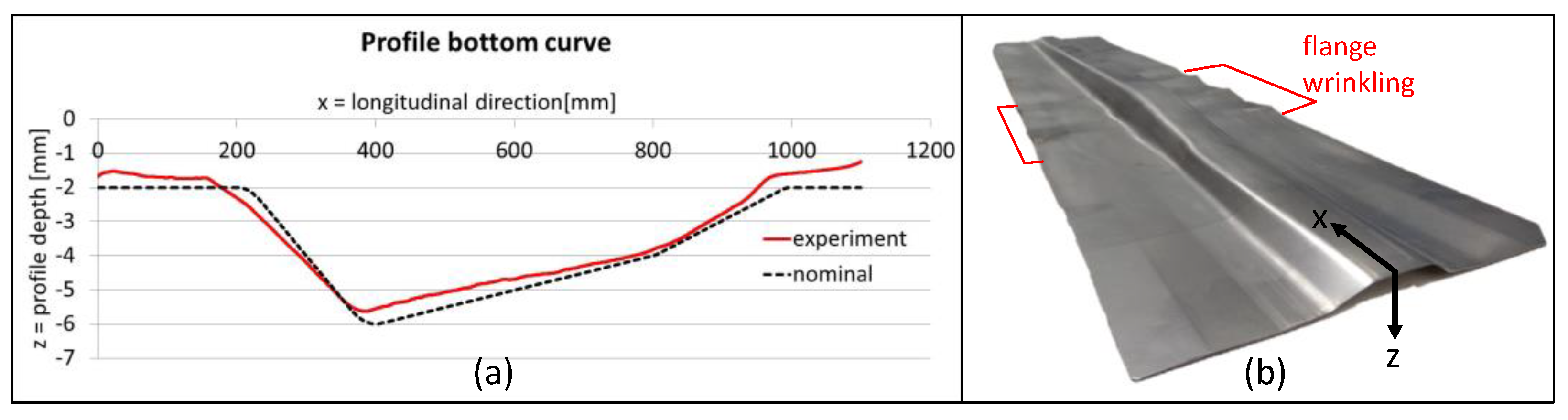
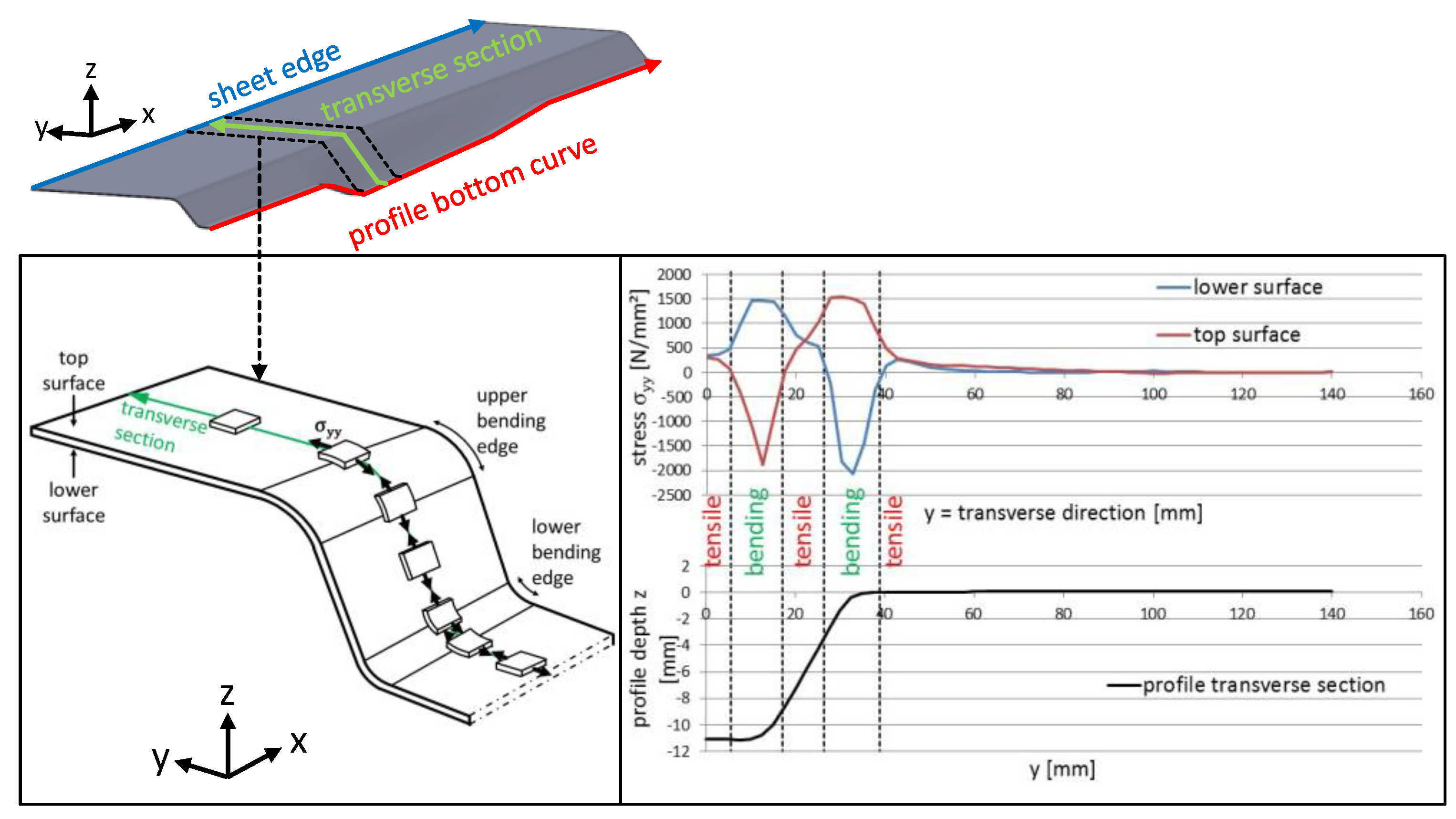
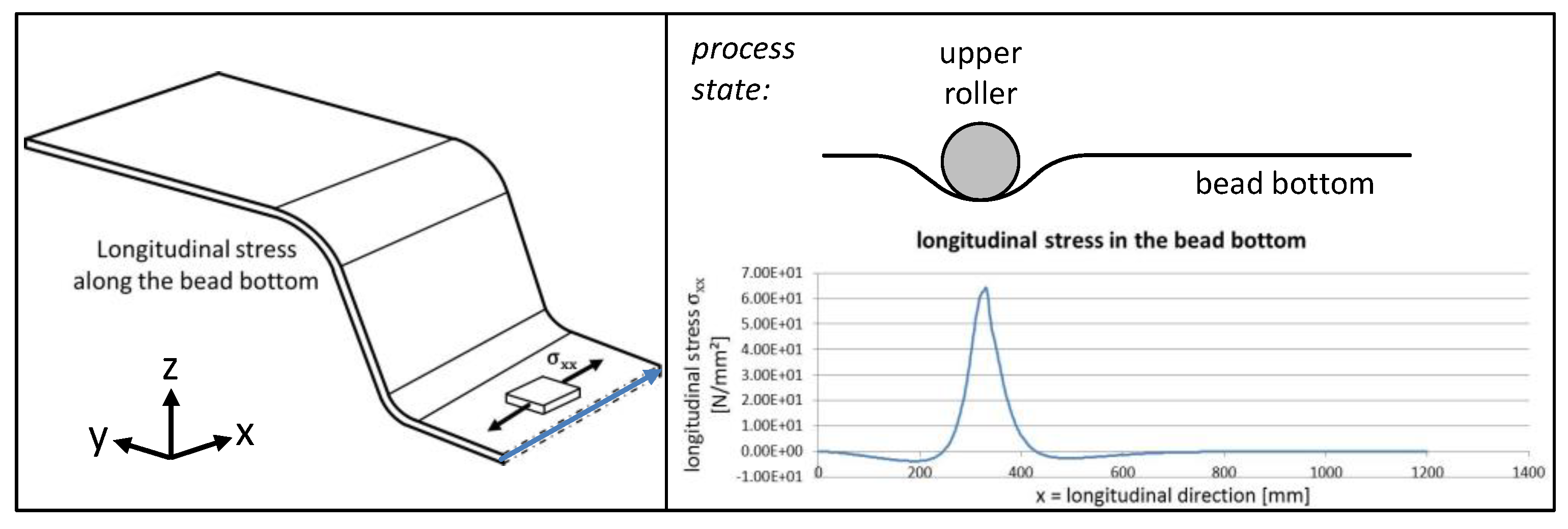
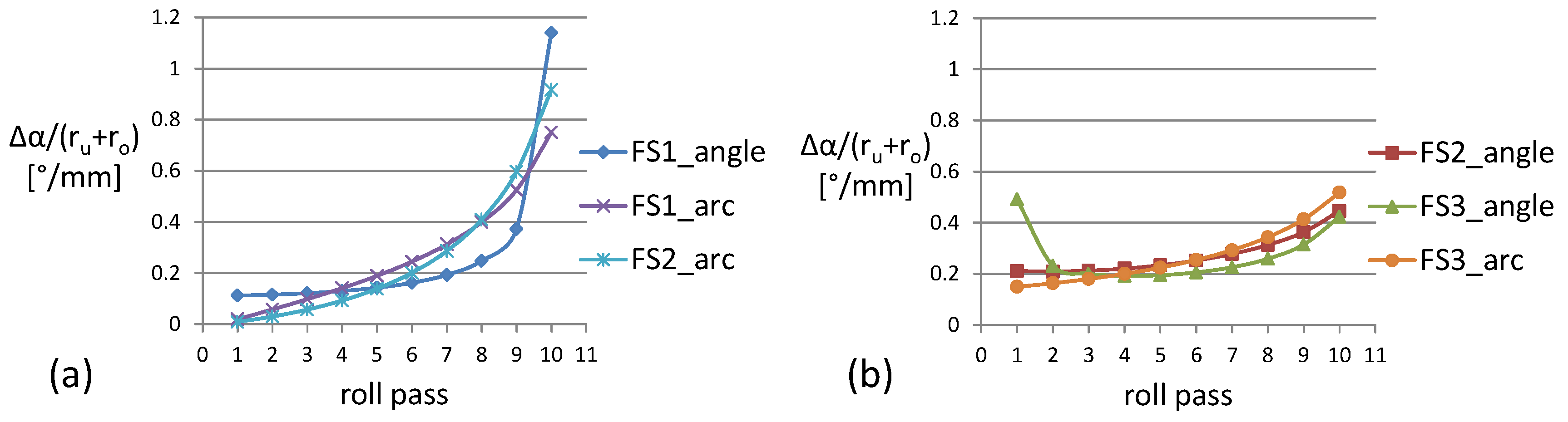
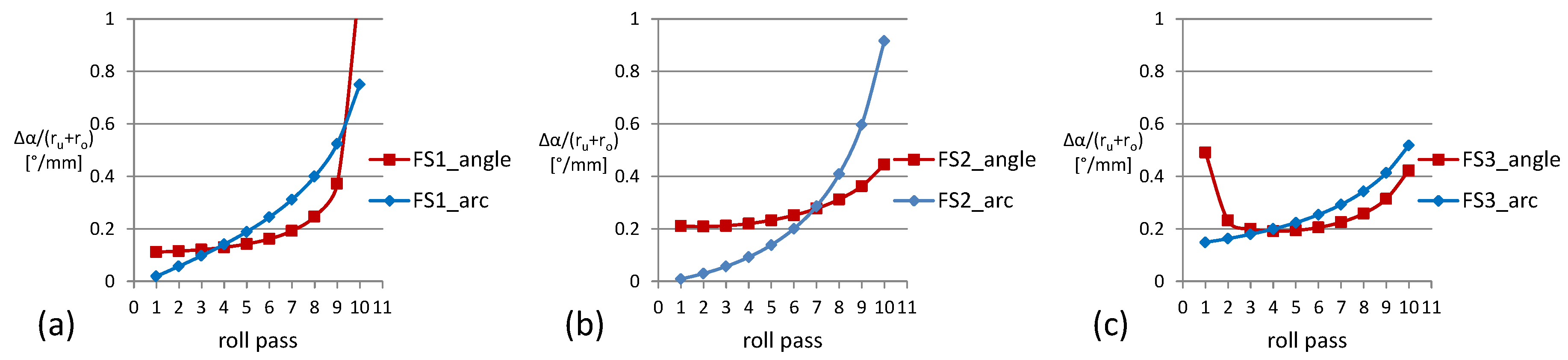
3.1. Process- and Tool-Side Variations: Effects of the Forming Sequence
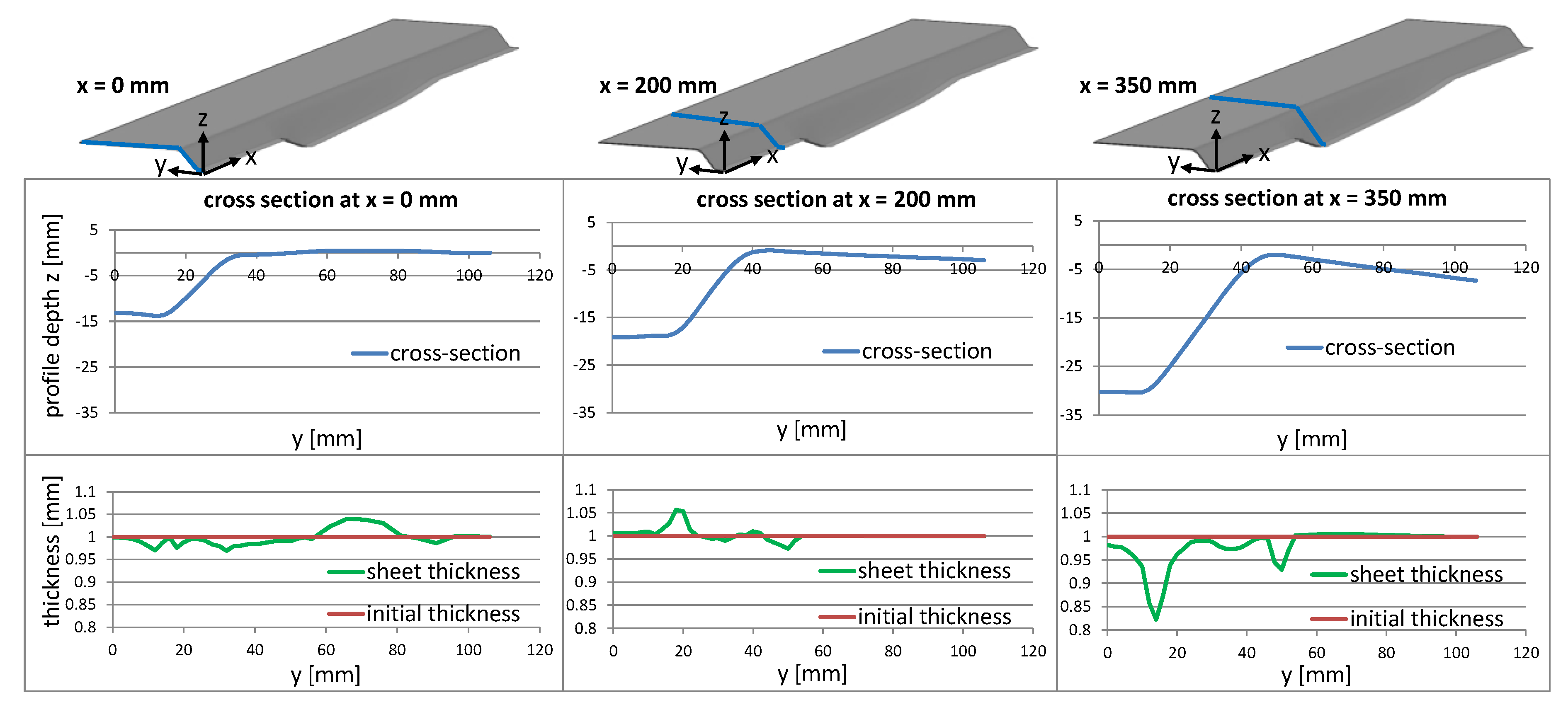
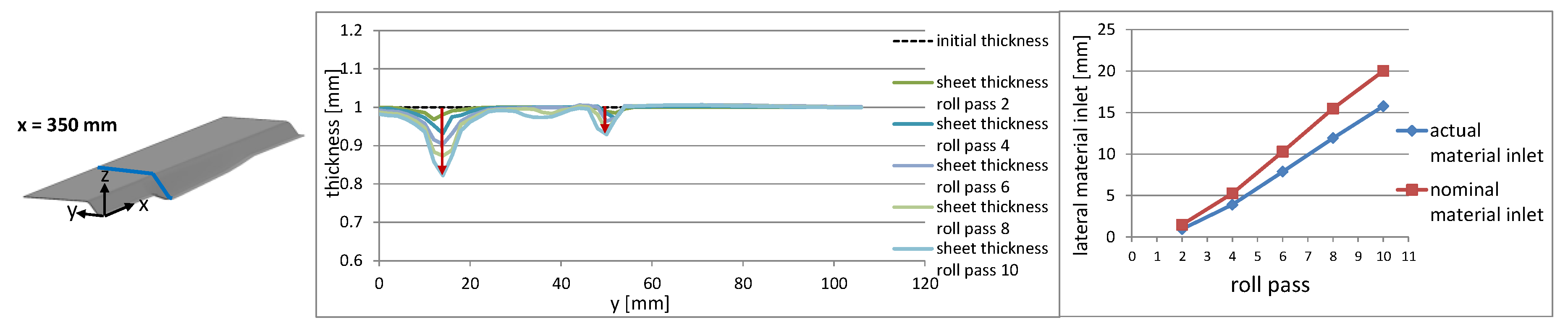
3.2. Effect on the Sheet Thickness
3.3. Workpiece-Side Variations
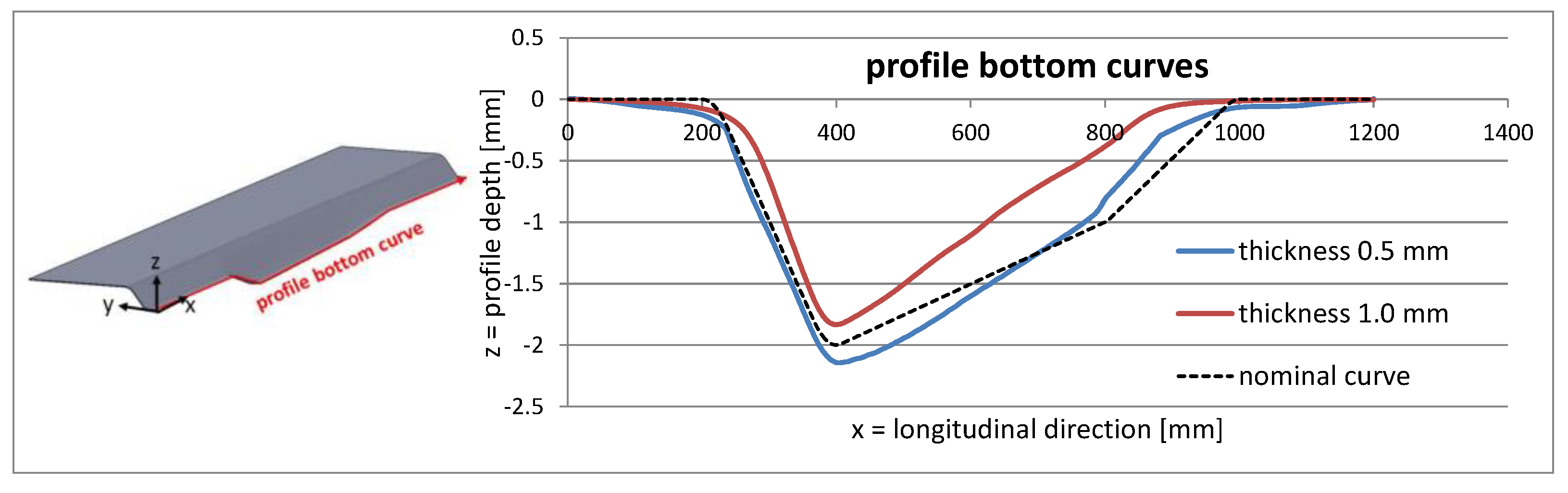
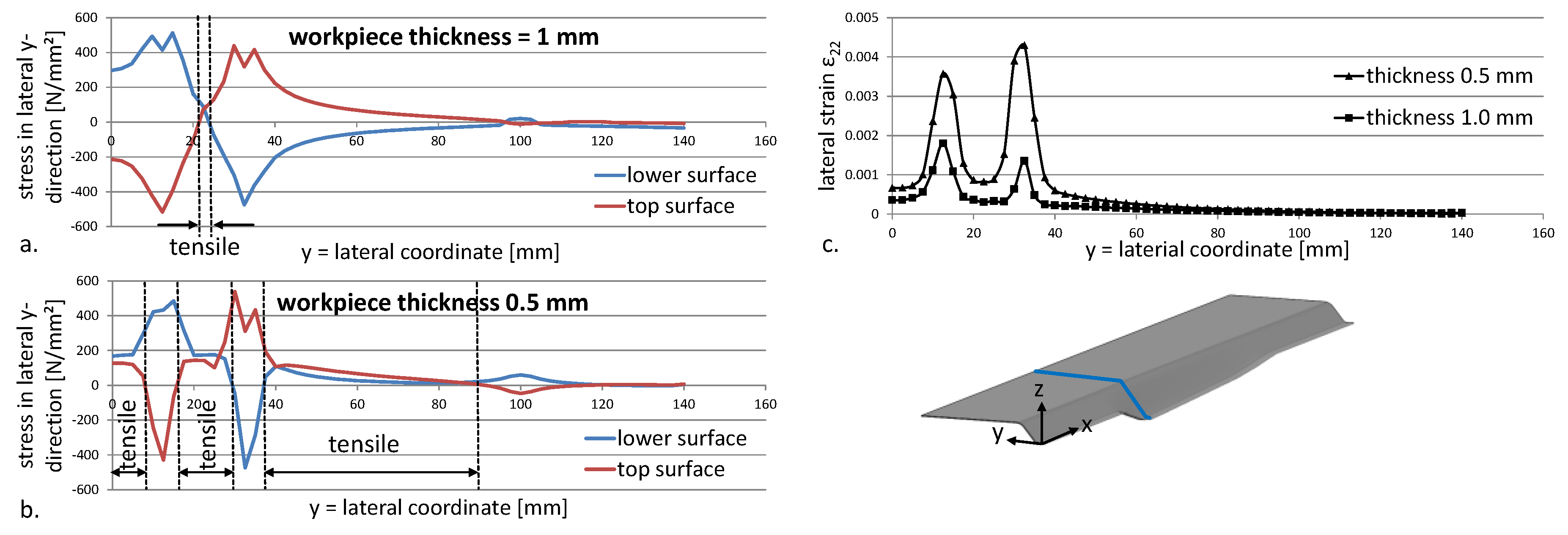
3.3.1. Geometric Properties: Workpiece Thickness
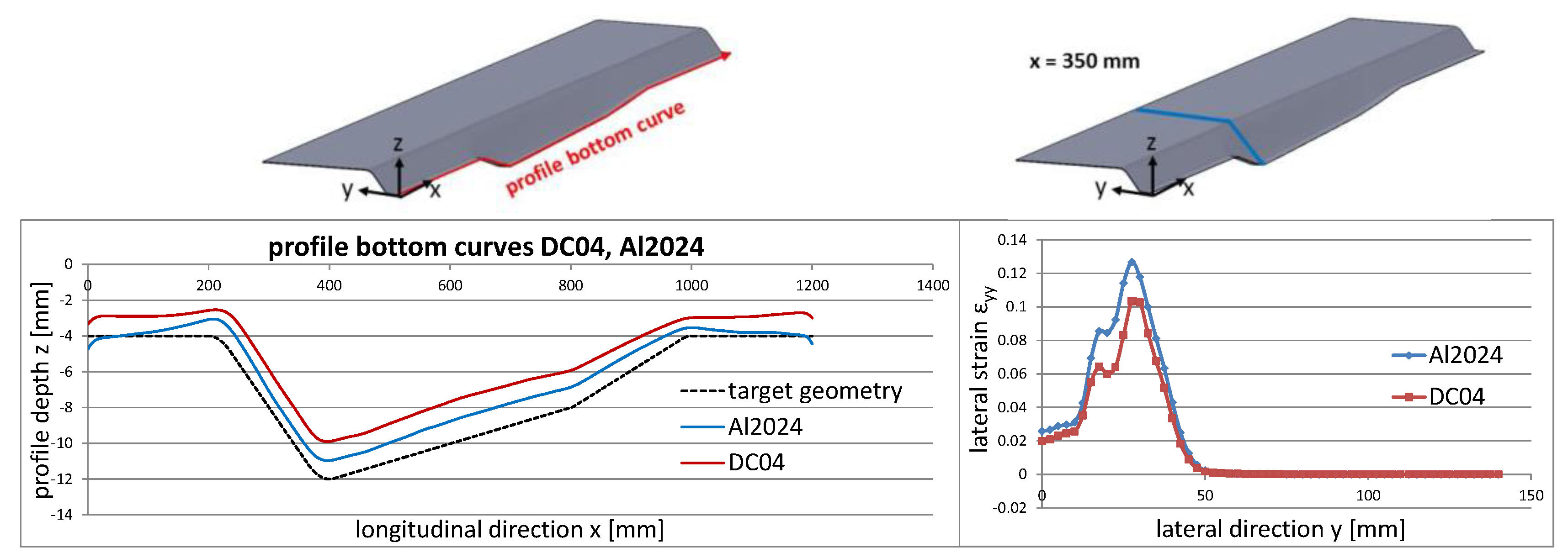
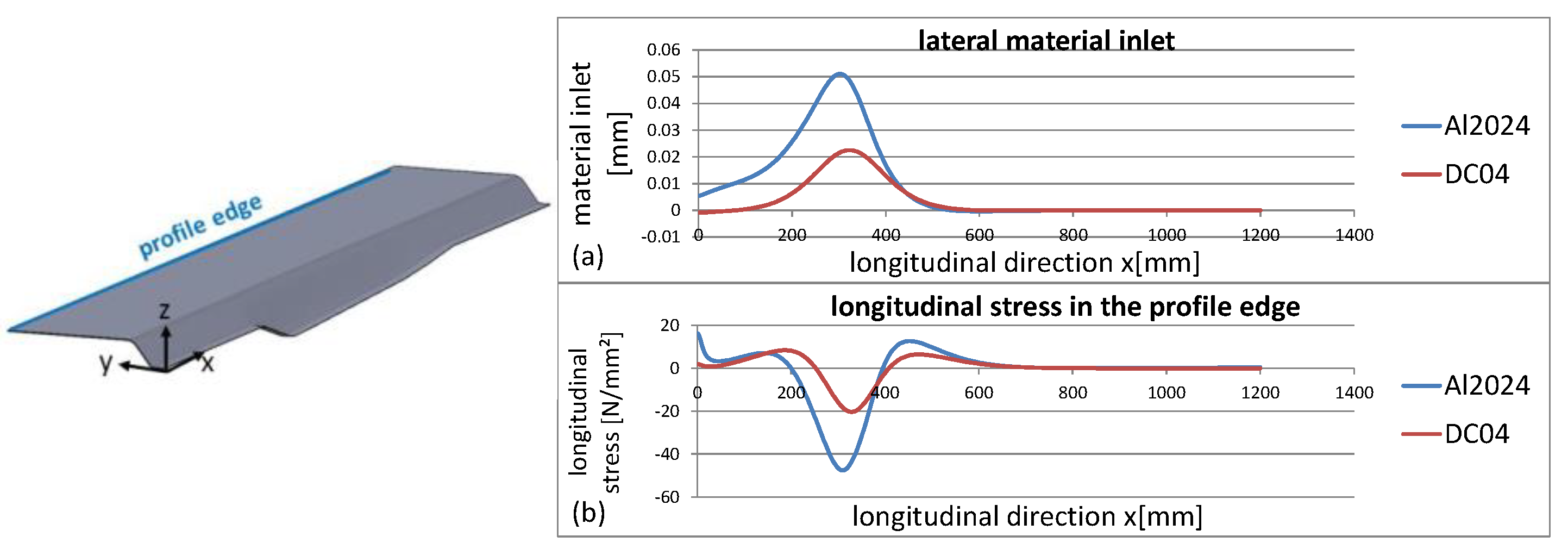
3.3.2. Material Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schwab, K. The Fourth Industrial Revolution; Crown Business: New York, NY, USA, 2017. [Google Scholar]
- Yang, D.Y.; Bambach, M.; Cao, J.; Duflou, J.R.; Groche, P.; Kuboki, T.; Sterzing, A.; Tekkaya, A.E.; Lee, C.W. Flexibility in metal forming. In CIRP Annals—Manufacturing Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2018; pp. 743–762. [Google Scholar]
- Mehrabi, M.G.; Ulsoy, A.G.; Koren, Y.; Heytler, P. Trends and perspectives in flexible and reconfigurable manufacturing systems. J. Intell. Manuf. 2002, 13, 135–146. [Google Scholar] [CrossRef]
- Allwood, J.M. Steel and Aluminium in a Low Carbon Future. In Proceedings of the 10th International Conference on Technology of Plasticity, ICTP 2011, Aachen, Germany, 25–30 September 2011; pp. 27–42. [Google Scholar]
- Broer, G.; Martin-Bullmann, R. Kaltprofile; Verlag Stahleisen mbH: Düsseldorf, Germany, 1993. [Google Scholar]
- Groche, P.; Von Breitenbach, G.; Jockel, M.; Zettler, A. New Tooling Concepts for Future Roll Forming Applications. In Proceedings of the ICIT, 4th International Conference on Industrial Tools, Celje, Slovenia, 10–12 December 2003; pp. 121–126. [Google Scholar]
- Ona, H.; Sho, R.; Nagamachi, T.; Hoshi, K. Development of Flexible Cold Roll Forming Machine Controlled by PLC. In Steel Research International; WILEY-VCH: Weinheim, Germany, 2010; pp. 182–185. [Google Scholar]
- Lindgren, M.; Ingmarsson, L.-O. 3D roll forming of hat-profile with variable depth and width. In Proceedings of the 1st International Congress on RollForming, Bilbao, Spain, 14–15 October 2009; pp. 1–8. [Google Scholar]
- Sedlmaier, A.; Dietl, T.; Harrasser, J. 3D Roll Forming in Automotive Industry. In Proceedings of the 5th International Conference on Steels in Cars and Trucks, Amsterdam, The Netherlands, 18–22 June 2017. [Google Scholar]
- Groche, P.; Storbeck, M.; Wang, T. Continuous forming of height-variable beads by flexible roller beading. J. Adv. Manuf. Technol. 2019. under review. [Google Scholar]
- Berner, S.; Storbeck, M.; Groche, P. A Study on Flexible Roll Formed Products Accuracy by Means of FEA and Experimental Tests. In Proceedings of the 14th International ESAFORM Conference on Material Forming, AIP Conference Proceedings, Belfast, Northern Ireland, 27–29 April 2011; pp. 345–350. [Google Scholar]
- Groche, P.; Zettler, A.; Berner, S.; Schneider, G. Development and verification of a one-step-model for the design of flexible roll formed parts. Int. J. Mater. Form. 2011, 4, 371–377. [Google Scholar] [CrossRef]
- Park, J.C.; Yang, D.Y.; Cha, M.H.; Kim, D.G.; Nam, J.B. Investigations of a new incremental counter forming in flexible roll forming to manufacture accurate profiles with variable cross-sections. Int. J. Mach. Tools Manuf. 2014, 86, 68–80. [Google Scholar] [CrossRef]
- Kiuchi, M.; Koudabashi, T. Automated design system of optimal roll profiles for cold roll forming. In Proceedings of the 3rd International Conference on Rotary Metalworking Processes, Kyoto, Japan, 8–10 September 1984; pp. 423–436. [Google Scholar]
- Rebelo, N.; Nagtegaal, J.C.; Taylor, L.M.; Passman, R. Comparison of implicit and explicit finite element methods in the simulation of metal forming processes. In Proceedings of the ABAQUS Users Conference, Newport, Rhode Island, 1 January 1992. [Google Scholar]
- Senanayake, R.S.; Cole, I.M.; Thiruvarudchelvan, S. The application of computational and experimental techniques to metal deformation in cold roll forming. J. Mater. Process. Technol. 1994, 45, 155–160. [Google Scholar] [CrossRef]
- Daniel, W.J.T.; Meehan, P.A. Implicit finite element study of non-steady effects in cold roll forming. In Proceedings of the 5th Australasian Congress on Applied Mechanics (ACAM 2007), Brisbane, Australia, 10–12 December 2007. [Google Scholar]
- Groche, P.; Mueller, C.; Traub, T. Experimental and Numerical Determination of Roll Forming Loads; Wiley: Weinheim, Germany, 2013; pp. 112–122. [Google Scholar]
- MARC. User Information—Volume A, Element Library—Volume B; MARC Analysis Research Corporation: Palo Alto, CA, USA, 2014. [Google Scholar]
- Gehring, A. Beurteilung der Eignung von Metallischem Band und Blech zum Walzprofilieren. Ph.D. Thesis, Universitätsverlag Karlsruhe, Karlsruhe, Germany, 2006. [Google Scholar]
- Traub, T.; Miks, C.; Groche, P. Force Measurements Supporting the Set-up Process in Roll Forming. In Proceedings of the 1st Annual International Conference on Mechanical Engineering, ATINER’s Conference Paper Series, MEC2017-2346, Athens, Greece, 17–20 July 2017. [Google Scholar]
- Boman, R.; Papeleux, L.; Bui, Q.V.; Ponthot, J.P. Application of the Arbitrary Lagrangian Eulerian formulation to the numerical simulation of cold roll forming process. J. Mater. Process. Technol. 2006, 177, 621–625. [Google Scholar] [CrossRef]
- Görtan, M.O.; Vucic, D.; Groche, P.; Livatyali, H. Roll forming of branched profiles. J. Mater. Process. Technol. 2009, 209, 5837–5844. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Groche, P. Sheet Metal Profiles with Variable Height: Numerical Analyses on Flexible Roller Beading. J. Manuf. Mater. Process. 2019, 3, 19. https://doi.org/10.3390/jmmp3010019
Wang T, Groche P. Sheet Metal Profiles with Variable Height: Numerical Analyses on Flexible Roller Beading. Journal of Manufacturing and Materials Processing. 2019; 3(1):19. https://doi.org/10.3390/jmmp3010019
Chicago/Turabian StyleWang, Tianbo, and Peter Groche. 2019. "Sheet Metal Profiles with Variable Height: Numerical Analyses on Flexible Roller Beading" Journal of Manufacturing and Materials Processing 3, no. 1: 19. https://doi.org/10.3390/jmmp3010019
APA StyleWang, T., & Groche, P. (2019). Sheet Metal Profiles with Variable Height: Numerical Analyses on Flexible Roller Beading. Journal of Manufacturing and Materials Processing, 3(1), 19. https://doi.org/10.3390/jmmp3010019



