Machining Forces Due to Turning of Bimetallic Objects Made of Aluminum, Titanium, Cast Iron, and Mild/Stainless Steel
Abstract
1. Introduction
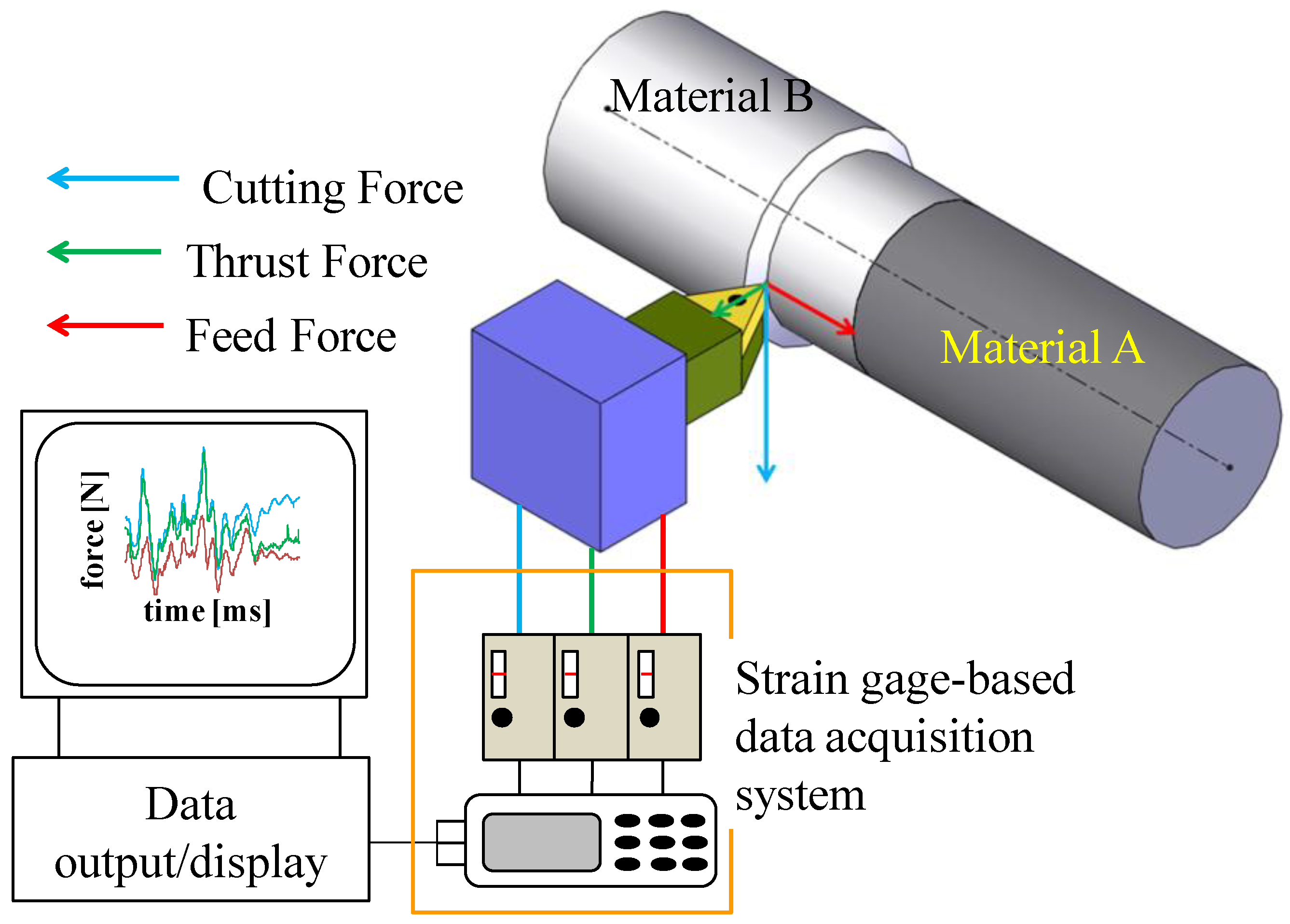
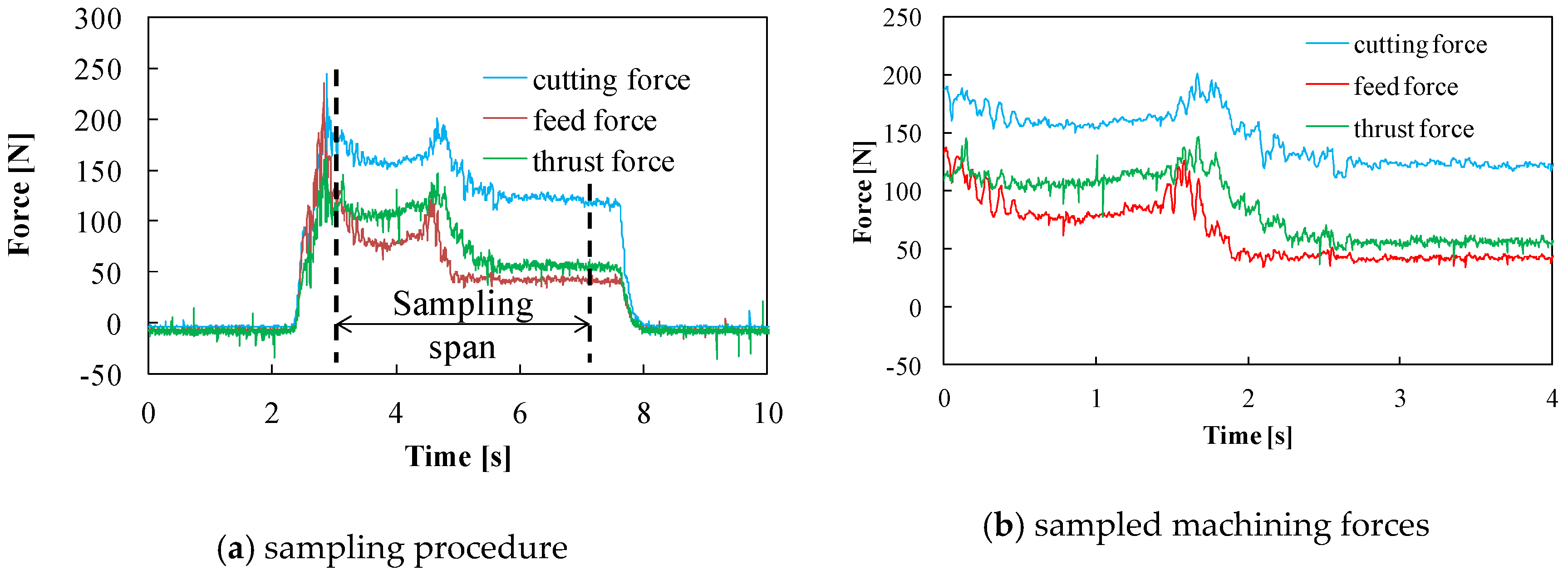
2. Machining Experiments and Data Acquisition
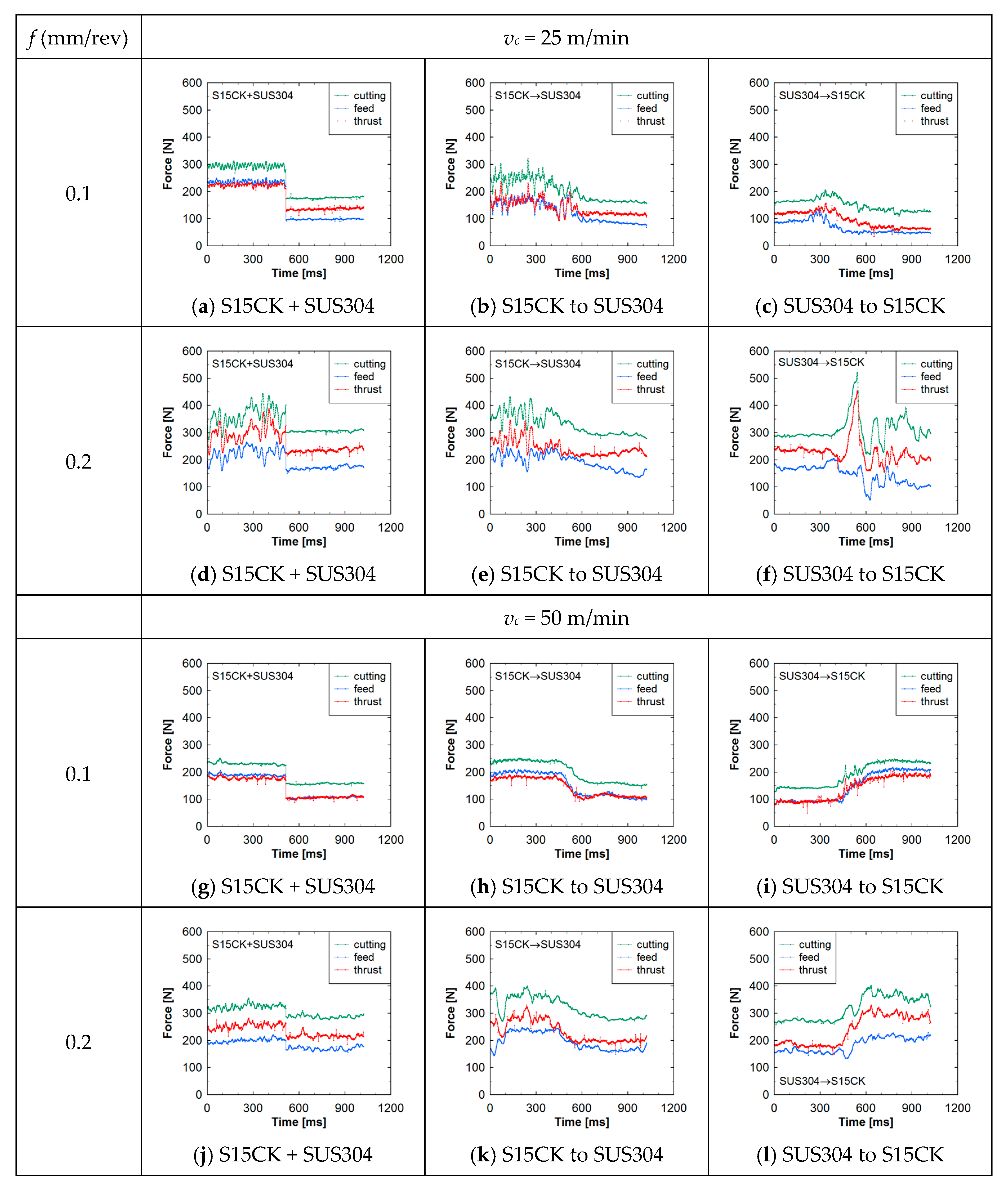
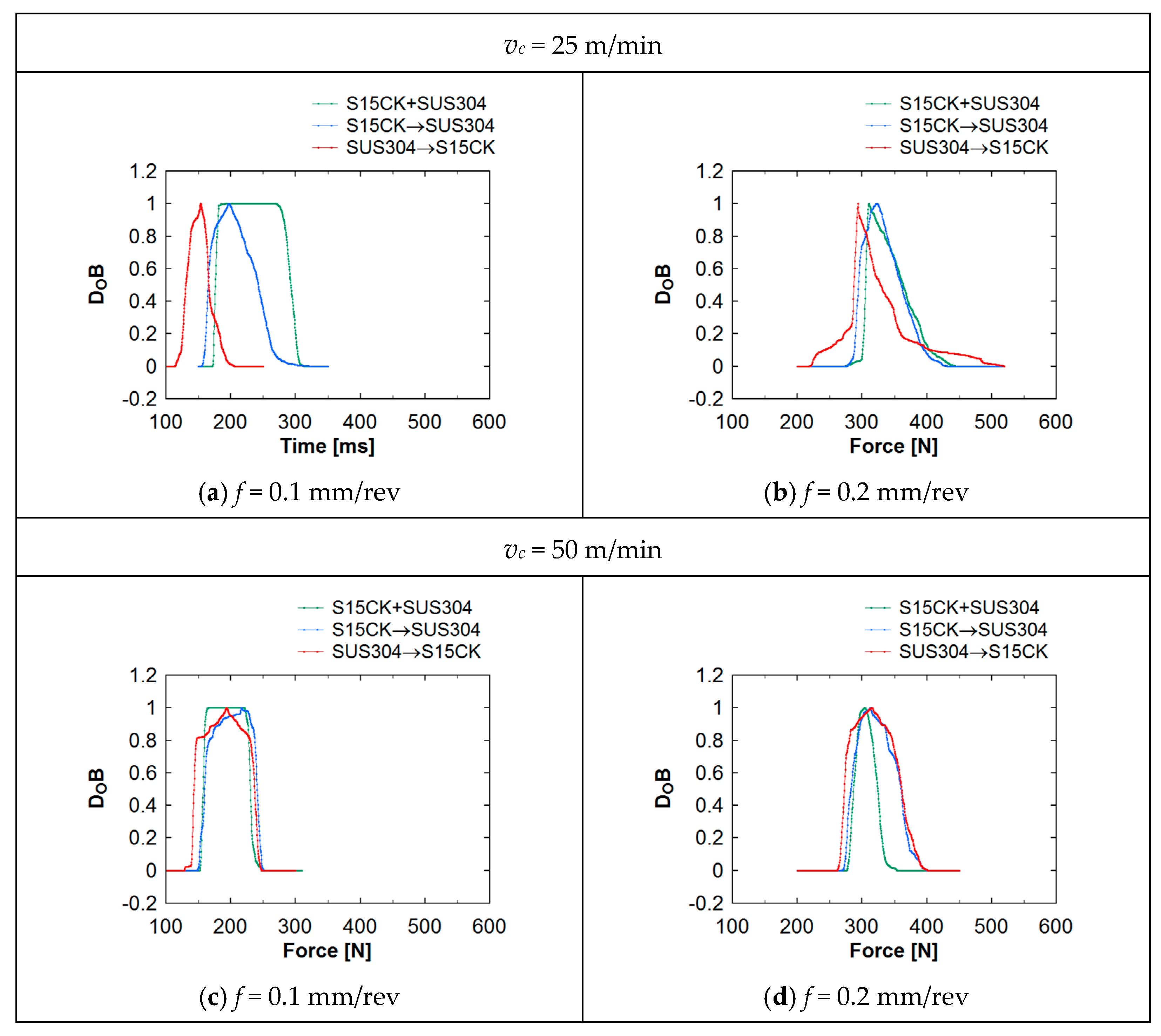
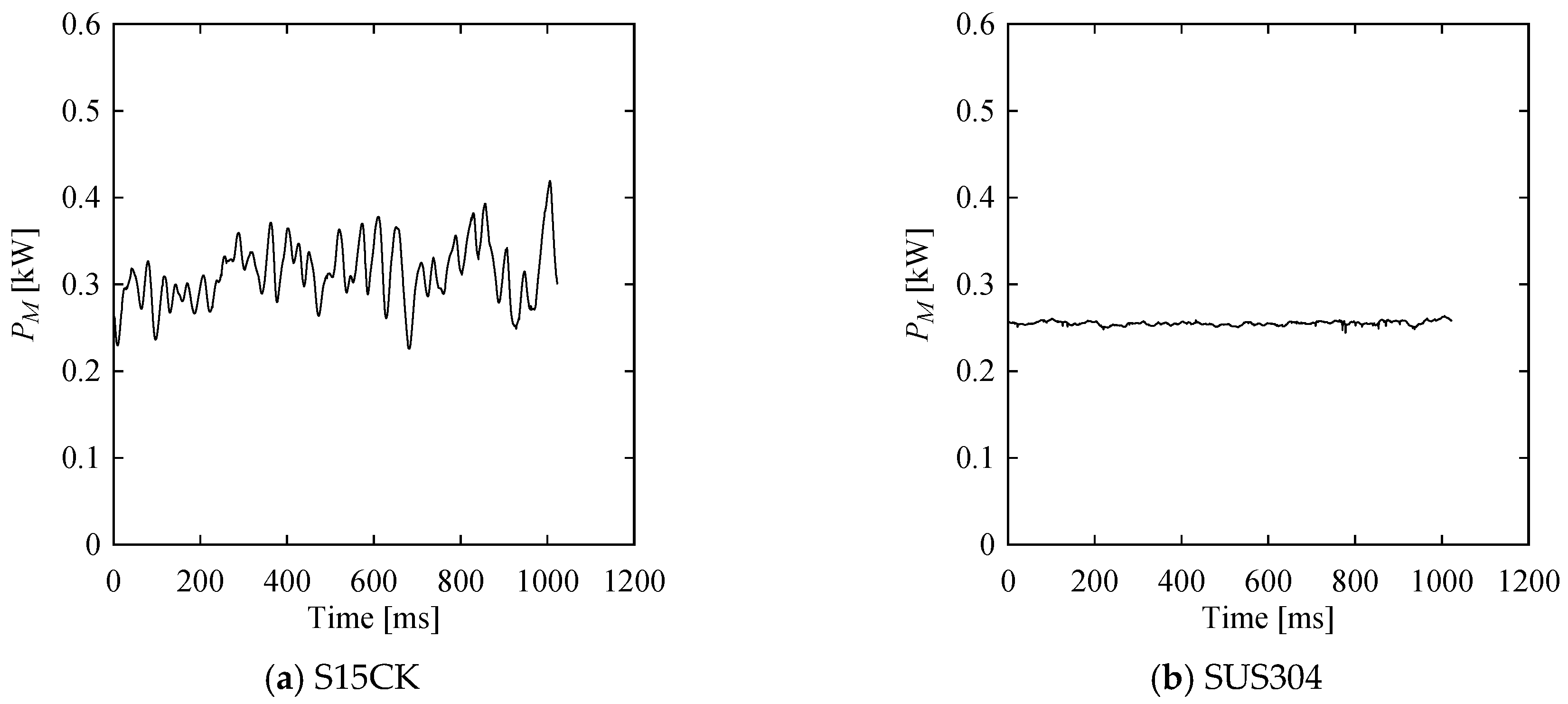
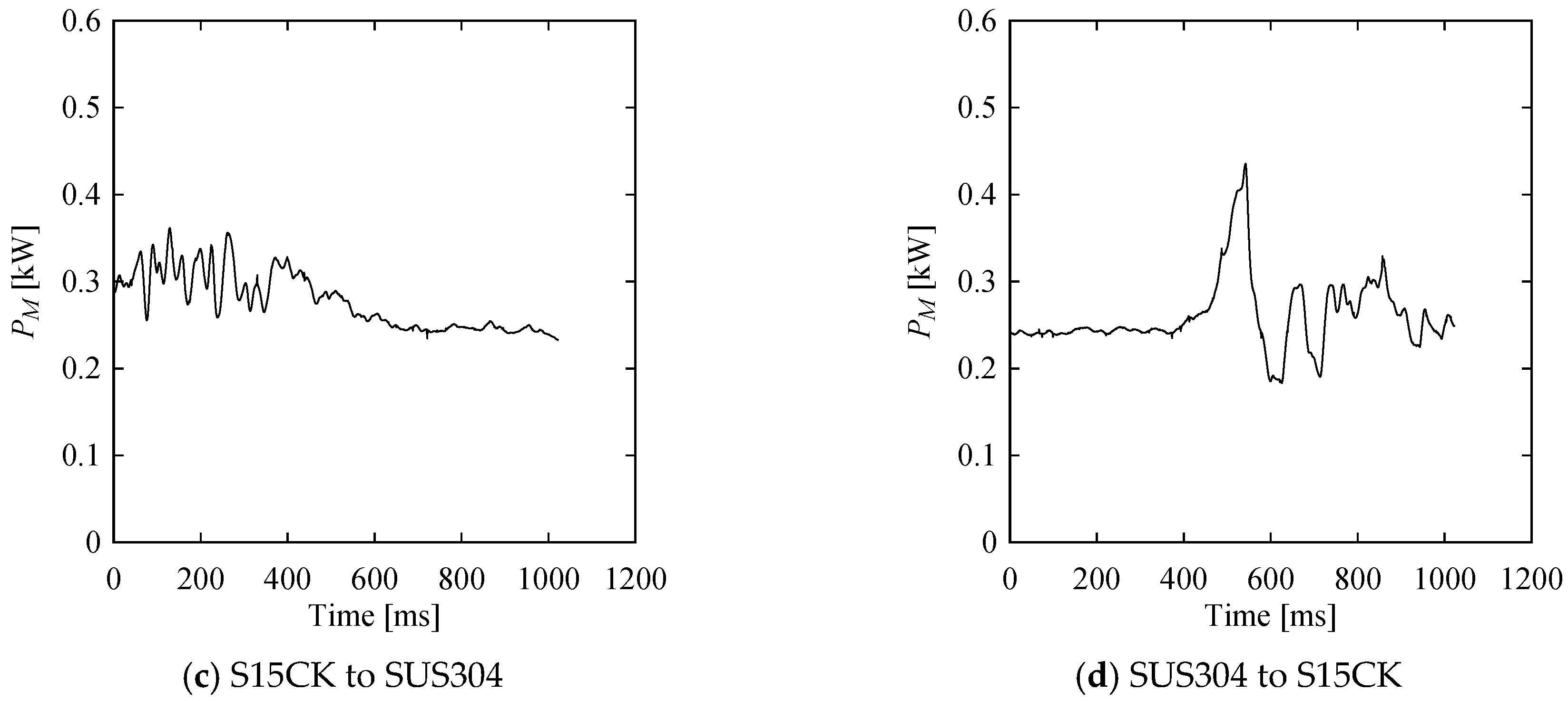
3. Analyzing Machining Forces Underlying SU–SC
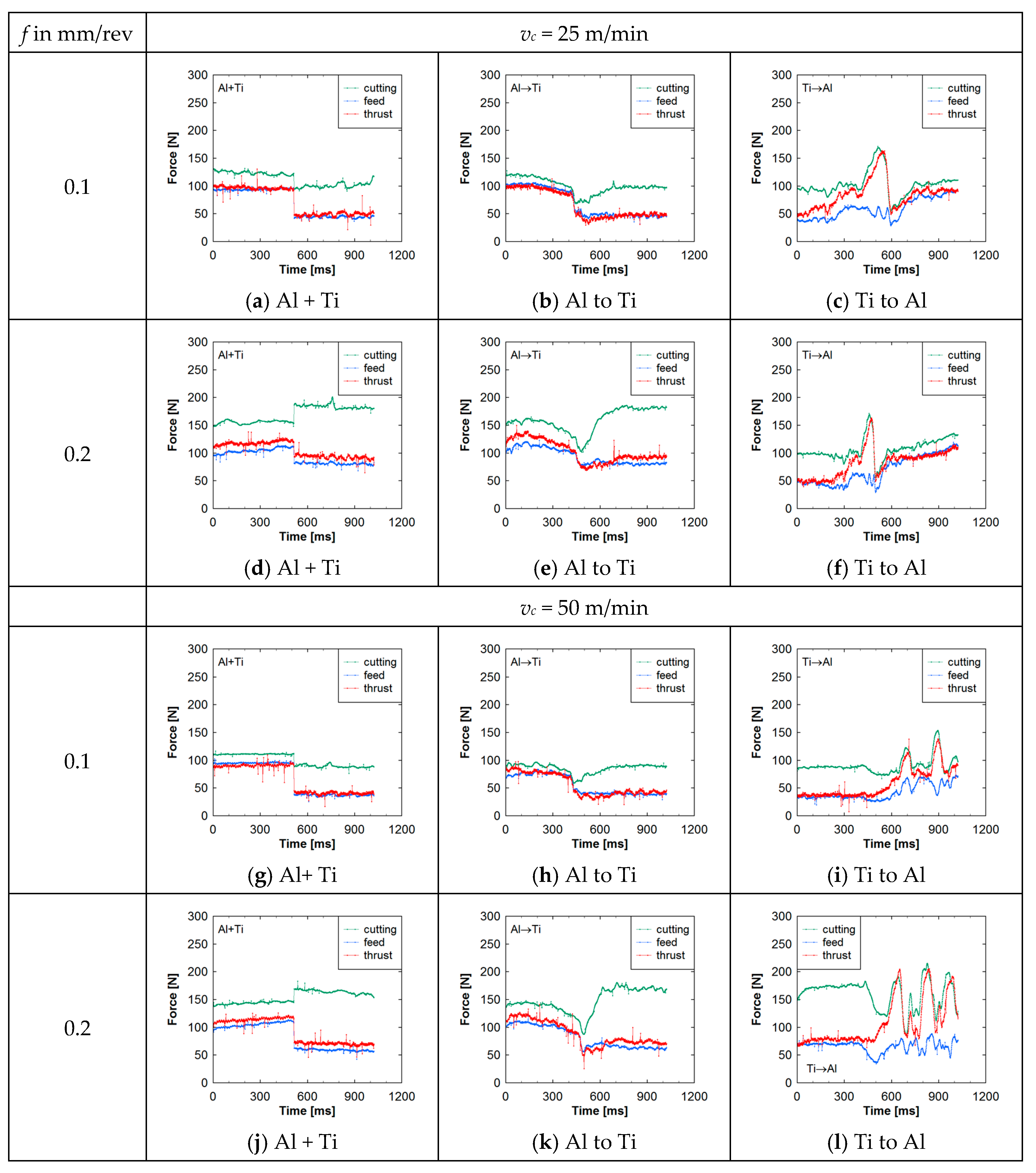
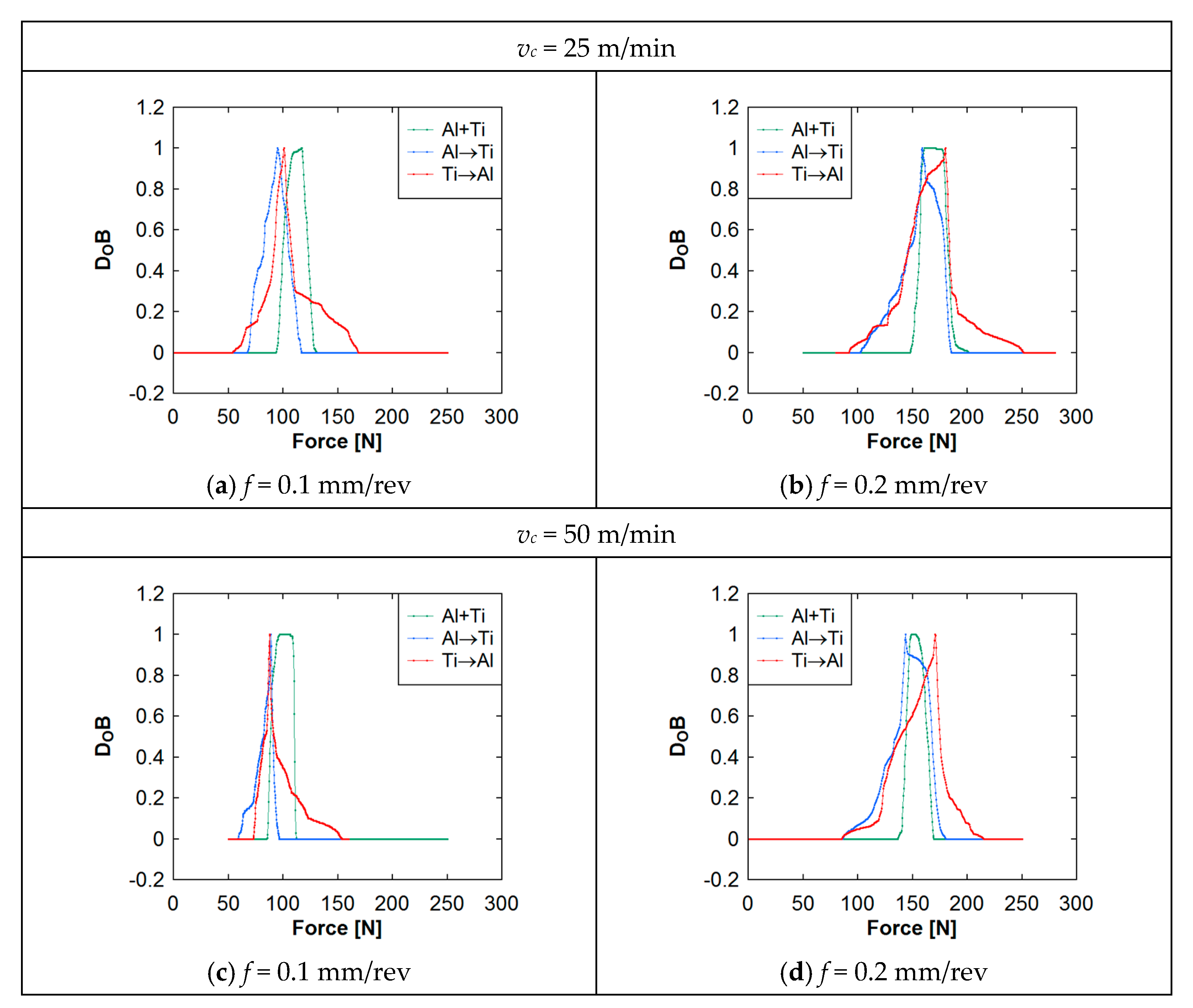
4. Analyzing Machining Forces Underlying Al–Ti
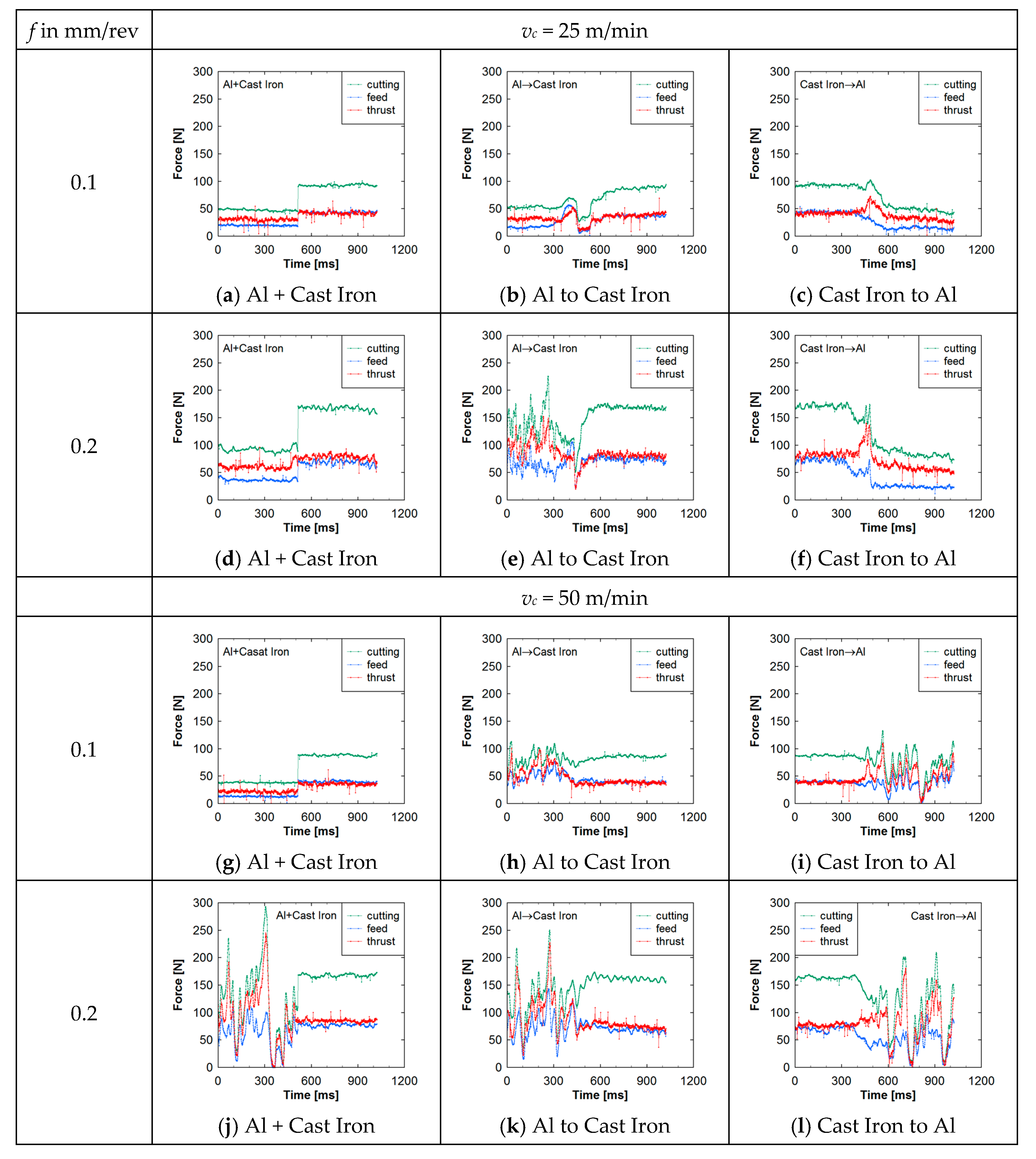
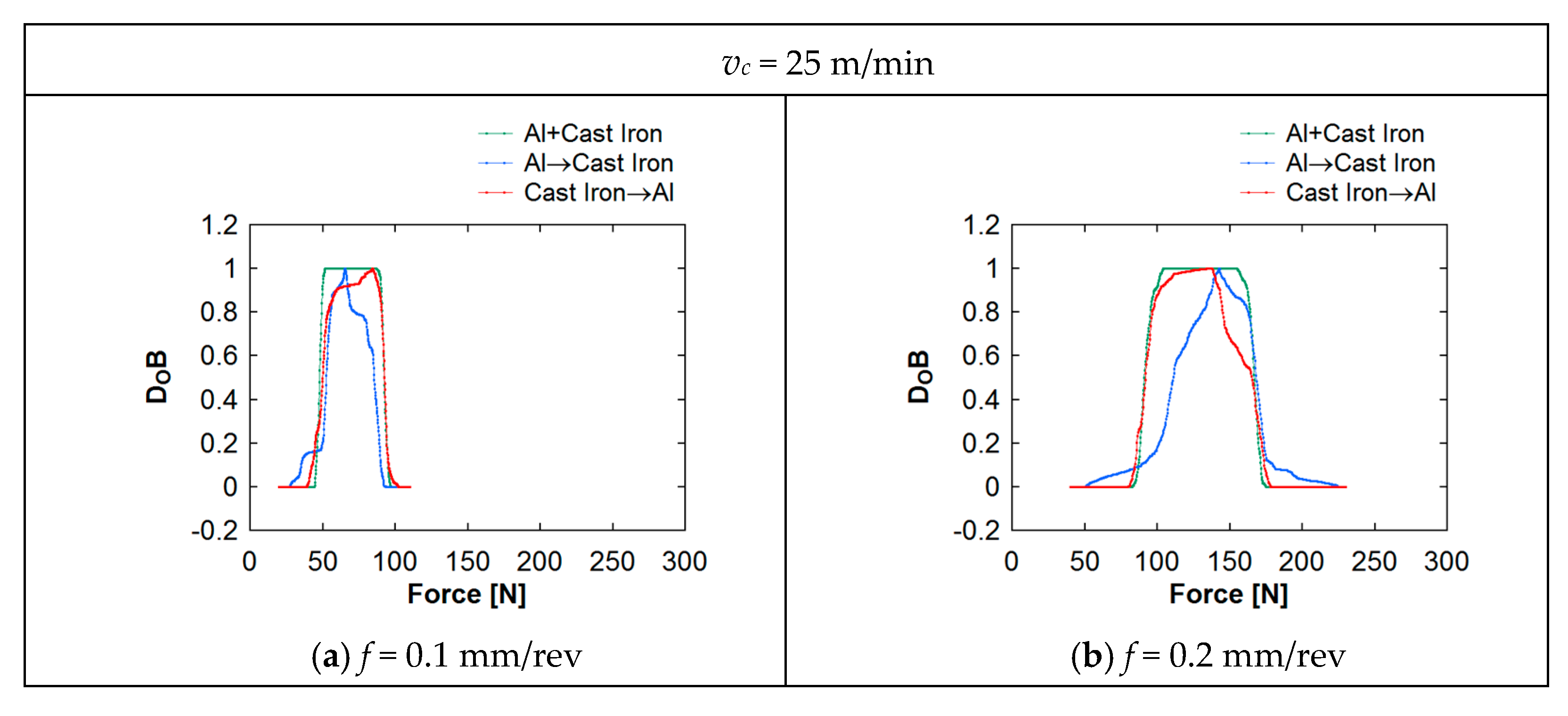
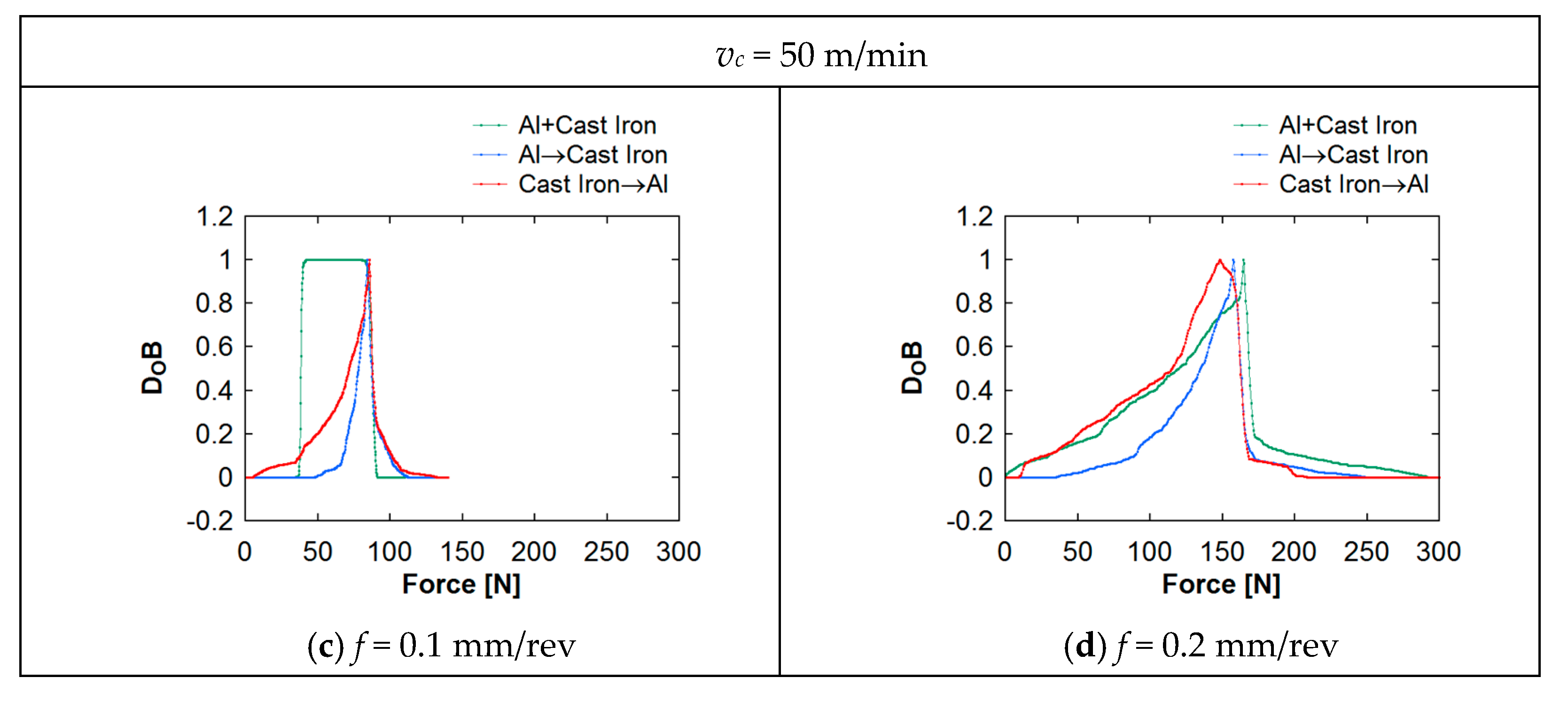
5. Analyzing Machining Forces Underlying Al–CI
6. Discussions
7. Concluding Remarks
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Pictures of the Bimetallic Specimens Taken after Machining



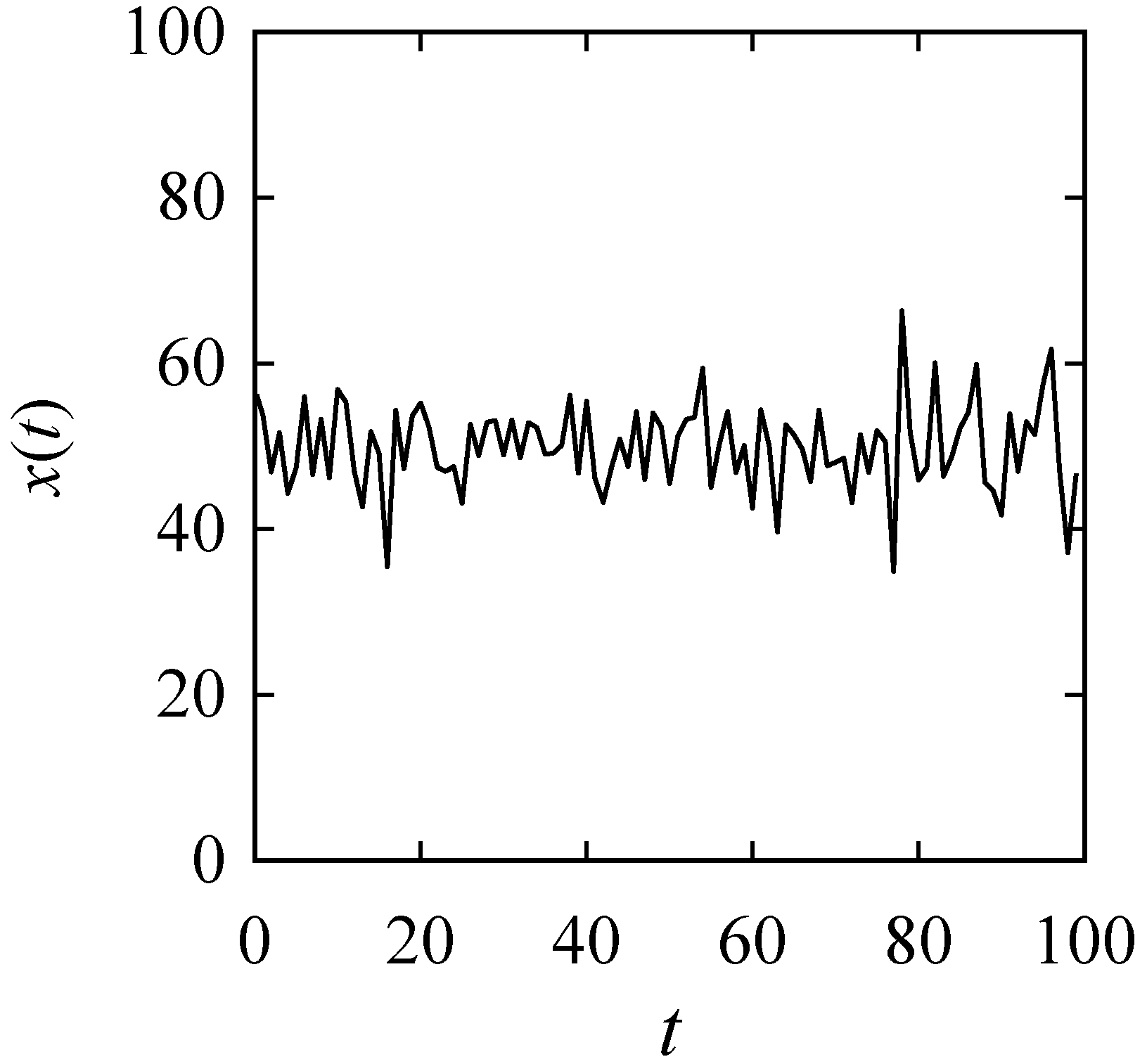
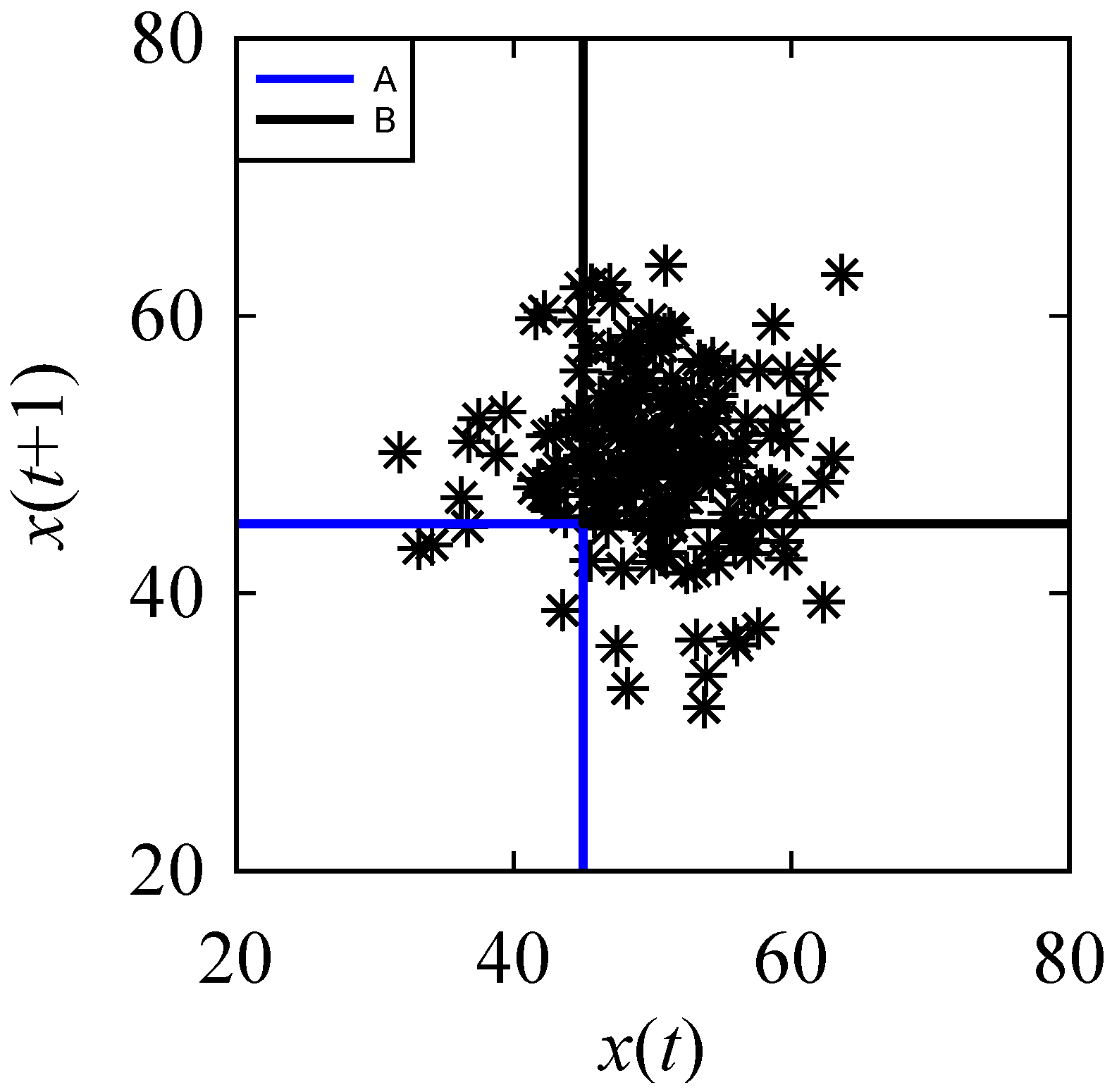
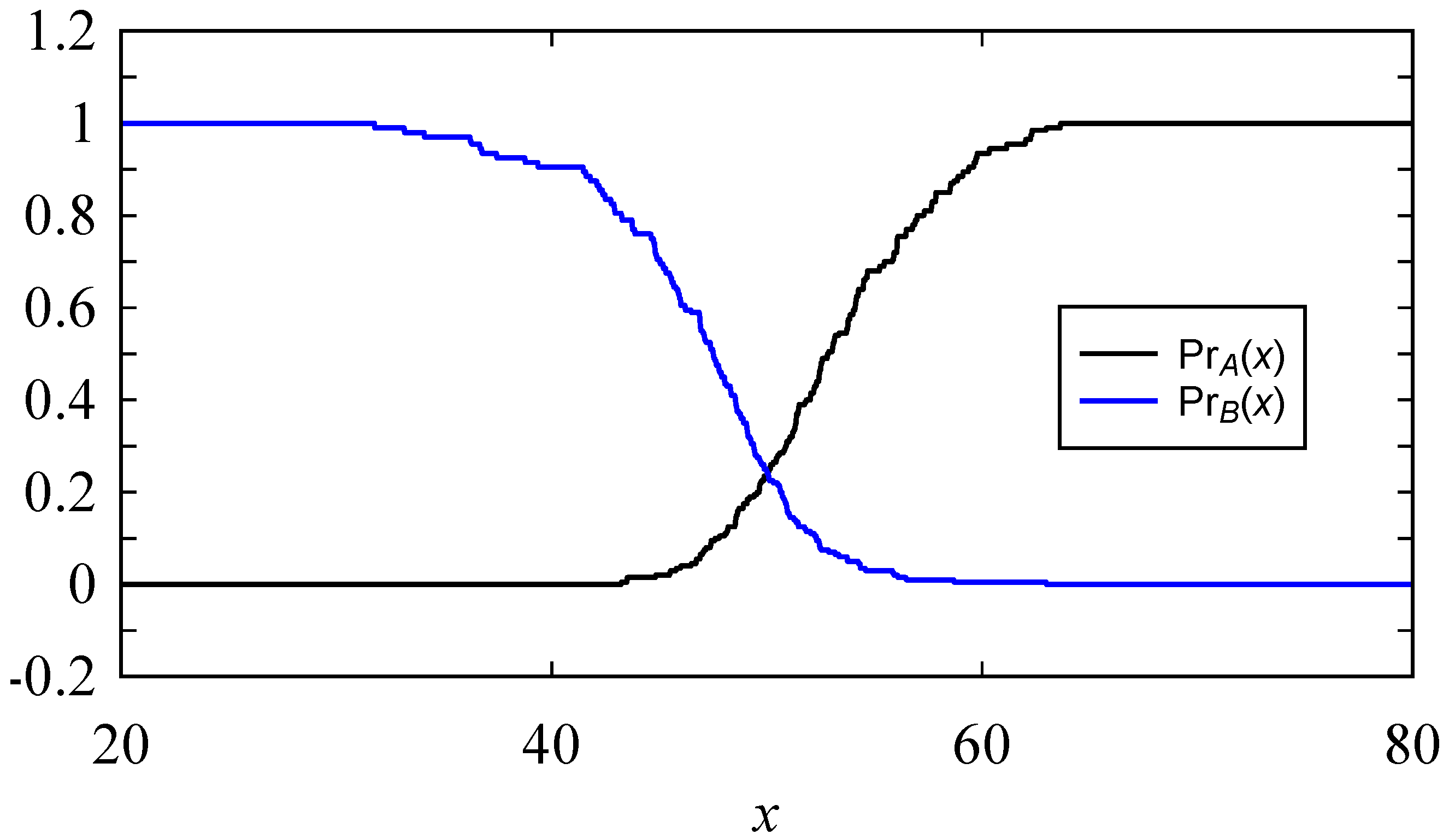
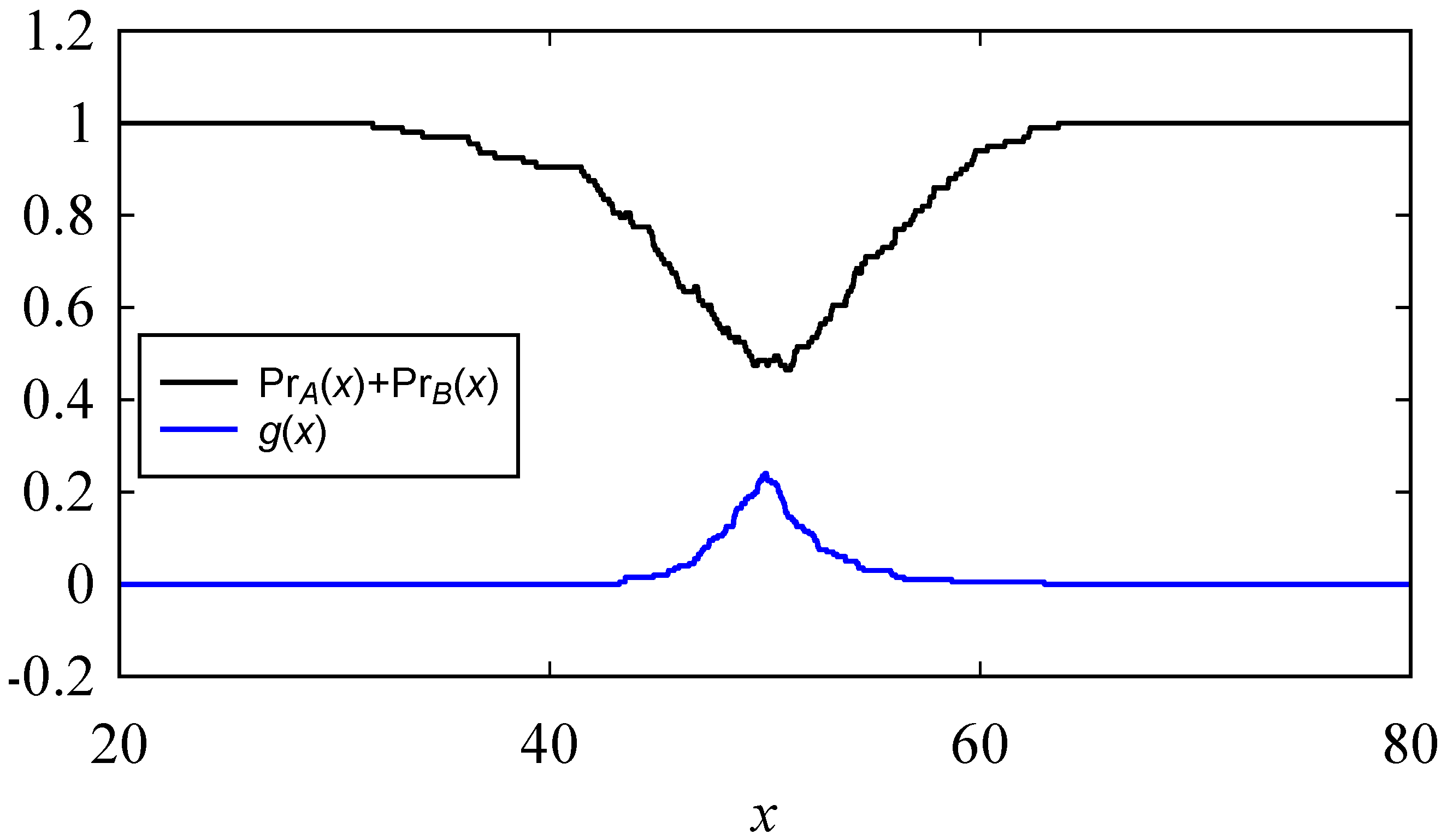
Appendix B. Inducing Possibility Distributions (Fuzzy Numbers) from Numerical Data
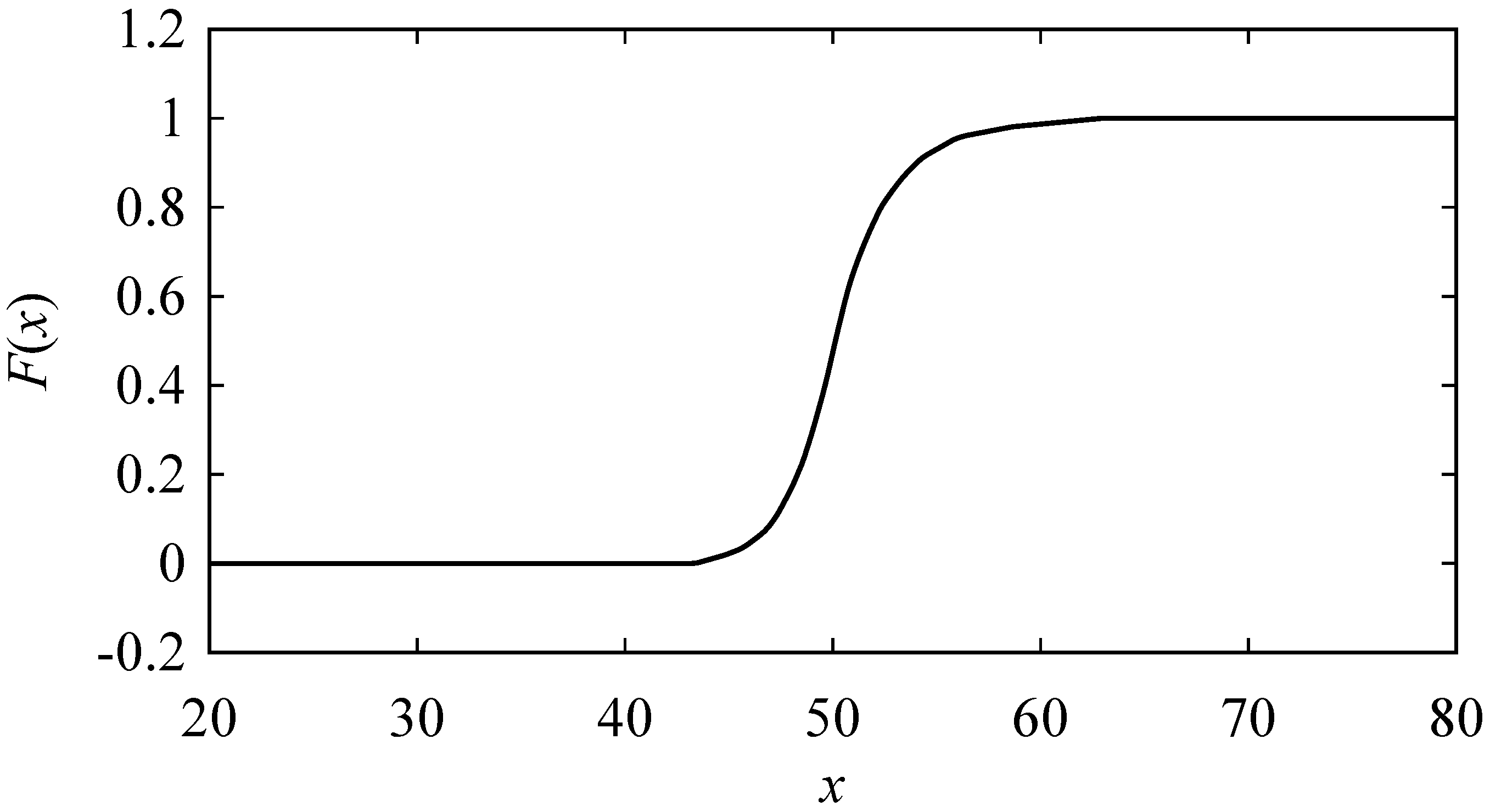
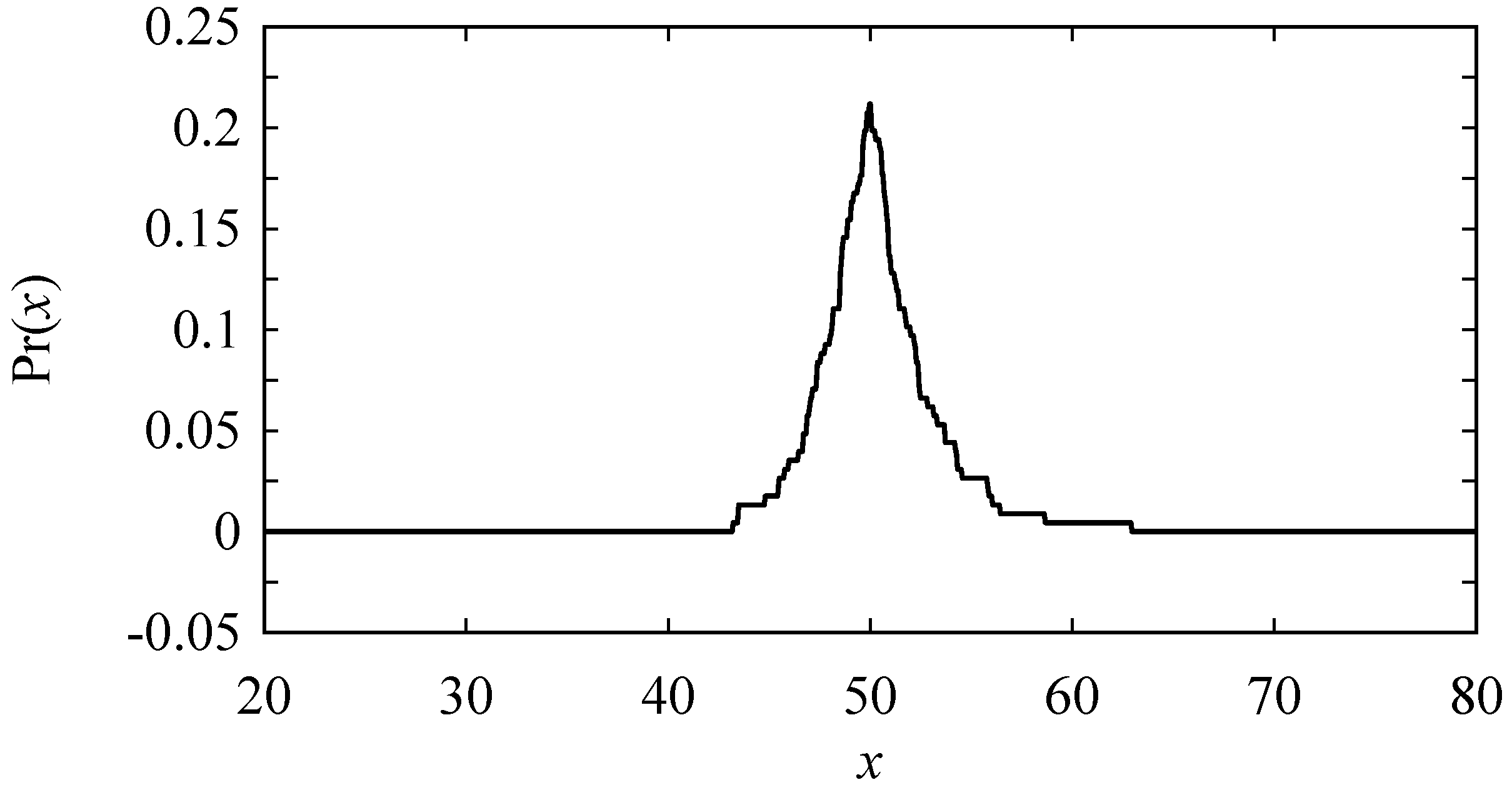
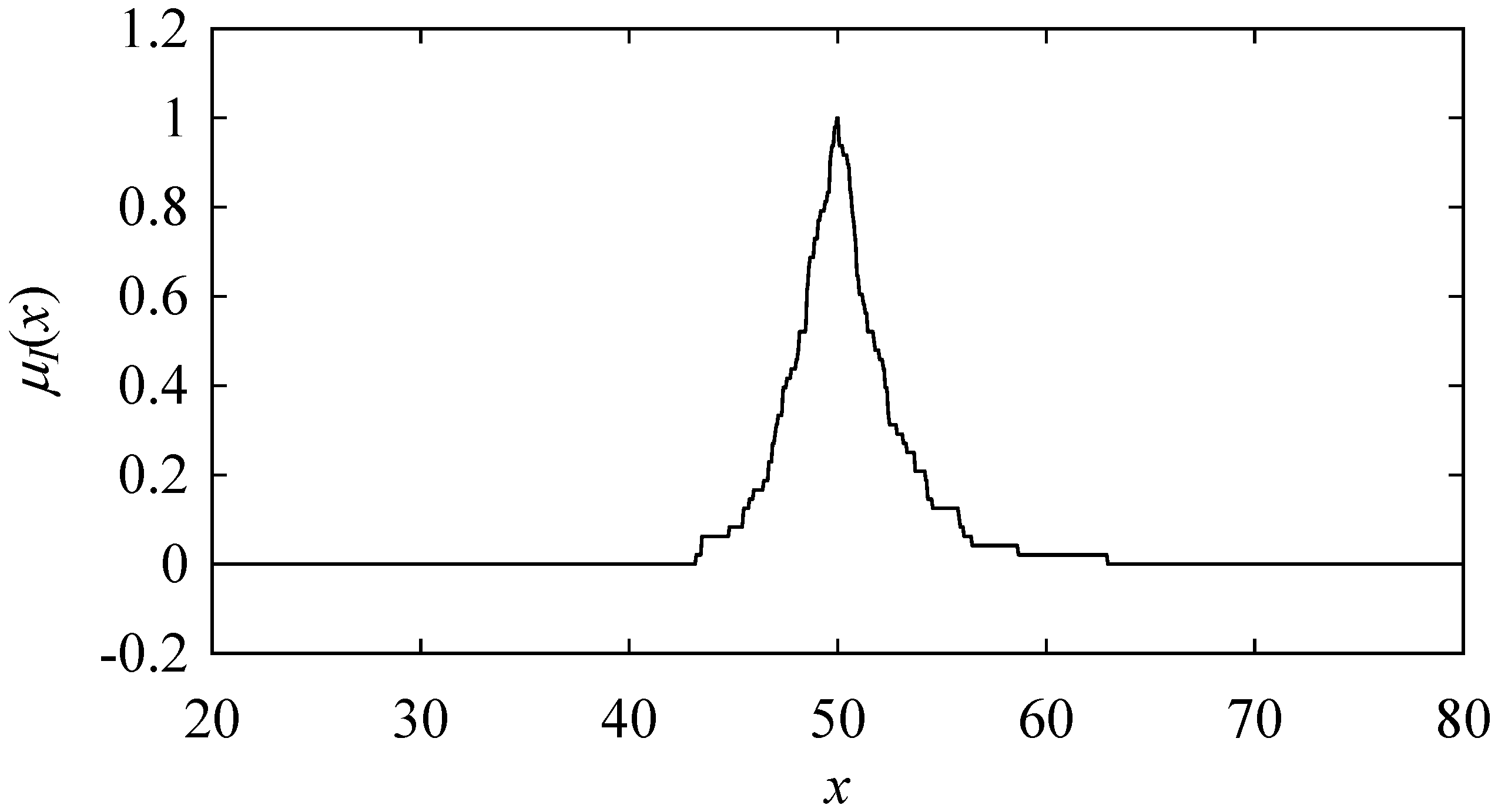
References
- United Nations Environment Program. Report of the World Commission on Environment and Development Annex to General Assembly Document a/42/427; United Nations: Nairobi, NY, USA, 1987. [Google Scholar]
- Ullah, A.M.M.S.; Fuji, A.; Kubo, A.; Tamaki, J. Analyzing the sustainability of bimetallic components. Int. J. Autom. Technol. 2014, 8, 745–753. [Google Scholar] [CrossRef]
- Allwood, J.M.; Ashby, M.F.; Gutowski, T.G.; Worrell, E. Material efficiency: A white paper. Resour. Conserv. Recycl. 2011, 55, 362–381. [Google Scholar] [CrossRef]
- Bian, J.; Mohrbacher, H.; Zhang, J.-S.; Zhao, Y.-T.; Lu, H.-Z.; Dong, H. Application potential of high performance steels for weight reduction and efficiency increase in commercial vehicles. Adv. Manuf. 2015, 3, 27–36. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Hashimoto, H.; Kubo, A.; Tamaki, J. Sustainability analysis of rapid prototyping: Material/resource and process perspectives. Int. J. Sustain. Manuf. 2013, 3, 20–36. [Google Scholar] [CrossRef]
- Kimura, M.; Kusaka, M.; Kaizu, K.; Fuji, A. Effect of post-weld heat treatment on joint properties of friction welded joint between brass and low carbon steel. Sci. Technol. Weld. Join. 2010, 15, 590–596. [Google Scholar] [CrossRef]
- Kimura, M.; Fuji, A.; Konno, Y.; Itoh, S.; Kim, Y.C. Investigation of fracture for friction welded joint between pure nickel and pure aluminium with post-weld heat treatment. Mater. Des. 2014, 57, 503–509. [Google Scholar] [CrossRef]
- Sahu, P.K.; Kumari, K.; Pal, S.; Pal, S.K. Hybrid fuzzy-grey-Taguchi based multi weld quality optimization of Al/Cu dissimilar friction stir welded joints. Adv. Manuf. 2016, 4, 237–247. [Google Scholar] [CrossRef]
- Buffa, G.; de Lisi, M.; Sciortino, E.; Fratini, L. Dissimilar titanium/aluminum friction stir welding lap joints by experiments and numerical simulation. Adv. Manuf. 2016, 4, 287–295. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing, 2nd ed.; Springer: New York, NY, USA, 2015. [Google Scholar]
- Bourell, D.L.; Rosen, D.W.; Leu, M.C. The Roadmap for Additive Manufacturing and Its Impact. Print. Addit. Manuf. 2016, 1, 231–238. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S. Design for additive manufacturing of porous structures using stochastic point-cloud: A pragmatic approach. Comput. Aided Des. Appl. 2018, 15, 138–146. [Google Scholar] [CrossRef]
- Tateno, T. Anisotropic Stiffness Design for Mechanical Parts Fabricated by Multi-Material Additive Manufacturing. Int. J. Autom. Technol. 2016, 10, 231–238. [Google Scholar] [CrossRef]
- Song, X.; Lieh, J.; Yen, D. Application of small-hole dry drilling in bimetal part. J. Mater. Process. Technol. 2007, 186, 304–310. [Google Scholar] [CrossRef]
- Uthayakumar, M.; Prabhaharan, G.; Aravindan, S.; Sivaprasad, J.V. Machining studies on bimetallic pistons with CBN tool using the Taguchi method—Technical communication. Mach. Sci. Technol. 2008, 12, 249–255. [Google Scholar] [CrossRef]
- Uthayakumar, M.; Prabhakaran, G.; Aravindan, S.; Sivaprasad, J.V. Influence of Cutting Force on Bimetallic Piston Machining by a Cubic Boron Nitride (CBN) Tool. Mater. Manuf. Process. 2012, 27, 1078–1083. [Google Scholar] [CrossRef]
- Manikandan, G.; Uthayakumar, M.; Aravindan, S. Machining and simulation studies of bimetallic pistons. Int. J. Adv. Manuf. Technol. 2013, 66, 711–720. [Google Scholar] [CrossRef]
- Malakizadi, I.; Sadik, L. Nyborg, Wear Mechanism of CBN Inserts During Machining of Bimetal Aluminum-grey Cast Iron Engine Block. Procedia CIRP 2013, 8, 188–193. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Fuji, A.; Kubo, A.; Tamaki, J.; Kimura, M. On the Surface Metrology of Bimetallic Components. Mach. Sci. Technol. 2015, 19, 339–359. [Google Scholar] [CrossRef]
- Matsui, S.; Ullah, S.; Kubo, A.; Fuji, A. Cutting force signal processing for machining bimetallic components. In Proceedings of the International Conference on Leading Edge Manufacturing in 21st Century: LEM21, Tokyo, Japan, 18–22 October 2015. [Google Scholar] [CrossRef]
- Wu, D.; Ullah, S.; Kubo, A.; Fuji, A. On the complexity in roughness quantification across bimetallic boundary. In Proceedings of the International Conference on Leading Edge Manufacturing in 21st Century: LEM21, Tokyo, Japan, 18–22 October 2015. [Google Scholar] [CrossRef]
- Kaynak, Y.; Kitay, O. Porosity, Surface Quality, Microhardness and Microstructure of Selective Laser Melted 316L Stainless Steel Resulting from Finish Machining. J. Manuf. Mater. Process. 2018, 2, 36. [Google Scholar] [CrossRef]
- Cabrera, C.G.; Araujo, A.C.; Castello, D.A. On the wavelet analysis of cutting forces for chatter identification in milling. Adv. Manuf. 2017, 5, 130–142. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Akamatsu, T.; Furuno, M.; Chowdhury, M.A.K.; Kubo, A. Strategies for Developing Milling Tools from the Viewpoint of Sustainable Manufacturing. Int. J. Autom. Technol. 2016, 10, 727–736. [Google Scholar] [CrossRef]
- Ullah, A.M.M.S.; Shamsuzzaman, M. Fuzzy Monte Carlo Simulation using point-cloud-based probability–possibility transformation. Simulation 2013, 89, 860–875. [Google Scholar] [CrossRef]
- Chowdhury, M.A.K.; Sharif Ullah, A.M.M.; Anwar, S. Drilling High Precision Holes in Ti6Al4V Using Rotary Ultrasonic Machining and Uncertainties Underlying Cutting Force, Tool Wear, and Production Inaccuracies. Materials 2017, 10, 1069. [Google Scholar] [CrossRef] [PubMed]

| Bimetallic Specimens | Materials | Tensile Strength | Elongation | Hardness |
|---|---|---|---|---|
| (MPa) | (%) | (Scale) | ||
| SU–SC | Stainless Steel | 663 | 55 | 182 |
| (JIS: SUS304) | (HV) | |||
| Mild Steel | 439 | 38 | 132 | |
| (JIS: S15CK) | (HV) | |||
| Al–Ti | Aluminum | 120 | 27 | 41 |
| (JIS: A1070) | (HV) | |||
| Commercial Pure (CP) Titanium | 401 | 35 | 146 | |
| (HV) | ||||
| Al–CI | Aluminum | 265 | 17.4 | 86 |
| (JIS: A5052) | (HV) | |||
| Ductile Cast Iron | 442 | 18.6 | 79.2 | |
| (HRB) |
| Friction Welding Conditions | Specimens | ||
|---|---|---|---|
| SU-SC | Al-Ti | Al-CI | |
| Rotating material | S15CK | A1070 | A5052 |
| Diameter of the rotating material (mm) | 12 | ||
| Friction speed (s−1) | 27.5 (1650 rpm) | ||
| Friction pressure (MPa) | 30 | ||
| Friction time (s) | 2 | 1 | 3 |
| Upset pressure (MPa) | 270 | 90 | 200 |
| Upset time (s) | 6 | ||
| Items | Descriptions |
|---|---|
| Machine Tool | Lathe Machine Make: WASHINO Model: LEO-80A |
| Cutting Tool | Carbide CVD Coated Insert Make: Sandvik™ Code: TNMG160404-MF |
| Cutting Speed (vc) (m/min) | 25, 50 |
| Rotational Speeds of the Chuck (rpm) | 1377 |
| Feed (f) (mm/rev) | 0.1, 0.2 |
| Depth of Cut (ap) (mm) | 1 |
| Cutting Direction | A to B, B to A (for the joint area) |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.S. Machining Forces Due to Turning of Bimetallic Objects Made of Aluminum, Titanium, Cast Iron, and Mild/Stainless Steel. J. Manuf. Mater. Process. 2018, 2, 68. https://doi.org/10.3390/jmmp2040068
Ullah AS. Machining Forces Due to Turning of Bimetallic Objects Made of Aluminum, Titanium, Cast Iron, and Mild/Stainless Steel. Journal of Manufacturing and Materials Processing. 2018; 2(4):68. https://doi.org/10.3390/jmmp2040068
Chicago/Turabian StyleUllah, AMM Sharif. 2018. "Machining Forces Due to Turning of Bimetallic Objects Made of Aluminum, Titanium, Cast Iron, and Mild/Stainless Steel" Journal of Manufacturing and Materials Processing 2, no. 4: 68. https://doi.org/10.3390/jmmp2040068
APA StyleUllah, A. S. (2018). Machining Forces Due to Turning of Bimetallic Objects Made of Aluminum, Titanium, Cast Iron, and Mild/Stainless Steel. Journal of Manufacturing and Materials Processing, 2(4), 68. https://doi.org/10.3390/jmmp2040068





