Energy Optimal Trajectory Planning for the Morphing Solar-Powered Unmanned Aerial Vehicle Based on Hierarchical Reinforcement Learning
Abstract
1. Introduction
1.1. Existing Research on Trajectory Planning for Solar-Powered Aircraft
1.2. Existing Research on Trajectory Planning Based on Deep Reinforcement Learning
1.3. The Potential of Hierarchical Reinforcement Learning
1.4. Work of This Study
- The simulation mathematical model for the Λ-shaped morphing solar-powered UAV is established, including its aerodynamic model, dynamics and kinematics model, solar energy absorption model, and energy storage and consumption model. These provide a modeling foundation for its trajectory planning.
- Based on the phased characteristics of the 24 h trajectory of solar-powered UAVs, a classification method for the operating conditions of the Λ-shaped solar-powered UAV during 24 h flight is proposed with energy as the reference. On the basis of classification, HRL is employed to address the energy-optimal trajectory planning problem for the UAV, and a complete hierarchical policy training process is designed.
- The trajectory planning policy based on HRL can adaptively respond to different flight operating conditions within a 24 h period. Based on flight information, it outputs appropriate real-time commands for thrust, attitude angles, and wing deflections, thereby continuously tracking the peak energy power and maintaining the optimal energy state.
2. Model
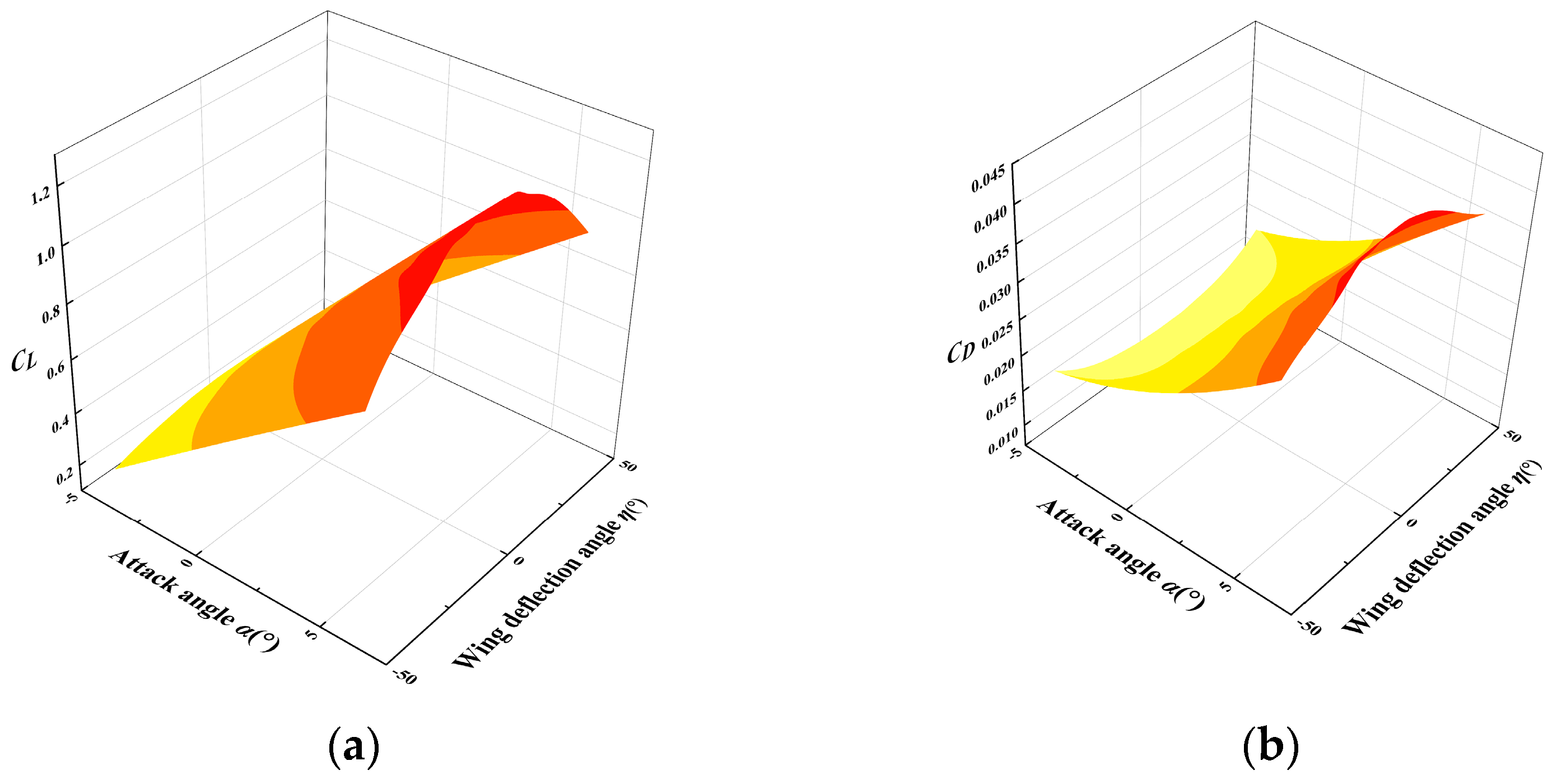
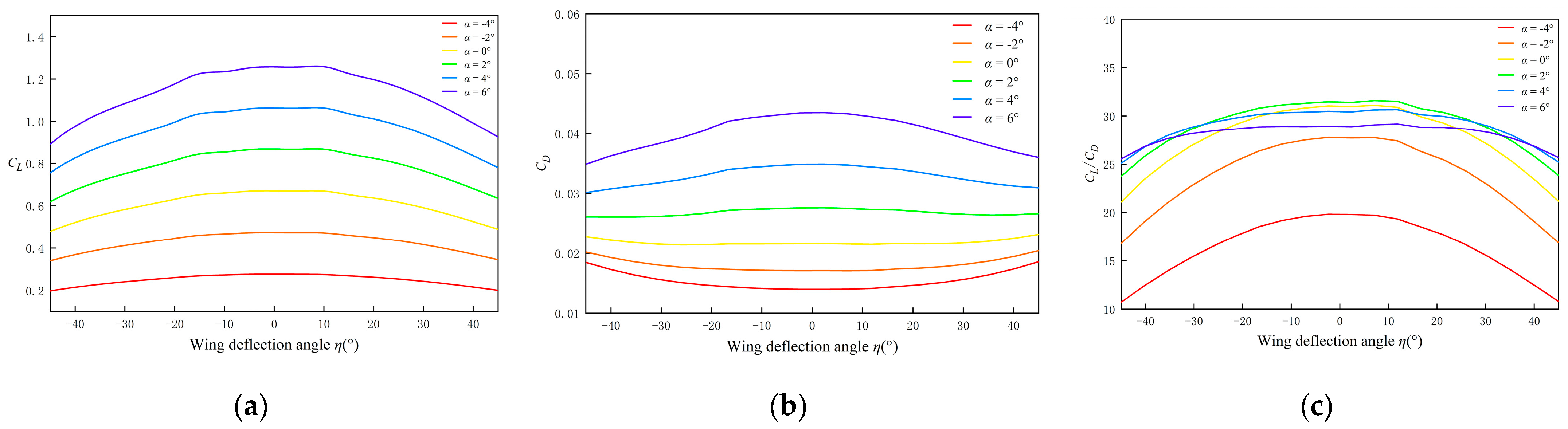
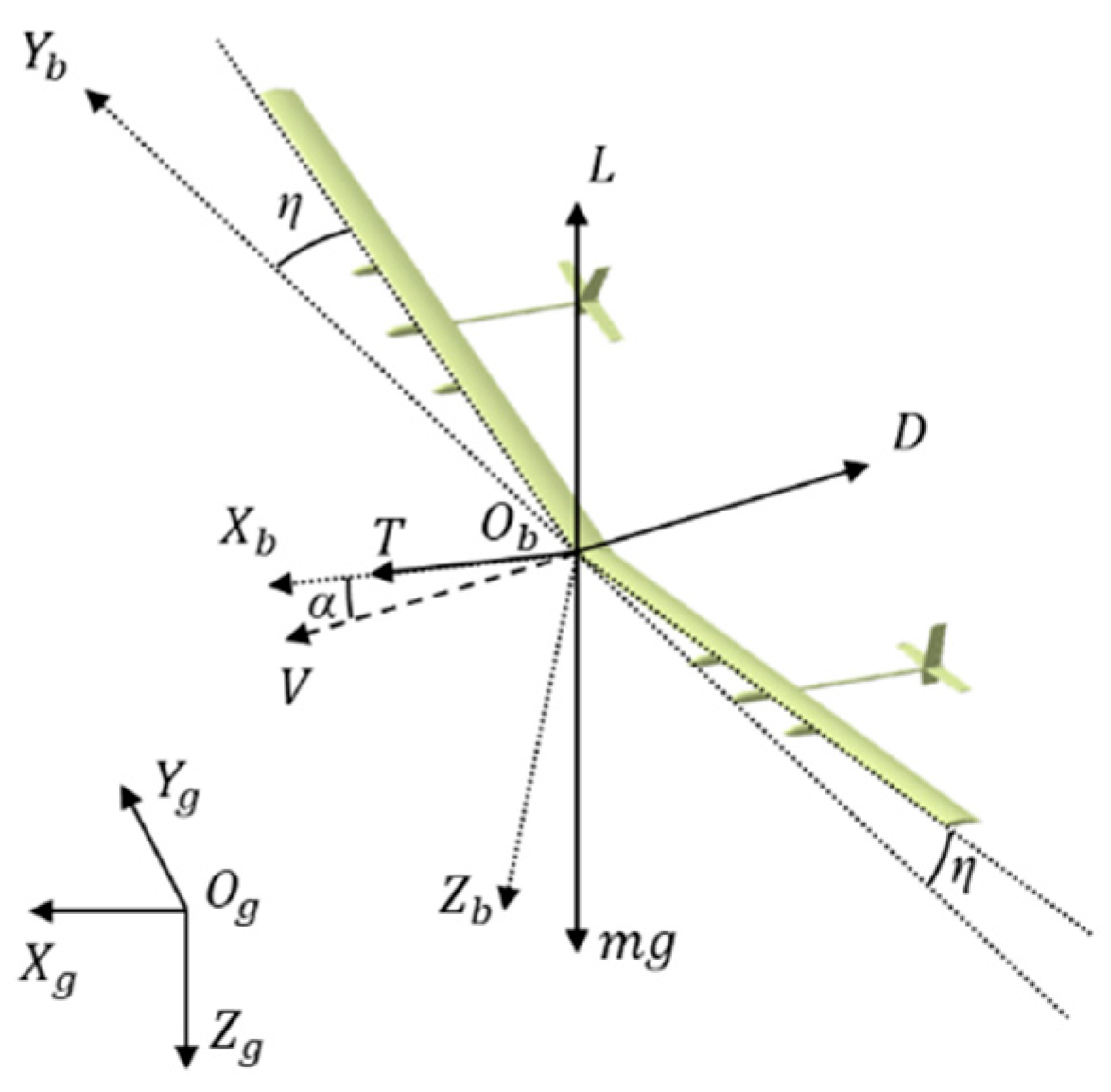
2.1. The Aerodynamic Model
2.2. The Dynamic and Kinematic Model
2.3. The Ideal Inner-Loop Response Model
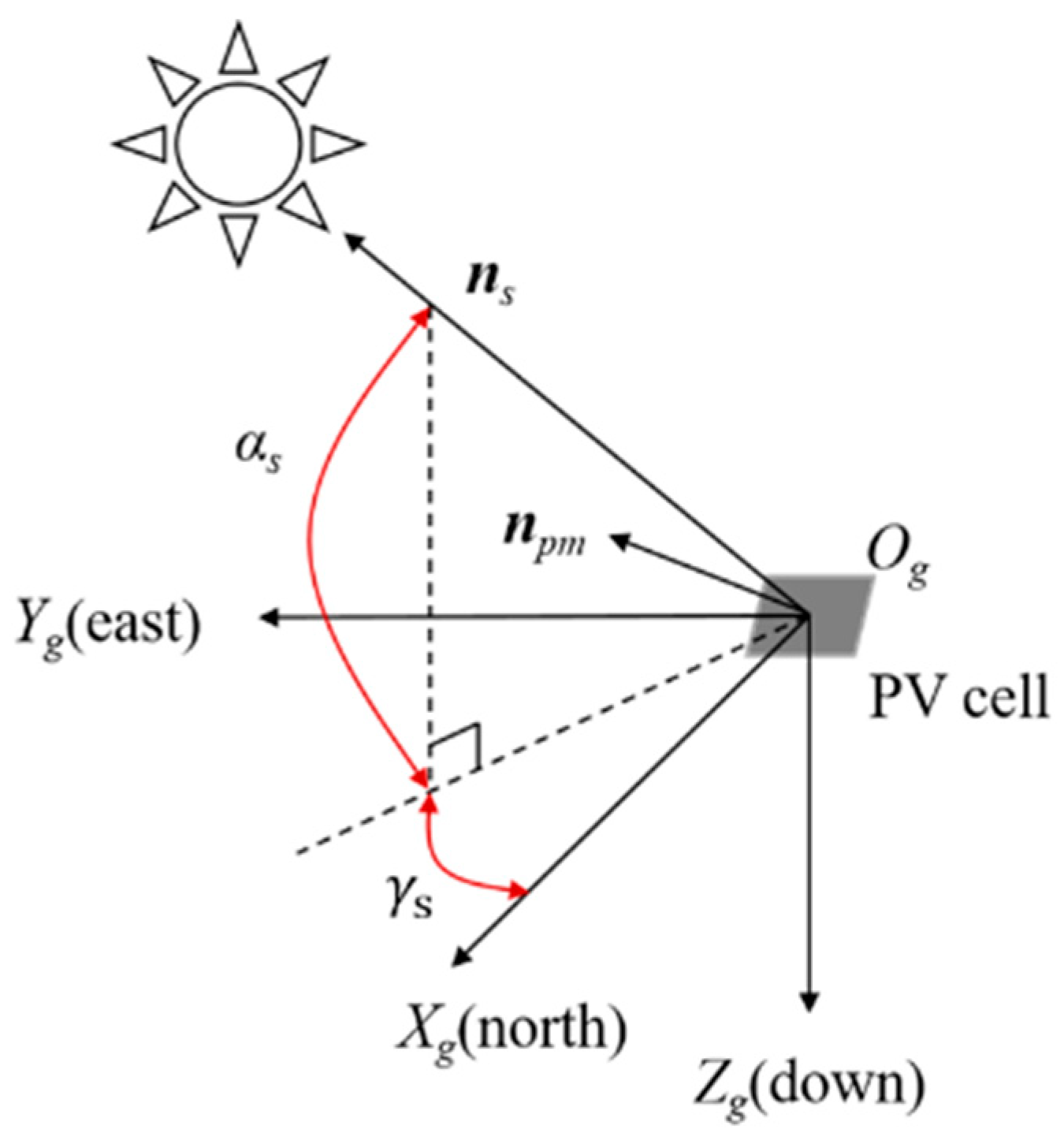
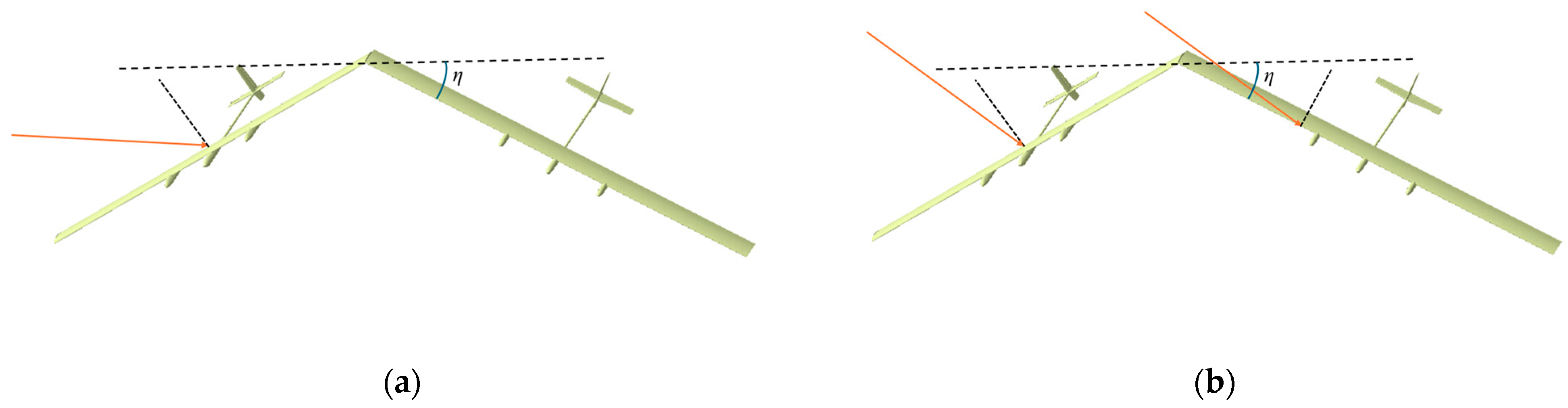
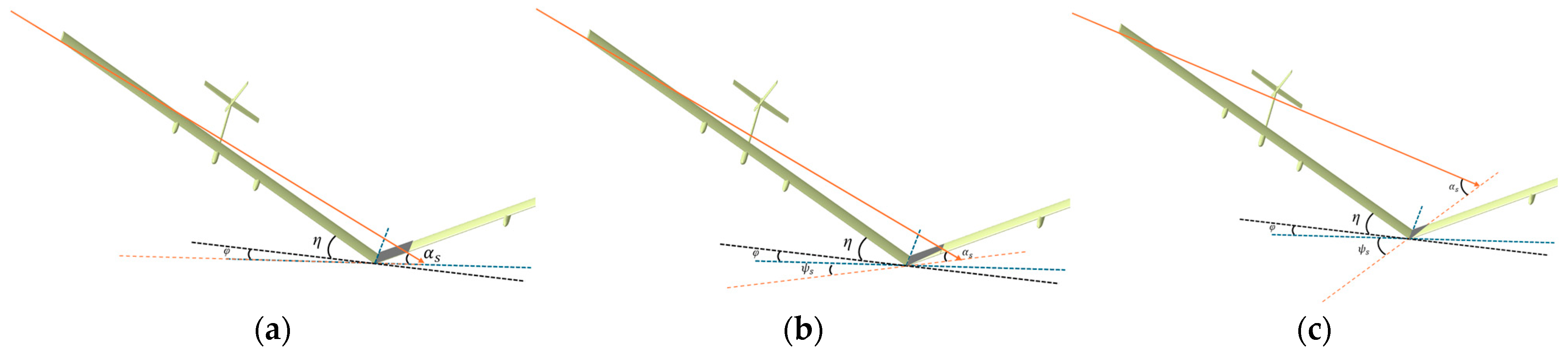
2.4. The Solar Irradiation Model
2.5. The Energy Absorption Model
2.6. The Energy Consumption Model
2.7. The Energy Storage Model
3. Minimum Energy Consumption Trajectory Analysis
3.1. Minimum Energy Consumption State-Machine Policy
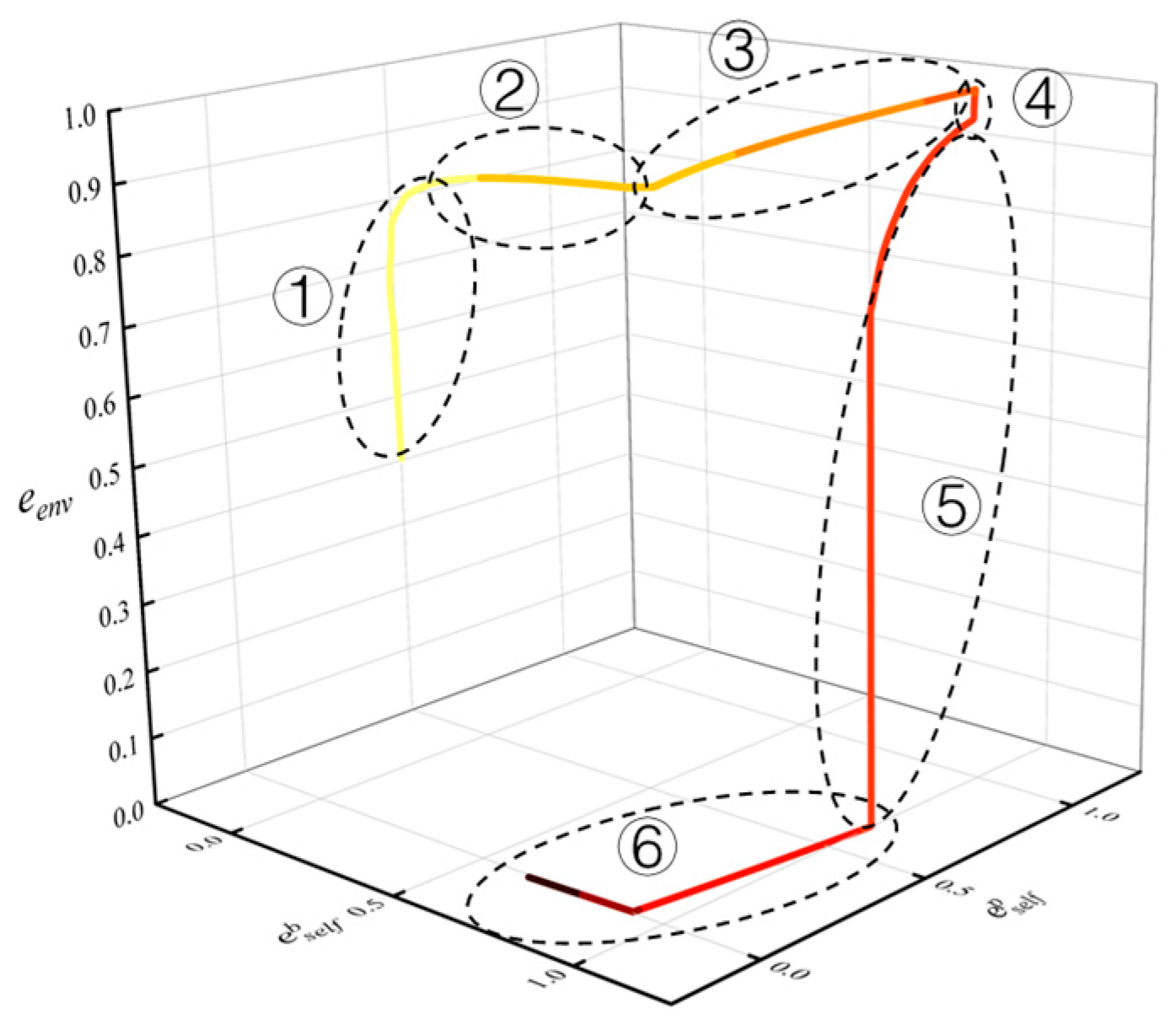
- Low-altitude charging cruising: The UAV cruises horizontally with minimum energy consumption power at the initial altitude until the SOC reaches a threshold.
- Climbing: After the SOC reaches the threshold, the UAV climbs until it reaches the maximum altitude or its SOC begins to decrease.
- High-altitude cruising: The UAV cruises horizontally at the end of the climbing until the SOC begins to decrease.
- Descent: The UAV descends to the lowest altitude.
- Low-altitude cruising: The UAV cruises horizontally after returning to the lowest altitude.
3.2. Classification of Flight Conditions
4. Hierarchical Reinforcement Learning
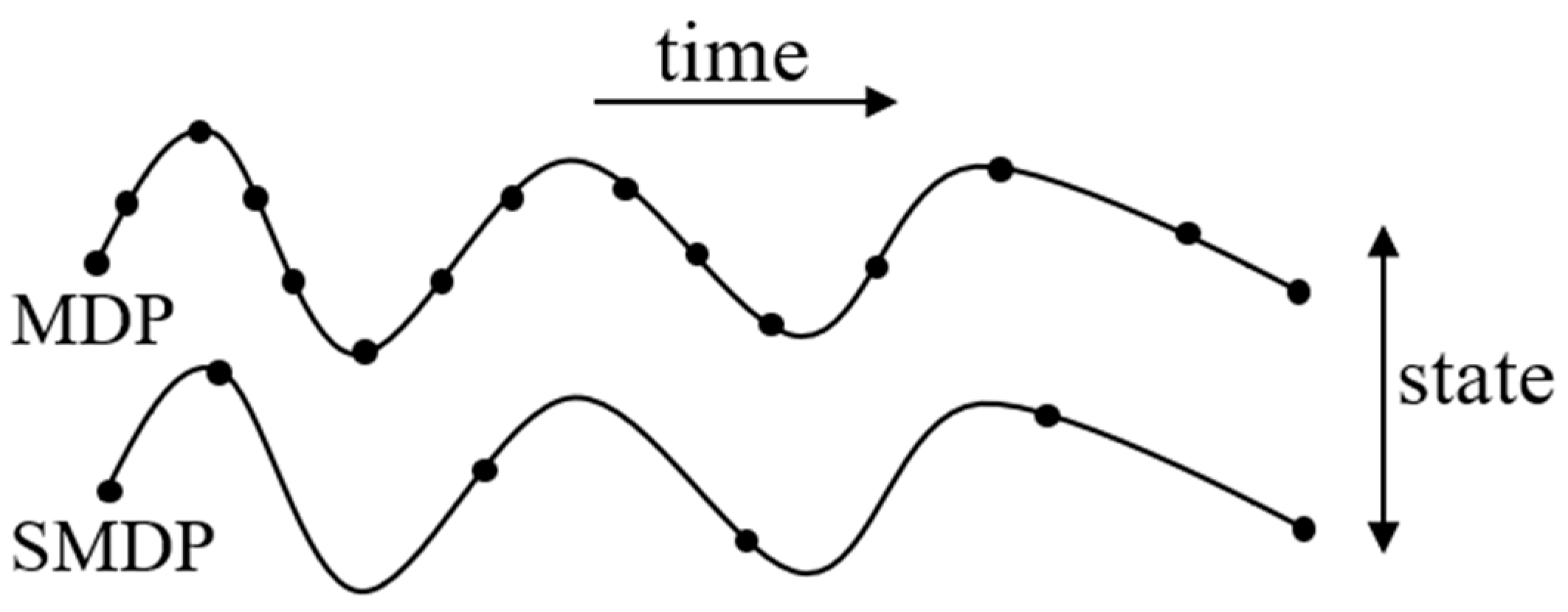
4.1. Option-Based HRL
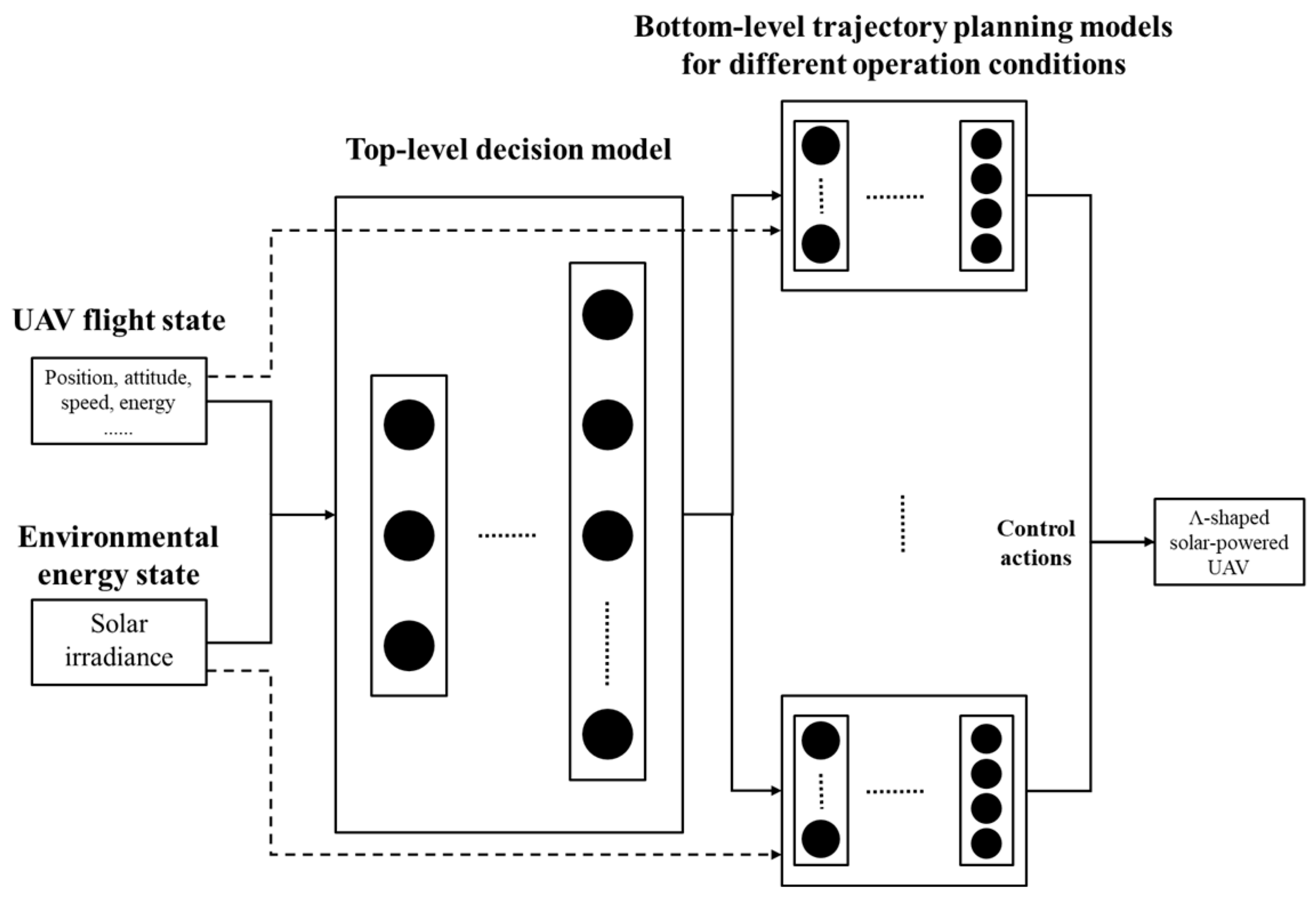
4.2. Option-Based Hierarchical Trajectory Planning Model
5. Hierarchical Trajectory Planning Policy
5.1. The Bottom-Level Policies
5.1.1. SAC Algorithm
| Algorithm 1. Soft Actor-Critic. |
| Input: , for each iteration do for each environment step do end for for each gradient step do end for end for Output: |
5.1.2. The Bottom-Level Policy for Operating Condition 1
5.1.3. The Bottom-Level Policy for Operating Condition 2
5.1.4. The Bottom-Level Policy for Operating Condition 3
5.1.5. Network Settings
5.2. The Top-Level Policy
| Algorithm 2. Deep Q-Network. |
| Input: , for each iteration do for each environment step do end for for each gradient step do where end for every C step do end for Output: |
6. Results and Discussion
6.1. Simulation Settings
6.2. Training and Testing
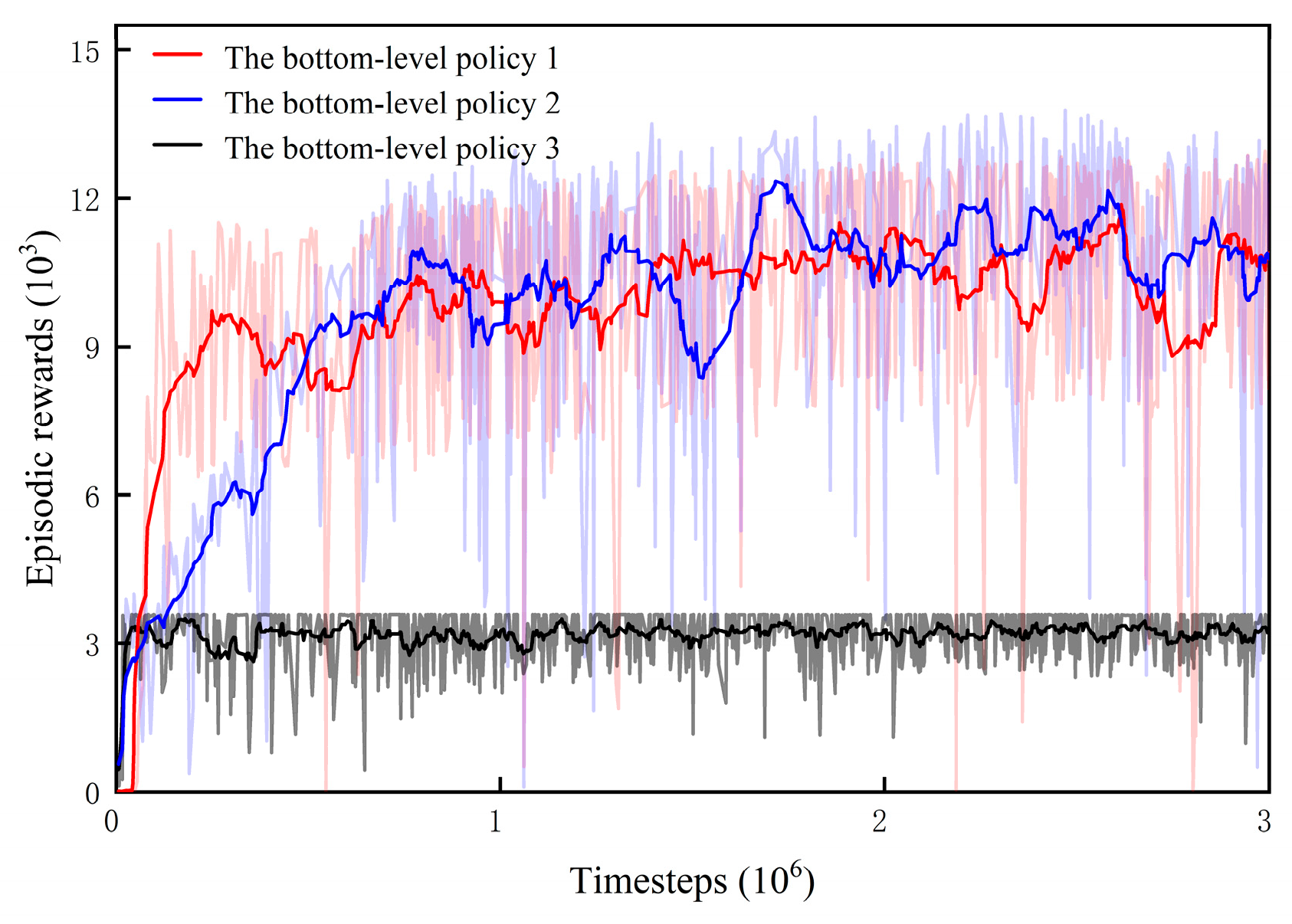
6.2.1. Training and Testing of the Bottom-Level Policies
- 1.
- Testing of bottom-level policy 1
- 2.
- Testing of bottom-level policy 2
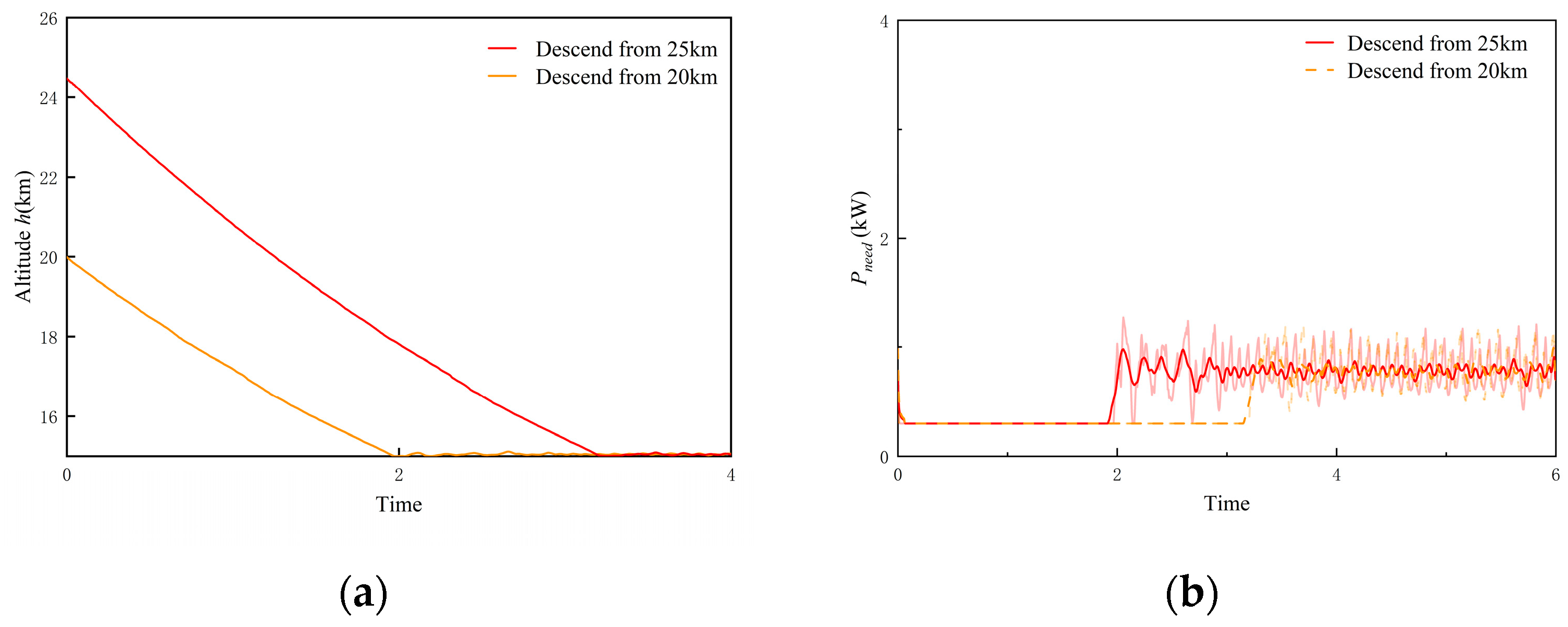
- 3.
- Testing of bottom-level policy 3
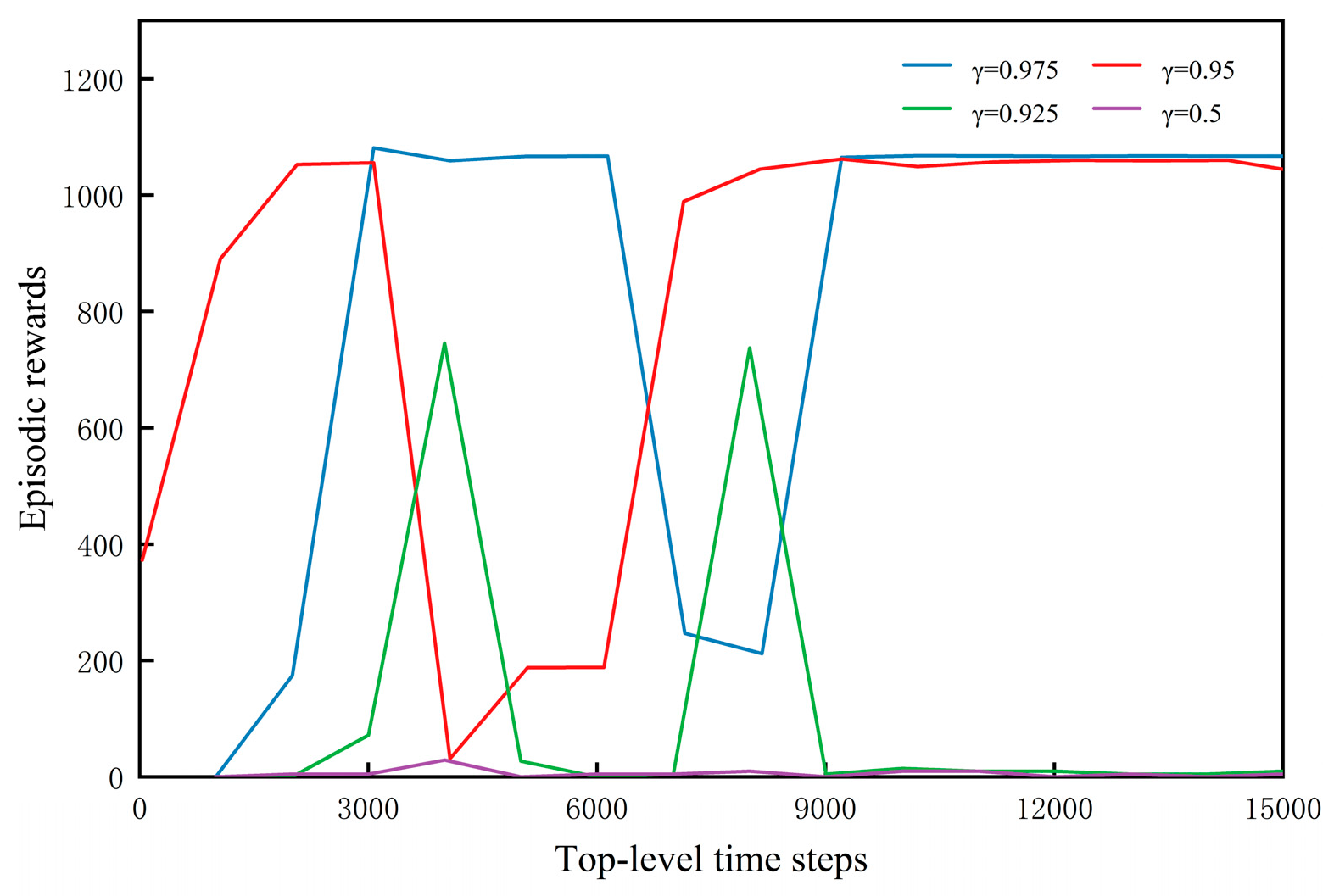
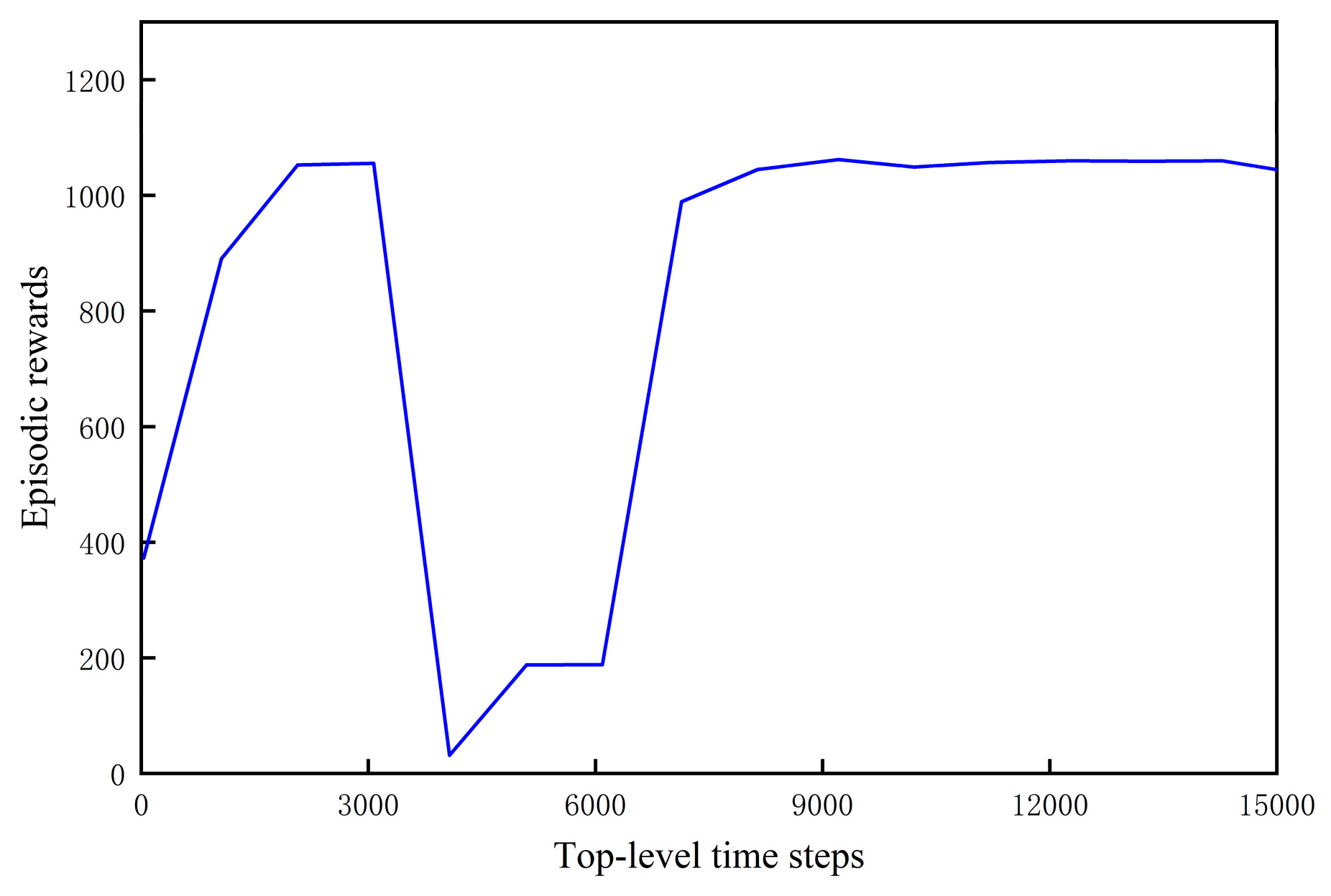
6.2.2. Training of the Top-Level Policy
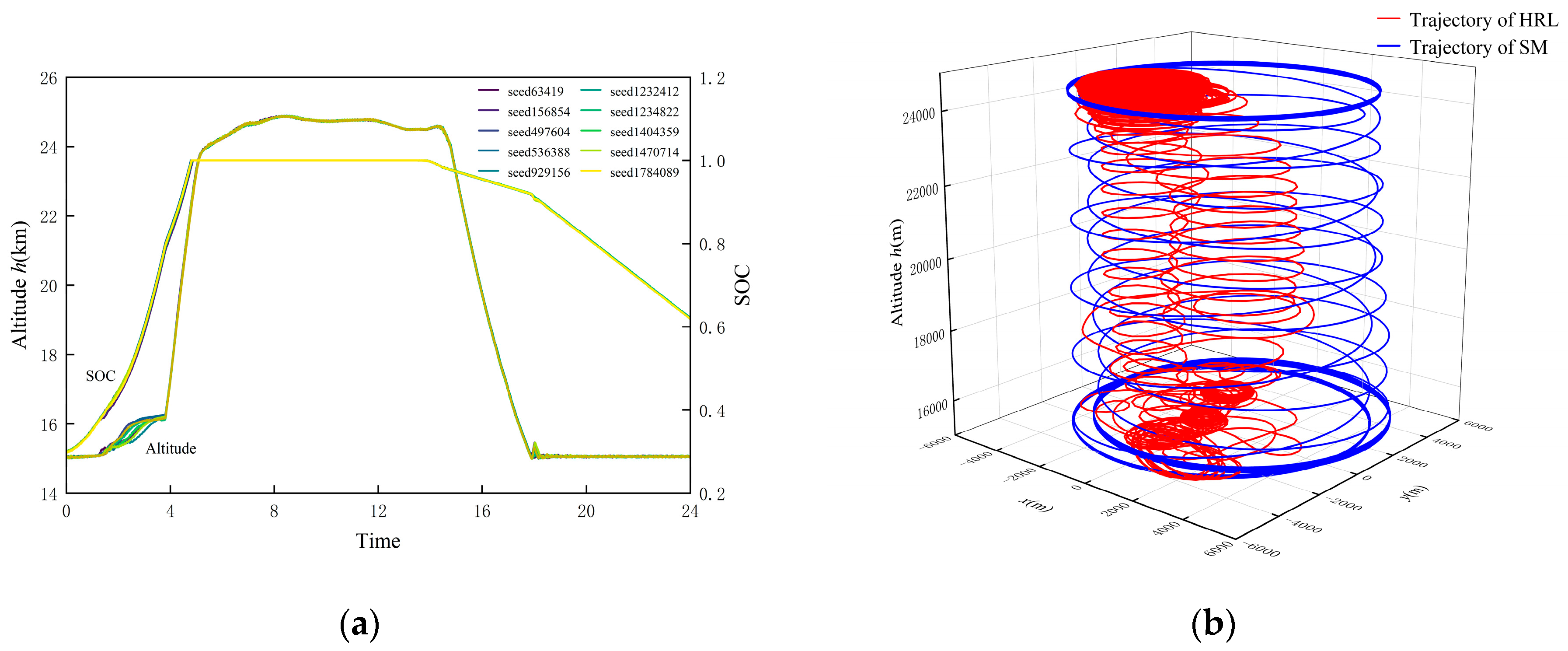
6.2.3. The 24 h Trajectory Simulation and Comparison
- Operating Condition 1: During daytime with scarce battery energy.
- 2.
- Operating Condition 2: During daytime with abundant battery energy.
- 3.
- Operating Condition 3: During nighttime.
- 4.
- Evaluation of the necessity of the top-level policy
- (1)
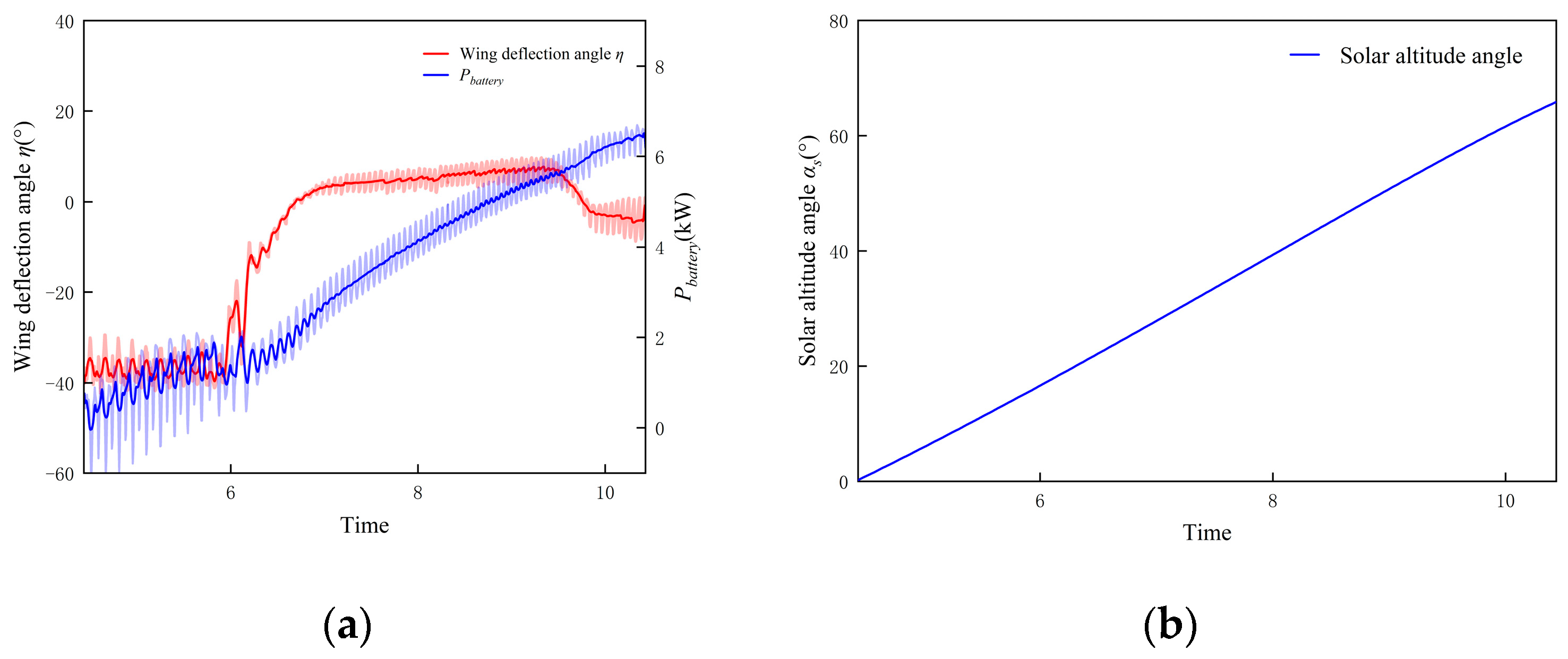
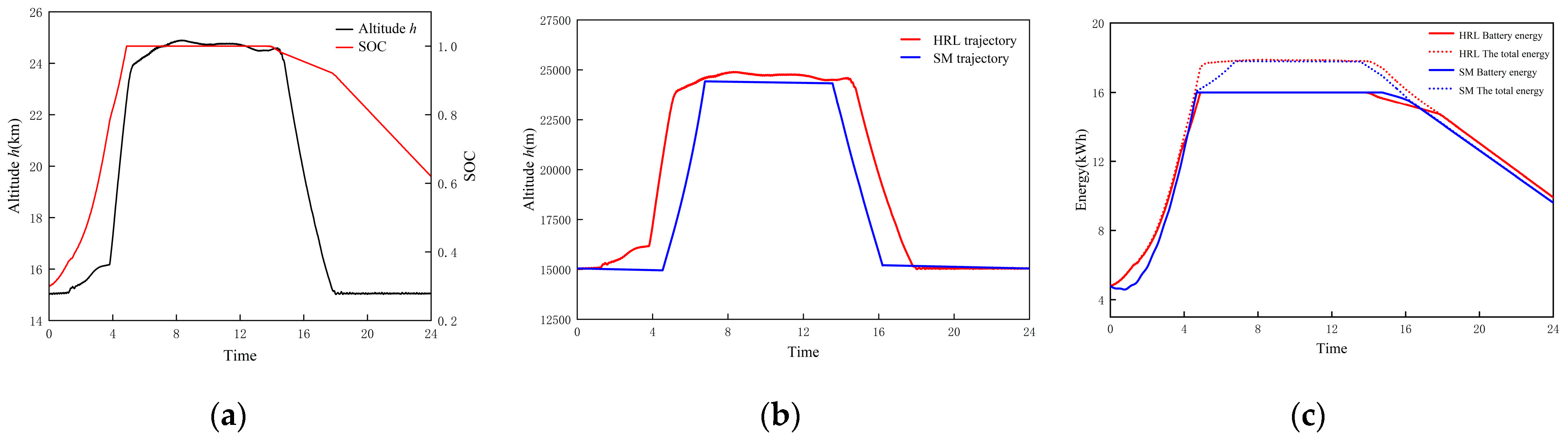
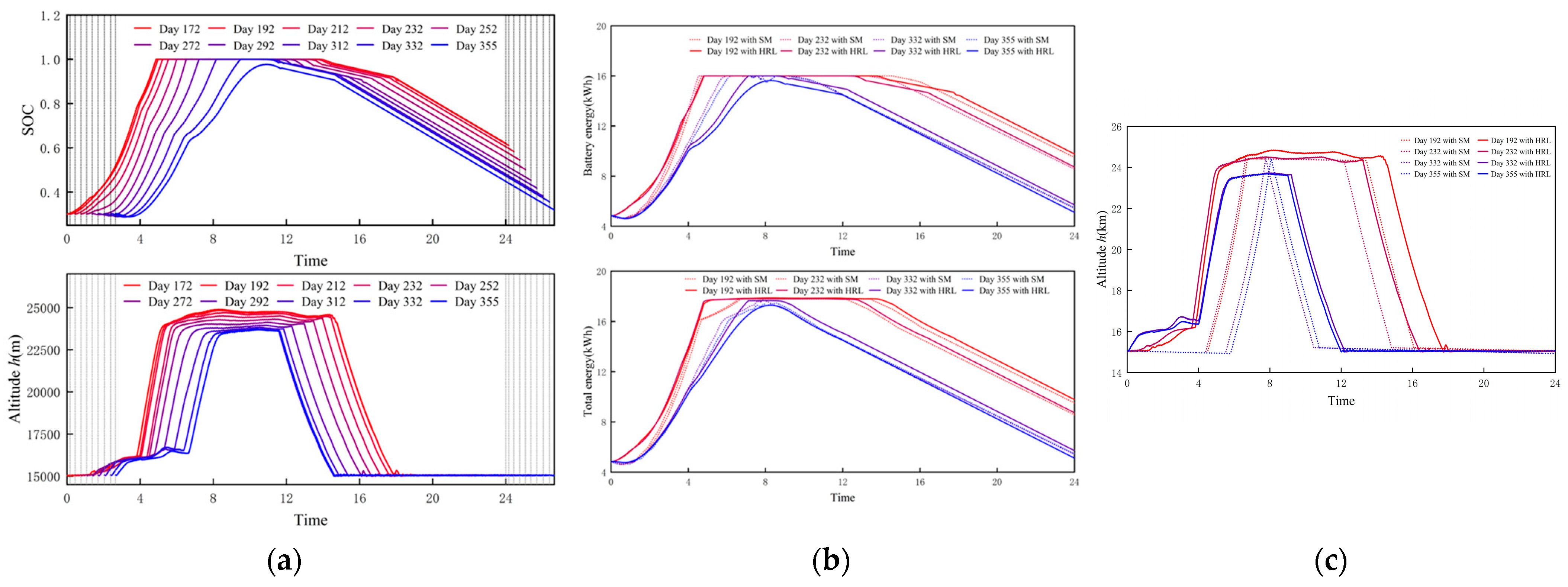
- Superior energy state during flight: This policy enables the UAV to achieve better solar energy absorption efficiency during the charging stage, allowing its SOC to continuously increase. In contrast, the battery energy of the UAV with the State-Machine policy experiences a brief decrease after takeoff. Regarding gravitational potential energy storage, this policy does not adhere to the traditional heuristic of climbing only after reaching full charge. Instead, it makes autonomous decisions based on its own energy status and environmental energy information. By starting to climb earlier, it achieves a longer duration of optimal total energy stored, and the comparison with the flat agent strongly corroborates this result. The superior solar energy absorption capability of this policy’s bottom-level sub-policy as sunset approaches further extends this period. This is specifically manifested as an additional 0.98 h of full-charge high-altitude cruising duration compared to the State-Machine policy.
- (2)
- More remaining energy: The remaining energy of the UAV after a 24 h flight is the most direct indicator for evaluating its energy-optimal trajectory planning policy. After completing the 24 h flight, the UAV guided by this policy has a remaining battery energy of 9.93 kWh, a remaining total stored energy of 9.94 kWh, and a remaining SOC of 62.04%. The UAV guided by the State-Machine policy has a remaining battery energy of 9.62 kWh, a remaining total stored energy of 9.63 kWh, and a remaining SOC of 60.12%. Compared to the latter, the former results in 0.31 kWh more remaining battery energy, 0.31 kWh more remaining total stored energy, and 1.92% higher remaining SOC, thus achieving better energy returns.
6.2.4. Testing of the Generalization Ability
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| CL | α = −4° | α = −2.57° | α = −1.14° | α = −0.286° | α = 1.71° | α = 3.14° | α = 4.57° | α = 6° |
|---|---|---|---|---|---|---|---|---|
| η = 45° | 0.2008 | 0.3038 | 0.4071 | 0.5105 | 0.6142 | 0.7178 | 0.8215 | 0.9251 |
| η = 30° | 0.2433 | 0.3674 | 0.4916 | 0.6159 | 0.7402 | 0.8644 | 0.9885 | 1.1124 |
| η = 20° | 0.2626 | 0.3964 | 0.5302 | 0.6639 | 0.7976 | 0.9310 | 1.0642 | 1.1969 |
| η = 15° | 0.2694 | 0.4065 | 0.5435 | 0.6805 | 0.8172 | 0.9537 | 1.0898 | 1.2254 |
| η = 10° | 0.2752 | 0.4163 | 0.5573 | 0.6981 | 0.8386 | 0.9788 | 1.1184 | 1.2576 |
| η = 5° | 0.2767 | 0.4176 | 0.5582 | 0.6986 | 0.8386 | 0.9783 | 1.1173 | 1.2559 |
| η = 0° | 0.2771 | 0.4182 | 0.5590 | 0.6995 | 0.8396 | 0.9791 | 1.1181 | 1.2565 |
| η = −5° | 0.2766 | 0.4172 | 0.5576 | 0.6975 | 0.8370 | 0.9759 | 1.1141 | 1.2515 |
| η = −10° | 0.2733 | 0.4122 | 0.5507 | 0.6887 | 0.8261 | 0.9630 | 1.0990 | 1.2344 |
| η = −15° | 0.2694 | 0.4065 | 0.5435 | 0.6805 | 0.8172 | 0.9537 | 1.0898 | 1.2254 |
| η = −20° | 0.2610 | 0.3938 | 0.5260 | 0.6575 | 0.7884 | 0.9186 | 1.0479 | 1.1763 |
| η = −30° | 0.2411 | 0.3638 | 0.4858 | 0.6072 | 0.7277 | 0.8475 | 0.9663 | 1.0841 |
| η = −45° | 0.1980 | 0.2994 | 0.4000 | 0.5000 | 0.5991 | 0.6973 | 0.7946 | 0.8909 |
| CL | α = −4° | α = −2.57° | α = −1.14° | α = −0.286° | α = 1.71° | α = 3.14° | α = 4.57° | α = 6° |
|---|---|---|---|---|---|---|---|---|
| η = 45° | 0.0186 | 0.0198 | 0.0215 | 0.0236 | 0.0261 | 0.0290 | 0.0323 | 0.0360 |
| η = 30° | 0.0156 | 0.0173 | 0.0195 | 0.0224 | 0.0258 | 0.0297 | 0.0342 | 0.0393 |
| η = 20° | 0.0146 | 0.0165 | 0.0191 | 0.0223 | 0.0262 | 0.0307 | 0.0358 | 0.0415 |
| η = 15° | 0.0143 | 0.0163 | 0.0190 | 0.0224 | 0.0264 | 0.0311 | 0.0364 | 0.0424 |
| η = 10° | 0.0141 | 0.0161 | 0.0188 | 0.0222 | 0.0264 | 0.0313 | 0.0368 | 0.0430 |
| η = 5° | 0.0140 | 0.0161 | 0.0189 | 0.0224 | 0.0267 | 0.0316 | 0.0372 | 0.0435 |
| η = 0° | 0.0140 | 0.0160 | 0.0189 | 0.0224 | 0.0266 | 0.0316 | 0.0372 | 0.0435 |
| η = −5° | 0.0140 | 0.0161 | 0.0189 | 0.0224 | 0.0266 | 0.0315 | 0.0371 | 0.0433 |
| η = −10° | 0.0141 | 0.0161 | 0.0189 | 0.0223 | 0.0264 | 0.0312 | 0.0367 | 0.0428 |
| η = −15° | 0.0143 | 0.0163 | 0.0190 | 0.0224 | 0.0264 | 0.0311 | 0.0364 | 0.0424 |
| η = −20° | 0.0146 | 0.0165 | 0.0190 | 0.0222 | 0.0260 | 0.0304 | 0.0354 | 0.0410 |
| η = −30° | 0.0156 | 0.0172 | 0.0194 | 0.0221 | 0.0254 | 0.0293 | 0.0336 | 0.0384 |
| η = −45° | 0.0185 | 0.0196 | 0.0212 | 0.0232 | 0.0256 | 0.0283 | 0.0314 | 0.0349 |
Appendix B
Appendix C
References
- Zhu, X.; Guo, Z.; Hou, Z. Solar-Powered Airplanes: A Historical Perspective and Future Challenges. Prog. Aerosp. Sci. 2014, 71, 36–53. [Google Scholar] [CrossRef]
- Alvi, O.U.R. Development of Solar Powered Aircraft for Multipurpose Application. In Collection of Technical Papers—AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference; American Institute of Aeronautics and Astronautics Inc. (AIAA): Reston, VA, USA, 2010. [Google Scholar]
- Wang, S.Q.; Ma, D.L. Three dimensional trajectory optimization of high-altitude solar powered unmanned aerial vehicles. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 936–943. [Google Scholar] [CrossRef]
- Richfield, P. Aloft for 5 Years: DARPA’s Vulture Project Aims for Ultra Long UAV Missions. Def. News 2007, 22, 30. [Google Scholar]
- Gao, Z.X. General planning method for energy optimal flight path of solar-powered aircraft in near space. Chin. J. Aeronaut. 2023, 44, 6–27. [Google Scholar]
- Klesh, A.; Kabamba, P. Energy-Optimal Path Planning for Solar-Powered Aircraft in Level Flight. In Collection of Technical Papers—AIAA Guidance, Navigation, and Control Conference 2007; AIAA: Hilton Head, SC, USA, 2007; Volume 3, pp. 2966–2982. [Google Scholar] [CrossRef]
- Spangelo, S.C.; Gilbert, E.G. Power Optimization of Solar-Powered Aircraft with Specified Closed Ground Tracks. J. Aircr. 2013, 50, 232–238. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.; Wang, H.; Su, G. A Method of 3D Path Planning for Solar-Powered UAV with Fixed Target and Solar Tracking. Aerosp. Sci. Technol. 2019, 92, 831–838. [Google Scholar] [CrossRef]
- Ailon, A. A Path Planning Approach for Unmanned Solar-Powered Aerial Vehicles. Renew. Energy Power Qual. J. 2023, 21, 109–114. [Google Scholar] [CrossRef]
- Gao, X.-Z.; Hou, Z.-X.; Guo, Z.; Liu, J.-X.; Chen, X.-Q. Energy Management Strategy for Solar-Powered High-Altitude Long-Endurance Aircraft. Energy Convers. Manag. 2013, 70, 20–30. [Google Scholar] [CrossRef]
- Ma, D.; Bao, W.; Qiao, Y. Study of flight path for solar-powered aircraft based on gravity energy reservation. Hangkong Xuebao/Acta Aeronaut. Astronaut. Sin. 2014, 35, 408–416. [Google Scholar]
- Marriott, J.; Tezel, B.; Liu, Z.; Stier-Moses, N.E. Trajectory Optimization of Solar-Powered High-Altitude Long Endurance Aircraft. In Proceedings of the 2020 6th International Conference on Control, Automation and Robotics, ICCAR 2020, Singapore, 20–23 April 2020; pp. 473–481. [Google Scholar] [CrossRef]
- Sun, M.; Shan, C.; Sun, K.-W.; Jia, Y.-H. Energy Management Strategy for High-Altitude Solar Aircraft Based on Multiple Flight Phases. Math. Probl. Eng. 2020, 2020, 6655031. [Google Scholar] [CrossRef]
- Ni, W.; Ying, B.I.; Di, W.U.; Xiaoping, M.A. Energy-Optimal Trajectory Planning for Solar-Powered Aircraft Using Soft Actor-Critic. Chin. J. Aeronaut. 2022, 35, 337–353. [Google Scholar] [CrossRef]
- Montalvo, C. Meta Aircraft Flight Dynamics and Controls. Ph.D. thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2014. [Google Scholar]
- Chao, A.; Xie, C.-C.; Meng, Y.; Liu, D.-X.; Yang, C. Flight dynamics and stable control analyses of multi-body aircraft. Gongcheng Lixue/Eng. Mech. 2021, 38, 248–256. [Google Scholar]
- Liu, D.; Xie, C.; Hong, G. Dynamic characteristics of wingtip-jointed composite aircraft. J. Beijing Univ. Aeronaut. Astronaut. 2021, 47, 2311–2321. [Google Scholar]
- Wang, X.; Yang, Y.; Wang, D.; Zhang, Z. Mission-Oriented Cooperative 3D Path Planning for Modular Solar-Powered Aircraft with Energy Optimization. Chin. J. Aeronaut. 2022, 35, 98–109. [Google Scholar] [CrossRef]
- Wu, M.; Xiao, T.; Ang, H.; Li, H. Optimal Flight Planning for a Z-Shaped Morphing-Wing Solar-Powered Unmanned Aerial Vehicle. J. Guid. Control. Dyn. 2018, 41, 497–505. [Google Scholar] [CrossRef]
- Wu, M.; Shi, Z.; Ang, H.; Xiao, T. Theoretical Study on Energy Performance of a Stratospheric Solar Aircraft with Optimum Λ-Shaped Rotatable Wing. Aerosp. Sci. Technol. 2020, 98, 105670. [Google Scholar] [CrossRef]
- Wu, M.; Shi, Z.; Xiao, T.; Ang, H. Flight Trajectory Optimization of Sun-Tracking Solar Aircraft under the Constraint of Mission Region. Chin. J. Aeronaut. 2021, 34, 140–153. [Google Scholar] [CrossRef]
- Li, Z.-r.; Yang, Y.-p.; Zhang, Z.-j.; Ma, X.-p. Overall Design and Energy Efficiency Optimization for Communication-Oriented Morphing Solar-Powered UAV. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48. [Google Scholar] [CrossRef]
- Ma, D.; Bao, W.; Qiao, Y. Study of solar-powered aircraft configuration beneficial to winter flight. Hangkong Xuebao/Acta Aeronaut. Et Astronaut. Sin. 2014, 35, 1581–1591. [Google Scholar]
- Wang, S.; Ma, D.; Yang, M.; Zhang, L.; Li, G. Flight Strategy Optimization for High-Altitude Long-Endurance Solar-Powered Aircraft Based on Gauss Pseudo-Spectral Method. Chin. J. Aeronaut. 2019, 32, 2286–2298. [Google Scholar] [CrossRef]
- Martin, R.A.; Gates, N.S.; Ning, A.; Hedengren, J.D. Dynamic Optimization of High-Altitude Solar Aircraft Trajectories under Station-Keeping Constraints. J. Guid. Control. Dyn. 2019, 42, 538–552. [Google Scholar] [CrossRef]
- Pandian, A.P.D. Sustainable Energy Efficient Unmanned Aerial Vehicles with Deep Q-Network and Deep Deterministic Policy Gradient. In Proceedings of the 2024 International Symposium on Networks, Computers and Communications, ISNCC 2024, Washington, DC, USA, 22–25 October 2024. [Google Scholar] [CrossRef]
- Chen, S.; Mo, Y.; Wu, X.; Xiao, J.; Liu, Q. Reinforcement Learning-Based Energy-Saving Path Planning for UAVs in Turbulent Wind. Electronics 2024, 13, 3190. [Google Scholar] [CrossRef]
- Li, Y.; Aghvami, A.H.; Dong, D. Path Planning for Cellular-Connected UAV: A DRL Solution With Quantum-Inspired Experience Replay. IEEE Trans. Wirel. Commun. 2022, 21, 7897–7912. [Google Scholar] [CrossRef]
- Reddy, G.; Wong-Ng, J.; Celani, A.; Sejnowski, T.J.; Vergassola, M. Glider Soaring via Reinforcement Learning in the Field. Nature 2018, 562, 236–239. [Google Scholar] [CrossRef]
- Xi, Z.; Wu, D.; Ni, W.; Ma, X. Energy-Optimized Trajectory Planning for Solar-Powered Aircraft in a Wind Field Using Reinforcement Learning. IEEE Access 2022, 10, 87715–87732. [Google Scholar] [CrossRef]
- Sutton, R.S.; Precup, D.; Singh, S. Between MDPs and Semi-MDPs: A Framework for Temporal Abstraction in Reinforcement Learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Chai, J.; Chen, W.; Zhu, Y.; Yao, Z.-X.; Zhao, D. A Hierarchical Deep Reinforcement Learning Framework for 6-DOF UCAV Air-to-Air Combat. IEEE Trans. Syst. Man Cybern.-Syst. 2023, 53, 5417–5429. [Google Scholar] [CrossRef]
- Lv, C.; Zhu, M.; Guo, X.; Ou, J.; Lou, W. Hierarchical Reinforcement Learning Method for Long-Horizon Path Planning of Stratospheric Airship. Aerosp. Sci. Technol. 2025, 160, 110075. [Google Scholar] [CrossRef]
- Raoufi, M.; Telikani, A.; Zhang, T.; Shen, J. Fire Front Path Planning and Tracking Control of Uncrewed Aerial Vehicles Using Deep Reinforcement Learning. Robot. Auton. Syst. 2025, 193, 105076. [Google Scholar] [CrossRef]
- Kong, W.; Zhou, D.-Y.; Du, Y.-J.; Zhou, Y.; Zhao, Y.-Y. Hierarchical Multi-Agent Reinforcement Learning for Multi-Aircraft Close-Range Air Combat. IET Control Theory Appl. 2023, 17, 1840–1862. [Google Scholar] [CrossRef]
- Wang, H.T.; Yu, C.M. Trajectory Planning of Morphing Aircraft Based on the Probability of Passing through Threat Zones. Aerosp. Control 2024, 42, 35–41. [Google Scholar] [CrossRef]
- Sachs, G.; Holzapfel, F. Flight Mechanic and Aerodynamic Aspects of Extremely Large Dihedral in Birds. In Collection of Technical Papers—45th AIAA Aerospace Sciences Meeting, Reno, NV, USA, 8–11 January 2007; AIAA: Reston, VA, USA, 2007. [Google Scholar] [CrossRef]
- Zhang, J.; Si, J. Study on the Wingbody Longitudinal Characters with Different Wing Dihedral Angles. Chin. J. Appl. Mech. 2013, 30, 167–172. [Google Scholar] [CrossRef]
- Etkin, B. Dynamics of Atmospheric Flight; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Keidel, B. Design and Simulation of High-Flying Permanently Stationary Solar Drones. Ph.D. Dissertation, Technical University of Munich Faculty of Mechanical Engineering, Munich, Bavaria, Germany, 2000. [Google Scholar]
- Asselin, M. An Introduction to Aircraft Performance; AIAA: Reston, VA, USA, 1997. [Google Scholar]
- Shiau, J.-K.; Ma, D.-M.; Yang, P.-Y.; Wang, G.-F.; Gong, J.H. Design of a Solar Power Management System for an Experimental UAV. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1350–1360. [Google Scholar] [CrossRef]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft Actor-Critic Algorithms and Applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Guo, S.; Zhao, X. Multi-agent deep reinforcement learning based transmission latency minimization for delay-sensitive cognitive satellite UAV networks. IEEE Trans. Commun. 2022, 71, 131–144. [Google Scholar] [CrossRef]



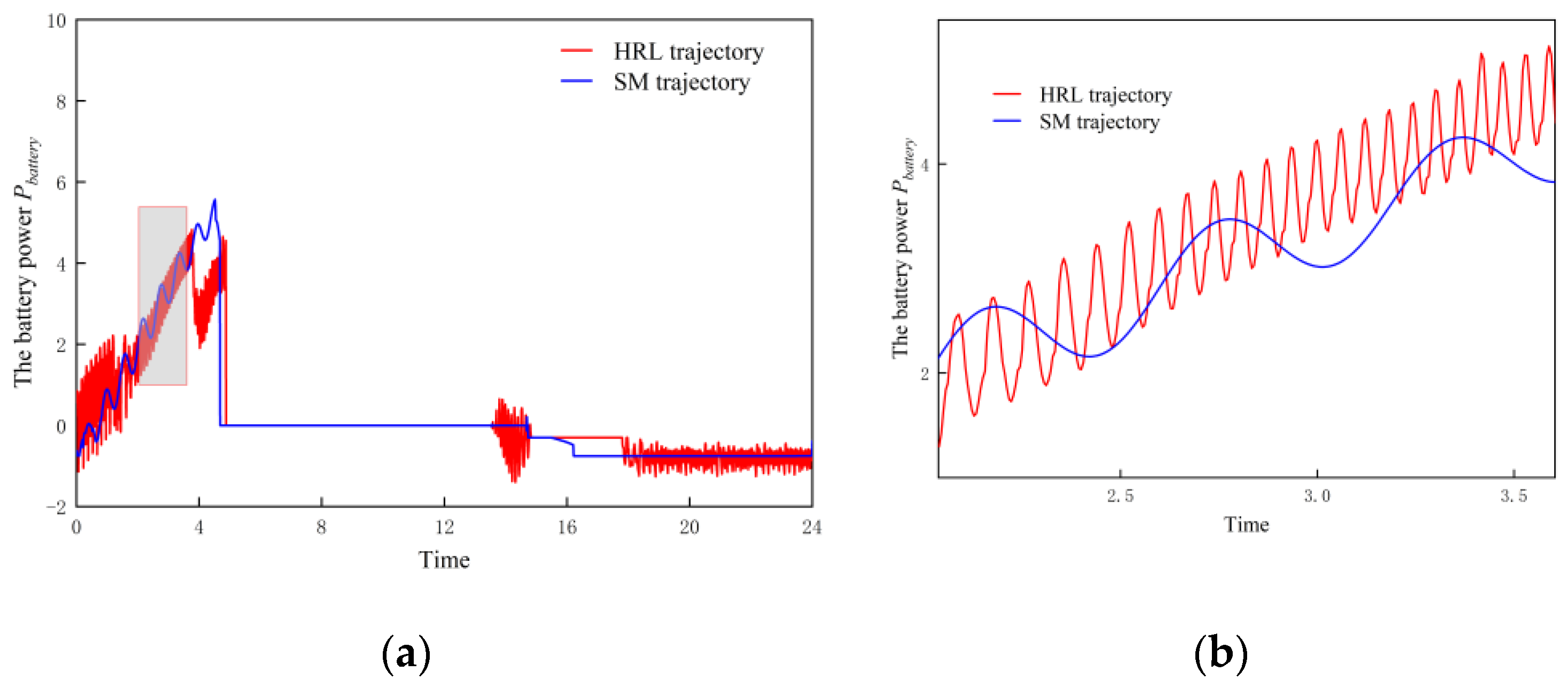


| Parameter | Description | Value | Parameter | Description | Range |
|---|---|---|---|---|---|
| m (kg) | Aircraft mass | 70 | h (m) | Altitude | [15,000, 25,000] |
| Sr,0 (m2) | Reference area when η is 0° | 31.84 | R (m) | Flight radius | [0, 5000] |
| c (m) | Chord length | 1.0272 | V (m/s) | Airspeed | [15, 80] |
| l (m) | Wingspan of a single wing | 15.1 | T (N) | Thrust | [0, 100] |
| SPV (m2) | Solar panel area of a single wing | 12 | α (°) | Attack angle | [−4, 6] |
| Ebattery,max (kWh) | Maximum battery energy | 16 | φ (°) | Bank angle | [−5, 5] |
| Pacc (kW) | Avionics power | 0.3 | η (°) | Wing deflection angle | [−45, 45] |
| ηMPPT | MPPT efficiency | 0.95 | θ (°) | Pitch angle | [−15, 15] |
| ηPV | Solar panel efficiency | 0.3 | ψ (°) | Yall angle | [−180, 180] |
| ηprop | Propeller efficiency | 0.82 | SOC | State of Charge | [0.15, 1] |
| ηmot | Motor efficiency | 0.9 | (°) | Solar altitude angle | [−90, 90] |
| ta (s) | Inner loop response time | 3.33 | (°) | Solar azimuth angle | [−180, 180] |
| Operation Condition | Stage | > 0 | = 0 | Energy Optimal Flight Strategies | ||
|---|---|---|---|---|---|---|
| 1 | ①② | √ | Enhancing solar energy absorption efficiency at low solar altitude angles through wing deflection. | |||
| 2 | ③④⑤ | √ | (1) Balancing battery energy and gravitational potential energy; (2) Shortening the duration of stage ⑤. | |||
| 3 | ⑥ | √ | Minimum energy consumption flight. | |||
| Action Command | Min Value | Max Value |
|---|---|---|
| −10 | 10 | |
| −5 | 5 | |
| −5 | 5 | |
| −10 | 10 |
| Parameter | Description | Value or Range |
|---|---|---|
| Initial time | 4:24 | |
| (h) | Training duration | 6 |
| (m) | Initial location | < 5000 |
| (m) | Initial altitude | 15,000 |
| Initial SOC | [0.15, 1] |
| Parameter | Description | Value or Range |
|---|---|---|
| Initial time | 7:24~10:24 | |
| (h) | Training duration | |
| (m) | Initial location | < 5000 |
| (m) | Initial altitude | [15,000, 15,200] |
| Initial SOC | [0.15, 1.0] |
| Parameter | Description | Value or Range |
|---|---|---|
| Initial time | ~ | |
| (h) | Training duration | 4 |
| (m) | Initial location | < 5000 |
| (m) | Initial altitude | [15,000, 25,000] |
| Initial SOC | [0.15, 1.0] |
| Parameter | Description | Value or Range |
|---|---|---|
| Initial time | 4:24 | |
| (h) | Training duration | |
| (m) | Initial location | < 5000 |
| (m) | Initial altitude | 15,000 |
| Initial SOC | 0.3 |
| Optimizer | Minibatch | Buffer | Learning Rate | α | γ | |
|---|---|---|---|---|---|---|
| Adam | 256 | 0.2 | 0.99 |
| Optimizer | Minibatch | Buffer | Learning Rate | γ | |
|---|---|---|---|---|---|
| Adam | 256 | 0.95 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Meng, W.; Zhang, J. Energy Optimal Trajectory Planning for the Morphing Solar-Powered Unmanned Aerial Vehicle Based on Hierarchical Reinforcement Learning. Drones 2025, 9, 498. https://doi.org/10.3390/drones9070498
Xu T, Meng W, Zhang J. Energy Optimal Trajectory Planning for the Morphing Solar-Powered Unmanned Aerial Vehicle Based on Hierarchical Reinforcement Learning. Drones. 2025; 9(7):498. https://doi.org/10.3390/drones9070498
Chicago/Turabian StyleXu, Tichao, Wenyue Meng, and Jian Zhang. 2025. "Energy Optimal Trajectory Planning for the Morphing Solar-Powered Unmanned Aerial Vehicle Based on Hierarchical Reinforcement Learning" Drones 9, no. 7: 498. https://doi.org/10.3390/drones9070498
APA StyleXu, T., Meng, W., & Zhang, J. (2025). Energy Optimal Trajectory Planning for the Morphing Solar-Powered Unmanned Aerial Vehicle Based on Hierarchical Reinforcement Learning. Drones, 9(7), 498. https://doi.org/10.3390/drones9070498








