Accuracy-Aware MLLM Task Offloading and Resource Allocation in UAV-Assisted Satellite Edge Computing

Abstract

This paper presents a novel framework for optimizing multimodal large language model (MLLM) inference through task offloading and resource allocation in UAV-assisted satellite edge computing (SEC) networks. MLLMs leverage transformer architectures to integrate heterogeneous data modalities for IoT applications, particularly real-time monitoring in remote areas. However, cloud computing dependency introduces latency, bandwidth, and privacy challenges, while IoT device limitations require efficient distributed computing solutions. SEC, utilizing low-earth orbit (LEO) satellites and unmanned aerial vehicles (UAVs), extends mobile edge computing to provide ubiquitous computational resources for remote IoTDs. We formulate the joint optimization of MLLM task offloading and resource allocation as a mixed-integer nonlinear programming (MINLP) problem, minimizing latency and energy consumption while optimizing offloading decisions, power allocation, and UAV trajectories. To address the dynamic SEC environment characterized by satellite mobility, we propose an action-decoupled soft actor–critic (AD-SAC) algorithm with discrete–continuous hybrid action spaces. The simulation results demonstrate that our approach significantly outperforms conventional deep reinforcement learning methods in convergence and system cost reduction compared to baseline algorithms.

1. Introduction

Multimodal large language models (MLLMs) powered by transformer architectures represent a breakthrough in artificial intelligence, fundamentally differing from ordinary AI optimization algorithms such as traditional machine learning models or heuristic optimization techniques. While conventional AI models typically process single-modality data with limited computational complexity, MLLMs integrate diverse data modalities for advanced pattern recognition and contextually rich output generation. However, this advanced functionality comes at the cost of massive computational requirements, often billions of parameters, making their deployment particularly challenging. The prevalent cloud-based deployment model introduces critical bottlenecks: prohibitive latency for real-time applications and excessive bandwidth consumption for multimodal data transmission [1]. These limitations are particularly acute in IoT environments where edge devices possess minimal computational capacity, creating an urgent need for distributed computing solutions specifically designed for MLLMs.

Mobile edge computing (MEC) emerged as a promising solution by bringing computational resources closer to data sources [2,3,4]. However, as IoT applications expand into remote terrestrial and maritime environments, areas crucial for applications like offshore monitoring and disaster response, traditional cellular-based MEC faces fundamental coverage limitations [5]. The prohibitive costs of infrastructure deployment in these regions demand alternative approaches. This gap has catalyzed the development of satellite edge computing (SEC), which leverages low Earth orbit (LEO) satellites augmented by unmanned aerial vehicles (UAVs) to create a ubiquitous computational layer [6,7]. UAVs serve as dynamic computing nodes that can process tasks locally, adapting their positions to optimize coverage and minimize latency, capabilities essential for supporting MLLM-based services in connectivity-challenged environments [8].

The integration of MLLMs into SEC networks unlocks unprecedented possibilities for intelligent edge applications. By enabling complex multimodal reasoning at the network edge, this paradigm supports autonomous decision-making while preserving data privacy. The key to realizing this potential lies in intelligent task distribution: determining optimal processing locations based on task characteristics, network conditions, and available resources. This requires sophisticated algorithms for task offloading and resource allocation that can navigate the trade-offs between computational capacity, communication latency, and energy constraints across heterogeneous computing nodes [9].

However, MLLM task offloading and resource allocation in SEC networks present unique challenges that far exceed traditional edge computing scenarios [10]. The massive parameter scale of MLLMs, often billions of parameters, creates extraordinary computational demands that strain the limited resources of satellite and UAV platforms [11]. Compounding this challenge, the inherent dynamics of SEC networks introduce additional complexity: LEO satellites’ rapid orbital motion causes frequent topology changes, time-varying channel conditions create unpredictable communication links, and the heterogeneous nature of computing nodes, including LEO satellites and UAVs, requires coordinated resource management [12]. These factors render static optimization approaches obsolete, as they cannot adapt to the continuously evolving network state [13].

The complexity and scale of this optimization problem exceed the capabilities of conventional approaches. While dynamic programming suffers from the curse of dimensionality, heuristic methods lack performance guarantees in highly dynamic environments. Deep reinforcement learning (DRL) offers a compelling alternative, learning adaptive policies through interaction with the environment [14,15,16]. However, the SEC task offloading problem presents a particularly challenging scenario: the action space combines discrete decisions (task offloading choices) with continuous variables (power allocation, UAV trajectories) [17]. Traditional DRL methods either discretize the entire action space, sacrificing precision and creating computational bottlenecks, or struggle to handle hybrid action spaces effectively.

Given the aforementioned challenges, this work addresses three key research questions. How can MLLMs be efficiently deployed in UAV-assisted SEC networks to provide ubiquitous services to IoT devices in remote areas? How can we jointly optimize discrete offloading decisions and continuous resource allocation variables to minimize system latency and energy consumption while ensuring MLLM service quality in dynamic SEC environments? How can we develop a DRL that effectively handles the hybrid discrete–continuous action space inherent in SEC task offloading problems?

To address these research questions, this paper aims to achieve comprehensive performance optimization for MLLM inference in UAV-assisted SEC networks through intelligent MLLM task offloading, bandwidth allocation, and UAV trajectory. The primary objective is to develop a framework that minimizes system-wide latency and energy consumption while ensuring reliable MLLM service delivery to remote IoTDs. This involves formulating the joint optimization problem as a mixed-integer nonlinear programming (MINLP) problem that simultaneously handles discrete offloading decisions and continuous resource allocation variables. To solve this challenging optimization problem, we propose an action-decoupled soft actor–critic (AD-SAC) algorithm specifically designed for hybrid discrete–continuous action spaces. This approach maintains the precision of continuous control while efficiently handling discrete decisions, enabling real-time adaptation to dynamic SEC environments. The framework aims to minimize system-wide latency and energy consumption while ensuring sustainable MLLM service delivery to IoTDs in remote environments. The main contributions of this work are summarized as follows.

• We develop a novel MLLM inference framework that jointly optimizes task offloading and resource allocation in UAV-assisted SEC networks, enabling ubiquitous MLLM services for IoT devices in remote environments through coordinated utilization of UAVs and LEO satellites.
• We formulate the joint optimization problem as an MINLP problem that minimizes the weighted sum of MLLM offloading latency and energy consumption. The formulation simultaneously optimizes discrete offloading decisions and continuous variables, including power allocation and UAV trajectories, while satisfying accuracy requirements and accounting for dynamic LEO satellite coverage.
• We propose an AD-SAC algorithm to solve the MINLP problem with hybrid discrete–continuous action spaces. By delegating discrete and continuous actions to specialized agents within a cooperative training framework, AD-SAC effectively leverages off-policy data to develop robust hybrid policies for real-time adaptation.
• Extensive simulation results demonstrate that our proposed method achieves a more effectively converged policy and exhibits enhanced performance in MLLM inference when compared to prevalent DRL baseline algorithms.

The organization of this manuscript is structured as follows. Section 2 reviews the related work. The system model and problem formulation are delineated in Section 3. A comprehensive description of the hybrid space SAC algorithm is provided in Section 4. The performance evaluation of the proposed algorithm is presented in Section 5, and the study is summarized in Section 6.

2. Related Work

This section reviews the relevant literature on LLM deployment in edge computing environments, examining both MEC and SEC paradigms.

2.1. LLM in MEC Networks

LLMs are characterized by their extensive parameter sets and significant computational demands. MEC facilitates data processing and computational tasks for LLM-based applications by performing operations close to end-users, thereby enhancing the efficiency and adaptability of AI services for mobile environments. The authors of [18] introduced an edge inference framework tailored for LLMs in wireless networks, utilizing distributed edge computing to mitigate challenges related to privacy, latency, and resource constraints. This framework employs a novel optimization algorithm, OT-GAH, to address the NP-hard problem of batch scheduling and resource allocation for real-time LLM inference on edge devices. Similarly, He et al. [19] proposed an active inference-based method for offloading LLM tasks and managing resources in cloud–edge systems, overcoming limitations of traditional DRL approaches. Their method enhances data efficiency, adaptability to varying task loads, and sensitivity to latency, with simulations demonstrating superior performance compared to conventional DRL techniques. The EdgeShard framework, presented in [20], leveraged cloud–edge collaboration (CEC) to optimize LLM inference by partitioning models into shards distributed across edge and cloud infrastructures. A dynamic programming algorithm minimizes inference latency and maximizes throughput, yielding significant performance gains in experimental evaluations. Yang et al. [21] introduced PerLLM, a personalized inference scheduling framework that optimizes resource allocation and scheduling in edge–cloud environments to meet diverse service demands while reducing energy consumption, with experiments confirming its efficacy across multiple model deployments. In [22], the Edge-LLM framework is proposed for deploying LLMs in resource-constrained edge settings, incorporating adaptive quantization, an FM cache mechanism, and a value-density-first scheduling algorithm to enhance computational efficiency and reduce task timeouts. Additionally, Hu et al. [23] presented Voltage, a distributed inference system that improves transformer model performance on resource-limited edge devices by distributing workloads across multiple devices, achieving notable gains in speed and efficiency compared to single-device deployments. However, high and variable transmission latency between edge devices and the central cloud infrastructure remains a critical challenge, significantly affecting the performance of LLM inference and finetuning processes.

2.2. LLMs in SEC Networks

The integration of LLM services into SEC networks can substantially enhance the intelligent management and optimization of these complex systems. By enabling the SEC to effectively adapt to dynamic and heterogeneous environments, AI contributes to the improvement of critical performance metrics, including latency, energy efficiency, bandwidth utilization, and real-time adaptability. This enhancement is particularly valuable given AI’s capacity to process extensive datasets and deliver instantaneous decisions, which is essential for addressing the intricate challenges inherent in the operation of the SEC. Tang et al. [24] investigated how LLMs, which are advanced AI systems capable of processing and generating human-like text, can be applied to optimize and intelligently manage space–air–ground integrated networks (SAGINs) that combine satellite, aerial, and terrestrial networks to ensure seamless connectivity and coverage. Xu et al. [10] jointly optimized model caching and inference to deliver LLM agents across SAGINs, minimizing bandwidth and computational and storage costs through an age-of-thought metric and a DRL–based auction mechanism for resource allocation. In [25], the authors developed a diffusion-model-driven digital-twin synchronization framework that orchestrates UAV, LEO satellite, and ground edge resources within space–air–ground integrated networks to deliver timely low-latency AI-generated content (AIGC) services. Zhang et al. [26] introduced generative-AI agents driven by LLM that auto-construct satellite-network optimization problems and solve them with a mixture-of-experts PPO transmission strategy, mitigating interference and boosting 6G satellite link performance. The authors in [27] devised a parameter-training-efficiency aware resource allocation (PARA) framework that co-optimizes user association, data offloading, and communication–compute resources in space–air–ground integrated networks to maximize parameter-efficient finetuning throughput for AIGC tasks under wireless constraints. Despite the advancements in leveraging LLMs for SAGIN and SEC networks, several critical research gaps persist. While existing research has made significant strides in deploying LLMs within MEC and SEC networks, critical gaps remain. The current work predominantly focuses on text-based LLMs and optimization strategies, overlooking the unique challenges posed by multimodal large language models (MLLMs) that process diverse data types, including text, images, and sensor data. This limitation is particularly acute in SEC environments where MLLMs could enable transformative applications such as real-time disaster response and multi-sensor remote monitoring.

Furthermore, existing approaches fail to adequately address the joint optimization of task offloading, resource allocation, and mobility management in highly dynamic SEC environments characterized by LEO satellite movement and heterogeneous computing resources. The hybrid discrete–continuous nature of this optimization problem, combining discrete offloading decisions with continuous power and trajectory variables, remains unexplored. To address these gaps, we propose a novel MLLM inference framework for UAV-assisted SEC networks that jointly optimizes offloading decisions, power allocation, and UAV trajectories. Our approach uniquely considers the computational demands of MLLMs while adapting to dynamic satellite coverage, filling a critical void in the current literature.

3. System Model

This section presents the system model for MLLM inference in UAV-assisted SEC networks. We first describe the network architecture and then introduce the task model, followed by the wireless transmission, latency, and energy consumption models.

3.1. Network Model

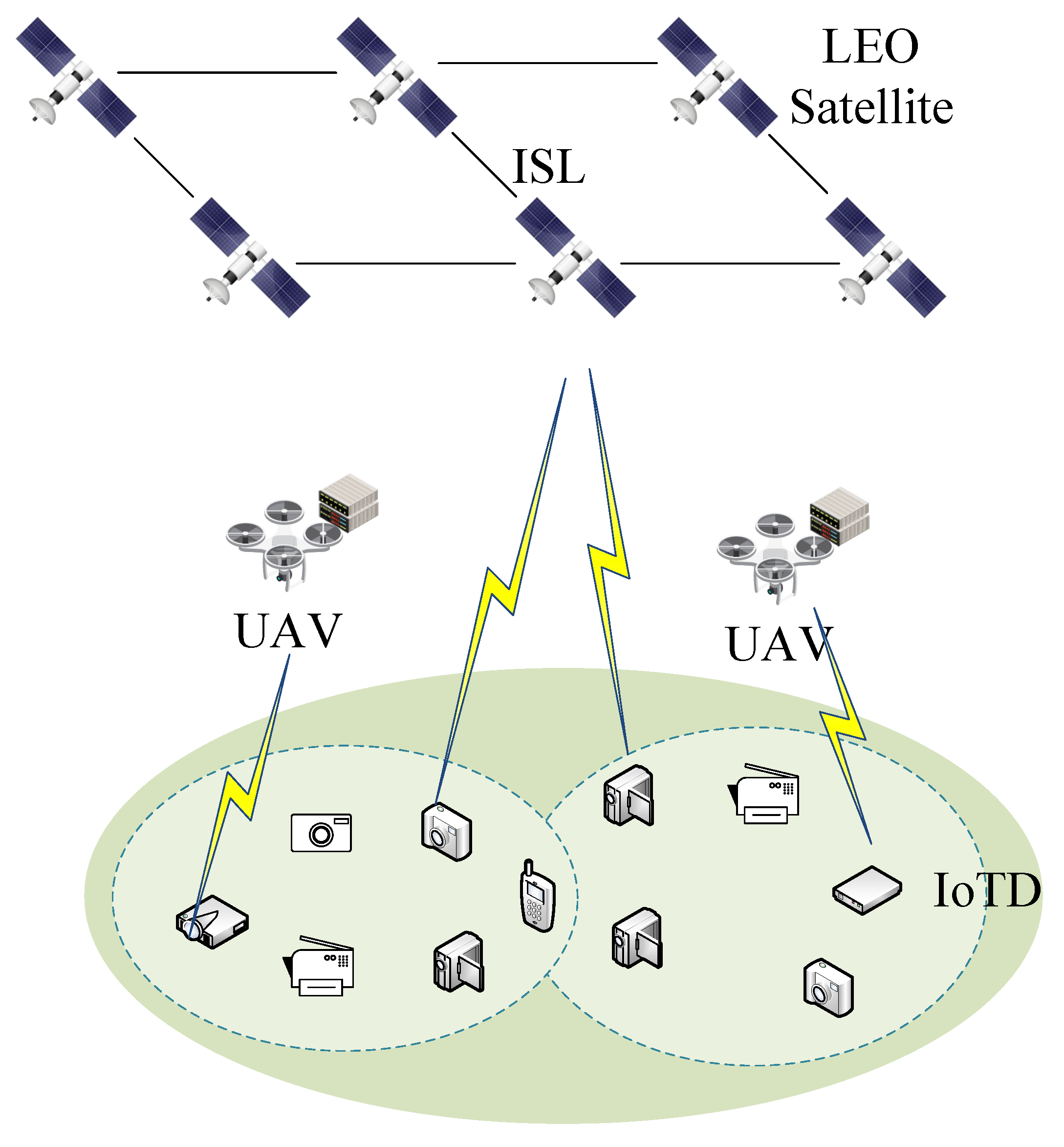
We consider a three-tier SEC network architecture as illustrated in Figure 1, comprising K IoTDs, M UAVs, and N LEO satellites, denoted by the sets $\mathcal{K}=1,2,\dots ,K$, $\mathcal{M}=1,2,\dots ,M$, and $\mathcal{N}=1,2,\dots ,N$, respectively. In this MLLM-enabled SEC framework, resource-constrained IoTDs are not capable of processing the MLLM task locally; thus, the MLLM task requests are offloaded to UAVs and LEO satellites. UAVs deploy smaller MLLMs, offering accuracy $A_m$, for processing tasks, while LEO satellites, equipped with high-performance computing capability, run larger MLLMs, achieving a higher inference accuracy $A_n$. For clarity, MLLMs deployed on UAVs will be referred to as MLMM m, while those deployed on LEO satellites will be referred to as MLMM n.

The system time is discrete into T time slots; within each time slot t, IoTDs can offload MLLM inference tasks to either UAVs through direct wireless links or to LEO satellites via ground-to-satellite communication. This hierarchical architecture enables flexible task distribution based on accuracy requirements, latency constraints, and resource availability.

While some IoTDs may have the ability to perform partial processing of smaller MLLM tasks, this work assumes that all MLLM tasks are offloaded to UAVs or LEO satellites. This assumption is grounded in the resource constraints of typical IoTDs with limited computational power, memory, and energy, which make local processing of large-scale MLLM or quantized MLLM tasks impractical, especially in remote or challenging environments like offshore monitoring or disaster response. By assuming full offloading, we simplify the system model and focus on optimizing task allocation across UAVs and LEO satellites, though extending the framework to include partial local processing remains an interesting avenue for future work.

3.2. Task Model

At each discrete time slot t, IoTD $k\in \mathcal{K}$ generates an MLLM service request characterized by the tuple ${\mathcal{T}}_k\left(t\right)=\langle u_k\left(t\right),o_k\left(t\right),T_k^{max}\left(t\right),a_k\left(t\right)\rangle$, where $u_k\left(t\right)$ denotes the multimodal input data size (bits), encompassing text, image, and video content, $o_k\left(t\right)\in O_1,O_2,\dots ,O_{max}$ represents the discrete output length level, determined by the service type and input characteristics, $T_k^{max}\left(t\right)$ specifies the maximum tolerable latency from task initiation to result reception, and $a_k\left(t\right)$ indicates the minimum acceptable inference accuracy.

The output length $o_k\left(t\right)$, selected from the discrete set $\{O_1,O_2,\dots ,O_{max}\}$, is determined by the specific MLLM application and the characteristics of the input data $u_k\left(t\right)$. For example, in translation tasks, $o_k\left(t\right)$ is typically proportional to the input size $u_k\left(t\right)$, reflecting the length of the translated text. In contrast, video summarization yields a fixed-length summary (e.g., a paragraph), while visual question answering produces a short fixed output (e.g., a few words). The discrete levels $O_1,O_2,\dots ,O_{max}$ are predefined based on the expected output sizes for different application types, allowing the system to accommodate varying computational and bandwidth demands.

Given the computational limitations of IoTDs, all MLLM tasks need to be offloaded to UAVs or LEO satellites. Upon task completion, the server node transmits the processed outcomes back to the IoTD. Formally, let $x_k\left(t\right)=(x_{k,m}\left(t\right),x_{k,n}\left(t\right))$ denote a binary variable for IoTD k, capturing the task offloading choice at time slot t. Here, $x_{k,m}\left(t\right)=1$ signifies that IoTD k assigns the task to UAV m, whereas $x_{k,n}\left(t\right)=1$ indicates that the task is offloaded to LEO satellite n, with $x_{k,n}\left(t\right)=0$ otherwise. A key constraint ensures that, within each time slot, an IoTD’s task is allocated to precisely one execution node. The subsequent constraints governing task offloading are as follows:

$$\sum _{m\in \mathcal{M}}{x}_{k,m}\left(t\right)+\sum _{n\in \mathcal{N}}{x}_{k,n}\left(t\right)=1,\forall k\in \mathcal{K}.$$

(1)

Additionally, accuracy constraints must be satisfied based on the selected computing node:

$$x_{k,m}\left(t\right)·A_m+x_{k,n}\left(t\right)·A_n\ge a_k\left(t\right),\forall k\in \mathcal{K}.$$

(2)

While IoTD locations and wireless channels remain stable within each time slot, inter-slot variations arise from device mobility and environmental dynamics, necessitating adaptive resource allocation strategies.

3.3. Service Coverage Model

The heterogeneous nature of the SEC network necessitates distinct coverage models for UAVs and LEO satellites, reflecting their different mobility patterns and communication characteristics.

3.3.1. UAV Service Coverage

Each UAV $m\in \mathcal{M}$ maintains a circular service coverage area with radius $R_m^{cov}$, within which IoTDs can establish communication links for task offloading. At time slot t, UAV m operates at position ${\mathbf{L}}_m\left(t\right)=(q_m^X\left(t\right),q_m^Y\left(t\right),q_m^Z)$, where $(q_m^X\left(t\right),q_m^Y\left(t\right))$ denote the horizontal coordinates, and $q_m^Z$ represents the fixed flight altitude. For IoTD k located at ${\mathbf{L}}_k=(q_k^X,q_k^Y,0)$ to successfully offload tasks to UAV m, the following coverage constraint must be satisfied:

$$d_{k,m}\left(t\right)=\sqrt{{(q_m^X\left(t\right)-q_k^X\left(t\right))}^2+{(q_m^Y\left(t\right)-q_k^Y\left(t\right))}^2}\le R_m^{cov}.$$

(3)

This constraint ensures that only IoTDs within the UAV’s coverage can access its computational resources, directly impacting the feasibility of offloading decisions.

3.3.2. LEO Satellite Service Coverage

Unlike stationary UAVs, LEO satellites exhibit continuous orbital motion, creating time-varying coverage windows for ground IoTDs. The visibility duration $T_{k,n}^{vis}$ during which IoTD k can communicate with satellite $n\in \mathcal{N}$ is determined by

$$T_{k,n}^{vis}={\displaystyle \frac{l_{k,n}}{v_{k,n}}},$$

(4)

where $v_{k,n}$ represents the linear velocity of the accessible LEO satellite n for IoTD k. Let $l_{k,n}=2(re+d_{k,n}){\omega }_{k,m}$ denote the arc length of the ground-to-satellite communication link between IoTD k and its accessible LEO satellite n, where ${\omega }_{k,m}$ is the coverage angle of the accessible LEO satellite n, calculated as follows:

$${\omega }_{k,m}=arccos{\displaystyle \frac{re}{re+d_{k,n}}}cos{\theta }_{k,n}-{\theta }_{k,n},$$

(5)

where $d_{k,n}$ signifies the altitude of the accessible LEO satellite n from the ground for IoTD k, $re$ denotes the Earth’s radius, and ${\theta }_{k,n}$ represents the elevation angle between IoTD k and its accessible LEO satellite n.

3.4. Communication Model

The wireless channels in the UAV-assisted SEC network exhibit distinct characteristics for UAV and satellite links. In this paper, we consider radio frequency (RF) wireless communication channels for both ground-to-UAV and ground-to-satellite links [28], rather than free space optical (FSO) channels [29]. The choice of RF communication is motivated by its robustness to weather conditions and lower pointing requirements compared to FSO, which is particularly important for mobile UAVs and fast-moving LEO satellites.

3.4.1. Ground-to-UAV Communication

Similar to the existing works [30], the channel between IoTD k and UAV m follows a Rician fading model, capturing both line-of-sight (LoS) and non-line-of-sight (NLoS) components. The channel coefficient is expressed as

$$h_{k,m}\left(t\right)=\sqrt{{\beta }_0{d}_{k,m}^{-\alpha }\left(t\right)}·{\widehat{h}}_{k,m}\left(t\right),$$

(6)

where ${\beta }_0$ represents the reference channel gain at unit distance, and $\alpha$ is the path-loss exponent (typically $\alpha =2$ for UAV communications). Then, the ${\widehat{h}}_{k,m}\left(t\right)$ denotes the small-scale fading component:

$${\widehat{h}}_{k,m}\left(t\right)=\sqrt{{\displaystyle \frac{\kappa }{\kappa +1}}}{\overline{h}}_{k,m}+\sqrt{{\displaystyle \frac{1}{\kappa +1}}}{\tilde{h}}_{k,m},$$

(7)

where $\kappa$ is the Rician factor, $|{\overline{h}}_{k,m}|=1$ represents the LoS component, and ${\tilde{h}}_{k,m}\sim \mathcal{CN}(0,1)$ denotes the NLoS component.

When the MLLM tasks are offloaded to the UAVs, the uplink transmission rate $R_{k,m}^{up}$ from the IoTD k to the UAV m is expressed as

$$R_{k,m}^{up}\left(t\right)=B_m{log}_2\left(1+{\displaystyle \frac{h_{k,m}\left(t\right)P_k\left(t\right)}{{\sum }_{j\in K\backslash \left\{k\right\}}{h}_{j,m}\left(t\right)P_j\left(t\right)+N_0}}\right),$$

(8)

where $P_k$ denotes the uplink transmit power of the IoTD k, $B_m$ signifies the channel bandwidth of the UAV m, and $N_0$ signifies the power spectral density of the AWGN. Correspondingly, the downlink transmission rate $R_{k,m}^{dl}$ is given as

$$R_{k,m}^{dl}\left(t\right)=B_m{log}_2\left(1+{\displaystyle \frac{h_{k,m}\left(t\right)P_m\left(t\right)}{{\sum }_{j\in M\backslash \left\{m\right\}}{h}_{k,j}\left(t\right)P_m\left(t\right)+N_0}}\right).$$

(9)

3.4.2. Ground-to-Satellite Communication

Satellite links experience more severe propagation conditions, modeled using the Rician-Shadowed fading distribution to capture atmospheric effects and shadowing. The uplink rate from IoTD k to satellite n is

$$R_{k,n}^{up}\left(t\right)=B_n{log}_2\left(1+{\displaystyle \frac{h_{k,n}\left(t\right)P_k\left(t\right)}{{\sum }_{i\in K\backslash \left\{k\right\}}{h}_{j,n}\left(t\right)P_j\left(t\right)+N_0}}\right),$$

(10)

where $h_{k,n}\left(t\right)$ represents the channel power gain between the IoTD k and the LEO satellite n following the Racian-Shadowed fading model [31], and $B_n$ indicates the channel bandwidth of LEO satellite n. For the downlink, the large propagation distance typically eliminates inter-satellite interference at the IoTD. Then, the downlink transmission rate $R_{k,n}^{dl}$ can be calculated as

$$R_{k,n}^{dl}\left(t\right)=B_n{log}_2\left(1+{\displaystyle \frac{h_{k,n}\left(t\right)P_n\left(t\right)}{N_0}}\right).$$

(11)

3.5. Computing Model

The MLLM inference process involves three sequential phases: uplink transmission of multimodal input data, inference computation, and downlink transmission of generated results. This section models the latency and energy consumption for both UAV and LEO satellite computing.

3.5.1. UAV Computing Latency

When IoTDs choose to offload their MLLM tasks to UAVs through wireless connections, the communication latency model encompasses both the upload transmission latency and the latency associated with returning the results. In this context, the term $T_k^{UAV}$ represents the total UAV computing latency, which includes the latency needed to upload multimodal data from IoTD k to UAV m, the inference processing latency at UAV m, and the transmission of the resulting data back to IoTD k. For a specified volume of multimodal input data $u_k\left(t\right)$, the upload transmission latency can be calculated by

$$T_{k,m}^{up}\left(t\right)={\displaystyle \frac{u_k\left(t\right)}{R_{k,m}^{up}\left(t\right)}}.$$

(12)

Hence, the energy consumption of upload transmission from IoTD k to UAV m is

$$E_{k,m}^{up}\left(t\right)=P_k\left(t\right)T_{k,m}^{up}\left(t\right).$$

(13)

Upon acquiring multimodal data, UAV m is able to handle the MLLM inference request for IoTD k. The inference execution duration, denoted as $T_{k,m}^{exe}\left(t\right)$, is influenced by the maximum floating-point operations per second (FLOPS) capacity of the onboard computing capability of UAV m, in addition to the total computational resources required for the inference process. Consequently, the computational latency for the MLLM on UAV m to generate content for IoTD k can be expressed as

$$T_{k,m}^{exe}\left(t\right)={\displaystyle \frac{v_m·o_k\left(t\right)}{f_m^{gpu}}},$$

(14)

where $v_m$ denotes the number of FLOPS used by one inference step of MLLM on UAV m per output word, and $f_m^{gpu}$ is the FLOPS capability of UAV m.

The energy consumption associated with the inference task of IoTD k on UAV m is expressed as

$$E_{k,m}^{exe}\left(t\right)=P_m^{exe}{T}_{k,m}^{exe}\left(t\right),$$

(15)

where $P_m^{exe}$ denotes the power consumption of UAV m’s processing unit.

During the result return phase, the output of the MLLM task for IoTD k is determined by multiplying the average data size per output word, denoted as $d^{token}$ (in bits per word), by the total number of output words. Consequently, the downlink transmission latency is defined as

$$T_{k,m}^{dl}\left(t\right)={\displaystyle \frac{d^{token}{o}_k\left(t\right)}{R_{k,m}^{dl}\left(t\right)}},$$

(16)

where $R_{km}^{dl}\left(t\right)$ represents the downlink transmission rate between IoTD k and UAV m.

The energy consumption associated with the downlink transmission from UAV m to IoTD k is computed as

$$E_{k,m}^{dl}\left(t\right)=P_m{T}_{k,m}^{dl}\left(t\right),$$

(17)

where $P_m$ represents the transmission power of UAV m.

In summary, the total UAV computing latency for IoTD k on UAV m at time slot t is expressed as

$$T_{k,m}^{UAV}\left(t\right)=T_{k,m}^{up}\left(t\right)+T_{k,m}^{exe}\left(t\right)+T_{k,m}^{dl}\left(t\right).$$

(18)

Thus, the total energy consumption for the MLLM task of IoTD k processed on UAV m is calculated as follows.

$$E_{k,m}^{UAV}\left(t\right)=E_{k,m}^{up}\left(t\right)+E_{k,m}^{exe}\left(t\right)+E_{k,m}^{dl}\left(t\right).$$

(19)

3.5.2. LEO Satellite Computing Latency

Analogous to the UAV computing latency, when IoTD k offloads its MLLM request to a LEO satellite, the process involves IoTD k initially transmitting multimodal data to the LEO satellite n through a ground-to-satellite link.

If an MLLM task is transmitted from accessible satellite n to satellite $n^{\prime }$ via a multi-hop path through inter-satellite links (ISL), the transmission latency of ISL needs to be considered. Let the path be a sequence of satellites $s_1,s_2,\dots ,s_h$, where $s_1=n$ and $s_h=n^{\prime }$. Then, the upload transmission latency from IoTD k to the satellite $n^{\prime }$ via accessible satellite n can be expressed as

$$T_{k,n,n^{\prime }}^{up}\left(t\right)={\displaystyle \frac{u_k\left(t\right)}{R_{kn}^{up}\left(t\right)}}+{\displaystyle \frac{d_{k,n}}{c}}+{\mathbb{I}}_{k,n,n^{\prime }}\left(t\right)\sum _{i=1}^{h-1}\left({\displaystyle \frac{d_{s_i,s_{i+1}}}{c}}+{\displaystyle \frac{u_k\left(t\right)}{R_{ISL}}}\right),$$

(20)

where c is the speed of light for propagation latency, $d_{s_i,s_{i+1}}$ is the distance between satellites $s_i$ and $s_{i+1}$, $H_{n,n^{\prime }}$ is the number of routing hops, and $R_{ISL}$ is the transmission rate of the ISL. Here, ${\mathbb{I}}_{k,n,n^{\prime }}\left(t\right)$ is the indicator function of whether or not the accessible satellite n and offloaded satellite $n^{\prime }$ are the same, which is defined as

$${\mathbb{I}}_{k,n,n^{\prime }}\left(t\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}n\ne n^{\prime },\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(21)

Consequently, the energy consumption for the upload transmission from IoTD k to LEO satellite $n^{\prime }$ via accessible satellite n is expressed as

$$\begin{array}{cc}\hfill E_{k,n}^{up}\left(t\right)& =P_k\left(t\right)\left({\displaystyle \frac{u_k\left(t\right)}{R_{kn}^{up}\left(t\right)}}+{\displaystyle \frac{d_{k,n}}{c}}\right)\hfill \\ \hfill & +{\mathbb{I}}_{k,n,n^{\prime }}\left(t\right)\sum _{i=1}^{h-1}{P}_{ISL}\left({\displaystyle \frac{d_{s_i,s_{i+1}}}{c}}+{\displaystyle \frac{u_k\left(t\right)}{R_{ISL}}}\right),\hfill \end{array}$$

(22)

where $P_{ISL}$ is the transmission power of the ISL.

When the MLLM task is executed on the LEO satellite, the inference latency for IoTD k at LEO satellite n is calculated as

$$T_{k,n}^{exe}\left(t\right)={\displaystyle \frac{v_n·o_k\left(t\right)}{f_n^{gpu}}},$$

(23)

where $v_n$ represents the number of FLOPs used by one inference step of MLLM on LEO satellite n per output word, and $f_n^{gpu}$ is the FLOPS of LEO satellite n.

The inference energy consumption for IoTD k’s task executed on LEO satellite n is

$$E_{k,n}^{exe}\left(t\right)=P_n^{exe}{T}_{k,n}^{exe}\left(t\right),$$

(24)

where $P_n^{exe}$ represents the device power of LEO satellite n.

The latency associated with transmitting the token results from LEO satellite $n^{\prime }$ to IoTD k through accessible satellite n is expressed as

$$\begin{array}{cc}\hfill T_{k,n^{\prime },n}^{dl}\left(t\right)& ={\mathbb{I}}_{k,n,n^{\prime }}\left(t\right)\sum _{i=1}^{h-1}\left({\displaystyle \frac{d_{s_i,s_{i+1}}}{c}}+{\displaystyle \frac{d^{token}{o}_k\left(t\right)}{R_{ISL}}}\right)\hfill \\ \hfill & +{\displaystyle \frac{d^{token}{o}_k\left(t\right)}{R_{km}^{dl}\left(t\right)}}+{\displaystyle \frac{d_{k,n}}{c}},\hfill \end{array}$$

(25)

where $R_{kn}^{dl}\left(t\right)$ represents the downlink transmission rate of the ground-to-satellite link.

The energy consumption for the resulting transmission from LEO satellite $n^{\prime }$ to IoTD k through accessible satellite n is given by

$$\begin{array}{cc}\hfill E_{k,n}^{dl}\left(t\right)& ={\mathbb{I}}_{k,n^{\prime },n}\left(t\right)\sum _{i=1}^{h-1}{P}_{ISL}\left({\displaystyle \frac{d_{s_i,s_{i+1}}}{c}}+{\displaystyle \frac{d^{token}{o}_k\left(t\right)}{R_{ISL}}}\right)\hfill \\ \hfill & +P_n\left({\displaystyle \frac{d^{token}{o}_k\left(t\right)}{R_{kn}^{dl}\left(t\right)}}+{\displaystyle \frac{d_{k,n}}{c}}\right),\hfill \end{array}$$

(26)

In summary, the LEO satellite computing latency for the MLLM task of IoTD k is calculated as

$$T_{k,n}^{sat}\left(t\right)=T_{k,n,n^{\prime }}^{up}\left(t\right)+T_{k,n^{\prime }}^{exe}\left(t\right)+T_{k,n^{\prime },n}^{dl}\left(t\right).$$

(27)

The energy consumption for LEO satellite computing associated with the MLLM task of IoTD k is expressed as

$$E_{k,n}^{sat}\left(t\right)=E_{k,n,n^{\prime }}^{up}\left(t\right)+E_{k,n^{\prime }}^{exe}\left(t\right)+E_{k,n^{\prime },n}^{dl}\left(t\right).$$

(28)

The total latency for the MLLM service request of IoTD k is

$$T_k\left(t\right)=\sum _{m=1}^M{x}_{k,m}\left(t\right)T_{k,m}^{UAV}\left(t\right)+\sum _{n=1}^N{x}_{k,n}\left(t\right)T_{k,n}^{sat}\left(t\right).$$

(29)

The total energy consumption for the MLLM task of IoTD k across all server nodes is given by

$$E_k\left(t\right)=\sum _{m=1}^M{x}_{k,m}\left(t\right)E_{k,m}^{UAV}\left(t\right)+\sum _{n=1}^N{x}_{k,n}\left(t\right)E_{k,n}^{sat}\left(t\right).$$

(30)

3.6. Problem Formulation

This section formulates the MLLM task offloading and resource allocation problem as an MINLP problem. The objective is to minimize the weighted sum of the system latency and energy consumption for MLLM task requests from IoTDs within UAV-assisted SEC networks. The optimization simultaneously optimizes the offloading decisions, transmission power allocation of IoTDs, and UAV trajectory while satisfying the accuracy requirements of the IoTDs. The optimization problem is structured as follows:

$${\mathcal{P}}_1:\underset{\mathbf{X},\mathbf{P},\mathbf{L}}{\min }\underset{T⟶\infty }{lim}{\displaystyle \frac{1}{T}}{\displaystyle \frac{1}{K}}\sum _{t=0}^{T-1}\sum _{k=1}^K{\eta }_l{T}_k\left(t\right)+{\eta }_e{E}_k\left(t\right)$$

(31)

$$\mathrm{such}\mathrm{that}\left(1\right),\left(2\right),$$

$$x_{k,m}\left(t\right),x_{k,n}\left(t\right)\in \{0,1\},\forall n\in \mathcal{N},m\in \mathcal{M},$$

(31a)

$$x_{k,m}\left(t\right)A_m+x_{k,n}\left(t\right)A_n\ge a_k,$$

(31b)

$$T_k\left(t\right)\le T_k^{max},$$

(31c)

$$P_k\left(t\right)\le P_k^{max},$$

(31d)

where $\mathit{X}={\{x_{k,m},x_{k,n}\}}_{k\in \mathcal{K},n\in \mathcal{N},m\in \mathcal{M}}$ represents the offloading decisions of IoTDs, $\mathit{P}={\left\{P_k\right\}}_{k\in \mathcal{K}}$ indicates the transmitted power allocation of IoTDs, and $\mathit{L}={\left\{L_k\right\}}_{k\in \mathcal{K}}$ denotes the locations of IoTDs. Constraint (31a) delineates the offloading decision for the MLLM task associated with IoTD k. Constraint (31b) signifies that the offloaded server node fulfills the minimum accuracy threshold specified by IoTD k. Constraint (31c) establishes the upper bound on acceptable latency for each MLLM task. Constraint (31d) enforces that the maximum transmission power of IoTD k.

In the objective function, the terms $T_k\left(t\right)$ and $E_k\left(t\right)$ have distinct physical units and cannot be summed directly. To resolve this, we employ weight factors ${\eta }_l$ and ${\eta }_e$ to form the weighted sum ${\eta }_l{T}_k\left(t\right)+{\eta }_e{E}_k\left(t\right)$. These factors serve dual purposes: (1) they ensure dimensional consistency by making the terms dimensionless or commensurable, and (2) they normalize the contributions of delay and energy, enabling a fair comparison in the optimization process. The values of ${\eta }_l$ and ${\eta }_e$ can be adjusted based on system requirements, such as typical latency and energy scales or the relative importance of each objective, allowing the framework to effectively balance real-time performance and energy efficiency.

4. Hybrid Action Space SAC-Based MLLM Task Offloading and Resource Allocation Scheme

In this section, we address the challenges of optimizing task offloading and resource allocation for MLLMs in the SEC environment. Specifically, we consider MLLM tasks that involve processing inputs from the MMMU dataset [32], which includes multimodal inputs consisting of text sequences of varying lengths and images. The MLLMs deployed on the servers include VILA1.5 (3B, 8B, 13B parameters) [33], Obsidian 3B [34], and Llava1.6 (7B, 13B parameters) [35]. To accommodate different computational constraints and accuracy requirements, these models are deployed with various quantization levels ranging from 4-bit to semi-precision, enabling flexible trade-offs between inference speed and model accuracy.

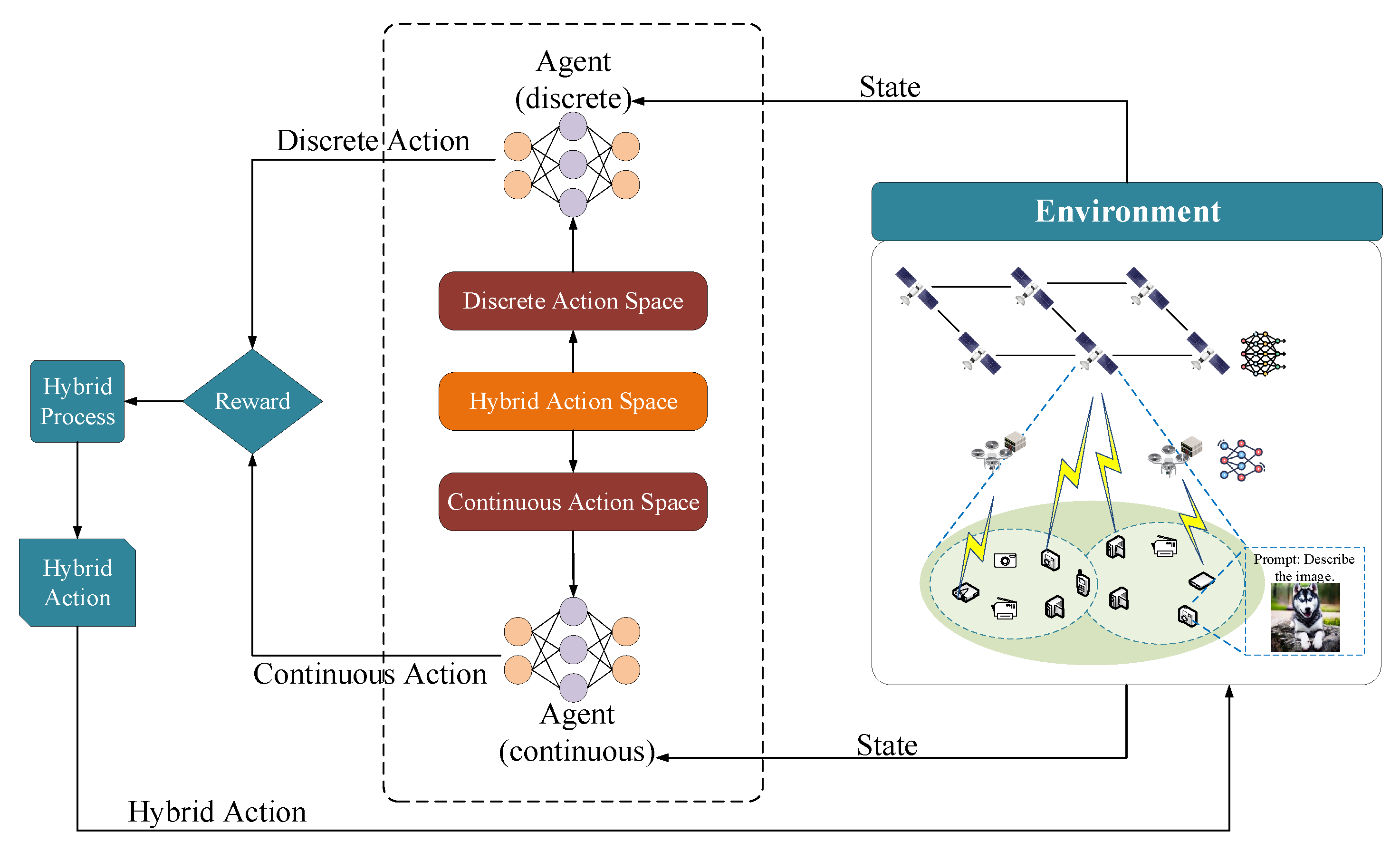
DRL is particularly effective for tackling the long-term optimization objectives of the identified challenges, despite the complications arising from complex hybrid discrete–continuous action spaces. Traditional methods, such as discretizing continuous actions or converting discrete actions to a continuous format, often result in excessively large action spaces or significant exploration demands. To address these challenges, we propose a hybrid action space framework that decouples actions and allocates them to separate agents for collaborative learning, thereby effectively integrating discrete and continuous policies.

4.1. Markov Decision Process

Prior to implementing DRL algorithms, it is essential to formulate each problem as an MDP. An MDP is characterized by three fundamental components: state, action, and reward.

4.1.1. State Space

The system state at any given time slot t is conceptualized as encompassing several distinct elements, which can be expressed as

$$\begin{array}{cc}\hfill s\left(t\right)=\{& {\left\{u_k\left(t\right)\right\}}_{k\in \mathcal{K}},{\left\{o_k\left(t\right)\right\}}_{k\in \mathcal{K}},{\left\{a_k\left(t\right)\right\}}_{k\in \mathcal{K}},{\left\{T_k^{max}\left(t\right)\right\}}_{k\in \mathcal{K}},\hfill \\ \hfill & {\{h_{k,n}\left(t\right),h_{k,m}\left(t\right)\}}_{k\in \mathcal{K},m\in \mathcal{M},n\in \mathcal{N}},\hfill \\ \hfill & {\{L_k\left(t\right)\}}_{k\in \mathcal{K}},{\left\{T_{k,n}^{\mathrm{vis}}\left(t\right)\right\}}_{k\in \mathcal{K},n\in \mathcal{N}}\},\hfill \end{array}$$

(32)

where ${\left\{u_k\left(t\right)\right\}}_{k\in \mathcal{K}}$ describes the input data size of IoTDs’ MLLM request, ${\left\{o_k\left(t\right)\right\}}_{k\in \mathcal{K}}$ represents the length of the generated text output of the k-th MLLM request, ${\left\{a_k\left(t\right)\right\}}_{k\in \mathcal{K}}$ indicates the required accuracy for the k-th MLLM request, and ${\left\{T_k^{max}\left(t\right)\right\}}_{k\in \mathcal{K}}$ denotes the maximum tolerable latency. ${\{h_{k,n}\left(t\right),h_{k,m}\left(t\right)\}}_{k\in \mathcal{K},m\in \mathcal{M},n\in \mathcal{N}}$ signifies the channel gains between IoTDs and UAVs and between IoTDs and LEO satellites. ${\left\{L_k\left(t\right)\right\}}_{k\in \mathcal{K}}$ represents the locations of IoTDs at each time slot t. ${\left\{T_{k,n}^{\mathrm{vis}}\left(t\right)\right\}}_{k\in \mathcal{K},n\in \mathcal{N}}$ indicates the visibility window of the accessible LEO satellite.

4.1.2. Action Space

After observing the state $s\left(t\right)$ at a specific time slot t, the agent undertakes an action $a\left(t\right)$, which is defined as

$$a\left(t\right)=\{\mathit{X},\mathit{P},\mathit{L}\},$$

(33)

where $\mathit{X}$ is the offloading decision, $\mathit{P}$ represents the power allocation strategies, and $\mathit{L}$ indicates the trajectory decisions of UAVs.

4.1.3. Reward Function

To align the DRL objective with the aim of minimizing the total energy consumption, which contrasts with the conventional goal of maximizing cumulative rewards, we define the reward function as the inverse of the weighted sum of system latency and energy consumption for MLLM task requests. The reward function can be defined as

$$r(s\left(t\right),a\left(t\right))={\displaystyle \frac{K{\beta }_r}{{\sum }_{k=1}^K\left({\eta }_l{T}_k\left(t\right)+{\eta }_e{E}_k\left(t\right)\right)}},$$

(34)

where ${\beta }_r$ is the adjustable coefficient.

4.2. SAC Framework

To optimize the decision variables in alignment with the MDP defined for Equation (34), we utilize the SAC algorithm to identify effective solutions. The SAC algorithm, an actor–critic method, integrates policy-based and value-based strategies, employing four neural networks: a value function network parameterized by $\varphi$, a soft Q-function network parameterized by $\theta$, a policy network parameterized by $\vartheta$, and a target value function network denoted by $\overline{\varphi }$. Then, we clarify the roles of different Q-function networks:

• $Q_{\varphi }\left(s\left(t\right)\right)$: the state value function network that estimates the expected return from state $s\left(t\right)$ under the entropy-regularized policy.
• $Q_{\theta }(s\left(t\right),a\left(t\right))$: the soft Q-function network that evaluates state-action pairs, incorporating entropy bonuses in the value estimation.
• $Q_{\overline{\varphi }}\left(s\left(t\right)\right)$: the target value function network, updated slowly for training stability.
• $\overline{Q}(s\left(t\right),a\left(t\right))$: the target Q-value computed using the Bellman equation: $\overline{Q}(s\left(t\right),a\left(t\right))=r(s\left(t\right),a\left(t\right))+\gamma Q_{\overline{\varphi }}\left(s(t+1)\right)$.

In practice, these networks require training to implement the SAC algorithm. The update rule for the value function is given as

$$\begin{array}{cc}\hfill J_{Q_{\varphi }}& =\mathbb{E}\left[{\displaystyle \frac{1}{2}}\left(Q_{\varphi }\left(s\left(t\right)\right)-\mathbb{E}\left[Q_{\theta }(s\left(t\right),a\left(t\right))\right.\right.{\left.\left.-log{\pi }_{\vartheta }\left(a\left(t\right)\right|s\left(t\right))\right]\right)}^2\right]\hfill \end{array},$$

(35)

where the Q-value associated with a given network is denoted by $Q_{·}$, the expectation operator by $\mathbb{E}[·]$, and the sample distribution by $\mathcal{D}$. The SAC algorithm minimizes the loss by leveraging the squared residual error for the value function. The gradient of the value function loss, as derived from Equation (35), is expressed as

$$\begin{array}{cc}\hfill {\nabla }_{\varphi }{J}_{Q_{\varphi }}=& {\nabla }_{\varphi }{Q}_{\varphi }\left(s\left(t\right)\right)(Q_{\varphi }\left(s\left(t\right)\right)-Q_{\theta }(s\left(t\right),a\left(t\right))+log{\pi }_{\vartheta }\left(a\left(t\right)\right|s\left(t\right))).\hfill \end{array}$$

(36)

Additionally, the loss function for updating the soft Q-network $Q_{\theta }$ is formulated as

$$J_{Q_{\theta }}=\mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\theta }(s\left(t\right),a\left(t\right))-\overline{Q}(s\left(t\right),a\left(t\right))\right)}^2\right],$$

(37)

where the target Q-value $\overline{Q}(s\left(t\right),a\left(t\right))$ is defined as

$$\overline{Q}(s\left(t\right),a\left(t\right))=r(s\left(t\right),a\left(t\right))+\gamma \mathbb{E}\left[Q_{\overline{\varphi }}\left(s(t+1)\right),\right],$$

(38)

with $\gamma$ representing the discount factor and $\rho$ denoting the state transition probability.

The corresponding gradient for the Q-network update is given by

$$\begin{array}{cc}\hfill {\nabla }_{\theta }{J}_{Q_{\theta }}& ={\nabla }_{\theta }{Q}_{\theta }(s\left(t\right),a\left(t\right))(Q_{\theta }(s\left(t\right),a\left(t\right))-r(s\left(t\right),a\left(t\right))-\gamma Q_{\overline{\varphi }}\left(s(t+1)\right)).\hfill \end{array}$$

(39)

Furthermore, the policy network is reformulated through a neural network transformation defined as $a\left(t\right)=f_{\vartheta }(\xi \left(t\right);s\left(t\right))$, where $\xi \left(t\right)$ represents a noise term adhering to a Gaussian distribution. The loss function for updating the policy network ${\pi }_{\vartheta }$ is computed as

$$\begin{array}{cc}\hfill J_{{\pi }_{\vartheta }}=& \mathbb{E}\left[log{\pi }_{\vartheta }\left(f_{\vartheta }(\xi \left(t\right);s\left(t\right))\right|s\left(t\right))-Q_{\theta }(s\left(t\right),f_{\vartheta }(\xi \left(t\right);s\left(t\right)))\right],\hfill \end{array}$$

(40)

where $\varphi$ signifies the normal distribution. The corresponding gradient is calculated by

$$\begin{array}{cc}\hfill {\nabla }_{\vartheta }{J}_{{\pi }_{\vartheta }}=& {\nabla }_{\vartheta }log{\pi }_{\vartheta }\left(a\left(t\right)\right|s\left(t\right))+({\nabla }_{a\left(t\right)}log{\pi }_{\vartheta }\left(a\left(t\right)\right|s\left(t\right))-\hfill \\ \hfill & {\nabla }_{a\left(t\right)}{Q}_{\theta }(s\left(t\right),a\left(t\right))){\nabla }_{\vartheta }{f}_{\vartheta }(\xi \left(t\right);s\left(t\right)),\hfill \end{array}$$

(41)

with the Q-value updated as

$$\begin{array}{cc}\hfill Q\left(s\right(t),a(t\left)\right)=& r(s\left(t\right),a\left(t\right))+\gamma \mathbb{E}\left[Q_{\overline{\varphi }}\left(s(t+1)\right)\right],\hfill \end{array}$$

(42)

where $\gamma$ denotes the discount factor, and $\rho$ represents the state transition probability.

4.3. Continuous–Discrete Action Space-Based SAC Algorithm

In the optimization challenges delineated in problem ${\mathcal{P}}_1$, the decision-making process involves a combination of discrete and continuous actions, presenting a substantial obstacle for traditional DRL algorithms [36]. Conventional techniques frequently address this issue by converting the continuous action space into a discrete form, which significantly expands the size of the action space. Alternatively, some methods attempt to reframe discrete actions as continuous, a strategy that increases complexity and obstructs the training process’s ability to converge effectively. To mitigate these difficulties, we propose the integration of an action decoupling algorithm within the SAC framework through decomposing the Q-functions into discrete and continuous components:

• Discrete agent networks: $Q_{\mu }^{\varphi }$, $Q_{\mu }^{\theta }$, $Q_{\mu }^{\vartheta }$ handle discrete actions (offloading decisions), where subscript $\mu$ denotes discrete components.
• Continuous agent networks: $Q_{\nu }^{\varphi }$, $Q_{\nu }^{\theta }$, $Q_{\nu }^{\vartheta }$ handle continuous actions (power allocation and UAV trajectories), where subscript $\nu$ denotes continuous components.

This approach entails a redefinition of both the action and the policy, enabling more efficient management of the hybrid action space. The policy function and action can be redefined as

$$\begin{array}{cc}\hfill Q_{\vartheta }\left(a\right|s)& =Q_{\mu }^{\vartheta }\left(a_{\mu }\right|s)·Q_{\nu }^{\vartheta }\left(a_{\nu }\right|s)=\prod _{a_i\in a_{\mu }}{Q}_{\mu }^{\vartheta }\left(a_i\right|s)·\prod _{a_j\in a_{\nu }}{Q}_{\nu }^{\vartheta }\left(a_j\right|s),\hfill \end{array}$$

(43)

$$A=\{\mu ,\nu \},$$

(44)

where, $\mu$ represents discrete actions, and $\nu$ denotes continuous actions. Here, $Q_{\vartheta }\left(a\right|s)$ represents the joint policy function obtained by combining the discrete and continuous policy components. This factorization enables independent learning of discrete and continuous action policies while maintaining their interdependence through the joint Q-value estimation.

Accordingly, we develop two independent agents, each utilizing a distinct SAC framework to optimize the discrete or continuous variables of problem ${\mathcal{P}}_1$. Consequently, the cost functions for the value networks of the discrete and continuous agents are expressed as

$$\begin{array}{cc}\hfill J_{Q_{\mu }^{\varphi }}=& \mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\mu }^{\varphi }\left(s\left(t\right)\right)-\mathbb{E}\left[Q_{\mu }^{\theta }(s\left(t\right),a\left(t\right))-log{Q}_{\mu }^{\vartheta }\left(a\left(t\right)\right|s\left(t\right))\right]\right)}^2\right]\hfill \end{array},$$

(45)

$$\begin{array}{cc}\hfill J_{Q_{\nu }^{\varphi }}=& \mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\nu }^{\varphi }\left(s\left(t\right)\right)-\mathbb{E}\left[Q_{\nu }^{\theta }(s\left(t\right),a\left(t\right))-log{Q}_{\nu }^{\vartheta }\left(a\left(t\right)\right|s\left(t\right))\right]\right)}^2\right]\hfill \end{array}.$$

(46)

Then, the cost functions for the soft Q-networks associated with discrete and continuous agents are defined as

$$J_{Q_{\mu }^{\theta }}=\mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\mu }^{\theta }(s\left(t\right),a\left(t\right))-{\overline{Q}}_{\mu }(s\left(t\right),a\left(t\right))\right)}^2\right],$$

(47)

$$J_{Q_{\nu }^{\theta }}=\mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\nu }^{\theta }(s\left(t\right),a\left(t\right))-{\overline{Q}}_{\nu }(s\left(t\right),a\left(t\right))\right)}^2\right].$$

(48)

Additionally, the cost functions for the policy networks of the discrete and continuous agents are given by

$$\begin{array}{cc}\hfill J_{Q_{\mu }^{\vartheta }}=& \mathbb{E}\left[log{Q}_{\mu }^{\vartheta }\left(f_{\vartheta }(\zeta \left(t\right);s\left(t\right))\right|s\left(t\right))-Q_{\mu }^{\theta }(s\left(t\right),f_{\vartheta }(\zeta \left(t\right);s\left(t\right)))\right]\hfill \end{array},$$

(49)

$$\begin{array}{cc}\hfill J_{Q_{\nu }^{\vartheta }}=& \mathbb{E}\left[log{Q}_{\nu }^{\vartheta }\left(f_{\vartheta }(\zeta \left(t\right);s\left(t\right))\right|s\left(t\right))-Q_{\nu }^{\theta }(s\left(t\right),f_{\vartheta }(\zeta \left(t\right);s\left(t\right)))\right]\hfill \end{array}.$$

(50)

To optimize the decoupled policies, we adopt the maximum a posteriori policy optimization algorithm, as described in [37]. For the hybrid action space within the SAC framework, we introduce a new policy ℓ to maximize expected Q-values while satisfying Kullback–Leibler (KL) divergence constraints to ensure stable policy updates:

$$J_{Q_{\ell }}=\mathbb{E}\left[\widehat{Q}(s,a)\right],$$

(51)

where $\widehat{Q}$ represents the Q-function derived from the replay buffer $\mathcal{C}$ [38]. To maintain stability, it is imperative to constrain the divergence between the new policy and the existing one. This is achieved through the following condition:

$$\mathbb{E}\left[\rho \left(Q_{\ell }\left(a\right|s)\Vert Q_{\overline{\ell }}\left(a\right|s)\right)\right]<\chi ,$$

(52)

where $\rho (·)$ denotes the Kullback–Leibler divergence, $\overline{\ell }$ represents the current hybrid policy, and $\chi$ is the stability threshold.

The updated policy is determined by optimizing the following objective:

$$\widehat{\ell }=arg\underset{\ell }{max}\mathbb{E}\left[\rho \left(Q_{\ell }\left(a\right|s)\Vert Q_{\mu }^{\ell }\left(a_{\mu }\right|s)Q_{\nu }^{\ell }\left(a_{\nu }\right|s)\right)\right],$$

(53)

subject to the constraints:

$$\mathbb{E}\left[\rho \left(Q_{\mu }^{\overline{\ell }}\left(a_{\mu }\right|s)\Vert Q_{\mu }^{\ell }\left(a_{\mu }\right|s)\right)\right]<{\chi }_{\mu },$$

(53a)

$$\mathbb{E}\left[{\displaystyle \frac{1}{\overline{o}}}\sum _{o=1}^{\overline{O}}\rho \left(Q_{\nu }^{\overline{\ell }}\left(a_{\nu }\right|s)\Vert Q_{\nu }^{\ell }\left(a_{\nu }\right|s)\right)\right]<{\chi }_{\nu },$$

(53b)

where ${\chi }_{\mu }$ and ${\chi }_{\nu }$ represent the stability thresholds for the discrete and continuous agents, respectively, and $\overline{o}$ denotes the number of discrete choices. The structure of the hybrid action space AD-SAC algorithm is illustrated in Figure 2.

The proposed algorithm decomposes the hybrid action space into discrete and continuous components, allocating each to a distinct agent trained within its own SAC framework. Subsequently, the maximum a posteriori policy optimization algorithm [37] is utilized to integrate the decoupled policies from all agents. This approach effectively tackles the complexities associated with hybrid action spaces in the addressed problems, offering a robust and adaptable framework for hybrid action selection. Algorithm 1 provides a comprehensive overview of the AD-SAC algorithm.

Algorithm 1 AD-SAC Algorithm for MLLM Task Offloading and Resource Allocation

1: Initialize all the networks, ${\varphi }^{\mu }$, ${\varphi }^{\nu }$, ${\overline{\varphi }}^{\mu }$, ${\overline{\varphi }}^{\nu }$, ${\theta }^{\mu }$, ${\theta }^{\nu }$, ${\vartheta }^{\mu }$, ${\vartheta }^{\nu }$ and ℓ.   2: repeat   3:     for each time slot do   4:         Obtain $a\left(t\right)$, $s(t+1)$, $r\left(s\right(t),a(t\left)\right)$ based on the policy ℓ and current state $s\left(t\right)$.   5:         Save the sample $\left\{s\right(t),a(t),s(t+1),r(s\left(t\right),a\left(t\right)\left)\right\}$ to replay $\mathcal{C}$.   6:         Generate samples for unavailable actions and save them to replay $\mathcal{C}$.   7:     end for   8:     for each training epoch do   9:         Update $Q_{\mu }^{\varphi }$ based on (45), $Q_{\mu }^{\theta }$ based on (47), $Q_{\mu }^{\vartheta }$ based on (49). 10:         Update $Q_{\nu }^{\varphi }$ based on (46), $Q_{\nu }^{\theta }$ based on (48), $Q_{\nu }^{\vartheta }$ based on (50). 11:         ;Soft update $Q_{\mu }^{\overline{\varphi }}$ and $Q_{\nu }^{\overline{\varphi }}$. 12:         Update ℓ based on (51), (52) and (53). 13:     end for 14: until convergence.

4.4. Complexity Analysis of AD-SAC

4.4.1. Time Complexity

The proposed AD-SAC algorithm employs two independent agents, each utilizing four neural networks (value network, soft Q-network, policy network, and target value network). Assuming each network consists of L fully-connected layers with hidden dimension H, the computational complexity for a single forward pass is $O\left(L{H}^2\right)$. During each training iteration with batch size B, the algorithm performs forward and backward propagation across all eight networks, resulting in a time complexity of $O\left(8BL{H}^2\right)$ per iteration. Additionally, the policy integration step using maximum a posteriori optimization introduces a computational overhead of $O\left(B{d}_{\mu }{d}_{\nu }\right)$, where $d_{\mu }$ and $d_{\nu }$ represent the discrete and continuous action dimensions, respectively. Therefore, the overall time complexity per training epoch is $O(BL{H}^2+B{d}_{\mu }{d}_{\nu })$, which scales linearly with the batch size and quadratically with the hidden layer dimension.

4.4.2. Space Complexity

The memory requirements of AD-SAC are primarily determined by the storage of network parameters and the experience replay buffer. Each neural network with L layers and hidden dimension H requires approximately $O(d_{s}H+L{H}^2+H{d}_a)$ parameters, where $d_s$ denotes the state dimension, and $d_a$ represents the corresponding action dimension. With eight networks in total, the parameter storage requires $O(8(d_{s}H+L{H}^2)+4H(d_{\mu }+d_{\nu }))$ memory. The experience replay buffer $\mathcal{C}$ stores tuples of states, actions, and rewards, consuming $O\left(\right|\mathcal{C}\left|(2d_s+d_{\mu }+d_{\nu })\right)$ memory, where $\left|\mathcal{C}\right|$ is the buffer capacity. Consequently, the total space complexity is $O(L{H}^2+|\mathcal{C}\left|(d_s+d_{\mu }+d_{\nu })\right)$, demonstrating that the algorithm maintains reasonable memory requirements even for large-scale MLLM task offloading scenarios.

5. Performance Evaluation

In this section, we initially outline the experimental framework and configuration for the MLLM-based SEC environment. Subsequently, we assess the performance of our algorithm in comparison to established benchmark algorithms across various conditions.

5.1. Parameter Settings

In the UAV-assisted SEC environment, we consider that multiple IoTDs are arbitrarily dispersed within a 500 m × 500 m region, where UAVs and LEO satellites, equipped with ESs, are capable of offering computational support to these IoTDs. Each IoTD generates an MLLM task request that necessitates processing, either via task offloading to UAVs or LEO satellites. We set the number of IoTDs $K=10$, the number of UAVs $M=3$, and the number of LEO satellites $N=4$, wherein UAVs fly at an altitude of $[40,60]$ m and LEO satellites at an altitude of 500 km. In this simulation, each UAV is assumed to be equipped with NVIDIA Jetson Orin NX with 1.88 TFLOPS and 16 GB memory, and the LEO satellite is equipped with NVIDIA Jetson AGX Orin with 3.33 TFLOPS and 32 GB memory [39].

We implement the proposed algorithm based on the HuggingFace [40]. To evaluate the inference performance of our algorithm, we implement a text generation benchmark. Utilizing the MMMU dataset provided by HuggingFace, we randomly selected a specific subset where each input sequence contains $[16,32,64,96]$ tokens and a picture; then, the server generated $[16,32,64,96]$ tokens based on these inputs. The duration of each time slot was set as 3 s. The MDs’ request arrivals were characterized by a Poisson distribution, with the rate parameter ranging from 1 to 1.5 requests at each time slot. The actor and critic learning rates were $LR\_A=0.0003$ and $LR\_C=0.0003$, respectively. The buffer size $\mathcal{C}=$ 10,000, the soft update coefficient $\tau$ was $0.01$, and the batch size is 128. The other simulation parameters are presented in

Table 1. Simulation parameter settings.

Parameters	Value
Number of IoTDs: K	10
Number of UAVs: M	3
Number of LEO satellites: N	4
FLOPS used by one inference step: $v_m$	[0.05, 0.6] TFLOPS
Noise power density: $N_0$	$-100$ dBm/Hz
Time slot: T	100
Computation power of UAV	25 W
Computation power of LEO satellite	50 W
Maximum uplink transmission power of IoTD	1 W
Transmission power of UAV, satellite	2 W, 4 W
Channel bandwidth: $B_n$, $B_m$	20 MHz, 10 MHz
Transmission rate between LEO satellites: $R_{ISL}$	1 Gbps
Input data size: $u_k$	[5.0, 10.0] Mbits
Maximum latency requirement: $T_k^{max}$	[2.0, 3.0] s
MMMU benchmark accuracy requirement: $a_k$	[0.3, 0.7]
Weighted coefficients: ${\eta }_l,{\eta }_e$	0.5, 0.5

. Similar experimental configurations were adopted in [18,41]. The hyperparameters of the AD-SAC algorithm are listed in

Table 2. The hyperparameters of the proposed AD-SAC algorithm.

Parameters	Value	Parameters	Value
Network type	Fully connected	Number of layers	3
Hidden units	[256, 256, 256]	Activation	ReLU
Optimizer	Adam	Entropy learning rate	0.001
Actor learning rate	0.001	Critic learning rate	0.001
Batch size	64	Replay buffer size	10,000
Discount factor $\gamma$	0.995	Soft update $\tau$	0.01
Training epochs	1000	Epoch length	100

. The simulations were conducted on a platform featuring an Intel(R) Xeon(R) Platinum 8370C CPU 2.80 GHz and an NVIDIA GeForce GTX 4090 graphics.

Benchmark: In our study, we evaluated the efficacy of our enhanced AD-SAC algorithm compared to four benchmarking schemes:

• Random: This method selects actions uniformly at random, serving as a baseline to assess the effectiveness of learning-based approaches.
• Proximal Policy Optimization (PPO): PPO is a policy optimization DRL technique that iteratively refines the policy to maximize expected cumulative rewards.
• Dueling Double Deep Q-Network (D3QN): D3QN builds upon the Deep Q-Network framework by incorporating a dueling architecture to estimate state values and action advantages separately.
• Deep Deterministic Policy Gradient (DDPG): DDPG is a policy gradient algorithm that learns a deterministic policy alongside a value function for optimization.
• Hybrid Proximal Policy Optimization (Hybrid-PPO): Hybrid-PPO introduces a parameterized PPO method based on the hybrid action space to solve the collaborative partial task offloading problem at the edge [42].

5.2. Numerical Results

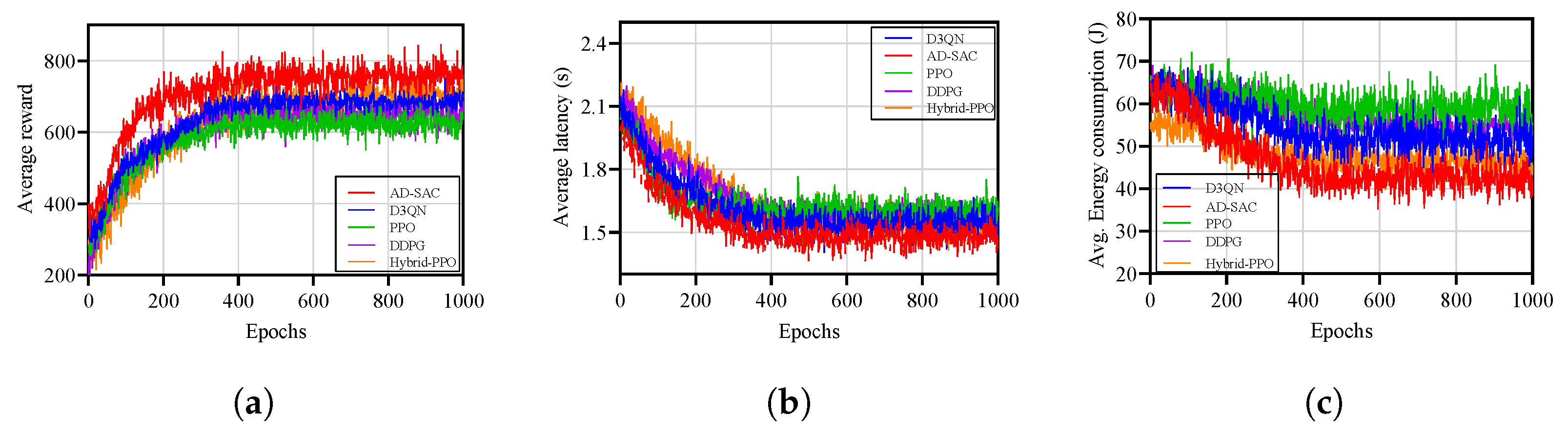
First, we analyze the convergence of the proposed AD-SAC algorithm and the comparative DRL algorithms. Figure 3 illustrates the learning curves for the AD-SAC, PPO, D3QN, DDPG, and Hybrid-PPO algorithms across 1000 epochs. AD-SAC demonstrates superior convergence speed and performance, outperforming the benchmark algorithms. Specifically, AD-SAC reaches a significantly higher final average reward, while Hybrid-PPO, DDPG, D3QN, and PPO obtain approximately 5.7–13.4% lower reward compared to the AD-SAC algorithm. This indicates that AD-SAC not only converges faster but also maintains better stability throughout training. While Hybrid-PPO exhibits a relatively stable learning curve and a higher final reward than DDPG, D3QN, and PPO, its performance is still notably lower than that of the AD-SAC algorithm. PPO and D3QN, on the other hand, exhibit greater reward fluctuations and slower convergence rates, ultimately stabilizing at lower reward levels. This analysis emphasizes AD-SAC’s superior stability, faster convergence, and overall effectiveness compared to the other algorithms.

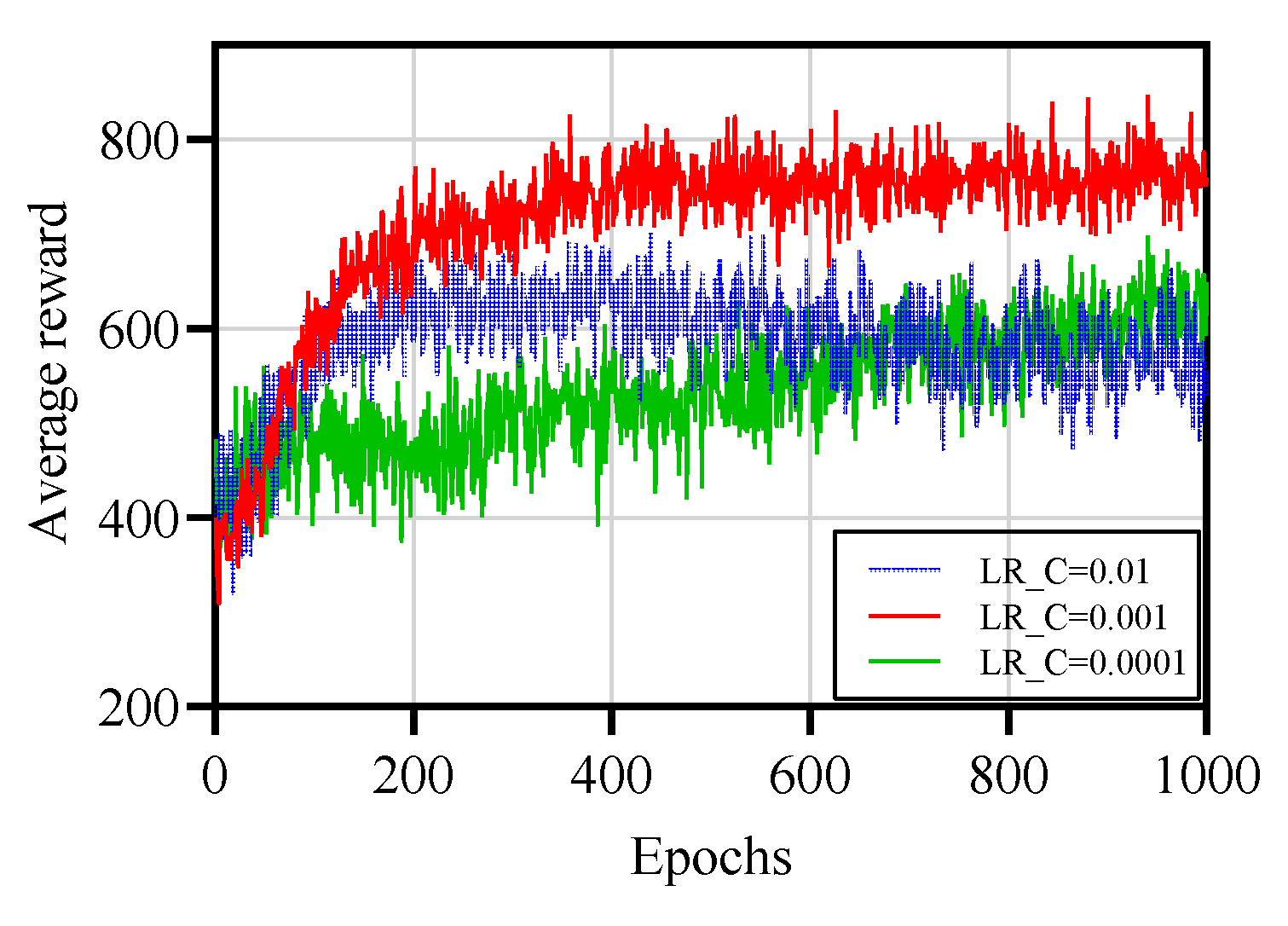
Figure 4 demonstrates the impact of varying the critic learning rate on the convergence behavior of the AD-SAC algorithm for MLLM task offloading in UAV-assisted SEC networks. The figure illustrates that a moderate critic learning rate facilitates rapid and stable convergence, with the average reward per episode increasing swiftly to a high plateau, indicating efficient minimization of the weighted sum of latency and energy consumption. In contrast, the lower critic learning rate with 0.0001 results in slower convergence, requiring more training episodes to achieve comparable performance, while the critic learning rate with 0.01 leads to oscillatory behavior and failure to stabilize, reflecting instability in the training process. These findings highlight the critical role of carefully tuning the critic learning rate to balance the learning speed and stability within the hybrid action space DRL framework, ensuring effective task allocation and resource management in the resource-constrained SEC environment. Therefore, in the subsequent experiments, we set the critic learning rate to 0.001 to ensure the efficiency and robustness of the AD-SAC algorithm.

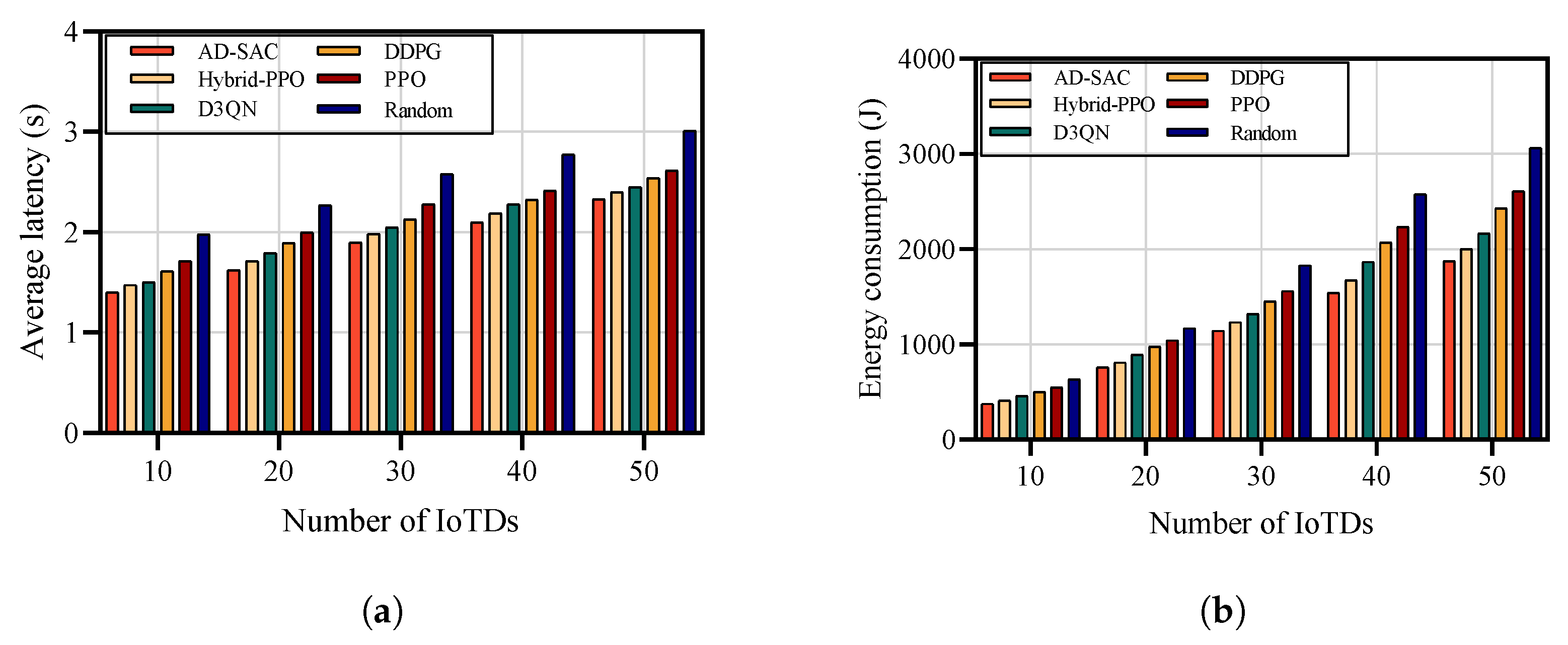
To investigate the impact of the number of IoTDs on the efficiency of the proposed algorithm, we conducted a series of comparative analyses involving five distinct algorithms, including AD-SAC, PPO, D3QN, DDPG, Hybrid-PPO, and Random. As illustrated in Figure 5, the increase in the number of IoTDs leads to higher service latency and energy consumption across all evaluated algorithms. This performance can be attributed to the diminishing resource availability of nearby UAVs, as the number of IoTDs increases, which necessitates offloading MLLM tasks to more distant LEO satellites, ultimately resulting in increased service latency and transmission energy consumption. Additionally, as the number of IoTDs rises, the AD-SAC algorithm consistently achieves the lowest service latency and energy consumption, showcasing a strong adaptability to varying environmental conditions. This is because our proposed AD-SAC algorithm stems from its integration of a hybrid action space to approximate optimal decisions on offloading and resource allocation, thereby optimizing convergence efficiency and reducing latency and energy consumption.

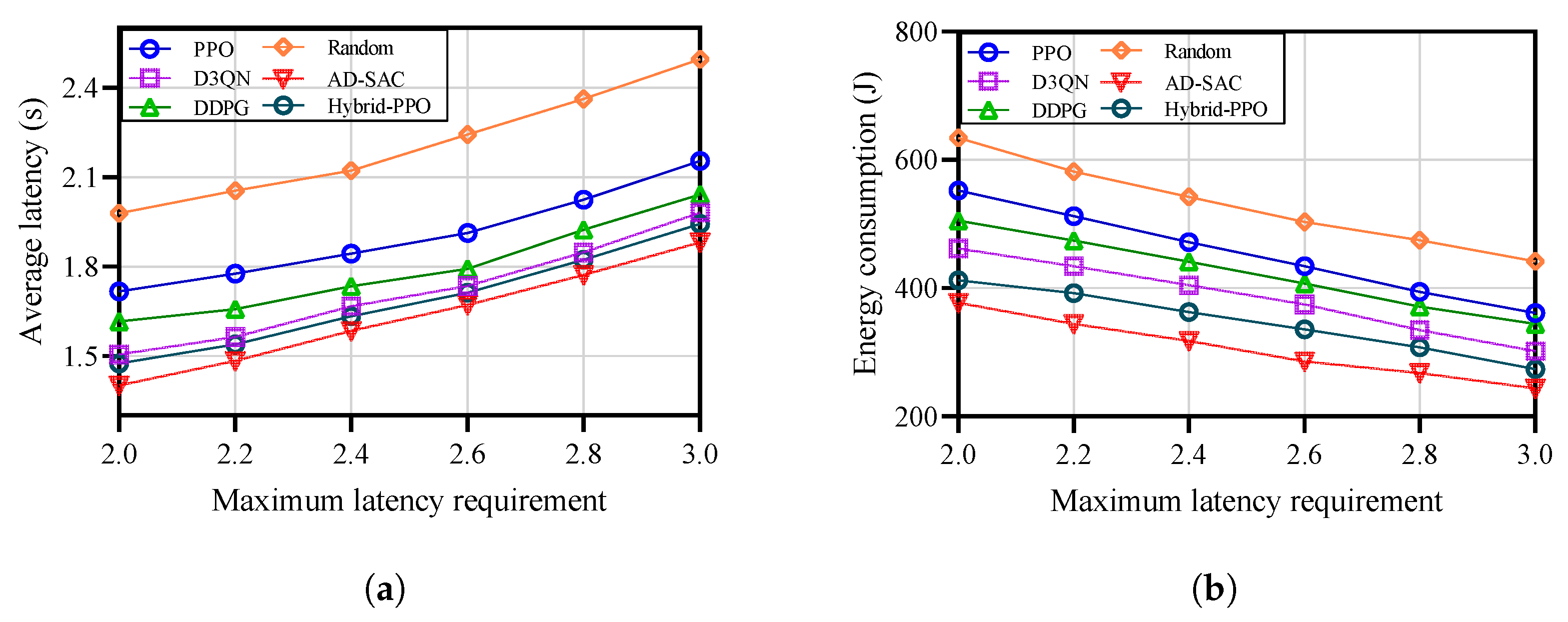
Figure 6 demonstrates the impact of maximum latency constraints $T^{max}$ on the performance of five distinct task offloading algorithms. It is intuitive that Figure 6a reveals a direct correlation between increasing $T^{max}$ and heightened service latency across all assessed algorithms. This trend can be attributed to the algorithms’ propensity to offload a greater number of tasks to LEO satellite infrastructure when latency constraints are more loose. While this scheme results in higher latency, it simultaneously enhances service reliability. Notably, the proposed AD-SAC algorithm consistently achieves the lowest service latency as $T^{max}$ increases. This outstanding performance is attributed to AD-SAC’s preference for offloading tasks to nearby UAVs and LEO satellites, effectively reducing communication latency. Figure 6b further emphasizes that the AD-SAC algorithm also shows the lowest energy consumption. This efficiency primarily arises from its inclination to offload tasks to proximate servers, unlike other algorithms that often rely on more distant LEO satellites, resulting in higher communication energy costs. Additionally, as the maximum service delay threshold expands, a marked reduction in energy consumption is observed across all algorithms. This decline is driven by the increased task offloading to LEO satellites, which utilize their advanced computational efficiency to lower overall energy demands.

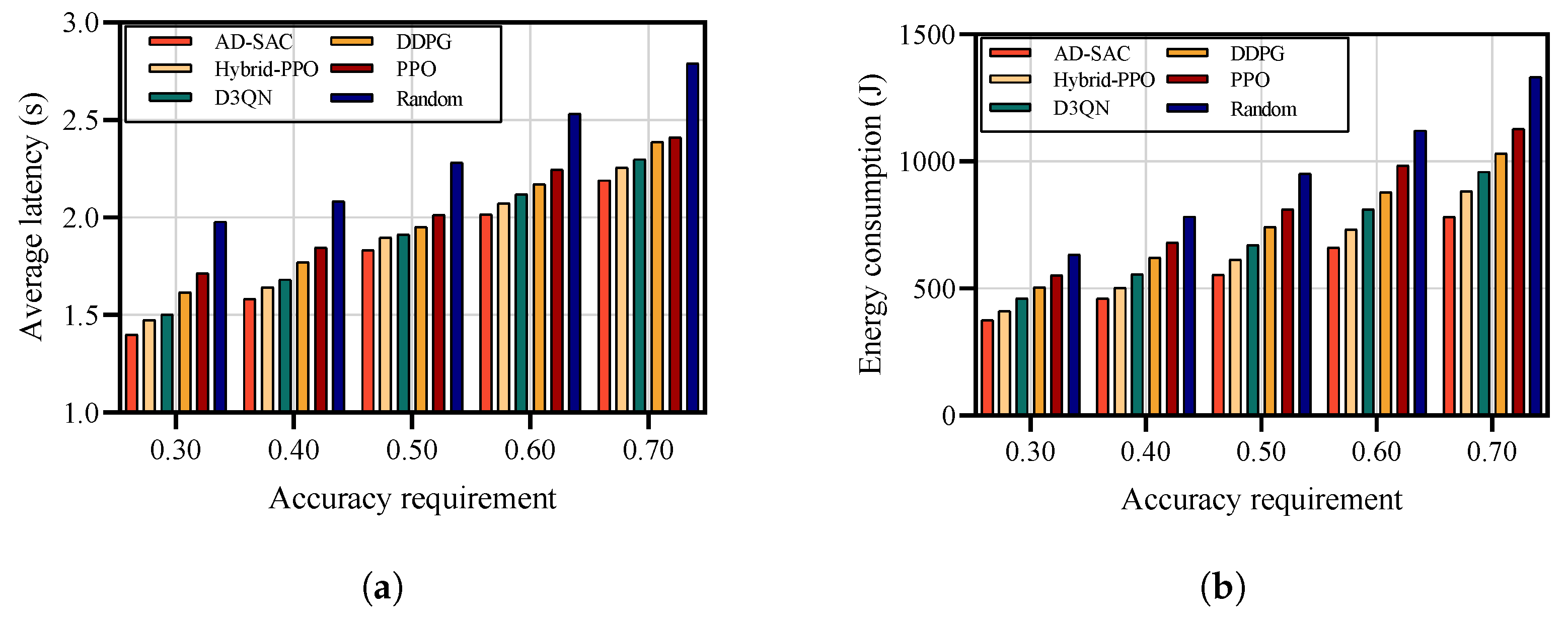
We evaluated the impact of varying MMMU accuracy requirements on system performance by conducting experiments with accuracy thresholds ranging from 0.3 to 0.7. Figure 7 illustrates the relationship between accuracy requirements and system metrics. The experimental results demonstrate an increase in both latency and energy consumption as accuracy requirements become more stringent. Specifically, when the accuracy requirement increases from 0.3 to 0.7, the average system latency rises from 1.41 s to 2.19 s, representing a 55.3% increase. Similarly, energy consumption exhibits a substantial growth from 377J per time slot to 782J per time slot, marking a 107.4% increase. The most significant performance degradation occurs in the transition from accuracy requirement 0.5 to 0.6, where we observe a sharp increase in latency and energy consumption. This indicates a critical threshold where the SEC system shifts from predominantly UAV-based processing to satellite-based processing. It can be observed that our proposed AD-SAC algorithm with a hybrid action space demonstrates significant advantages compared to D3QN, PPO, DDPG, Hybrid-PPO, and Random methods. The superiority of AD-SAC stems from its ability to effectively handle the mixed discrete–continuous action space inherent in our problem. In contrast, Hybrid-PPO addresses the discrete–continuous action space by parameterization, because the single network needs to learn two different types of action mappings simultaneously, which is prone to achieving suboptimal performance. In addition, while D3QN struggles with the continuous power allocation and UAV trajectory optimization, and DDPG faces challenges in discrete offloading decisions, our decoupled approach allows specialized agents to optimize each action type. The discrete agent efficiently learns offloading patterns based on accuracy requirements, while the continuous agent finetunes power allocation and UAV positioning to minimize interference and reduce transmission latency.

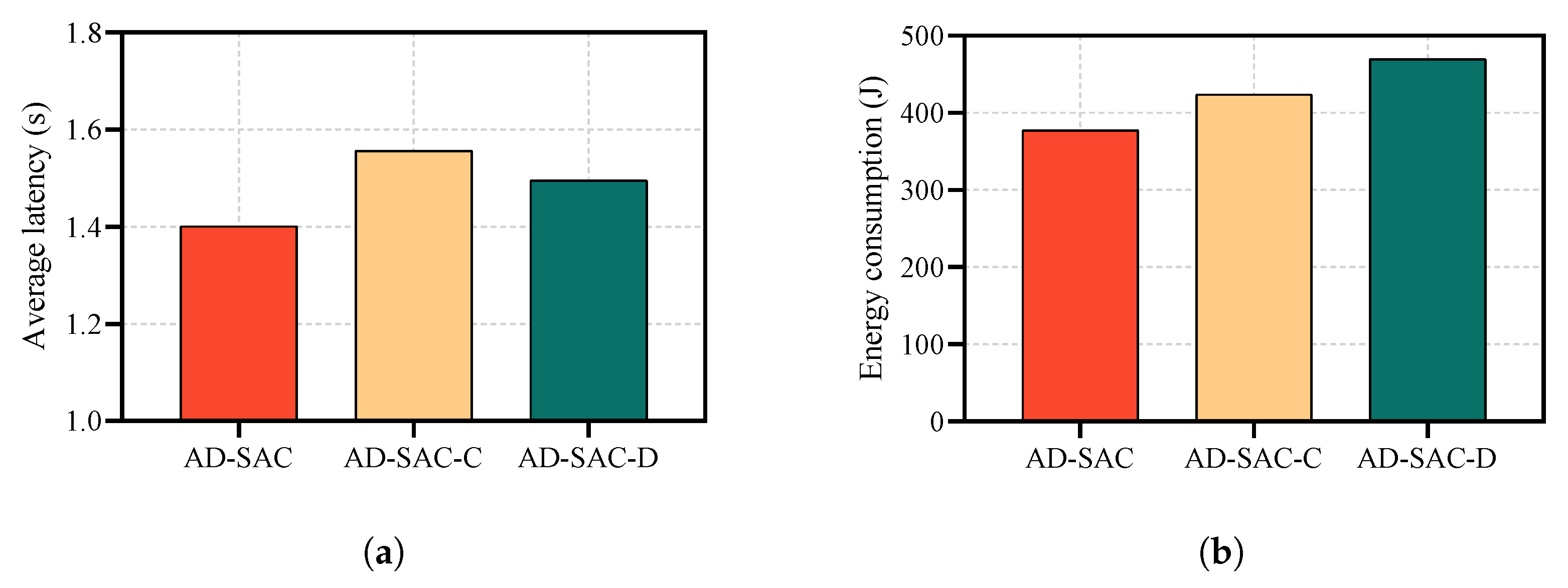
To validate the effectiveness of our hybrid action space decoupling approach, Figure 8 ablation studies comparing our proposed AD-SAC, AD-SAC-D (discrete agent with continuous actions mapped to discrete space), and AD-SAC-C (continuous agent with discrete actions mapped to continuous space). The results demonstrate that the proposed AD-SAC achieves optimal performance in terms of latency and energy consumption. AD-SAC-D shows a 7.4% latency increase and 24.3% energy increase due to discretization loss in power allocation and trajectory, while AD-SAC-C exhibits the worst latency performance 11.7% increase but better energy efficiency 13.5% increase due to the continuous representation of discrete offloading decisions. This cross-advantage phenomenon validates our theoretical analysis that latency is primarily dominated by offloading decisions, while energy is dominated by power allocation and trajectory. The results conclusively demonstrate that forcing action space conversions leads to significant performance degradation, proving the necessity of our decoupling design that preserves the native characteristics of both discrete and continuous actions.

5.3. Discussion

In our study, deployment feasibility is a core consideration, particularly in addressing the inherent challenges of intermittent connectivity in low Earth orbit (LEO) satellite networks. To this end, we explicitly introduce the visibility time window $T_{k,n}^{\mathrm{vis}}\left(t\right)$ into the MDP state space. This parameter represents the dynamic communication window between an IoTD k and satellite n at time t. This design captures the time-varying availability characteristics of LEO satellites due to their orbital motion. By incorporating $T_{k,n}^{\mathrm{vis}}\left(t\right)$ into the MDP state space, our framework can adaptively respond to the dynamic changes in satellite connectivity. For instance, during task offloading and resource allocation, the algorithm makes optimized decisions based on the real-time visibility window of the satellite, choosing to offload tasks to the satellite only when the communication window is sufficient to support computation and data transmission. This mechanism effectively mitigates the impact of intermittent satellite connectivity on service reliability, thereby enhancing the system’s robustness.

While our proposed framework for MLLM inference in UAV-assisted SEC networks achieves significant performance improvements in terms of latency and energy efficiency, certain simplifying assumptions in the system model warrant further exploration to enhance its applicability to real-world scenarios. Below, we discuss key limitations and potential avenues for future research. In this work, we assume that IoTD locations remain static within each time slot to simplify the optimization problem and focus on the joint task offloading and resource allocation challenge. This assumption facilitates the development and evaluation of our AD-SAC algorithm by reducing the complexity of the dynamic environment. However, in practical IoT deployments, such as disaster response or maritime monitoring, IoTDs may exhibit mobility, leading to variations in network topology, channel conditions, and UAV coverage requirements. While our model accounts for inter-slot variations due to device mobility (as noted in Section 3.2), explicitly incorporating intra-slot IoTD mobility could improve the framework’s robustness. Future work could extend our approach by integrating mobility models for IoTDs, such as random waypoint or trajectory-based patterns, and developing adaptive algorithms that dynamically adjust offloading decisions and UAV trajectories in response to these changes.

Another limitation of our current model is the absence of explicit energy constraints or depletion models for UAVs and LEO satellites. We opted not to include these factors to maintain focus on optimizing MLLM task offloading and resource allocation, rather than energy management of the computing nodes. In our formulation, energy consumption is minimized from a system-wide perspective (e.g., transmission and inference energy), but the battery life and recharge cycles of UAVs and satellites are not directly modeled. In real-world deployments, especially in remote areas where recharging infrastructure is scarce, energy constraints are critical for ensuring the sustained operation of these mobile nodes. For instance, UAVs may need to return to base for recharging, and satellites may rely on solar energy with limited storage capacity. Future research could enhance our framework by incorporating energy-aware mechanisms, such as battery depletion models, recharge scheduling, or energy harvesting strategies (e.g., solar panels for UAVs and satellites). This would enable a more holistic optimization that balances computational performance with operational longevity.

6. Conclusions and Future Work

In this paper, we investigate the challenging problem of MLLM task offloading and resource allocation in UAV-assisted SEC networks. We formulate an MINLP problem to minimize the weighted sum of system latency and energy consumption while satisfying accuracy requirements for diverse MLLM services. The problem poses significant challenges due to the hybrid discrete–continuous action space, involving discrete offloading decisions and continuous power allocation and UAV trajectory optimization. To address these challenges, we proposed a novel AD-SAC algorithm that effectively handles the hybrid action space by employing separate agents for discrete and continuous actions. Our approach leverages the maximum a posteriori policy optimization to integrate the decoupled policies, ensuring stable learning and efficient exploration. The AD-SAC framework enables intelligent decision-making that considers the trade-offs between UAV-based edge computing with lower latency but limited accuracy and satellite-based computing with higher accuracy but increased communication overhead. Extensive experiments demonstrate the superiority of our proposed AD-SAC algorithm over state-of-the-art baselines.

While our work demonstrates the advantages of SEC-based MLLM deployment, a limitation of this study is the lack of a comprehensive quantitative comparison with cloud-based deployment scenarios. In future work, we will expand the research scope to include cloud computing deployment scenarios for MLLM services and provide concrete real-world examples and quantitative data, such as latency metrics from actual IoT deployments, bandwidth consumption patterns for multimodal data transmission, and comparative analysis between cloud, UAV, and SEC paradigms. This expanded investigation will offer comprehensive empirical evidence to justify the bottlenecks in different IoT environments.