Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks
Abstract
1. Introduction
2. Problem Formulation
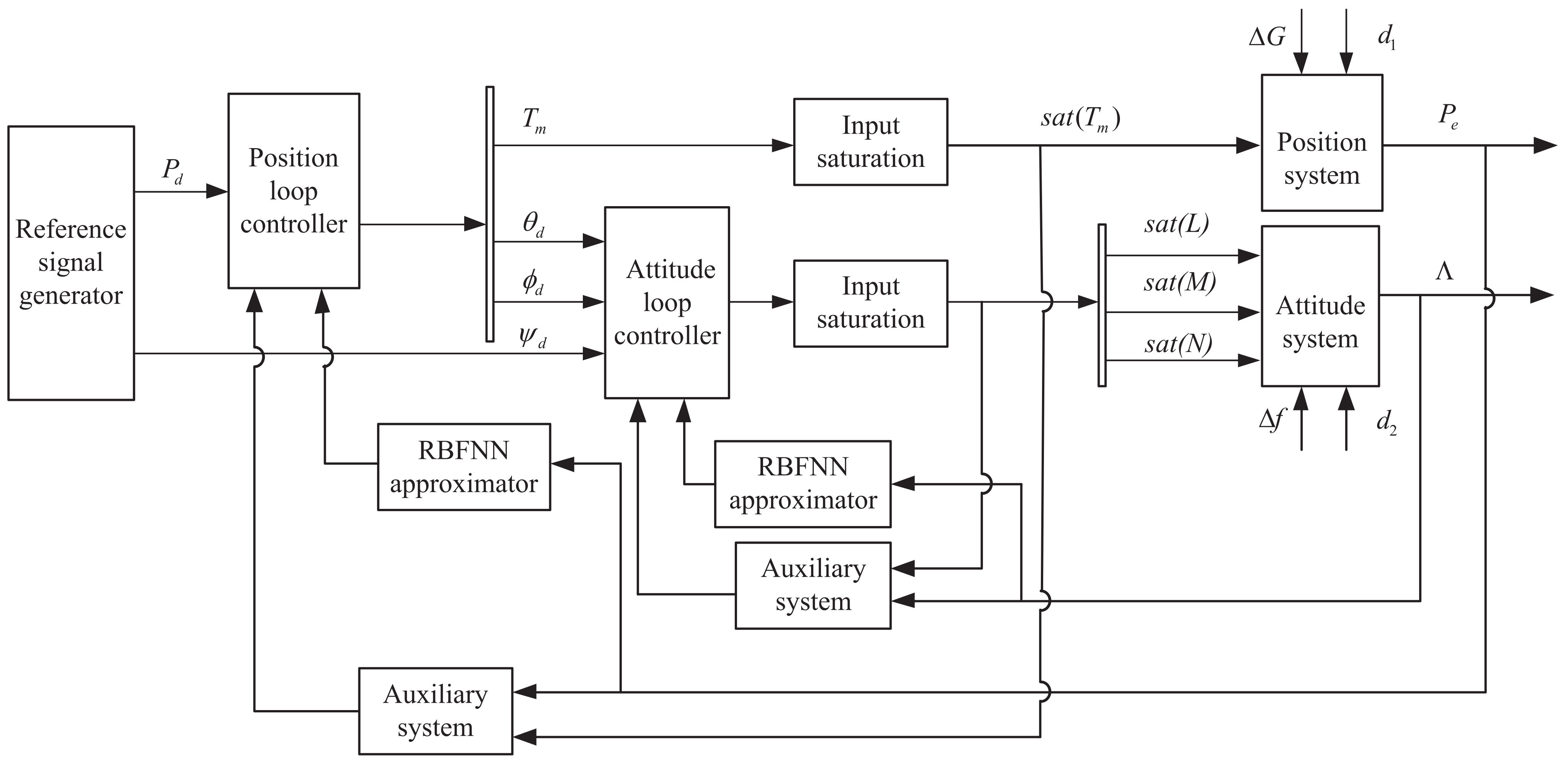
3. Controller Design of the UAH with Input Saturation, Disturbances and Uncertainty
3.1. Positional Subsystem Controller
3.2. Attitude Subsystem Controller
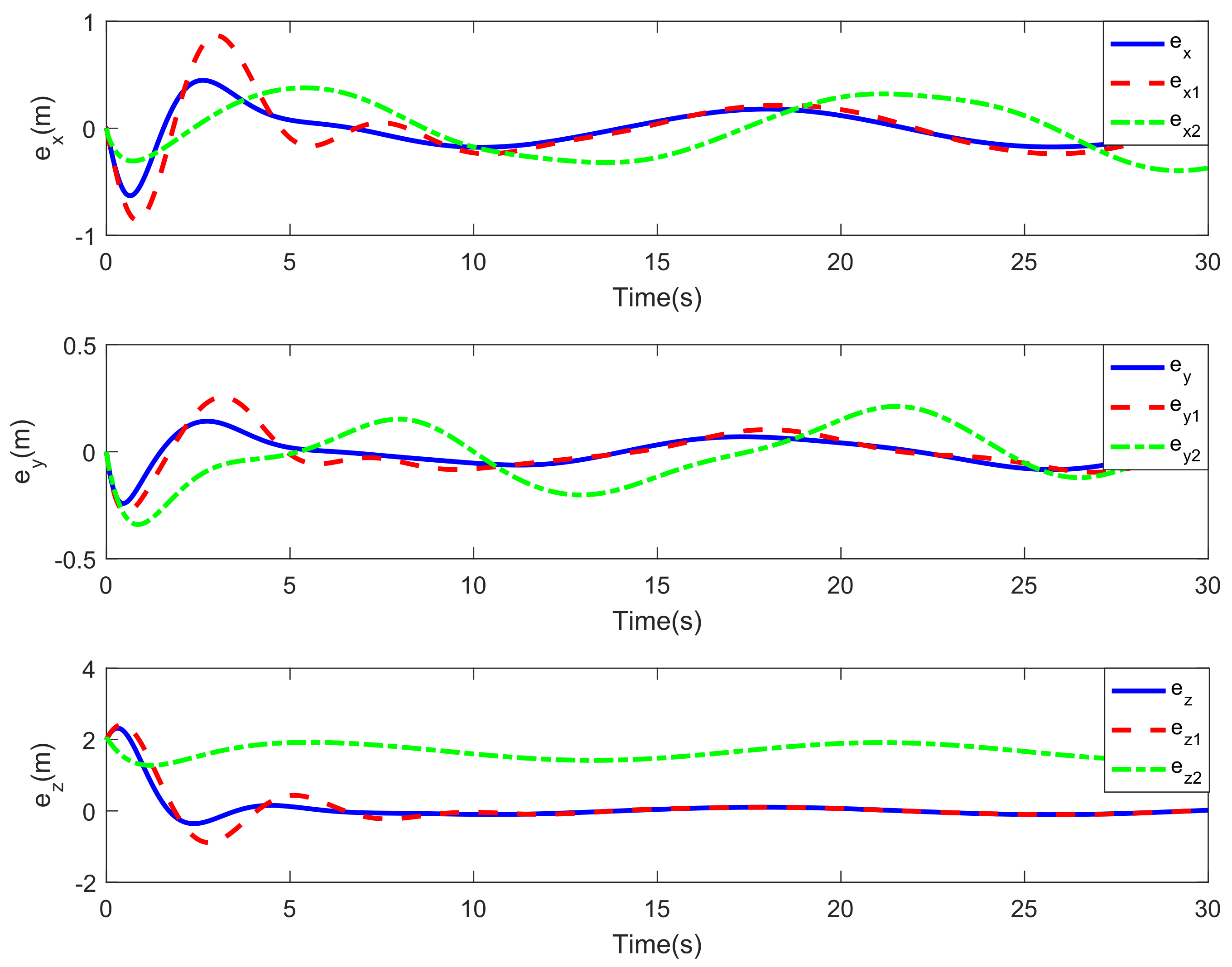
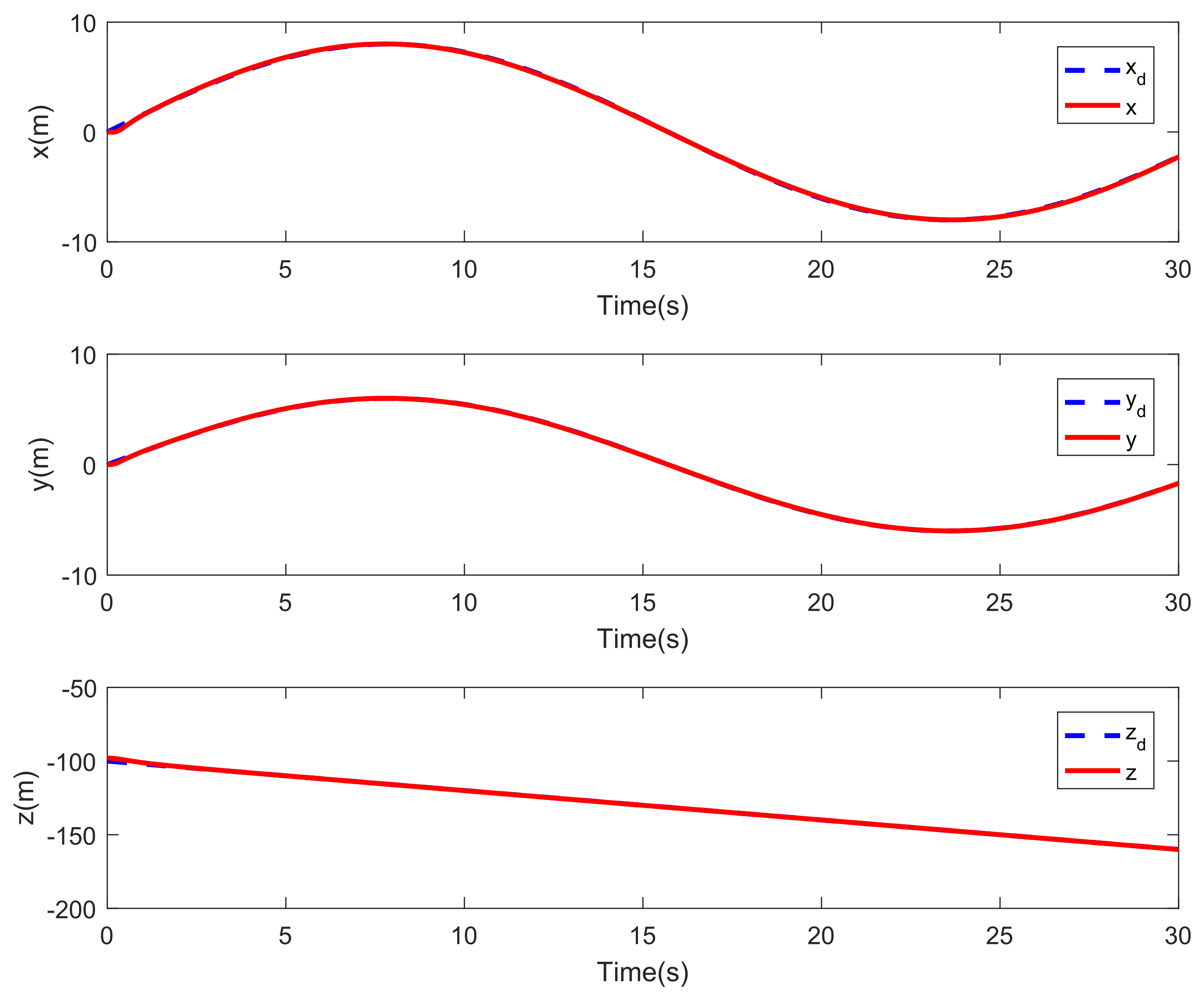
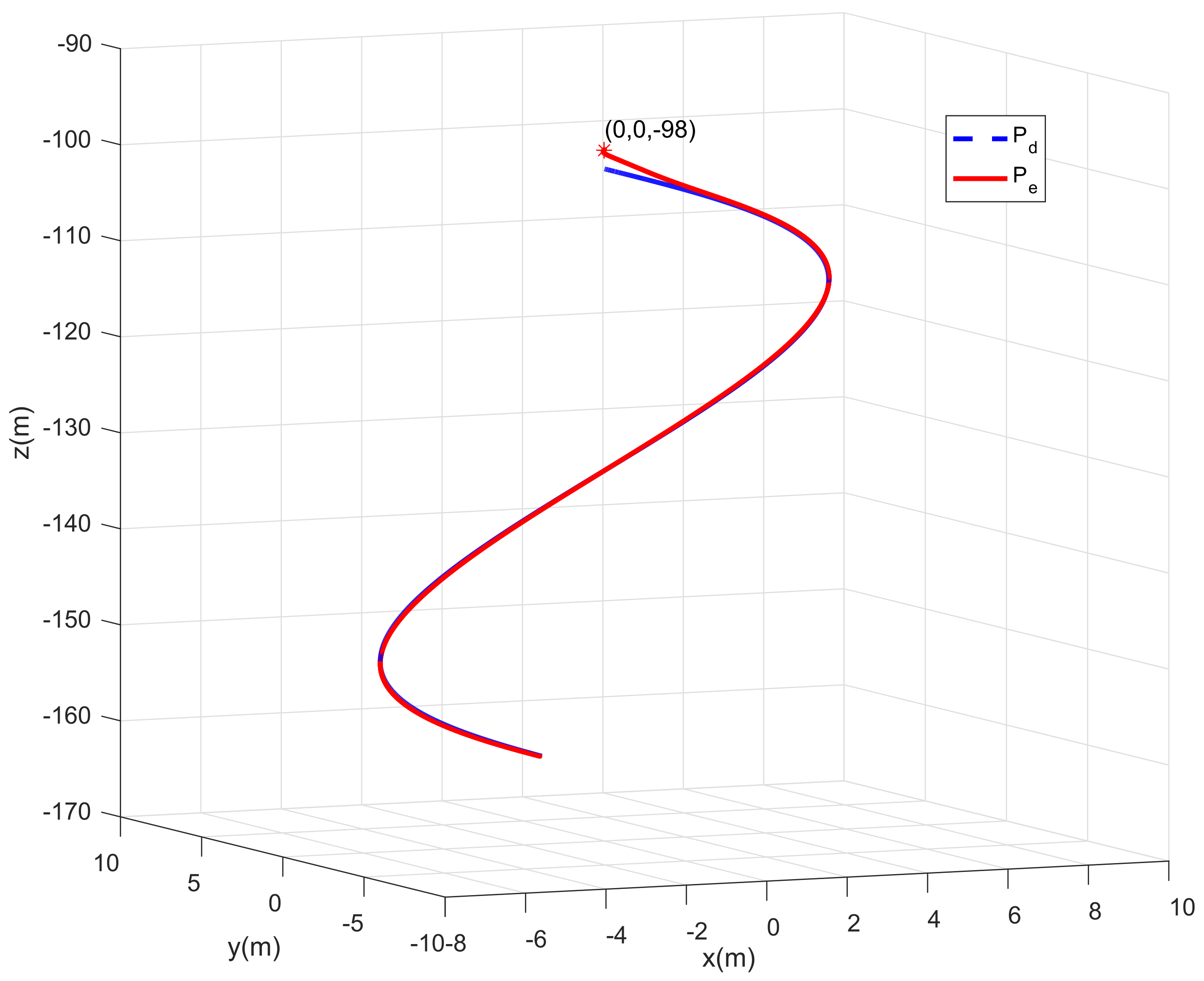
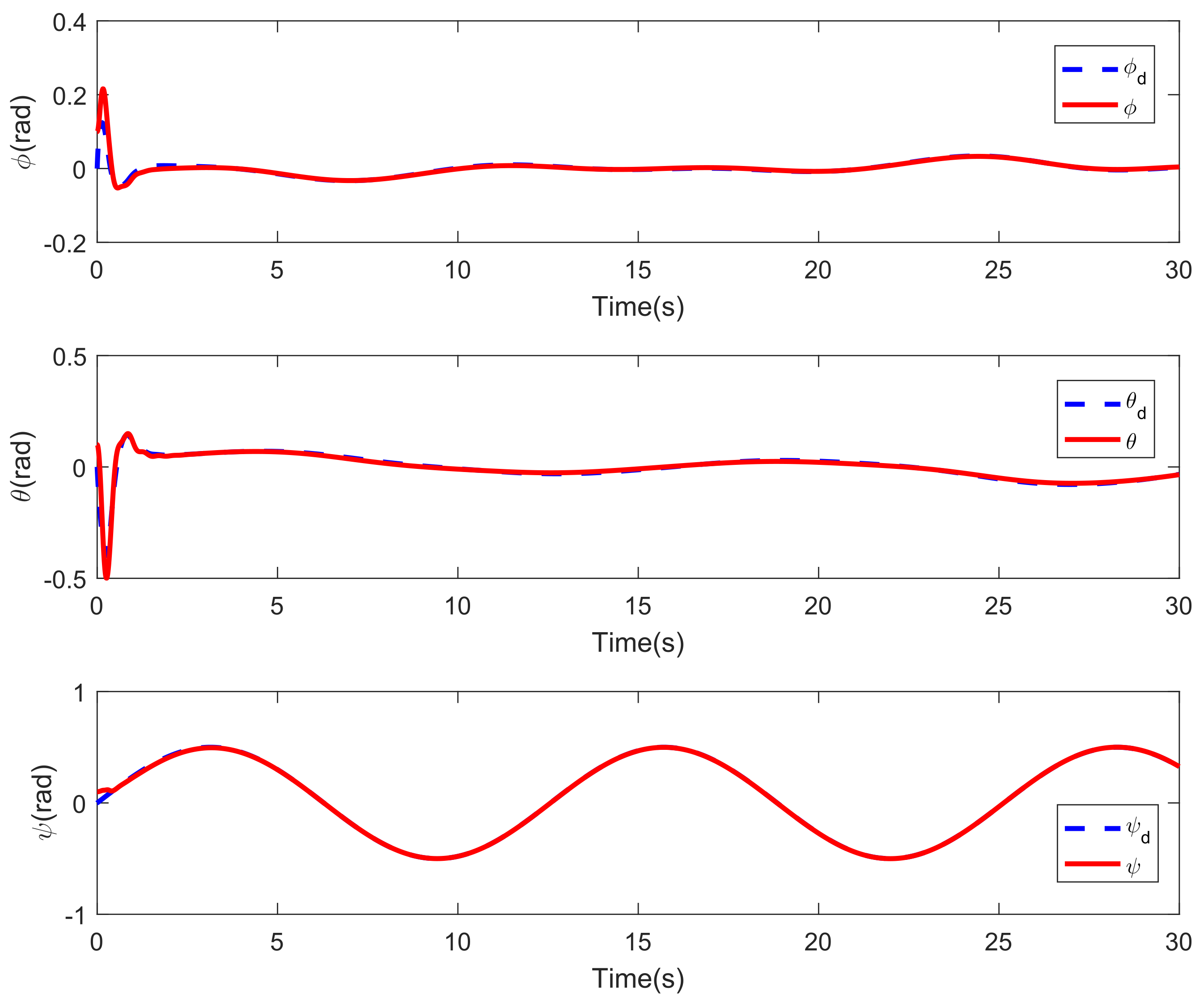
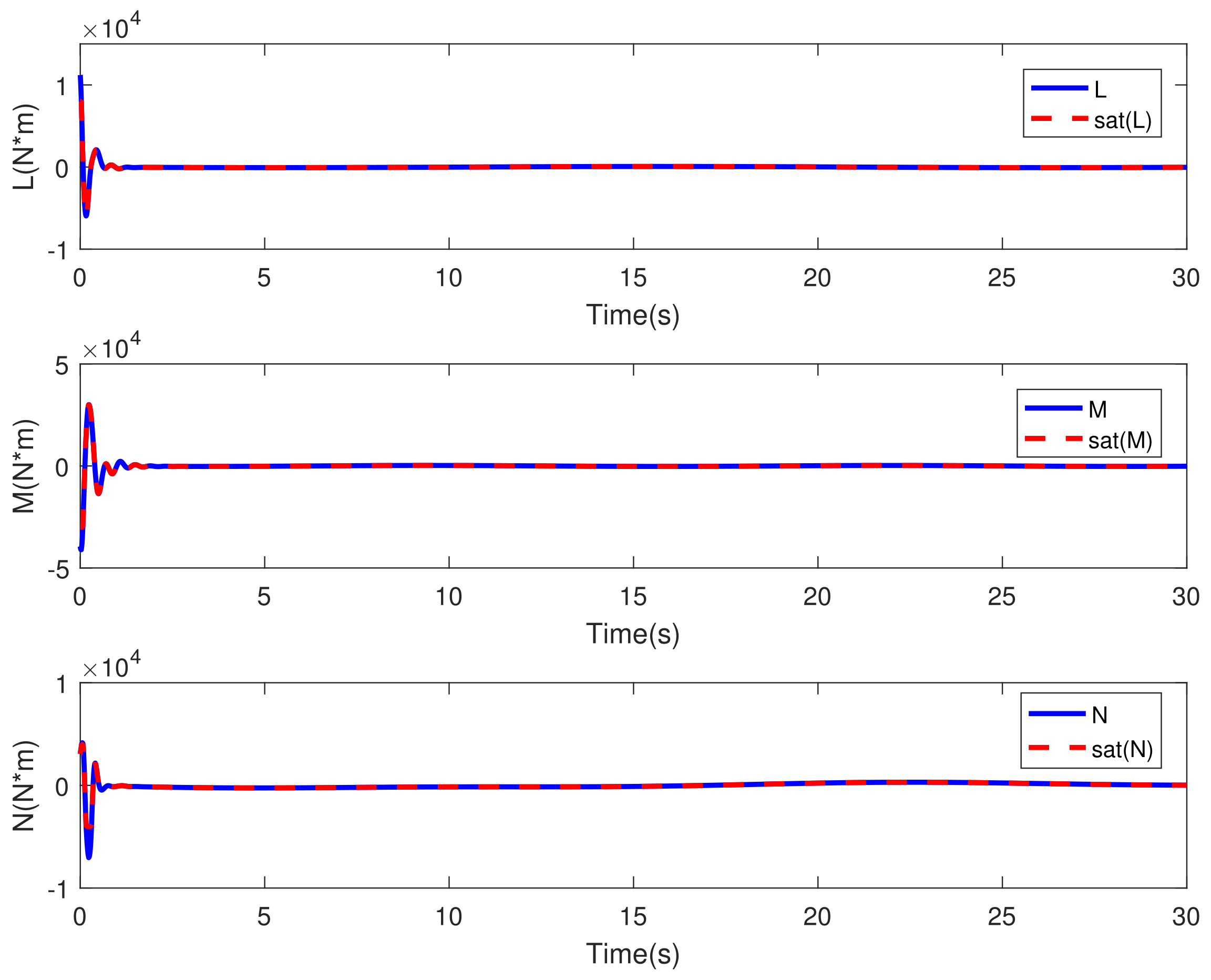
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.D. Helicopter Flight Control, 3rd ed.; National Defense Industry Press: Beijing, China, 2007; pp. 32–70. [Google Scholar]
- Yan, K.; Chen, M.; Wu, Q.; Jiang, B. Extended state observer-based sliding mode fault-tolerant control for unmanned autonomous helicopter with wind gusts. IET Control Theory Appl. 2019, 10, 1500–1513. [Google Scholar] [CrossRef]
- Chaudhary, S.; Kumar, A. Control of Twin Rotor MIMO system using 1-degree-of-freedom PID, 2-degree-of-freedom PID and fractional order PID controller. In Proceedings of the 2019 3rd International conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 12–14 June 2019; pp. 746–751. [Google Scholar]
- Pounds, P.E.; Dollar, A.M. Stability of helicopters in compliant contact under PD-PID control. IEEE Trans. Robot. 2014, 30, 1472–1486. [Google Scholar] [CrossRef]
- He, M.; He, J.; Scherer, S. Model-based real-time robust controller for a small helicopter. Mech. Syst. Signal Process. 2021, 14, 107022. [Google Scholar] [CrossRef]
- Okyere, E.; Bousbaine, A.; Poyi, G.T.; Joseph, A.K.; Andrade, J.M. LQR controller design for quad-rotor helicopters. J. Eng. 2019, 17, 4003–4007. [Google Scholar] [CrossRef]
- Mollov, L.; Kralev, J.; Slavov, T.; Petkov, P. μ-synthesis and hardware-in-the-loop simulation of miniature helicopter control system. J. Intell. Robot. Syst. 2014, 76, 315–351. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, Y.; Li, S.; Zhou, Y. Fuzzy controller design of micro-unmanned helicopter relying on improved genetic optimization algorithm. Aerosp. Sci. Technol. 2020, 98, 105685. [Google Scholar] [CrossRef]
- Lee, J.; Seo, J.; Choi, J. Output feedback control design using Extended High-Gain Observers and dynamic inversion with projection for a small scaled helicopter. Automatica 2021, 133, 109883. [Google Scholar] [CrossRef]
- Suprijono, H.; Kusumoputro, B. Direct inverse control based on neural network for unmanned small helicopter attitude and altitude control. J. Telecommun. Electron. Comput. 2017, 9, 99–102. [Google Scholar]
- Mokhtari, A.; Msirdi, N.K.; Meghriche, K. Feedback linearization and linear observer for a quadrotor unmanned aerial vehicle. Adv. Robot. 2006, 20, 71–91. [Google Scholar] [CrossRef]
- Aboudonia, A.; El-Badawy, A.; Rashad, R. Disturbance observer-based feedback linearization control of an unmanned quadrotor helicopter. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2016, 230, 877–891. [Google Scholar] [CrossRef]
- Zhu, B.; Huo, W. Adaptive backstepping control for a miniature autonomous helicopter. In Proceedings of the 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 5413–5418. [Google Scholar]
- Sun, X.Y.; Fang, Y.C.; Sun, N. Backstepping-based adaptive attitude and height control of a small-scale unmanned helicopter. Control. Theory Appl. 2012, 29, 381–388. [Google Scholar]
- Raptis, I.A.; Valavanis, K.P.; Moreno, W.A. A novel nonlinear backstepping controller design for helicopters using the rotation matrix. IEEE Trans. Control. Syst. Technol. 2011, 19, 465–473. [Google Scholar] [CrossRef]
- Lee, C.T.; Tsai, C.C. Adaptive backstepping integral control of a small-scale helicopter for airdrop missions. Asian J. Control. 2010, 12, 531–541. [Google Scholar] [CrossRef]
- Hamida, M.A.; Leon, J.D.; Glumineau, A. High-order sliding mode observers and integral backstepping sensorless control of IPMS motor. Int. J. Control. 2014, 87, 2176–2193. [Google Scholar] [CrossRef]
- Poultney, A.; Gong, P.; Ashrafiuon, H. Integral backstepping control for trajectory and yaw motion tracking of quadrotors. Robotica 2019, 37, 300–320. [Google Scholar] [CrossRef]
- Din, S.U.; Khan, Q.; Rehman, F.U.; Akmeliawanti, R. A comparative experimental study of robust sliding mode control strategies for underactuated systems. IEEE Access 2017, 5, 10068–10080. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N. Continuous sliding mode control strategy for a class of nonlinear underactuated systems. IEEE Trans. Autom. Control. 2018, 63, 3471–3478. [Google Scholar] [CrossRef]
- Ullah, S.; Mehmood, A.; Khan, Q.; Rehman, S.; Iqbal, J. Robust integral sliding mode control design for stability enhancement of under-actuated quadcopter. Int. J. Control. Autom. Syst. 2020, 18, 1671–1678. [Google Scholar] [CrossRef]
- Bessa, W.M.; Otto, S.; Kreuzer, E.; Seifried, R. An adaptive fuzzy sliding mode controller for uncertain underactuated mechanical systems. J. Vib. Control. 2019, 25, 1521–1535. [Google Scholar] [CrossRef]
- Rsetam, K.; Cao, Z.; Man, Z. Design of robust terminal sliding mode control for underactuated flexible joint robot. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 4272–4285. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, Y.; Cheng, X. An enhanced coupling PD with sliding mode control method for underactuated double-pendulum overhead crane systems. Int. J. Control. Autom. Syst. 2019, 17, 1579–1588. [Google Scholar] [CrossRef]
- Adhikary, N.; Mahanta, C. Integral backstepping sliding mode control for underactuated systems: Swing-up and stabilization of the Cart–Pendulum System. ISA Trans. 2013, 52, 870–880. [Google Scholar] [CrossRef]
- Jia, Z.; Yu, J.; Mei, Y.; Chen, Y.; Shen, Y.; Ai, X. Integral backstepping sliding mode control for quadrotor helicopter under external uncertain disturbances. Aerosp. Sci. Technol. 2017, 68, 299–307. [Google Scholar] [CrossRef]
- Nodland, D.; Zargarzadeh, H.; Jagannathan, S. Neural network-based optimal adaptive output feedback control of a helicopter UAV. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1061–1073. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Zhang, H. Neural network based adaptive dynamic inversion flight control system design. In Proceedings of the 2011 2nd International Conference on Intelligent Control and Information Processing, Harbin, China, 25–28 July 2011; pp. 135–137. [Google Scholar]
- Lee, T.; Kim, Y. Nonlinear adaptive flight control using backstepping and neural networks controller. J. Guidance Control Dyn. 2012, 24, 675–682. [Google Scholar] [CrossRef]
- Mokhtari, S.; Abbaspour, A.; Yen, K.K.; Sargolzaei, A. Neural Network-Based Active Fault-Tolerant Control Design for Unmanned Helicopter with Additive Faults. Remote Sens. 2021, 13, 2396. [Google Scholar] [CrossRef]
- Wang, D.; Zong, Q.; Tian, B.; Shao, S.; Zhang, X.; Zhao, X. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters. ISA Trans. 2018, 73, 208–226. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Y.; Dong, L.; Xue, L.; Sun, C. Adaptive control based on neural networks for an uncertain 2-DOF helicopter system with input deadzone and output constraints. IEEE/CAA J. Autom. Sin. 2019, 6, 807–815. [Google Scholar] [CrossRef]
- Chen, M.; Ma, H.; Kang, Y.; Wu, Q. Adaptive neural safe tracking control design for a class of uncertain nonlinear systems with output constraints and disturbances. IEEE Trans. Cybern. 2021, 52, 12571–12582. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Tao, G.; Jiang, B. Dynamic surface control using neural networks for a class of uncertain nonlinear systems with input saturation. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2086–2097. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Chen, M. Adaptive neural prescribed performance tracking control for near space vehicles with input nonlinearity. Neurocomputing 2016, 174, 780–789. [Google Scholar] [CrossRef]
- Chen, M.; Yan, K.; Wu, Q. Multiapproximator-based fault-tolerant tracking control for unmanned autonomous helicopter with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 5710–5722. [Google Scholar] [CrossRef]
- Wu, B.; Wu, J.; Zhang, J.; Tang, G.; Zhao, Z. Adaptive neural control of a 2DOF helicopter with input saturation and time-varying output constraint. Actuators 2022, 11, 336. [Google Scholar] [CrossRef]
- Cai, G.; Chen, B.M.; Lee, T.H. Unmanned Rotorcraft Systems; Springer Science and Business Media: New York, NY, USA, 2011; pp. 97–128. [Google Scholar]
- Chen, M.; Shi, P.; Lim, C. Adaptive neural fault-tolerant control of a 3-DOF model helicopter system. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 260–270. [Google Scholar] [CrossRef]
- Chen, M. Robust tracking control for self-balancing mobile robots using disturbance observer. IEEE/CAA J. Autom. Sin. 2017, 4, 458–465. [Google Scholar] [CrossRef]
- Ge, S.S.; Wang, C. Adaptive neural control of uncertain MIMO nonlinear systems. IEEE Trans. Neural Netw. 2004, 15, 674–692. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Ge, S.S.; How, B.V.E. Robust adaptive neural network control for a class of uncertain MIMO nonlinear systems with input nonlinearities. IEEE Trans. Neural Netw. 2010, 21, 796–812. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, J. Neural network-based adaptive dynamic surface control for a class of uncertain nonlinear systems in strict-feedback form. IEEE Trans. Neural Netw. 2005, 16, 195–202. [Google Scholar] [CrossRef]
- Mokhtari, M.R.; Cherki, B.; Braham, A.C. Disturbance observer based hierarchical control of coaxial-rotor UAV. ISA Trans. 2017, 67, 466–475. [Google Scholar] [CrossRef]






| Symbol | Definition | Value(unit) |
|---|---|---|
| m | Mass of UAH | 800 kg |
| g | Acceleration of gravity | 9.8 m/s2 |
| Moment of inertia along x axis | 358.4 kg · m2 | |
| Moment of inertia along y axis | 777.9 kg · m2 | |
| Moment of inertia along z axis | 601.4 kg · m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, M.; Chen, M.; Lungu, M. Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks. Drones 2023, 7, 154. https://doi.org/10.3390/drones7030154
Wan M, Chen M, Lungu M. Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks. Drones. 2023; 7(3):154. https://doi.org/10.3390/drones7030154
Chicago/Turabian StyleWan, Min, Mou Chen, and Mihai Lungu. 2023. "Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks" Drones 7, no. 3: 154. https://doi.org/10.3390/drones7030154
APA StyleWan, M., Chen, M., & Lungu, M. (2023). Integral Backstepping Sliding Mode Control for Unmanned Autonomous Helicopters Based on Neural Networks. Drones, 7(3), 154. https://doi.org/10.3390/drones7030154








