Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery
Abstract
:1. Introduction
1.1. Vegetation Mapping with Unmanned Aerial Vehicles
1.2. From Imagery to Reflectance Measurements
1.3. Problems in Radiometric Calibration
1.4. Effects of Illumination Geometry
1.5. Flying Height
1.6. Objectives and Research Questions
- How sensitive to changing solar elevation and azimuth are reflectance and NDVI measured by the Sequoia in individual images and orthomosaics?
- Does flying height influence surface reflectance in Sequoia images and orthomosaics?
- How consistent is reflectance measured by the Sequoia with ground measurements from a field spectrometer?
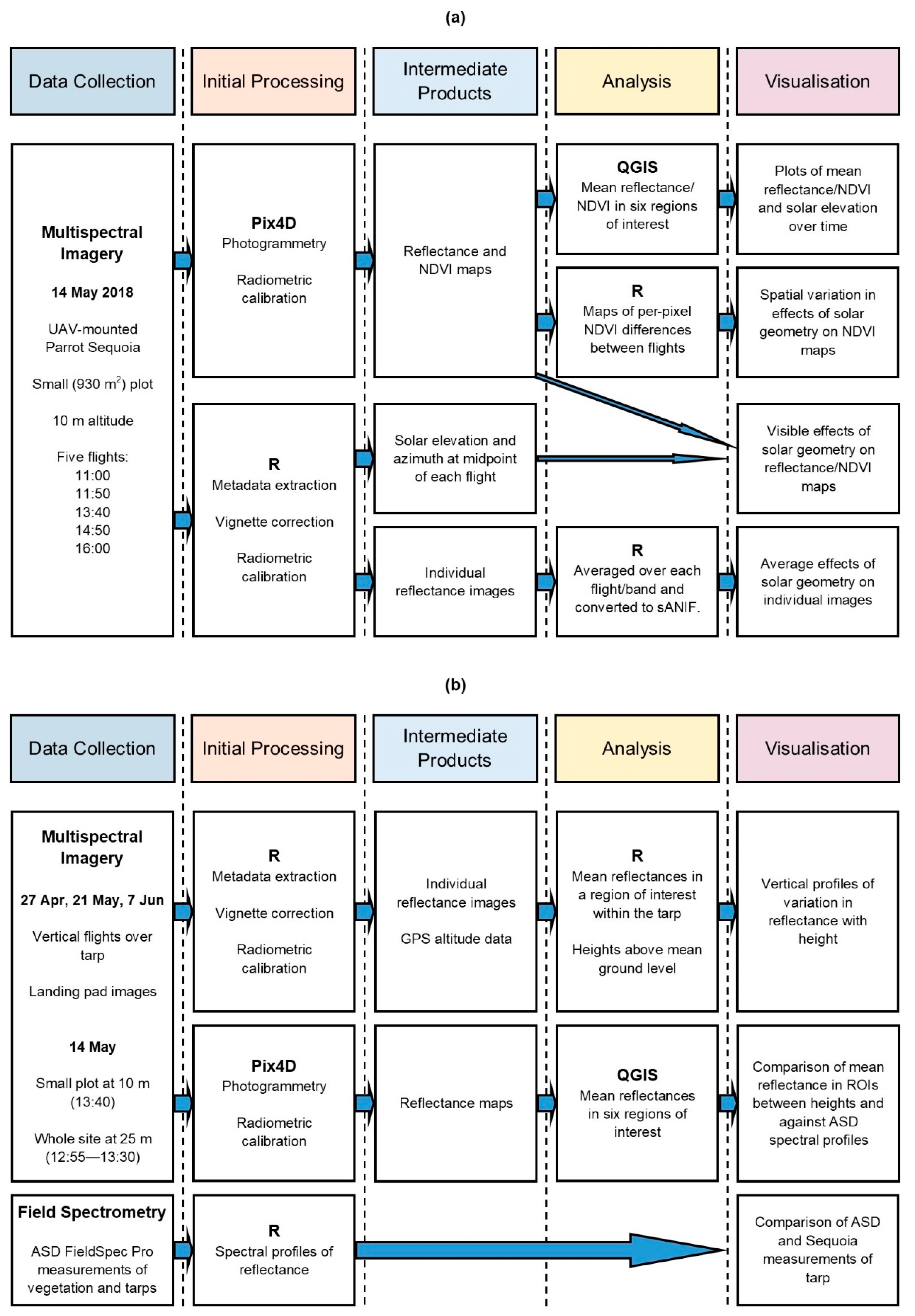
2. Materials and Methods
2.1. Data Collection
2.1.1. Study Site
2.1.2. UAS Platform and Sensor
2.1.3. Image Acquisition
2.1.4. Ground Reference Data
2.2. Image Processing
2.2.1. Correction and Calibration of Individual Images
2.2.2. Reflectance and NDVI Maps
2.3. Analysis and Visualisation
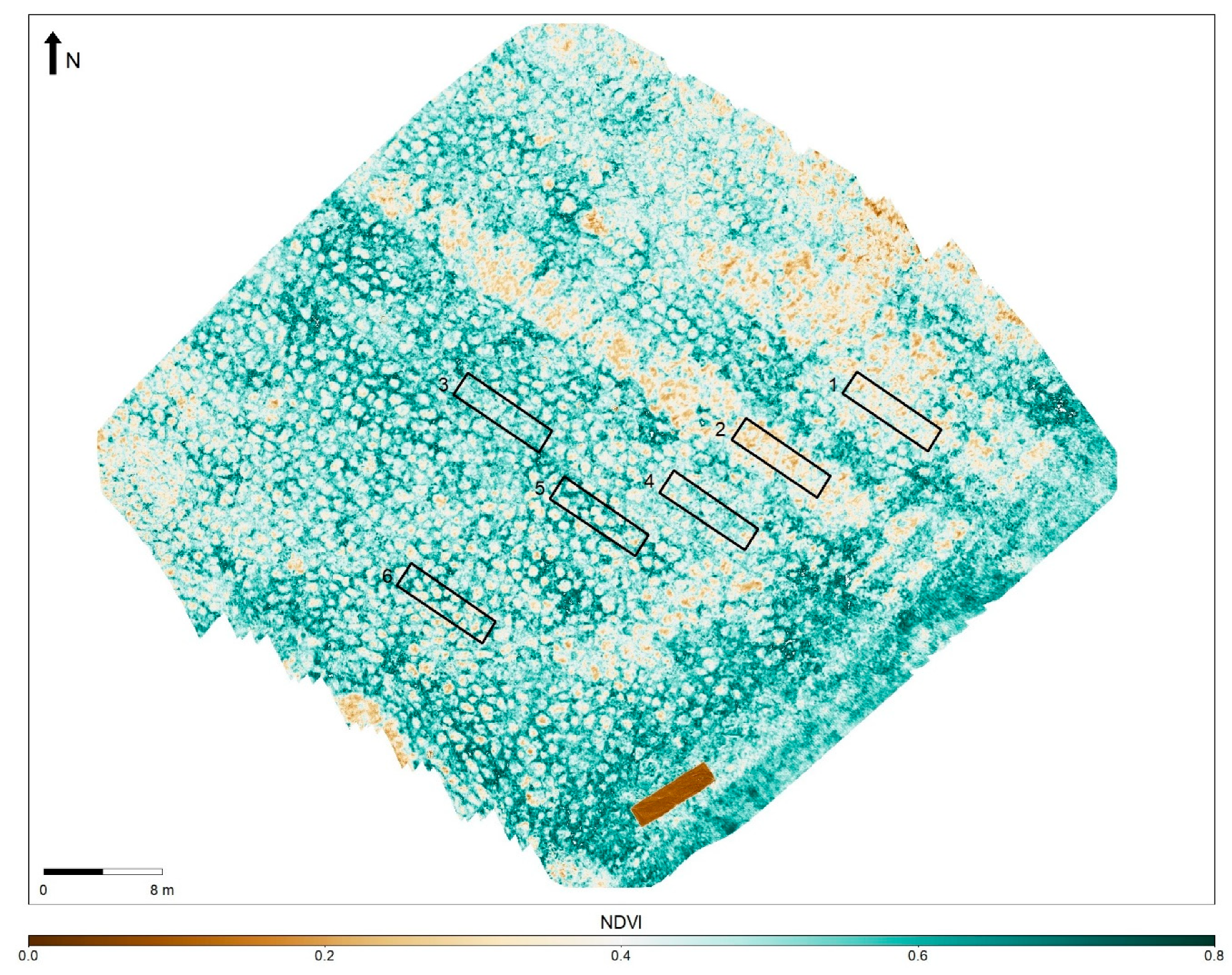
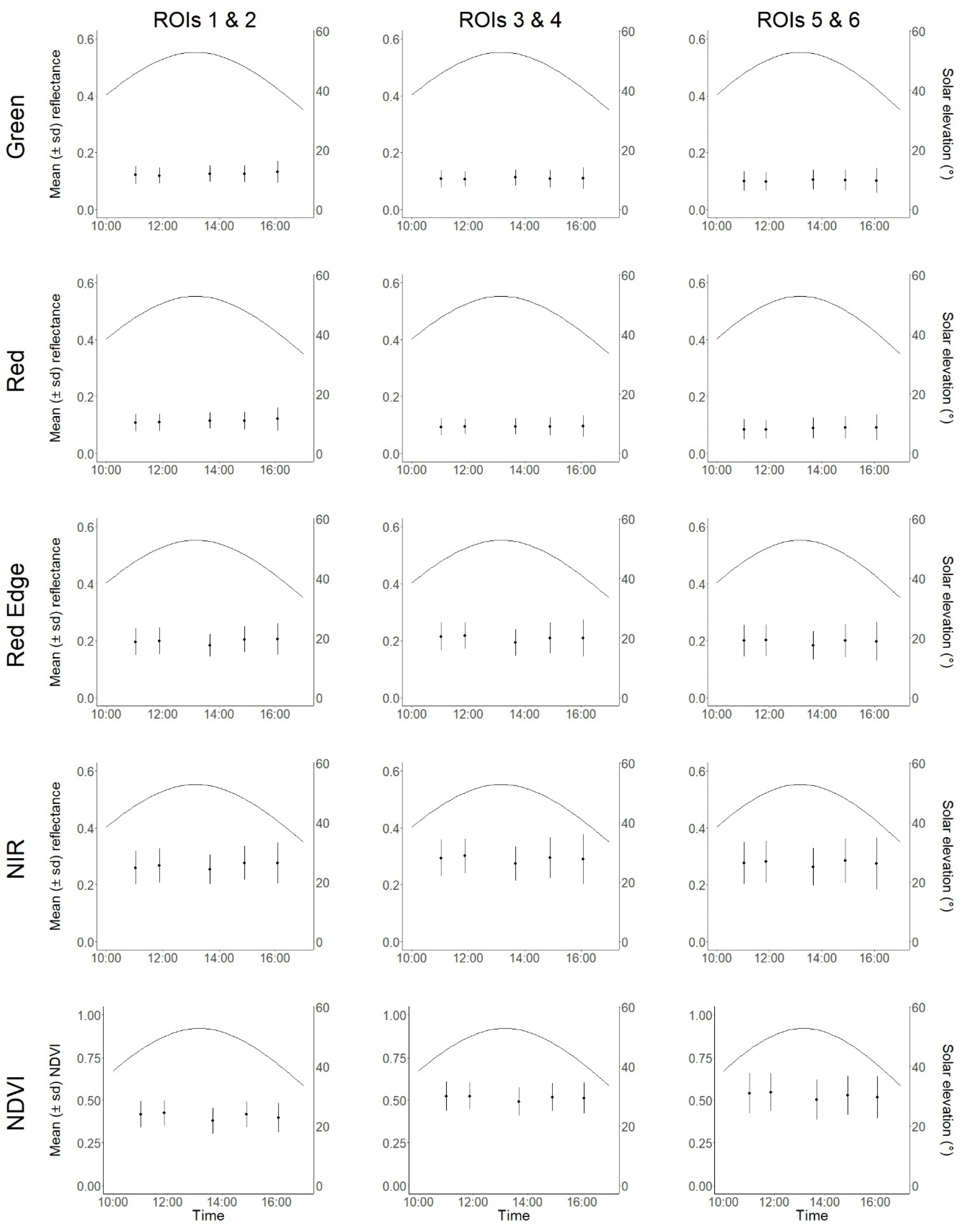
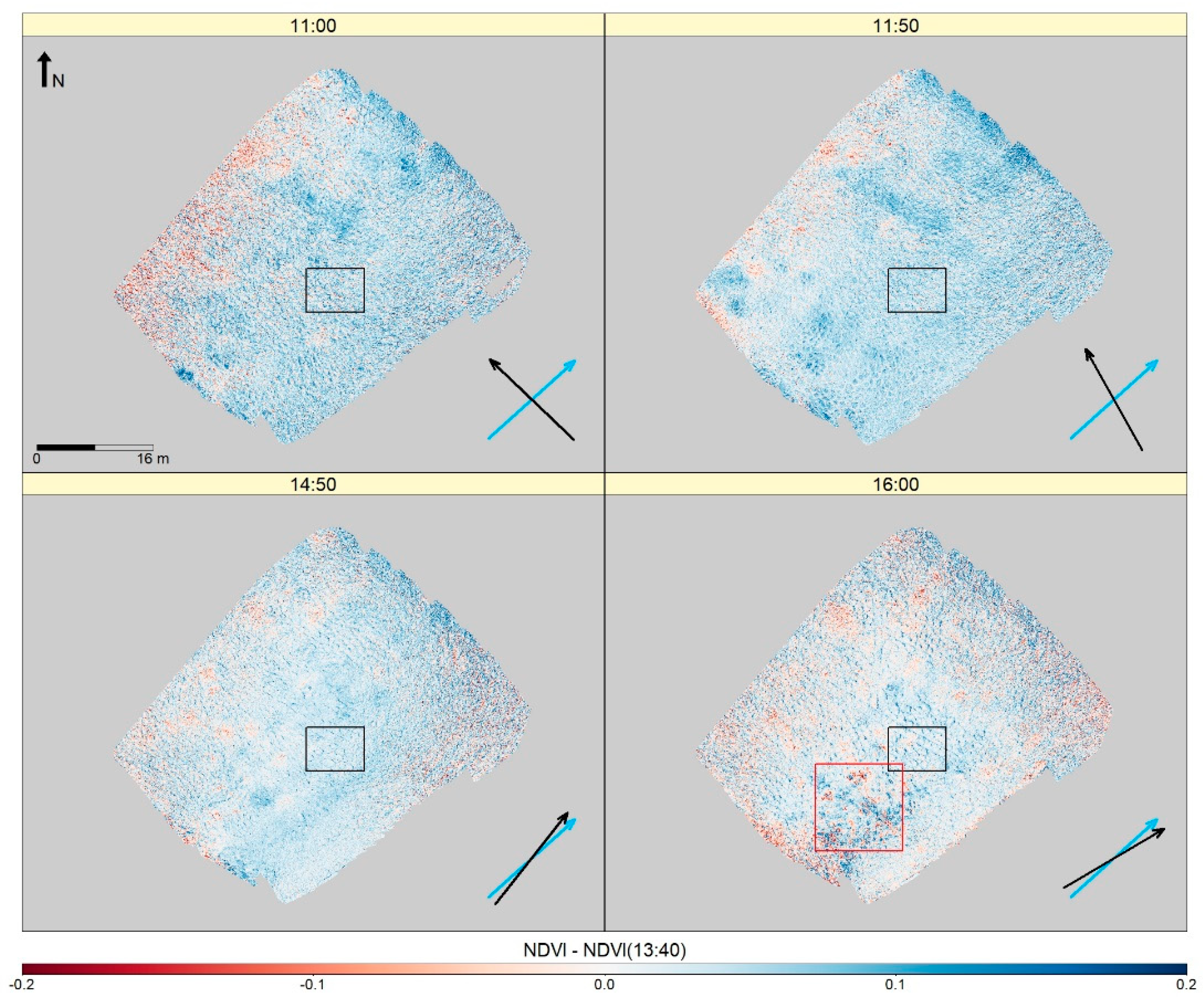
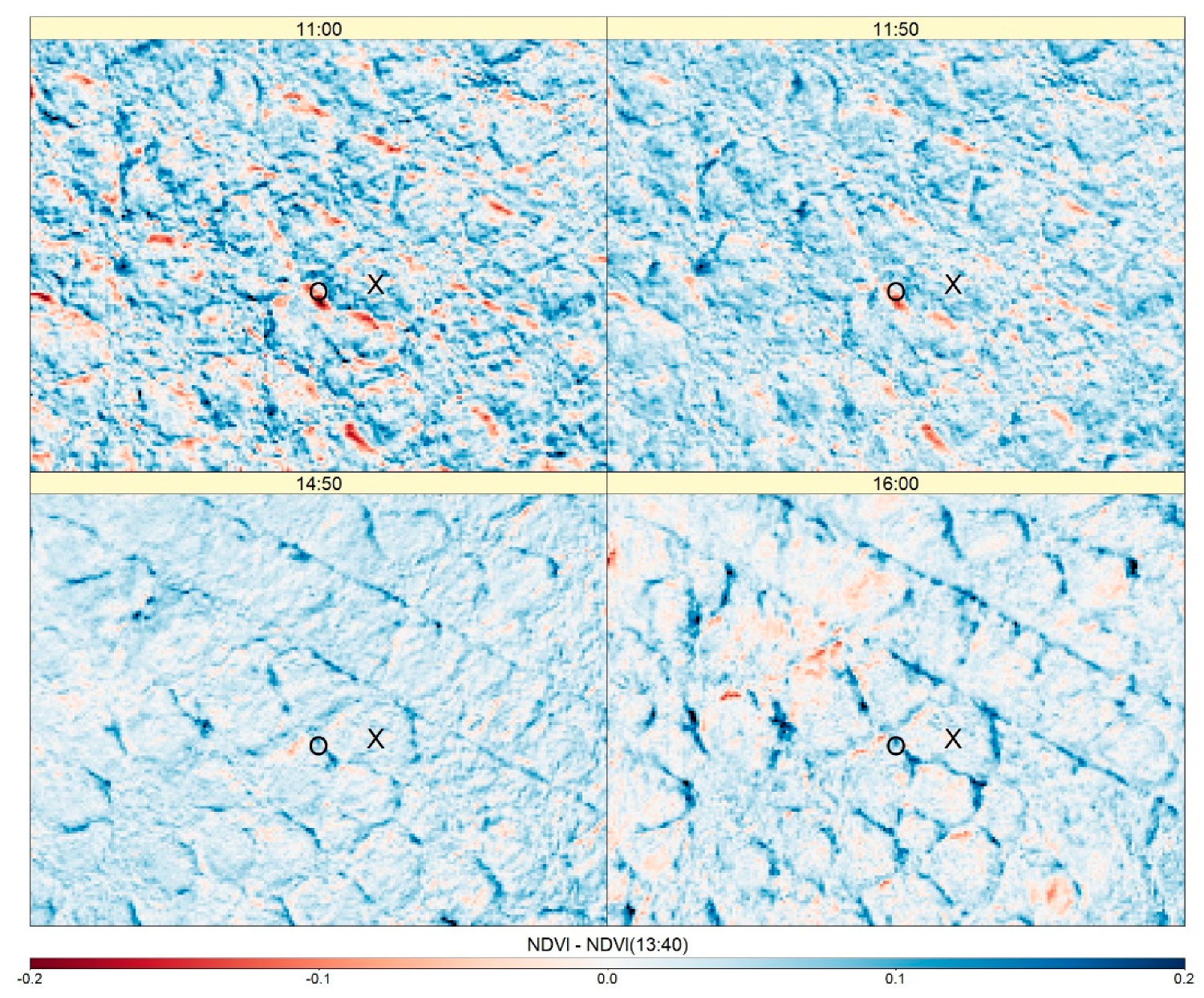
2.3.1. Illumination Geometry
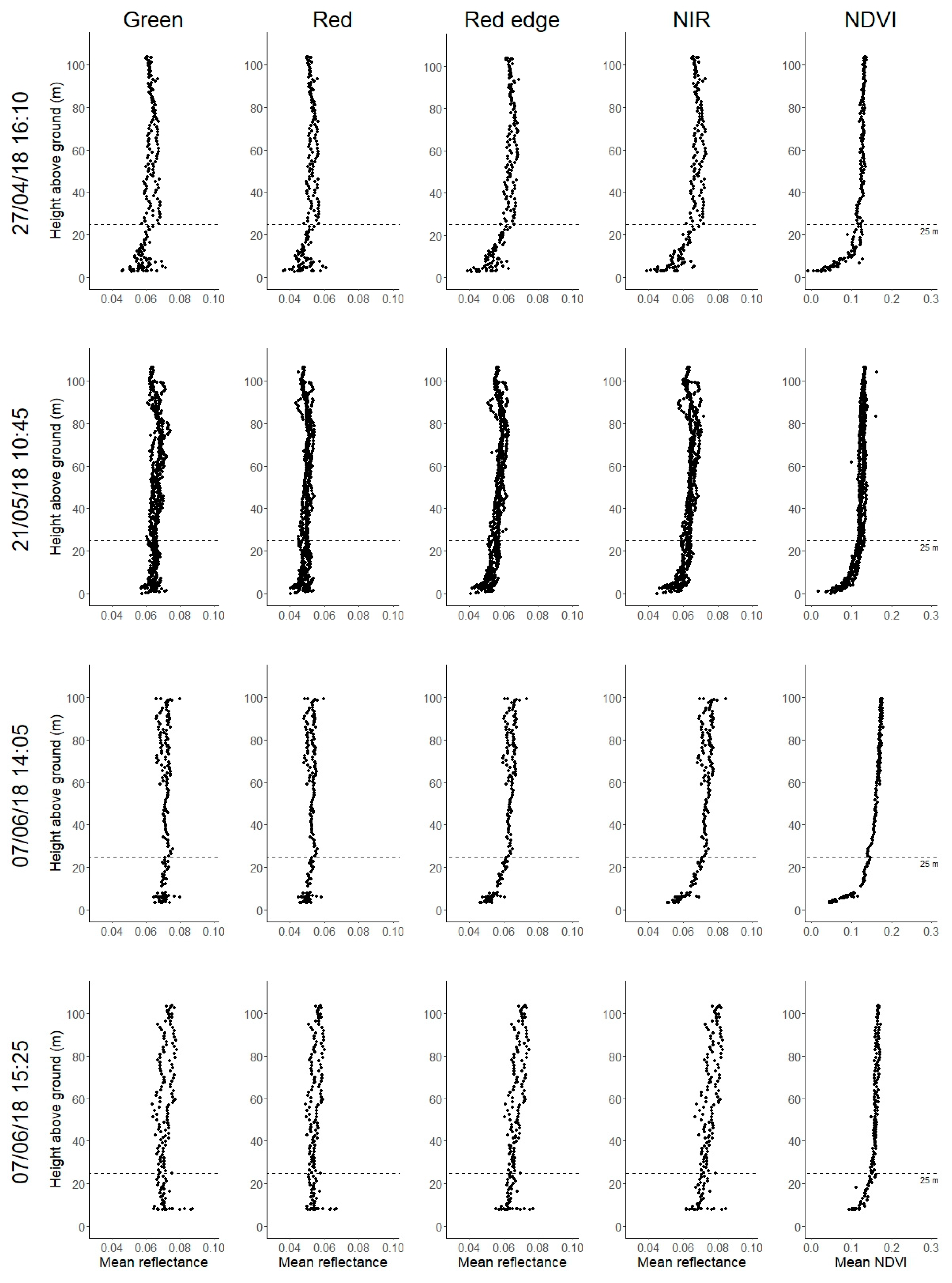
2.3.2. Flying Height
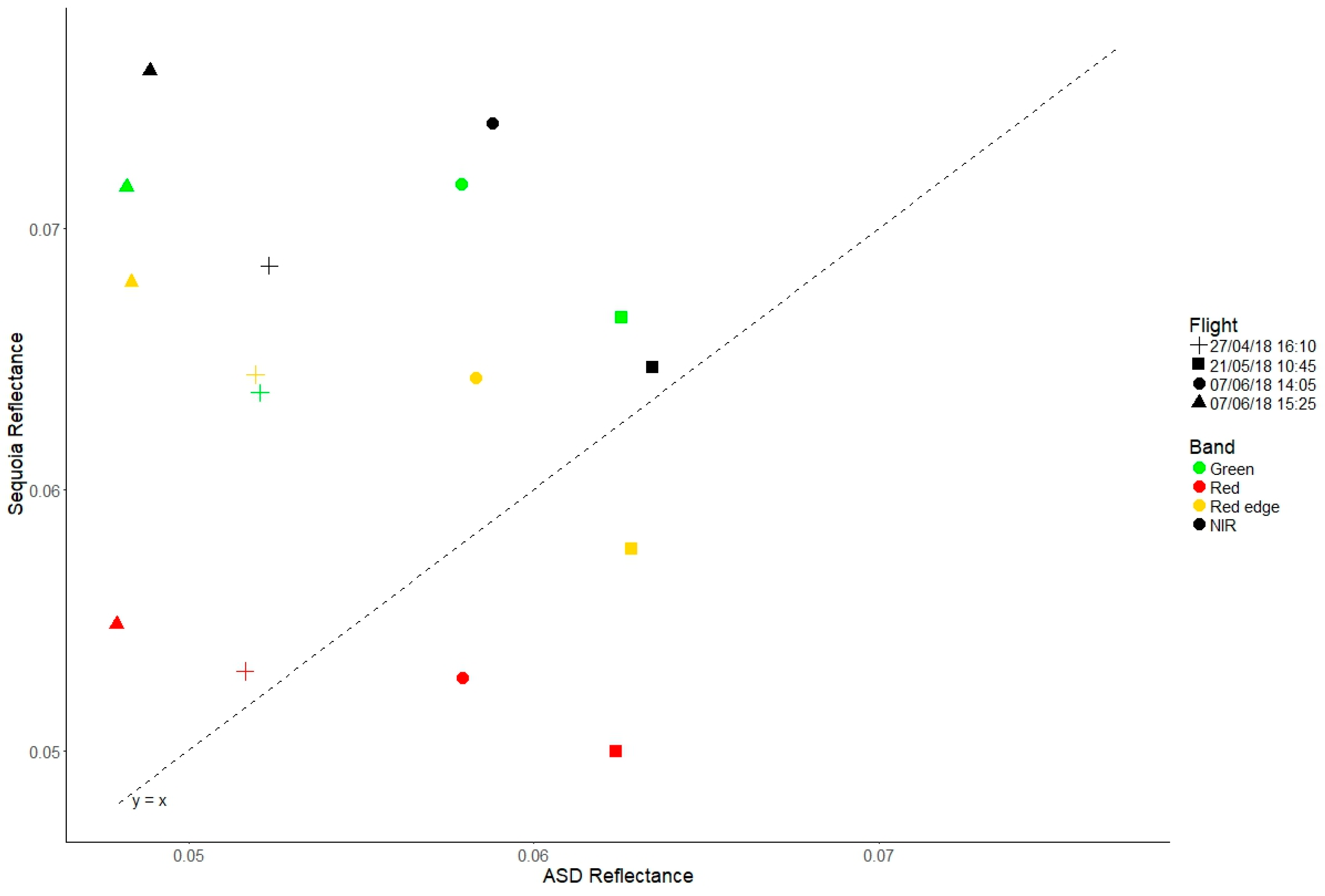
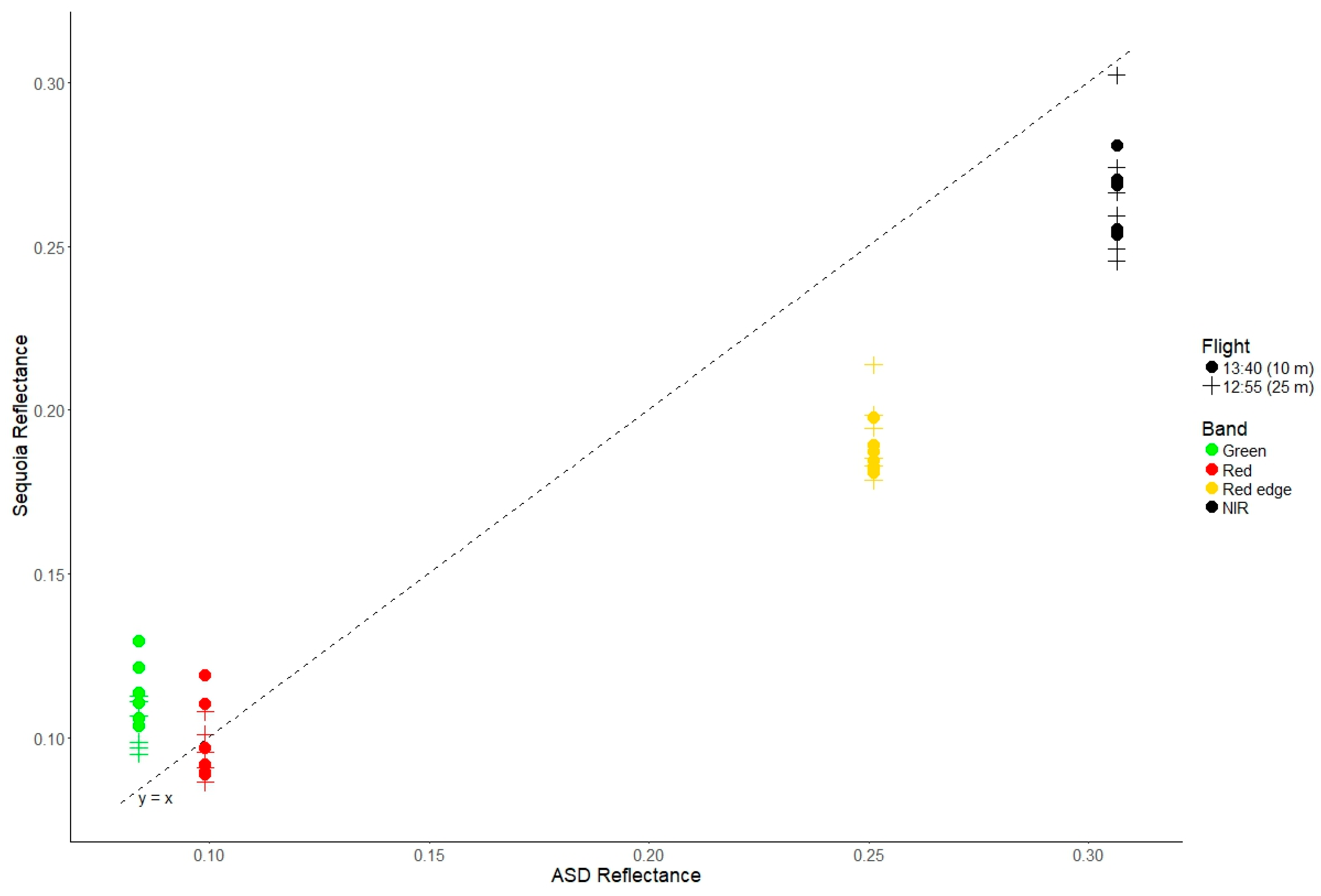
2.3.3. Comparison between UAS and Ground Reference Data
- Mean reflectance in each Sequoia band from images collected above 25 m in vertical profile flights.
- Mean reflectance in each band in the six ROIs for reflectance maps of the 25-m flight and the 13:40 10-m flight on 14 May.
3. Results
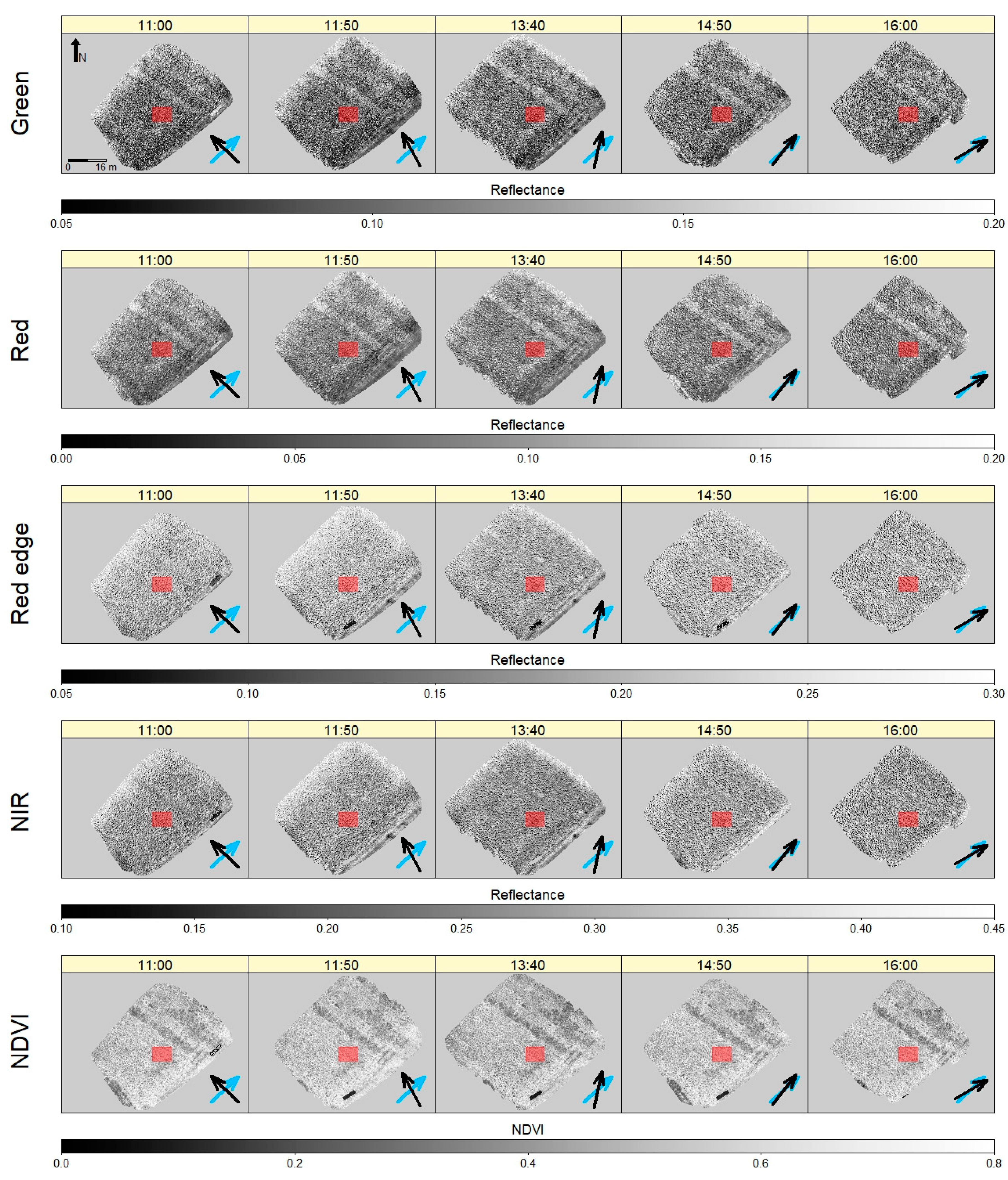
3.1. Effects of Illumination Geometry
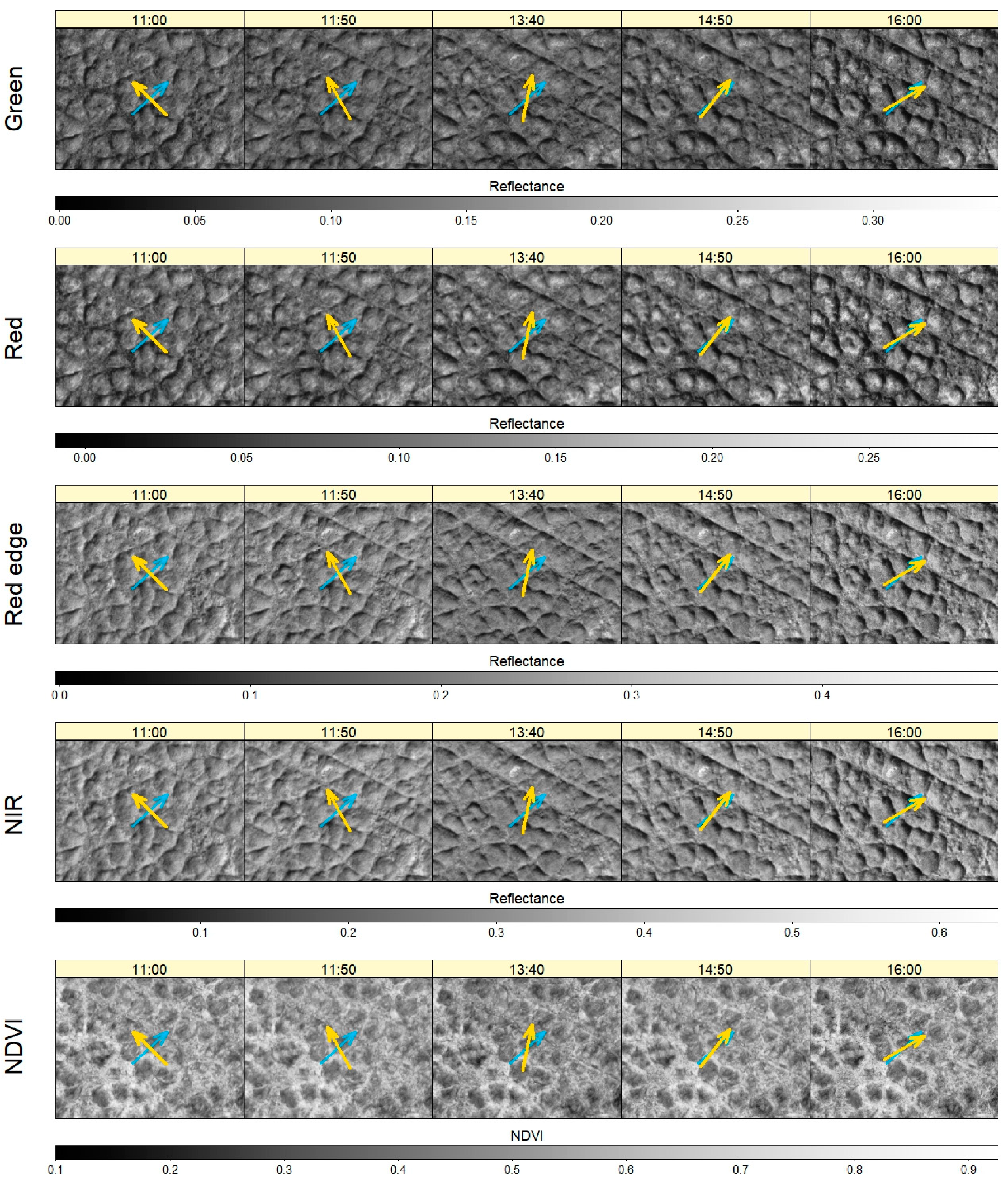
3.2. Effects of Flying Height
3.3. Comparison between Sequoia and Ground Reference Data
4. Discussion
4.1. Anisotropic Reflectance
4.2. Flight Planning
4.3. Flying Height
4.4. Radiometric Calibration
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo Madrigal, V.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Cruzan, M.B.; Weinstein, B.G.; Grasty, M.R.; Kohrn, B.F.; Hendrickson, E.C.; Arredondo, T.M.; Thompson, P.G. Small unmanned aerial vehicles (micro-UAVs, drones) in plant ecology. Appl. Plant Sci. 2016, 4, 1600041. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef] [Green Version]
- Pádua, L.; Vanko, J.; Hruška, J.; Adão, T.; Sousa, J.J.; Peres, E.; Morais, R. UAS, sensors, and data processing in agroforestry: A review towards practical applications. Int. J. Remote Sens. 2017, 38, 2349–2391. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Gennaro, S.F.D.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: A review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Salamí, E.; Barrado, C.; Pastor, E. UAV flight experiments applied to the remote sensing of vegetated areas. Remote Sens. 2014, 6, 11051–11081. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Cowley, D.; Moriarty, C.; Geddes, G.; Brown, G.; Wade, T.; Nichol, C. UAVs in Context: Archaeological Airborne Recording in a National Body of Survey and Record. Drones 2017, 2, 2. [Google Scholar] [CrossRef]
- Singh, K.K.; Frazier, A.E. A meta-analysis and review of unmanned aircraft system (UAS) imagery for terrestrial applications. Int. J. Remote Sens. 2018. [Google Scholar] [CrossRef]
- Aasen, H.; Honkavaara, E.; Lucieer, A.; Zarco-Tejada, P.J. Quantitative Remote Sensing at Ultra-High Resolution with UAV Spectroscopy: A Review of Sensor Technology, Measurement Procedures, and Data Correction Workflows. Remote Sens. 2018, 10, 1091. [Google Scholar] [CrossRef]
- Dandois, J.; Olano, M.; Ellis, E. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef] [Green Version]
- Kelcey, J.; Lucieer, A. Sensor Correction of a 6-Band Multispectral Imaging Sensor for UAV Remote Sensing. Remote Sens. 2012, 4, 1462–1493. [Google Scholar] [CrossRef] [Green Version]
- Assmann, J.J.; Kerby, J.T.; Cunliffe, A.M.; Myers-Smith, I.H. Vegetation monitoring using multispectral sensors - best practices and lessons learned from high latitudes. bioRxiv 2018. [Google Scholar] [CrossRef]
- Berra, E.F.; Gaulton, R.; Barr, S. Commercial Off-the-Shelf Digital Cameras on Unmanned Aerial Vehicles for Multitemporal Monitoring of Vegetation Reflectance and NDVI. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4878–4886. [Google Scholar] [CrossRef] [Green Version]
- Lebourgeois, V.; Bégué, A.; Labbé, S.; Mallavan, B.; Prévot, L.; Roux, B. Can Commercial Digital Cameras Be Used as Multispectral Sensors? A Crop Monitoring Test. Sensors 2008, 8, 7300–7322. [Google Scholar] [CrossRef]
- Lelong, C.C.D.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of Unmanned Aerial Vehicles Imagery for Quantitative Monitoring of Wheat Crop in Small Plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef]
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Wang, C.; Myint, S.W. A Simplified Empirical Line Method of Radiometric Calibration for Small Unmanned Aircraft Systems-Based Remote Sensing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1876–1885. [Google Scholar] [CrossRef]
- Aasen, H.; Bolten, A. Multi-temporal high-resolution imaging spectroscopy with hyperspectral 2D imagers—From theory to application. Remote Sens. Environ. 2018, 205, 374–389. [Google Scholar] [CrossRef]
- Domenzain, L. Reflectance Estimation. Available online: https://forum.developer.parrot.com/t/reflectance-estimation/5597/2 (accessed on 3 May 2018).
- Parrot Drones SAS. Application note: Pixel value to irradiance using the sensor calibration model. Available online: https://forum.developer.parrot.com/uploads/default/original/2X/3/383261d35e33f1f375ee49e9c7a9b10071d2bf9d.pdf (accessed on 3 May 2018).
- Ortega-Terol, D.; Hernandez-Lopez, D.; Ballesteros, R.; Gonzalez-Aguilera, D. Automatic Hotspot and Sun Glint Detection in UAV Multispectral Images. Sensors 2017, 17, 2352. [Google Scholar] [CrossRef]
- Sandmeier, S.; Müller, C.; Hosgood, B.; Andreoli, G. Physical Mechanisms in Hyperspectral BRDF Data of Grass and Watercress. Remote Sens. Environ. 1998, 66, 222–233. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Kooistra, L.; Clevers, J.G.P.W. Mapping Reflectance Anisotropy of a Potato Canopy Using Aerial Images Acquired with an Unmanned Aerial Vehicle. Remote Sens. 2017, 9, 417. [Google Scholar] [CrossRef]
- Roosjen, P.P.J.; Suomalainen, J.M.; Bartholomeus, H.M.; Clevers, J.G.P.W. Hyperspectral Reflectance Anisotropy Measurements Using a Pushbroom Spectrometer on an Unmanned Aerial Vehicle—Results for Barley, Winter Wheat, and Potato. Remote Sens. 2016, 8, 909. [Google Scholar] [CrossRef]
- Burkart, A.; Aasen, H.; Alonso, L.; Menz, G.; Bareth, G.; Rascher, U. Angular Dependency of Hyperspectral Measurements over Wheat Characterized by a Novel UAV Based Goniometer. Remote Sens. 2015, 7, 725–746. [Google Scholar] [CrossRef] [Green Version]
- Grenzdörffer, G.J.; Niemeyer, F. UAV Based BRDF-Measurements of Agricultural Surfaces with PFIFFikus. ISPRS - Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-1/C22, 229–234. [Google Scholar]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of Bidirectional Reflectance Factor Dataset Using a Micro Unmanned Aerial Vehicle and a Consumer Camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, J.; Ntakos, G.; Nielsen, J.; Svensgaard, J.; Poulsen, R.N.; Christensen, S. Are vegetation indices derived from consumer-grade cameras mounted on UAVs sufficiently reliable for assessing experimental plots? Eur. J. Agron. 2016, 74, 75–92. [Google Scholar] [CrossRef]
- Brede, B.; Suomalainen, J.; Bartholomeus, H.; Herold, M. Influence of solar zenith angle on the enhanced vegetation index of a Guyanese rainforest. Remote Sens. Lett. 2015, 6, 972–981. [Google Scholar] [CrossRef]
- Yu, X.; Liu, Q.; Liu, X.; Liu, X.; Wang, Y. A physical-based atmospheric correction algorithm of unmanned aerial vehicles images and its utility analysis. Int. J. Remote Sens. 2017, 38, 3101–3112. [Google Scholar] [CrossRef]
- NERC Centre for Ecology & Hydrology. Auchencorth Moss Fieldsite. Available online: http://www.auchencorth.ceh.ac.uk/ (accessed on 7 March 2018).
- NERC Centre for Ecology & Hydrology. Auchencorth Moss: An atmospheric observatory. Available online: https://www.ceh.ac.uk/our-science/monitoring-site/auchencorth-moss-atmospheric-observatory (accessed on 7 March 2018).
- Parrot Drones SAS. Parrot Sequoia. Available online: https://www.parrot.com/uk/parrot-professional/parrot-sequoia (accessed on 7 March 2018).
- NERC Field Spectroscopy Facility. Field Guide for the ASD FieldSpec Pro – White Reference Mode. Available online: http://fsf.nerc.ac.uk/resources/guides/pdf_guides/asd_guide_v2_wr.pdf (accessed on 23 April 2018).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Hijmans, R. raster: Geographic Data Analysis and Modeling. 2017. Available online: https://cran.r-project.org/package=raster (accessed on 3 May 2018).
- Parrot Drones SAS. Application note: How to correct vignetting in images. Available online: https://forum.developer.parrot.com/uploads/default/original/2X/b/b9b5e49bc21baf8778659d8ed75feb4b2db5c45a.pdf (accessed on 3 May 2018).
- Domenzain, L. Details of Irradiance List tag for Sunshine sensor in exif data of Sequoia. Available online: https://forum.developer.parrot.com/t/details-of-irradiance-list-tag-for-sunshine-sensor-in-exif-data-of-sequoia/5261/2 (accessed on 3 May 2018).
- Bashir, M. How to convert Sequoia images to reflectance? Available online: https://onedrive.live.com/?authkey=%21ACzNLk1ORe37aRQ&cid=C34147D823D8DFEF&id=C34147D823D8DFEF%2115414&parId=C34147D823D8DFEF%21106&o=OneUp (accessed on 3 May 2018).
- Pix4D SA. Radiometric corrections. Available online: https://support.Pix4D.com/hc/en-us/articles/202559509 (accessed on 7 March 2018).
- Agafonkin, V.; Thieurmel, B. suncalc: Compute Sun Position, Sunlight Phases, Moon Position and Lunar Phase, R package version 0.4; 2018. Available online: https://CRAN.R-project.org/package=suncalc (accessed on 3 May 2018).
- QGIS Development Team. QGIS Geographic Information System. Open Source Geospatial Foundation Project. 2017. Available online: http://www.qgis.org (accessed on 3 May 2018).
- Kimes, D.S. Dynamics of directional reflectance factor distributions for vegetation canopies. Appl. Opt. 1983, 22, 1364–1372. [Google Scholar] [CrossRef]
- Ishihara, M.; Inoue, Y.; Ono, K.; Shimizu, M.; Matsuura, S. The Impact of Sunlight Conditions on the Consistency of Vegetation Indices in Croplands—Effective Usage of Vegetation Indices from Continuous Ground-Based Spectral Measurements. Remote Sens. 2015, 7, 14079–14098. [Google Scholar] [CrossRef]






| Band | Centre Wavelength (nm) | Band Width (nm) | Focal Length (mm) | Image Size (pixels) | Field of View |
|---|---|---|---|---|---|
| Green | 550 | 40 | 3.98 | 1280 × 960 | Horizontal: 61.9° Vertical: 48.5° Diagonal: 73.7° |
| Red | 660 | 40 | |||
| Red Edge | 735 | 10 | |||
| NIR | 790 | 40 |
| Date | Target | Time of Measurements (UTC+0100) | Number of Measurements |
|---|---|---|---|
| 27 April | Tarp | 11:29–11:31 | 4 |
| Vegetation | 11:35–12:05 | 20 | |
| 14 May | Vegetation | 12:10–12:35 | 14 |
| 21 May | Tarp | 11:00–11:04 | 10 |
| Vegetation | 12:15–12:50 | 22 | |
| 7 June | Tarp | 13:58 | 9 |
| 14:56 | 10 | ||
| 15:53 | 10 | ||
| Vegetation | 16:04–16:16 | 10 |
| Flight Time | Flying Height (m) | Average GSD (cm) |
|---|---|---|
| 11:00 | 10 | 1.15 |
| 11:50 | 10 | 1.29 |
| 13:40 | 10 | 1.05 |
| 14:50 | 10 | 1.09 |
| 16:00 | 10 | 0.85 |
| 12:55 | 25 | 2.92 |
| Flight Time | Mean Absolute NDVI Difference |
|---|---|
| 11:00 | 0.0572 |
| 11:50 | 0.0484 |
| 14:50 | 0.0432 |
| 16:00 | 0.0445 |
| Band | 10 m vs. 25 m | Sequoia vs. ASD | |||
|---|---|---|---|---|---|
| Vegetation | Tarp | ||||
| 10-m Flights | 25-m Flights | All Flights | All Flights | ||
| Green | 0.0116 | 0.0315 | 0.0208 | 0.0267 | 0.0149 |
| Red | 0.0068 | 0.0114 | 0.0089 | 0.0103 | 0.0076 |
| Red edge | 0.0083 | 0.0642 | 0.0600 | 0.0621 | 0.0123 |
| NIR | 0.0098 | 0.0439 | 0.0444 | 0.0441 | 0.0176 |
| NDVI | 0.0193 | 0.0789 | 0.0621 | 0.0710 | 0.1394 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stow, D.; Nichol, C.J.; Wade, T.; Assmann, J.J.; Simpson, G.; Helfter, C. Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery. Drones 2019, 3, 55. https://doi.org/10.3390/drones3030055
Stow D, Nichol CJ, Wade T, Assmann JJ, Simpson G, Helfter C. Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery. Drones. 2019; 3(3):55. https://doi.org/10.3390/drones3030055
Chicago/Turabian StyleStow, Daniel, Caroline J. Nichol, Tom Wade, Jakob J. Assmann, Gillian Simpson, and Carole Helfter. 2019. "Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery" Drones 3, no. 3: 55. https://doi.org/10.3390/drones3030055
APA StyleStow, D., Nichol, C. J., Wade, T., Assmann, J. J., Simpson, G., & Helfter, C. (2019). Illumination Geometry and Flying Height Influence Surface Reflectance and NDVI Derived from Multispectral UAS Imagery. Drones, 3(3), 55. https://doi.org/10.3390/drones3030055





