Fuzzy Convexity Under cr-Order with Control Operator and Fractional Inequalities

Abstract

This study is organized to introduce the concept of center–radius $\left(cr\right)$-ordered fuzzy number-valued convex mappings. Based on this class of mappings, we have initiated the idea of fuzzy number-valued extended $cr$-ℏ convex mappings incorporating control mapping ℏ. Furthermore, several potential new classes of convexity will be provided to discuss its generic nature. Also, some essential properties, criteria, and detailed characterizations through Jensen’s and Hermite–Hadamard-like inequalities are provided, incorporating Riemann–Liouville fractional operators, which are defined by $\rho$-level mappings. To validate the proposed fractional bounds through simulations, we consider both triangular and trapezoidal fuzzy numbers. Our results are based on totally ordered fuzzy-valued mappings, which are new and generic. The under-consideration class also includes a blend of new classes of convexity, which are controlled by non-negative mapping ℏ. In previous studies, the researchers have focused on different partially ordered relations.

1. Introduction and Preliminaries

Convex mapping theory is a bridge between geometrical and analytical properties and modernizes various concepts. Also, it provides unified approaches to assessing the various problems of optimization, operational research, differential equations, and inequalities. Observing the dominance of convexity, various new concepts of convex sets and mappings have been explored, relying on weighted means and more general frameworks like interval-valued calculus, fuzzy-valued calculus, and stochastic analysis. The fundamental goal of such a theory is to define new generalizations of convexity and its characterization through inequalities. For more details, see [1,2,3,4,5].

The role of inequalities is fundamental in the analysis of complex mathematical expressions that appear in most branches of the physical sciences. Their work has grown out of multiple viewpoints: the extension of applicability and overcoming the shortcomings of classical results, the use of tools of functional analysis, further developments in calculus, and convexity. The inequalities were originally devised to bound mappings and integrals but have evolved into essential tools for the uniqueness and stability of solutions, for estimating errors in numerical integration, and for dealing with problems in information theory, among other things. Convex analysis has substantially enriched this field, because many classical inequalities arise naturally from properties of convex functions. For more information, see [6,7].

Let us mention the premises of convex mappings.

Definition 1

([8]). Any mapping $\mathcal{F}:[{\eta }_3,{\eta }_4]\to \mathbb{R}$ is said to be convex if

$$\begin{array}{c}\hfill \mathcal{F}({\eta }_3+g({\eta }_4-{\eta }_3))\le (1-g)\mathcal{F}\left({\eta }_3\right)+g\mathcal{F}\left({\eta }_4\right),g\in [0,1].\end{array}$$

To highlight the strong enhancement between inequalities and convexity, we recover some fundamental results. First, we furnish Jensen’s inequality:

Theorem 1

([8]). If $\mathcal{F}:[{\eta }_3,{\eta }_4]\to \mathbb{R}$ is a convex mapping, ${\vartheta }_i\in [{\eta }_3,{\eta }_4]$, and ${\sum }_{i=1}^n{g}_i=1$ then

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \sum _{i=1}^n}{g}_i{\vartheta }_i\right)\le {\displaystyle \sum _{i=1}^n}{g}_i\mathcal{F}\left({\vartheta }_i\right).\end{array}$$

Likewise, another attracting double inequality due to convex mapping is Hermite–Hadamard inequality and is given as

Theorem 2

([8]). If $\mathcal{F}:I=\left[{\eta }_3,{\eta }_4\right]\to \mathbb{R}$ is a convex mapping then for ${\eta }_3,{\eta }_4\in I$, as well as ${\eta }_3<{\eta }_4$, the inequality

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\le {\displaystyle \frac{1}{{\eta }_4-{\eta }_3}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(\epsilon \right)\mathrm{d}\epsilon \le {\displaystyle \frac{\mathcal{F}\left({\eta }_3\right)+\mathcal{F}\left({\eta }_4\right)}{2}}.\end{array}$$

Set-valued analysis is an effective and attractive branch of mathematics; it generalizes single-valued mappings. Interval-valued and fuzzy-valued are specific cases of it. These kinds of mappings are quite applicable to approximating the error analysis of numerical methods. The subject of interval analysis was pioneered by Moore [9], and monographs authored by him are regarded as fundamental to exploring this subject further. In recent times, it has influenced every aspect of mathematical sciences because a natural problem is under what condition single-valued results can be updated for set-valued maps. In the following context, Breckner [10] proved the Hermite–Hadamard leveraging the set-valued convexity, which is given as follows:

Let $\mathcal{F}:[{\eta }_3,{\eta }_4]\subseteq \mathbb{R}\to P\left(\mathbb{R}\right)$ be a set-valued convex mapping; then,

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\supseteq {\displaystyle \frac{1}{{\eta }_4-{\eta }_3}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(\vartheta \right)\mathrm{d}g\supseteq {\displaystyle \frac{\mathcal{F}\left({\eta }_3\right)+\mathcal{F}\left({\eta }_4\right)}{2}}.\end{array}$$

In 1965, Zadeh [11] generalized the idea of characteristic mapping and defined membership mapping to deal with quantities having vagueness. He delivered the premises of the convex set and mapping in a fuzzy context. Moreover, the concept of convexity has a fundamental role in defining fuzzy numbers. These concepts provide a new strategy of estimating quantities and models with certain attributes other than statistical approaches. Zadeh’s contributions are fundamental in the progression of possibility theory; they are marvelous contributions to exploring the problems of computer science and dynamical systems. In 1982, Dubois and Prade [12] worked on fuzzy calculus and explored the preliminary concepts. In 1992, Nanda and Kar [13] studied the numerous classes of convexity, including their essential attributes.

In order to prove our main result, let us mention the facts and rules regarding interval and fuzzy analysis. Throughout the investigation, we denote the space compact intervals and non-negative compact intervals by $K_c$ and $K_c^{+}$, respectively. Let ${\widehat{B}}_1,{\mathcal{E}}_1\in K_c$, and $c\in \mathbb{R}$; then, Minkowski’s operations are given as

$$\begin{array}{cc}\hfill & c.\mathcal{E}:=\left\{\begin{array}{cc}\hfill \begin{array}{c}[c{\mathcal{E}}_{*},c{\mathcal{E}}^{*}]ifc\ge 0,\end{array}& \\ \\ \hfill \begin{array}{c}[c{\mathcal{E}}^{*},c{\mathcal{E}}_{*}]ifc<0.\end{array}\end{array}\right.\hfill \end{array}$$

Then, the Minkowski difference $\widehat{B}-\mathcal{E}$, addition $\mathcal{E}+\widehat{B}$, and $\mathcal{E}\times \widehat{B}$ for $\mathcal{E},\widehat{B}\in K_c$ are defined by

$$\begin{array}{cc}\hfill & [{\widehat{B}}_{*},{\widehat{B}}^{*}]-[{\mathcal{E}}_{*},{\mathcal{E}}^{*}]:=[{\widehat{B}}_{*}-{\mathcal{E}}_{*},{\widehat{B}}^{*}-{\mathcal{E}}^{*}]\hfill \\ \hfill & [{\widehat{B}}_{*},{\widehat{B}}^{*}]+[{\mathcal{E}}_{*},{\mathcal{E}}^{*}]:=[{\widehat{B}}_{*}+{\mathcal{E}}_{*},{\widehat{B}}^{*}+{\mathcal{E}}^{*}]\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & [{\widehat{B}}_{*},{\widehat{B}}^{*}]\times [{\mathcal{E}}_{*},{\mathcal{E}}^{*}]:=[min\{{\widehat{B}}_{*}{\mathcal{E}}_{*},{\widehat{B}}^{*}{\mathcal{E}}_{*},{\widehat{B}}_{*}{\mathcal{E}}^{*},{\widehat{B}}^{*}{\mathcal{E}}^{*}\},max\{{\widehat{B}}_{*}{\mathcal{E}}_{*},{\widehat{B}}^{*}{\mathcal{E}}_{*},{\widehat{B}}_{*}{\mathcal{E}}^{*},{\widehat{B}}^{*}{\mathcal{E}}^{*}\}].\hfill \end{array}$$

Definition 2

([14]). The "${\le }_{\rho }$" relation over $K_c$ is demonstrated as

$$[{\widehat{B}}_{*},{\widehat{B}}^{*}]{\le }_{\rho }[{\mathcal{E}}_{*},{\mathcal{E}}^{*}]$$

if and only if

$${\widehat{B}}_{*}\le {\mathcal{E}}_{*},{\widehat{B}}^{*}\le {\mathcal{E}}^{*};$$

for all $[{\widehat{B}}_{*},{\widehat{B}}^{*}],[{\mathcal{E}}_{*},{\mathcal{E}}^{*}]\in K_c$ is a pseudo-order or left–right (LR) ordering relation.

The ranking relation defined based on center and radius of interval is reported as follows.

Definition 3

([14]). The $cr$ relation between two intervals $\widehat{B}=\left[{\widehat{B}}_{★},{\widehat{B}}^{★}\right]=⟨{\widehat{B}}_c,{\widehat{B}}_r⟩$ and $\mathcal{E}=\left[{\mathcal{E}}_{★},{\mathcal{E}}^{★}\right]=⟨{\mathcal{E}}_c,{\mathcal{E}}_r⟩$ is defined as

$$\begin{array}{c}\hfill \widehat{B}{⪯}_{cr}\mathcal{E}\iff \left\{\begin{array}{c}{\widehat{B}}_c<{\mathcal{E}}_c,if{\widehat{B}}_c\ne {\mathcal{E}}_c\\ {\widehat{B}}_r\le {\mathcal{E}}_r,if{\widehat{B}}_c={\mathcal{E}}_c.\end{array}\right.\end{array}$$

Thus, for any two intervals $\widehat{B},\mathcal{E}\in {\mathbb{R}}_I$, either $\widehat{B}{⪯}_{\mathcal{cr}}\mathcal{E}$ or $\mathcal{E}{⪯}_{\mathcal{cr}}\widehat{B}$.

Theorem 3

([14,15]). Consider $\rho \in [0,1]$ and fuzzy set ξ. Its ρ-level is defined as of ${\xi }_{\rho }=\{g\in \mathbb{R}:\xi \left(g\right)\ge \rho \}$, and $supp\left(\xi \right)=cl\{g\in \mathbb{R}:\xi (g)>0\}$.

For greater conciseness, we symbolize the space of all real fuzzy sets and fuzzy numbers by $\mathbb{M}\left(\mathbb{R}\right)$ and ${\mathbb{M}}_F$, respectively. If a fuzzy set meets the conditions, such as normality, semi-continuity, fuzzy convexity, and being compactly supported, then it is called fuzzy number (interval).

Let $\xi \in {\mathbb{M}}_F$ be a fuzzy interval ⇔$\rho$-levels ${\left[\xi \right]}^{\rho }$ is a compact convex set of $\mathbb{R}$.

Its $\rho$-level form is given as

$$\begin{array}{c}\hfill {\left[\xi \right]}^{\rho }=[{\xi }_{*}\left(\rho \right),{\xi }^{*}\left(\rho \right)],\end{array}$$

where

$$\begin{array}{c}\hfill {\xi }_{*}\left(\rho \right):=inf\{g\in \mathbb{R}:\xi \left(g\right)\ge \rho \},{\xi }^{*}\left(\rho \right):=sup\{g\in \mathbb{R}:\xi \left(g\right)\ge \rho \}.\end{array}$$

Also, fuzzy numbers can be studied and explored in triplet, depending on the parameters, as follows:

$$\begin{array}{c}\hfill \left\{{\xi }_{*}\left(\rho \right),{\xi }^{*}\left(\rho \right);\rho \in [0,1]\right\}.\end{array}$$

The aforementioned representation is more instrumental for studying fuzzy numbers in different fields. To become more familiar with these concepts, consult [16].

Proposition 1.

If $\widehat{B},\mathcal{E}\in {\mathbb{M}}_F$ then the relation “≼" expressed on ${\mathbb{M}}_F$ by

$$\widehat{B}\preccurlyeq \mathcal{E} \mathit{if} \mathit{and} \mathit{only} \mathit{if} {\left[\widehat{B}\right]}^{\rho }{\le }_{\rho }{\left[\mathcal{E}\right]}^{\rho } \mathit{for} \mathit{all} \rho \in [0,1].$$

The following relation satisfies the properties of partial order relation. For $\widehat{B},\mathcal{E}\in {\mathbb{M}}_F$ and $c\in \mathbb{R}$ the scalar product sum with constant, the sum and product of two fuzzy numbers, are expressed by

$$\begin{array}{cc}\hfill {[c·\widehat{B}]}^{\rho }& =c·{\left[\widehat{B}\right]}^{\rho },\hfill \\ \hfill [c\widetilde{+}\widehat{B}{]}^{\rho }& =c+{\left[\widehat{B}\right]}^{\rho }.\hfill \\ \hfill [\widehat{B}\widetilde{+}{\mathcal{E}]}^{\rho }& ={\left[\widehat{B}\right]}^{\rho }+{\left[\mathcal{E}\right]}^{\rho },\hfill \\ \hfill [\widehat{B}\tilde{\times }{\mathcal{E}]}^{\rho }& ={\left[\widehat{B}\right]}^{\rho }\times {\left[\mathcal{E}\right]}^{\rho }.\hfill \end{array}$$

Definition 4

([17]). A fuzzy mapping $\mathcal{F}:[{\eta }_3,{\eta }_4]\subset \mathbb{R}\to {\mathbb{M}}_F$ is fuzzy number-valued. If $\rho \in [0,1]$ then ρ-cuts showcase the cluster of I.V.F, such that ${\mathcal{F}}_{\rho }:[{\eta }_3,{\eta }_4]\subset \mathbb{R}\to K_c$ are given by ${\mathcal{F}}_{\rho }\left(g\right)=[{\mathcal{F}}_{*}(g,\rho ),{\mathcal{F}}^{*}(g,\rho )]$ for all $g\in [{\eta }_3,{\eta }_4]$. Also, left and right real-valued mappings ${\mathcal{F}}_{*}(g,\rho ),{\mathcal{F}}^{*}(g,\rho ):[{\eta }_3,{\eta }_4]\to \mathbb{R}$ are termed as end-point mappings of $\mathcal{F}$.

Definition 5

([18]). Presume that $\mathcal{F}:[{\eta }_3,{\eta }_4]\subset \mathbb{R}\to {\mathbb{M}}_F$ is an F.I.V mapping. Then, the fuzzy Riemann definite integral of $\mathcal{F}$ over $[{\eta }_3,{\eta }_4]$, represented by $\left(FR\right){\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(g\right)\mathrm{d}g$,

$$\begin{array}{cc}\hfill {\left[\left(FR\right){\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(g\right)\mathrm{d}g\right]}^{\rho }& =\left(FR\right){\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{\mathcal{F}}_{\rho }\left(g\right)\mathrm{d}g\hfill \\ \hfill & =\left\{{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}(g,\rho )\mathrm{d}g:\mathcal{F}(g,\rho )\in {\mathcal{R}}_{([{\eta }_3,{\eta }_4],\rho )}\right\},\hfill \end{array}$$

for all $\rho \in [0,1]$, where ${\mathcal{R}}_{([{\eta }_3,{\eta }_4],\rho )}$ describes the space of integrable mappings.

Definition 6

([13]). The fuzzy numbered mapping $\mathcal{F}:[{\eta }_3,{\eta }_4]\to {\mathbb{M}}_F$ is termed as a convex mapping on $[{\eta }_3,{\eta }_4]$ if

$$\begin{array}{c}\hfill \mathcal{F}((1-g)\vartheta +gy)\preccurlyeq (1-g)\mathcal{F}\left(\vartheta \right)\widetilde{+}g\mathcal{F}\left(y\right),\end{array}$$

for all $\vartheta ,y\in [{\eta }_3,{\eta }_4],g\in [0,1]$.

Over the years, fractional calculus has forced researchers to focus on the transformation of existing mathematical models to general concepts. Fractional derivatives and integral operators are used to showcase the various physical quantities with more precision. Although these operators have few limitations, they generalize classical operators, and by utilizing fractional operators one can attain the analytical solution for those differential systems whose analytical solutions do not exist or are difficult to calculate. Recently, mathematicians have focused on an approach combining fractional and fuzzy calculus to study differential systems. Let us reformulate the notion of fuzzy Riemann–Liouville fractional operators relying on $\rho$-levels.

Definition 7

([19]). Let $\varrho >0$, and $\mathrm{Ł}({\eta }_3,{\eta }_4,{\mathbb{M}}_F)$ contains the collection of fuzzy-valued Lebesgue measurable mapping on $[{\eta }_3,{\eta }_4]$. Then,

$$\begin{array}{c}\hfill J_{{{\eta }_3}^{+}}^{\alpha }\mathcal{F}\left({\eta }_3\right)={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{(g-{\eta }_3)}^{\varrho -1}\mathcal{F}\left(g\right)\mathrm{d}g,g\ge {\eta }_3\end{array}$$

and

$$\begin{array}{c}\hfill J_{{{\eta }_4}^{-}}^{\alpha }\mathcal{F}\left({\eta }_4\right)={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{({\eta }_4-g)}^{\varrho -1}\mathcal{F}\left(g\right)\mathrm{d}g,g\le {\eta }_4.\end{array}$$

Furthermore, the left and right RL-fractional operator based on left and right end-point mappings can be defined; that is,

$$\begin{array}{cc}\hfill {\left[J_{{{\eta }_3}^{+}}^{\alpha }\mathcal{F}\left({\eta }_3\right)\right]}^{\rho }& ={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{(g-{\eta }_3)}^{\varrho -1}{\mathcal{F}}_{\rho }\left(g\right)\mathrm{d}g\hfill \\ \hfill & ={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{(g-{\eta }_3)}^{\varrho -1}{\mathcal{F}}_{\rho }\left[{\mathcal{F}}_{*}(g,\rho ),{\mathcal{F}}^{*}(g,\rho )\right]\mathrm{d}g,\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill J_{{{\eta }_3}^{+}}^{\alpha }{\mathcal{F}}_{*}({\eta }_3,\rho )& ={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{(g-{\eta }_3)}^{\varrho -1}{\mathcal{F}}_{*}(g,\rho )\mathrm{d}g\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill J_{{{\eta }_3}^{+}}^{\alpha }{\mathcal{F}}^{*}({\eta }_3,\rho )& ={\displaystyle \frac{1}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}{(g-{\eta }_3)}^{\varrho -1}{\mathcal{F}}^{*}(g,\rho )\mathrm{d}g.\hfill \end{array}$$

By a similar argument, we can define the right operator.

In [20], the authors constructed the various kinds of inequalities in association with approximately interval-valued convexity. Nwaeze et al. [21] discussed interval-valued n-polynomials to establish new generalized inequalities. In [22], the authors presented unified $cr$ convexity to analyze new counterparts of existing results of inequalities. Liu et al. [23,24] formulated some novel consequences of totally ordered $log$ and harmonic convexity. Budak and his co-authors [25] employed classical interval-valued convexity RL operators to explore fractional analogs for the first time within an interval-valued setting. In [26], the authors focused on generalizing the existing classes of convexity and delivered the conception of $\vartheta$ totally ordered convexity along with essential inequalities. The authors of [27] studied fractional coordinated harmonic inequalities through unified fractional operators. For deep information, read [28,29,30,31,32]. Fahad et al. [33] discussed interval-valued $cr$-$GA$ convexity and associated inequalities with application to divergence measures. Javed et al. [34] worked on stochastic generalized convexity leveraging the idea of quasi mean and looked at various kinds of inequalities. In [35,36], the authors transformed superquadraticity to interval-valued via partial and total ranking relation. Also, they furnished the analysis of both classes through an inequality perspective. In 1998, Furukawa [37] discussed the Lipschitz continuity of convex fuzzy number-valued mappings. Costa et al. [38] employed fuzzy number-valued mappings to approximate the bounds of Ostrowski’s inequality. Gong and Hai [39] transformed the idea of vector-valued fuzzy mappings to n-dimensional fuzzy numbers and discussed various important results. Zhang et al. [14] initiated the LR set and fuzzy-valued mappings and proved a few Jensen’s inequalities for Aumann integrals. Cheng and his colleagues [40] delivered fuzzy variants of trapezium-like inequalities. Khan et al. [41,42] bridged the concepts of fuzzy-valued convexity and RL operators to deduce new general bounds of fuzzy integrals and utilized the weighted p-mean fuzzy ordered relation to introduce a new class of fuzzy-valued convexity and deliver some interesting inequalities. Abbaszadeh and Eshaghi [43] developed the idea of fuzzy number-valued r convexity to examine inequalities. Allahviranloo et al. [44] presented the idea of extended fuzzy-valued mappings along with applications to inequalities. Bin-Mohsin [45] put forward the idea of fuzzy number-valued bi-convexity through a bi-mapping and characterized it through classical inequalities. For a deeper understanding, read [46,47,48,49].

From the previous studies, we observe that all the classes of fuzzy-valued convex mappings are constructed by means of various partial ordering relations. An interesting question comes to mind: is it possible to define fuzzy-valued convexity utilizing total order relation? The principle of intent is to define fuzzy number-valued mapping by the $cr$ ordering relation. First, we will define the class of fuzzy number-valued cr convex mappings. To extend it for a larger space of mappings, we will introduce fuzzy number-valued extended $cr$ convex mappings via non-negative mapping. We will furnish some basic properties, criteria, examples, and characterizations through fractional integral inequalities. Lastly, some simulations and applications of the obtained results via two kinds of fuzzy number will be derived. We hope this class will be beneficial for studying further inequalities.

2. Results and Discussions

This part is attributed with the development of a novel generic totally ordered fuzzy number-valued convex mapping and its essential characterization.

Proposition 2.

If $\widehat{B},\mathcal{E}\in {\mathbb{M}}_F$ then the relation “${\preccurlyeq }_{cr}$" demonstrated on ${\mathbb{M}}_F$ by

$$\widehat{B}{\preccurlyeq }_{cr}\mathcal{E} \mathit{if} \mathit{and} \mathit{only} \mathit{if} {\left[\widehat{B}\right]}^{\rho }{⪯}_{cr}{\left[\mathcal{E}\right]}^{\rho } \mathit{for} \mathit{all} \rho \in [0,1].$$

First, we give the idea of fuzzy number-valued $cr$ convex mapping.

Definition 8.

Let $\mathcal{F}:[{\eta }_3,{\eta }_4]\to {\mathbb{M}}_F$ be a fuzzy number-valued mapping. It is regarded as $cr$ convex mapping if

$$\begin{array}{c}\hfill \mathcal{F}((1-g){\eta }_3+g{\eta }_4){\preccurlyeq }_{cr}(1-g)\mathcal{F}\left({\eta }_3\right)\oplus g\mathcal{F}\left({\eta }_4\right),g\in [0,1].\end{array}$$

Throughout the investigation, $\hslash :(0,1)\to (0,\infty )$ is a non-negative mapping and ℏ is said to be supermultiplicative if

$$\begin{array}{c}\hfill \hslash \left(\nu g\right)\ge \hslash \left(\nu \right)\hslash \left(g\right),\end{array}$$

for all $\nu ,g\in [0,1]$. The reverse statement holds for submultiplicative mapping. Let $\hslash \left(\vartheta \right)={(\vartheta -c)}^{p-1}$ for all $\vartheta \ge 0$. If $c=0$ then ℏ is multiplicative. If $c\ge 1$ and $p\in (0,1)$ then ℏ is supermultiplicative and $p>1$ is submultiplicative. For further details, see [50]. In our next definition, ℏ has a governing role. We control different classes of convexity through different choices of ℏ: that is why we named it as the control operator.

3. On Fuzzy Number-Valued Extended $\mathbf{cr}$-ℏ-Convex Mappings

Definition 9.

Let $\mathcal{F}:[{\eta }_3,{\eta }_4]\to {\mathbb{R}}_I^{+}$ be a fuzzy number-valued mapping, such that $\mathcal{F}=[{\mathcal{F}}_c,{\mathcal{F}}_r]$. Then, $\mathcal{F}$ is known as a fuzzy number-valued $cr$-ℏ convex mapping if

$$\begin{array}{c}\hfill \mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right){\preccurlyeq }_{cr}g\hslash \left(g\right)\mathcal{F}\left({\eta }_3\right)\oplus (1-g)\hslash (1-g)\mathcal{F}\left({\eta }_4\right),\end{array}$$

(1)

for all ${\eta }_3,{\eta }_4\in \zeta$, and $g\in [0,1]$.

Now, we enlist some potential totally ordered subclasses of Definition 9. We deduce the classes of fuzzy number-valued $cr$ convex mapping, $cr$-P mapping, $cr$-s convex mapping, $cr$-s-Godunova–Levin mapping, and $cr$-tgs convex mapping by taking $\hslash \left(g\right)=1,g^{-1},g^{s-1},g^{-s-1},1-g$ in (1), respectively.

Remark 1.

Through the utilization of different values of ℏ, we obtain the various classes of totally ordered fuzzy number-valued convex mappings, like exponential convexity, n-polynomial convexity, trigonometric convexity, and many more. Assuming that ${\mathcal{F}}_c={\mathcal{F}}_r$ in Definition 9, then we recover the class of generalized ℏ convexity.

The space of all generalized ℏ convex mappings and the space of all fuzzy number-valued extended $cr$-ℏ convex mappings are represented by $SGX\left(\hslash ,[{\eta }_3,{\eta }_4],\mathbb{R}\right)$ and

$$SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right),$$

respectively.

Proposition 3.

Consider ${\hslash }_1,{\hslash }_2>0$, such that ${\hslash }_2\left(g\right)\le {\hslash }_1\left(g\right)$ with $g\in [0,1]$.

If $\mathcal{F}\in SFEX\left(cr-{\hslash }_2,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ then $\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$.

Proof. 

Since $\mathcal{F}\in SFEX\left(cr-{\hslash }_2,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, then for all ${\eta }_3,{\eta }_4\in [{\eta }_3,{\eta }_4]$ and $g\in [0,1]$ we have

$$\begin{array}{cc}\hfill \mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)& {\preccurlyeq }_{cr}g{\hslash }_2\left(g\right)\mathcal{F}\left({\eta }_3\right)\oplus (1-g){\hslash }_2(1-g)\mathcal{F}\left({\eta }_4\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}g{\hslash }_1\left(g\right)\mathcal{F}\left({\eta }_3\right)\oplus (1-g){\hslash }_1(1-g)\mathcal{F}\left({\eta }_4\right).\hfill \end{array}$$

Hence, $\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$. □

Proposition 4.

Let$\mathcal{F}:[{\eta }_3,{\eta }_4]\to {\mathbb{M}}_F$ be a fuzzy number-valued mapping, such that $\mathcal{F}=[{\mathcal{F}}_c(\vartheta ,\rho ),{\mathcal{F}}_r(\vartheta ,\rho )]=⟨{\mathcal{F}}_c(\vartheta ,\rho ),{\mathcal{F}}_r(\vartheta ,\rho )⟩$. If ${\mathcal{F}}_c(g,\rho ),{\mathcal{F}}_r(g,\rho )\in SGX\left(\hslash [{\eta }_3,{\eta }_4],\mathbb{R}\right)$ then $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$.

Proof. 

If ${\mathcal{F}}_c,{\mathcal{F}}_r\in SFEX\left({\hslash }_1,[{\eta }_3,{\eta }_4],\mathbb{R}\right)$ then for $g\in [0,1]$ and $\vartheta ,y\in [{\eta }_3,{\eta }_4]$ we obtain

$$\begin{array}{c}\hfill {\mathcal{F}}_c\left(g\vartheta +\left(1-g\right)y,\rho \right)\le g\hslash \left(g\right){\mathcal{F}}_c(\vartheta ,\rho )+(1-g)\hslash (1-g){\mathcal{F}}_c(y,\rho )\end{array}$$

and

$$\begin{array}{c}\hfill {\mathcal{F}}_r\left(g\vartheta +\left(1-g\right)y,\rho \right)\le g\hslash \left(g\right){\mathcal{F}}_r(\vartheta ,\rho )+(1-g)\hslash (1-g){\mathcal{F}}_r(y,\rho ).\end{array}$$

If

$$\begin{array}{c}\hfill {\mathcal{F}}_c\left(g\vartheta +\left(1-g\right)y,\rho \right)\ne g\hslash \left(g\right){\mathcal{F}}_c(\vartheta ,\rho )+(1-g)\hslash (1-g){\mathcal{F}}_c(y,\rho ),\end{array}$$

and

$$\begin{array}{c}\hfill {\mathcal{F}}_c\left(g\vartheta +\left(1-g\right)y,\rho \right)<g\hslash \left(g\right){\mathcal{F}}_c(\vartheta ,\rho )+(1-g)\hslash (1-g){\mathcal{F}}_c(y,\rho )\end{array}$$

then by the definition of $cr$-ordering relation we obtain

$$\begin{array}{c}\hfill \mathcal{F}\left(\vartheta +\left(1-g\right)y,\rho \right){\preccurlyeq }_{cr}g\hslash \left(g\right)\mathcal{F}(\vartheta ,\rho )\oplus (1-g)\hslash (1-g)\mathcal{F}(y,\rho ).\end{array}$$

Otherwise, we have

$$\begin{array}{c}\hfill {\mathcal{F}}_r\left(\vartheta +\left(1-g\right)y,\rho \right)\le g\hslash \left(g\right){\mathcal{F}}_r(\vartheta ,\rho )+(1-g)\hslash (1-g){\mathcal{F}}_r(y,\rho ).\end{array}$$

Again, considering the definition of $cr$ relation, we obtain

$$\begin{array}{c}\hfill \mathcal{F}\left(\vartheta +\left(1-g\right)y,\rho \right){\preccurlyeq }_{cr}g\hslash \left(g\right)\mathcal{F}(\vartheta ,\rho )\oplus (1-g)\hslash (1-g)\mathcal{F}(y,\rho ).\end{array}$$

This completes the proof. □

Now, we give some illustrative examples in favor of the newly developed class of convexity.

Example 1.

Let $\mathcal{F}\left(\vartheta \right)=(0,2{\vartheta }^3,6{\vartheta }^3)$ be a triangular fuzzy number, and its membership mapping is defined as follows:

$$\begin{array}{c}\hfill {\mathcal{F}}_{\vartheta }\left(g\right)=\left\{\begin{array}{cc}{\displaystyle \frac{g}{2{\vartheta }^3}},\hfill & 0<g\le 2{\vartheta }^3\hfill \\ \\ {\displaystyle \frac{6{\vartheta }^3-g}{4{\vartheta }^3}},\hfill & 2{\vartheta }^3<g\le 6{\vartheta }^3\hfill \\ \\ 0,\hfill & g>6{\vartheta }^3.\hfill \end{array}\right.\end{array}$$

Moreover, the ρ-level representation is $\mathcal{F}(\vartheta ,\rho )=\left[2\rho {\vartheta }^3,6{\vartheta }^3-4\rho {\vartheta }^3\right]$. Also, ${\mathcal{F}}_c(\vartheta ,\rho )=3{\vartheta }^3-\rho {\vartheta }^3$ and ${\mathcal{F}}_r(\vartheta ,\rho )=3{\vartheta }^3-3\rho {\vartheta }^3$. Note that both ${\mathcal{F}}_c(\vartheta ,\rho )$ and ${\mathcal{F}}_r(\vartheta ,\rho )$ are generalized ℏ convex. This implies that $\mathcal{F}\left(\vartheta \right)$ is a $cr$-ℏ fuzzy-valued convex mapping.

Now, we deliver the graphical depiction of triangular fuzzy number-valued mapping for $\vartheta =2$ (Figure 1).

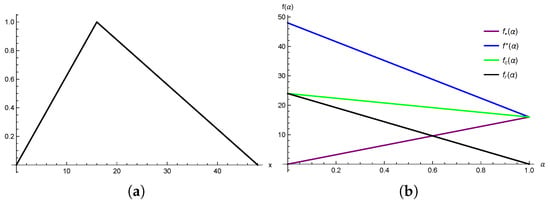
Figure 1. Graphical depiction of membership mapping (a) and its $\rho$-level given representation (b) in Example 1.

Example 2.

Let $\mathcal{S}\left(\vartheta \right)=(1,2{\vartheta }^3,5{\vartheta }^3,6{\vartheta }^3)$ be a trapezoidal fuzzy number, and its membership mapping is defined as follows:

$$\begin{array}{c}\hfill {\mathcal{S}}_{\vartheta }\left(g\right)=\left\{\begin{array}{cc}0,\hfill & g\le 1\hfill \\ \\ {\displaystyle \frac{g-1}{3{\vartheta }^3-1}},\hfill & 1<g\le 3{\vartheta }^3\hfill \\ \\ 1,\hfill & 3{\vartheta }^3<g\le 5{\vartheta }^3\hfill \\ \\ {\displaystyle \frac{6{\vartheta }^3-g}{{\vartheta }^3}},\hfill & 5{\vartheta }^3<g\le 6{\vartheta }^3\hfill \\ \\ 0,\hfill & g>6{\vartheta }^3.\hfill \end{array}\right.\end{array}$$

Moreover, the ρ-level representation is $\mathcal{S}(\vartheta ,\rho )=\left[3\rho {\vartheta }^3+(1-\rho ),6{\vartheta }^3-\rho {\vartheta }^3\right]$. Also, ${\mathcal{F}}_c(\vartheta ,\rho )=3{\vartheta }^3+\rho {\vartheta }^3+{\displaystyle \frac{1-\rho }{2}}$ and ${\mathcal{S}}_r(\vartheta ,\rho )=3{\vartheta }^3-2\rho {\vartheta }^3+{\displaystyle \frac{\rho -1}{2}}$. Note that both ${\mathcal{S}}_c^{\rho }$ and ${\mathcal{S}}_r^{\rho }$ are convex. This implies that $\mathcal{S}\left(\vartheta \right)$ is a $cr$-ℏ fuzzy-valued convex mapping.

Now, we deliver the graphical depiction of trapezoidal fuzzy number-valued mapping for $\vartheta =2$ (Figure 2).

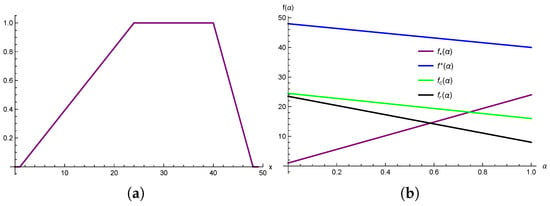
Figure 2. Graphical depiction of membership mapping (a) and its $\rho$-level given representation (b) in Example 2.

3.1. Jensen’s-Type Inequalities

This section contains some celebrated Jensen’s-like inequalities. First, we prove Jensen’s inequality for $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$.

Theorem 4.

If $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and ℏ is supermultiplicative mapping then

$$\begin{array}{c}\hfill \mathcal{F}\left(\frac{1}{{\mathcal{V}}_e}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}\left(\frac{g_j}{{\mathcal{V}}_e}\right)\hslash \left(\frac{g_j}{{\mathcal{V}}_e}\right)\mathcal{F}\left({\vartheta }_j\right),\end{array}$$

(2)

where ${\mathcal{V}}_e={\displaystyle \sum _{j=1}^e}{g}_j$.

Proof. 

Suppose that $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$. For $g=2$, we obtain

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{g_1}{{\mathcal{V}}_2}}{\vartheta }_1+{\displaystyle \frac{g_2}{{\mathcal{V}}_2}}{\vartheta }_2\right){\preccurlyeq }_{cr}{\displaystyle \frac{g_1}{{\mathcal{V}}_2}}\hslash \left({\displaystyle \frac{g_1}{{\mathcal{V}}_2}}\right)\mathcal{F}\left({\vartheta }_1\right)\oplus {\displaystyle \frac{g_2}{{\mathcal{V}}_2}}\hslash \left({\displaystyle \frac{g_2}{{\mathcal{V}}_2}}\right)\mathcal{F}\left({\vartheta }_2\right).\end{array}$$

Consider (2) satisfies for $g=e$; then,

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_e}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right)\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right)\mathcal{F}\left({\vartheta }_j\right).\end{array}$$

This inequality can be transformed as

$$\begin{array}{cc}\hfill & ⟨{\mathcal{F}}_c\left({\displaystyle \frac{1}{{\mathcal{V}}_e}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j,\rho \right),{\mathcal{F}}_r\left({\displaystyle \frac{1}{{\mathcal{V}}_e}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j,\rho \right)⟩\hfill \\ \hfill & {\preccurlyeq }_{cr}⟨{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right)\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right){\mathcal{F}}_c\left({\vartheta }_j,\rho \right),{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right)\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_e}}\right){\mathcal{F}}_r\left({\vartheta }_j,\rho \right)⟩.\hfill \end{array}$$

Now, we prove (2) for $g=e+1$:

$$\begin{array}{cc}\hfill & \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e+1}}{g}_j{\vartheta }_j\right)\hfill \\ \hfill & =⟨{\mathcal{F}}_c\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e+1}}{g}_j{\vartheta }_j,\rho \right),{\mathcal{F}}_r\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e+1}}{g}_j{\vartheta }_j,\rho \right)⟩\hfill \\ \hfill & =⟨{\mathcal{F}}_c\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right),\hfill \\ \hfill & {\mathcal{F}}_r\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right)⟩.\hfill \end{array}$$

From the definition of the fuzzy number-valued extended $cr$-ℏ convexity of the mapping $\mathcal{F}$ and utilizing the supermultiplicative property of ℏ, we have

$$\begin{array}{cc}\hfill & {\mathcal{F}}_c\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right)\hfill \\ \hfill & \le {\displaystyle \sum _{j=1}^{e-1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_j,\rho )+\left({\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\right)\right){\mathcal{F}}_c\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}},\rho \right)\hfill \\ \hfill & \le {\displaystyle \sum _{j=1}^{e-1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_j,\rho )+\left({\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\right)\right)\times \hfill \\ \hfill & \left[\left({\displaystyle \frac{g_e}{g_e+g_{e+1}}}\hslash \left({\displaystyle \frac{g_e}{g_e+g_{e+1}}}\right)\right){\mathcal{F}}_c({\vartheta }_e,\rho )+\left({\displaystyle \frac{g_{e+1}}{g_e+g_{e+1}}}\hslash \left({\displaystyle \frac{g_{e+1}}{g_e+g_{e+1}}}\right)\right){\mathcal{F}}_c({\vartheta }_{e+1},\rho )\right]\hfill \\ \hfill & \le \left({\displaystyle \frac{g_e}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_e}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_e,\rho )\oplus {\displaystyle \frac{g_{e+1}}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_{e+1}}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_{e+1},\rho )\right)\oplus {\displaystyle \sum _{j=1}^{e-1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_j,\rho )\hfill \\ \hfill & ={\displaystyle \sum _{j=1}^{e+1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_j,\rho )\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\mathcal{F}}_r\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right)\hfill \\ \hfill & \le {\displaystyle \sum _{j=1}^{e+1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_r({\vartheta }_j,\rho ).\hfill \end{array}$$

Finally, we obtain

$$\begin{array}{cc}\hfill & ⟨{\mathcal{F}}_c\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{e+1}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right),\hfill \\ \hfill & {\mathcal{F}}_r\left({\displaystyle \frac{1}{{\mathcal{V}}_{e+1}}}{\displaystyle \sum _{j=1}^{e-1}}{g}_j{\vartheta }_j+{\displaystyle \frac{g_e+g_{e+1}}{{\mathcal{V}}_{e+1}}}\left({\displaystyle \frac{g_e{\vartheta }_e}{g_e+g_{e+1}}}+{\displaystyle \frac{g_{e+1}{\vartheta }_{e+1}}{g_e+g_{e+1}}}\right),\rho \right)⟩\hfill \\ \hfill & {\preccurlyeq }_{cr}⟨{\displaystyle \sum _{j=1}^{e+1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_c({\vartheta }_j,\rho ),{\displaystyle \sum _{j=1}^{e+1}}{\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\hslash \left({\displaystyle \frac{g_j}{{\mathcal{V}}_{e+1}}}\right){\mathcal{F}}_r({\vartheta }_j,\rho )⟩.\hfill \end{array}$$

Hence, totally ordered Jensen’s inequality is acquired. □

Here are some useful deductions of fuzzy number-valued Jensen’s inequality (2):

• Substituting $\hslash \left(g\right)=1$ in (2) produces Jensen inequality for fuzzy number-valued $cr$ convex mappings.

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_g}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{g_j}{{\mathcal{V}}_g}}\right)\mathcal{F}\left({\vartheta }_j\right).\end{array}$$
• To obtain fuzzy-valued Jensen’s inequality for $cr$-P convex mappings, we take $\hslash \left(g\right)=g^{-1}$ in (2):

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_g}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}\mathcal{F}\left({\vartheta }_j\right).\end{array}$$
• For $\hslash \left(g\right)=g^{s-1}$, the inequality (2) generates the following inequality:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_g}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}{\left({\displaystyle \frac{g_j}{{\mathcal{V}}_g}}\right)}^s\mathcal{F}\left({\vartheta }_j\right).\end{array}$$
• We obtain totally ordered fuzzy-valued Jensen’s inequality for $cr$-Godunova–Levin convex mapping by substituting $\hslash \left(g\right)=g^{-s-1}$ in (2):

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{1}{{\mathcal{V}}_g}}{\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}{\left({\displaystyle \frac{g_j}{{\mathcal{V}}_g}}\right)}^{-s}\mathcal{F}\left({\vartheta }_j\right).\end{array}$$
• Setting ${\mathcal{V}}_g={\displaystyle \sum _{j=1}^e}{g}_j=1$ in inequality (2), we obtain another unified Jensen’s inequality.

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \sum _{j=1}^e}{g}_j{\vartheta }_j\right){\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}{g}_j\hslash \left(g_j\right)\mathcal{F}\left({\vartheta }_j\right).\end{array}$$

For $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, we prove another Jensen’s inequality.

Theorem 5.

Let $\hslash \ge 0$ be a supermultiplicative mapping. If $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and for ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3\in [{\eta }_3,{\eta }_4]$, ${\epsilon }_1<{\epsilon }_2<{\epsilon }_3$, such that ${\epsilon }_3-{\epsilon }_1,{\epsilon }_3-{\epsilon }_2,{\epsilon }_2-{\epsilon }_1\in (0,1)$, then

$$\begin{array}{c}\hfill ({\epsilon }_3-{\epsilon }_1)\hslash ({\epsilon }_3-{\epsilon }_1)\mathcal{F}\left({\epsilon }_2\right){\preccurlyeq }_{cr}({\epsilon }_3-{\epsilon }_2)\hslash ({\epsilon }_3-{\epsilon }_2)\mathcal{F}\left({\epsilon }_1\right)\oplus ({\epsilon }_2-{\epsilon }_1)\hslash ({\epsilon }_2-{\epsilon }_1)\mathcal{F}\left({\epsilon }_3\right).\end{array}$$

(3)

Proof. 

Let $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$. Let ${\epsilon }_1,{\epsilon }_2,{\epsilon }_3\in [{\eta }_3,{\eta }_4]$ and $\hslash \left({\epsilon }_3-{\epsilon }_1\right)>0$; then,

$$\begin{array}{cc}\hfill & \hslash \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right)\le {\displaystyle \frac{\hslash \left({\epsilon }_3-{\epsilon }_2\right)}{\hslash \left({\epsilon }_3-{\epsilon }_1\right)}},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \hslash \left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right)\le {\displaystyle \frac{\hslash \left({\epsilon }_2-{\epsilon }_1\right)}{\hslash \left({\epsilon }_3-{\epsilon }_1\right)}}.\hfill \end{array}$$

Selecting $g={\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}},{\eta }_3={\epsilon }_1,{\eta }_4={\epsilon }_3$, then from (1) we obtain

$$\begin{array}{cc}\hfill {\mathcal{F}}_c\left({\epsilon }_2,\rho \right)& \le \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right)\hslash \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right){\mathcal{F}}_c({\epsilon }_1,\rho )+\left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right)\hslash \left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right){\mathcal{F}}_c({\epsilon }_3,\rho )\hfill \\ \hfill & \le \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_3-{\epsilon }_2)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}{\mathcal{F}}_c({\epsilon }_1,\rho )+\left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_2-{\epsilon }_1)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}{\mathcal{F}}_c({\epsilon }_3,\rho ).\hfill \end{array}$$

(4)

Similarly,

$$\begin{array}{cc}\hfill {\mathcal{F}}_r\left({\epsilon }_2,\rho \right)& \le \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right)\hslash \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right){\mathcal{F}}_r({\epsilon }_1,\rho )+\left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right)\hslash \left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right){\mathcal{F}}_r({\epsilon }_3,\rho )\hfill \\ \hfill & \le \left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_3-{\epsilon }_2)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}{\mathcal{F}}_r({\epsilon }_1,\rho )\left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_2-{\epsilon }_1)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}{\mathcal{F}}_r({\epsilon }_3,\rho ).\hfill \end{array}$$

(5)

From (4) and (5), we have

$$\begin{array}{cc}\hfill & ⟨{\mathcal{F}}_c\left({\epsilon }_2,\rho \right),{\mathcal{F}}_r\left({\epsilon }_2,\rho \right)⟩\hfill \\ \hfill & {\preccurlyeq }_{cr}\left({\displaystyle \frac{{\epsilon }_3-{\epsilon }_2}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_3-{\epsilon }_2)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}⟨{\mathcal{F}}_c({\epsilon }_1,\rho ),{\mathcal{F}}_r({\epsilon }_1,\rho )⟩\hfill \\ \hfill & +\left({\displaystyle \frac{{\epsilon }_2-{\epsilon }_1}{{\epsilon }_3-{\epsilon }_1}}\right){\displaystyle \frac{\hslash ({\epsilon }_2-{\epsilon }_1)}{\hslash ({\epsilon }_3-{\epsilon }_1)}}⟨{\mathcal{F}}_c({\epsilon }_3,\rho ),{\mathcal{F}}_r({\epsilon }_3,\rho )⟩.\hfill \end{array}$$

From the above inequality, we deduce our desired Jensen’s-like inequality. □

By incorporating the Jenesn’s-type inequality (3), we prove another refinement of it.

Theorem 6.

Let $\hslash \ge 0$, ${\epsilon }_j\in [{\eta }_3,{\eta }_4]$ and $g_j\in {\mathbb{R}}^{+}$. If $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and $(\sigma ,P)\subseteq [{\eta }_3,{\eta }_4]$ then

$$\begin{array}{cc}\hfill \mathcal{F}\left({\epsilon }_j\right){\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right)\hslash \left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right)& {\preccurlyeq }_{cr}{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right)\hslash \left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right){\displaystyle \frac{(P-{\epsilon }_j)}{(P-\sigma )}}{\displaystyle \frac{\hslash (P-{\epsilon }_j)}{\hslash (\mathfrak{M}-\sigma )}}\mathcal{F}\left(\sigma \right)\hfill \\ \hfill & +{\displaystyle \sum _{j=1}^e}\left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right)\hslash \left({\displaystyle \frac{{\mathfrak{q}}_j}{Q_g}}\right){\displaystyle \frac{({\epsilon }_j-\sigma )}{(P-\sigma )}}{\displaystyle \frac{\hslash ({\epsilon }_j-\sigma )}{\hslash (P-\sigma )}}\mathcal{F}\left(P\right),\hfill \end{array}$$

where $Q_g={\displaystyle \sum _{j=1}^e}{g}_j$.

Proof. 

The result is obvious. □

For $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, we construct the continuous analogue of inequality (2).

Theorem 7.

Let $\mathcal{S}:\left[{\eta }_3,{\eta }_4\right]\to \mathbb{R}$ be an integrable mapping, and $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$. If

$$\begin{array}{c}\hfill \underset{\vartheta \to 0^{+}}{lim}{\displaystyle \frac{\hslash \left(\vartheta \right)}{\vartheta }}=\varrho >0,\end{array}$$

exists and is finite then

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{S}\left(g\right)dg}{{\eta }_4-{\eta }_3}}\right){\preccurlyeq }_{cr}{\displaystyle \frac{\omega }{({\eta }_4-{\eta }_3)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(\mathcal{S}\left(g\right)\right)dg.\end{array}$$

Proof. 

Let $P\left(\varrho ,\left[{\eta }_3,{\eta }_4\right]\right)$ be the collection of all partitions of $[{\eta }_3,{\eta }_4]$, and $p_1\in P\left(\varrho ,\left[{\eta }_3,{\eta }_4\right]\right)$ is given by

$$\begin{array}{c}\hfill \left\{{\eta }_3=y_0<y_1<\dots <y_e={\eta }_4\right\},\end{array}$$

where $y_j={\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)$ for $0\le j\le e$. By selecting $g_j={\eta }_3+{\displaystyle \frac{j-1}{e}}\left({\eta }_4-{\eta }_3\right)$, then, utilizing the Riemann sum,

$$\begin{array}{c}\hfill S\left(\mathcal{F},P_1,\varrho \right)={\displaystyle \sum _{j=1}^e}\mathcal{F}\left(g_j\right)\left(y_j-y_{j-1}\right).\end{array}$$

Since $\mathcal{S}\in R_{\left(\left[{\eta }_3,{\eta }_4\right]\right)}$, then

$$\begin{array}{c}\hfill {\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{S}\left(g\right)dg=\underset{e\to \infty }{lim}{\displaystyle \sum _{j=1}^e}\mathcal{S}\left(g_j\right)\left(y_j-y_{j-1}\right)=\underset{e\to \infty }{lim}{\displaystyle \frac{{\eta }_4-{\eta }_3}{e}}{\displaystyle \sum _{j=1}^e}\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right).\end{array}$$

Since $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and, continuous, $\mathcal{F}\left(g\right)=⟨{\mathcal{F}}_c\left(g\right),{\mathcal{F}}_r\left(g\right)⟩$, then the composition mapping $\mathcal{F}\left(\mathcal{S}\left(g\right)\right)\in FI{R}_{\left(⟨{\eta }_3,{\eta }_4⟩\right)}$ and we have

$$\begin{array}{cc}\hfill & \mathcal{F}\left({\displaystyle \frac{1}{e}}{\displaystyle \sum _{j=1}^e}\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right)\right)\hfill \\ \hfill & =⟨{\mathcal{F}}_c\left({\displaystyle \frac{1}{e}}{\displaystyle \sum _{j=1}^e}\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right),\rho \right)\right),{\mathcal{F}}_r\left({\displaystyle \frac{1}{e}}{\displaystyle \sum _{j=1}^e}\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right),\rho \right)⟩\hfill \\ \hfill & {\preccurlyeq }_{cr}⟨{\displaystyle \sum _{j=1}^e}{\displaystyle \frac{1}{e}}\hslash \left({\displaystyle \frac{1}{e}}\right){\mathcal{F}}_c\left(\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right),\rho \right),{\displaystyle \sum _{j=1}^e}{\displaystyle \frac{1}{e}}\hslash \left({\displaystyle \frac{1}{e}}\right){\mathcal{F}}_r\left(\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right),\rho \right)⟩\hfill \\ \hfill & =⟨{\displaystyle \sum _{j=1}^e}{\displaystyle \frac{1}{e({\eta }_4-{\eta }_3)}}{\displaystyle \frac{\hslash \left(\frac{1}{e}\right)}{\frac{1}{e}}}{\displaystyle \frac{{\eta }_4-{\eta }_3}{e}}{\mathcal{F}}_c\left(\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right),\rho \right),{\displaystyle \sum _{j=1}^e}{\displaystyle \frac{1}{e({\eta }_4-{\eta }_3)}}{\displaystyle \frac{\hslash \left(\frac{1}{e}\right)}{\frac{1}{e}}}{\displaystyle \frac{{\eta }_4-{\eta }_3}{e}}{\mathcal{F}}_r\left(\mathcal{S}\left({\eta }_3+{\displaystyle \frac{j}{e}}\left({\eta }_4-{\eta }_3\right)\right),\rho \right)⟩.\hfill \end{array}$$

Applying limit $e\to \infty$, we obtain

$$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{S}\left(g\right)dg}{{\eta }_4-{\eta }_3}}\right){\preccurlyeq }_{cr}{\displaystyle \frac{\omega }{({\eta }_4-{\eta }_3)}}{\displaystyle \underset{{\eta }_3}{\overset{{\eta }_4}{\int }}}\mathcal{F}\left(\mathcal{S}\left(g\right)\right)dg.\end{array}$$

Since $\underset{\vartheta \to 0^{+}}{lim}{\displaystyle \frac{\hslash \left(\vartheta \right)}{\vartheta }}=\varrho >0$ and ${\displaystyle \frac{\varrho }{e}}=\omega .$, this completes the proof. □

3.2. Hermite–Hadamard’s Inequalities

In the following segment, we investigate trapezium-type inequalities via fuzzy number-valued extended $cr$-h convex mappings. First, we aim to develop the fractional fuzzy number-valued trapezoid inequality.

Theorem 8.

Let $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, and $\mathcal{F}$ is a fuzzy-valued Riemann integrable mapping. Then, for $\alpha >0$ we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)& {\preccurlyeq }_{cr}{\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{2\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \frac{\varrho }{2}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

Proof. 

Using the definition of fuzzy number-valued extended $cr$-ℏ convex mapping, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}\mathcal{F}\left({\displaystyle \frac{\vartheta +y}{2}}\right){\preccurlyeq }_{cr}\mathcal{F}\left(\vartheta \right)\oplus \mathcal{F}\left(y\right).\end{array}$$

Inserting $\vartheta =g{\eta }_3+\left(1-g\right){\eta }_4,y=g{\eta }_4+\left(1-g\right){\eta }_3$, taking the product on both sides by $g^{\varrho }$, and integrating over $[0,1]$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)dg\hfill \\ \hfill & {⪯}_{cr}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left[\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\right]dg.\hfill \end{array}$$

This above inequality can be written as

$$\begin{array}{cc}\hfill & ⟨{\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}{\mathcal{F}}_c\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)dg,{\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}{\mathcal{F}}_r\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)dg⟩\hfill \\ \hfill & {⪯}_{cr}⟨{\int }_0^1{g}^{\varrho -1}\left[{\mathcal{F}}_c\left(g{\eta }_3+\left(1-g\right){\eta }_4,\rho \right)+{\mathcal{F}}_c\left(g{\eta }_4+\left(1-g\right){\eta }_3,\rho \right)\mathrm{d}g\right],\hfill \\ \hfill & {\int }_0^1{g}^{\varrho -1}\left[{\mathcal{F}}_r\left(g{\eta }_3+\left(1-g\right){\eta }_4,\rho \right)+{\mathcal{F}}_r\left(g{\eta }_4+\left(1-g\right){\eta }_3,\rho \right)\mathrm{d}g\right]⟩.\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill & ⟨{\displaystyle \frac{2}{\alpha \hslash \left(\frac{1}{2}\right)}}{\mathcal{F}}_c\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right),{\displaystyle \frac{2}{\alpha \hslash \left(\frac{1}{2}\right)}}{\mathcal{F}}_r\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)⟩\hfill \\ \hfill & {⪯}_{cr}⟨{\displaystyle \frac{\Gamma \left(\alpha \right)}{{({\eta }_4-{\eta }_3)}^{\alpha }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }{\mathcal{F}}_c\left({\eta }_4,\rho \right)+J_{{{\eta }_4}^{-}}^{\varrho }{\mathcal{F}}_c\left({\eta }_3,\rho \right)\right],\hfill \\ \hfill & {\displaystyle \frac{\Gamma \left(\alpha \right)}{{({\eta }_4-{\eta }_3)}^{\alpha }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }{\mathcal{F}}_r\left({\eta }_4,\rho \right)+J_{{{\eta }_4}^{-}}^{\varrho }{\mathcal{F}}_r\left({\eta }_3,\rho \right)\right]⟩.\hfill \end{array}$$

Some simple computations produce the left Hermite–Hadamard’s inequality.

Again, considering the notion of fuzzy number-valued extended $cr$-ℏ convex mappings, we have the following inequality:

$$\begin{array}{cc}\hfill & \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg\hfill \\ \hfill & {\preccurlyeq }_{cr}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

This implies

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}\varrho {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

Hence, the desired right-Hadamard’s inequality is achieved. □

Theorem 8 reduces to the following potential inequalities:

• Taking $\hslash \left(g\right)=1$ in Theorem 8 yields the trapezium inequality for fuzzy number-valued $cr$ convex mappings:

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}{\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{2\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]{\preccurlyeq }_{cr}{\displaystyle \frac{\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]}{2}}.\end{array}$$
• For $\hslash \left(g\right)=g^{-1}$ in Theorem 8, we obtain following double inequality.

  $$\begin{array}{c}\hfill \mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}{\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]{\preccurlyeq }_{cr}2\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right].\end{array}$$
• Selecting $\hslash \left(g\right)=g^{s-1}$ in Theorem 8 produces the following fuzzy-valued inequality:

  $$\begin{array}{cc}\hfill & 2^{s-1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}{\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{2\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \frac{\varrho [\mathcal{F}\left({\eta }_3\right)+\mathcal{F}\left({\eta }_4\right)]}{2}}\left[{\displaystyle \frac{1}{\varrho +s}}+\widehat{B}(\varrho ,s+1)\right].\hfill \end{array}$$
• To generate the double fuzzy-valued inequality associated $cr$-$tgs$ convex mappings, we take $\hslash \left(g\right)=g(1-g)$ in Theorem 8:

  $$\begin{array}{cc}\hfill 4\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}& {\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{2\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\right]\hfill \\ & {\preccurlyeq }_{cr}{\displaystyle \frac{\varrho }{(\varrho +1)(\varrho +2)}}\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

Example 3.

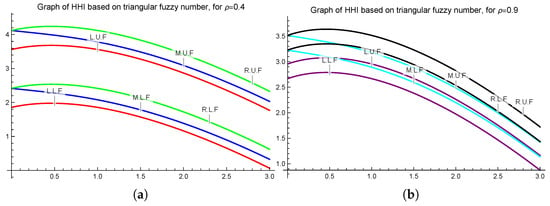
Let $\mathcal{F}:[1,3]\to {\mathbb{M}}_F$ be a triangular fuzzy number-valued extended $cr$ convex mapping, as defined in Example 1. Since $\mathcal{F}(\vartheta ,\rho )$ satisfies all the credentials of Theorem 8, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 3a,b, we consider the triangular fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures affirm the accuracy of the inequality proved in Theorem 8.

Figure 3. Graphical demonstration of Theorem 8 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

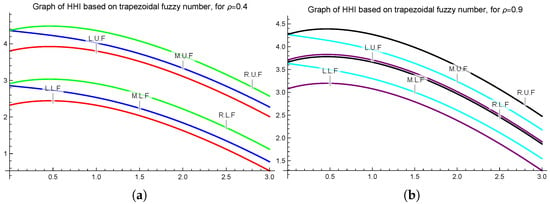
Let $\mathcal{F}:[1,3]\to {\mathbb{M}}_F$ be a trapezoidal fuzzy number-valued extended $cr$ convex mapping, as defined in Example 2. Since $\mathcal{F}(\vartheta ,\rho )$ satisfies all the credentials of Theorem 8, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 4a,b, we consider the trapezoidal fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures highlight the accuracy of inequality proved in Theorem 8.

Figure 4. Depiction of Theorem 8 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

Next, we build the weighted Hermite–Hadamrad’s inequality, based on the newly proposed class of convexity and symmetric mappings about the mid-point.

Theorem 9.

Let $\mathcal{F}\in SFEX\left(cr-\hslash ,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, let $\mathcal{F}$ be a fuzzy-valued Riemann integrable mapping, and let $P:[{\eta }_3,{\eta }_4]\to {\mathbb{R}}_I^{+},P>0$ be a symmetric with respect to ${\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}$; then, for $\alpha >0$,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\left[J_{{{\eta }_3}^{+}}^{\varrho }P\left({\eta }_4\right)+J_{{{\eta }_4}^{-}}^{\varrho }P\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)P\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \frac{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

Proof. 

Using the definition of fuzzy number-valued extended $cr$-ℏ convex mapping and taking the product on both sides by $g^{\varrho }$ and integrating over $[0,1]$,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & +{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)P\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg.\hfill \end{array}$$

(6)

Then,

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{\hslash \left(\frac{1}{2}\right)}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & ={\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\left[{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\right.\hfill \\ \hfill & \left.+{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)P\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg\right]\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\varrho \right)}{\hslash \left(\frac{1}{2}\right){\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\left[J_{{{\eta }_3}^{+}}^{\varrho }P\left({\eta }_4\right)+J_{{{\eta }_4}^{-}}^{\varrho }P\left({\eta }_3\right)\right].\hfill \end{array}$$

(7)

Also,

$$\begin{array}{cc}\hfill & {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & +{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)P\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg.\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\varrho \right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)P\left({\eta }_3\right)\right].\hfill \end{array}$$

(8)

Finally, by comparing (6), (7), and (8), we obtain the left Fejer inequality:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\hslash \left(\frac{1}{2}\right)}}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\left[J_{{{\eta }_3}^{+}}^{\varrho }P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }P\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)P\left({\eta }_3\right)\right].\hfill \end{array}$$

For the second fuzzy number-valued Fejer inequality, again considering fuzzy number-valued extended $cr$-ℏ convex mapping and taking the product of the resultant inequality by $P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)$, we obtain

$$\begin{array}{cc}\hfill & \mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right].\hfill \end{array}$$

Taking the product of $g^{\varrho -1}$ with the aforementioned inequality, then applying integration, we have

$$\begin{array}{cc}\hfill & \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & +\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & {\preccurlyeq }_{cr}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)+(1-g)\hslash (1-g)\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

This yields

$$\begin{array}{cc}\hfill & \left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)P\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \frac{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}{\Gamma \left(\varrho \right)}}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\hslash \left(g\right)\oplus (1-g)\hslash (1-g)\right)P\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]dg.\hfill \end{array}$$

Hence, the intended inequality is attained. □

Under certain constraints, Theorem 9 reduces to the following significant inequalities:

• Inserting $\hslash \left(g\right)=1$ into Theorem 9 produces the following inequality:

  $$\begin{array}{cc}\hfill & \mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)\left[J_{{{\eta }_3}^{+}}^{\varrho }P\left({\eta }_4\right)+J_{{{\eta }_4}^{-}}^{\varrho }P\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)P\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)P\left({\eta }_3\right)\right]{\preccurlyeq }_{cr}{\displaystyle \frac{\left[\mathcal{F}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\right]}{2}}\left[J_{{{\eta }_3}^{+}}^{\varrho }P\left({\eta }_4\right)+J_{{{\eta }_4}^{-}}^{\varrho }P\left({\eta }_3\right)\right].\hfill \end{array}$$

Example 4.

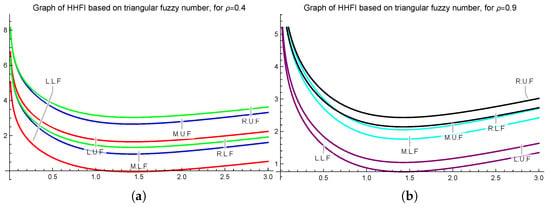
Let $\mathcal{F}:[0,2]\to {\mathbb{M}}_F$ be a triangular fuzzy number-valued extended $cr$ convex mapping, as defined in Example 1, and let $\mathcal{S}\left(\vartheta \right)={(1-\vartheta )}^2$ be a symmetric mapping about 1. Since $\mathcal{F}(\vartheta ,\rho )$ and $\mathcal{S}$ satisfy all the credentials of Theorem 9, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 5a,b, we consider the triangular fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures affirm the accuracy of inequality proved in Theorem 9.

Figure 5. Graphical demonstration of Theorem 9 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

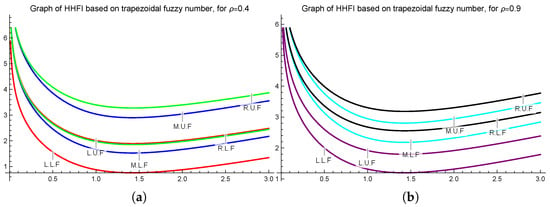
Let $\mathcal{F}:[0,2]\to {\mathbb{M}}_F$ be a trapezoidal fuzzy number-valued extended $cr$ convex mapping, as defined in Example 2, and let $\mathcal{S}\left(\vartheta \right)={(1-\vartheta )}^2$ be a symmetric mapping about 1. Since $\mathcal{F}(\vartheta ,\rho )$ and $\mathcal{S}$ satisfy all the credentials of Theorem 9, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 6a,b, we consider the trapezoidal fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures highlight the accuracy of the inequality proved in Theorem 9.

Figure 6. Depiction of Theorem 9 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

Now, we develop new bounds for the product of two generalized convex mappings.

Theorem 10.

Let ${\hslash }_1,{\hslash }_2:(0,1)\to (0,\infty )$ be two non-negative mappings. If

$$\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$$

and $\mathcal{S}\in SFEX\left(cr-{\hslash }_2,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ then

$$\begin{array}{cc}\hfill & \frac{4}{{\hslash }_1\left(\frac{1}{2}\right){\hslash }_2\left(\frac{1}{2}\right)\varrho }\mathcal{F}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)\mathcal{S}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}\frac{\Gamma \left(\varrho \right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_3\right)\right]\hfill \\ \hfill & \oplus {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left[g\left(1-g\right)\left({\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)+{\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right)\right]{\varphi }_1\left({\eta }_3,{\eta }_4\right)dg\hfill \\ \hfill & \oplus {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left[g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)+{\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right]{\varphi }_2\left({\eta }_3,{\eta }_4\right)dg,\hfill \end{array}$$

where ${\varphi }_1\left({\eta }_3,{\eta }_4\right)$ and ${\varphi }_2\left({\eta }_3,{\eta }_4\right)$ are defined in Theorem 11.

Proof. 

Since $\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and $\mathcal{S}\in SFEX\left(cr-{\hslash }_2,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{2}{{\hslash }_1\left(\frac{1}{2}\right)}}\mathcal{F}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\hfill \\ \hfill & {\displaystyle \frac{2}{{\hslash }_2\left(\frac{1}{2}\right)}}\mathcal{S}\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right){\preccurlyeq }_{cr}\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right).\hfill \end{array}$$

This results in

$$\begin{array}{cc}\hfill & \frac{4}{{\hslash }_1\left(\frac{1}{2}\right){\hslash }_2\left(\frac{1}{2}\right)}\mathcal{F}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)\mathcal{S}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\hfill \\ \hfill & \oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right).\hfill \end{array}$$

Also, by the definition of fuzzy number-valued extended $cr$ convex mappings, we have

$$\begin{array}{cc}\hfill & \mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\oplus \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}\left[g\left(1-g\right)\left({\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)\oplus {\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right)\right]{\varphi }_1\left({\eta }_3,{\eta }_4\right)\hfill \\ \hfill & \oplus \left[g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)\oplus {\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right]{\varphi }_2\left({\eta }_3,{\eta }_4\right).\hfill \end{array}$$

From the previous inequality, we have

$$\begin{array}{cc}\hfill & \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\frac{4}{{\hslash }_1\left(\frac{1}{2}\right){\hslash }_2\left(\frac{1}{2}\right)}\mathcal{F}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)\mathcal{S}\left(\frac{{\eta }_3+{\eta }_4}{2}\right)dg\hfill \\ \hfill & {\preccurlyeq }_{cr}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & \oplus \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg\hfill \\ \hfill & \oplus \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left[g\left(1-g\right)\left({\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)\oplus {\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right)\right]{\varphi }_1\left({\eta }_3,{\eta }_4\right)dg\hfill \\ \hfill & \oplus \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left[g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)\oplus {\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right]{\varphi }_2\left({\eta }_3,{\eta }_4\right)dg.\hfill \end{array}$$

Finally, some simple computations deliver the desired inequality. □

Example 5.

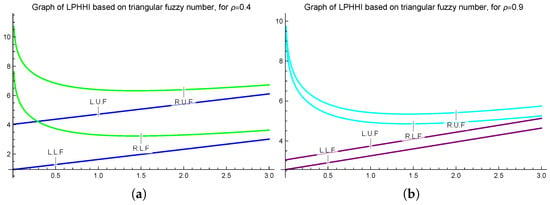
Let $\mathcal{F},\mathcal{S}:[0,2]\to {\mathbb{M}}_F$ be two triangular fuzzy number-valued extended $cr$ convex mappings, $\mathcal{F}$ is defined in Example 1, and

$\mathcal{S}\left(\vartheta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{g}{2{\vartheta }^2}},\hfill & 0<g\le 2{\vartheta }^2\hfill \\ \\ {\displaystyle \frac{4{\vartheta }^2-g}{2{\vartheta }^2}},\hfill & 2{\vartheta }^3<g\le 4{\vartheta }^2.\hfill \end{array}\right.$

Since $\mathcal{F}(\vartheta ,\rho )$ and $\mathcal{S}(\vartheta ,\rho )=[2\rho {\vartheta }^2,(4-2\rho ){\vartheta }^2]$, all the credentials of Theorem 10 are satisfied. We have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 7a,b, we consider the triangular fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures affirm the accuracy of the inequality proved in Theorem 10.

Figure 7. Graphical demonstration of Theorem 10 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

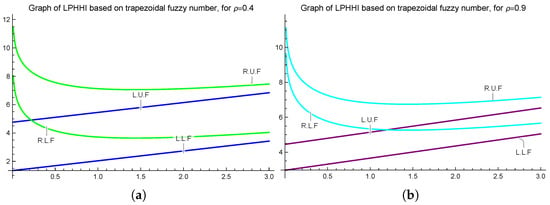
Let $\mathcal{F},\mathcal{S}:[0,2]\to {\mathbb{M}}_F$ be a trapezoidal fuzzy number-valued extended $cr$ convex mapping, such that

$$\begin{array}{c}\hfill {\mathcal{F}}_{\vartheta }\left(g\right)=\left\{\begin{array}{cc}{\displaystyle \frac{g-1}{3{\vartheta }^3}},\hfill & 0<g\le 3{\vartheta }^3\hfill \\ \\ 1,\hfill & 3{\vartheta }^3<g\le 5{\vartheta }^3\hfill \\ \\ {\displaystyle \frac{6{\vartheta }^3-g}{{\vartheta }^3}},\hfill & 5{\vartheta }^3<g\le 6{\vartheta }^3\hfill \\ \\ 0,\hfill & g>6{\vartheta }^3.\hfill \end{array}\right.\\ \hfill \mathit{and}\\ \hfill {\mathcal{S}}_{\vartheta }\left(g\right)=\left\{\begin{array}{cc}{\displaystyle \frac{g}{2{\vartheta }^2}},\hfill & 0<g\le 2{\vartheta }^2\hfill \\ \\ 1,\hfill & {\vartheta }^2<g\le 4{\vartheta }^2\hfill \\ \\ {\displaystyle \frac{6{\vartheta }^2-g}{2{\vartheta }^2}},\hfill & 4{\vartheta }^2<g\le 6{\vartheta }^2\hfill \\ \\ 0,\hfill & g>6{\vartheta }^2.\hfill \end{array}\right.\end{array}$$

Since $\mathcal{F}(\vartheta ,\rho )=[3\rho {\vartheta }^3,(6-\rho ){\vartheta }^3]$ and $\mathcal{S}(\vartheta ,\rho )=[2\rho {\vartheta }^2,(6-2\rho ){\vartheta }^2]$, all the credentials of Theorem 10 are satisfied. We have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 8a,b, we consider the trapezoidal fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures highlight the accuracy of the inequality proved in Theorem 9.

Figure 8. Depiction of Theorem 10 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

Lastly, we construct the right-product inequality.

Theorem 11.

Suppose ${\hslash }_1,{\hslash }_2>0$ are two mappings. If $\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ and $\mathcal{S}\in SFEX\left(cr-{\hslash }_2,[{\eta }_3,{\eta }_4],{\mathbb{M}}_F\right)$ then

$$\begin{array}{cc}\hfill & \frac{\Gamma \left(\varrho \right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)+{\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right){\varphi }_1\left({\eta }_3,{\eta }_4\right)dg\hfill \\ \hfill & \oplus {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\left(1-g\right){\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)+g\left(1-g\right){\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right){\varphi }_2\left({\eta }_3,{\eta }_4\right)dg,\hfill \end{array}$$

where

$$\begin{array}{c}\hfill {\varphi }_1\left({\eta }_3,{\eta }_4\right)=\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_3\right)\oplus \mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right),\\ \hfill {\varphi }_2\left({\eta }_3,{\eta }_4\right)=\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_4\right)\oplus \mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_3\right).\end{array}$$

Proof. 

Since $\mathcal{F}\in SFEX\left(cr-{\hslash }_1,[{\varrho }_2,{\eta }_4],{\mathbb{M}}_F\right)$ and $\mathcal{S}\in SFEX\left(cr-{\hslash }_2,[{\varrho }_2,{\eta }_4],{\mathbb{M}}_F\right)$, then

$$\begin{array}{cc}\hfill & \mathcal{F}\left(g{\varrho }_2+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\varrho }_2+\left(1-g\right){\eta }_4\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}{g}^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)\mathcal{F}\left({\varrho }_2\right)\mathcal{S}\left({\varrho }_2\right)\oplus g\left(1-g\right){\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_4\right)\hfill \\ \hfill & \oplus g\left(1-g\right){\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_3\right)\oplus {\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right).\hfill \end{array}$$

(9)

Likewise,

$$\begin{array}{cc}\hfill & \mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\hfill \\ \hfill & {\preccurlyeq }_{cr}{g}^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right)\oplus g\left(1-g\right){\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_3\right)\hfill \\ \hfill & \oplus g\left(1-g\right){\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_4\right)\oplus {\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_3\right).\hfill \end{array}$$

(10)

Summing (9) and (10), taking product by $g^{\varrho -1}$, and integrating over $[0,1]$, we have

$$\begin{array}{cc}\hfill & \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)\mathcal{S}\left(g{\eta }_3+\left(1-g\right){\eta }_4\right)dg\hfill \\ \hfill & \oplus \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\mathcal{F}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)\mathcal{S}\left(g{\eta }_4+\left(1-g\right){\eta }_3\right)dg\hfill \\ \hfill & {\preccurlyeq }_{cr}\left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)+{\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right){\varphi }_1\left({\eta }_3,{\eta }_4\right)dg\hfill \\ \hfill & \oplus \left(FR\right){\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\left(1-g\right){\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)+g\left(1-g\right){\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right){\varphi }_2\left({\eta }_3,{\eta }_4\right)dg.\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill & \frac{\Gamma \left(\varrho \right)}{{\left({\eta }_4-{\eta }_3\right)}^{\varrho }}\left[J_{{{\eta }_3}^{+}}^{\varrho }\mathcal{F}\left({\eta }_4\right)\mathcal{S}\left({\eta }_4\right)\oplus J_{{{\eta }_4}^{-}}^{\varrho }\mathcal{F}\left({\eta }_3\right)\mathcal{S}\left({\eta }_3\right)\right]\hfill \\ \hfill & {\preccurlyeq }_{cr}{\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g^2{\hslash }_1\left(g\right){\hslash }_2\left(g\right)+{\left(1-g\right)}^2{\hslash }_1\left(1-g\right){\hslash }_2\left(1-g\right)\right){\varphi }_1\left({\eta }_3,{\eta }_4\right)dg\hfill \\ \hfill & \oplus {\displaystyle \underset{0}{\overset{1}{\int }}}{g}^{\varrho -1}\left(g\left(1-g\right){\hslash }_1\left(g\right){\hslash }_2\left(1-g\right)+g\left(1-g\right){\hslash }_1\left(1-g\right){\hslash }_2\left(g\right)\right){\varphi }_2\left({\eta }_3,{\eta }_4\right)dg.\hfill \end{array}$$

Final inequality is achieved. □

Example 6.

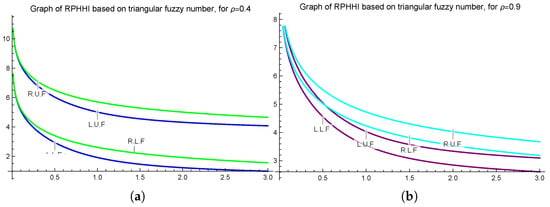
Let $\mathcal{F},\mathcal{S}:[0,2]\to {\mathbb{M}}_F$ be two triangular fuzzy number-valued extended $cr$ convex mappings, as defined in Example 5. Since $\mathcal{F}(\vartheta ,\rho )$ and $\mathcal{S}(\vartheta ,\rho )=[2\rho {\vartheta }^2,(4-2\rho ){\vartheta }^2]$ satisfy all the credentials of Theorem 11, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 9a,b, we consider the triangular fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures affirm the accuracy of the inequality proved in Theorem 11.

Figure 9. Graphical demonstration of Theorem 11 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

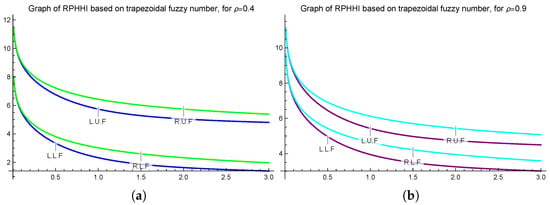
Let $\mathcal{F},\mathcal{S}:[0,2]\to {\mathbb{M}}_F$ be a trapezoidal fuzzy number-valued extended $cr$ convex mapping, as defined in Example 5. Since $\mathcal{F}(\vartheta ,\rho )$ and $\mathcal{S}(\vartheta ,\rho )$ satisfy all the credentials of Theorem 11, we have the following graphical representations for $\rho =0.4$ and $\rho =0.9$.

To construct Figure 10a,b, we consider the trapezoidal fuzzy number-valued extended $cr$-ℏ convex mappings, $\varrho \in (0,3]$ and specific values ρ. Both figures highlight the accuracy of the inequality proved in Theorem 11.

Figure 10. Depiction of Theorem 11 for $\rho$ = 0.4 (a), 0.9 (b) plotted on Mathematica 13.

Remark 2.

It is interesting to note that by utilizing the values of ℏ in Theorems 4–11 we obtain the various classes of totally ordered fuzzy number-valued convex mappings, like s convexity in all four senses, Godunova–Levin convexity, tgs convexity, exponential convexity, n-polynomial convexity, trigonometric convexity, and many more. Assuming that ${\mathcal{F}}_c={\mathcal{F}}_r$ in Definition 9, then we recover the class of generalized ℏ convexity. Moreover, for $\hslash =1$ and $\varrho =1$ in Theorems 4–11 we obtain the Jensen,’s, Schur’s, Hermite–Hadamard’s, Fejer, and left- and right-product Hermite-Hadamard inequality for fuzzy number-valued $cr$ convex mappings. All these results are new and novel.

4. Applications

Here, we supply some applications of trapezoid and fuzzy-valued Jensen’s inequalities. The well known two kinds of binary means are defined as

(1)

The arithmetic mean:

$$A({\eta }_3,{\eta }_4)={\displaystyle \frac{{\eta }_3+{\eta }_4}{2}};$$

(2)

The extended log-mean:

$$L_e({\eta }_3,{\eta }_4)={\left[{\displaystyle \frac{{{\eta }_4}^{e+1}-{{\eta }_3}^{e+1}}{(e+1)({\eta }_4-{\eta }_3)}}\right]}^{{\displaystyle \frac{1}{e}}};e\in \Re \setminus \{-1,0\}.$$

Proposition 5.

If ${\eta }_3,{\eta }_4\ge 0$ then

$$\begin{array}{cc}\hfill \left[2\rho A^3({\eta }_3,{\eta }_4),(6-4\rho )A^3({\eta }_3,{\eta }_4)\right]& {⪯}_{cr}\left[2\rho L_3^3({\eta }_3,{\eta }_4),(6-4\rho )L_3^3({\eta }_3,{\eta }_4)\right]\hfill \\ \hfill & {⪯}_{cr}\left[2\rho A({{\eta }_3}^3,{{\eta }_4}^3),(6-4\rho )A({{\eta }_3}^3,{{\eta }_4}^3)\right].\hfill \end{array}$$

Proof. 

The intended inequality follows by substituting $\mathcal{F}\left(\vartheta \right)=[2\rho {\vartheta }^3,(6-4\rho ){\vartheta }^3]$ on Theorem 8 and taking $\varrho =1$ and $\hslash =1$. □

Next, we establish two new refinements of triangular inequality.

Proposition 6.

Let $\left\{{\vartheta }_j\right\}\in [{\eta }_3,{\eta }_4]$ be an increasing positive sequence. Then, Theorem 4 transforms into the following results:

$$\begin{array}{c}\hfill \left|{\displaystyle \sum _{j=1}^g}{\vartheta }_j\right|\le {\displaystyle \sum _{j=1}^g}\left|{\vartheta }_j\right|,\end{array}$$

and

$$\begin{array}{c}\hfill ∥{\displaystyle \sum _{j=1}^g}{\vartheta }_j∥\le {\displaystyle \sum _{j=1}^g}\parallel {\vartheta }_j\parallel .\end{array}$$

Proof. 

We plug the values of ${\hslash }_{\circ }\left(\vartheta \right)={\displaystyle \frac{1}{\vartheta }}$, ${\mathcal{V}}_g=1$, ${\mathcal{F}}_{*}(\vartheta ,\rho )={\mathcal{F}}^{*}(\vartheta ,\rho )$, and $\rho =1$ into Theorem 4 and take $\mathcal{F}\left(\vartheta \right)=\left|\vartheta \right|$ and $\mathcal{F}\left(\vartheta \right)=\parallel \vartheta \parallel$. □

Now, we establish an inequality for the modified Bessel mapping. In this regard, we recall the modified Bessel mapping, which is given in [51] as

$$\begin{array}{c}\hfill I_p\left(\vartheta \right)={\displaystyle \sum _{\lambda =0}^{\infty }}{\displaystyle \frac{{\left(\frac{\vartheta }{2}\right)}^{p+2\lambda }}{\lambda !\Gamma (p+\lambda +1)}},\vartheta \in \mathbb{R}.\end{array}$$

Let us define a mapping associated with $I_p\left(\vartheta \right)$. Let $\mathcal{G}:[0,\infty )\to [0,\infty )$, such that ${\mathcal{G}}_p\left(\vartheta \right)={\vartheta }^p{I}_p\left(\vartheta \right)$ for $p\ge 2$. Its few derivatives are given as

$$\begin{array}{cc}\hfill & {\mathcal{G}}_p\left(\vartheta \right)={\vartheta }^p{I}_p\left(\vartheta \right)\hfill \\ \hfill & {\mathcal{G}}_p^{\prime }\left(\vartheta \right)={\vartheta }^p{I}_{p-1}\left(\vartheta \right)\hfill \\ \hfill & {\mathcal{G}}_p^{″}\left(\vartheta \right)={\vartheta }^{p-1}{I}_{p-1}\left(\vartheta \right)+{\vartheta }^p{I}_{p-2}\left(\vartheta \right).\hfill \end{array}$$

The above formulations affirm that ${\mathcal{G}}_p$ is convex because ${\mathcal{G}}^{″}\ge 0$ for all $p\ge 2$.

Proposition 7.

For $p\ge 2$, we obtain the following fractional inequality,

$$\begin{array}{cc}\hfill {\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)}^p{I}_p\left({\displaystyle \frac{{\eta }_3+{\eta }_4}{2}}\right)& \le {\displaystyle \frac{\Gamma \left(\varrho +1\right)}{{2\left({\eta }_4-{\eta }_3\right)}^{\varrho }}}\left[{\eta }_4^p{J}_{{{\eta }_3}^{+}}^{\varrho }{I}_p\left({\eta }_4\right)+{\eta }_3^p{J}_{{{\eta }_4}^{-}}^{\varrho }{I}_p\left({\eta }_3\right)\right]\hfill \\ \hfill & {\displaystyle \frac{\left[{\eta }_3^p{I}_p\left({\eta }_3\right)+{\eta }_4^p{I}_p\left({\eta }_4\right)\right]}{2}}.\hfill \end{array}$$

Proof. 

To prove the required inequality, we take ${\mathcal{F}}_c={\mathcal{F}}_r$ in Theorem 8, $\varrho =1$, and $\hslash =1$. The result follows direct by takingly $\mathcal{F}\left(\vartheta \right)={\mathcal{G}}_p\left(\vartheta \right)$. □

5. Conclusions

Exploration of inequalities through convexity and its consequences is intriguing and captivating research. The dominance of inequalities in diverse directions has secured the attention of researchers. In the following context, the construction of fuzzy-valued inequalities motivated us to develop new counterparts of existing results for a larger space of mappings. We have derived Jensen’s and fractional Hermite–Hadamard’s-like inequalities based on the newly proposed class of fuzzy-valued convexity. It is worth mentioning that from our proposed class, we can analyze the up and down and left and right fuzzy-valued convex, whose center and radius are both convex for all $\rho \in [0,1]$, whereas an up-and-down fuzzy-valued convex function need not be an LR fuzzy-valued convex mapping. To the extent of our knowledge, the idea of totally ordered fuzzy-valued convexity is new in the literature, which makes our results significant. Also, this class can be investigated from an optimization viewpoint. It would be a good problem to investigate the coordinated inequalities utilizing this idea. By following a similar strategy, several new classes of convex mappings, like strong convex mappings, uniform convex mappings, and superquadratic mappings, could be defined. Several other inequalities linked with convexity could be explored. In future, we will derive the fractal, fractional, and quantum fuzzy-valued inequalities, leveraging the concepts of various other classes of totally ordered fuzzy-valued mappings.