Fractional and Integrable Perspectives on a Variable-Coefficient Semi-Discrete NLS Equation: Analytical Method and Engineering Applications

Abstract

The method of deriving fractional-order differential equations using Riesz fractional-order calculus is a new breakthrough, and it is possible to use the inverse scattering transform (IST) to solve the analytical solutions of the derived equations. However, there are still relatively few examples of using discrete Riesz fractional (DRF) order calculations. This article focuses on using discrete Riesz fractional-order calculations to derive a variable-coefficient fractional integrable semi-discrete nonlinear Schrödinger (vcfISDNLS) equation. On the one hand, we derive the vcfISDNLS equation through dispersion relation (DR) and DRF order calculations. On the other hand, we obtain the explicit expressions of the one-soliton solution, two-soliton solution, and three-soliton solution of this equation without reflection potentials (RPs). By deriving and solving the equation and displaying the obtained soliton solutions, possible evidential support can be provided for control engineering, automotive engineering, image processing, and optical communication systems.

1. Introduction

As described in [1,2,3], a semi-discrete system (SDS) is a kind of system where spatial independent variable(s) is/are discrete but the temporal independent variable remains continuous. Therefore, an SDS combines some characteristics of discrete systems with certain features of continuous systems. For example, in the lattice model, atoms are discretely distributed in space, while time can be viewed as continuous [4,5,6]. When studying nonlinear issues like wave propagation in discrete lattices, an SDS can accurately characterize the relevant physical processes. Meanwhile, there are some methods for finding solutions for SDSs, such as the Jacobian elliptic function method [7], the exp-function technique [8], the double commutation method, and IST [9]. Nevertheless, compared with continuous systems, solving SDSs is still relatively difficult. These methods are mainly used to solve some semi-discrete NLS equations [4,5], the Toda hierarchy [9,10,11], etc. In addition, SDSs have wide applications in digital control systems [12], signal processing and communication [13], robotics [14], etc.

Fractional calculus [15,16] is an extension of the concept of integer calculus, making the analysis of functions more refined. Integer calculus can only describe change in a function at integer orders, while fractional calculus can capture the more subtle variation characteristics of functions [17,18]. For some functions with fractal properties, integer calculus cannot fully reflect their complex local properties. However, fractional calculus can describe the variation rules of functions at multi-scales through different fractional orders, providing a powerful tool for studying the local singularity and irregularity of functions. Combining fractional calculus with Laplace transform [16,19,20,21] and/or Fourier transform [18] expands the application scope and theoretical depth of these transformations. Fractional calculus not only has wide applications in mathematics and physics [22,23,24] but also plays an important role in engineering, such as proportional integral derivative (PID) control [25], robotics [26], image processing [27], and automotive engineering [28].

However, we know that for integrable partial differential equations, they are not necessarily integrable after being partially discretized. Discrete integrable systems can be studied from different angles. It is known from the book [5] by Ablowitz, Prinari, and Trubatch that they studied the NLS, integrable discrete NLS (IDNLS), matrix NLS (MNLS), and integrable discrete MNLS (IDMNLS) equations, with the NLS equation remaining integrable after discretization. In 2022, Ablowitz, Been, and Carr [29] utilized the discrete Fourier transform/Z-transform to obtain the fractional IDNLS (fIDNLS) equation and the fractional averaged NLS (fADNLS) equation after studying the fractional mKdV (fmKdV), fractional sine-Gordon (fsine-G), and fractional sinh-Gordon (fsinh-G) equations [30] by extending the method of [15]. This is due to the use of the chosen Riesz fractional-order derivative (RFD) [15], denoted by ${\left|-{\mathit{\partial }}_x^2\right|}^{\omega }$:

$${\left|-{\partial }_x^2\right|}^{\omega }v(x,t)={\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_{-\infty }^{\infty }\widehat{v}(p,t){\left|p^2\right|}^{\omega }}{e}^{ipx}dp, \widehat{v}(p,t)={\displaystyle {\int }_{-\infty }^{\infty }v(x,t)e^{-ipx}}dx,$$

which has the Fourier multiplier ${\left|p^2\right|}^{\omega }$ for $\left|\omega \right|<1$. The discrete RFD used in this article, namely, the DRF derivative, also has a similar multiplier to RFD, as shown in Equations (13) and (14). Although there are many other fractional-order derivatives [31], such as the Riemann–Liouville fractional derivative, the Caputo fractional derivative, the Grünwald–Letnikov fractional derivative, etc., this multiplier is not possessed by these nonlocal fractional derivatives. Compared to other nonlocal fractional derivatives, the advantage of RFDs is that they are particularly intuitive and easy to understand for physicists who do not specialize in this mathematical field, and they are an ideal tool for describing isotropic anomalous diffusion. In addition, RFDs have an extremely concise form in the frequency domain, making theoretical analysis and numerical solutions very effective. This is an effective tool for describing the behavior of complex systems due to the close correlation between RFDs and non-Gaussian statistics [32], as indicated in [30], and it has physical applications in describing the motion of water in porous media and power law decay in materials. It can be seamlessly extended to high-dimensional space, with an invariant definition, and is suitable for solving fractional-order partial differential equations in space.

The core idea of Ablowitz et al.’s method [15,29] includes three elements, one of which is to link a set of integrable nonlinear equations or semi-discrete equations to linear scattering problems to characterize the fractional equation with an RFD or DRF derivative to be solved through a power law DR. The second is to determine the fractional operator corresponding to the DR based on the completeness of the squared eigenfunctions of the relevant scattering equations. The third is to follow the steps of the IST [33] to obtain the solution of the fractional equation being solved. The method proposed by Ablowitz et al. [15,29] is not only suitable for the fractional equations [15,29,30] mentioned above but has also been successfully applied to other models with RFDs, such as fractional higher-order NLS equations [34] and combined mKdV hierarchy [35], fractional coupled multi-component NLS models [36,37], fractional coupled Hirota and Gerdjikov–Ivanov equations [38,39], the fractional derivative NLS equation [40] and generalized NLS equations [41], the fractional Fokas–Lenells equation [42], variable-coefficient fractional KdV and generalized NLS equations [43,44], and fractional Toda lattice and hierarchy [45].

In the complex and diverse real world, many profound natural phenomena and inherent rules can all be precisely depicted through ingenious mathematical physics equations. Variable-coefficient equations [43,44] with detailed descriptions of the parameter evolution characteristics in dynamic systems have broken through the limitations of constant-coefficient equations, endowed complex problems with higher descriptive accuracy, and have become powerful tools for revealing the essence of nature. However, proving the existence and solvability of solutions for nonlinear equations with variable coefficients has always been a difficult problem in the field of mathematical physics. Such equations are not only limited by their own nonlinear characteristics in analytical methods but also need to deal with the dynamic effects caused by variable coefficients, which poses a dual challenge that makes the related research much more difficult than that of constant-coefficient equations. The fractional NLS-type equation under the framework of continuous systems has successfully revealed the soliton structure characteristics of fractional integrable models solved by the IST constrained with the dual action [44] of RFDs and variable coefficients, providing an important reference for research in the related field. However, it is worth noting that up to now, within the framework of IST integrability conditions defined by Ablowitz et al. [29], there have been no systematic studies on variable-coefficient semi-discrete equations with DRF derivatives reported in the public literature, and this research gap urgently needs to be filled. In view of this, this paper is based on the DRF derivative theory and the variable-coefficient analysis method and is committed to deeply exploring the existence, analytical properties, and soliton structure characteristics of IST integrable Riesz fractional semi-discrete models. This research is not only expected to explore the integrability of the theoretical system of fractional-order nonlinear equations but also provides solid theoretical support and innovative research ideas for solving practical problems in multiple interdisciplinary fields such as nonlinear physics, control engineering, and communication engineering.

This paper introduces the DRF calculus ${\Delta }_n^{(1+\delta )}$ with $\delta \in (-1,1)$ [46,47], and in a similar way to that of [29], to obtain the following vcfISDNLS equation:

$$i{\partial }_t{u}_n+{[2\alpha (t)I-\beta (t)\Delta -\beta (t)({\Theta }_{+}+{\Theta }_{+}^{-})]}^{(1+\delta )}{u}_n=0,$$

(1)

where $u_n={(q_n,r_n)}^T$ with $r_n=\mp q_n^{\ast }$; using the index number, $n$, as the lattice point or spatial position, the time variable is $t$, and $\alpha (t)$ and $\beta (t)$ are real functions of $t$ that are independent of each other. When $\alpha (t)=\beta (t)=1$, Equation (1) degenerates into Ablowitz et al.’s fIDNLS equation [29], $i{\partial }_t{u}_n+{[2I-\Delta -({\Theta }_{+}+{\Theta }_{+}^{-})]}^{(1+\delta )}{u}_n=0$. In general, a step size, $c$, exists in Equation (1). In this paper, we take $c=1$ without losing generality. To generate Equation (1), we only need to convert $c{q}_n$ and $c{r}_n$ into $q_n$ and $r_n$. Given the condition of $\delta =0$, Equation (1) can generate new equations:

$$\left\{\begin{array}{l}i{\partial }_t{q}_n-[\beta (t)q_{n+1}-2\alpha (t)q_n+\beta (t)q_{n-1}]\mp \beta (t){\left|q_n\right|}^2(q_{n+1}+q_{n-1})=0\hfill \\ -i{\partial }_t{r}_n-[\beta (t)r_{n+1}-2\alpha (t)r_n+\beta (t)r_{n-1}]\mp \beta (t){\left|r_n\right|}^2(r_{n+1}+r_{n-1})=0\hfill \end{array}\right..$$

(2)

In this article, we derive the vcfISDNLS Equation (1) using the DRF order derivative and solve it through the IST. In Section 2, we derive the vcfISDNLS equation, Equation (1), by using the DR. In Section 3, we first obtain the Jost functions and summation equations and prove their existence and analytical properties. Secondly, we obtain scattering data and normal constants and prove the symmetry of the solution. In Section 4, we first introduce the boundary conditions and residues, and then, we consider two cases of no poles and poles. Finally, we obtain reflectionless potentials, the Gel’fand–Levitan–Marchenko (GLM) equation, and time evolution. In Section 5, when $\mathcal{K}=\tilde{\mathcal{K}}=1,\hspace{0.33em}2,\hspace{0.33em}3$, we determine the one-, three-, and three-soliton solutions and conduct nonlinear dynamic analysis on them. In the final section, we present the corresponding conclusions and opinions and point out the shortcomings and their implications for engineering applications.

2. Derivation of the vcfISDNLS Equation

In order to obtain Equation (1), we first consider the discrete problem:

$${\kappa }_{n+1}-{\kappa }_n=\left(\begin{array}{cc}-ik& q_n\\ r_n& ik\end{array}\right){\kappa }_n.$$

(3)

When $z=e^{-ik}=1-ik$, we rewrite Equation (3) as

$${\kappa }_{n+1}=\left(\begin{array}{cc}z& q_n\\ r_n& z^{-1}\end{array}\right){\kappa }_n$$

(4)

and introduce the following time-dependent equation:

$${\displaystyle \frac{d{\kappa }_n}{dt}}=\left(\begin{array}{cc}i\beta (t)q_n{r}_{n-1}-{\displaystyle \frac{i}{2}}[\beta (t)(z^2+z^{-2})-2\alpha (t)]& -i\beta (t)(z{q}_n-z^{-1}{q}_{n-1})\\ i\beta (t)(z^{-1}{r}_n-z{r}_{n-1})& -i\beta (t)r_n{q}_{n-1}+{\displaystyle \frac{i}{2}}[\beta (t)(z^2+z^{-2})-2\alpha (t)]\end{array}\right){\kappa }_n$$

(5)

Then, the compatibility condition of Equations (4) and (5) is equivalent to Equation (2).

However, obtaining Equation (2) is not the starting point of this article but rather draws inspiration from it and derives Equation (1). For this, we need to find the DR corresponding to Equation (1). Before that, we introduce the following nonlinear evolution equation:

$$\sigma {\displaystyle \frac{d{u}_n}{dt}}+\theta ({\mathrm{ƛ}}_n)u_n=0, \sigma =\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).$$

(6)

The operator, ${\mathrm{ƛ}}_n$, introduced here consists of two factors, and in fact, it is necessary to divide this operator into two factors. The first factor is composed of $2\alpha (t)I-\beta (t)\Delta$. When applying the second factor, we introduce operator ${\Theta }_{+}$ and the inverse operator, which is ${\Theta }_{+}^{-}$. Note that operator ${\Theta }_{+}$ satisfies [29]

$${\Theta }_{+}{\chi }_n=({\epsilon }_n-1)\left(\begin{array}{cc}{\Delta }_n^{+}& 0\\ 0& {\Delta }_n^{-}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right)+\left(\begin{array}{cc}{q}_n{\displaystyle {\sum }_{n-1}^{+}{r}_{i-1}}& q_n{\displaystyle {\sum }_{n-2}^{+}{q}_{i+1}}\\ -r_n{\displaystyle {\sum }_{n-1}^{+}{r}_{i-1}}& -r_n{\displaystyle {\sum }_{n-2}^{+}{q}_{i+1}}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right)+{\epsilon }_n\left(\begin{array}{cc}{q}_{n+1}{\displaystyle {\sum }_{n+1}^{+}\frac{r_i}{h_i}}& q_{n+1}{\displaystyle {\sum }_{n+1}^{+}\frac{q_i}{h_i}}\\ -r_{n-1}{\displaystyle {\sum }_n^{+}\frac{r_i}{h_i}}& -r_{n-1}{\displaystyle {\sum }_n^{+}\frac{q_i}{h_i}}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right),$$

(7)

and the inverse operator, ${\Theta }_{+}^{-}$, satisfies [29]

$${\Theta }_{+}^{-}{\chi }_n=({\epsilon }_n-1)\left(\begin{array}{cc}{\Delta }_n^{-}& 0\\ 0& {\Delta }_n^{+}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right)+\left(\begin{array}{cc}-q_n{\displaystyle {\sum }_n^{+}{r}_{i+1}}& -q_n{\displaystyle {\sum }_{n+1}^{+}{q}_{i-1}}\\ r_n{\displaystyle {\sum }_{n-1}^{+}{r}_{i+1}}& r_n{\displaystyle {\sum }_n^{+}{q}_{i-1}}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right)+{\epsilon }_n\left(\begin{array}{cc}-q_{n-1}{\displaystyle {\sum }_n^{+}\frac{r_i}{h_i}}& -q_{n-1}{\displaystyle {\sum }_n^{+}\frac{q_i}{h_i}}\\ r_{n+1}{\displaystyle {\sum }_{n+1}^{+}\frac{r_i}{h_i}}& -r_{n+1}{\displaystyle {\sum }_{n+1}^{+}\frac{q_i}{h_i}}\end{array}\right)\left(\begin{array}{c}{\chi }_i^{(1)}\\ {\chi }_i^{(2)}\end{array}\right),$$

(8)

where ${\epsilon }_n=1-r_n{q}_n$, ${\sum }_n^{+}={\sum }_{i=n}^{\infty }$, and ${\Delta }_n^{\pm }{\chi }_i^{(s)}={\chi }_{n\pm 1}^{(s)}\hspace{0.33em}$ with $s=1, 2$, providing the definition of $\Delta$, which satisfies

$$\Delta =\left(\begin{array}{cc}{\Delta }_n^{+}+{\Delta }_n^{-}& 0\\ 0& {\Delta }_n^{-}+{\Delta }_n^{+}\end{array}\right).$$

(9)

Specifically, when $\theta ({\mathrm{ƛ}}_n)$ is a fully regular function, it is related to the linearized DR, and then, we can solve Equation (1) by using the IST. For Equation (1), we can determine the corresponding operator, $\theta ({\mathrm{ƛ}}_n)$, with a fractional power:

$$\theta ({\mathrm{ƛ}}_n)=-i{[2\alpha (t)I-\beta (t)\Delta -\beta (t)({\Theta }_{+}+{\Theta }_{+}^{-})]}^{(1+\delta )}.$$

(10)

In fact, by utilizing the method of [29], we let $\underset{n\to \infty }{\lim }{q}_n=0$ and determine the linear part of Equation (6):

$$i{\partial }_t{u}_n+{[2\alpha (t)I-\beta (t)\Delta ]}^{(1+\delta )}{u}_n=0.$$

(11)

In this paper, the DRF derivative of ${\Delta }_n^{(1+\delta )}$ is defined by

$${\Delta }_n^{(1+\delta )}(\mathcal{l}[n])={\displaystyle \frac{1}{2\pi }}{\displaystyle {\int }_{-\pi }^{\pi }{e}^{j\tau (1+\delta )}\mathcal{L}(e^{j\tau n})d\tau },$$

(12)

$$\mathcal{L}(e^{j\tau })={\displaystyle {\sum }_{-\infty }^{\infty }\mathcal{l}[n]}{e}^{-j\tau n}$$

(13)

Then, the DR, $\upsilon (z)$, corresponding to Equation (11), is obtained as

$$\upsilon (z)=-{[2\alpha (t)-\beta (t)(z^2+z^{-2})]}^{(1+\delta )}.$$

(14)

In addition, the operator, ${\mathrm{ƛ}}_n$, can be directly related to the DR, $\upsilon (z)$. As described by ${\mathrm{ƛ}}_n\to 2\alpha (t)I-\beta (t)\Delta \equiv {\nabla }_n$, the linear part of Equation (6) can be obtained:

$$\sigma {\displaystyle \frac{d{u}_n}{dt}}+\theta ({\nabla }_n)u_n=0.$$

(15)

Further substituting $q_n=z^{2n}{e}^{-i{\displaystyle {\int }_0^t\upsilon (z)dm}}$ into Equation (15), we obtain

$$\theta ({\nabla }_n)=i\upsilon (z).$$

(16)

By comparing Equations (14) and (16), we conclude that

$$\theta ({\nabla }_n)=-i{[2\alpha (t)-\beta (t)(z^2+z^{-2})]}^{(1+\delta )}.$$

(17)

Using Equations (11) and (14), we ultimately obtain Equation (10), thus proving the existence of Equation (1).

3. Scattering Problem of the vcfISDNLS Equation

3.1. Jost Functions and Summation Equations

When $n\to \pm \infty$, $q_n$, and $r_n\to 0$, it is established that a unique asymptotic condition exists for the special solution of Equation (4), which can be expressed as follows:

$${\kappa }_{n+1}=\left(\begin{array}{cc}z& 0\\ 0& z^{-1}\end{array}\right){\kappa }_n.$$

(18)

Therefore, we can present Equation (18), as defined by the following boundary conditions:

$${\vartheta }_n(z)~z^n\left(\begin{array}{c}1\\ 0\end{array}\right), {\vartheta }_n(z)~z^{-n}\left(\begin{array}{c}0\\ 1\end{array}\right), n\to -\infty ,$$

(19)

$${\nu }_n(z)~z^{-n}\left(\begin{array}{c}0\\ 1\end{array}\right), {\tilde{\nu }}_n(z)~z^n\left(\begin{array}{c}1\\ 0\end{array}\right), n\to +\infty .$$

(20)

In the ensuing analysis, we consider it more convenient to examine functions that comply with constant boundary conditions. Accordingly, we define the Jost functions in the following forms:

$${\mathcal{A}}_n(z)=z^{-n}{\vartheta }_n(z), \widetilde{{\mathcal{A}}_n}(z)=z^n{\tilde{\vartheta }}_n(z),$$

(21)

$${\mathcal{B}}_n(z)=z^n{\nu }_n(z), \widetilde{{\mathcal{B}}_n}(z)=z^{-n}{\tilde{\nu }}_n(z).$$

(22)

If the scattering problem (4) is reformulated as

$${\kappa }_{n+1}-P{\kappa }_n={\tilde{T}}_n{\kappa }_n, P=\left(\begin{array}{cc}z& 0\\ 0& z^{-1}\end{array}\right), {\tilde{T}}_n=\left(\begin{array}{cc}0& q_n\\ r_n& 0\end{array}\right),$$

(23)

then we can articulate the solution of the above difference equations in terms of Jost functions,

$${\mathcal{A}}_{n+1}(z)-z^{-1}P{\mathcal{A}}_n(z)=z^{-1}{\tilde{T}}_n{\mathcal{A}}_n(z),$$

(24)

$${\tilde{\mathcal{A}}}_{n+1}(z)-zP{\tilde{\mathcal{A}}}_n(z)=z{\tilde{T}}_n{\tilde{\mathcal{A}}}_n(z),$$

(25)

$${\mathcal{B}}_{n+1}(z)-zP{\mathcal{B}}_n(z)=z{\tilde{T}}_n{\mathcal{B}}_n(z),$$

(26)

$${\tilde{\mathcal{B}}}_{n+1}(z)-z^{-1}P{\tilde{\mathcal{B}}}_n(z)=z^{-1}{\tilde{T}}_n{\tilde{\mathcal{B}}}_n(z),$$

(27)

with the constant boundary conditions:

$${\mathcal{A}}_n(z)\to \left(\begin{array}{c}1\\ 0\end{array}\right), {\tilde{\mathcal{A}}}_n(z)\to \left(\begin{array}{c}0\\ 1\end{array}\right), n\to -\infty ,$$

(28)

$${\mathcal{B}}_n(z)\to \left(\begin{array}{c}0\\ 1\end{array}\right), {\tilde{\mathcal{B}}}_n(z)\to \left(\begin{array}{c}1\\ 0\end{array}\right), n\to +\infty .$$

(29)

To establish the existence of the Jost functions, we will first introduce the following Green’s function. Equations (28) and (29) represent their solution:

$${\mathcal{G}}_{n+1}-z^{-1}P{\mathcal{G}}_n=z^{-1}{\mathcal{s}}_{0,n}I, {\mathcal{s}}_{0,n}=\left\{\begin{array}{c}0,\hspace{0.33em}n\ne 0\\ 1, n=0\end{array}\right.,$$

(30)

and ${\kappa }_n$ satisfies the summation of Equation (31):

$${\kappa }_n=\varsigma +{\displaystyle {\sum }_{i=-\infty }^{+\infty }{\mathcal{G}}_{n-i}}{\tilde{T}}_i{\kappa }_i,$$

(31)

with

$$\varsigma -z^{-1}P\varsigma =0.$$

(32)

When $q_n$, $r_n\to 0$ as $n\to \pm \infty$ is considered, and the summation equation involving ${\mathcal{A}}_n(z)$, ${\tilde{\mathcal{A}}}_n(z)$, ${\mathcal{B}}_n(z)$, and ${\tilde{\mathcal{B}}}_n(z)$ can be derived as follows:

$${\mathcal{A}}_n(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)+{\displaystyle {\sum }_{i=-\infty }^{+\infty }{\mathcal{G}}_{n-i}^{ℂ}}(z){\tilde{T}}_n{\mathcal{A}}_i(z), {\tilde{\mathcal{A}}}_n(z)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\displaystyle {\sum }_{i=-\infty }^{+\infty }{\tilde{\mathcal{G}}}_{n-i}^{ℂ}}(z){\tilde{T}}_n{\tilde{\mathcal{A}}}_i(z),$$

(33)

$${\mathcal{B}}_n(z)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\displaystyle {\sum }_{i=-\infty }^{+\infty }{\mathcal{G}}_{n-i}^{\mathbb{Q}}}(z){\tilde{T}}_n{\mathcal{B}}_i(z), {\tilde{\mathcal{B}}}_n(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)+{\displaystyle {\sum }_{i=-\infty }^{+\infty }{\tilde{\mathcal{G}}}_{n-i}^{\mathbb{Q}}}(z){\tilde{T}}_n{\tilde{\mathcal{B}}}_n(z),$$

(34)

where

$${\mathcal{G}}_n^{ℂ}(z)=z\varpi (n-1)\left(\begin{array}{cc}{z}^{2(n-1)}& 0\\ 0& 1\end{array}\right), {\tilde{\mathcal{G}}}_n^{ℂ}(z)=z^{-1}\varpi (n-1)\left(\begin{array}{cc}1& 0\\ 0& z^{-2(n-1)}\end{array}\right),$$

(35)

$${\tilde{\mathcal{G}}}_n^{\mathbb{Q}}(z)=-z^{-1}\varpi (-n)\left(\begin{array}{cc}1& 0\\ 0& z^{-2(n-1)}\end{array}\right), {\mathcal{G}}_n^{\mathbb{Q}}(z)=-z\varpi (-n)\left(\begin{array}{cc}{z}^{2(n-1)}& 0\\ 0& 1\end{array}\right),$$

(36)

$$\varpi (n)={\displaystyle {\sum }_{k=-\infty }^n{\mathcal{s}}_{0,k}}=\left\{\begin{array}{c}1,\hspace{0.17em}\hspace{0.17em}n\ge 0\hspace{0.33em}\\ 0,\hspace{0.17em}\hspace{0.17em}n<0\end{array}\right..$$

(37)

3.2. Existence and Analyticity of the Jost Functions

Firstly, we establish the existence and analytical properties of the Jost functions, ${\mathcal{A}}_n(z)$ and ${\mathcal{B}}_n(z)$. Taking ${\mathcal{A}}_n(z)$ as an exemplary case, we consider the Neumann series given by

$${\mathcal{A}}_n(z)={\displaystyle {\sum }_{m=0}^{\infty }{\Re }_n^m}(z),$$

(38)

where

$${\Re }_n^0(z)=\left(\begin{array}{c}1\\ 0\end{array}\right),$$

(39)

$${\Re }_n^{m+1}(z)={\displaystyle {\sum }_{i=-\infty }^{+\infty }{\mathcal{G}}_{n-i}^{ℂ}}(z){\tilde{T}}_i{\Re }_i^m(z), i\ge 0.$$

(40)

We impose a restriction on ${\Re }_n^m$ such that the series presented in Equation (38) converges absolutely and uniformly with respect to $n$, as well as uniformly with respect to $z$, within the specified region, $\left|z\right|>1$.

The equation for the component-wise summation of ${\mathcal{A}}_n(z)$ is as follows:

$${\mathcal{A}}_n^{(1)}(z)=1+z^{-1}{\displaystyle {\sum }_{i=-\infty }^{n-1}{q}_i}{\mathcal{A}}_i^{(2)}(z),$$

(41)

$${\mathcal{A}}_n^{(2)}(z)={\displaystyle {\sum }_{i=-\infty }^{n-1}{z}^{-2(n-i-1)-1}{r}_i}{\mathcal{A}}_i^{(1)}(z),$$

(42)

and its component form is as follows:

$${\Re }_n^{m+1,(1)}(z)=z^{-1}{q}_i{\Re }_i^{m,(2)}(z),$$

(43)

$${\Re }_n^{m+1,(2)}(z)=z^{-1}{\displaystyle {\sum }_{i=-\infty }^{n-1}{z}^{-2(n-1-i)}}{r}_i{\Re }_i^{m,(1)}(z).$$

(44)

Since ${\Re }_n^{0,(2)}=0$ holds, it consequently follows that ${\Re }_n^{2m+1,(1)}=0$ and ${\Re }_n^{2m,(2)}=0$ are valid for any $m\ge 0$. Our next step is to establish bounds for ${\Re }_n^{2m,(1)}$ and ${\Re }_n^{2m+1,(2)}$. Subsequently, we will demonstrate through the induction of $m$ that, for $\left|z\right|\ge 1$,

$$\left|{\Re }_n^{2m+1,(2)}(z)\right|\le {\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|r_i\right|})}^{m+1}}{(m+1)!}}{\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|q_i\right|})}^m}{m!}},$$

(45)

$$\left|{\Re }_n^{2m+1,(1)}(z)\right|\le {\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|r_i\right|})}^{m+1}}{(m+1)!}}{\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|q_i\right|})}^{m+1}}{(m+1)!}}.$$

(46)

Applying Formula (44) twice, it can be determined in the first iteration that

$$\left|{\Re }_n^{2m+1,(2)}(z)\right|\le {\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|q_i\right|})}^m}{m!}}{\displaystyle {\sum }_{i=-\infty }^{n-1}\left|r_i\right|}{\displaystyle \frac{{({\displaystyle {\sum }_{ℂ=-\infty }^{i-1}\left|r_{ℂ}\right|})}^m}{m!}}.$$

(47)

The next iteration of Equation (44) yields for $\left|z\right|\ge 1$:

$$\left|{\Re }_n^{2m+2,(1)}(z)\right|\le {\displaystyle \frac{{({\displaystyle {\sum }_{i=-\infty }^{n-1}\left|r_i\right|})}^{m+1}}{(m+1)!}}{\displaystyle {\sum }_{i=-\infty }^{n-1}\left|q_i\right|}{\displaystyle \frac{{({\displaystyle {\sum }_{ℂ=-\infty }^{k-1}\left|q_{ℂ}\right|})}^m}{m!}}.$$

(48)

The above calculations demonstrate that ${\mathcal{B}}_n(z)$ exists continuously within region $\left|z\right|\ge 1$. Furthermore, under the conditions specified by ${‖q‖}_1$, ${‖r‖}_1<\infty$, ${\tilde{\mathcal{A}}}_n(z)$, and ${\tilde{\mathcal{B}}}_n(z)$ exist within region $\left|z\right|\le 1$ and remain continuous. Under the same conditions, ${\mathcal{B}}_n(z)$ is solvable within region $\left|z\right|>1$, while ${\tilde{\mathcal{A}}}_n(z)$ and ${\tilde{\mathcal{B}}}_n(z)$ exhibit solvability within region $\left|z\right|<1$.

3.3. Scattering Data and Normalization Constants

To prove that the two eigenfunctions are linearly independent when $\left|n\right|\to \infty$, we then introduce the Wronskian of these solutions:

$$W({\mathcal{X}}_1,{\mathcal{X}}_2)=\det \left|{\mathcal{X}}_1,{\mathcal{X}}_2\right|={\mathcal{X}}_1^{\left(1\right)}{\mathcal{X}}_2^{(2)}-{{\mathcal{X}}_1}^{(2)}{\mathcal{X}}_2^{\left(1\right)},$$

(49)

for any two vectors, ${\mathcal{X}}_1={({{\mathcal{X}}_1}^{(1)},{{\mathcal{X}}_1}^{(2)})}^T$ and ${\mathcal{X}}_2={({{\mathcal{X}}_2}^{(1)},{{\mathcal{X}}_2}^{(2)})}^T$. If $W({\mathcal{X}}_{1,n},{\mathcal{X}}_{2,n})=0$ holds for all $n$, then the vector sequences ${\mathcal{X}}_{1,n}$ and ${\mathcal{X}}_{2,n}$ are linearly independent. Furthermore, if ${\mathcal{X}}_{1,n}$ and ${\mathcal{X}}_{2,n}$ represent any two solutions to the scattering problem (4), their Wronskian adheres to a recursive relationship:

$$W({\mathcal{X}}_{1,n+1},{\mathcal{X}}_{2,n+1})=(1-r_n{q}_n)W({\mathcal{X}}_{1,n},{\mathcal{X}}_{2,n}).$$

(50)

We then get

$$W({\vartheta }_n(z),{\tilde{\vartheta }}_n(z))={\displaystyle {\prod }_{i=-\infty }^{n-1}(1-r_i{q}_i)},$$

(51)

$$W({\nu }_n(z),{\tilde{\nu }}_n(z))={\displaystyle {\prod }_{i=n}^{+\infty }{(1-r_i{q}_i)}^{-1}}.$$

(52)

Thus, we can express ${\vartheta }_n(z)$ and ${\tilde{\vartheta }}_n(z)$ as linear combinations of ${\nu }_n(z)$ and ${\nu }_n(z)$, or vice versa. The coefficients involved in these linear combinations are contingent upon $z$. Therefore, the following relationships hold,

$${\vartheta }_n(z)=\mathcal{g}(z){\nu }_n(z)+\mathcal{f}(z){\tilde{\nu }}_n(z),$$

(53)

$${\tilde{\vartheta }}_n(z)=\tilde{\mathcal{f}}(z){\nu }_n(z)+\tilde{\mathcal{g}}(z){\tilde{\nu }}_n(z),$$

(54)

for any $z$ such that the four eigenfunctions ${\vartheta }_n(z)$, ${\tilde{\vartheta }}_n(z)$, ${\nu }_n(z)$, and ${\tilde{\nu }}_n(z)$ exist. In particular, Equations (53) and (54) hold on $\left|z\right|=1$, and we can define the scattering coefficients $\mathcal{f}(z)$, $\tilde{\mathcal{f}}(z)$, $\mathcal{g}(z)$, and $\tilde{\mathcal{g}}(z)$.

The scattering coefficients can be expressed as the Wronskians of the Jost functions. Indeed, by utilizing Equations (53) and (54), where ${\Im }_n={\displaystyle {\prod }_{i=n}^{+\infty }(1-r_i{q}_i)}$, it is noteworthy that ${\nu }_n(z)$ is meromorphic within region $\left|z\right|>1$, exhibiting poles that correspond to the zeros of $\mathcal{f}(z)$. In parallel, ${\tilde{\nu }}_n(z)$ is also meromorphic in region $\left|z\right|<1$, possessing poles situated at the zeros of $\tilde{\mathcal{f}}(z)$. Furthermore, we advance a definition for the reflection coefficients:

$$\mathcal{H}(z)={\displaystyle \frac{\mathcal{g}(z)}{\mathcal{f}(z)}}, \tilde{\mathcal{H}}(z)={\displaystyle \frac{\tilde{\mathcal{g}}(z)}{\tilde{\mathcal{f}}(z)}},$$

(55)

so that the Conditions (53) and (54) are equivalent to the following:

$${\nu }_n(z)-{\tilde{\mathcal{B}}}_n(z)=z^{-2n}\mathcal{H}(z){\mathcal{B}}_n(z),$$

(56)

$${\tilde{\nu }}_n(z)-{\mathcal{B}}_n(z)=z^{2n}\tilde{\mathcal{H}}(z)\widetilde{{\mathcal{B}}_n}(z).$$

(57)

These occur whenever $\mathcal{f}(z_k)=0$ for some $z_k$ values, such that $\left|z_k\right|>1$ or $\tilde{\mathcal{f}}({\tilde{z}}_{ℂ})=0$ with $\left|{\tilde{z}}_{ℂ}\right|<1$. For such values of the spectral parameter, $W({\vartheta }_n(z_k),{\nu }_n(z_k))=0$ and $W({\tilde{\vartheta }}_n({\tilde{z}}_{ℂ}),{\tilde{\nu }}_n({\tilde{z}}_{ℂ}))=0$, and therefore, ${\vartheta }_n(z_k)$, ${\nu }_n(z_k)$ and ${\tilde{\vartheta }}_n({\tilde{z}}_{ℂ})$, ${\tilde{\nu }}_n({\tilde{z}}_{ℂ})$ are linearly dependent, that is

$${\vartheta }_n(z_k)={\tilde{\mathcal{g}}}_k{\nu }_n(z_k), {\tilde{\vartheta }}_n({\tilde{z}}_{ℂ})={\tilde{\mathcal{g}}}_{ℂ}{\tilde{\nu }}_n({\tilde{z}}_{ℂ}),$$

(58)

for the complex constants ${\mathcal{g}}_k$ and ${\tilde{\mathcal{g}}}_{ℂ}$. In terms of the Jost functions, Equation (58) can be written as

$${\mathcal{A}}_n(z_k)={\mathcal{g}}_k{z}_k^{-2n}{\mathcal{B}}_n(z_k), {\tilde{\mathcal{A}}}_n({\tilde{z}}_k)={\tilde{\mathcal{g}}}_k{\tilde{z}}_k^{2n}{\tilde{\mathcal{B}}}_n({\tilde{z}}_k),$$

(59)

which hold if, and only if, $z_k$ and ${\tilde{z}}_{ℂ}$ are eigenvalues. Note that the boundary conditions, (28) and (29), together with Equation (58), imply that ${\vartheta }_n(z_k)$, ${\tilde{\vartheta }}_n({\tilde{z}}_{ℂ})\to 0$ for $\left|n\right|\to \infty$. Let us assume $\mathcal{f}(z)$ has $\mathcal{K}$ simple zeros, ${\left\{z_k:\left|z_k\right|>1\right\}}_{k=1}^{\mathcal{K}}$, and $\tilde{\mathcal{f}}(z)$ has $\mathcal{K}$ simple zeros at the points ${\left\{{\tilde{z}}_k:\left|{\tilde{z}}_k\right|<1\right\}}_{k=1}^{\tilde{\mathcal{K}}}$. Then, we can obtain

$$\mathrm{Res}({\nu }_n;z_k)={\displaystyle \frac{{\mathcal{A}}_n(z_k)}{{\mathcal{f}}^{\prime }(z_k)}}={\displaystyle \frac{{\mathcal{g}}_k}{{\mathcal{f}}^{\prime }(z_k)}}{z}_k^{-2n}{\mathcal{B}}_n(z_k)=z_k^{-2n}{\Re }_k{\mathcal{B}}_n(z_k),$$

(60)

$$\mathrm{Res}({\tilde{\nu }}_n;{\tilde{z}}_{ℂ})={\displaystyle \frac{{\tilde{\mathcal{A}}}_n({\tilde{z}}_{ℂ})}{{\tilde{\mathcal{f}}}^{\prime }({\tilde{z}}_{ℂ})}}={\displaystyle \frac{{\tilde{\mathcal{g}}}_{ℂ}}{\widetilde{{\mathcal{f}}^{\prime }}({\tilde{z}}_{ℂ})}}{\tilde{z}}_{ℂ}^{2n}{\tilde{\mathcal{B}}}_n({\tilde{z}}_{ℂ})={\tilde{z}}_{ℂ}^{2n}{\tilde{\Re }}_{ℂ}{\tilde{\mathcal{B}}}_n({\tilde{z}}_{ℂ}).$$

(61)

If the potentials $q_n$ and $r_n$ decay sufficiently rapidly as $\left|n\right|\to \infty$, such that ${\mathcal{g}}_k$ and ${\tilde{\mathcal{g}}}_{ℂ}$ can be extended beyond the unit circle in correspondence with the discrete eigenvalues $z_k$ and ${\tilde{z}}_{ℂ}$, respectively, then the normalization constants are simply given by

$${\Re }_k={\displaystyle \frac{\mathcal{g}(z_k)}{{\mathcal{f}}^{\prime }(z_k)}}, {\tilde{\Re }}_{ℂ}={\displaystyle \frac{\tilde{\mathcal{g}}(z_{ℂ})}{\widetilde{{\mathcal{f}}^{\prime }}({\tilde{z}}_{ℂ})}}.$$

(62)

3.4. Symmetries and Trace Formula

First, we observe that the expansions of $\mathcal{f}(z)$ and $\tilde{\mathcal{f}}(z)$ include only even powers of $z^{-1}$ and $z$, respectively. Consequently, if $z_k$ is a root of $\mathcal{f}(z)$, then $-z_k$ must also be a root, and the same applies to $\tilde{\mathcal{f}}(z)$. Thus, the eigenvalues manifest in the pairs $\pm z_k$ and ${\Re }_k^{\pm }$. We denote the normalization constants associated with the paired poles, $\pm z_k$, as ${\Re }_k^{\pm }$.

Similarly, we denote the constants, ${\mathcal{f}}_k^{\pm }$, in Equation (59) related to $\pm z_k$. Given the expansions

$${\mathcal{A}}_n(z)=\left(\begin{array}{c}1+O(z^{-2}, \mathrm{even})\\ z^{-1}{r}_{n-1}+O(z^{-3}, \mathrm{odd})\end{array}\right), {\mathcal{B}}_n(z)=\left(\begin{array}{c}-z^{-1}{\Im }_n^{-1}{q}_n+O(z^{-3}, \mathrm{odd})\\ {\Im }_n^{-1}+O(z^{-2} \mathrm{even}),\end{array}\right),$$

we conclude that ${\mathcal{g}}_k^{-}=-{\mathcal{g}}_k^{+}$. On the other hand, $\mathcal{f}(z)$ is even, so ${\mathcal{f}}^{\prime }(z)$ is an odd function of $z$. Thus, we have

$${\Re }_k^{-}={\displaystyle \frac{{\mathcal{g}}_k^{-}}{{\mathcal{f}}^{\prime }(-z_k)}}={\displaystyle \frac{-{\mathcal{g}}_k^{+}}{-{\mathcal{f}}^{\prime }(z_k)}}={\displaystyle \frac{{\mathcal{g}}_k^{+}}{{\mathcal{f}}^{\prime }(z_k)}}={\Re }_k^{+}.$$

(63)

Given that the two normalization constants associated with $\pm z_k$ are identical, we shall henceforth omit the superscript $\pm$ from the normalization constants and collectively refer to both constants as ${\Re }_k$. In a similar vein, it can be demonstrated that

$${\tilde{\Re }}_{ℂ}^{-}={\tilde{\Re }}_{ℂ}^{+}={\tilde{\Re }}_{ℂ},$$

(64)

for the normalization constants, ${\tilde{\Re }}_{ℂ}^{\pm }$, that are intricately linked to $\pm {\tilde{z}}_{ℂ}$. Furthermore, we also have

$$\mathcal{H}(-z)=-\mathcal{H}(z), \tilde{\mathcal{H}}(-z)=-\tilde{\mathcal{H}}(z).$$

(65)

The eigenvalues ${\left\{\pm z_k\right\}}_{k=1}^{\mathcal{K}}$ and ${\left\{\pm {\tilde{z}}_k\right\}}_{k=1}^{\tilde{\mathcal{K}}}$, along with the corresponding normalization constants, ${\left\{{\Re }_k\right\}}_{k=1}^{\mathcal{K}}$ and ${\left\{{\tilde{\Re }}_k\right\}}_{k=1}^{\tilde{\mathcal{K}}}$, in conjunction with the reflection coefficients (55), collectively form the comprehensive set of scattering data, $\mathcal{S}(z)$.

Indeed, a meticulous computation reveals that Green’s functions, (35) and (36), fulfill the specified identities:

$${\widehat{\mathcal{P}}}_{\mp }({\mathcal{G}}_n^{ℂ}(1/z^{\ast }))*{{\widehat{\mathcal{P}}}_{\mp }}^{-1}={\tilde{\mathcal{G}}}_n^{ℂ}(z), {\widehat{\mathcal{P}}}_{\mp }({\mathcal{G}}_n^{\mathbb{Q}}(1/z^{\ast }))*{{\widehat{\mathcal{P}}}_{\mp }}^{-1}={\tilde{\mathcal{G}}}_n^{\mathbb{Q}}(z),$$

(66)

where

$${\widehat{\mathcal{P}}}_{\mp }=\left(\begin{array}{cc}0& \mp 1\\ 1& 0\end{array}\right).$$

(67)

Moreover, under the symmetry reductions, $r_n=\mp q_n^{\ast }$, the matrix potential, ${\tilde{T}}_n(z)$, in Equation (23) is such that

$${\widehat{\mathcal{P}}}_{\mp }{\tilde{T}}_n^{\ast }{\widehat{\mathcal{P}}}_{\mp }^{-1}={\widehat{T}}_n.$$

(68)

From Equations (67) and (68), it can be deduced that ${\widehat{\mathcal{P}}}_{\mp }{\mathcal{A}}_n^{\ast }(1/z^{\ast })$ and ${\widehat{\mathcal{P}}}_{\mp }{\mathcal{B}}_n^{\ast }(1/z^{\ast })$ adhere to the same summation relations as ${\tilde{\mathcal{A}}}_n(z)$ and $\mp {\tilde{\mathcal{B}}}_n(z)$, specifically articulated in Equations (33) and (34). Consequently, should these equations possess unique solutions, we are led to uncover the underlying symmetries:

$${\tilde{\mathcal{A}}}_n(z)={\widehat{\mathcal{P}}}_{\mp }{\mathcal{A}}_n^{\ast }(1/z^{\ast }), {\tilde{\mathcal{B}}}_n(z)=\mp {\widehat{\mathcal{P}}}_{\mp }{\mathcal{B}}_n^{\ast }(1/z^{\ast }).$$

(69)

If the potentials exhibit the symmetries of $r_n=\mp q_n$, then it follows that the scattering coefficients will also adhere to the inherent symmetries:

$$\tilde{\mathcal{f}}(z)={\mathcal{f}}^{\ast }(1/z^{\ast }), \tilde{\mathcal{H}}(z)=\mp {\mathcal{H}}^{\ast }(1/z^{\ast }).$$

(70)

It follows that ${\tilde{z}}_k=1/z_k^{\ast }$ constitutes an eigenvalue under the condition that $\left|{\tilde{z}}_k\right|<1$ holds true if, and only if, ${\mathit{z}}_{\mathit{k}}$ represents an eigenvalue such that $\left|z_k\right|>1$ is satisfied. Consequently, $\mathcal{K}=\tilde{\mathcal{K}}$ emerges; specifically, the count of eigenvalues residing within the unit circle corresponds precisely to the number of those situated beyond it. Moreover, these eigenvalues manifest in elegant quartets:

$${\left\{\pm z_k, \pm 1/z_k^{\ast }\right\}}_{k=1}^{\mathcal{K}}.$$

(71)

Furthermore, the normalization constants corresponding to these paired eigenvalues exhibit remarkable symmetries:

$${\tilde{\Re }}_k=\pm {(z_k^{\ast })}^{-2}{\Re }_k^{\ast }.$$

(72)

We assume that $\mathcal{f}(z)$ and $\tilde{\mathcal{f}}(z)$ have the simple zeros, ${\left\{\pm z_k: \left|z_k\right|>1\right\}}_{k=1}^{\mathcal{K}}$ and ${\left\{\pm {\tilde{z}}_k: \left|{\tilde{z}}_k\right|<1\right\}}_{k=1}^{\tilde{\mathcal{K}}}$, respectively. Moreover, we define

$$\mathcal{Q}(z)={\displaystyle {\prod }_{i=1}^{\mathcal{K}}\frac{z^2-{(z_i^{\ast })}^{-2}}{z^2-z_i^2}}\mathcal{f}(z), \tilde{\mathcal{Q}}(z)={\displaystyle {\prod }_{i=1}^{\tilde{\mathcal{K}}}\frac{z^2-{({\tilde{z}}_i^{\ast })}^{-2}}{z^2-{\tilde{z}}_i^2}}\tilde{\mathcal{f}}(z).$$

(73)

According to these definitions, the function, $\mathcal{Q}(z)$, is analytic in the exterior of the unit circle, where it possesses no zeros. In contrast, $\tilde{\mathcal{Q}}(z)$ is analytic within the confines of the unit circle and similarly lacks any zeros; furthermore, $\mathcal{Q}(z)\to 1$ behaves analogously to $\left|z\right|\to \infty$. Consequently, considering that both $\mathcal{f}$ and $\tilde{\mathcal{f}}$ are even functions of $z$, we arrive at the following conclusions:

$$\log \mathcal{Q}(z)=-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log \mathcal{Q}(\wp )}{{\wp }^2-z^2}}d\wp , {\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log \tilde{\mathcal{Q}}(\wp )}{{\wp }^2-z^2}}d\wp =0, \left|z\right|>1,$$

(74)

$$\log \tilde{\mathcal{Q}}(z)=-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log \tilde{\mathcal{Q}}(\wp )}{{\wp }^2-z^2}}d\wp , {\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log \mathcal{Q}(\wp )}{{\wp }^2-z^2}}d\wp =0, \left|z\right|>1.$$

(75)

Subtracting the above equations from one another and using Equation (73) yields

$$\log \mathcal{Q}(z)={\displaystyle {\sum }_{i=1}^{\mathcal{K}}\log \left(\frac{z^2-z_i^2}{z^2-{(z_i^{\ast })}^{-2}}\right)}-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log (\mathcal{Q}(\wp )\tilde{\mathcal{Q}}(\wp ))}{{\wp }^2-z^2}}d\wp , \left|z\right|>1,$$

(76)

$$\log \tilde{\mathcal{Q}}(z)={\displaystyle {\sum }_{i=1}^{\tilde{\mathcal{K}}}\log \left(\frac{z^2-{\tilde{z}}_m^2}{z^2-{({\tilde{z}}_i^{\ast })}^{-2}}\right)}+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log (\mathcal{Q}(\wp )\tilde{\mathcal{Q}}(\wp ))}{{\wp }^2-z^2}}d\wp , \left|z\right|<1.$$

(77)

This allows one to recover $\mathcal{Q}(z)$ and $\tilde{\mathcal{Q}}(z)$ from knowledge of ${\left\{\pm z_k: \left|z_k\right|>1\right\}}_{k=1}^{\mathcal{K}}$, ${\left\{\pm {\tilde{z}}_k:\left|{\tilde{z}}_k\right|<1\right\}}_{k=1}^{\tilde{\mathcal{K}}}$, and $\mathcal{f}(\wp )\tilde{\mathcal{f}}(\wp )={\Im }_{-\infty }{(1-\mathcal{H}(\wp )\tilde{\mathcal{H}}(\wp ))}^{-1}$ for $\left|\wp \right|=1$.

Note that if $r_n=-q_n^{\ast }$, then it follows that $\mathcal{f}(\wp )\tilde{\mathcal{f}}(\wp )={\Im }_{-\infty }{(1+{\left|\mathcal{H}(\wp )\right|}^2)}^{-1}$ for $\left|\wp \right|=1$, and consequently, Equation (76) can be written as

$$\log \mathcal{Q}(z)={\displaystyle {\sum }_{i=1}^{\mathcal{K}}\log \left(\frac{z^2-z_i^2}{z^2-{(z_i^{\ast })}^{-2}}\right)}-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\wp \log (1+{\left|\mathcal{H}(\wp )\right|}^2)}{{\wp }^2-z^2}}d\wp , \left|z\right|>1.$$

(78)

4. Inverse Scattering Problem of the vcfISDNLS Equation

4.1. Boundary Conditions and Residues

The inverse problem entails the reconstruction of potentials based on the scattering data: $\left\{\mathcal{H}(\wp ),\tilde{\mathcal{H}}(\wp ) for \left|\wp \right|=1\right\}\cup {\left\{\pm z_k: \left|z_k\right|>1\right\}}_{k=1}^{\mathcal{K}}\cup {\left\{\pm {\tilde{z}}_k: \left|{\tilde{z}}_k\right|<1\right\}}_{k=1}^{\tilde{\mathcal{K}}}$. In the preceding section, we demonstrated that the functions ${\mathcal{B}}_n(z)$ and $\widetilde{{\mathcal{B}}_n}(z)$ exist and are analytic within the domains $\left|z\right|>1$ and $\left|z\right|<1$, respectively, provided ${‖q‖}_1$, ${‖r‖}_1<1$ holds true. Additionally, it is imperative to acquire information regarding the residues of the poles. Moreover, to uniquely determine the solution, it is essential to delineate appropriate boundary conditions.

Note that the functions ${\nu }_n(z)$ and ${\mathcal{B}}_n(z)$ are meromorphic in region $\left|z\right|>1$ and have the limits:

$${\mathcal{B}}_n(z)\to \left(\begin{array}{c}1\\ {\Im }_n^{-1}\end{array}\right),{\nu }_n(z)\to \left(\begin{array}{c}1\\ 0\end{array}\right), \left|z\right|\to \infty ,$$

(79)

where ${\Im }_n={\displaystyle {\prod }_{m=n}^{+\infty }(1-r_m{q}_m)}$. The boundary condition for ${\mathcal{B}}_n(z)$ depends on $q_m$ and $r_m$ for all $m\ge n$. However, $q_n$ and $r_n$ are unknowns in the inverse problem. To remove this dependence, we introduce the functions

$${{\mathcal{B}}_n}^{\prime }=\left(\begin{array}{cc}1& 0\\ 0& {\Im }_n\end{array}\right){\mathcal{B}}_n=\left(\begin{array}{c}-z^{-1}{\Im }_n^{-1}{q}_n\\ 1\end{array}\right)+O(z^{-2}), \left|z\right|\to \infty ,$$

(80)

$${{\nu }_n}^{\prime }=\left(\begin{array}{cc}1& 0\\ 0& {\Im }_n\end{array}\right){\nu }_n=\left(\begin{array}{c}1\\ z^{-1}{\Im }_n{r}_{n-1}\end{array}\right)+O(z^{-2}), \left|z\right|\to \infty ,$$

(81)

$${{\tilde{\mathcal{B}}}_n}^{\prime }=\left(\begin{array}{cc}1& 0\\ 0& {\Im }_n\end{array}\right){\mathcal{B}}_n=\left(\begin{array}{c}{\Im }_n^{-1}\\ -z{r}_n\end{array}\right)+O(z^2), z\to 0,$$

(82)

$${{\tilde{\nu }}_n}^{\prime }=\left(\begin{array}{cc}1& 0\\ 0& {\Im }_n\end{array}\right){\tilde{\nu }}_n=\left(\begin{array}{c}z{q}_{n-1}\\ {\Im }_n\end{array}\right)+O(z^2), z\to 0.$$

(83)

These modified functions also satisfy the jump conditions, (56) and (57), on $\left|z\right|=1$; that is,

$${{\tilde{\nu }}_n}^{\prime }(z)-\tilde{{{\mathcal{B}}_n}^{\prime }}(z)=z^{-2n}\mathcal{H}(z){{\mathcal{B}}_n}^{\prime }(z),$$

(84)

$${{\tilde{\nu }}_n}^{\prime }(z)-{{\mathcal{B}}_n}^{\prime }(z)=z^{2n}\tilde{\mathcal{H}}(z)\tilde{{{\mathcal{B}}_n}^{\prime }}(z).$$

(85)

Moreover, the poles of ${{\tilde{\nu }}_n}^{\prime }(z)$ and ${{\tilde{\nu }}_n}^{\prime }(z)$ are the same as the poles of ${\nu }_n(z)$ and ${\tilde{\nu }}_n(z)$, respectively, and the residues of these poles are determined by the relations

$$\mathrm{Res}({{\tilde{\nu }}_n}^{\prime };z_k)=z_k^{-2n}{\Re }_k{{\mathcal{B}}_n}^{\prime }(z_k), \mathrm{Res}({{\tilde{\nu }}_n}^{\prime };{\tilde{z}}_k)={\tilde{z}}_k^{2n}{\tilde{\Re }}_k{{\tilde{\mathcal{B}}}_n}^{\prime }({\tilde{z}}_k).$$

(86)

4.2. Cases of No Poles and Poles

Let us first delve into the scenario where discrete eigenvalues are absent, meaning that matrices ${{\tilde{\nu }}_n}^{\prime }(z)$ and ${\tilde{\nu }}_n(z)$ exhibit no poles. To facilitate our analysis, we shall introduce 2 × 2 matrices:

$${\mathcal{m}}_n(z)=({{\tilde{\nu }}_n}^{\prime }(z),{{\mathcal{B}}_n}^{\prime }(z)), {\tilde{\mathcal{m}}}_n(z)=({{\tilde{\mathcal{B}}}_n}^{\prime }(z),{{\tilde{\nu }}_n}^{\prime }(z)),$$

(87)

with ${\mathcal{m}}_n(z)$ being analytical outside the unit circle, $\left|z\right|=1$, and ${\tilde{\mathcal{m}}}_n(z)$ being analytical inside the same unit circle.

We can write the jump conditions, (84) and (85), as

$${\mathcal{m}}_n(z)-{\tilde{\mathcal{m}}}_n(z)={\tilde{\mathcal{m}}}_n(z){\mathcal{W}}_n(z), \left|z\right|=1,$$

(88)

where

$${\mathcal{W}}_n(z)=\left(\begin{array}{cc}-\mathcal{H}(z)\tilde{\mathcal{H}}(z)& -z^{2n}\tilde{\mathcal{H}}(z)\\ z^{-2n}\mathcal{H}(z)& 0\end{array}\right),$$

(89)

and

$${\mathcal{m}}_n(z)\to I, \left|z\right|\to \infty .$$

(90)

Then, we consider the integral operators,

$$\tilde{\mathcal{T}}(\mathcal{h})(z)=\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\mathcal{h}(\wp )}{\wp -\zeta }}d\wp ,$$

(91)

$$\mathcal{T}(\mathcal{h})(z)=\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|>1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{\mathcal{h}(\wp )}{\wp -\zeta }}d\wp ,$$

(92)

defined for $\left|z\right|>1$ and $\left|z\right|<1$, respectively, for any function, $\mathcal{h}(\wp )$, continuous on $\left|\wp \right|=1$. Applying $\tilde{\mathcal{T}}$ to both sides of Equation (88) yields

$${\tilde{\mathcal{m}}}_n(z)=I-\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{{\tilde{\mathcal{m}}}_n(\wp ){\mathcal{W}}_n(\wp )}{\wp -\zeta }}d\wp ,$$

(93)

which, in theory, provides the means to ascertain ${\tilde{\mathcal{m}}}_n(z)$. In its component form, Equation (93) produces

$${{\tilde{\mathcal{B}}}_n}^{\prime }(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)-\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\mathcal{H}(\wp ){{\tilde{\mathcal{V}}}_n}^{\prime }(\wp )-\mathcal{H}(\wp )\tilde{\mathcal{H}}(\wp ){{\tilde{\mathcal{B}}}_n}^{\prime }(\wp )}{\wp -\zeta }}d\wp ,$$

(94)

$${{\tilde{\nu }}_n}^{\prime }(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)+\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{{\wp }^{2n}\tilde{\mathcal{H}}(\wp ){{\tilde{\mathcal{B}}}_n}^{\prime }(\wp )}{\wp -\zeta }}d\wp .$$

(95)

Similarly, by employing the external projector $\mathcal{T}$ on both sides of Equations (84) and (85), we derive the following:

$${{\mathcal{B}}_n}^{\prime }(z)=\left(\begin{array}{c}0\\ 1\end{array}\right)+\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|>1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{{\wp }^{2n}\tilde{\mathcal{H}}(\wp ){{\tilde{\mathcal{B}}}_n}^{\prime }(\wp )}{\wp -\zeta }}d\wp ,$$

(96)

$${{\tilde{\nu }}_n}^{\prime }(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)-\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\mathcal{H}(\wp ){{\mathcal{B}}_n}^{\prime }(\wp )}{\wp -\zeta }}d\wp ,$$

(97)

$${\tilde{\mathcal{m}}}_n(z)=I-{\displaystyle \frac{z}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{-2}}{\tilde{\mathcal{m}}}_n(\wp ){\mathcal{W}}_n(\wp )d\wp +O(z^{-2}).$$

(98)

Thus, we obtain

$$q_n={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{2n}\tilde{\mathcal{H}}(\wp ){\tilde{\mathcal{B}}}_{n+1}^{\prime \left(1\right)}(\wp )}d\wp ,$$

(99)

$$r_n={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{-2(n+1)}\mathcal{H}(\wp ){{\tilde{\nu }}_n}^{\prime (2)}(\wp )-{\wp }^{-2}\mathcal{H}(\wp )\tilde{\mathcal{H}}(\wp ){\tilde{\mathcal{B}}}_n^{\prime \left(2\right)}(\wp )}d\wp .$$

(100)

By leveraging the symmetrical relation (65) that exists between the reflection coefficients $\mathcal{H}$ and $\tilde{\mathcal{H}}$, we can express the potential as

$$q_n={\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{2n}{\mathcal{H}}^{\ast }(\wp ){\tilde{\mathcal{B}}}_{n+1}^{\prime \left(1\right)}(\wp )}d\wp .$$

(101)

The solution method requires an extra step if ${{\nu }_n}^{\prime }(z)$ and ${{\tilde{\nu }}_n}^{\prime }(z)$ have poles. We obtain

$${{\mathcal{B}}_n}^{\prime }(z)=\left(\begin{array}{c}1\\ 0\end{array}\right)+{\displaystyle {\sum }_{k=1}^{\mathcal{K}}{\Re }_k}{z}_k^{-2n}\left[{\displaystyle \frac{1}{z-z_k}}{{\mathcal{B}}_n}^{\prime }(z_k)+{\displaystyle \frac{1}{z+z_k}}{{\mathcal{B}}_n}^{\prime }(-z_k)\right]-\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\mathcal{H}(\wp ){{\mathcal{B}}_n}^{\prime }(\wp )}{\wp -\zeta }d\wp },$$

(102)

$${{\mathcal{B}}_n}^{\prime }=\left(\begin{array}{c}1\\ 0\end{array}\right)+{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_k}{\tilde{z}}_k^{-2n}\left[{\displaystyle \frac{1}{z-{\tilde{z}}_k}}\tilde{{{\mathcal{B}}_n}^{\prime }}(z_k)+{\displaystyle \frac{1}{z+{\tilde{z}}_k}}\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_k)\right]-\underset{\begin{array}{l}\zeta \to z\\ \left|\zeta \right|<1\end{array}}{\lim }{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\tilde{\mathcal{H}}(\wp )\tilde{{{\mathcal{B}}_n}^{\prime }}(\wp )}{\wp -\zeta }d\wp }.$$

(103)

This system is fundamentally reliant on the vectors ${\left\{{{\mathcal{B}}_n}^{\prime }(z_k),{{\mathcal{B}}_n}^{\prime }(-z_k)\right\}}_{k=1}^{\mathcal{K}}$ and ${\left\{\tilde{{{\mathcal{B}}_n}^{\prime }}({\tilde{z}}_k),\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_k)\right\}}_{k=1}^{\tilde{\mathcal{K}}}$. We derive the expressions for these vectors by meticulously evaluating Equation (102) at the designated points, $\pm {\tilde{z}}_k$, and Equation (103) at the specified points, $\pm z_k$. This process culminates in a sophisticated linear algebraic–integral framework, intricately woven from Equations (102) and (103), along with

$$\tilde{{{\mathcal{B}}_n}^{\prime }}({\tilde{z}}_k)=\left(\begin{array}{c}1\\ 0\end{array}\right)+{\displaystyle {\sum }_{i=1}^{\mathcal{K}}{\Re }_i}{z}_i^{-2n}\left[{\displaystyle \frac{1}{{\tilde{z}}_k-z_i}}{{\mathcal{B}}_n}^{\prime }(z_i)+{\displaystyle \frac{1}{{\tilde{z}}_k+z_i}}{{\mathcal{B}}_n}^{\prime }(-z_i)\right]-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\mathcal{H}(\wp ){{\mathcal{B}}_n}^{\prime }(\wp )}{\wp -{\tilde{z}}_k}d\wp },$$

(104)

$$\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_k)=\left(\begin{array}{c}1\\ 0\end{array}\right)-{\displaystyle {\sum }_{i=1}^{\mathcal{K}}{\Re }_i}{z}_i^{-2n}\left[{\displaystyle \frac{1}{{\tilde{z}}_k+z_i}}{{\mathcal{B}}_n}^{\prime }(z_i)+{\displaystyle \frac{1}{{\tilde{z}}_k-z_i}}{{\mathcal{B}}_n}^{\prime }(-z_i)\right]-{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\tilde{\mathcal{H}}(\wp ){{\mathcal{B}}_n}^{\prime }(\wp )}{\wp +{\tilde{z}}_k}d\wp },$$

(105)

$${{\mathcal{B}}_n}^{\prime }(z_k)=\left(\begin{array}{c}0\\ 1\end{array}\right)+{\displaystyle {\sum }_{i=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_i}{\tilde{z}}_i^{2n}\left[{\displaystyle \frac{1}{z_k-{\tilde{z}}_i}}\tilde{{{\mathcal{B}}_n}^{\prime }}({\tilde{z}}_i)+{\displaystyle \frac{1}{z_k+{\tilde{z}}_i}}\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_i)\right]+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{-2n}\tilde{\mathcal{H}}(\wp )\tilde{{{\mathcal{B}}_n}^{\prime }}(\wp )}{\wp -z_k}d\wp },$$

(106)

$${{\mathcal{B}}_n}^{\prime }(-z_k)=\left(\begin{array}{c}0\\ 1\end{array}\right)-{\displaystyle {\sum }_{i=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_i}{\tilde{z}}_i^{2n}\left[{\displaystyle \frac{1}{z_k+{\tilde{z}}_i}}\tilde{{{\mathcal{B}}_n}^{\prime }}({\tilde{z}}_i)+{\displaystyle \frac{1}{z_k-{\tilde{z}}_i}}\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_i)\right]+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{2n}\tilde{\mathcal{H}}(\wp )\tilde{{{\mathcal{B}}_n}^{\prime }}(\wp )}{\wp +z_k}d\wp }.$$

(107)

Instead, we apply $\tilde{\mathcal{T}}$ to both sides of Equation (85) to obtain the representation

$${{\tilde{\upsilon }}_n}^{\prime }(z)=\left(\begin{array}{c}0\\ 1\end{array}\right)-{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_k}{\tilde{z}}_k^{2n}\left[{\displaystyle \frac{1}{z-{\tilde{z}}_k}}\tilde{{{\mathcal{B}}_n}^{\prime }}({\tilde{z}}_k)+{\displaystyle \frac{1}{z+{\tilde{z}}_k}}\tilde{{{\mathcal{B}}_n}^{\prime }}(-{\tilde{z}}_k)\right]+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {∳}_{\left|\wp \right|=1}\frac{{\wp }^{2n}\tilde{\mathcal{H}}(\wp )\tilde{{{\mathcal{B}}_n}^{\prime }}(\wp )}{\wp -z}d\wp }.$$

(108)

By meticulously analyzing the power series expansions on the right-hand sides of Equations (102) and (108), in conjunction with their corresponding expansions presented, we arrive at the following conclusions:

$$r_n=2{\displaystyle {\sum }_{k=1}^{\mathcal{K}}{\Re }_k{z}_k^{-2(n+1)}}{{\mathcal{B}}_n}^{\prime (2)}(z_k)+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{-2(n+1)}\mathcal{H}(\wp ){{\mathcal{B}}_n}^{\prime (2)}(\wp )}d\wp ,$$

(109)

$$q_{n-1}=-2{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_k{\tilde{z}}_k^{2(n-1)}}{{\mathcal{B}}_n}^{\prime (1)}({\tilde{z}}_k)+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{2(n-1)}\tilde{\mathcal{H}}(\wp ){{\mathcal{B}}_n}^{\prime (1)}(\wp )}d\wp .$$

(110)

Note that from Equations (97) and (108) it also follows that

$${\Im }_n=1-2{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_k{\tilde{z}}_k^{2n-1}}{{\tilde{\mathcal{B}}}_n}^{\prime (2)}({\tilde{z}}_k)+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|\wp \right|=1}{\wp }^{2n-1}\tilde{\mathcal{H}}(\wp ){{\tilde{\mathcal{B}}}_n}^{\prime (2)}(\wp )}d\wp .$$

(111)

4.3. Reflectionless Potentials and GLM Equation

Similar to the continuous case, we can also achieve a reconstruction of the potentials utilizing the GLM integral equations. In fact, let us express the eigenfunctions ${\xi }_n$ and ${\tilde{\xi }}_n$ through triangular kernels:

$${\xi }_n(z)={\displaystyle {\sum }_{i=n}^{+\infty }{z}^{-i}}J(n,i), \left|z\right|>1,$$

(112)

$${\tilde{\xi }}_n(z)={\displaystyle {\sum }_{i=n}^{+\infty }{z}^{-i}}\tilde{J}(n,i), \left|z\right|<1,$$

(113)

where $J(n,i)={(J^{(1)}(n,i),J^{(2)}(n,i))}^T$ and $\tilde{J}(n,i)={({\tilde{J}}^{(1)}(n,i),{\tilde{J}}^{(2)}(n,i))}^T$, and with the triangular representations, (112) and (113), we obtain

$$\tilde{J}(n,m)+{\displaystyle {\sum }_{i=n}^{+\infty }J(n,i)H(m+i)}=\left(\begin{array}{c}1\\ 0\end{array}\right){\mathcal{s}}_{m,n}, m\ge n,$$

(114)

where

$$H(n)={\displaystyle {\sum }_{k=1}^{\mathcal{K}}{z}_k^{-n-1}}{\Re }_k+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|z\right|=1}{z}^{-n-1}\mathcal{H}(z)dz}.$$

(115)

Analogously, we also obtain

$$J(n,m)+{\displaystyle {\sum }_{k=n}^{+\infty }\tilde{J}(n,k)\tilde{H}(m+k)}=\left(\begin{array}{c}1\\ 0\end{array}\right){\mathcal{s}}_{m,n}, m\ge n,$$

(116)

where

$$\tilde{H}(n)=-{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{z}}_k^{n-1}}{\tilde{\Re }}_k+{\displaystyle \frac{1}{2\pi i}}{\displaystyle {\oint }_{\left|z\right|=1}{z}^{n-1}\tilde{\mathcal{H}}(z)dz}.$$

(117)

By comparing representations (112) and (113) for the eigenfunctions with their asymptotic behaviors, we can derive, while recalling Equation (22), a reconstruction of the potentials in terms of the kernels of the GLM equations, specifically,

$$J^{(1)}(n,n)={\tilde{J}}^{(2)}(n,n)=0, {\tilde{J}}^{(1)}(n,n)=J^{(2)}(n,n)={\Im }_n^{-1},$$

(118)

$$q_n=-{\displaystyle \frac{J^{(1)}(n,n+1)}{J^{(2)}(n,n)}}, r_n=-{\displaystyle \frac{{\tilde{J}}^{(2)}(n,n+1)}{{\tilde{J}}^{(1)}(n,n)}}.$$

(119)

For convenience, we introduce $\mathcal{k}(n,m)$ and $\tilde{\mathcal{k}}(n,m)$ such that

$$\mathcal{k}(n,n)=\left(\begin{array}{c}0\\ 1\end{array}\right), \tilde{\mathcal{k}}(n,n)=\left(\begin{array}{c}1\\ 0\end{array}\right),$$

(120)

and for $m>n$,

$$J(n,m)={\displaystyle {\prod }_{k=n}^{+\infty }(1-r_k{q}_k)}\mathcal{k}(n,m),$$

(121)

$$\tilde{J}(n,m)={\displaystyle {\prod }_{k=n}^{+\infty }(1-r_k{q}_k)}\tilde{\mathcal{k}}(n,m),$$

(122)

Then Equations (121) and (122) become

$$\tilde{\mathcal{k}}(n,m)+\left(\begin{array}{c}0\\ 1\end{array}\right)H(m+n)+{\displaystyle {\sum }_{k=n+1}^{+\infty }\mathcal{k}(n,k)}F(m+k)=0, m>n,$$

(123)

$$\mathcal{k}(n,m)+\left(\begin{array}{c}1\\ 0\end{array}\right)\tilde{H}(m+n)+{\displaystyle {\sum }_{k=n+1}^{+\infty }\tilde{\mathcal{k}}(n,k)}\tilde{H}(m+k)=0, m>n,$$

(124)

and the potentials are obtained from

$$q_n=-{\mathcal{k}}^{(1)}(n,n+1), r_n=-{\tilde{\mathcal{k}}}^{(2)}(n,n+1).$$

(125)

4.4. Time Evolution

We can derive the time evolution of the scattered data by using operator (5). When $n\to \pm \infty$, we assume that $q_n$, $r_n\to 0$; then, the asymptotic form of the time evolution Equation (5) is

$${\partial }_t{\kappa }_n=\left(\begin{array}{cc}-i\Lambda & 0\\ 0& i\Lambda \end{array}\right){\kappa }_n, n\to \pm \infty ,$$

(126)

where

$$\Lambda ={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z^2+z^{-2})]}^{(1+\delta )}}ds.$$

(127)

The system has linear combinations of solutions determined by the fixed boundary conditions of the Jost functions, and these solutions satisfy ${\kappa }_n^{+}={(e^{-i\Lambda },0)}^T$ and ${\kappa }_n^{-}={(0,e^{i\Lambda })}^T$, so we define the following functions:

$${\mathcal{Z}}_n(z,t)=e^{-i\Lambda }{\mathcal{A}}_n(z,t), {\tilde{\mathcal{Z}}}_n(z,t)=e^{i\Lambda }\widetilde{{\mathcal{A}}_n}(z,t),$$

(128)

$${\mathcal{R}}_n(z,t)=e^{i\Lambda }{\mathcal{B}}_n(z,t), {\tilde{\mathcal{R}}}_n(z,t)=e^{-i\Lambda }\widetilde{{\mathcal{B}}_n}(z,t).$$

(129)

To serve as solutions to the time-dependent equation, Equation (5), these time-dependent functions fulfill the following relations:

$${\mathcal{Z}}_n(z,t)=z^{-2n}{e}^{-2i\Lambda }\mathcal{g}(z,t){\mathcal{R}}_n(z,t)+\mathcal{f}(z,t){\tilde{\mathcal{R}}}_n(z,t),$$

(130)

$${\tilde{\mathcal{Z}}}_n(z,t)=z^{2n}{e}^{2i\Lambda }\tilde{\mathcal{g}}(z,t){\tilde{\mathcal{R}}}_n(z,t)+\tilde{\mathcal{f}}(z,t){\mathcal{R}}_n(z,t).$$

(131)

To find the expressions for the evolution of the scattering coefficients, we first differentiate Equations (130) and (131) with respect to $t$ and obtain

$${\partial }_t{\mathcal{Z}}_n(z,t)=z^{-2n}{e}^{-2i\Lambda }\left\{\mathcal{g}(z,t){\partial }_t{\mathcal{R}}_n(z,t)+[{\mathcal{g}}_t(z,t)-2i{\Lambda }_t\mathcal{g}(z,t)]{\mathcal{R}}_n(z,t)\right\}+{\mathcal{f}}_t(z,t){\tilde{\mathcal{R}}}_n(z,t)+\mathcal{f}(z,t){\partial }_t{\tilde{\mathcal{R}}}_n(z,t),$$

(132)

$${\partial }_t{\tilde{\mathcal{Z}}}_n(z,t)=z^{-2n}{e}^{-2i\Lambda }\left\{\tilde{\mathcal{g}}(z,t){\partial }_t{\tilde{\mathcal{R}}}_n(z,t)+[{\tilde{\mathcal{g}}}_t(z,t)-2i{\Lambda }_t\tilde{\mathcal{g}}(z,t)]{\tilde{\mathcal{R}}}_n(z,t)\right\}+{\tilde{\mathcal{f}}}_t(z,t){\mathcal{R}}_n(z,t)+\tilde{\mathcal{f}}(z,t){\partial }_t{\mathcal{R}}_n(z,t).$$

(133)

On the other hand, because the functions ${\mathcal{Z}}_n(z,t)$, ${\mathcal{R}}_n(z,t)$, ${\tilde{\mathcal{R}}}_n(z,t)$, and ${\tilde{\mathcal{Z}}}_n(z,t)$ satisfy Equation (5), we have

$${\partial }_t{\mathcal{Z}}_n(z,t)=z^{-2n}{e}^{-2i\Lambda }\mathcal{g}(z,t){\partial }_t{\mathcal{R}}_n(z,t)+\mathcal{f}(z,t){\partial }_t{\tilde{\mathcal{R}}}_n(z,t),$$

(134)

$${\partial }_t{\tilde{\mathcal{Z}}}_n(z,t)=z^{2n}{e}^{2i\Lambda }\tilde{\mathcal{g}}(z,t){\partial }_t{\tilde{\mathcal{R}}}_n(z,t)+\tilde{\mathcal{f}}(z,t){\mathcal{R}}_n(z,t).$$

(135)

Comparing Equations (128) and (129) with, respectively, Equations (138) and (139) and examining the asymptotes of these expressions as $n\to +\infty$ gets

$${\mathcal{g}}_t(z,t)=2i{\Lambda }_t\mathcal{g}(z,t), {\mathcal{f}}_t(z,t)=0,$$

(136)

$${\tilde{\mathcal{f}}}_t(z,t)=0, {\tilde{\mathcal{g}}}_t(z,t)=2i{\Lambda }_t\tilde{\mathcal{g}}(z,t),$$

(137)

and, therefore, we have

$$\mathcal{g}(z,t)=\mathcal{g}(z,0)e^{2i\Lambda }, \mathcal{f}(z,t)=\mathcal{f}(z,0),$$

(138)

$$\tilde{\mathcal{f}}(z,t)=\tilde{\mathcal{f}}(z,0), \tilde{\mathcal{g}}(z,t)=\tilde{\mathcal{g}}(z,0)e^{-2i\Lambda }.$$

(139)

The evolution of the reflection coefficients is thus given by

$$\mathcal{H}(z,t)=\mathcal{H}(z,0)e^{2i\Lambda }, \tilde{\mathcal{H}}(z,t)=\tilde{\mathcal{H}}(z,0)e^{-2i\Lambda }.$$

(140)

It is evident that the eigenvalues remain constant as the solution progresses. Not only is the number of eigenvalues fixed, but their positions are also invariant. Consequently, these eigenvalues represent time-independent discrete states within the evolution process. In contrast, the normalization constants do not maintain a fixed value. Their evolution can be derived in a similar manner and is expressed as follows:

$${\Re }_k(t)={\Re }_k(0)e^{2i{\Lambda }_k}, {\tilde{\Re }}_k(t)={\tilde{\Re }}_k(0)e^{-2i{\tilde{\Lambda }}_k},$$

(141)

where

$${\Lambda }_k={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_k^2+z_k^{-2})]}^{(1+\delta )}}ds, {\tilde{\Lambda }}_k={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)({\tilde{z}}_k^2+{\tilde{z}}_k^{-2})]}^{(1+\delta )}}ds.$$

(142)

4.5. Infinite Conservation Quantities

In order to obtain the conservation law of the vcfISDNLS Equation (1), we reconsider the following matrix,

$$S_n=\left(\begin{array}{cc}z& q_n\\ r_n& z^{-1}\end{array}\right),$$

(143)

which satisfies the semi-discrete zero-curvature equation:

$$S_{n,t}=T_{n+1}{S}_n-S_n{T}_n.$$

(144)

It is worth noting that $T_n$ here does not have its specific form; we only know its asymptotic form from Equation (126). In other words, we cannot use the Lax integrability when deriving the conservation law.

Here, we reintroduce the Jost functions from the previous section and reference Equations (19), (20), (53) and (54). When $n\to +\infty$, there are

$${\vartheta }_n\sim \mathcal{f}(z)z^n, {\tilde{\vartheta }}_n\sim \tilde{\mathcal{g}}(z)z^n,$$

(145)

and

$$\left(\begin{array}{c}{\vartheta }_{n+1}\\ {\tilde{\vartheta }}_{n+1}\end{array}\right)=S_n\left(\begin{array}{c}{\vartheta }_n\\ {\tilde{\vartheta }}_n\end{array}\right).$$

(146)

We, therefore, obtain the corresponding scattering equations from Equation (146):

$${\vartheta }_{n+1}=z{\vartheta }_n+q_n{\tilde{\vartheta }}_n,$$

(147)

$${\tilde{\vartheta }}_{n+1}=r_n{\vartheta }_n+{\displaystyle \frac{1}{z}}{\tilde{\vartheta }}_n.$$

(148)

Then, we define the ratio function:

$${\mathrm{\Gamma }}_n={\displaystyle \frac{{\tilde{\vartheta }}_n}{{\vartheta }_n}}.$$

(149)

Dividing Equations (147) and (148) by ${\vartheta }_n$ and simplifying them yields

$${\mathrm{\Gamma }}_{n+1}={\displaystyle \frac{r_n+\frac{1}{z}{\mathrm{\Gamma }}_n}{z+q_n{\mathrm{\Gamma }}_n}},$$

(150)

and at the same time, we can also obtain

$${\vartheta }_n={\vartheta }_{-\infty }{\displaystyle {\prod }_{\mathcal{m}=-\infty }^{n-1}(z+q_m{\mathrm{\Gamma }}_m)}.$$

(151)

Taking ${\vartheta }_{-\infty }=z^{-\infty }$ yields

$$\mathcal{f}(z)={\displaystyle {\prod }_{n=-\infty }^{\infty }(1+\frac{q_n{\mathrm{\Gamma }}_n}{z})}.$$

(152)

Then, we define the following equation:

$$\ln \mathcal{f}(z)={\displaystyle {\sum }_{n=-\infty }^{\infty }\frac{C_k}{z^k}}.$$

(153)

Since $\mathcal{f}(z)$ does not change with time, $C_k$ is a conserved quantity. Furthermore, due to Equation (152), it can be concluded that

$$C_k={\displaystyle {\sum }_{n=-\infty }^{\infty }\frac{{(-1)}^{k+1}}{k}}{(q_n{\mathrm{\Gamma }}_n)}^k.$$

(154)

From Equation (150), it can be recursively derived that

$${\mathrm{\Gamma }}_n={\displaystyle \frac{1}{z}}{r}_{n-1}+{\displaystyle \frac{1}{z^2}}(r_{n-2}-q_{n-1}{r}_{n-1}^2)+{\displaystyle \frac{1}{z^3}}[r_{n-3}-q_{n-1}{r}_{n-1}{r}_{n-2}-q_{n-2}{r}_{n-2}{r}_{n-1}+q_{n-1}^2{r}_{n-1}^3]+\mathrm{O}(z^{-4}).$$

(155)

Substituting $q_n{\mathrm{\Gamma }}_n$ and calculating $C_k$ yields the first conservation quantity,

$$C_1={\displaystyle {\sum }_{n=-\infty }^{\infty }{q}_n{r}_{n-1}},$$

(156)

the second conservation quantity,

$$C_2={\displaystyle {\sum }_{n=-\infty }^{\infty }\left[q_n{r}_{n-2}-\frac{1}{2}{(q_n{r}_{n-1})}^2\right]},$$

(157)

and the third conservation quantity,

$$C_3={\displaystyle {\sum }_{n=-\infty }^{\infty }[q_n{r}_{n-3}-q_n{r}_{n-1}{q}_{n-1}{r}_{n-2}-q_n{r}_{n-1}{q}_n{r}_{n-2}+\frac{1}{3}{(q_n{r}_{n-1})}^3]}.$$

(158)

Continuing the operation, we can obtain other conservation quantities for Equation (1) but only write out the first three exact expressions, (156)–(158), for convenience. We note that $\mathcal{f}(z)$ does not contain the time variable, while $\tilde{\mathcal{g}}(z)$ does. However, in the process of computation, $\tilde{\mathcal{g}}(z)$ is eliminated, and therefore, the coefficients $\alpha (t)$ and $\beta (t)$ and the fractional order, $\delta$, do not affect the expression of the conservation quantities.

5. Soliton Solutions

In the case where the scattering data comprise proper eigenvalues but $\mathcal{H}(z)=\tilde{\mathcal{H}}(z)=0$ on $\left|z\right|=1$, the algebraic–integral system, (104)–(107), reduces to the linear algebraic system. Moreover, the potentials are given by

$$q_{n-1}=-2{\displaystyle {\sum }_{k=1}^{\tilde{\mathcal{K}}}{\tilde{\Re }}_k{\tilde{z}}_k^{2(n-1)}}{\tilde{\mathcal{B}}}_n^{\prime (1)}({\tilde{z}}_k),$$

(159)

$$r_n=2{\displaystyle {\sum }_{k=1}^{\mathcal{K}}{\Re }_k{z}_k^{-2(n+1)}}{\tilde{\mathcal{B}}}_n^{\prime (2)}(z_k).$$

(160)

When $\tilde{\mathcal{K}}=\mathcal{K}=1$, the eigenvalues are $\left\{\pm z_1, \pm {\tilde{z}}_1\right\}$, where ${\tilde{z}}_1=1/z_1^{\ast }$ with $\left|z_1\right|>1$ and $\left|{\tilde{z}}_1\right|<1$; then, we can solve for ${\widetilde{{\mathcal{B}}_n}}^{\prime }$ and ${{\mathcal{B}}_n}^{\prime }$, obtaining, in particular,

$${\tilde{\mathcal{B}}}_n^{\prime (1)}({\tilde{z}}_1)={\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2(n-1)}{\tilde{z}}_1^{2n}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1},$$

(161)

$${\mathcal{B}}_n^{\prime (2)}(z_1)={\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2n}{\tilde{z}}_1^{2(n+1)}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}.$$

(162)

Then, it follows that

$$q_n=-{\displaystyle \frac{2{\aleph }_1{\tilde{z}}_1^{2(n+1)}}{1+4{\Re }_1{\aleph }_1{(z_1^2-{\tilde{z}}_1^2)}^{-2}{z}_1^{-2n}{\tilde{z}}_1^{2(n+2)}}},$$

(163)

$$r_n={\displaystyle \frac{2{\Re }_1{z}_1^{-2(n+1)}}{1+4{\Re }_1{\aleph }_1{(z_1^2-{\tilde{z}}_1^2)}^{-2}{z}_1^{-2n}{\tilde{z}}_1^{2(n+2)}}},$$

(164)

where we introduce the modified normalization constants

$${\aleph }_1={\tilde{z}}_1^{-2}{\tilde{\Re }}_1, {\Re }_1(t)={\Re }_1(0)e^{2i{\Lambda }_1}, {\tilde{\Re }}_1(t)={\tilde{\Re }}_1(0)e^{-2i{\tilde{\Lambda }}_1},$$

(165)

$${\Lambda }_1={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_1^2+z_1^{-2})]}^{(1+\delta )}}ds, {\tilde{\Lambda }}_1={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)({\tilde{z}}_1^2+{\tilde{z}}_1^{-2})]}^{(1+\delta )}}ds.$$

(166)

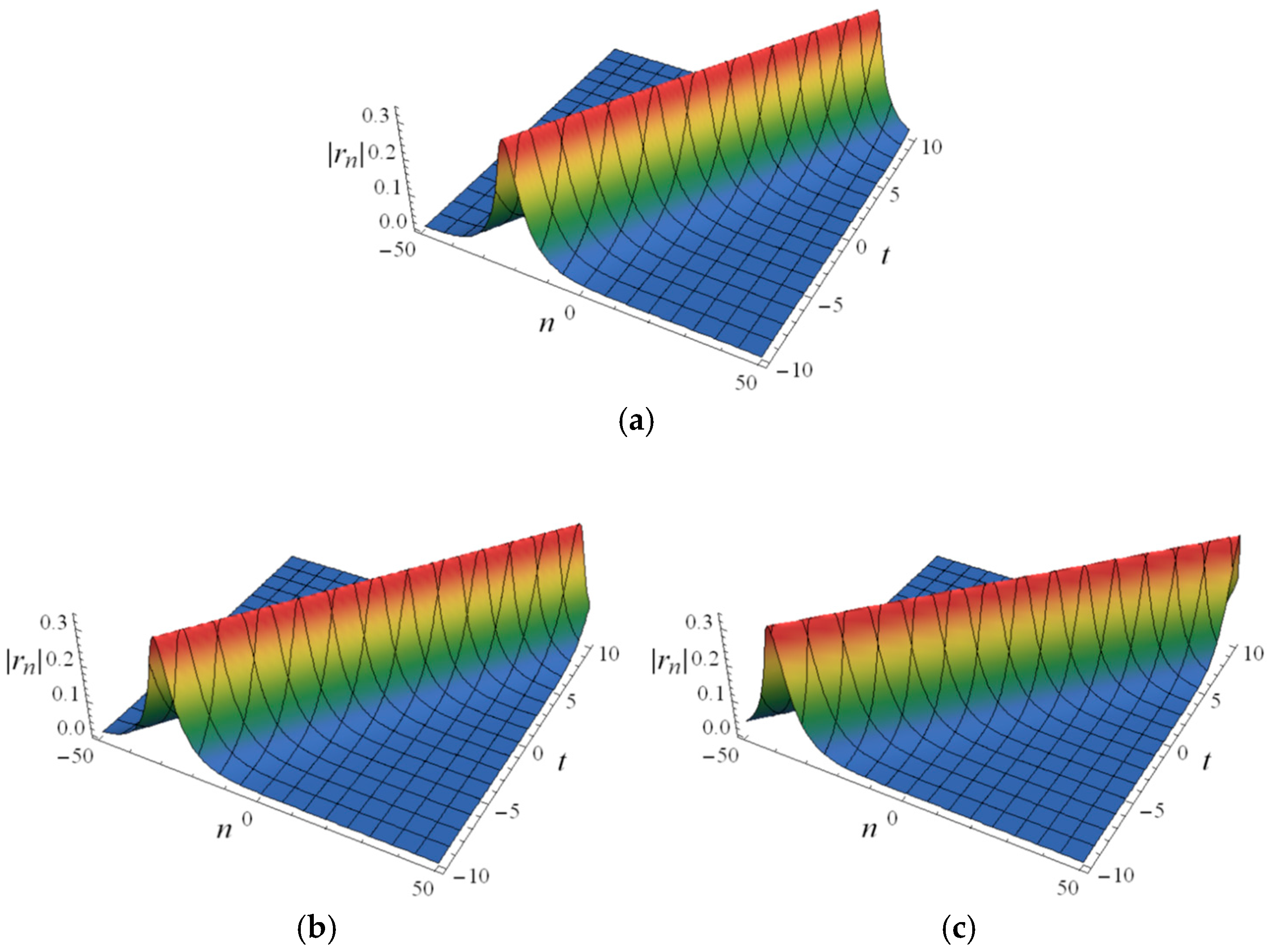
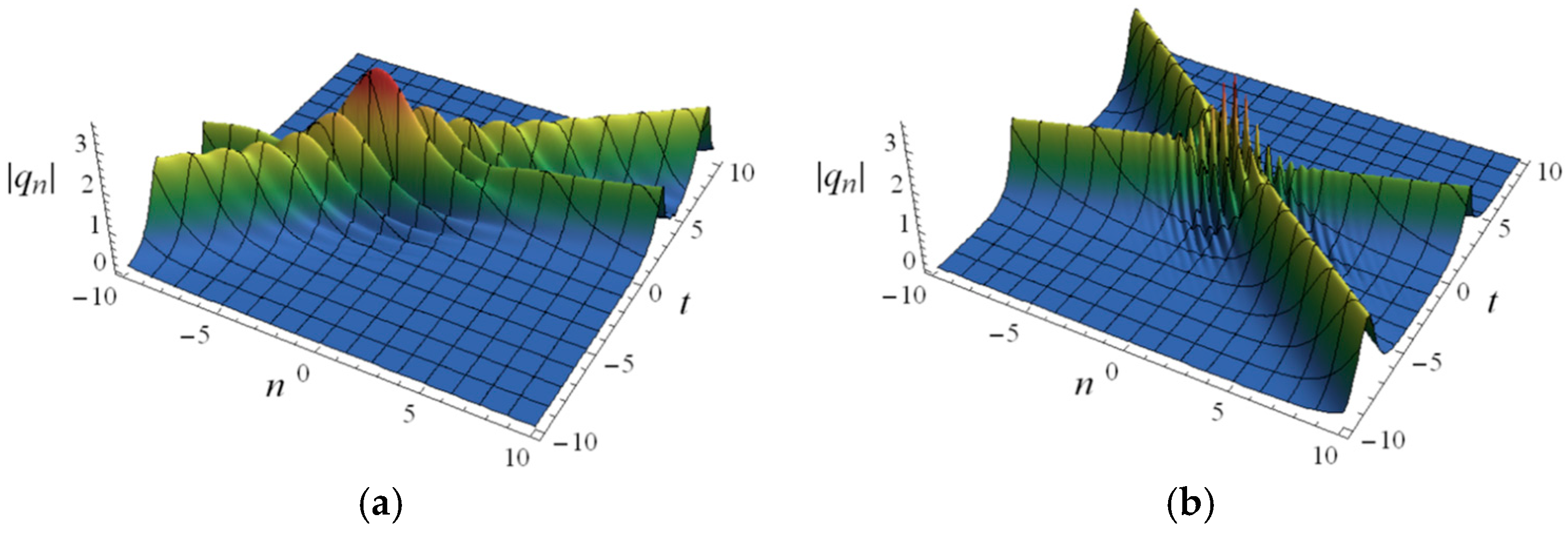
We simulate the spatiotemporal structures of the semi-discrete one-soliton solutions, (151) and (152), in Figure 1 and Figure 2 by taking different DRF orders, $\delta =0$, $\delta =0.1$, and $\delta =-0.1$, where $\alpha (t)=-1$, $\beta (t)=-2$, ${\Re }_1(0)={\tilde{\Re }}_1(0)=1$, and $z_1=e^{0.1+i}$, ${\tilde{z}}_1=e^{-0.1+i}$. It can be seen that the bell-solitons formed by solutions (151) and (152) propagate in the positive direction of the n-axis and have very similar shapes on the n-axis, and the amplitudes $\left|q_n\right|$ and $\left|r_n\right|$ of these bell-solitons are not significantly different. When other parameters remain unchanged and the value of $\delta$ changes from −0.1 to 0 and then to 0.1, we find that the shape of the bell-soliton remains unchanged, but the angle between the trajectory of the bell-soliton on the coordinate plane and the n-axis decreases, indicating that the distance traveled by the soliton per unit time increases; that is, the velocity increases.

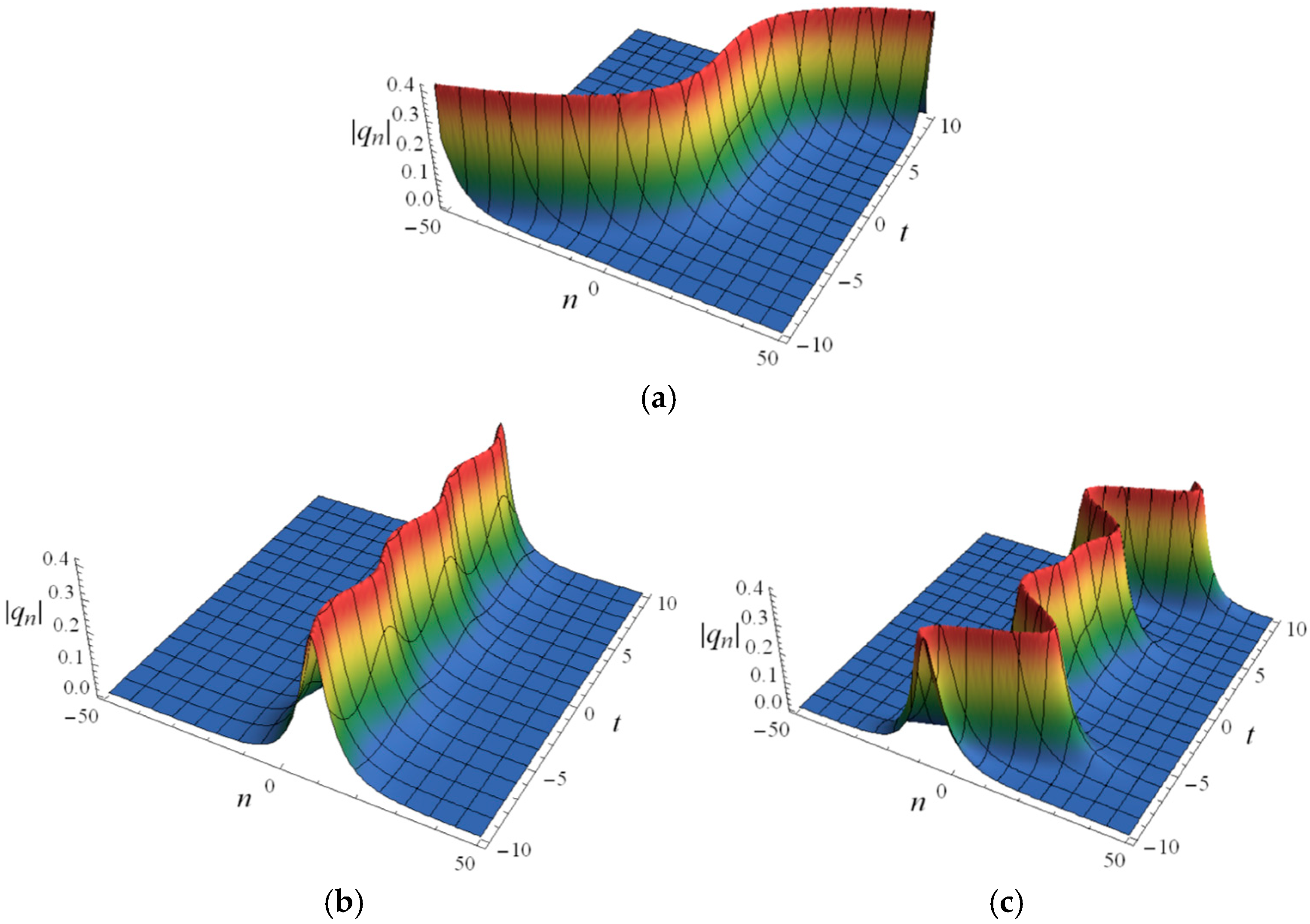
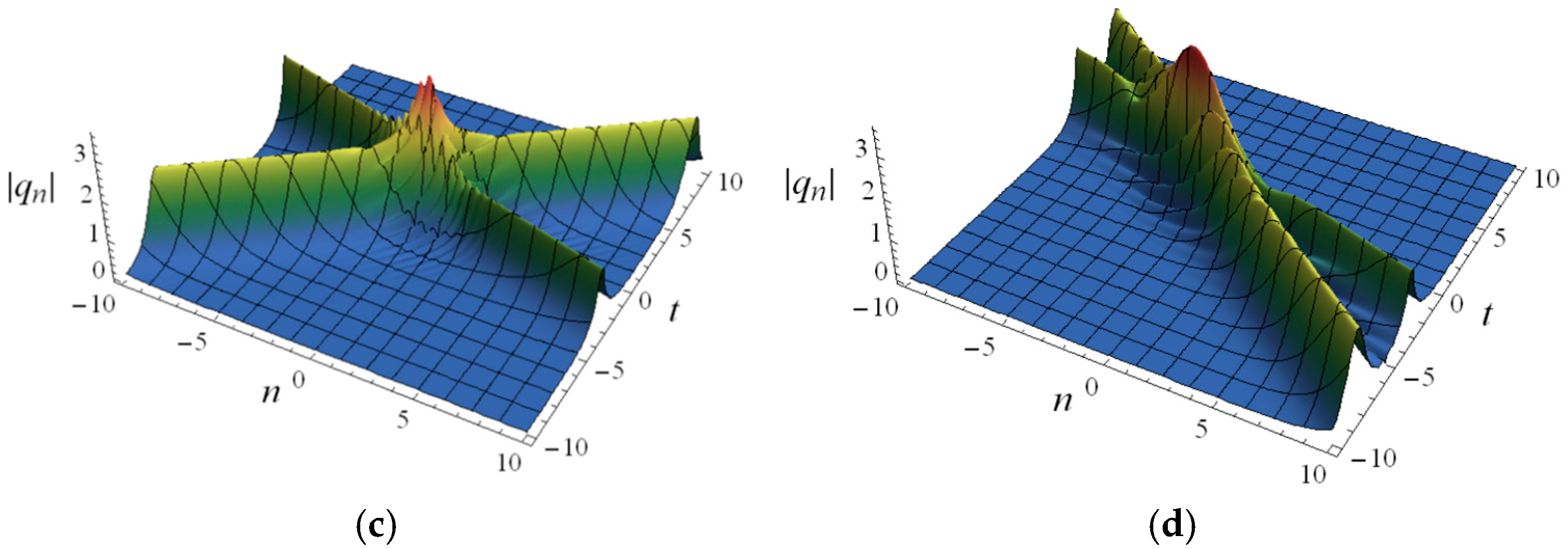
Figure 1 and Figure 2 illustrate that the value of fractional order, $\delta$, has no significant effect on the shape and amplitude of a soliton but has a visible impact on the soliton velocity (only in terms of quantity rather than direction). Figure 3 shows that although the coefficients $\alpha (t)$ and $\beta (t)$ do not have a significant effect on the shape and amplitude of the soliton, they can affect the soliton velocity in both quantity and direction. As a result, the soliton forms a curved plane trajectory, which is completely different from the straight plane trajectory formed when $\alpha (t)$ and $\beta (t)$ are constants (see Figure 1 and Figure 2). In the case where $\delta$ is zero, Figure 4 shows that $\alpha (t)$ and $\beta (t)$, with time, become factors that constrain soliton velocity, resulting in the formation of rich curved plane trajectory curves, some of which may also have periodicity. Figure 1, Figure 2, Figure 3 and Figure 4 indicate that $\alpha (t)$, $\beta (t)$, and $\delta$ can jointly control the velocity of the solitons together, including the quantity and direction of velocity, but changing them will not result in energy loss or diffusion of soliton propagation.

In fact, when the eigenvalues satisfy (i) the relation ${\tilde{z}}_1=1/z_1^{\ast }$, (ii) the product of the normalization constants ${\Re }_1$ and ${\aleph }_1$ are complex numbers, and (iii) the exponential forms $z_1=e^{{\gamma }_1-{\rho }_{1}i}$ with ${\gamma }_1,{\rho }_1\in ℝ$; thus, the solutions, (163) and (164), can be rewritten in the forms

$$q_n=\sinh (2{\gamma }_1)e^{2i\mathrm{Im}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_1^2+z_1^{-2})]}^{(1+\delta )}}ds-{\rho }_{1}n-i[\arg {\Re }_1(0)-\pi /2]}\mathrm{sech}\{2{\gamma }_1(n-n_0)-2\mathrm{Re}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_1^2+z_1^{-2})]}^{(1+\delta )}}ds\},$$

(167)

$$r_n=\sinh (2{\gamma }_1)e^{-2i\mathrm{Im}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_1^2+z_1^{-2})]}^{(1+\delta )}}ds+{\rho }_{1}n+i[\arg {\Re }_1(0)-\pi /2]}\mathrm{sech}\{2{\gamma }_1(n-n_0)-2\mathrm{Re}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_1^2+z_1^{-2})]}^{(1+\delta )}}ds\}.$$

(168)

Then, the velocity of the solitons formed by Equations (167) and (168) can be expressed mathematically as

$$v={\displaystyle \frac{\mathrm{Re}{[-2\alpha (t)+\beta (t)(z_1^2+z_1^{-2})]}^{(1+\delta )}}{{\gamma }_1}}.$$

(169)

This theoretically elucidates the dual effects on the velocity of solitons from the coefficients $\alpha (t)$ and $\beta (t)$ and the fractional order, $\delta$. Meanwhile, we can also see from Equations (167) and (168) that the amplitude of solitons is theoretically unaffected by the choice of $\alpha (t)$, $\beta (t)$, and $\delta$.

When $\tilde{\mathcal{K}}=\mathcal{K}=2$, the eigenvalues are $\left\{\pm z_1, \pm {\tilde{z}}_1, \pm z_2, \pm {\tilde{z}}_2\right\}$, where ${\tilde{z}}_1=1/z_1^{\ast }$, ${\tilde{z}}_2=1/z_2^{\ast }$ with $\left|z_1\right|$, $\left|z_2\right|>1$ and $\left|{\tilde{z}}_1\right|$, $\left|{\tilde{z}}_2\right|<1$; then, we can solve for ${\widetilde{{\mathcal{B}}_n}}^{\prime }$ and ${{\mathcal{B}}_n}^{\prime }$, obtaining, in particular,

$${\tilde{\mathcal{B}}}_n^{\prime (1)}({\tilde{z}}_2)=\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2(n-1)}{\tilde{z}}_1^{2n}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{(z_2^2-{\tilde{z}}_1^2)({\tilde{z}}_2^2-z_1^2)}}\right\}{\left[1+4{\Re }_2{\tilde{\Re }}_2{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{{({\tilde{z}}_2^2-z_2^2)}^2}}\right]}^{-1},$$

(170)

$${\mathcal{B}}_n^{\prime (2)}(z_2)=\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2n}{\tilde{z}}_1^{2(n+1)}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{({\tilde{z}}_2^2-z_1^2)(z_2^2-{\tilde{z}}_1^2)}}\right\}{\left[1+4{\Re }_2{\tilde{\Re }}_2{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{{({\tilde{z}}_2^2-z_2^2)}^2}}\right]}^{-1}.$$

(171)

Then, it follows that

$$q_n=-2\left[({\tilde{\Re }}_1{\tilde{z}}_1^{2n}){\tilde{\mathcal{B}}}_{n+1}^{\prime (1)}({\tilde{z}}_1)+({\tilde{\Re }}_2{\tilde{z}}_2^{2n}){\tilde{\mathcal{B}}}_{n+1}^{\prime (1)}({\tilde{z}}_2)\right],$$

(172)

$$r_n=2\left[{\Re }_1{z}_1^{-2(n+1)}{{\mathcal{B}}_n}^{\prime (2)}(z_1)+{\Re }_2{z}_2^{-2(n+1)}{{\mathcal{B}}_n}^{\prime (2)}(z_2)\right],$$

(173)

where we introduced the modified normalization constants,

$${\Re }_2(t)={\Re }_2(0)e^{2i{\Lambda }_2}, {\tilde{\Re }}_2(t)={\tilde{\Re }}_2(0)e^{-2i{\tilde{\Lambda }}_2},$$

(174)

$${\Lambda }_2={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_2^2+z_2^{-2})]}^{(1+\delta )}}ds, {\tilde{\Lambda }}_2={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)({\tilde{z}}_2^2+{\tilde{z}}_2^{-2})]}^{(1+\delta )}}ds.$$

(175)

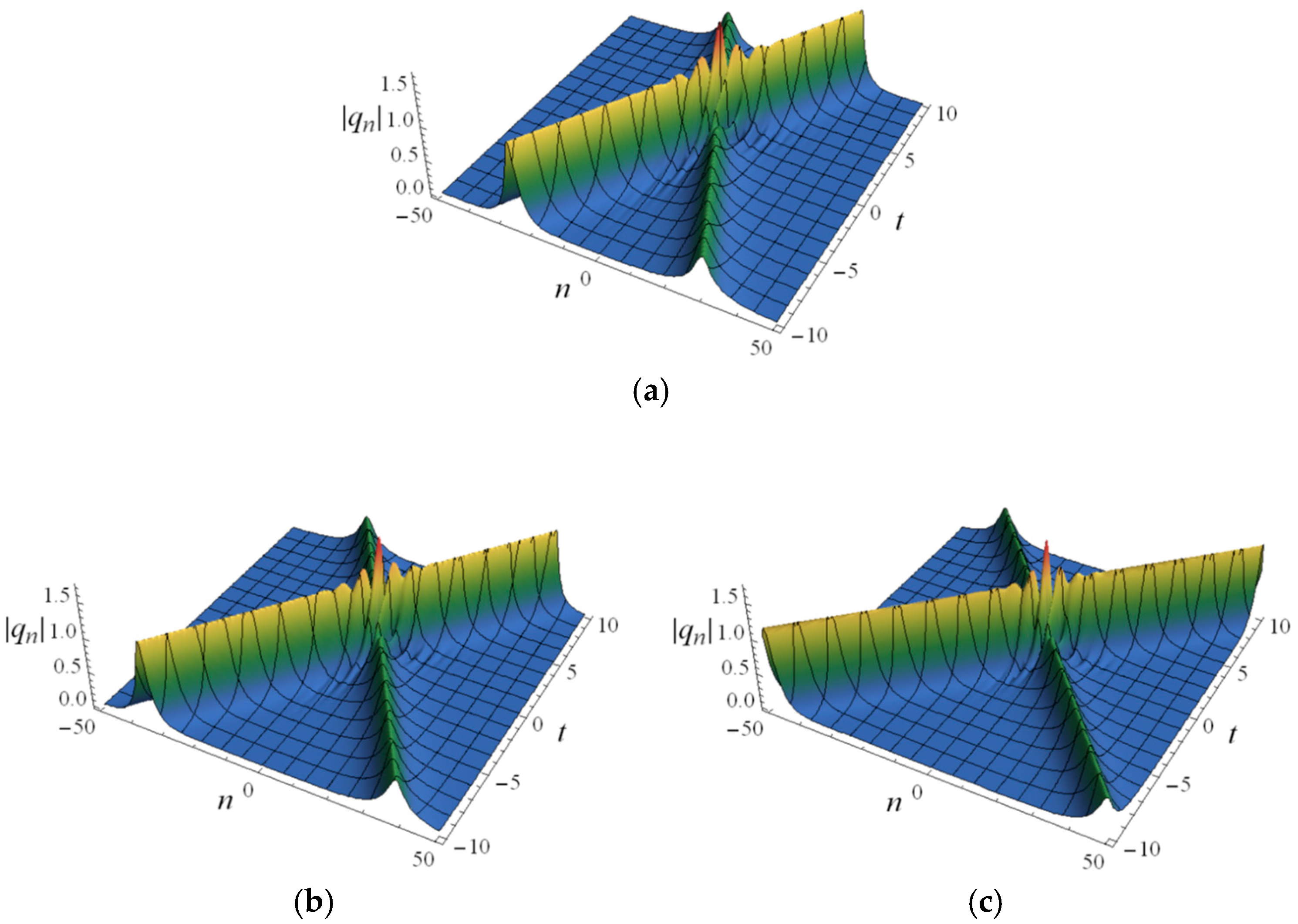
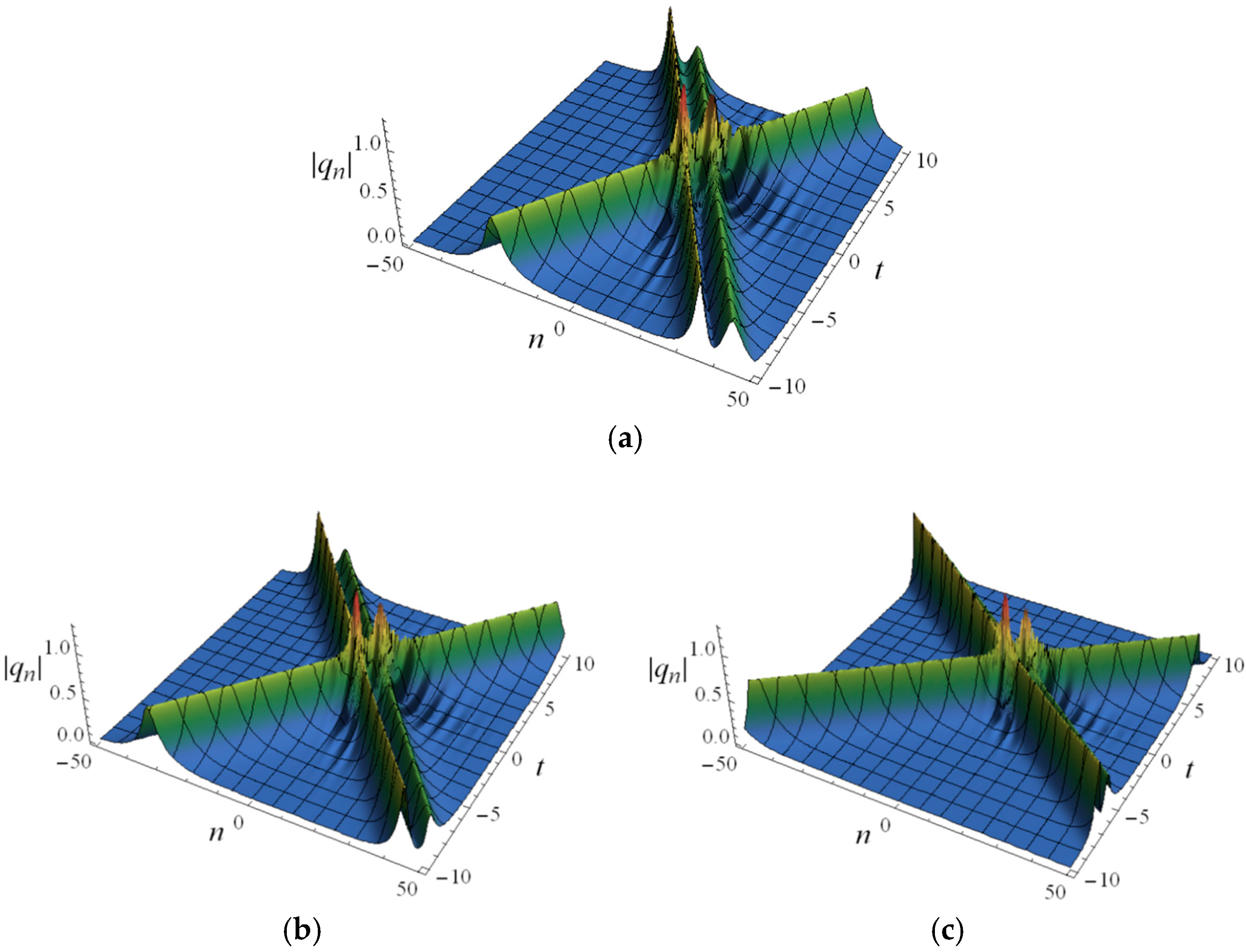
In Figure 5, the spatiotemporal structures of the semi-discrete two-soliton (172) are shown, and we can see that two types of waves propagate in both positive and negative directions, forming an X-shape. By changing $\delta$ from 0 to 0.1 and then to 0.3, the distance between the two solitons increases sequentially, but there is no significant difference in soliton amplitude. Figure 6 indicates that without considering the variation in $\delta$, a clear characteristic of soliton propagation is that two seemingly stationary solitons collide and travel opposite to each other with a sharp increase in velocity. This tells us that the coefficient, $\beta (t)$, has a decisive impact on the soliton velocity.

In Figure 7, we specifically set $\delta =0$, and we can see that the two solitons propagate in both positive and negative directions, as shown in Figure 5 and Figure 6, forming an X-shape. We can clearly see that when the sign of the imaginary part of z changes, the direction of the velocity also changes. If the imaginary parts of two solitons have the same sign, the propagation direction is the same; when the imaginary parts have different signs, the propagation direction is opposite, and the amplitudes of the two solitons are also different. Furthermore, it is clear that the two solitons completely penetrate each other, and there is no loss or diffusion during the propagation process.

When $\tilde{\mathcal{K}}=\mathcal{K}=3$, the eigenvalues are $\left\{\pm z_1, \pm {\tilde{z}}_1, \pm z_2, \pm {\tilde{z}}_2, \pm z_3, \pm {\tilde{z}}_3\right\}$, where ${\tilde{z}}_1=1/z_1^{\ast }$, ${\tilde{z}}_2=1/z_2^{\ast }$, ${\tilde{z}}_3=1/z_3^{\ast }$ with $\left|z_1\right|$, $\left|z_2\right|$, $\left|z_3\right|>1$ and $\left|{\tilde{z}}_1\right|$, $\left|{\tilde{z}}_2\right|$, $\left|{\tilde{z}}_3\right|<1$; then, we can solve for ${\widetilde{{\mathcal{B}}_n}}^{\prime }$ and ${{\mathcal{B}}_n}^{\prime }$, obtaining, in particular,

$$\begin{array}{cc}\hfill {\tilde{\mathcal{B}}}_n^{\prime (1)}({\tilde{z}}_3)& =\left\{4{\Re }_2{\tilde{\Re }}_2\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2(n-1)}{\tilde{z}}_1^{2n}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{(z_2^2-{\tilde{z}}_1^2)({\tilde{z}}_2^2-z_1^2)}}\right\}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \\ & +\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2(n-1)}{\tilde{z}}_1^{2n}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{(z_3^2-{\tilde{z}}_1^2)({\tilde{z}}_3^2-z_1^2)}}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \\ & +\left\{{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{(z_3^2-{\tilde{z}}_2^2)({\tilde{z}}_3^2-z_2^2)}}{\left[1+4{\Re }_2{\tilde{\Re }}_2{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{{({\tilde{z}}_2^2-z_2^2)}^2}}\right]}^{-1}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \end{array},$$

(176)

$$\begin{array}{c}{{\mathcal{B}}_n}^{\prime (2)}(z_3)=\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2n}{\tilde{z}}_1^{2(n+1)}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{({\tilde{z}}_3^2-z_1^2)(z_3^2-{\tilde{z}}_1^2)}}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \\ +\left\{4{\Re }_2{\tilde{\Re }}_2\left\{1+4{\Re }_1{\tilde{\Re }}_1{\left[1+4{\Re }_1{\tilde{\Re }}_1{\displaystyle \frac{z_1^{-2n}{\tilde{z}}_1^{2(n+1)}}{{(z_1^2-{\tilde{z}}_1^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_1^{1-2n}{\tilde{z}}_1^{2n+1}}{({\tilde{z}}_2^2-z_1^2)(z_2^2-{\tilde{z}}_1^2)}}\right\}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \\ +\left\{{\left[1+4{\Re }_2{\tilde{\Re }}_2{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{{({\tilde{z}}_2^2-z_2^2)}^2}}\right]}^{-1}{\displaystyle \frac{z_2^{1-2n}{\tilde{z}}_2^{2n+1}}{({\tilde{z}}_3^2-z_2^2)(z_3^2-{\tilde{z}}_2^2)}}\right\}{\left[1+4{\Re }_3{\tilde{\Re }}_3{\displaystyle \frac{z_3^{1-2n}{\tilde{z}}_3^{2n+1}}{{({\tilde{z}}_3^2-z_3^2)}^2}}\right]}^{-1}\hfill \end{array}.$$

(177)

Then, it follows that

$$q_n=-2\left[({\tilde{\Re }}_1{\tilde{z}}_1^{2n}){{\mathcal{B}}_{n+1}}^{\prime (2)}({\tilde{z}}_1)+({\tilde{\Re }}_2{\tilde{z}}_2^{2n}){{\mathcal{B}}_{n+1}}^{\prime (2)}({\tilde{z}}_2)+({\tilde{\Re }}_3{\tilde{z}}_3^{2n}){{\tilde{\mathcal{B}}}_{n+1}}^{\prime (2)}({\tilde{z}}_3)\right],$$

(178)

$$r_n=2\left[{\Re }_1{z}_1^{-2(n+1)}{{\mathcal{B}}_n}^{\prime (2)}(z_1)+{\Re }_2{z}_2^{-2(n+1)}{{\mathcal{B}}_n}^{\prime (2)}(z_2)+{\Re }_3{z}_3^{-2(n+1)}{{\mathcal{B}}_n}^{\prime (2)}(z_3)\right],$$

(179)

where we introduce the modified normalization constants,

$${\Re }_3(t)={\Re }_3(0)e^{2i{\Lambda }_3}, {\tilde{\Re }}_3(t)={\tilde{\Re }}_3(0)e^{-2i{\tilde{\Lambda }}_3},$$

(180)

$${\Lambda }_3={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)(z_3^2+z_3^{-2})]}^{(1+\delta )}}ds, {\tilde{\Lambda }}_3={\displaystyle \frac{1}{2}}{\displaystyle {\int }_0^t{[-2\alpha (s)+\beta (s)({\tilde{z}}_3^2+{\tilde{z}}_3^{-2})]}^{(1+\delta )}}ds.$$

(181)

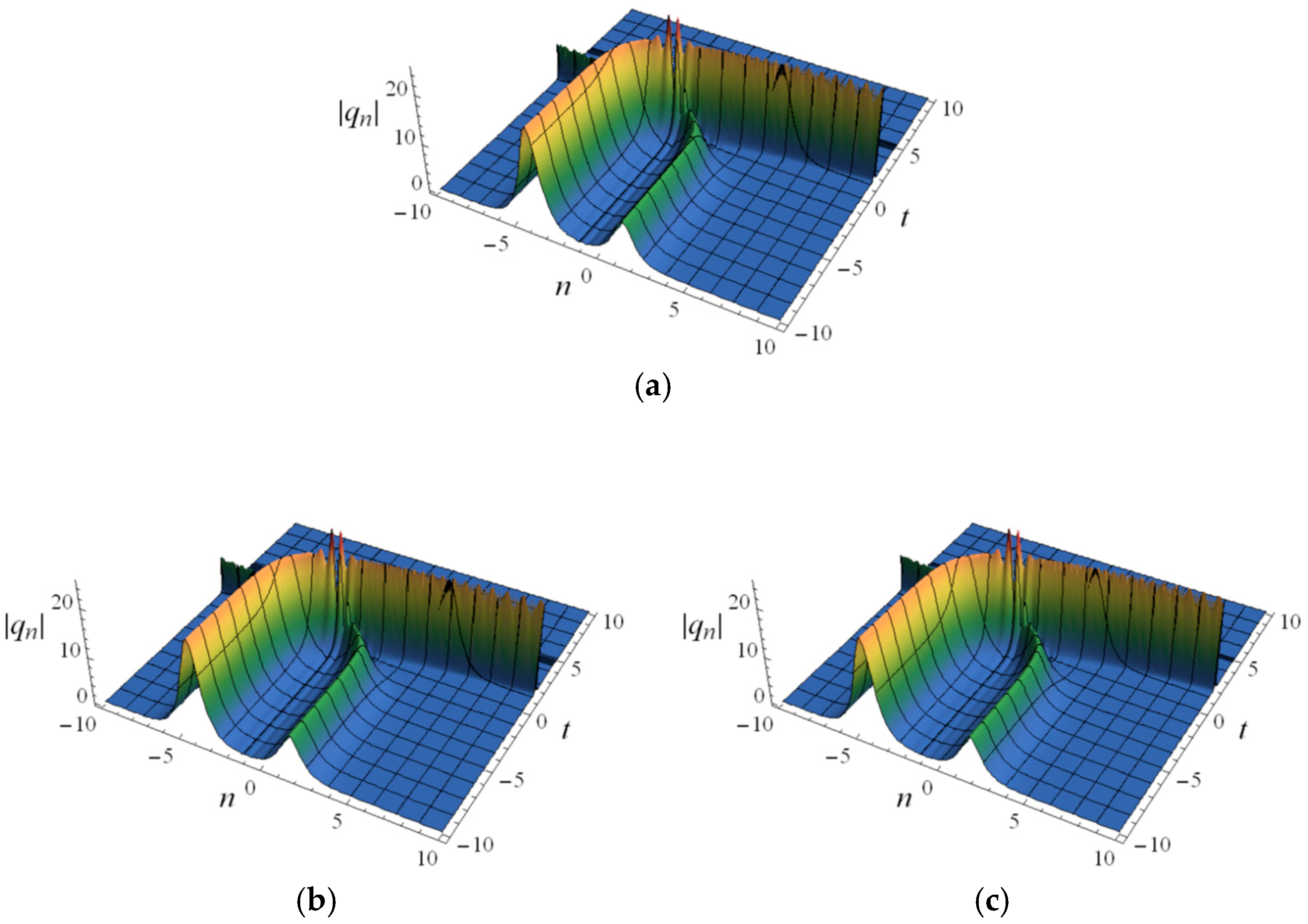
In Figure 8, we show the spatiotemporal structures of the semi-discrete three-soliton solution (178). We range the fractional order, $\delta$, from 0 to 0.1 and then to 0.3, where the directions of the three solitons are different. Two of them travel along the positive n-axis, but the third one travels in the opposite direction. Figure 8 shows that the three solitons penetrate each other after interaction without diffusion or loss, and the larger the value of $\delta$, the greater the distance between solitons moving in opposite directions.

6. Conclusions

We derived the vcfISDNLS equation, Equation (1), based on the DRF derivative and studied its integrability within the IST framework. As a result, we derived the $\mathcal{K}$-soliton solution of the vcfISDNLS equation, Equation (1), with a focus on analyzing the one-soliton solutions, (163) and (164) or (176) and (168); two-soliton solutions, (172) and (173); and three-soliton solutions, (178) and (179). Equation (1) is first proposed in this article, and there are no other results besides our research here. Due to the coupling of variable coefficients $\alpha (t)$ and $\beta (t)$; the fractional order, $\delta$; and the discrete variable, $n$, in the obtained solutions, (163), (164), (172), (173), (176), and (178), it is difficult to directly substitute them back into Equation (1) to verify their correctness. As for the validity of these solutions, we only verified them with the help of computers in the case of $\delta =0$. The verification of single-soliton solutions for continuous Riesz fractional KdV and NLS equations has been achieved based on their explicit representations, as shown in [15]. In order to demonstrate the completeness of the derivation and calculations, some necessary results from [5] have been referenced and used in this article. Due to the presence of coefficient functions $\alpha (t)$ and $\beta (t)$ in Equation (1), it is important to distinguish between the conclusions cited in [5], which imply different development patterns related to time as used in the present work. As for the shortcomings of the research work, we would like to mention that we have not yet obtained the display of a Lax pair associated with Equation (1). In this work, the integrability of Equation (1) is limited to the meaning of inverse scattering solvability through Ablowitz et al.’s method [29], but its integrability cannot be verified under the traditional Lax integrability framework. This point was first emphasized by Ablowitz et al. in [15]. It should be made clear here that for higher-order soliton solutions in the case $\tilde{\mathcal{K}}=\mathcal{K}>3$, they can be derived by substituting Equations (104)–(107) into Equations (163) and (164). However, given the sufficient complexity of expressions (176) and (177) for the three-soliton solutions, (163) and (164), this article does not specifically elaborate on the derivation of such higher-order soliton solutions. For this reason, it should be noted that this article only considers a few situations. When we take other values for the DRF order, $\delta$, we find that the image is sometimes chaotic or exhibits singularity. Therefore, this article does not provide images of solutions corresponding to other values of DRF order $\delta$.

Regarding the research conclusions, we particularly point out the following four points: (1) The DRF order, $\delta$, does not change the overall spatial structures of the soliton, and its structure is mainly influenced by $\alpha (t)$ and $\beta (t)$. (2) The velocity of the soliton is also affected by not only coefficients $\alpha (t)$ and $\beta (t)$ but also fractional order $\delta$ when $\alpha (t)$ and $\beta (t)$ are fixed; the velocity of the one-soliton, two-soliton, and three-soliton increases with the increase in $\delta$. (3) Whether it is a 1one-soliton, two-soliton, or three-soliton, their amplitudes are not affected by $\alpha (t)$, $\beta (t)$, and $\delta$, which means that the soliton propagation process will not experience amplitude increase or attenuation except for the interaction process. (4) When $c\to 0$, the characteristics of the three-soliton solution (178) are similar to those of the vcRfgNLS equation [32], indicating that the “continuous” system and the “discrete” system are just as concluded at the beginning of the article.

The vcfISDNLS equation, Equation (1), plays a vital role in the nonlinear field: (i) The vcfISDNLS equation, Equation (1), can be used to describe the propagation of optical pulses in optical fibers. Optical solitons reduce signal attenuation and distortion and improve communication capacity and quality. (ii) The vcfISDNLS equation, Equation (1), can describe the interactions between atoms and the spatial distribution and evolution of Bose–Einstein condensates. (iii) The vcfISDNLS equation, Equation (1), can be used to describe nonlinear wave phenomena in plasmas, such as Langmuir waves, ion acoustic waves, etc. (iv) The successful derivation of the vcfISDNLS equation, Equation (1), through DRF calculations provides a theoretical basis for other SDS equations, which can also be derived and solved using the same method. (v) In automotive suspension systems, the system structure can be optimized to reduce unnecessary vibration reflections, minimize fatigue damage to mechanical components, and improve system stability and lifespan. Given that semi-discrete solitons can maintain stability from chaotic/singular states by considering the dual influence factors of DRF order and coefficient functions, it is expected that such a control mechanism can provide assistance for optimizing automotive suspension systems. However, the application of this control mechanism in practical engineering still needs to be explored. (vi) The nonlinear property of the vcfISDNLS equation, Equation (1), implies that the inclusion of nonlinear components is helpful in designing nonlinear circuits that can generate stable oscillation or pulse signals, which are applied in signal generators, oscillators, and other devices to provide high-quality signal sources for electronic devices. Furthermore, due to the particularity of DRF calculus, we did not utilize or find the explicit form of a Lax pair corresponding to the vcfISDNLS equation, Equation (1), but instead found that the asymptotic forms consist of Equations (18) and (130), which match the explicit Lax pair, which is not contradictory to the statement in [33]. In addition, for Equation (1), we need to analyze its existence and stability, but the stability is not discussed theoretically here. This is both the weakness of our work and the unsolved problem in the study of such Riesz fractional-integrable systems. At the same time, we believe that Equation (1) still has a lot to learn from a scientific and engineering perspective. This is because the semi-discrete NLS equation has practical applications in optics (all-optical switches), electronic engineering (nonlinear transmission pulse sources), and acoustic engineering (topological phononic crystals).