The Crank-Nicolson Mixed Finite Element Scheme and Its Reduced-Order Extrapolation Model for the Fourth-Order Nonlinear Diffusion Equations with Temporal Fractional Derivative

Abstract

This paper presents a Crank–Nicolson mixed finite element method along with its reduced-order extrapolation model for a fourth-order nonlinear diffusion equation with Caputo temporal fractional derivative. By introducing the auxiliary variable $v=-{\epsilon }^2\Delta u+f(u)$, the equation is reformulated as a second-order coupled system. A Crank–Nicolson mixed finite element scheme is established, and its stability is proven using a discrete fractional Gronwall inequality. Error estimates for the variables u and v are derived. Furthermore, a reduced-order extrapolation model is constructed by applying proper orthogonal decomposition to the coefficient vectors of the first several finite element solutions. This scheme is also proven to be stable, and its error estimates are provided. Theoretical analysis shows that the reduced-order extrapolation Crank–Nicolson mixed finite approach reduces the degrees of freedom from tens of thousands to just a few, significantly cutting computational time and storage requirements. Numerical experiments demonstrate that both schemes achieve spatial second-order convergence accuracy. Under identical conditions, the CPU time required by the reduced-order extrapolation Crank–Nicolson mixed finite model is only $1/60$ of that required by the Crank–Nicolson mixed finite scheme. These results validate the theoretical analysis and highlight the effectiveness of the methods.

1. Introduction

We consider the following nonlinear fourth-order time fractional diffusion equations.

Problem 1.

Find $u(\mathbf{x},t)\in C^2(J;C^2(\mathrm{\Omega }))$ satisfying

$$\left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }u-\kappa \Delta (-{\epsilon }^2\Delta u+f(u))=0,(\mathbf{x},t)\in \mathrm{\Omega }\times J,\hfill \\ u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\hfill \\ {\partial }_{n}u={\partial }_n({\epsilon }^2\Delta u+f(u))=0,(\mathbf{x},t)\in \partial \mathrm{\Omega }\times J,\hfill \end{array}\right.$$

(1)

in which $\mathrm{\Omega }\subset R^d(d=1,2,3)$ is a bounded domain and has a smooth boundary $\partial \mathrm{\Omega }$; $J=(0,T]$, $u_0(\mathbf{x})$ is a given initial function. Where κ is the diffusion mobility constant, ε is a positive constant. The function $f(u)$ satisfies $|f(u)|\le C\left|u\right|$ and the Lipschitz condition

$$|f(u_1)-f(u_2)|\le L|u_1-u_2|,\forall u_1,u_2\in R,$$

(2)

where $L>0$ is a constant.

${}_0{}^{C}D_t^{\alpha }u$ represents the Caputo fractional derivative with $\alpha \in (0,1)$ defined by

$${}_0{}^{C}D_t^{\alpha }u(\mathbf{x},t)=\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^t\frac{\partial u(\mathbf{x},r)}{\partial r}\frac{1}{{(t-r)}^{\alpha }}dr,$$

(3)

where $\mathrm{\Gamma }(z)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt$ is the Gamma function. Throughout this work, C is defined as a positive constant that could take different values at different places.

Diffusion is a fundamental physical process for mass and energy transport. Its classical description relies on Fick’s law, which leads to an integer-order diffusion equation [1]. However, numerous experiments have revealed non-classical phenomena in diffusion processes, such as slow diffusion and long-term memory effects. These observations have motivated the development of time-fractional diffusion equations, with applications to seepage in porous media [2], anomalous transport [3], and bioengineering [4]. By replacing the first-order time derivative with Caputo, Gr$\ddot{u}$nwald−Letnikov or Riemann−Liouville fractional derivatives, these models provide a more precise mathematical framework for anomalous diffusion [5,6]. Despite the advantages of time-fractional models for physical modeling, their analytical solutions typically involve complex Mittag–Leffler functions [7], which hinders practical application. Thus, the development of efficient numerical methods is essential. For spatial discretization, common techniques include finite difference [8], Galerkin finite element [9], weak Galerkin finite element [10], discontinuous Galerkin [11], and spectral methods [12]. However, when these numerical methods solve directly for the primary variable (e.g., concentration or temperature), their approximations for the corresponding flux (e.g., mass or heat flux) are typically of low order. In contrast, the mixed finite element method (MFE) introduces the flux as an independent variable, yielding a coupled system that simultaneously approximates both the primary variable and the flux field with high precision [13,14]. This characteristic gives it a significant advantage in fields where high-precision approximation of the flux field is essential, such as groundwater flow simulation [15] and composite material mechanics [16]. The non-local nature of time-fractional derivatives poses severe challenges for computation and storage. For the temporal discretization of such problems, the Crank–Nicolson (CN) scheme is widely adopted because of its unconditional stability and accuracy [17,18,19]. In practice, the CN scheme is often combined with the $L1$ formula. This approach effectively handles the historical memory term while preserving numerical accuracy [20,21]. Nevertheless, the high degrees of freedom in MFE methods, combined with the full-history dependence of fractional operators, leads to high computational costs. This limits the practicality of high-accuracy CN mixed finite element schemes for problems requiring multiple simulations.

To overcome this bottleneck, model reduction techniques are considered effective. Among them, the Proper Orthogonal Decomposition (POD) method is one of the most prominent spatial reduction techniques [22,23]. Its core idea is to extract solutions from the full-order model at specific parameters or time instances (known as “snapshots”) to construct an optimal orthogonal basis. A reduced-order model is then built by projecting the original system onto the low-dimensional subspace spanned by this POD basis. This method has been successfully applied to various partial differential equations, including parabolic equations [24] and two-dimensional Sobolev equations [25,26]. However, the traditional spatial dimensionality reduction method has certain limitations. The global basis functions it generates are highly dependent on the initial and boundary conditions of the problem. When these parameters change, the precomputed POD basis may become ineffective, necessitating the regeneration of snapshots and the reconstruction of new basis functions. This process is not only computationally expensive but also lacks clear criteria for updating the basis, which limits its flexibility in tackling complex problems. To circumvent this, Luo et al. proposed a novel approach where the POD method is applied directly to the solution coefficient vectors obtained from finite element discretization, rather than to the physical function space. This method is called reduced-order extrapolated Crank–Nicolson mixed finite element (ROECNMFE). This significantly improves computational efficiency and has been successfully applied to Sobolev equations [27], Stokes equations [28], and hyperbolic equations [29]. In recent years, this method has also been used to solve fractional partial differential equations [30,31,32].

In this work, the solution coefficient vector dimensionality reduction technique is applied to the fourth-order nonlinear diffusion equations with temporal fractional derivative for the first time. The core innovation lies in the integration of a high-precision CNMFE model with a solution coefficient vector dimensionality reduction technique. The main contributions of this work are threefold:

1. We construct a CNMFE scheme for the time-fractional diffusion equation. This scheme is designed to achieve high-order accuracy in both temporal and spatial discretizations, enabling the simultaneous and high-precision approximation of the primary variable and its associated flux variable.

2. To address the significant computational cost of the high-fidelity CNMFE model, we introduce a ROECNMFE method that acts directly on the solution coefficient vectors. By constructing an optimal POD basis from a set of snapshot solutions obtained from the full-order finite element model, we establish a reduced-order model that dramatically improves computational efficiency while maintaining satisfactory accuracy.

3. The designed numerical examples serve to verify the correctness of both schemes and the superior efficiency of the ROECNMFE model.

The remainder of this paper is organized as follows. Section 2 is devoted to formulating the CNMFE scheme for the time-fractional diffusion equation, followed by a rigorous analysis of its stability and a priori error estimates. Section 3 elaborates on the detailed construction process of the ROECNMFE model based on the coefficient vector reduction technique. This section also provides a theoretical analysis of the stability and error estimates. Section 4 verifies the effectiveness and advantages of the proposed method through a series of numerical experiments. Finally, Section 5 concludes the paper with a summary of our findings and a discussion on potential future research directions.

2. The CNMFE Method for the Diffusion Equation

First, introduce an intermediate variable $v=-{\epsilon }^2\Delta u+f(u)$. Thereby, a system of second-order coupled equations is obtained.

Problem 2.

Find $(u,v):\mathrm{\Omega }\times J\to \mathbb{R}$ satisfies

$$\left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }u=\kappa \Delta v,(\mathbf{x},t)\in \mathrm{\Omega }\times J,\hfill \\ v=-{\epsilon }^2\Delta u+f(u),(\mathbf{x},t)\in \mathrm{\Omega }\times J,\hfill \\ u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\hfill \\ {\partial }_{n}u{{|}_{\partial \mathrm{\Omega }}={\partial }_{n}v|}_{\partial \mathrm{\Omega }}=0,t\in J.\hfill \end{array}\right.$$

(4)

The Sobolev space and their norms in this article are classical [33,34]. The space of square-integrable functions on $\mathrm{\Omega }$, denoted by $L^2(\mathrm{\Omega })$, is defined as

$$L^2(\mathrm{\Omega })=\{u:\mathrm{\Omega }\to \mathbb{R}|{\int }_{\mathrm{\Omega }}{\left|u(\mathbf{x})\right|}^{2}d\mathbf{x}<\infty \}.$$

It is a Hilbert space equipped with the inner product

$${(u,v)}_{L^2(\mathrm{\Omega })}={\int }_{\mathrm{\Omega }}u(\mathbf{x})v(\mathbf{x})d\mathbf{x},$$

which induces the norm

$${\parallel u\parallel }_{L^2(\mathrm{\Omega })}=\sqrt{{(u,u)}_{L^2(\mathrm{\Omega })}}=({\int }_{\mathrm{\Omega }}{\left|u(\mathbf{x})\right|}^2{d\mathbf{x})}^{\frac{1}{2}}.$$

Let $\mathbb{V}=H_0^1(\mathrm{\Omega })$. Then the variational form for equations as follows:

Problem 3.

For $0<t\le T$, find $(u,v)\in \mathbb{V}\times \mathbb{V}$ that satisfies

$$\left\{\begin{array}{c}({}_0{}^{C}D_t^{\alpha }u,\psi )+\kappa (\nabla v,\nabla \psi )=0,\forall \psi \in \mathbb{V},\hfill \\ (v,\varphi )={\epsilon }^2(\nabla u,\nabla \varphi )+(f(u),\varphi ),\forall \varphi \in \mathbb{V}.\hfill \end{array}\right.$$

(5)

The time interval $[0,T]$ is partitioned as: $0=t_0<t_1<\dots <t_N=T$, where N is a positive integer. For convenience, we introduce some symbols

$$\begin{array}{cc}\hfill & t_{n-\frac{1}{2}}=\frac{t_n+t_{n-1}}{2},u(t_{n-\frac{1}{2}})=u(\mathbf{x},t_{n-\frac{1}{2}}),v(t_{n-\frac{1}{2}})=v(\mathbf{x},t_{n-\frac{1}{2}}),\hfill \\ \hfill & u^{n-\frac{1}{2}}=\frac{u^n+u^{n-1}}{2},v^{n-\frac{1}{2}}=\frac{v^n+v^{n-1}}{2}.\hfill \end{array}$$

(6)

Then, we consider the discretization for the Caputo fractional derivative of $u(t_{n-\frac{1}{2}})$ [35]

$$\begin{array}{cc}\hfill & {}_0{}^{C}D_{\tau }^{\alpha }u(t_{n-\frac{1}{2}})\hfill \\ \hfill & =\frac{1}{\mathrm{\Gamma }(1-\alpha )}{\int }_0^{t_{n-\frac{1}{2}}}{(t_{n-\frac{1}{2}}-r)}^{-\alpha }{u}^{\prime }(r)dr\hfill \\ \hfill & =(b_{0}u(t_{n-\frac{1}{2}})-\sum _{j=2}^{n-1}(b_{n-j-1}-b_{n-j})u(t_{j-\frac{1}{2}})-(b_{n-2}-B_n)u(t_{\frac{1}{2}})-B_{n}u(t_0))+R_1^{n-\frac{1}{2}}\hfill \\ \hfill & =(b_{0}u(t_{n-\frac{1}{2}})-\sum _{j=1}^{n-1}(b_{n-j-1}-b_{n-j})u(t_{j-\frac{1}{2}})-(b_{n-1}-B_n)u(t_{\frac{1}{2}})-B_{n}u(t_0))+R_1^{n-\frac{1}{2}}\hfill \\ \hfill & =D_t^{\alpha }{u}^{n-\frac{1}{2}}+R_1^{n-\frac{1}{2}},\hfill \end{array}$$

(7)

where $R_1^{n-\frac{1}{2}}=O({\tau }^{2-\alpha })$ [35] is the truncation error, and

$$\begin{array}{cc}\hfill & b_{n-j}=\frac{{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}({(n-j+1)}^{1-\alpha }-{(n-j)}^{1-\alpha }),\hfill \\ \hfill & B_n=\frac{2{\tau }^{-\alpha }}{\mathrm{\Gamma }(2-\alpha )}({(n-\frac{1}{2})}^{1-\alpha }-{(n-1)}^{1-\alpha }).\hfill \end{array}$$

(8)

At $t=t_{n-\frac{1}{2}}$, (5) can be reformulated into the following form:

$$\left\{\begin{array}{c}({}_0{}^{C}D_t^{\alpha }u(t_{n-\frac{1}{2}}),\psi )+\kappa (\nabla v(t_{n-\frac{1}{2}}),\nabla \psi )=0,\forall \psi \in \mathbb{V},\hfill \\ (v(t_{n-\frac{1}{2}}),\varphi )={\epsilon }^2(\nabla u(t_{n-\frac{1}{2}}),\nabla \varphi )+(f(u(t_{n-\frac{1}{2}})),\varphi ),\forall \varphi \in \mathbb{V}.\hfill \end{array}\right.$$

(9)

Furthermore, the equivalent weak form of (5) is obtained as follows:

$$\left\{\begin{array}{c}(D_t^{\alpha }{u}^{n-\frac{1}{2}},\psi )+\kappa (\nabla v^{n-\frac{1}{2}},\nabla \psi )=-(R_1^{n-\frac{1}{2}},\psi ),\forall \psi \in \mathbb{V},\hfill \\ (v^{n-\frac{1}{2}},\varphi )={\epsilon }^2(\nabla u^{n-\frac{1}{2}},\nabla \varphi )+(f(u^{n-\frac{1}{2}}),\varphi ),\forall \varphi \in \mathbb{V}.\hfill \end{array}\right.$$

(10)

Let $T_h$ be the quasi-uniform triangulation of $\mathrm{\Omega }$, h denote the spatial grid size. Then the M-dimensional finite element subspace can be defined as follows:

$$\begin{array}{cc}\hfill {\mathbb{V}}_h& =\{v_h\in (H_0^1(\mathrm{\Omega })\cap C(\mathrm{\Omega })):v_h{|}_K\in {\mathbb{P}}_{m-1}(K),\forall K\in T_h\}\hfill \\ \hfill & =\mathrm{span}\{{\mathit{\zeta }}_{\mathit{i}}(\mathbf{x}):1\le i\le M\},\hfill \end{array}$$

(11)

where ${\mathbb{P}}_{m-1}(K)$ denotes the space of polynomials with no more than $m-1$ degrees on $K\in T_h$, and ${\left\{{\mathit{\zeta }}_{\mathit{i}}(\mathbf{x})\right\}}_{i=1}^M$ forms a set of orthonormal bases under the inner product in $L^2(\mathrm{\Omega })$. To ensure the subsequent error estimates are valid, we make the following regularity assumption on the exact solution $u\in C^2([0,T];H^m(\mathrm{\Omega }))$. This implies that the solution has sufficient smoothness in both time and space. We introduce the Ritz projection operator $R_h:\mathbb{V}\to {\mathbb{V}}_h$, which satisfies

$$\begin{array}{c}\hfill (\nabla (R_h\varphi -\varphi ),\nabla \chi )=0,\forall \chi \in {\mathbb{V}}_h,\end{array}$$

(12)

and the operator satisfies the following inequality [36]:

$$\begin{array}{c}\hfill \parallel \varphi -R_h{\varphi \parallel }_p+h\parallel \varphi -R_h{\varphi \parallel }_{1,p}\le C{h}^m{\parallel \varphi \parallel }_{m,p},\forall 1\le p\le \infty .\end{array}$$

(13)

Using the subspace ${\mathbb{V}}_h$, we can build the CNMFE scheme as follows:

Problem 4.

Find $(u_h^{n-\frac{1}{2}},v_h^{n-\frac{1}{2}})\in {\mathbb{V}}_h\times {\mathbb{V}}_h(n=1,2,\dots ,N)$ that satisfies

$$\left\{\begin{array}{c}(a)(D_t^{\alpha }{u}_h^{n-\frac{1}{2}},{\psi }_h)+\kappa (\nabla v_h^{n-\frac{1}{2}},\nabla {\psi }_h)=0,\forall {\psi }_h\in {\mathbb{V}}_h,\hfill \\ (b)(v_h^{n-\frac{1}{2}},{\varphi }_h)={\epsilon }^2(\nabla u_h^{n-\frac{1}{2}},\nabla {\varphi }_h)+(f(u_h^{n-\frac{1}{2}}),{\varphi }_h),\forall {\varphi }_h\in {\mathbb{V}}_h.\hfill \end{array}\right.$$

(14)

where the finite element space ${\mathbb{V}}_h$, defined in (11), is a standard Lagrange finite element space consisting of continuous piecewise polynomials. Both the solution u and the auxiliary variable v are approximated in this same space.

Lemma 1

([35]). For the coefficients of (7), it holds that

$$\begin{array}{cc}\hfill & 0\le b_n\le b_{n-1},B_n\le b_{n-1},n\ge 1,\hfill \\ \hfill & b_n\le B_n,n\ge 0.\hfill \end{array}$$

(15)

Lemma 2

((Discrete Fractional $Gr\ddot{o}nwall$ Inequality) [17]). Suppose that the nonnegative sequence $\left\{u^{n-\frac{1}{2}}\right|n=1,2,\dots \}$ and $\left\{g^{n-\frac{1}{2}}\right|n=1,2,\dots \}$ satisfies

$$\begin{array}{c}\hfill D_t^{\alpha }{u}^{n-\frac{1}{2}}\le {\mu }_1{u}^{n-\frac{1}{2}}+{\mu }_2{u}^{n-1-\frac{1}{2}}+g^{n-\frac{1}{2}},n>1,\end{array}$$

(16)

where $R_1^{n-\frac{1}{2}}$ is well defined in (7), ${\mu }_1\ge 0$ and ${\mu }_2\ge 0$ are constants independent of τ. Especially, we let $D_{\tau }^{\alpha }{u}^{\frac{1}{2}}\le {\mu }_1{u}^{\frac{1}{2}}+{\mu }_2{u}^0+g^{\frac{1}{2}}$ when $n=1$. There exist positive constant ${\tau }^{*}$, when $\tau \le {\tau }^{*}$,

$$\begin{array}{c}\hfill u^{n-\frac{1}{2}}\le 2(u^0+g^{n-\frac{1}{2}})E_{\alpha }(2\mu t_{n-\frac{1}{2}}^{\alpha }),1\le n\le N,\end{array}$$

(17)

where $\mu ={\mu }_1+\frac{{\mu }_2{B}_1}{b_0-B_2}$ and $E_{\alpha }(z)={\sum }_{k=0}^{\infty }\frac{z^k}{\mathrm{\Gamma }(1+k\alpha )}$ is the Mittag–Leffler function.

Theorem 1.

The mixed finite element solution $(u_h^{n-\frac{1}{2}},v_h^{n-\frac{1}{2}})$ is unconditionally stable.

Proof. 

We let ${\psi }_h={\epsilon }^2{u}_h^{n-\frac{1}{2}},{\varphi }_h=\kappa v_h^{n-\frac{1}{2}}$ at (14)

$$\left\{\begin{array}{c}{\epsilon }^2(D_t^{\alpha }{u}_h^{n-\frac{1}{2}},u_h^{n-\frac{1}{2}})+\kappa {\epsilon }^2(\nabla v_h^{n-\frac{1}{2}},\nabla u_h^{n-\frac{1}{2}})=0,\forall {\psi }_h\in {\mathbb{V}}_h,\hfill \\ \kappa (v_h^{n-\frac{1}{2}},v_h^{n-\frac{1}{2}})={\epsilon }^2\kappa (\nabla u_h^{n-\frac{1}{2}},\nabla v_h^{n-\frac{1}{2}})+\kappa (f(u_h^{n-\frac{1}{2}}),v_h^{n-\frac{1}{2}}),\forall {\varphi }_h\in {\mathbb{V}}_h.\hfill \end{array}\right.$$

(18)

The sum of the above two formulas is obtained

$${\epsilon }^2(D_t^{\alpha }{u}_h^{n-\frac{1}{2}},u_h^{n-\frac{1}{2}})+\kappa (v_h^{n-\frac{1}{2}},v_h^{n-\frac{1}{2}})=\kappa (f(u_h^{n-\frac{1}{2}}),v_h^{n-\frac{1}{2}}).$$

(19)

Using the definition of $D_t^{\alpha }{u}_h^{n-\frac{1}{2}}$ and Lemma 1, the first term on the left side of the equation can be treated as

$$\begin{array}{cc}\hfill & (D_t^{\alpha }{u}_h^{n-\frac{1}{2}},u_h^{n-\frac{1}{2}})\hfill \\ \hfill & =(b_0{u}_h^{n-\frac{1}{2}}-\sum _{j=2}^{n-1}(b_{n-j-1}-b_{n-j})u_h^{j-\frac{1}{2}}-(b_{n-2}-B_n)u_h^{\frac{1}{2}}-B_n{u}_h^0,u_h^{n-\frac{1}{2}})\hfill \\ \hfill & \ge b_0\parallel u_h^{n-\frac{1}{2}}{\parallel }^2-\sum _{j=2}^{n-1}(b_{n-j-1}-b_{n-j})\frac{\parallel u_h^{j-\frac{1}{2}}{\parallel }^2+\parallel u_h^{n-\frac{1}{2}}{\parallel }^2}{2}\hfill \\ \hfill & -(b_{n-2}-B_n)\frac{\parallel u_h^{\frac{1}{2}}{\parallel }^2+\parallel u_h^{n-\frac{1}{2}}{\parallel }^2}{2}-B_n\frac{\parallel u_h^0{\parallel }^2+\parallel u_h^{n-\frac{1}{2}}{\parallel }^2}{2}\hfill \\ \hfill & =\frac{1}{2}(b_0\parallel u_h^{n-\frac{1}{2}}{\parallel }^2-\sum _{j=2}^{n-1}(b_{n-j-1}-b_{n-j})\parallel u_h^{j-\frac{1}{2}}{\parallel }^2-(b_{n-2}-B_n)\parallel u_h^{\frac{1}{2}}{\parallel }^2-B_n\parallel u_h^0{\parallel }^2)\hfill \\ \hfill & =\frac{1}{2}{D}_t^{\alpha }\parallel u_h^{n-\frac{1}{2}}{\parallel }^2.\hfill \end{array}$$

(20)

Substitute it into (19), using Cauchy inequality and $\parallel f(u_h^{n-\frac{1}{2}})\parallel \le C\parallel u_h^{n-\frac{1}{2}}\parallel$

$$\begin{array}{cc}\hfill \frac{{\epsilon }^2}{2}{D}_t^{\alpha }\parallel u_h^{n-\frac{1}{2}}{\parallel }^2+\kappa \parallel v_h^{n-\frac{1}{2}}{\parallel }^2& \le \kappa (f(u_h^{n-\frac{1}{2}}),v_h^{n-\frac{1}{2}})\hfill \\ \hfill & \le \frac{\kappa }{2}(\parallel f(u_h^{n-\frac{1}{2}}){\parallel }^2+\parallel v_h^{n-\frac{1}{2}}{\parallel }^2)\hfill \\ \hfill & \le C\parallel u_h^{n-\frac{1}{2}}{\parallel }^2+\frac{\kappa }{2}\parallel v_h^{n-\frac{1}{2}}{\parallel }^2.\hfill \end{array}$$

(21)

Further organizing the above equation and applying lemma 2, we obtain

$$\parallel u_h^{n-\frac{1}{2}}\parallel \le C\parallel u_h^0\parallel .$$

(22)

Combining the above two formulas, the following is obtained:

$$\parallel v_h^{n-\frac{1}{2}}\parallel \le C\parallel u_h^{n-\frac{1}{2}}\parallel \le C\parallel u_h^0\parallel .$$

(23)

The above results prove that solution is unconditionally stable. □

Theorem 2.

Let $(u(t_{n-\frac{1}{2}}),v(t_{n-\frac{1}{2}}))and(u_h^{n-\frac{1}{2}},v_h^{n-\frac{1}{2}})$ be solutions of (9) and (14) respectively. The following estimator is satisfied

$$\begin{array}{c}\hfill \parallel u(t_{n-\frac{1}{2}})-u_h^{n-\frac{1}{2}}\parallel +\parallel v(t_{n-\frac{1}{2}})-v_h^{n-\frac{1}{2}}\parallel \le C({\tau }^{2-\alpha }+h^2).\end{array}$$

(24)

Proof. 

First give some symbols

$$\begin{array}{cc}\hfill & {\overline{e}}^{n-\frac{1}{2}}=u(t_{n-\frac{1}{2}})-R_{h}u(t_{n-\frac{1}{2}}),e^{n-\frac{1}{2}}=u_h^{n-\frac{1}{2}}-R_{h}u(t_{n-\frac{1}{2}}),\hfill \\ \hfill & {\overline{\eta }}^{n-\frac{1}{2}}=v(t_{n-\frac{1}{2}})-R_{h}v(t_{n-\frac{1}{2}}),{\eta }^{n-\frac{1}{2}}=v_h^{n-\frac{1}{2}}-R_{h}v(t_{n-\frac{1}{2}}).\hfill \end{array}$$

(25)

Then, using the above relationship, from Equations (9) and (14), we can obtain

$$\left\{\begin{array}{c}(D_t^{\alpha }{e}^{n-\frac{1}{2}},{\psi }_h)+\kappa (\nabla {\eta }^{n-\frac{1}{2}},\nabla {\psi }_h)=(D_t^{\alpha }{\overline{e}}^{n-\frac{1}{2}},{\psi }_h)+\kappa (\nabla {\overline{\eta }}^{n-\frac{1}{2}},\nabla {\psi }_h)+(R_1^{n-\frac{1}{2}},{\psi }_h),\hfill \\ -{\epsilon }^2(\nabla e^{n-\frac{1}{2}},\nabla {\varphi }_h)+({\eta }^{n-\frac{1}{2}},{\varphi }_h)\hfill \\ =-{\epsilon }^2(\nabla {\overline{e}}^{n-\frac{1}{2}},\nabla {\varphi }_h)+({\overline{\eta }}^{n-\frac{1}{2}},{\varphi }_h)+(f(u_h^{n-\frac{1}{2}})-f(u^{n-\frac{1}{2}}),{\varphi }_h).\hfill \end{array}\right.$$

(26)

Take ${\psi }_h={\epsilon }^2{e}^{n-\frac{1}{2}},{\varphi }_h=\kappa {\eta }^{n-\frac{1}{2}}$ in (26). Obtain two equations and add them

$$\begin{array}{cc}\hfill {\epsilon }^2(D_t^{\alpha }{e}^{n-\frac{1}{2}},e^{n-\frac{1}{2}})+\kappa ({\eta }^{n-\frac{1}{2}},{\eta }^{n-\frac{1}{2}})& ={\epsilon }^2(D_t^{\alpha }{\overline{e}}^{n-\frac{1}{2}},e^{n-\frac{1}{2}})+{\epsilon }^2(R_1^{n-\frac{1}{2}},e^{n-\frac{1}{2}})\hfill \\ \hfill & +\kappa ({\overline{\eta }}^{n-\frac{1}{2}},{\eta }^{n-\frac{1}{2}})+\kappa (f(u_h^{n-\frac{1}{2}})-f(u^{n-\frac{1}{2}}),{\eta }^{n-\frac{1}{2}}).\hfill \end{array}$$

(27)

Similar to (20), we have $(D_t^{\alpha }{e}^{n-\frac{1}{2}},e^{n-\frac{1}{2}})\ge \frac{1}{2}{D}_t^{\alpha }\parallel e^{n-\frac{1}{2}}{\parallel }^2$. Then, by using the Cauchy inequality, the above equation can be organized as

$$\begin{array}{cc}\hfill \frac{{\epsilon }^2}{2}{D}_t^{\alpha }\parallel e^{n-\frac{1}{2}}{\parallel }^2+\kappa \parallel {\eta }^{n-\frac{1}{2}}{\parallel }^2& \le \parallel D_t^{\alpha }{\overline{e}}^{n-\frac{1}{2}}{\parallel }^2+\parallel R_1^{n-\frac{1}{2}}{\parallel }^2+\frac{{\epsilon }^4}{2}\parallel e^{n-\frac{1}{2}}{\parallel }^2\hfill \\ \hfill & +\kappa \parallel {\overline{\eta }}^{n-\frac{1}{2}}{\parallel }^2+\kappa \parallel f(u_h^{n-\frac{1}{2}})-f(u^{n-\frac{1}{2}}){\parallel }^2+\frac{\kappa }{2}\parallel {\eta }^{n-\frac{1}{2}}{\parallel }^2.\hfill \end{array}$$

(28)

Using (13), we obtain the estimation of the first term on the right

$$\begin{array}{cc}\hfill \parallel D_t^{\alpha }{\overline{e}}^{n-\frac{1}{2}}{\parallel }^2& =\parallel D_t^{\alpha }(u(t_{n-\frac{1}{2}})-R_{h}u(t_{n-\frac{1}{2}})){\parallel }^2\hfill \\ \hfill & =\parallel D_t^{\alpha }u(t_{n-\frac{1}{2}})-D_t^{\alpha }{R}_{h}u(t_{n-\frac{1}{2}}){\parallel }^2\hfill \\ \hfill & =\parallel D_t^{\alpha }u(t_{n-\frac{1}{2}})-{}_0{}^{C}D_t^{\alpha }u(t_{n-\frac{1}{2}})+{}_0{}^{C}D_t^{\alpha }u(t_{n-\frac{1}{2}})-D_t^{\alpha }{R}_{h}u(t_{n-\frac{1}{2}}){\parallel }^2\hfill \\ \hfill & \le \parallel D_t^{\alpha }u(t_{n-\frac{1}{2}})-{}_0{}^{C}D_t^{\alpha }u(t_{n-\frac{1}{2}}){\parallel }^2+\parallel {}_0{}^{C}D_t^{\alpha }u(t_{n-\frac{1}{2}})-D_t^{\alpha }{R}_{h}u(t_{n-\frac{1}{2}}){\parallel }^2\hfill \\ \hfill & \le C{({\tau }^{2-\alpha })}^2+C{(h^2)}^2.\hfill \end{array}$$

(29)

Therefore, (28) can be concluded

$$\begin{array}{c}\hfill D_t^{\alpha }\parallel e^{n-\frac{1}{2}}{\parallel }^2\le C\parallel e^{n-\frac{1}{2}}{\parallel }^2+C{({\tau }^{2-\alpha })}^2+C{(h^2)}^2.\end{array}$$

(30)

By using Lemma 2, we obtain

$$\begin{array}{c}\hfill \parallel e^{n-\frac{1}{2}}\parallel \le C({\tau }^{2-\alpha }+h^2)\end{array}$$

(31)

The above results, combined with (28), yield the following error estimation

$$\begin{array}{c}\hfill \parallel {\eta }^{n-\frac{1}{2}}\parallel \le C{\tau }^{2-\alpha }+C{h}^2+\parallel e^{n-\frac{1}{2}}\parallel \le C({\tau }^{2-\alpha }+h^2).\end{array}$$

(32)

□

Let ${\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}=(u_{h1}^{n-\frac{1}{2}},u_{h2}^{n-\frac{1}{2}},\dots ,u_{hM}^{n-\frac{1}{2}}),{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}=(v_{h1}^{n-\frac{1}{2}},v_{h2}^{n-\frac{1}{2}},\dots ,v_{hM}^{n-\frac{1}{2}})$. By using the orthonormal basis ${\left\{{\mathit{\zeta }}_{\mathit{i}}\right\}}_{i=1}^M$, we can obtain the matrix model for Problem 4.

Problem 5.

Find $({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\in {\mathbb{R}}^M\times {\mathbb{R}}^M$ that satisfies

$$\left\{\begin{array}{c}(a)D_t^{\alpha }{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa {\mathbf{BV}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}=0,1\le n\le N,\hfill \\ (b){\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}={\epsilon }^2{\mathbf{BU}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}+\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}),1\le n\le N,\hfill \\ (c)u_h^{n-\frac{1}{2}}=\sum _{i=1}^M{u}_i^{n-\frac{1}{2}}{\mathit{\zeta }}_{\mathit{i}}={\mathbf{U}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta },v_h^{n-\frac{1}{2}}=\sum _{i=1}^M{v}_i^{n-\frac{1}{2}}{\mathit{\zeta }}_{\mathit{i}}={\mathbf{V}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }.\hfill \end{array}\right.$$

(33)

where $\mathbf{B}={(\nabla {\mathit{\zeta }}_{\mathit{i}},\nabla {\mathit{\zeta }}_{\mathit{j}})}_{M\times M},\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}})={(f({\sum }_{i=1}^M{u}_i^{n-\frac{1}{2}}{\mathit{\zeta }}_{\mathit{i}}),{\mathit{\zeta }}_{\mathit{j}})}_{M\times M}$. And we can find that $\mathbf{B}$ is a positive definite symmetric matrix. To demonstrate the stability of the solution obtained by CNMFE scheme, we introduce a properties of $\mathbf{B}$ from Problem 5.

Lemma 3.

Matrix $\mathbf{B}$ satisfies the following inequality [34,37]

$$\begin{array}{c}\hfill {\parallel \mathbf{B}\parallel }_{\infty }\le C,{\parallel {\mathbf{B}}^{-1}\parallel }_{\infty }\le C.\end{array}$$

(34)

3. The ROECNMFE Method Based on POD for the Diffusion Equation

3.1. Construction of POD Bases

First, we choose the first L layers of solution vectors ${\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}}(n=1,2,\dots ,L)$ and ${\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}}(n=1,2,\dots ,L)$ of the solutions ${\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}}(n=1,2,\dots ,N)$ and ${\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}}(n=1,2,\dots ,N)$ of Problem 5, forming two snapshot matrices ${\mathbf{G}}_{\mathbf{1}}=({\mathbf{U}}_{\mathbf{h}}^{\mathbf{1}},{\mathbf{U}}_{\mathbf{h}}^{\mathbf{2}},\dots ,{\mathbf{U}}_{\mathbf{h}}^{\mathbf{L}})$ and ${\mathbf{G}}_{\mathbf{2}}=({\mathbf{V}}_{\mathbf{h}}^{\mathbf{1}},{\mathbf{V}}_{\mathbf{h}}^{\mathbf{2}},\dots ,{\mathbf{V}}_{\mathbf{h}}^{\mathbf{L}})$, respectively. Let ${\lambda }_{i,j}>0(i=1,2,j=1,2,\dots ,r_i=rank({\mathbf{G}}_{\mathbf{i}}))$ be the positive eigenvalues of ${{\mathbf{G}}_{\mathbf{i}}{\mathbf{G}}_{\mathbf{i}}}^T$ arranged degressively and ${\overline{\mathsf{\Phi }}}_{\mathit{i}}=({\phi }_{\mathit{i},\mathbf{1}},{\phi }_{\mathit{i},\mathbf{2}},\dots ,{\phi }_{\mathit{i},{\mathit{r}}_{\mathit{i}}})$ be the homologous orthonormal eigenvectors of ${{\mathbf{G}}_{\mathbf{i}}{\mathbf{G}}_{\mathbf{i}}}^T$. Thus, two sets of POD bases ${\mathsf{\Phi }}_{\mathit{i}}=({\phi }_{\mathit{i},\mathbf{1}},{\phi }_{\mathit{i},\mathbf{2}},\dots ,{\phi }_{\mathit{i},\mathit{d}})(d\le r_i,i=1,2)$ are obtained from the first d vectors in ${\overline{\mathsf{\Phi }}}_{\mathit{i}}$, and satisfy the following equation [38]:

$$\begin{array}{cc}\hfill & \parallel {\mathbf{G}}_{\mathbf{1}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{G}}_{\mathbf{1}}{\parallel }_{2,2}=\sqrt{{\lambda }_{1,d+1}},\hfill \\ \hfill & \parallel {\mathbf{G}}_{\mathbf{2}}-{\mathsf{\Phi }}_{\mathbf{2}}{{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{G}}_{\mathbf{2}}{\parallel }_{2,2}=\sqrt{{\lambda }_{2,d+1}}.\hfill \end{array}$$

(35)

where $\parallel {\mathbf{G}}_{\mathbf{i}}{\parallel }_{2,2}=su{p}_{\chi \ne 0}\frac{\parallel {\mathbf{G}}_{\mathbf{i}}{\chi \parallel }_2}{{\parallel \chi \parallel }_2}$ and ${\parallel \chi \parallel }_2$ is the Euclidean norm for vectors $\chi$. It follows that

$$\begin{array}{cc}\hfill & \parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}}\parallel =\parallel ({\mathbf{G}}_{\mathbf{1}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{G}}_{\mathbf{1}}){ϵ}^{\mathit{n}}\parallel \le \parallel {\mathbf{G}}_{\mathbf{1}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{G}}_{\mathbf{1}}{\parallel }_{2,2}\parallel {ϵ}^{\mathit{n}}\parallel \le \sqrt{{\lambda }_{1,d+1}},\hfill \\ \hfill & \parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel =\parallel ({\mathbf{G}}_{\mathbf{1}}-{{\mathsf{\Phi }}_{\mathbf{1}}{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{G}}_{\mathbf{1}}){ϵ}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \hfill \\ \hfill & \le \parallel {\mathbf{G}}_{\mathbf{1}}-{{\mathsf{\Phi }}_{\mathbf{1}}{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{G}}_{\mathbf{1}}{\parallel }_{2,2}\parallel {ϵ}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le \sqrt{{\lambda }_{1,d+1}},\hfill \\ \hfill & \parallel {\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathsf{\Phi }}_{\mathbf{2}}{{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel =\parallel ({\mathbf{G}}_{\mathbf{2}}-{{\mathsf{\Phi }}_{\mathbf{2}}{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{G}}_{\mathbf{2}}){ϵ}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \hfill \\ \hfill & \le \parallel {\mathbf{G}}_{\mathbf{2}}-{{\mathsf{\Phi }}_{\mathbf{2}}{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{G}}_{\mathbf{2}}{\parallel }_{2,2}\parallel {ϵ}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le \sqrt{{\lambda }_{2,d+1}}.\hfill \end{array}$$

(36)

where ${ϵ}^{\mathit{n}}(n=1,2,\dots ,L)$ are the unit vectors whose nth component is 1. Thereupon, two sets of POD bases ${\mathsf{\Phi }}_{\mathit{i}}=({\phi }_{\mathit{i},\mathbf{1}},{\phi }_{\mathit{i},\mathbf{2}},\dots ,{\phi }_{\mathit{i},\mathit{d}})(d\le r_i,i=1,2)$ are obtained.

Remark 1.

The eigenvalues ${\lambda }_{i,j}$ are positive because the snapshot matrix ${\mathbf{G}}_{\mathbf{i}}$ is real-valued, making ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}$ a positive semi-definite matrix. Furthermore, in practice, the number of snapshots $L+1$ is typically much smaller than the dimension of the system M ($L+1\ll M$), and the snapshots are linearly independent, which ensures that ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}$ is strictly positive definite. Consequently, all its eigenvalues are real and positive. The error term $\sqrt{{\lambda }_{i,d+1}}(i=1,2)$ in (36) is caused by the reduced dimension for the CNMFE solution coefficient vectors, but it may serve as the suggestion to elect the POD bases, namely it is only necessary to elect the number d of POD bases such that $\sqrt{{\lambda }_{i,d+1}}(i=1,2)\le {\tau }^{2-\alpha }+h^2$, the error estimates are optimal order. In our setup ($h={10}^{-2}$, $\tau ={10}^{-3}$), we find $\sqrt{{\lambda }_{1,3}}+\sqrt{{\lambda }_{2,3}}\le 7.6104\times {10}^{-15}$, which satisfies the inequality. Thus, $d=2$ is selected. And the POD basis is generated for a specific set of parameters and is not reused for different α or ε. Since ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}$ and ${{\mathbf{G}}_{\mathbf{i}}{\mathbf{G}}_{\mathbf{i}}}^T$ have the same positive eigenvalue, and $L+1\ll M$. Therefore, by calculating the eigenvalue ${\lambda }_{i,j}$ and the eigenvector ${\mathit{\delta }}_{\mathit{i},\mathit{j}}$ of ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}$ and using the relation ${\mathit{\phi }}_{\mathit{i},\mathit{j}}=\frac{{\mathbf{G}}_{\mathbf{i}}{\mathit{\delta }}_{\mathit{i},\mathit{j}}}{\sqrt{{\lambda }_{i,j}}}$, the eigenvalue ${\lambda }_{i,j}$ of ${{\mathbf{G}}_{\mathbf{i}}{\mathbf{G}}_{\mathbf{i}}}^T$ and the corresponding orthogonal eigenvector ${\mathit{\phi }}_{\mathit{i},\mathit{j}}$ can be quickly obtained.

Remark 2.

The term “extrapolation” in the ROECNMFE method specifically refers to the technique used to generate an advanced initial guess for the solutions coefficient vectors at each new time level, thereby accelerating the solution of the reduced-order system. Before solving for the unknowns ${\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ and ${\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ in the system below, their initial values are predicted using CNMFE solutions from previously computed solutions. This simple yet effective extrapolation step leverages the temporal continuity of the solution, providing a high-quality initial guess that significantly reduces the number of iterations for the solver to converge, which is a key contributor to the computational efficiency of the overall method.

3.2. ROECNMFE Scheme

The form of the reduced order extrapolation mixed finite element solution in the first L time layer is as follows:

$$\begin{array}{cc}\hfill & u_d^{n-\frac{1}{2}}={\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }=(u_{d1}^{n-\frac{1}{2}},u_{d2}^{n-\frac{1}{2}},\dots ,u_{dM}^{n-\frac{1}{2}})·\mathit{\zeta }={{\mathsf{\Phi }}_{\mathbf{1}}{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }={\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta },1\le n\le L,\hfill \\ \hfill & v_d^{n-\frac{1}{2}}={\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }=(v_{d1}^{n-\frac{1}{2}},v_{d2}^{n-\frac{1}{2}},\dots ,v_{dM}^{n-\frac{1}{2}})·\mathit{\zeta }={{\mathsf{\Phi }}_{\mathbf{2}}{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }={\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta },1\le n\le L.\hfill \end{array}$$

(37)

where ${\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}=({\alpha }_1^{n-\frac{1}{2}},{\alpha }_2^{n-\frac{1}{2}},\dots ,{\alpha }_d^{n-\frac{1}{2}}),{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}=({\beta }_1^{n-\frac{1}{2}},{\beta }_2^{n-\frac{1}{2}},\dots ,{\beta }_d^{n-\frac{1}{2}})$.

In Problem 5, replace ${\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ and ${\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ with ${\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ and ${\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}$. The ROECNMFE matrix model is as follows.

Problem 6.

Find $({\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})\in {\mathbb{R}}_d\times {\mathbb{R}}_d,({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\in {\mathbb{V}}_h\times {\mathbb{V}}_h$ satisfies

$$\left\{\begin{array}{c}(a){\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},1\le n\le L,\hfill \\ (b)D_t^{\alpha }{\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa \mathbf{B}{\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}=0,L+1\le n\le N,\hfill \\ (c){\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\epsilon }^2\mathbf{B}{\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\mathbf{F}({\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}),L+1\le n\le N,\hfill \\ (d)u_d^{n-\frac{1}{2}}={\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }={\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta },v_d^{n-\frac{1}{2}}={\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }={\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta },1\le n\le N.\hfill \end{array}\right.$$

(38)

Remark 3.

Borrowing ${\mathsf{\Phi }}_{\mathbf{1}}$ and ${\mathsf{\Phi }}_{\mathbf{2}}$, it is not difficult to determine that Problem 5 and Problem 6 have the same form, which means that the ROECNMFE matrix model has a unique solution. More importantly, Problem 6 has only $2d$ degrees of freedom while Problem 5 has $2M(M\gg d)$ degrees of freedom at the same time level. Therefore, Problem 6 greatly reduces the number of unknowns, which greatly saves calculation time in practical problems. Therefore, the ROECNMFE matrix format is similar to the CNMFE format. In addition, since Problem 5 and Problem 6 have the same basis function, they have the same error precision.

Theorem 3.

Under the same assumptions as Theorem 2, suppose that $(u^{n-\frac{1}{2}},v^{n-\frac{1}{2}})\in \mathbb{V}\times \mathbb{V}$ is a weak solution to Problem 2, $(u_d^{n-\frac{1}{2}},v_d^{n-\frac{1}{2}})\in {\mathbb{V}}_h\times {\mathbb{V}}_h$ is a solution to Problem 6. For any $1\le n\le N$, the unconditional stability of the solution can be obtained and the following convergence results are obtained:

$$\begin{array}{c}\hfill \parallel u^{n-\frac{1}{2}}-u_d^{n-\frac{1}{2}}\parallel +\parallel v^{n-\frac{1}{2}}-v_d^{n-\frac{1}{2}}\parallel \le C({\tau }^{2-\alpha }+h^2+\sqrt{{\lambda }_{1,d+1}}+\sqrt{{\lambda }_{2,d+1}}).\end{array}$$

(39)

Proof. (1)

Prove unconditional stability

When $1\le n\le L$, combine the orthogonality of ${\mathsf{\Phi }}_{\mathit{i}}(i=1,2)$ and Theorem 2

$$\begin{array}{cc}\hfill \parallel u_d^{n-\frac{1}{2}}\parallel +\parallel v_d^{n-\frac{1}{2}}\parallel & =\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel +\parallel {\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel \hfill \\ \hfill & =\parallel {\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel +\parallel {\mathsf{\Phi }}_{\mathbf{2}}{{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel \hfill \\ \hfill & \le C(\parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel +\parallel {\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}·\mathit{\zeta }\parallel )\hfill \\ \hfill & =C(\parallel u_h^{n-\frac{1}{2}}\parallel +\parallel v_h^{n-\frac{1}{2}}\parallel )\hfill \\ \hfill & \le C\parallel u_h^0\parallel ,1\le n\le L.\hfill \end{array}$$

(40)

When $L+1\le n\le N$, since ${\mathsf{\Phi }}_{\mathbf{1}}{\mathit{\alpha }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathsf{\Phi }}_{\mathbf{2}}{\mathit{\beta }}_{\mathit{d}}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$, $\mathbf{B}$ is a positive definite symmetric matrix, rewrite ((38)$(b)$) and ((38))$(c)$), we have

$$\left\{\begin{array}{c}(a)D_t^{\alpha }{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa {\mathbf{BV}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}=0,L+1\le n\le N,\hfill \\ (b){\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\epsilon }^2{\mathbf{BU}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}),L+1\le n\le N.\hfill \end{array}\right.$$

(41)

Substitute ((41)$(b)$) into ((41)$(a)$), we obtain

$$\begin{array}{c}\hfill D_t^{\alpha }{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa {\epsilon }^2{\mathbf{B}}^2{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa \mathbf{BF}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})=0,L+1\le n\le N.\end{array}$$

(42)

Take the inner product with ${\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$, we get the following formula

$$\begin{array}{c}\hfill (D_t^{\alpha }{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})+\kappa {\epsilon }^2({\mathbf{B}}^2{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})+\kappa (\mathbf{BF}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}),{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})=0,L+1\le n\le N.\end{array}$$

(43)

Similar to (20), we have $(D_t^{\alpha }{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\ge \frac{1}{2}{D}_t^{\alpha }\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2$. Then, by using the Cauchy inequality and $\parallel \mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\parallel \le C\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel$, the above equation can be organized as

$$\begin{array}{cc}\hfill \frac{1}{2}{D}_t^{\alpha }\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2+\kappa {\epsilon }^2\parallel {\mathbf{BU}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2& \le -\kappa (\mathbf{BF}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}),{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\hfill \\ \hfill & \le \kappa \parallel \mathbf{BF}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}){\parallel }^2+\frac{\kappa }{4}\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2\hfill \\ \hfill & \le {\kappa \parallel \mathbf{B}\parallel }_{\infty }^2\parallel \mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}){\parallel }^2+\frac{\kappa }{4}\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2\hfill \\ \hfill & \le C\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2,L+1\le n\le N.\hfill \end{array}$$

(44)

By using Lemma 2 and $()$, we obtain

$$\begin{array}{c}\hfill \parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{L}}\parallel \le C\parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{0}}\parallel ,L+1\le n\le N.\end{array}$$

(45)

Using ((41)$(b)$) and $\parallel \mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\parallel \le C\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel$, we have

$$\begin{array}{c}\hfill \parallel {\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{0}}\parallel ,L+1\le n\le N.\end{array}$$

(46)

The above results prove that solution is unconditionally stable.

(2) Prove convergence

When $1\le n\le L$, due to $\parallel \mathit{\zeta }\parallel \le C$ and (36), we can conclude that

$$\begin{array}{cc}\hfill & \parallel u_h^{n-\frac{1}{2}}-u_d^{n-\frac{1}{2}}\parallel +\parallel v_h^{n-\frac{1}{2}}-v_d^{n-\frac{1}{2}}\parallel \hfill \\ \hfill \le & \parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }_{\infty }\parallel \mathit{\zeta }\parallel +\parallel {\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }_{\infty }\parallel \mathit{\zeta }\parallel \hfill \\ \hfill \le & C(\parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathsf{\Phi }}_{\mathbf{1}}{{\mathsf{\Phi }}_{\mathbf{1}}}^T{\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel +\parallel {\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathsf{\Phi }}_{\mathbf{2}}{{\mathsf{\Phi }}_{\mathbf{2}}}^T{\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel )\hfill \\ \hfill \le & C(\sqrt{{\lambda }_{1,d+1}}+\sqrt{{\lambda }_{2,d+1}}),1\le n\le L.\hfill \end{array}$$

(47)

When $L+1\le n\le N$, Assuming ${\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$ and ${\rho }^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}$, combine (33) and (41), we derive

$$\left\{\begin{array}{c}(a)D_t^{\alpha }{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa \mathbf{B}{\rho }^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}=0,L+1\le n\le N,\hfill \\ (b){\rho }^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}={\epsilon }^2\mathbf{B}{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}),L+1\le n\le N.\hfill \end{array}\right.$$

(48)

Substitute ((48)$(b)$) into ((48)$(a)$), we have

$$\begin{array}{c}\hfill D_t^{\alpha }{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa {\epsilon }^2{\mathbf{B}}^2{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}+\kappa \mathbf{B}(\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}))=0,L+1\le n\le N.\end{array}$$

(49)

Take the inner product with ${\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}$, we obtain

$$\begin{array}{c}\hfill (D_t^{\alpha }{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})+\kappa {\epsilon }^2({\mathbf{B}}^2{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})+\kappa (\mathbf{B}(\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})),{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})=0.\end{array}$$

(50)

Similar to (20), we have $(D_t^{\alpha }{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}},{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})\ge \frac{1}{2}{D}_t^{\alpha }\parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2$. Then, by using the Cauchy inequality and $\parallel \mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\parallel \le L\parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel$, the above equation can be organized as

$$\begin{array}{cc}\hfill \frac{1}{2}{D}_t^{\alpha }\parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2+\kappa {\epsilon }^2\parallel \mathbf{B}{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2& \le -\kappa (\mathbf{B}(\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})),{\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}})\hfill \\ \hfill & \le \kappa \parallel \mathbf{B}(\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})){\parallel }^2+\frac{\kappa }{4}\parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2\hfill \\ \hfill & \le {\kappa \parallel \mathbf{B}\parallel }_{\infty }^2\parallel \mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}){\parallel }^2+\frac{\kappa }{4}\parallel {\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2\hfill \\ \hfill & \le C\parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}{\parallel }^2,L+1\le n\le N.\hfill \end{array}$$

(51)

By using Lemma 2 and (47), we obtain

$$\begin{array}{c}\hfill \parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\parallel {\mathit{\delta }}^{\mathit{L}}\parallel \le C\sqrt{{\lambda }_{1,d+1}},L+1\le n\le N.\end{array}$$

(52)

Using ((48)(b)) and $\mathbf{F}({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})-\mathbf{F}({\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})\le C({\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}}-{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\frac{\mathbf{1}}{\mathbf{2}}})$, we have

$$\begin{array}{c}\hfill \parallel {\rho }^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\parallel {\mathit{\delta }}^{\mathit{n}-\frac{\mathbf{1}}{\mathbf{2}}}\parallel \le C\sqrt{{\lambda }_{1,d+1}},L+1\le n\le N.\end{array}$$

(53)

Further utilizing $\parallel \mathit{\zeta }\parallel \le C$, we obtain

$$\begin{array}{cc}\hfill & \parallel u_h^{n-1/2}-u_d^{n-1/2}\parallel +\parallel v_h^{n-1/2}-v_d^{n-1/2}\parallel \hfill \\ \hfill & \le \parallel {\mathbf{U}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}-{\mathbf{U}}_{\mathbf{d}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}\parallel \parallel \mathit{\zeta }\parallel +\parallel {\mathbf{V}}_{\mathbf{h}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}-{\mathbf{V}}_{\mathbf{d}}^{\mathbf{n}-\mathbf{1}/\mathbf{2}}\parallel \parallel \mathit{\zeta }\parallel \hfill \\ \hfill & \le C(\parallel {\mathbf{U}}_h^{n-1/2}-{\mathbf{U}}_d^{n-1/2}\parallel +\parallel {\mathbf{V}}_h^{n-1/2}-{\mathbf{V}}_d^{n-1/2}\parallel )\hfill \\ \hfill & \le C(\sqrt{{\lambda }_{1,d+1}}+\sqrt{{\lambda }_{2,d+1}}),L+1\le n\le N.\hfill \end{array}$$

Using triangular inequalities, we obtain

$$\begin{array}{cc}\hfill & \parallel u^{n-1/2}-u_d^{n-1/2}\parallel +\parallel v^{n-1/2}-v_d^{n-1/2}\parallel \hfill \\ \hfill & \le \parallel u^n-u_h^{n-1/2}\parallel +\parallel u_h^n-u_d^{n-1/2}\parallel +\parallel v^{n-1/2}-v_h^{n-1/2}\parallel +\parallel v_h^{n-1/2}-v_d^{n-1/2}\parallel \hfill \\ \hfill & \le C({\tau }^{2-\alpha }+h^2+\sqrt{{\lambda }_{1,d+1}}+\sqrt{{\lambda }_{2,d+1}}),1\le n\le N.\hfill \end{array}$$

□

Remark 4.

The generic constant C appearing in the stability estimate and the convergence estimate is independent of the time step τ, the mesh size h, the number of POD modes d, and the final time T. However, it may depend on the parameters of the problem, such as the diffusion coefficient ε, the constant κ, the Lipschitz constant C of the nonlinear term $f(u)$ and the initial condition $u_0$.

Remark 5.

The convergence result in Theorem 3 provides a rigorous upper bound for the total error, which combines the errors from temporal discretization, spatial discretization, and model reduction. The term ${\tau }^{2-\alpha }$ represents the temporal error, which is of order $\mathcal{O}({\tau }^{2-\alpha })$. The temporal order approaches the classical second-order convergence $\mathcal{O}({\tau }^2)$ of the Crank–Nicolson scheme when the fractional order $\alpha \to 1$. For $\alpha <1$, the temporal order decreases smoothly with α. The term $h^2$ represents the spatial error introduced by the mixed finite element method, achieving optimal second-order convergence in space. The terms $\sqrt{{\lambda }_{1,d+1}}$ and $\sqrt{{\lambda }_{2,d+1}}$ represent the model reduction errors due to the POD approximation. These errors are controlled by the truncation of POD modes and can be made arbitrarily small by choosing a sufficiently large d.

4. The Numerical Examples for the Diffusion Equation

Solve the following system of equations: find $(u,v):\mathrm{\Omega }\times J\to \mathbb{R}$ satisfy

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }u-\kappa \Delta (-{\epsilon }^2\Delta u+f(u))=g(\mathbf{x},t),(\mathbf{x},t)\in \mathrm{\Omega }\times J,\hfill \\ u(\mathbf{x},0)=u_0(\mathbf{x}),\mathbf{x}\in \mathrm{\Omega },\hfill \\ {\partial }_{n}u={\partial }_n({\epsilon }^2\Delta u+f(u))=0,(\mathbf{x},t)\in \partial \mathrm{\Omega }\times J.\hfill \end{array}\right.\end{array}$$

The ROECNMFE solutions can be solved in the following four steps.

Step 1. Calculate out two sets of initial $L=20$ CNMFE solution coefficient vectors ${\mathit{\xi }}^{\mathbf{1}},{\mathit{\xi }}^{\mathbf{2}},\mathit{\dots },{\mathit{\xi }}^{\mathbf{20}}$ by Problem 5. Here, the nonlinear system at each time step is solved using the Newton-Raphson iterative method. These vectors are used to compose two snapshot matrices ${\mathbf{G}}_{\mathbf{i}}=({\mathit{\xi }}^{\mathbf{1}},{\mathit{\xi }}^{\mathbf{2}},\dots ,{\mathit{\xi }}^{\mathbf{20}})(i=1,2,\mathit{\xi }={\mathbf{U}}_{\mathbf{h}},{\mathbf{V}}_{\mathbf{h}})$, when $\epsilon =1,\alpha =0.2$(in different calculation examples, parameters can be changed).

Step 2. By using the technique in Section 3.1, calculate four sets of non-negative eigenvalues ${\lambda }_{i,1}\ge {\lambda }_{i,2}\ge \dots \ge {\lambda }_{i,20}\ge 0$ and the corresponding four sets of orthonormal eigenvectors ${\overline{\mathsf{\Phi }}}_{\mathit{i},\mathit{j}}(i=1,2,1\le j\le 20)$ for matrices ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}(i=1,2)$.

Step 3. By estimating, we come to the conclusion that $\sqrt{{\lambda }_{1,3}}+\sqrt{{\lambda }_{2,3}}\le 7.6104\times {10}^{-15}$. Thereupon, with two sets of formulas ${\mathit{\phi }}_{\mathit{i},\mathit{j}}=\frac{{\mathbf{G}}_{\mathbf{i}}{\mathit{\delta }}_{\mathit{i},\mathit{j}}\sqrt{{\lambda }_{i,j}}}{(}i=1,2,1\le j\le 3$ and the eigenvector ${\mathit{\delta }}_{\mathit{i},\mathit{j}}$ of ${{\mathbf{G}}_{\mathbf{i}}}^T{\mathbf{G}}_{\mathbf{i}}$). We obtain four POD bases ${\mathsf{\Phi }}_{\mathit{i}}=({\mathit{\phi }}_{\mathit{i},\mathbf{1}},{\mathit{\phi }}_{\mathit{i},\mathbf{2}},{\mathit{\phi }}_{\mathit{i},\mathbf{3}})(i=1,2)$.

Step 4. By substituting ${\mathsf{\Phi }}_{\mathbf{i}}$ into Problem 6, we calculate the ROECNMFE solutions.

According to the above calculation steps, we designed two sets of experiments with parameters $\alpha =0.1,0.2,0.4,$$0.5,0.8,0.9$ and $\epsilon =1,0.1,0.01$. The key findings are summarized as follows:

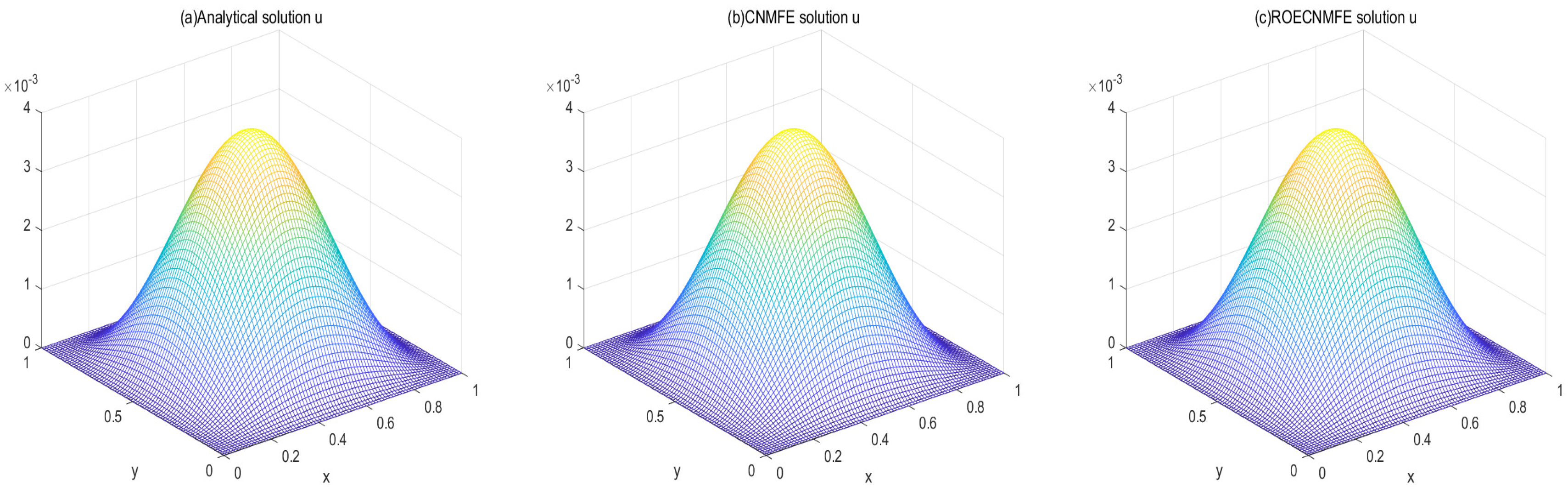
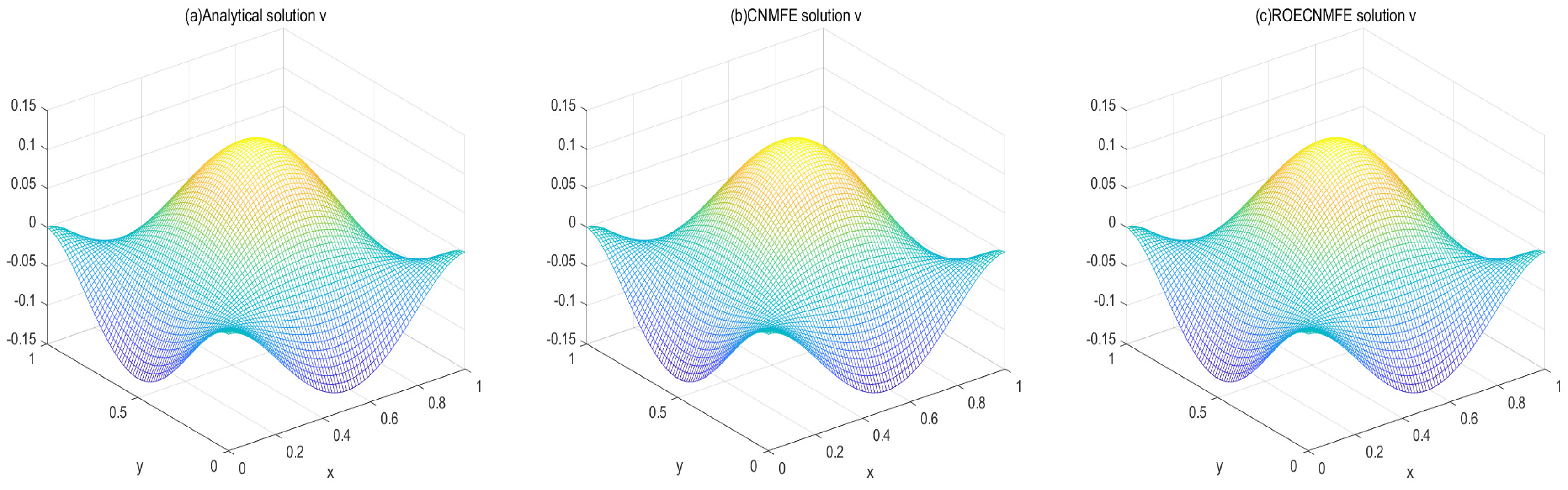
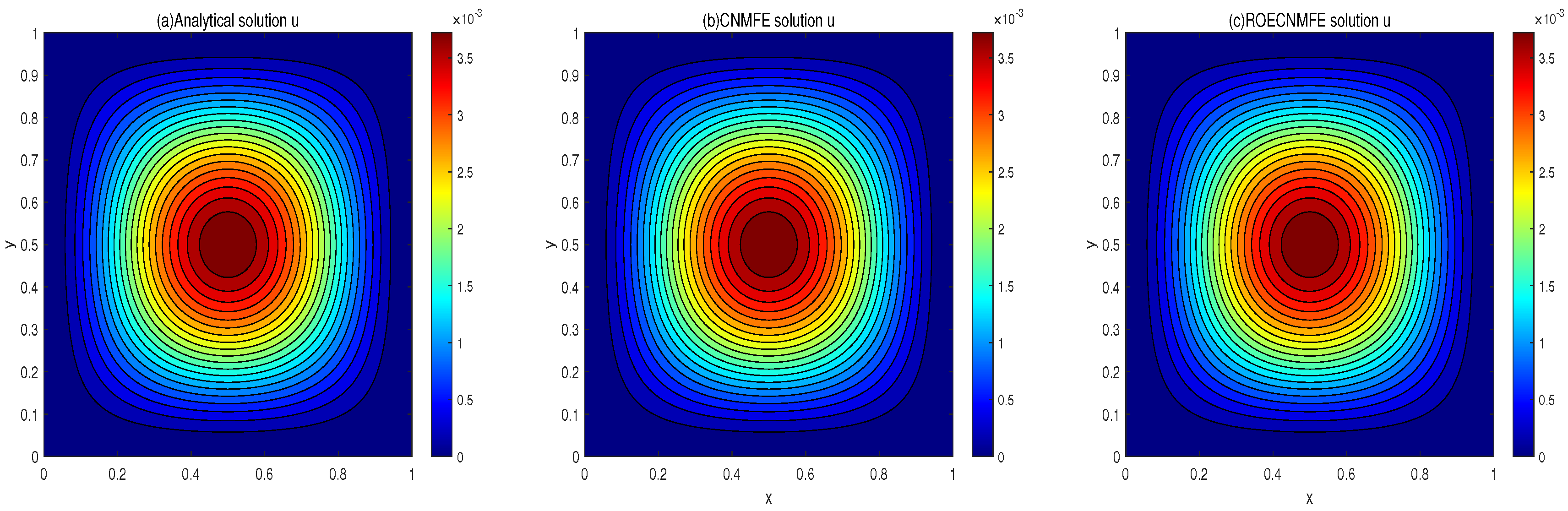
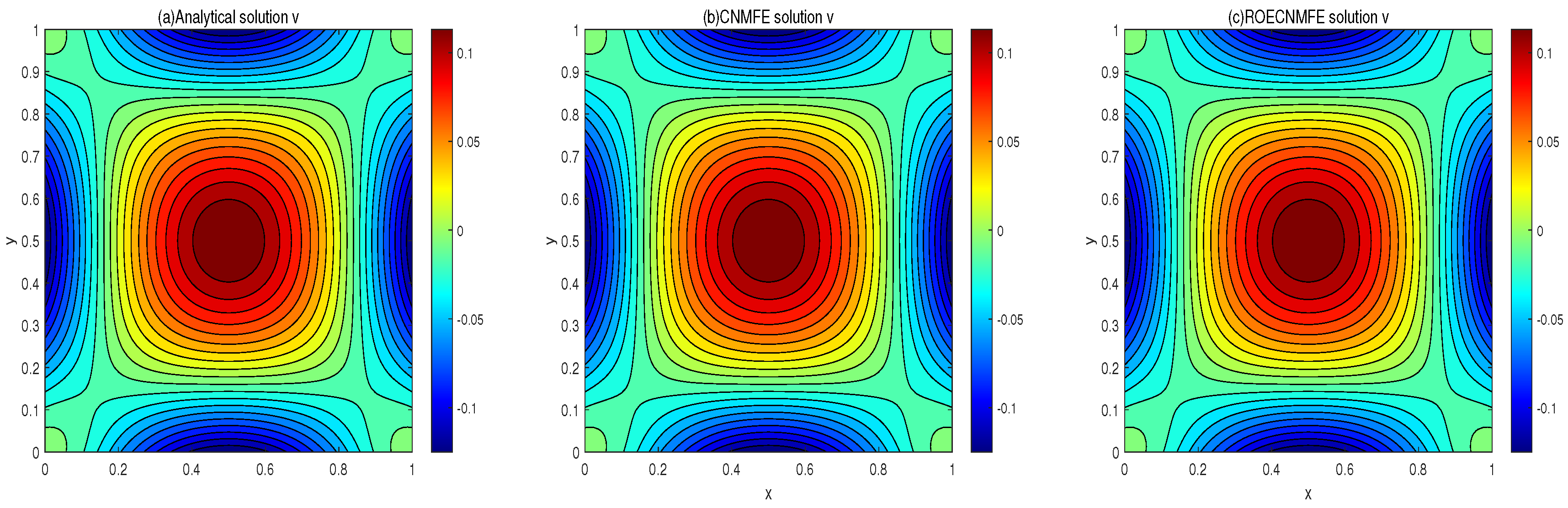
(i) Surface and contour plots at $t=T$ compare the analytical solution with the CNMFE and ROECNMFE solutions for u and v. The three sets of results are visually nearly identical.

(ii) The $L^2$ errors and convergence orders for both variables were computed under different $\alpha$ and $\epsilon$.

(iii) Under the same experimental setup, the CPU time of the ROECNMFE method is only about $1/60$ of that required by the CNMFE method, highlighting the significant computational advantage of the reduced-order approach.

Example 1.

Consider the source term $g(x,t)=cos(\pi x)cos(\pi y)(\frac{2}{\mathrm{\Gamma }(3-\alpha )}{t}^{2-\alpha }+2\kappa {\pi }^2{t}^2(2{\pi }^2{\epsilon }^2+cos(t^{2}cos(\pi x)cos(\pi y))))+\kappa {\pi }^2{t}^{4}sin(t^{2}cos(\pi x)cos(\pi y))({sin}^2(\pi x){cos}^2(\pi y)+{cos}^2(\pi x)$${sin}^2(\pi y))$. $f(u)=sinu$, $u(x,y,t)=t^{2}cos(\pi x)cos(\pi y),\mathrm{\Omega }=[-1,1]\times [-1,1]$, with parameters κ = 1 and ε = 1, 0.1, 0.01. The computational domain is discretized using spatial step size $h=2/100$ and temporal step size $\Delta t=T/1000$.

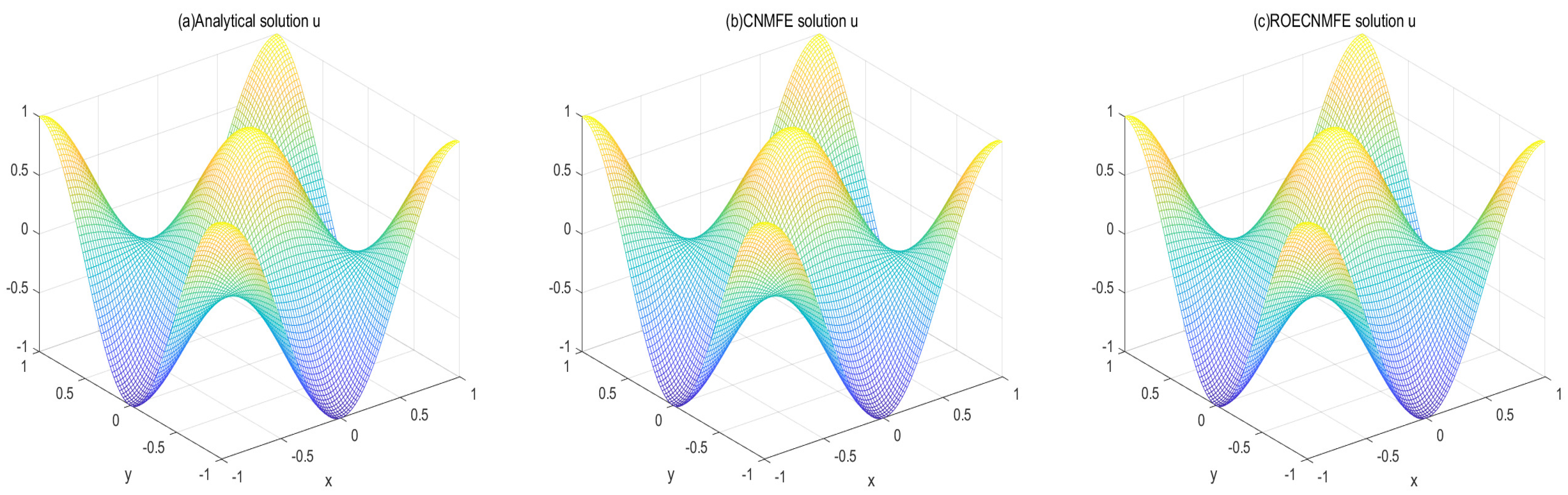
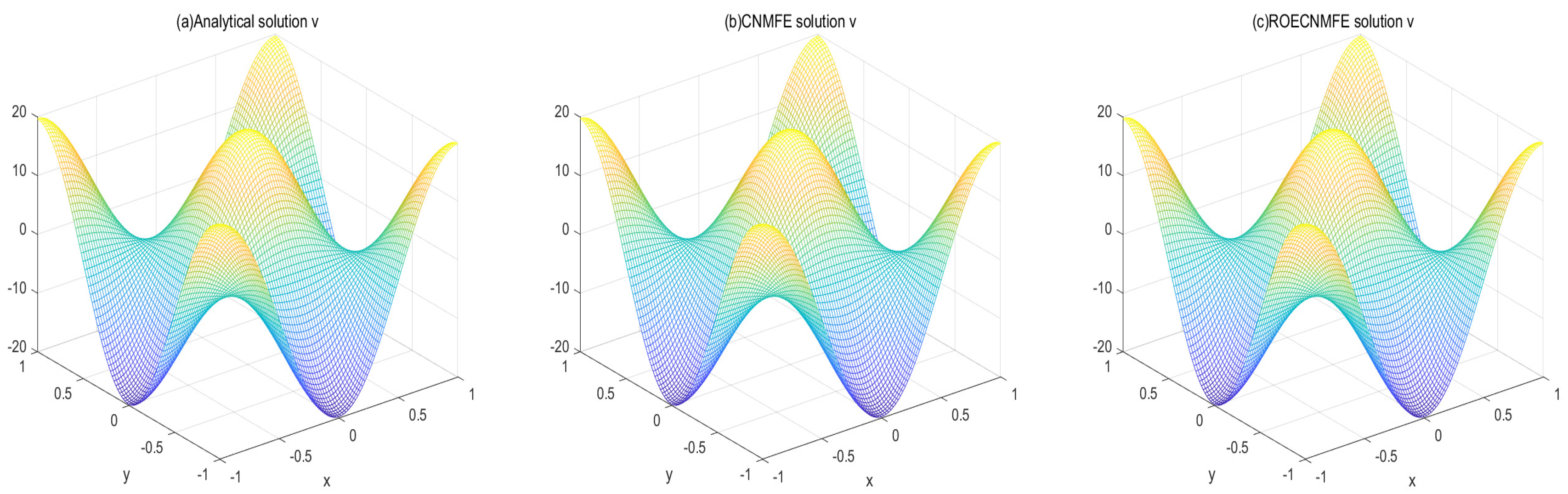
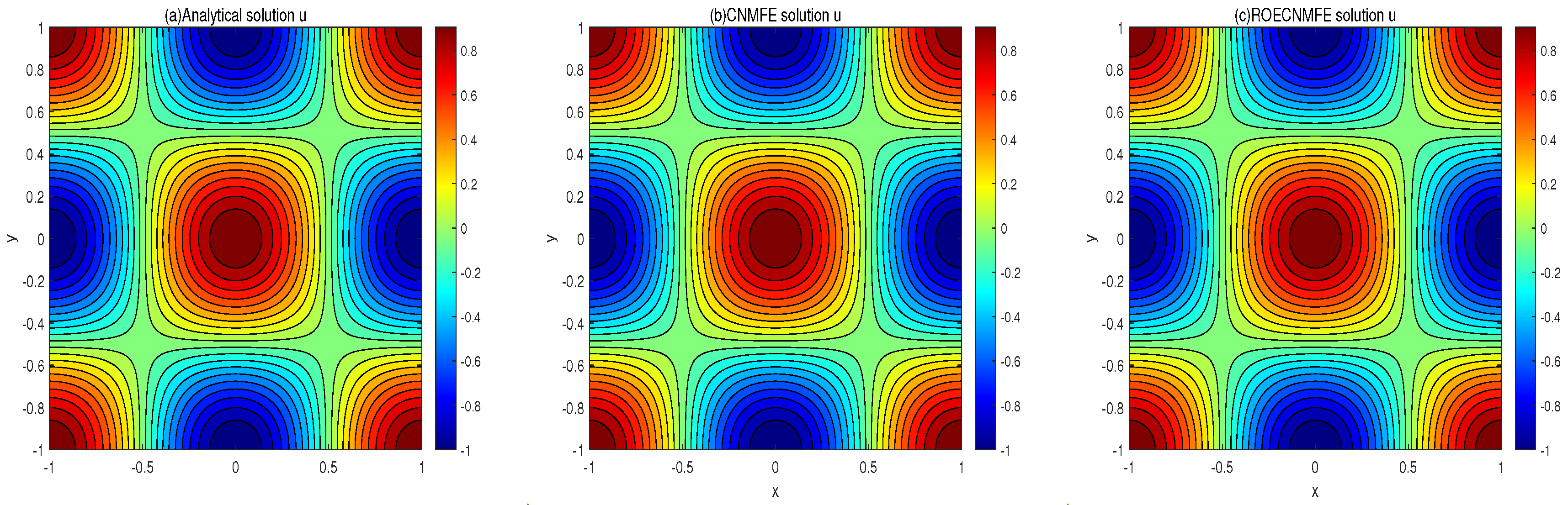
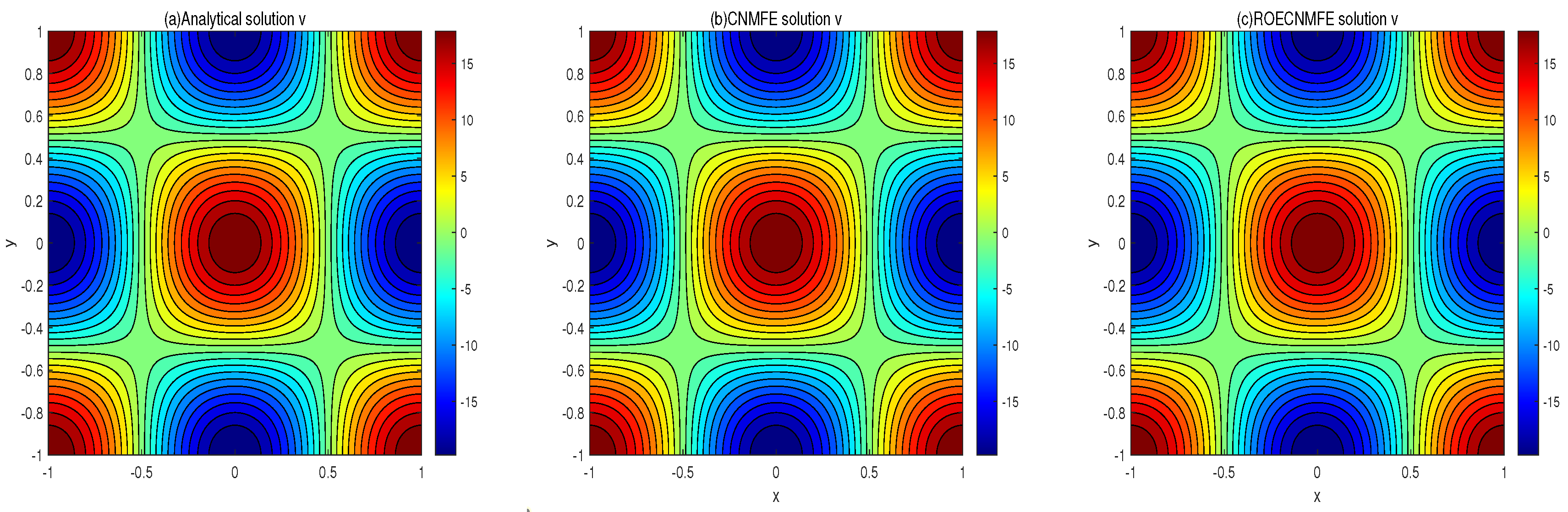
Figure 1 and Figure 2 compare the analytical, CNMFE, and ROECNMFE solutions for variables u and v at $T=1$, respectively. The three solutions in each figure show close visual agreement. Similarly, Figure 3 and Figure 4 present contour plots of the same solutions at $T=1$, where the contour distributions are nearly identical across all three methods. These comparisons preliminarily demonstrate the effectiveness of the proposed scheme in solving the time-fractional fourth-order nonlinear diffusion equation. To further quantify the accuracy, we conducted two sets of experiments: (i) with $\epsilon =1$ fixed and $\alpha =0.2,0.4,0.8$. (ii) with $\alpha =0.5$ fixed and $\epsilon =1,0.1,0.01$. In each case, the $L^2$ errors and convergence orders were computed for both the CNMFE and ROECNMFE solutions against the analytical solution.

Table 1. Comparison of the Error and Order of Convergence for the Two Methods (u at $T=1$, $\epsilon =1$).

	Norm	$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$		$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{d}}^{\mathit{n}}\parallel$
$\mathit{\alpha }$	Mesh	Error	Order	Error	Order
0.2	$8\times 8$	$1.0287\times {10}^{-1}$	—	$1.0287\times {10}^{-1}$	—
	$16\times 16$	$2.6585\times {10}^{-2}$	1.952	$2.6585\times {10}^{-2}$	1.9525
	$32\times 32$	$6.7018\times {10}^{-3}$	1.988	$6.7018\times {10}^{-3}$	1.988
	$64\times 64$	$1.6789\times {10}^{-3}$	1.997	$1.6789\times {10}^{-3}$	1.997
0.4	$8\times 8$	$1.0282\times {10}^{-1}$	—	$1.0282\times {10}^{-1}$	—
	$16\times 16$	$2.6573\times {10}^{-2}$	1.952	$2.6573\times {10}^{-2}$	1.952
	$32\times 32$	$6.6986\times {10}^{-3}$	1.988	$6.6986\times {10}^{-3}$	1.988
	$64\times 64$	$1.6781\times {10}^{-3}$	1.997	$1.6781\times {10}^{-3}$	1.997
0.8	$8\times 8$	$1.0273\times {10}^{-1}$	—	$1.0273\times {10}^{-1}$	—
	$16\times 16$	$2.6547\times {10}^{-2}$	1.952	$2.6547\times {10}^{-2}$	1.995
	$32\times 32$	$6.6917\times {10}^{-3}$	1.988	$6.6917\times {10}^{-3}$	1.998
	$64\times 64$	$1.6760\times {10}^{-3}$	1.997	$1.6760\times {10}^{-3}$	1.999

,

Table 2. Comparison of the Error and Order of Convergence for the Two Methods (v at $T=1$, $\epsilon =1$).

	Norm	$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{h}}^{\mathit{n}}\left|\right|$		$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{d}}^{\mathit{n}}\left|\right|$
$\mathit{\alpha }$	Mesh	Error	Order	Error	Order
0.2	$8\times 8$	$1.1953$	—	$1.1953$	—
	$16\times 16$	$2.9881\times {10}^{-1}$	2.000	$2.9881\times {10}^{-1}$	2.000
	$32\times 32$	$7.4707\times {10}^{-2}$	2.000	$7.4707\times {10}^{-2}$	2.000
	$64\times 64$	$1.8677\times {10}^{-2}$	2.000	$1.8677\times {10}^{-2}$	2.000
0.4	$8\times 8$	$1.1945$	—	$1.1945$	—
	$16\times 16$	$2.9859\times {10}^{-1}$	2.000	$2.9859\times {10}^{-1}$	2.000
	$32\times 32$	$7.4651\times {10}^{-2}$	2.000	$7.4651\times {10}^{-2}$	2.000
	$64\times 64$	$1.8663\times {10}^{-2}$	2.000	$1.8663\times {10}^{-2}$	2.000
0.8	$8\times 8$	$1.1929$	—	$1.1929$	—
	$16\times 16$	$2.9815\times {10}^{-1}$	2.000	$2.9815\times {10}^{-1}$	2.000
	$32\times 32$	$7.4530\times {10}^{-2}$	2.000	$7.4530\times {10}^{-2}$	2.000
	$64\times 64$	$1.8626\times {10}^{-2}$	2.001	$1.8626\times {10}^{-2}$	2.001

,

Table 3. Comparison of the Error and Order of Convergence for the Two Methods (u at $T=1$, $\alpha =0.5$).

	Norm	$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$		$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{d}}^{\mathit{n}}\parallel$
$\mathit{\epsilon }$	Mesh	Error	Order	Error	Order
1	$8\times 8$	$1.0280\times {10}^{-1}$	—	$1.0280\times {10}^{-1}$	—
	$16\times 16$	$2.6567\times {10}^{-2}$	1.952	$2.6567\times {10}^{-2}$	1.952
	$32\times 32$	$6.6970\times {10}^{-3}$	1.988	$6.6970\times {10}^{-3}$	1.988
	$64\times 64$	$1.6777\times {10}^{-3}$	1.997	$1.6777\times {10}^{-3}$	1.997
0.1	$8\times 8$	$7.9464\times {10}^{-2}$	—	$7.9464\times {10}^{-2}$	—
	$16\times 16$	$2.0037\times {10}^{-2}$	1.988	$2.0037\times {10}^{-2}$	1.988
	$32\times 32$	$5.0168\times {10}^{-3}$	1.998	$5.0168\times {10}^{-3}$	1.998
	$64\times 64$	$1.2525\times {10}^{-3}$	2.002	$1.2525\times {10}^{-3}$	2.002
0.01	$8\times 8$	$3.5011\times {10}^{-2}$	—	$3.5011\times {10}^{-2}$	—
	$16\times 16$	$8.2977\times {10}^{-3}$	2.077	$8.2977\times {10}^{-3}$	2.077
	$32\times 32$	$2.0455\times {10}^{-3}$	2.020	$2.0455\times {10}^{-3}$	2.020
	$64\times 64$	$5.0899\times {10}^{-4}$	2.007	$5.0899\times {10}^{-4}$	2.007

and

Table 4. Comparison of the Error and Order of Convergence for the Two Methods (v at $T=1$, $\alpha =0.5$).

	Norm	$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{h}}^{\mathit{n}}\left|\right|$		$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{d}}^{\mathit{n}}\left|\right|$
$\mathit{\epsilon }$	Mesh	Error	Order	Error	Order
1	$8\times 8$	$1.1941$	—	$1.1941$	—
	$16\times 16$	$2.9848\times {10}^{-1}$	2.000	$2.9848\times {10}^{-1}$	2.000
	$32\times 32$	$7.4622\times {10}^{-2}$	2.000	$7.4622\times {10}^{-2}$	2.000
	$64\times 64$	$1.8655\times {10}^{-2}$	2.000	$1.8655\times {10}^{-2}$	2.000
0.1	$8\times 8$	$8.2288\times {10}^{-3}$	—	$8.2288\times {10}^{-3}$	—
	$16\times 16$	$1.9690\times {10}^{-3}$	2.063	$1.9690\times {10}^{-3}$	2.063
	$32\times 32$	$4.8643\times {10}^{-4}$	2.017	$4.8643\times {10}^{-4}$	2.017
	$64\times 64$	$1.2098\times {10}^{-4}$	2.007	$1.2098\times {10}^{-4}$	2.007
0.01	$8\times 8$	$1.2004\times {10}^{-4}$	—	$1.2004\times {10}^{-4}$	—
	$16\times 16$	$2.9311\times {10}^{-5}$	2.034	$2.9311\times {10}^{-5}$	2.034
	$32\times 32$	$7.3014\times {10}^{-6}$	2.005	$7.3014\times {10}^{-6}$	2.005
	$64\times 64$	$1.8424\times {10}^{-6}$	1.987	$1.8424\times {10}^{-6}$	1.987

present the numerical errors and convergence orders under successive spatial refinement ($h\to h/2$) and a fixed time step $\Delta t=1/1000$. The results indicate that for different fractional orders $\alpha$, both the CNMFE and ROECNMFE schemes yield nearly identical error estimates for the variables u and v, and consistently achieve second-order convergence—in full agreement with theoretical predictions. It is also observed that smaller values of $\epsilon$ lead to smaller numerical errors. To further assess computational performance, we compare the CPU runtimes of the CNMFE and ROECNMFE methods.

Theoretically, at each time level, the CNMFE method requires solving for $2\times {101}^2$ unknowns, whereas the ROECNMFE method only needs to dolve for $2\times 2^2$ unknowns. As a result, the ROECNMFE method is expected to have a significantly shorter CPU runtime. To validate this theoretical expectation, we compared the computation times of both methods on the same computer.

Table 5. Comparison of errors and CPU runtime for the CNMFE method and the ROECNMFE method.

Time Point	CPU Runtime (s)		Speed-Up
	CNMFE	ROECNMFE	Ratio
$T=1$	263.825	2.540	103.9
$T=2$	269.341	4.223	63.8
$T=3$	165.695	4.198	39.5
$T=4$	156.278	2.577	60.6

presents the CPU running time when the spatial step is $h=2/100$ and the time step is $\Delta t=0.5/1000,1/1000,2/1000$ and $3/1000$. The data unequivocally show that under identical conditions, the ROECNMFE method is faster than the CNMFE method, with a speed-up factor ranging from approximately 40 to 104 times across different time points. These findings highlight the considerable advantage of the ROECNMFE method in drastically reducing computational time.

Example 2.

Consider the source term $g(x,t)=\frac{2t^{2-\alpha }}{\mathrm{\Gamma }(3-\alpha )}\varphi (x,y)-\kappa t^2(\Delta \varphi -{\epsilon }^2{\Delta }^2\varphi )$, $f(u)=u$, $u(x,y,t)=t^2\varphi$, $\varphi (x,y)={(x(1-x)y(1-y))}^2,\mathrm{\Omega }=[0,1]\times [0,1]$, with parameters κ = 1 and ε = 1, 0.1, 0.01. The computational domain is discretized using spatial step size $h=1/80$ and temporal step size $\Delta t=T/1000$.

Figure 5 and Figure 6 compare the analytical, CNMFE, and ROECNMFE solutions for variables u and v at $T=1$, respectively. The three solutions in each figure show close visual agreement. Similarly, Figure 7 and Figure 8 present contour plots of the same solutions at $T=1$, where the contour distributions are nearly identical across all three methods. These comparisons preliminarily demonstrate the effectiveness of the proposed scheme in solving the time-fractional fourth-order nonlinear diffusion equation. To further quantify the accuracy, we conducted two sets of experiments: (i) with $\epsilon =0.1$ fixed and $\alpha =0.1,0.5,0.9$; (ii) with $\alpha =0.4$ fixed and $\epsilon =1,0.1,0.01$. In each case, the $L^2$ errors and convergence orders were computed for both the CNMFE and ROECNMFE solutions against the analytical solution.

Table 6. Comparison of the Error and Order of Convergence for the Two Methods (u at $T=1$, $\epsilon =0.1$).

	Norm	$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$		$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{d}}^{\mathit{n}}\parallel$
$\mathit{\alpha }$	Mesh	Error	Order	Error	Order
0.1	$8\times 8$	$6.5908\times {10}^{-5}$	—	$6.5908\times {10}^{-5}$	—
	$16\times 16$	$1.6955\times {10}^{-5}$	1.959	$1.6955\times {10}^{-5}$	1.959
	$32\times 32$	$4.2686\times {10}^{-6}$	1.990	$4.2686\times {10}^{-6}$	1.990
	$64\times 64$	$1.0690\times {10}^{-6}$	1.997	$1.0687\times {10}^{-6}$	1.998
0.5	$8\times 8$	$6.5593\times {10}^{-5}$	—	$6.5593\times {10}^{-5}$	—
	$16\times 16$	$1.6868\times {10}^{-5}$	1.959	$1.7545\times {10}^{-5}$	1.902
	$32\times 32$	$4.2458\times {10}^{-6}$	1.990	$4.2460\times {10}^{-6}$	2.046
	$64\times 64$	$1.0627\times {10}^{-6}$	1.998	$1.0628\times {10}^{-6}$	1.998
0.9	$8\times 8$	$6.5243\times {10}^{-5}$	—	$6.5242\times {10}^{-5}$	—
	$16\times 16$	$1.6757\times {10}^{-5}$	1.961	$1.6757\times {10}^{-5}$	1.961
	$32\times 32$	$4.2028\times {10}^{-6}$	1.995	$4.2030\times {10}^{-6}$	1.995
	$64\times 64$	$1.0380\times {10}^{-6}$	2.017	$1.0379\times {10}^{-6}$	2.017

,

Table 7. Comparison of the Error and Order of Convergence for the Two Methods (v at $T=1$, $\epsilon =0.1$).

	Norm	$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{h}}^{\mathit{n}}\left|\right|$		$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{d}}^{\mathit{n}}\left|\right|$
$\mathit{\alpha }$	Mesh	Error	Order	Error	Order
0.1	$8\times 8$	$1.8930\times {10}^{-5}$	—	$1.8930\times {10}^{-5}$	—
	$16\times 16$	$4.8458\times {10}^{-6}$	1.966	$4.8458\times {10}^{-6}$	1.966
	$32\times 32$	$1.2185\times {10}^{-6}$	1.992	$1.2185\times {10}^{-6}$	1.992
	$64\times 64$	$3.0505\times {10}^{-7}$	1.998	$3.0505\times {10}^{-7}$	1.998
0.5	$8\times 8$	$1.8849\times {10}^{-5}$	—	$1.8849\times {10}^{-5}$	—
	$16\times 16$	$4.8224\times {10}^{-6}$	1.967	$4.8224\times {10}^{-6}$	1.967
	$32\times 32$	$1.2130\times {10}^{-6}$	1.991	$1.2130\times {10}^{-6}$	1.991
	$64\times 64$	$3.0343\times {10}^{-7}$	1.999	$3.0343\times {10}^{-7}$	1.999
0.9	$8\times 8$	$1.8761\times {10}^{-5}$	—	$1.8761\times {10}^{-5}$	—
	$16\times 16$	$4.7956\times {10}^{-6}$	1.968	$4.7956\times {10}^{-6}$	1.968
	$32\times 32$	$1.2018\times {10}^{-6}$	1.997	$1.2018\times {10}^{-6}$	1.997
	$64\times 64$	$2.9728\times {10}^{-7}$	2.015	$2.9728\times {10}^{-7}$	2.015

,

Table 8. Comparison of the Error and Order of Convergence for the Two Methods (u at $T=1$, $\alpha =0.4$).

	Norm	$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{h}}^{\mathit{n}}\parallel$		$\parallel \mathit{u}({\mathit{t}}_{\mathit{n}})-{\mathit{u}}_{\mathit{d}}^{\mathit{n}}\parallel$
$\mathit{\epsilon }$	Mesh	Error	Order	Error	Order
1	$8\times 8$	$6.6827\times {10}^{-5}$	—	$6.6827\times {10}^{-5}$	—
	$16\times 16$	$1.7208\times {10}^{-5}$	1.957	$1.7208\times {10}^{-5}$	1.957
	$32\times 32$	$4.3334\times {10}^{-6}$	1.989	$4.3334\times {10}^{-6}$	1.990
	$64\times 64$	$1.0853\times {10}^{-6}$	1.997	$1.0852\times {10}^{-6}$	1.997
0.1	$8\times 8$	$6.5675\times {10}^{-5}$	—	$6.5675\times {10}^{-5}$	—
	$16\times 16$	$1.6891\times {10}^{-5}$	1.959	$1.6891\times {10}^{-5}$	1.959
	$32\times 32$	$4.2519\times {10}^{-6}$	1.990	$4.2520\times {10}^{-6}$	1.990
	$64\times 64$	$1.0646\times {10}^{-6}$	1.998	$1.0646\times {10}^{-6}$	1.998
0.01	$8\times 8$	$5.5042\times {10}^{-5}$	—	$5.5042\times {10}^{-5}$	—
	$16\times 16$	$1.4252\times {10}^{-5}$	1.949	$1.4252\times {10}^{-6}$	1.949
	$32\times 32$	$3.5996\times {10}^{-6}$	1.985	$3.5972\times {10}^{-6}$	1.986
	$64\times 64$	$9.0203\times {10}^{-7}$	1.997	$8.9797\times {10}^{-7}$	2.002

and

Table 9. Comparison of the Error and Order of Convergence for the Two Methods (v at $T=1$, $\alpha =0.4$).

	Norm	$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{h}}^{\mathit{n}}\left|\right|$		$\left|\right|\mathit{v}({\mathit{t}}_{\mathit{n}})-{\mathit{v}}_{\mathit{d}}^{\mathit{n}}\left|\right|$
$\mathit{\epsilon }$	Mesh	Error	Order	Error	Order
1	$8\times 8$	$1.9178\times {10}^{-3}$	—	$1.9178\times {10}^{-3}$	—
	$16\times 16$	$4.9141\times {10}^{-4}$	1.964	$4.9141\times {10}^{-4}$	1.964
	$32\times 32$	$1.2359\times {10}^{-4}$	1.991	$1.2367\times {10}^{-4}$	1.990
	$64\times 64$	$3.0945\times {10}^{-5}$	1.998	$3.0944\times {10}^{-5}$	1.999
0.1	$8\times 8$	$1.8870\times {10}^{-5}$	—	$1.9025\times {10}^{-5}$	—
	$16\times 16$	$4.8291\times {10}^{-6}$	1.966	$4.8301\times {10}^{-6}$	1.978
	$32\times 32$	$1.2141\times {10}^{-6}$	1.992	$1.2652\times {10}^{-6}$	1.933
	$64\times 64$	$3.0390\times {10}^{-7}$	1.998	$3.0390\times {10}^{-7}$	2.056
0.01	$8\times 8$	$2.5973\times {10}^{-7}$	—	$2.5973\times {10}^{-7}$	—
	$16\times 16$	$6.4684\times {10}^{-8}$	2.005	$6.5069\times {10}^{-8}$	1.997
	$32\times 32$	$1.6081\times {10}^{-8}$	2.008	$1.6361\times {10}^{-8}$	1.992
	$64\times 64$	$4.0162\times {10}^{-9}$	2.001	$4.1754\times {10}^{-9}$	1.970

present the numerical errors and convergence orders under successive spatial refinement ($h\to h/2$) and a fixed time step $\Delta t=1/1000$. The results indicate that for different fractional orders $\alpha$, both the CNMFE and ROECNMFE schemes yield nearly identical error estimates for the variables u and v, and consistently achieve second-order convergence in full agreement with theoretical predictions. It is also observed that smaller values of $\epsilon$ lead to smaller numerical errors. To further assess computational performance, we compare the CPU runtimes of the CNMFE and ROECNMFE methods.

Theoretically, at each time level, the CNMFE method requires solving for $2\times {101}^2$ unknowns, whereas the ROECNMFE method only needs to solve for $2\times 2^2$ unknowns. As a result, the ROECNMFE method is expected to have a significantly shorter CPU runtime. To validate this theoretical expectation, we compared the computation times of both methods on the same computer.

Table 10. Comparison of errors and CPU runtime for the CNMFE method and the ROECNMFE method.

Time Point	CPU Runtime (s)		Speed-Up
	CNMFE	ROECNMFE	Ratio
$T=0.5$	171.928	3.195	53.8
$T=1$	167.136	3.286	50.9
$T=2$	316.584	6.442	49.1
$T=3$	332.517	6.383	52.1

presents the CPU running time when the spatial step is $h=2/100$ and the time step is $\Delta t=0.5/1000,1/1000,2/1000$ and $3/1000$. The data unequivocally show that under identical conditions, the ROECNMFE method is faster than the CNMFE method, with a speed-up factor ranging from approximately 50 times across different time points. These findings highlight the considerable advantage of the ROECNMFE method in drastically reducing computational time.

5. Conclusions

This paper investigates a nonlinear fourth-order diffusion equation with a time-fractional derivative. By introducing an auxiliary variable $v=-{\epsilon }^2\Delta u+f(u)$, the original equation is reformulated into a second-order coupled system. A CNMFE scheme is constructed, which achieves $(2-\alpha )$ order temporal accuracy and high-precision spatial approximations for both u and v. The numerical stability is rigorously established using a discrete fractional $Gr\ddot{o}nwall$ inequality, and detailed error estimates are derived. Numerical examples confirm the theoretical correctness and convergence order of the scheme. To alleviate the high computational cost resulting from the large number of degrees of freedom in the CNMFE model, a dimensionality reduction technique is applied to the solution coefficient vectors. Proper orthogonal decomposition is performed on snapshots from a small number of time steps to construct a low-dimensional ROECNMFE model. Theoretical analysis and numerical experiments show that the ROECNMFE model preserves the second-order convergence accuracy of the CNMFE scheme, while reducing the degrees of freedom from tens of thousands to only a few. As a result, the computational time is shortened to approximately $1/60$ of that required by the CNMFE model, demonstrating a significant improvement in computational efficiency and storage requirements.

Although the proposed method achieves promising results in simulating fourth-order nonlinear diffusion equations, several directions warrant further investigation. Future work may extend the approach to more complex models, such as coupled reaction–diffusion systems, variable-coefficient fourth-order equations, or other types of fractional partial differential equations. The method could be extended to higher-dimensional problems, and corresponding computational frameworks should be developed to address larger-scale practical engineering simulations.