Abstract
The segmentation analysis of the Golding–Cox mRNA dataset clarifies the description of these trajectories as a Fractional Lévy Stable Motion (FLSM). The FLSM method has several important advantages. Using only a few parameters, it allows for the detection of jumps in segmented trajectories with non-Gaussian confined parts. The value of each parameter indicates the contribution of confined segments. Non-Gaussian features in mRNA trajectories are attributed to trajectory segmentation. Each segment can be in one of the following diffusion modes: free diffusion, confined motion, and immobility. When free diffusion segments alternate with confined or immobile segments, the mean square displacement of the segmented trajectory resembles subdiffusion. Confined segments have both Gaussian (normal) and non-Gaussian statistics. If random trajectories are estimated as FLSM, they can exhibit either subdiffusion or Lévy diffusion. This approach can be useful for analyzing empirical data with non-Gaussian behavior, and statistical classification of diffusion trajectories helps reveal anomalous dynamics.
1. Introduction
The study of trajectories, resulting from single-molecule microscopy and imaging technologies, is very popular for understanding biological processes within living cells [1,2,3,4]. This method is known as single-particle tracking (SPT). The SPT data often show different types of diffusion [5,6,7]. In addition to ordinary diffusion, there are directed and confined motions. The cytoplasmic particles exhibit large jumps, which could be attributed to metabolic activities [8]. In many cases the confined diffusion is a result of the “crowding effect”, as 40% of the cell volume is occupied by biomacromolecules [9]. In general, trajectories may have anomalous behavior resembling subdiffusion and superdiffusion [10]. Estimation of mean square displacement (MSD) in random trajectories is often used to distinguish diffusion types [11]. However, due to a number of causes (finite localization precision of observations, stochastic nature of particle motion, and others), it is not easy to extract unambiguous information from MSDs [12]. Moreover, the movement of individual molecules tends to switch diffusion types even within the same trajectory. This effect within a trajectory is called segmentation. In this case, each segment appears in one from different diffusive modes. If the MSD method does not account for the segmentation in such a trajectory, then it provides a result that is too rough. Consequently, it is not surprising that a trajectory consisting of alternating segments of normal diffusion and confined movement may overall appear to exhibit subdiffusion. A more accurate method uses the model of fractional Lévy stable motion (FLSM) [13,14]. The stochastic process is characterized by the memory parameter d, where the sign of d reflects the diffusion behavior. FLSM incorporates jumps typical for the Lévy stable motion. This extension is appropriate because it accounts for the jumps detected in SPT trajectories. Until recently, the reason for their appearance in trajectories remained unclear. An in-depth study of confined segments and their statistics opens up new opportunities for understanding the role of FLSM in describing SPT trajectories. Let us examine it in greater detail from this perspective.
Pioneering experiments by Golding, Cox, and co-workers [15,16,17] examined the random motion of mRNA molecules inside E. coli cells. According to their study, the trajectories of molecules resemble subdiffusion. This suggests a dominant interaction between molecules and obstacles in their surroundings. However, the behavior can be caused by various physical origins. In particular, the fractional Brownian motion (FBM) has a power-law trend for MSD. Subdiffusion is also typical for Brownian motion subordinated by an inverse α-stable process. In addition, there are other reasons that lead to subdiffusion [18]. Let us recall here the result of [19]. Based on a statistical test for subdiffusive dynamics the authors proved that the best description for the evolution of mRNA molecules is not determined by either continuous time random walk (CTRW) or FBM models. This prompted others to further analyze the Golding–Cox data using various statistical tools [20,21,22]. Although FBM is a Gaussian, non-stationary, self-similar process, it does not always correspond to empirical data. The FLSM model is one of the promising approaches [23]. It extends the FBM model to stable laws. Therefore, the FLSM model has wider possibilities for studying both extreme local irregularity and scaling behavior in single-particle experiments. On the one hand, FLSM is a very natural extension of FBM, and on the other hand, it helps to detect heavy tails in experimental data. Unfortunately, as noted above, it does not give clear answers to all questions. One of the most important questions concerns the reason for Lévy jumps in the Golding–Cox trajectories. Another equally important question is what causes subdiffusive behavior in the data. In this article, the trajectories from the Golding and Cox experiments are classified differently. We use a new special algorithm for the transient motion analysis of molecular trajectories, termed “divide-and-conquer moment scaling spectrum” (DC–MSS) [24]. Using the DC–MSS classification, trajectory segments are identified according to diffusive modes. This allows us to clarify the FLSM description as applied to the Golding–Cox mRNA dataset and to answer the questions asked.
2. Fractional Lévy Stable Motion
Our consideration starts with a brief overview of the FLSM and its features. The standard Brownian motion
can be generalized by the
to integration over
as
where
, and
. The stochastic process
describes the FBM, which is characterized by the Hurst parameter
and is responsible for both the long-range memory and fractal properties of its trajectories [14,25]. If
, the process
simplifies to the standard Brownian motion
. When
(or
), the increments of
exhibit negative correlation and negative long-range dependence. Conversely, when
(or
), they show positive correlation, indicating positive long-term dependence. Note that this behavior is determined by the kernel function of Equation (1).
The FLSM process is more general than
[26,27,28]. It has a non-Gaussian distribution and is expressed in terms of the following formula:
where
is a Lévy
-stable motion (LSM), and the memory parameter d depends on
and
as the equality
[28]. Here, the kernel function also plays an important role. In the case of
it has singularities, when
and
. But, for
the kernel is bounded and positive at all
. Therefore, for
(
) the increments of the process are positively long-range dependent and typical for superdiffusion, while the negative dependence
(
) leads to another behavior, subdiffusion. The parameter
indicates stationary increments following an
-stable distribution. Moreover, this process, like FBM with
for every
, is H-self-similar, i.e.,
, where
means identical distributions. Such a variety of properties in the FLSM makes it very useful for different applications [14,27,29,30,31]. It is easy to see in Equation (2) that when
, the FLSM becomes the mean-zero Gaussian process
as a partial case.
The experimental data analysis uses a discrete-time data series. Denote the sample as
of length
. The sample MSD is written as
Let us also introduce its incremental process
. If the sample behaves H-self-similar Lévy
-stable, for a large N the value of
depends on the memory parameter d, namely
where
means similarity in distribution and
[32]. Since
is a random variable, it can play the role of superstatistics [33] due to to the randomization of the parameter d, which varies from trajectory to trajectory. Superstatistics is based on a model with random parameters that remain fixed for each trajectory [34]. It can be explained as each observed trajectory depends on its own neighborhood, which has distinct properties affecting the motion [35]. However, these properties are supposed to not vary significantly at temporal and spatial scales (slow environmental fluctuations) specific to the observed trajectories [36]. As a consequence, the sign of d determines the character of anomalous diffusion in the sample
. For
(or
), it has subdiffusive dynamics, whereas for
(or
), the sample is superdiffusive.
Applying experimental data analysis, the classification of samples (trajectories) as the FLSM involves several testing procedures [23]. First, we determine the parameter
from the
-stable hypothesis for the displacement distribution. This step utilizes a regression-based method to the increments, separately for both coordinates. The sample MSD exponent for the FLSM model depends on the Hurst parameter H and is given by
. Specifically, we can express the memory parameter d as
.
3. Segment Analysis of Diffusive Trajectories
Otherwise, a segment analysis of single-particle trajectories is constructed. We assume that each trajectory can comprise segments of different lengths, and the segments exhibit different types of diffusion. First, we identify the segments within the trajectories, and subsequently, we estimate their probabilistic properties.
3.1. Identification of Motion Switches
There are several ways for detecting the motion switch between different types of diffusion. Most transient study algorithms employ either a rolling analysis window [37] or many-state hidden Markov models [38], but each of them has its drawbacks [24]. To mitigate these drawbacks, a newly popular transient analysis algorithm—referred to as DC–MSS—has emerged. It includes three steps. The first step begins with calculating a local movement descriptor based on the maximum pairwise distance (MPD) between particle positions inside a window. The distance value reflects the extent of a molecule’s movement. The smallest value is typical for immobile diffusion, while the largest corresponds to the directed motion. Segments exhibiting confined and free diffusion fall within intermediate MPD values. Consequently, a rule like MPD (immobile) < MPD (confined) < MPD (free) < MPD (directed) detects switching between different diffusion types. The second step is that the track segments found before are classified, using the moment scaling spectrum analysis of single-particle displacements. In the last step, this algorithm verifies the possibility of merging adjacent segments, correcting the initial track oversegmentation. More information about the DC-MSS classification procedure and computer codes can be found in [24]. Knowing where each segment starts and ends, we can analyze them separately and investigate their statistical properties. However, this approach substantially increases the amount of additional information to analyze and extends the overall analysis time.
3.2. Types of Confined Motion
Following our previous experience in studying SPT trajectories [39,40], we find that confined segments are nearly as common as free segments. Moreover, these confined trajectories and segments exhibit not only Gaussian statistics, but also non-Gaussian behavior. Gaussian confinement behavior is well-described by the Ornstein–Uhlenbeck model [41], which is typical for Brownian motion under a harmonic potential. The emergence of confined diffusion with non-Gaussian distributions has several possible origins [40]:
- •
- Brownian motion subordinated by special random processes;
- •
- coupled Langevin equations;
- •
- stochastic resetting.
The first case is based on the conjugate property of Bernstein functions. Consider the Laplace exponent of a tempered
-stable process given by
, where
is a positive constant and
. This process has a conjugate partner expressed as
. When the ordinary Brownian motion serves as the parent process, and the directing stochastic process is determined by the Laplace exponent of this conjugate partner, the subordinated process exhibits a stationary distribution in explicit Laplace form. In other words, the subordinator is responsible for the confinement with a Laplace distribution. Furthermore, this case can be generalized to confinement with the Linnik distribution.
In a system of coupled Langevin equations, one equation (related to Brownian motion) is “driven” by another (such as the Cox–Ingersoll–Ross process or a square root process) through the diffusion coefficient. This phenomenon is still referred to as the “diffusing diffusivity”. The stationary state for the system is described by a distribution known as the generalized Laplace or variance gamma distribution. One of its particular cases corresponds to the ordinary Laplace distribution.
Stochastic resetting describes the evolution of a stochastic system that repeatedly returns to a steady (or equilibrium) state. When the resetting process follows a power-law time distribution using the Mittag–Leffler function, Brownian motion under resetting exhibits confined diffusion with Laplace and Linnik distributions. On the other hand, if stochastic resetting occurs with exponentially distributed times, the confined diffusion motion follows the Laplace distribution, while power-law distributed times contribute to the Linnik distribution in confined modes. Notably, the Laplace distribution represents a specific case of the more general Linnik distribution.
Each of these models indicates conditions necessary for its implementation. The statistics of confined trajectories/segments shed light on physical processes responsible for the occurrence of confinement. In particular, G proteins of coupled receptors have the non-Gaussian confined diffusion in two types: Laplace and Linnik ones [39]. These distributions produce jump-like stochastic processes [42]. Let us recall here that the Linnik distribution is a generalization of the Laplace one, and the Linnik confined motion is characterized by a heavier tail in its distribution and longer jumps. Following [39], the SPT trajectories under confined diffusion can have both Gaussian and non-Gaussian distributions. The empirical data analysis includes two test procedures. The first uses the difference between normal and Laplace-like distributions in the logarithm of the ratio of maximized likelihoods [43]. The ratio depends on the mean, variance, and median of the time series, which are easy to calculate. If the ratio is greater than zero, then the sample satisfies the normal distribution. Otherwise, the sample has a non-Gaussian distribution (either Laplace or Linnik). The second test procedure uses the minimization of the objective function [44]. In fact, this method compares the empirical characteristic function, obtained for the data, with the theoretical one. The objective function is written as
where
, and
is a data sampling. It is important that the minimization allows one to estimate the parameter
. The value
approximately equal to 2 indicates the Laplace distribution, whereas
(especially far from 2) corresponds to the Linnik distribution. All this analysis reveals the statistical properties of any confined segment depending on its distribution: normal, Laplace, and Linnik. Let us also note that examining the ensemble of cytoplasmic RNA-protein particles reveals a Laplace distribution [45].
4. Transient Motion Classification Results for the Golding–Cox Data
In their experiments Golding, Cox, and co-workers directly measured trajectories of mRNA molecules where no organelles were present. Moreover, there are no known active transport mechanisms for mRNA and proteins. Therefore, the features of cytoplasmic subdiffusion can be investigated using direct tracking of individual particles. The dataset contains 27 trajectories of different lengths. Unfortunately, the original trajectories also contain missing values (gaps). Therefore, just like in the paper [23], we study only the longest parts of the trajectories that do not have gaps. On the other hand, this simplifies the process of comparing our results with ones obtained in that work. Results of the analysis based on the FLSM model are shown in Table 1. It should be noticed that they are similar for Tables 1 and 2 from [23]. However, unfortunately, those tables have confused values in the column with the memory parameter d. Our table corrects this inconvenience.

Table 1.
The parameters
, d and H are estimated for Golding–Cox trajectories using the FLSM model.
The segment analysis of the Golding–Cox trajectories shows that about half of the trajectories (thirteen) are single-segmented, five trajectories are two-segmented, four are three-segmented, two trajectories each have either four or five segments, and one trajectory is eight-segmented (see the histogram in Figure 1). Depending on the diffusive type, each segment will be designated by the first letter of its name: ‘i’ indicates immobile, ‘c’ denotes confined, and ‘f’ is free. Such classification indicates the most common diffusive modes among segments (Figure 2). The number of confined segments (31) predominates, free segments are slightly smaller (24), and there are only six immobile segments. The confined diffusion segments can be presented by the following types of statistics: Gaussian, Laplace, and Linnik ones (Table 2). The distributions of the two last types produce jump-like stochastic processes [42]. It should also be noticed that the confined diffusion modes may be different in statistics for each coordinate. The analysis of confined segments for the Golding–Cox trajectories detects all three kinds of statistics. This suggests jumps in such trajectories. Another cause of jumps may be the transient character of trajectories, i.e., switching between different diffusive modes. The classification results are also illustrated in Figure 3, which presents the longest continuous parts of 27 trajectories from the Golding–Cox mRNA dataset. As applied to the classification, we analyzed the x- and y-coordinates together. This figure clearly shows the dominance of confined and free segments despite the overlap of trajectories.
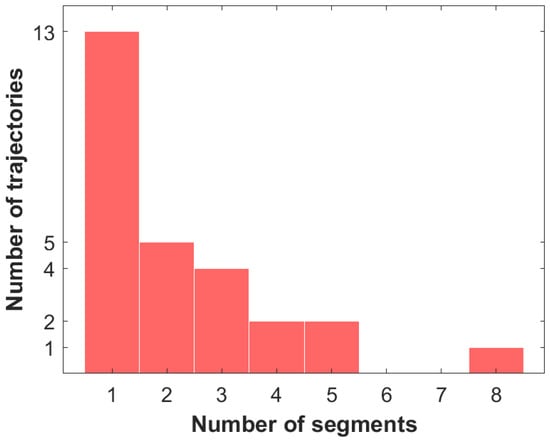
Figure 1.
Discrete distribution of Golding–Cox trajectories with respect to the number of segments.
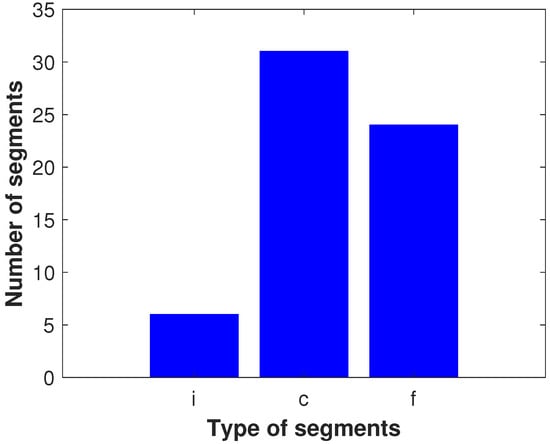
Figure 2.
Histogram of segments according to the type of diffusion.

Table 2.
Segmentation analysis of the Golding–Cox data. Statistics of confined segments are shown from left to right, according to the sequence of letters in their “words”.
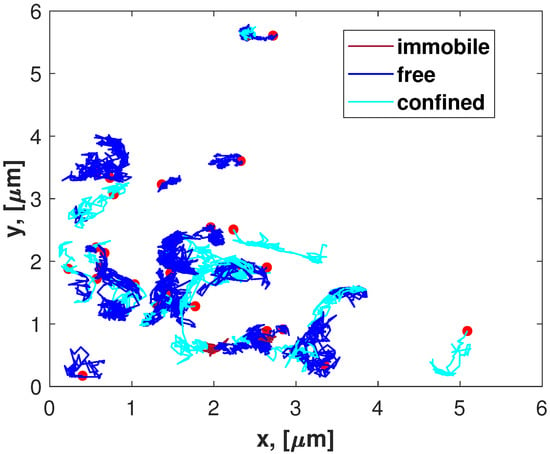
Figure 3.
The longest parts of trajectories from the Golding–Cox mRNA dataset marked according to the result of segment classification. The red circles indicate starting points of trajectories.
5. Simulation Study
An unpleasant feature of the Golding–Cox dataset is the small number of trajectories for statistical analysis. However, they also have different numbers of segments in different types of diffusion. This disadvantage can be compensated by numerical simulation of such random trajectories. To do this, we simulated 500 five-segment random trajectories, each 500 points long. In each simulated trajectory the even segments are confined, while the odd segments are free diffusion. Moreover, the segments are randomly long within 500 points. The free segments have the same diffusion coefficient and resemble one-dimensional Brownian motion. Within each trajectory, the confined segments are the same kind: either normal or Laplace or Linnik distribution. Thus, each trajectory can be written as the word ‘cfcfc’, and it was analyzed as FLSM. Consequently, we found their parameters (
, d and H).
Figure 4 displays histograms for three cases. The first case, denoted by (a), has only normal confined segments. The second case (b) corresponds to alternating free segments with Laplace confined ones. In the third case, the confined segments follow the Linnik distribution (with the index equal to 1.2). From these simulations we observe the following trends. When confined segments are too short, the trajectory closely resembles one-dimensional Brownian motion. In this scenario, the memory parameter d approaches 0,
approaches 2, and
equals 1/2. Longer confined segments lead to a negative change in the memory parameter d. Normal confinement has a minimal impact on the parameter
, which is typical for free segments. However, the Laplace and the Linnik distributions in confined segments result in a decrease in the value of
. This decrease indicates the contribution of jumps in the trajectory. Overall, the trajectory becomes similar to Lévy diffusion, as observed in [23]. Most of the d estimator values fall within the interval of approximately (−0.5, 0.1). The histograms show that negative values of d estimates are more probable than the positive ones. Interestingly, the Golding–Cox data exhibits similar behavior concerning the parameter d.
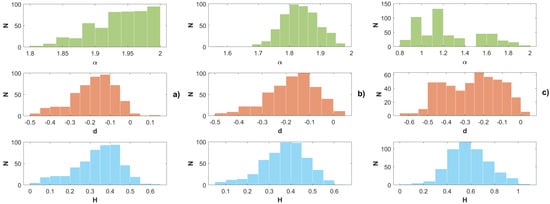
Figure 4.
Estimation of FLSM parameters in the form of their histograms after simulation of the segmented diffusion trajectories having (a) normal confined segments; (b) Laplace confined ones; and (c) Linnik confined ones.
These sets of simulated trajectories can be classified by the classical statistical hypothesis testing procedure named by Neymann–Pearson [46,47]. The classification of trajectories in diffusion types verifies the following hypotheses:
- •
- : a data sampling is free diffusion;
- •
- : a data sampling is subdiffusion;
- •
- : a data sampling is superdiffusion.
Next, we use the maximum (MAX) test [48]. Considering a trajectory traveled by a particle from a starting point during the time interval
, the largest distance reads
. The standardized maximal distance
of the trajectory takes the form
where
is a consistent estimator of the parameter
, namely
The important property of this approach is that the distribution of the random value
is independent of
for free diffusion. Given the distribution of the MAX test statistic
, we can estimate the value of
for each simulated trajectory from our sets. Specifically, we consider the quantiles of order
and
(for example,
= 5%). The decision rule is that
is typical for subdiffusion, whereas
indicates superdiffusion. If the MAX test gives
, then the trajectory corresponds to free diffusion. Consequently, this allows us to analyze the trajectories available for three cases mentioned above. Recall that they consist of two types of segments: free diffusion and confined diffusion. Moreover, confined segments can have three different distributions: normal, Laplace, and Linnik. Importantly, the statistical framework remains the same for each trajectory type. The classification result is presented in Table 3. None of the trajectories were detected as following superdiffusion. In the cases of (a) and (b), most of the trajectories (i.e., 57.8% and 52.4%, respectively) were classified as subdiffusive. However, trajectories with Linnik confined segments exhibit a different behavior: they show a dominance of free diffusion over subdiffusion. This behavior is connected with the heavier tail of the Linnik distribution. In real data, confined segments with such statistics are very rare. Notably, the classification results for cases (a) and (b) closely align with the percentages of the Golding–Cox trajectories classified into one of the three types of diffusion (as shown in Table 3 of [23]). The robustness of the simulated data was tested using different numbers of trajectories. The results remained very similar.

Table 3.
Percentages of the simulated trajectories classified into one of the three types of diffusion. The significance level
was set to 5%.
6. Discussion and Conclusions
The segmentation analysis of the Golding–Cox mRNA dataset provides clarity regarding the description of these trajectories as FLSM. The FLSM method offers several important advantages. By utilizing only a few parameters (, d and H), it enables the detection of jumps in segmented trajectories with non-Gaussian confined parts. Each parameter reflects the contribution of confined segments within the entire trajectory. Long confined segments contribute to the memory effects of their trajectory, resulting in a negative estimated memory parameter d. The parameter
, different of two, indicates jumps in the trajectory. These jumps originate from either Laplace or Linnik confined segments in trajectories, as well as transitions between diffusive modes. Trajectories containing only segments with normal statistics do not exhibit the typical jumps associated with Lévy diffusion. Note also that confined diffusion has the MSD exponent close to zero. In contrast, for free diffusion, the MSD value behaves proportionally to time. Since the number of confined segments dominates over the freely diffusing segments, the complete trajectories of mRNA molecules resemble subdiffusion, with the MSD expressed as a power function of time, where the MSD exponent is less than one.
Now it is clear why the FLSM description yields significantly better results than either CTRW or FBM. The point is that FLSM, unlike FBM and CTRW, naturally accounts for the heavy tails that are typical for the Golding–Cox experimental data. According to the statistical tests [23], the stable distribution hypothesis is acceptable for many trajectories in the dataset. This effect is hardwired into segments of SPT trajectories.
The FLSM method is no less useful than segment analysis. Although the latter is more sophisticated, it takes longer to obtain results. On the other hand, the FLSM approach can be employed to devise an adequate strategy for analyzing unknown experimental data. By knowing their parameters, it allows us to gain insights into the classification of the trajectories and, if necessary, to conduct a thorough analysis. Furthermore, the FLSM method can ensure that only trajectories with the required properties are selected, thereby reducing the time spent on detailed analysis. Therefore, its application to non-standard data is highly desirable.
Author Contributions
Conceptualization, A.A.S. and A.W.; Methodology, A.A.S. and A.W.; Software, A.A.S.; Formal analysis, A.W.; Investigation, A.W.; Writing—original draft, A.A.S. Writing—review and editing, A.A.S. and A.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data were obtained from I. Golding and E.C. Cox and are available from I. Golding and E.C. Cox with the permission of I. Golding and E.C. Cox.
Acknowledgments
The authors would like to thank I. Golding and E.C. Cox for providing the experimental data analyzed in Section 4 as well as J. Janczura and L. Kirichenko for useful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Saxton, M.J.; Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 373–399. [Google Scholar] [CrossRef]
- El Beheiry, M.; Dahan, M. High-speed localization microscopy and single-particle tracking. In Encyclopedia of Cell Biology; Bradshaw, R.A., Stahl, P.D., Eds.; Academic Press: Cambridge, MA, USA, 2016; Volume 2, pp. 121–128. [Google Scholar]
- Manzo, C.; Garcia-Parajo, M.F. A review of progress in single particle tracking: From methods to biophysical insights. Rep. Prog. Phys. 2015, 78, 124601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Welsher, K. Information-efficient, off-center sampling results in improved precision in 3D single-particle tracking microscopy. Entropy 2021, 23, 498. [Google Scholar] [CrossRef]
- Saxton, M.J. Anomalous diffusion due to obstacles: A Monte Carlo study. Biophys. J. 1994, 66, 394–401. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J. Single-particle tracking: The distribution of diffusion coefficients. Biophys. J. 1997, 72, 1744–1753. [Google Scholar] [CrossRef] [PubMed]
- Kowalek, P.; Loch-Olszewska, H.; Szwabiński, J. Classification of diffusion modes in single-particle tracking data: Feature-based versus deep-learning approach. Phys. Rev. E 2019, 100, 032410. [Google Scholar] [CrossRef]
- Parry, B.R.; Surovtsev, I.V.; Cabeen, M.T.; O’Hern, C.S.; Dufresne, E.R.; Jacobs-Wagner, C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell 2014, 156, 183–194. [Google Scholar] [CrossRef]
- Zhou, H.-X.; Rivas, G.; Minton, A.P. Macromolecular crowding and confinement: Biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008, 37, 375–397. [Google Scholar] [CrossRef]
- Weber, S.C.; Spakowitz, A.J.; Theriot, J.A. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys. Rev. Lett. 2010, 104, 238102. [Google Scholar] [CrossRef]
- Muñoz-Gil, G.; Garcia-March, M.A.; Manzo, C.; Martín-Guerrero, J.D.; Lewenstein, M. Single trajectory characterization via machine learning. New J. Phys. 2020, 22, 013010. [Google Scholar] [CrossRef]
- Han, D.; Korabel, N.; Chen, R.; Johnston, M.; Gavrilova, A.; Allan, V.J.; Fedotov, S.; Waigh, T.A. Deciphering anomalous heterogeneous intracellular transport with neural networks. eLife 2020, 9, e52224. [Google Scholar] [CrossRef] [PubMed]
- Stoev, S.; Taqqu, M.S. Simulation methods for linear fractional stable motion and FARIMA using the fast Fourier transform. Fractals 2004, 12, 95–121. [Google Scholar] [CrossRef]
- Weron, A.; Burnecki, K.; Mercik, S.; Weron, K. Complete description of all self-similar models driven by Lévy stable noise. Phys. Rev. E 2005, 71, 016113. [Google Scholar] [CrossRef] [PubMed]
- Golding, I.; Cox, E.C. RNA dynamics in live Escherichia coli cells. Proc. Natl. Acad. Sci. USA 2004, 101, 11310. [Google Scholar] [CrossRef] [PubMed]
- Golding, I.; Paulsson, J.; Zawilski, S.M.; Cox, E.C. Real-time kinetics of gene activity in individual bacteria. Cell 2005, 123, 1025. [Google Scholar] [CrossRef] [PubMed]
- Golding, I.; Cox, E.C. Physical nature of bacterial cytoplasm. Phys. Rev. Lett. 2006, 96, 098102. [Google Scholar] [CrossRef] [PubMed]
- Sikora, G.; Burnecki, K.; Wylomanska, A. Mean-squared-displacement statistical test for fractional Brownian motion. Phys. Rev. E 2017, 95, 032110. [Google Scholar] [CrossRef] [PubMed]
- Burnecki, K. Identification, Validation and Prediction of Fractional Dynamical Systems; Oficyna Wydawnicza Politechniki Wroclawskiej: Wroclaw, Poland, 2012. [Google Scholar]
- Balcerek, M.; Burnecki, K. Testing of fractional Brownian motion in a noisy environment. Chaos Solitons Fractals 2020, 140, 110097. [Google Scholar] [CrossRef]
- Klafter, J.; Lim, S.C.; Metzler, R. Fractional Dynamics. Recent Advances; World Scientific: Singapore, 2012. [Google Scholar]
- Burnecki, K. FARIMA processes with application to biophysical data. J. Stat. Mech. 2012, P05015. [Google Scholar] [CrossRef]
- Janczura, J.; Burnecki, K.; Muszkieta, M.; Stanislavsky, A.; Weron, A. Classification of random trajectories based on the fractional Lévy stable motion. Chaos Solitons Fractals 2022, 154, 111606. [Google Scholar] [CrossRef]
- Vega, A.R.; Freeman, S.A.; Grinstein, S.; Jaqaman, K. Multistep track segmentation and motion classification for transient mobility analysis. Biophys. J. 2018, 114, 1018. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Lutz, E. Fractional Langevin equation. Phys. Rev. E 2001, 64, 051106. [Google Scholar] [CrossRef] [PubMed]
- Watkins, N.W.; Credgington, D.; Sanchez, R.; Rosenberg, S.J.; Chapman, S.C. Kinetic equation of linear fractional stable motion and applications to modeling the scaling of intermittent bursts. Phys. Rev. E 2009, 79, 041124. [Google Scholar] [CrossRef] [PubMed]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes; Chapman & Hall: New York, NY, USA, 1994. [Google Scholar]
- Burnecki, K.; Sikora, G. Identification and validation of stable ARFIMA processes with application to UMTS data. Chaos Solitons Fractals 2017, 102, 456–466. [Google Scholar] [CrossRef]
- Dybiec, B.; Gudowska-Nowak, E.; Chechkin, A. To hit or to pass it over—Remarkable transient behavior of first arrivals and passages for Lévy flights in finite domains. J. Phys. A Math Theor. 2016, 49, 504001. [Google Scholar] [CrossRef]
- Song, W.; Chen, J.; Wang, Z.; Kudreyko, A.; Qi, D.; Zio, E. Remaining useful life prediction of lithium-ion battery based on adaptive fractional Lévy stable motion with capacity regeneration and random fluctuation phenomenon. Fractal Fract. 2023, 7, 827. [Google Scholar] [CrossRef]
- Teuerle, M.; Wyłomańska, A.; Sikora, G. Modeling anomalous diffusion by a subordinated fractional Lévy-stable process. J. Stat. Mech. 2013, 2013, P05016. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Beck, C. Generalized statistical mechanics for superstatistical systems. Phil. Trans. R. Soc. A 2011, 369, 453–465. [Google Scholar] [CrossRef]
- Ślęzak, J.; Burnecki, K.; Metzler, R. Random coefficient autoregressive processes describe Brownian yet non-Gaussian diffusion in heterogeneous systems. New J. Phys. 2019, 21, 073056. [Google Scholar] [CrossRef]
- Sadoon, A.; Wang, Y. Anomalous, non-Gaussian, viscoelastic, and age-dependent dynamics of histonelike nucleoid-structuring proteins in live Escherichia coli. Phys. Rev. E 2018, 98, 042411. [Google Scholar] [CrossRef]
- Huet, S.; Karatekin, E.; Tran, V.S.; Fanget, I.; Cribier, S.; Henry, J.P. Analysis of transient behavior in complex trajectories: Application to secretory vesicle dynamics. Biophys. J. 2006, 91, 3542–3559. [Google Scholar] [CrossRef]
- Das, R.; Cairo, C.W.; Coombs, D. A hidden Markov model for single particle tracks quantifies dynamic interactions between LFA-1 and the actin cytoskeleton. PLoS Comput. Biol. 2009, 5, e1000556. [Google Scholar] [CrossRef] [PubMed]
- Stanislavsky, A.A.; Weron, A. Confined random motion with Laplace and Linnik statistics. J. Phys. A Math. Theor. 2021, 54, 055009. [Google Scholar] [CrossRef]
- Stanislavsky, A.A.; Weron, A. Confined modes of single-particle trajectories induced by stochastic resetting. Phys. Rev. E 2023, 108, 044130. [Google Scholar] [CrossRef]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of Brownian motion. Phys. Rev. 1930, 36, 823–841. [Google Scholar] [CrossRef]
- Kotz, S.; Kozubowski, T.; Podgórski, K. The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Kundu, D. Discriminating between normal and Laplace distributions. In Advances in Ranking and Selection, Multiple Comparisons, and Reliability. Statistics for Industry and Technology; Balakrishnan, N., Nagaraja, H.N., Kannan, N., Eds.; Birkhäuser: Boston, MA, USA, 2005; pp. 65–79. [Google Scholar]
- Anderson, D.N.; Arnold, B.C. Linnik distributions and processes. J. Appl. Probab. 1993, 30, 330–340. [Google Scholar] [CrossRef]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef]
- Neyman, J.; Pearson, E.S. On the problem of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Ser. A 1933, 231, 289–337. [Google Scholar]
- Neyman, J. Outline of a theory of statistical estimation based on the classical theory of probability. Philos. Trans. R. Soc. Ser. A 1937, 236, 333–380. [Google Scholar]
- Briane, M.V.; Kervrann, C.; Vimond, M. A statistical analysis of particle trajectories in living cells. Phys. Rev. E 2018, 97, 062121. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).