An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach
Abstract
1. Introduction
2. Problem Formulation
2.1. Flying Range
2.2. Terrain Model
- is the height of the i indexed peak.
- (,) are the coordinates of the i indexed peak.
- is the amplitude or height of the i indexed peak.
- and are the standard deviations or widths of the i indexed peak along the X and Y directions, respectively.
2.3. Objective Function
- denotes the cost associated with the route length for UAV I.
- represents the expense related to navigating through mountainous terrain for UAV i.
- signifies the cost attributed to collisions for UAV i.
- N is the total number of UAVs in the swarm.
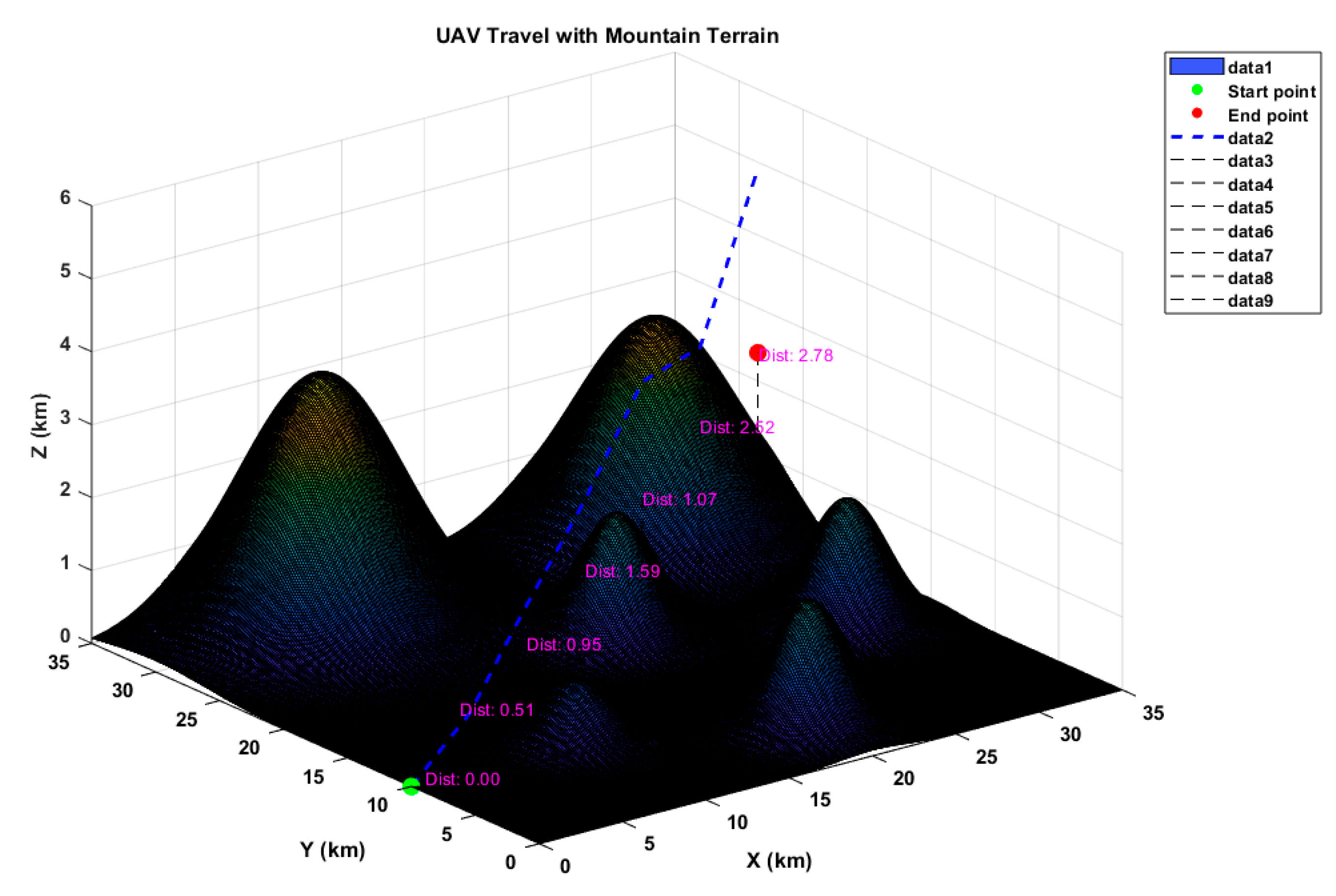
2.3.1. Flying Path Length Cost
- indicates the summation of all path leg lengths from i = 1 to i = n.
- n is the total number of legs in the route.
- i is the index of each path leg in the route.
- denotes the length of i indexed leg in the route.
2.3.2. Mountain Terrain Cost
2.3.3. Collision Cost Function
2.4. Constraints
3. Introduction to UAV Formation with Communication Latency
Concept of UAV Communication Network Topology
4. Formation Dynamics and Modeling
4.1. Modeling of Fixed-Wing UAVs
4.2. Formation Control with Leader–Follower Dynamics
5. Hybrid Approach for Formation Control
5.1. Classical PSO
5.2. Velocity-Pausing PSO
5.3. Fractional Order Hybrid PSO
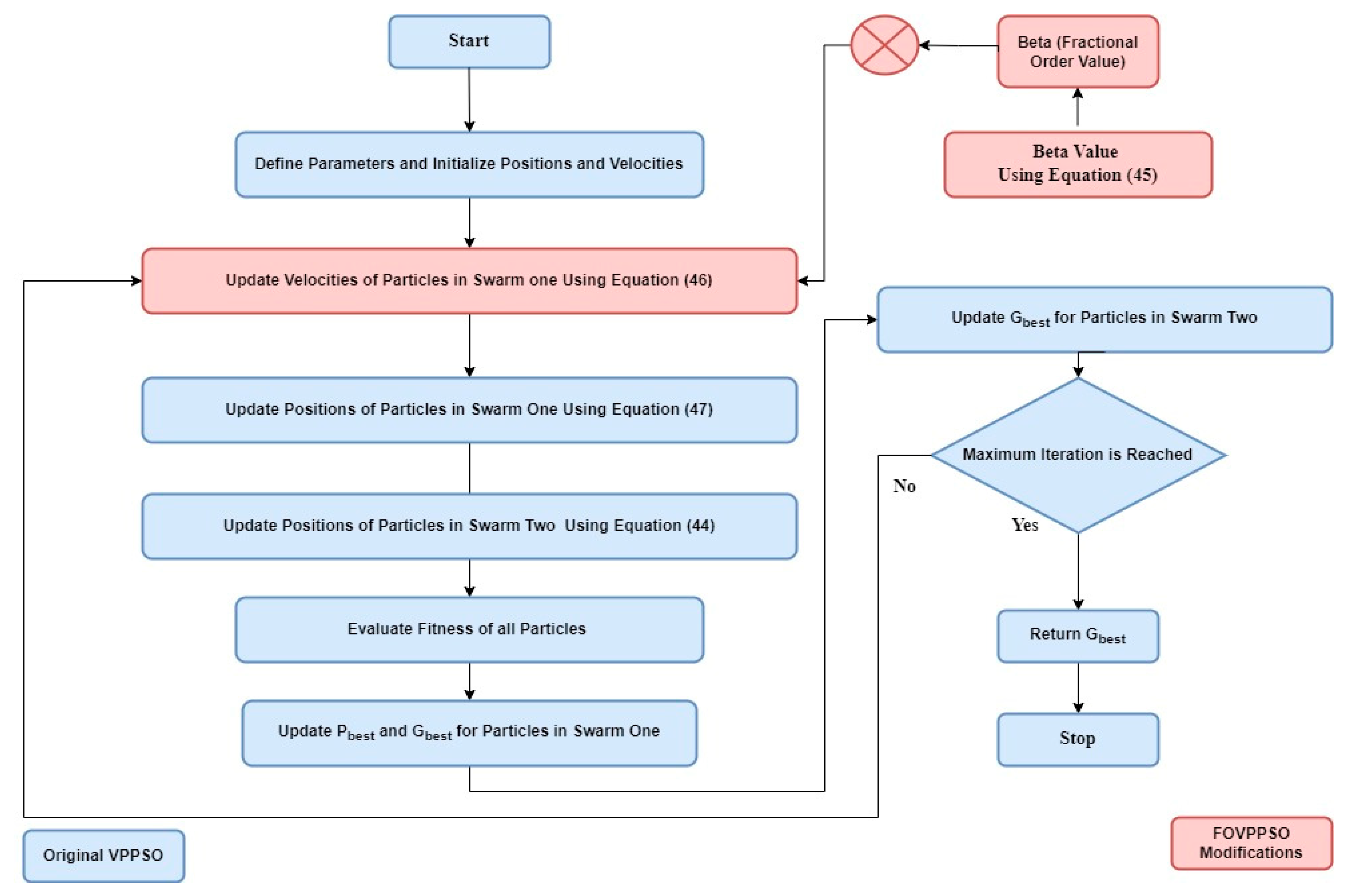
5.4. Hybrid Algorithm
- Step 1:
- The 3D mission environment and terrain model are developed based on the specifications of the task. The starting and ending points for the UAV swarm are established.
- Step 2:
- The parameters are initialized, including the total particle number N, the particle position and velocity matrices, β (fractional order), c1, c2, the maximum number of iterations T, the communication range, and other relevant parameters.
- Step 3:
- The fitness function is designed considering the objectives and constraints of the optimization problem. The fitness function should reflect the performance metrics to be optimized, such as the flight length, terrain cost, and collision cost.
- Step 4:
- Objective functions:The objectives (flight length, terrain cost, and collision cost) are aggregated into the fitness function that evaluates each UAV’s (particle’s) performance.The fitness function directly influences the velocity and position updates, guiding the swarm towards optimal solutions that balance these objectives.
- Step 5:
- The fitness functions of the entire swarm are monitored, and the optimal positions for each UAV are computed as well as the optimal position for the formation.
- Step 6:
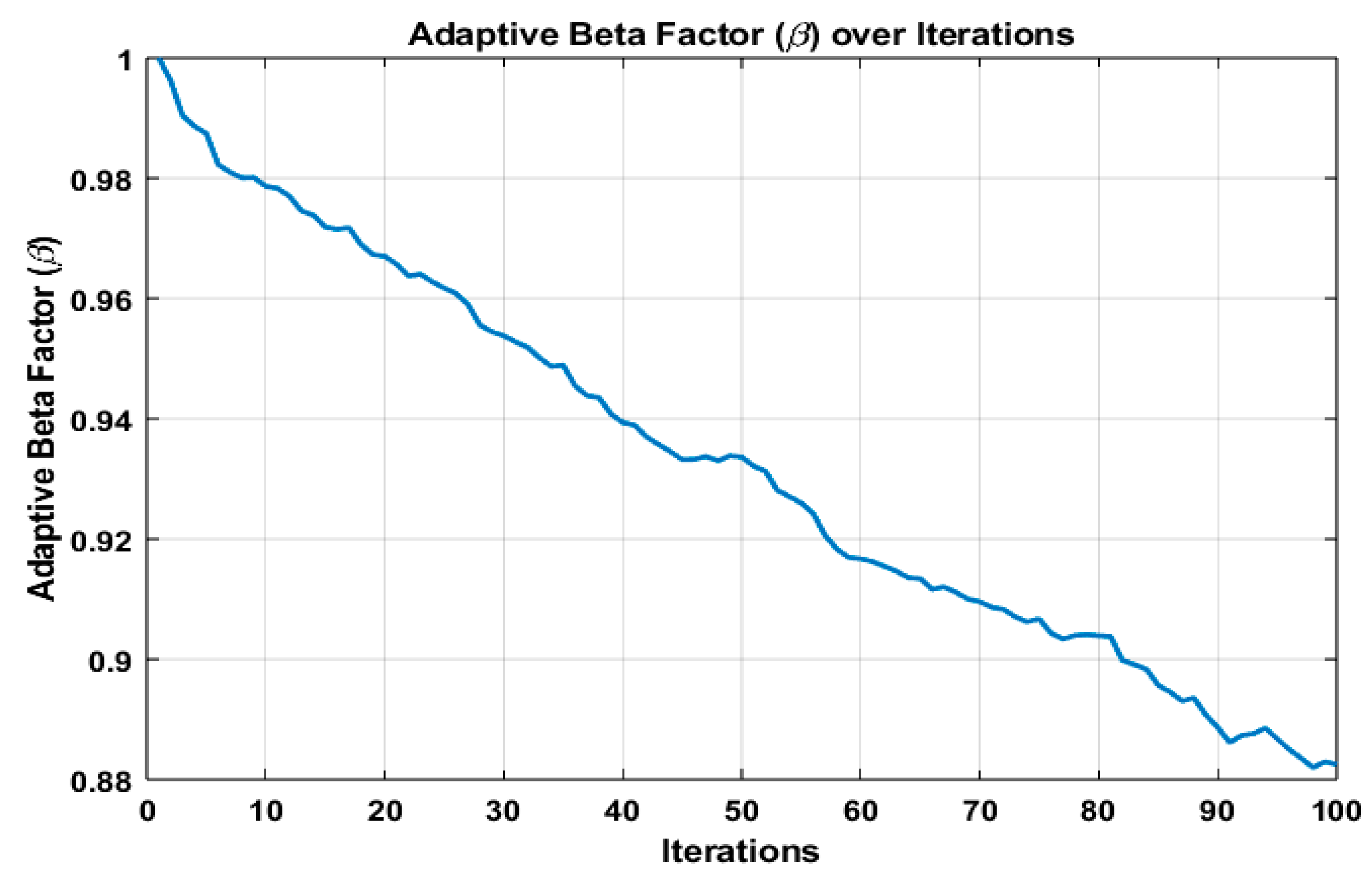
- Updating the parameters dynamically:The fractional order β is updated based on the convergence trend using the calculate_adaptive_beta function. The inertia weight w and c1 and c2 coefficients are adjusted if necessary to balance exploration and exploitation.
- Step 7:
- Updating the particles:The velocity and position of the particles are updated using the FOVPPSO algorithm with velocity pausing and fractional-order dynamics.
- Step 8:
- Tuning parameters to swarm position:The position of each UAV in the swarm is updated using the velocity update Equation (44) of FO-VPPSO, which is influenced by the adaptive value β and coefficients c1 and c2.As the UAVs navigate the 3D mission environment, their positions represent the search space explored by the FO-VPPSO particles.
- Step 9:
- Steps 4–6 are repeated until the maximum iterations T are reached.
- Step 10:
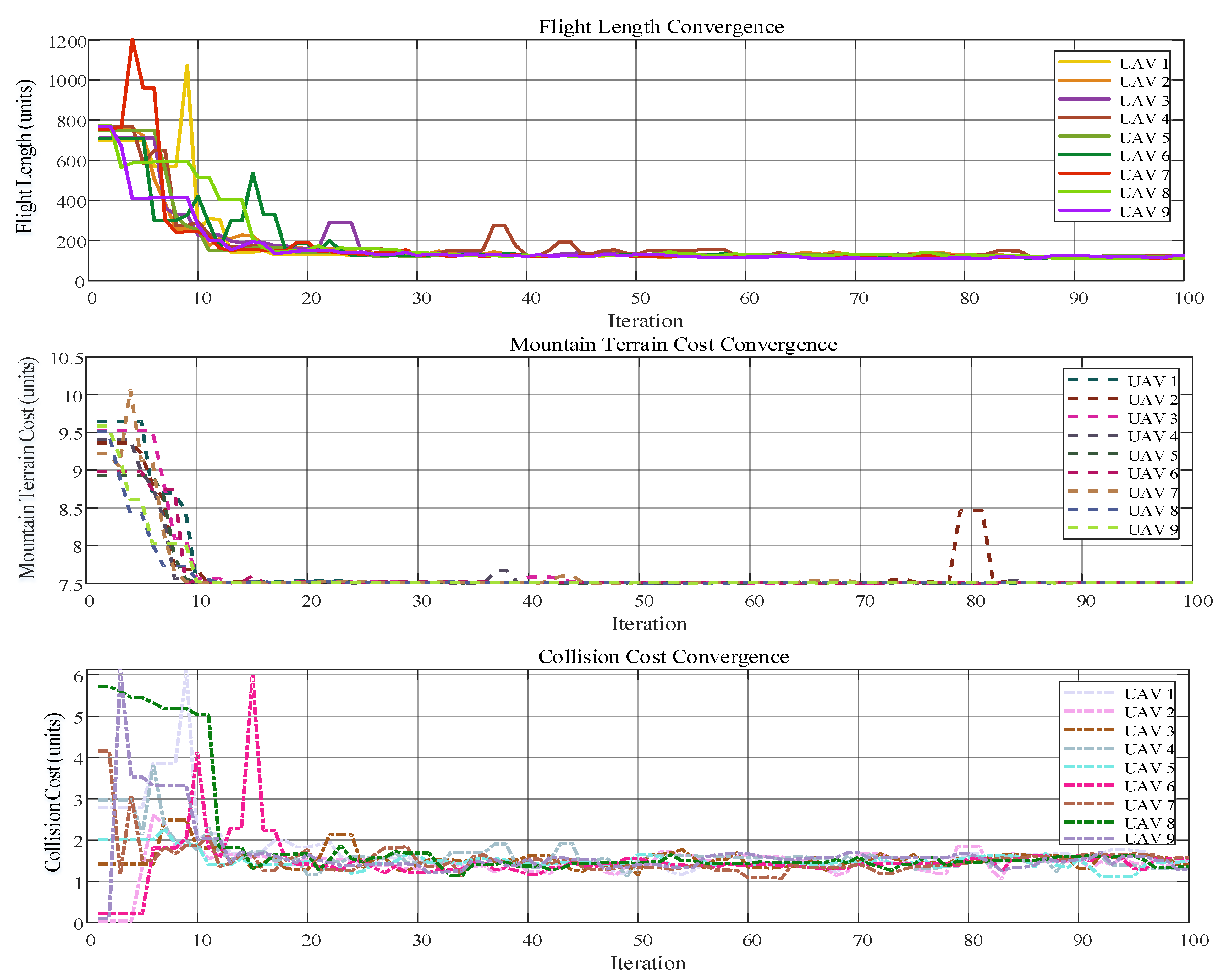
- The hybrid algorithm is finished, and the results are analyzed:The convergence of the fitness functions is plotted over the iterations to observe the algorithm’s performance.A visual graphical abstract, explaining the complete scenario is provided here in Figure 6.
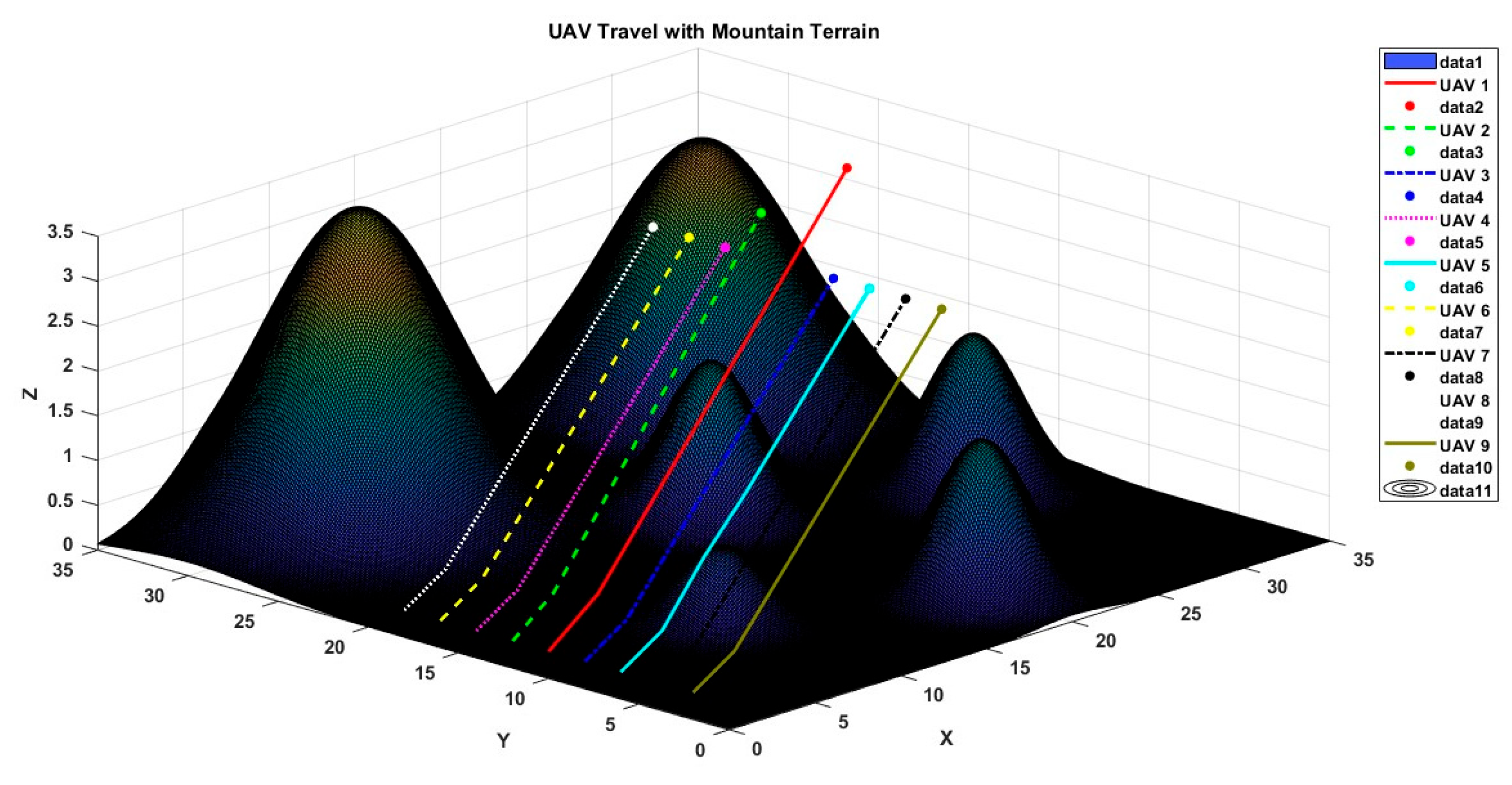
6. Experimental Analysis and Findings
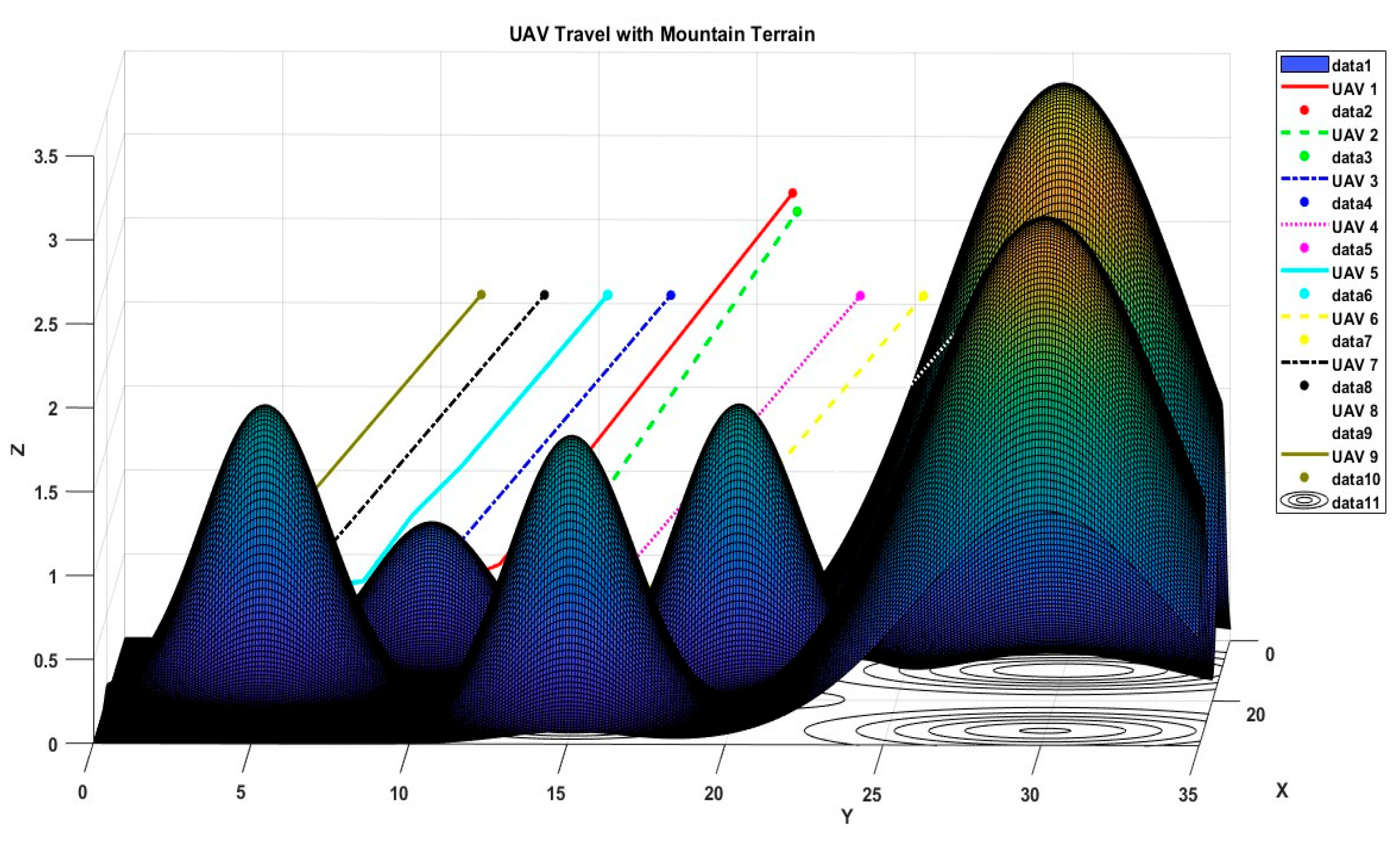
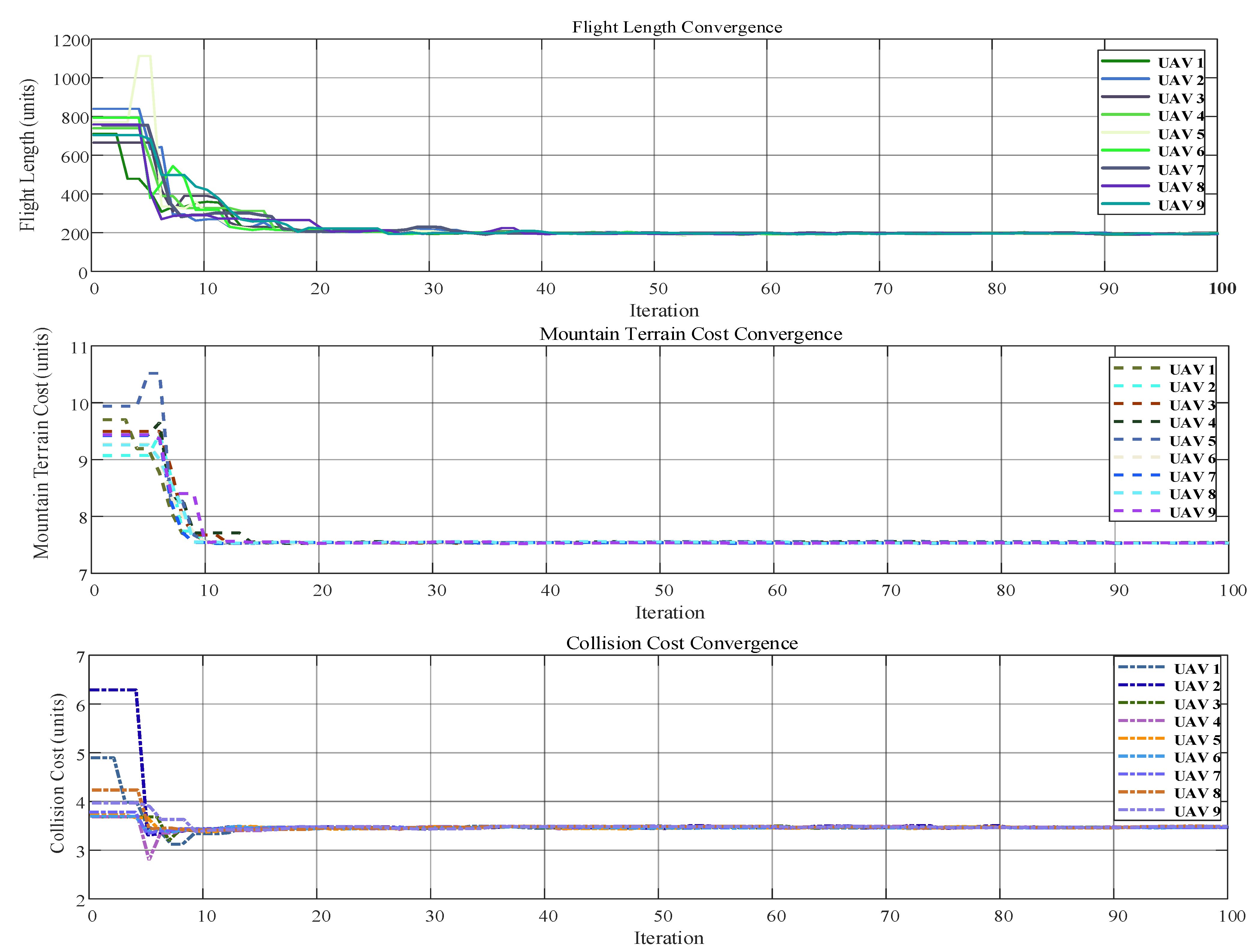
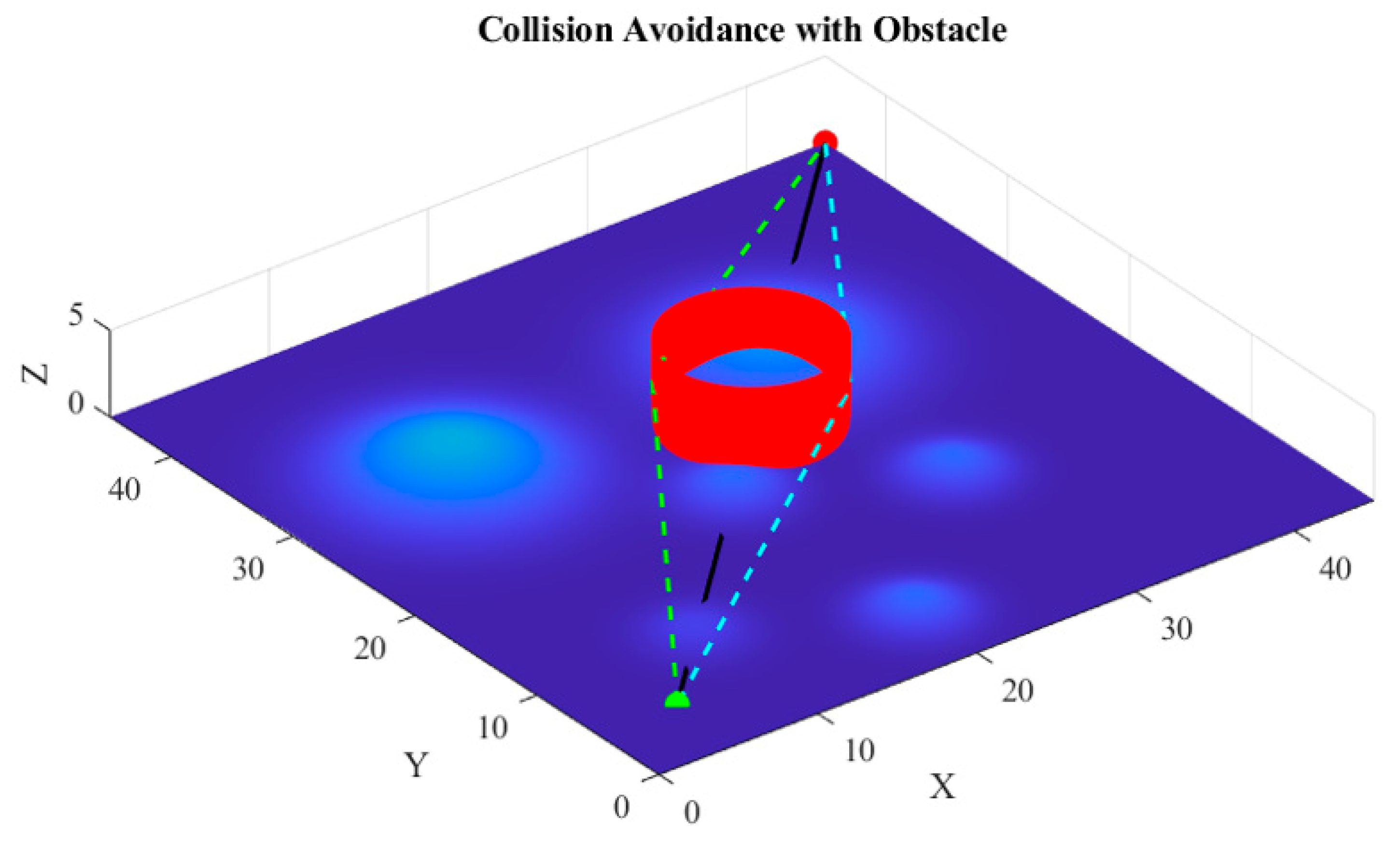
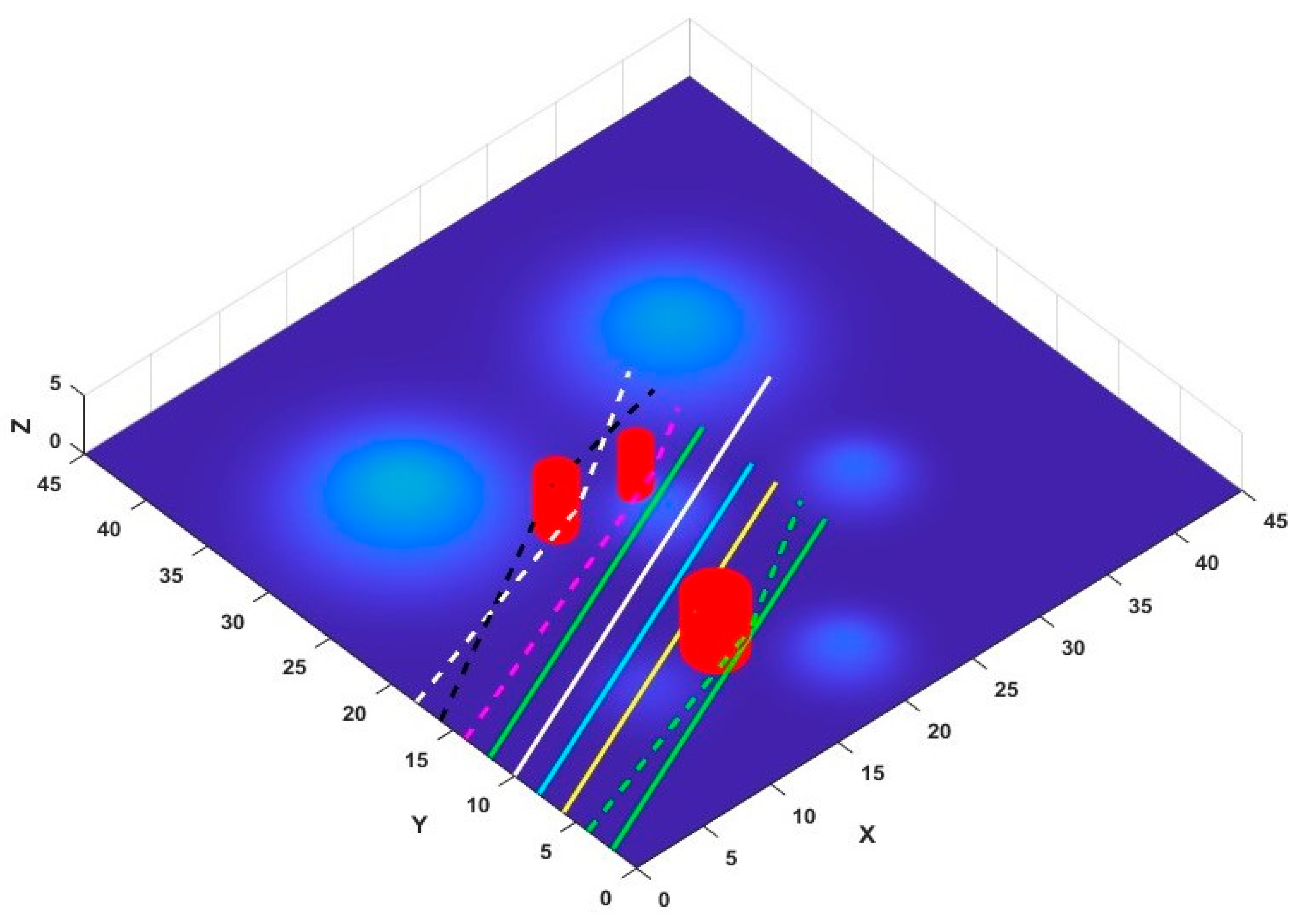
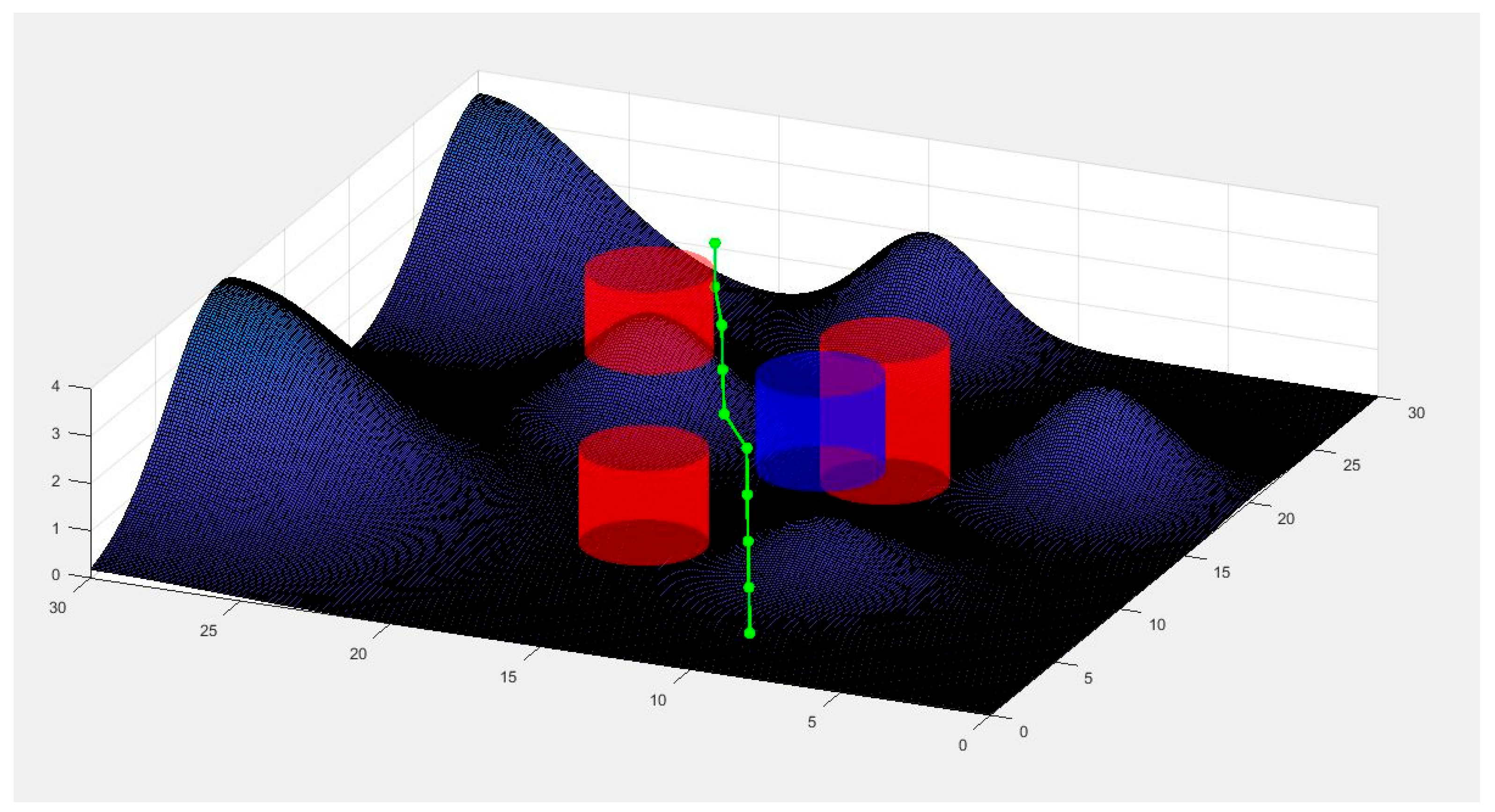
6.1. Scenario 1
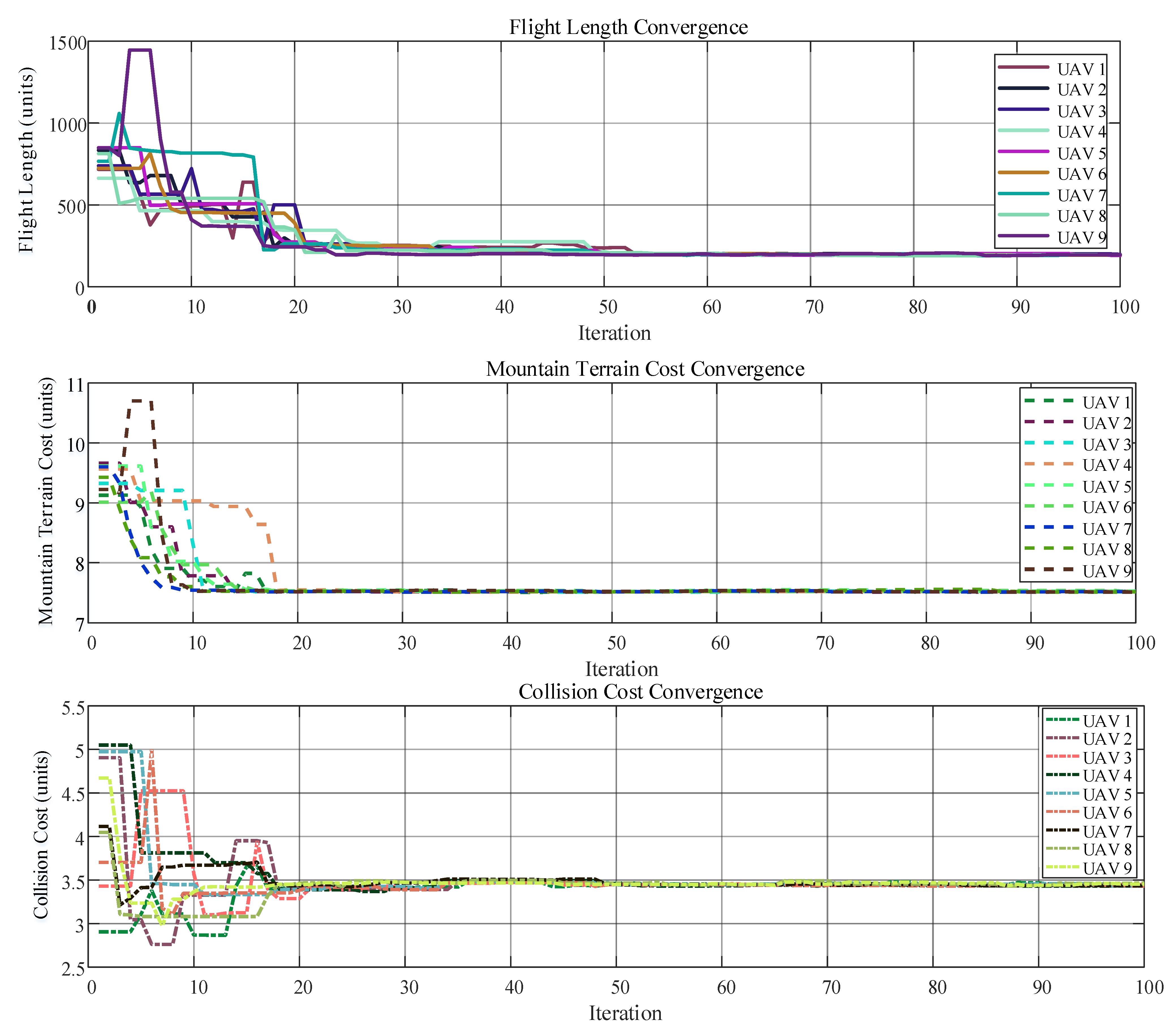
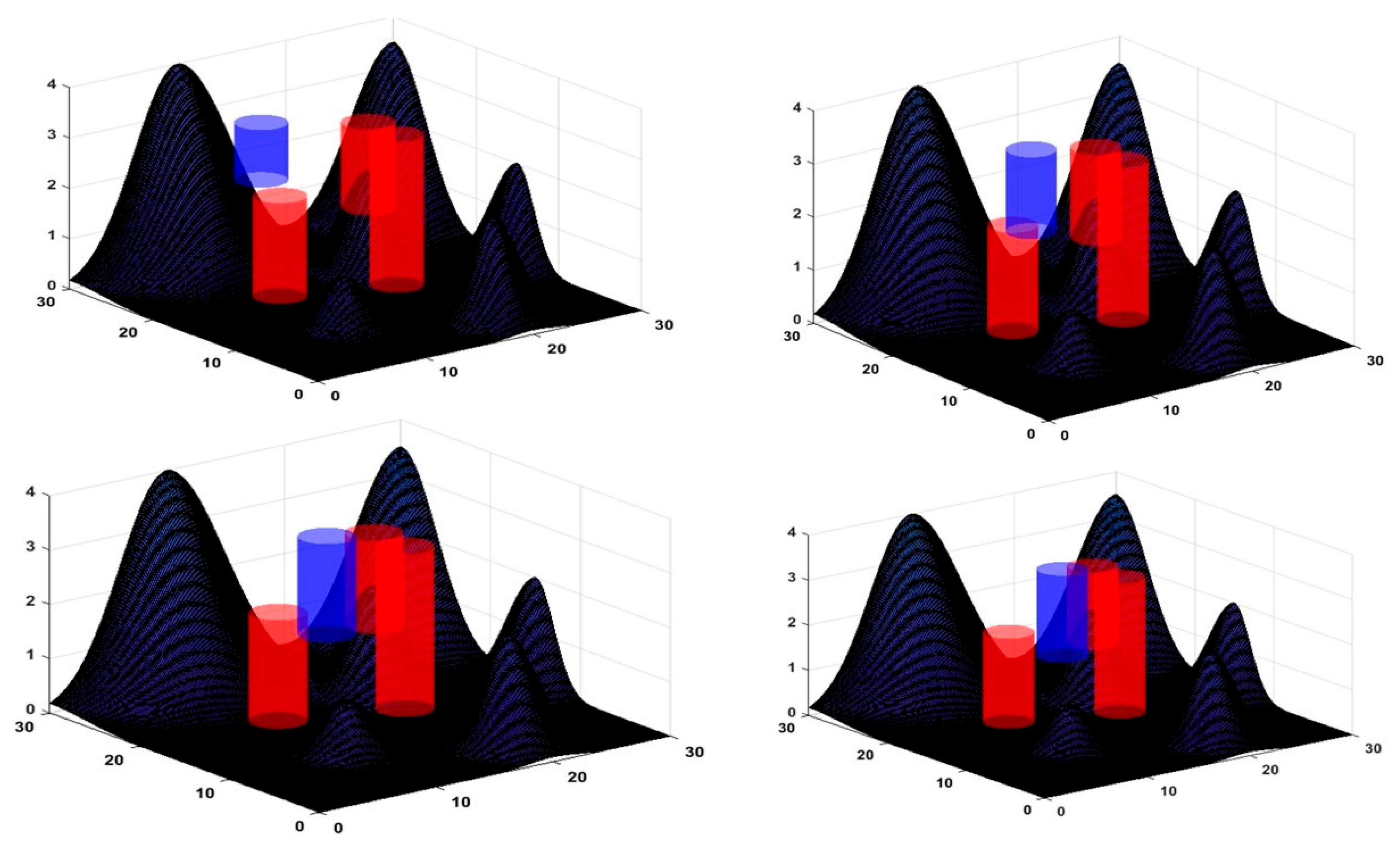
6.2. Scenario 2
7. Implementations
7.1. Sensors
7.2. Potential Challenges
7.3. Computational Complexities
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Qingtian, H. Research on Cooperate Search Path Planning of Multiple UAVs Using Dubins Curve. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications, ICPECA 2021, Shenyang, China, 22–24 January 2021; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2021; pp. 584–588. [Google Scholar]
- Ali, Z.A.; Han, Z.; Masood, R.J. Collective motion and self-organization of a swarm of UAVS: A cluster-based architecture. Sensors 2021, 21, 3820. [Google Scholar] [CrossRef] [PubMed]
- Cetin, O.; Yilmaz, G. Real-time Autonomous UAV Formation Flight with Collision and Obstacle Avoidance in Unknown Environment. J. Intell. Robot. Syst. 2016, 84, 415–433. [Google Scholar] [CrossRef]
- Duan, Z.; Shen, J. Synchronization problem of 2-D coupled dynamical networks with communication delays and missing measurements. Multidimens. Syst. Signal Process. 2017, 30, 39–67. [Google Scholar] [CrossRef]
- Jabbarpour, M.R.; Malakooti, H.; Noor, R.M.; Anuar, N.B.; Khamis, N. Ant colony optimisation for vehicle traffic systems: Applications and challenges. Int. J. Bio-Inspired Comput. 2014, 6, 32–56. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y.V. A new vibrational genetic algorithm enhanced with a Voronoi diagram for path planning of autonomous UAV. Aerosp. Sci. Technol. 2012, 16, 47–55. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–420. [Google Scholar] [CrossRef]
- Ren, W. Consensus strategies for cooperative control of vehicle formations. IET Control. Theory Appl. 2007, 1, 505–512. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, L.; Han, Z.; Fu, M. Distributed formation control of multi-agent systems using complex laplacian. IEEE Trans. Autom. Control. 2014, 59, 1765–1777. [Google Scholar] [CrossRef]
- Nor, M.H.M.; Ismail, Z.H.; Ahmad, M.A. Broadcast control of multi-robot systems with norm-limited update vector. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420945958. [Google Scholar] [CrossRef]
- Ren, R.; Zhang, Y.-Y.; Luo, X.-Y.; Li, S.-B. Automatic generation of optimally rigid formations using decentralized methods. Int. J. Autom. Comput. 2010, 7, 557–564. [Google Scholar] [CrossRef]
- McCune, R.R.; Madey, G.R. Swarm control of UAVs for cooperative hunting with DDDAS. Procedia Comput. Sci. 2013, 18, 2537–2544. [Google Scholar] [CrossRef]
- Weng, L.; Liu, Q.; Xia, M.; Song, Y. Immune network-based swarm intelligence and its application to unmanned aerial vehicle (UAV) swarm coordination. Neurocomputing 2014, 125, 134–141. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Yao, P. Energy-optimal path planning for Solar-powered UAV with tracking moving ground target. Aerosp. Sci. Technol. 2016, 53, 241–251. [Google Scholar] [CrossRef]
- Sun, J.; Tang, J.; Lao, S. Collision Avoidance for Cooperative UAVs with Optimized Artificial Potential Field Algorithm. IEEE Access 2017, 5, 18382–18390. [Google Scholar] [CrossRef]
- Yaghoobi, T.; Esmaeili, E. An improved artificial bee colony algorithm for global numerical optimisation. Int. J. Bio-Inspired Comput. 2017, 9, 251–258. [Google Scholar] [CrossRef]
- Mazal, J.; Stodola, P. Applying the ant colony optimisation algorithm to the capacitated multi-depot vehicle routing problem. Int. J. Bio-Inspired Comput. 2016, 8, 228. [Google Scholar] [CrossRef]
- Danancier, K.; Ruvio, D.; Sung, I.; Nielsen, P. Comparison of path planning algorithms for an unmanned aerial vehicle deployment under threats. IFAC-Pap. 2019, 52, 1978–1983. [Google Scholar] [CrossRef]
- Israr, A.; Ali, Z.A.; Alkhammash, E.H.; Jussila, J.J. Optimization Methods Applied to Motion Planning of Unmanned Aerial Vehicles: A Review. Drones 2022, 6, 126. [Google Scholar] [CrossRef]
- Zhao, S.; Dimarogonas, D.V.; Sun, Z.; Bauso, D. A General Approach to Coordination Control of Mobile Agents with Motion Constraints. IEEE Trans. Autom. Control. 2018, 63, 1509–1516. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998. [Google Scholar]
- Tian, D.; Shi, Z. MPSO: Modified particle swarm optimization and its applications. Swarm Evol. Comput. 2018, 41, 49–68. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.; Gao, M.; Cao, S.; Guo, A.; Wang, J. Heterogeneous comprehensive learning and dynamic multi- swarm particle swarm optimizer with two mutation operators. Inf. Sci. 2020, 540, 175–201. [Google Scholar] [CrossRef]
- Shami, T.M.; Mirjalili, S.; Al-Eryani, Y.; Daoudi, K.; Izadi, S.; Abualigah, L. Velocity pausing particle swarm optimization: A novel variant for global optimization. Neural Comput. Appl. 2023, 35, 9193–9223. [Google Scholar] [CrossRef]
- Karagiannis, D.; Sassano, M.; Astolfi, A. Dynamic scaling and observer design with application to adaptive control. Automatica 2009, 45, 2883–2889. [Google Scholar] [CrossRef]
- Razmjooei, H.; Palli, G.; Janabi-Sharifi, F.; Alirezaee, S. Adaptive fast-finite-time extended state observer design for uncertain electro-hydraulic systems. Eur. J. Control. 2023, 69, 100749. [Google Scholar] [CrossRef]
- Ali, Z.A.; Zhangang, H. Multi-unmanned aerial vehicle swarm formation control using hybrid strategy. Trans. Inst. Meas. Control. 2021, 43, 2689–2701. [Google Scholar] [CrossRef]
- Huang, C.; Fei, J. UAV Path Planning Based on Particle Swarm Optimization with Global Best Path Competition. Int. J. Pattern Recognit. Artif. Intell. 2018, 32, 1859008. [Google Scholar] [CrossRef]
- Shafiq, M.; Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M. A Multi-Colony Social Learning Approach for the Self-Organization of a Swarm of UAVs. Drones 2022, 6, 104. [Google Scholar] [CrossRef]
- Shafiq, M.; Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M.; Jussila, J.J. Convergence Analysis of Path Planning of Multi-UAVs Using Max-Min Ant Colony Optimization Approach. Sensors 2022, 22, 5395. [Google Scholar] [CrossRef]
- Wang, X.; Yadav, V.; Balakrishnan, S.N. Cooperative UAV formation flying with obstacle/collision avoidance. IEEE Trans. Control. Syst. Technol. 2007, 15, 672–679. [Google Scholar] [CrossRef]
- Do, H.; Nguyen, H.; Nguyen, C.; Nguyen, M.; Nguyen, M. Formation control of multiple unmanned vehicles based on graph theory: A Comprehensive Review. ICST Trans. Mob. Commun. Appl. 2022, 7, e3. [Google Scholar] [CrossRef]
- Wang, J.; Xin, M. Integrated optimal formation control of multiple unmanned aerial vehicles. IEEE Trans. Control. Syst. Technol. 2012, 21, 1731–1744. [Google Scholar] [CrossRef]
- Abdul-Razaq, Y. Leader-Follower Formation Control of ROS Enabled Mobile Robots Subject to Robots Failure. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2022. [Google Scholar]
- Dong, X.; Chen, M.; Wang, X.; Gao, F. Intelligent Coordination of UAV Swarm Systems; MDPI: Basel, Switzerland, 2023. [Google Scholar]
- Xuan-Mung, N.; Hong, S.K. Robust adaptive formation control of quadcopters based on a leader–follower approach. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419862733. [Google Scholar] [CrossRef]
- Ali, Z.A.; Israr, A.; Alkhammash, E.H.; Hadjouni, M. A Leader-Follower Formation Control of Multi-UAVs via an Adaptive Hybrid Controller. Complexity 2021, 2021, 9231636. [Google Scholar] [CrossRef]
- Eberhart, R.; Shi, Y. Tracking and optimizing dynamic systems with particle swarms. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Republic of Korea, 27–30 May 2001. [Google Scholar]
- Ahmed, W.A.E.M.; Mageed, H.M.A.; Mohamed, S.A.; Saleh, A.A. Fractional order Darwinian particle swarm optimization for parameters identification of solar PV cells and modules. Alex. Eng. J. 2021, 61, 1249–1263. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]





| Functions | Dim | MFO [42] | PSO [42] | GSA [42] | BA [42] | FOVPPSO | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| 100 | 0.000117 | 0.00015 | 1.32115 | 1.15388 | 608.232 | 464.654 | 20792.4 | 5892.40 | 0.0031 | 0.0023 | |
| 100 | 0.000639 | 0.000877 | 7.71556 | 4.13212 | 22.7526 | 3.36513 | 89.785 | 41.9577 | 0.0042 | 0.0017 | |
| 100 | 696.730 | 188.527 | 736.393 | 361.781 | 135760. | 48652.6 | 62481.3 | 29769.1 | 1.4110 × 103 | 1.5645 × 103 | |
| 100 | 70.6864 | 5.27505 | 12.9728 | 2.63443 | 78.7819 | 2.81410 | 49.7432 | 10.14363 | 33.9004 | 10.2286 | |
| 100 | 139.148 | 120.260 | 77,360.83 | 51156.15 | 741.003 | 781.2393 | 199,512 | 125,238 | 112.1192 | 182.9603 | |
| 100 | 0.00011 | 9.87 × 10−5 | 286.651 | 107.079 | 3080.96 | 898.635 | 17,053.4 | 4917.56 | 0.0032 | 0.0021 | |
| 100 | 0.091155 | 0.04642 | 1.037316 | 0.310315 | 0.112975 | 0.037607 | 6.045055 | 3.045277 | 0.0209 | 0.0065 | |
| 100 | 8496.78 | 725.8737 | −3571 | 430.7989 | −2352.32 | 382.167 | 65535 | 0 | −9.4068 × 103 | 545.8885 | |
| 100 | 84.600 | 16.1665 | 124.29 | 14.2509 | 31.0001 | 13.6605 | 96.2152 | 19.5875 | 73.4391 | 24.2290 | |
| 100 | 1.2603 | 0.72956 | 9.1679 | 1.56898 | 3.74098 | 0.17126 | 15.9460 | 0.77495 | 0.1078 | 0.4614 | |
| 100 | 0.0190 | 0.02173 | 12.418 | 4.16583 | 0.04978 | 0.04978 | 220.281 | 54.7066 | 0.0181 | 0.0151 | |
| 100 | 0.894006 | 0.88127 | 13.87378 | 5.85373 | 0.46344 | 0.137598 | 28,934,354 | 2,178,683 | 0.5711 | 0.6499 | |
| 100 | 0.115824 | 0.193042 | 11,813.5 | 30,701.9 | 7.617114 | 1.22532 | 1.09 × 108 | 1.05 × 108 | 0.0616 | 0.2539 | |
| Functions | Dim | FPA [42] | SMS [42] | FA [42] | GA [42] | FOVPPSO | |||||
| Mean | STD | Mean | STD | Mean | STD | Mean | STD | Mean | STD | ||
| 100 | 203.638 | 78.3984 | 120 | 0 | 7480.74 | 894.849 | 21886.0 | 2879.58 | 0.0031 | 0.0023 | |
| 100 | 11.1687 | 2.91959 | 0.0205 | 0.00471 | 39.3253 | 2.46586 | 56.5175 | 5.66085 | 0.0042 | 0.0017 | |
| 100 | 237.56 | 136.6463 | 37820 | 0 | 17,357.3 | 1740.11 | 37,010.2 | 5572.21 | 1.4110 × 103 | 1.5645 × 103 | |
| 100 | 12.5728 | 42.29 | 69.1700 | 3.87666 | 33.9535 | 1.86966 | 59.14331 | 4.648526 | 33.9004 | 10.2286 | |
| 100 | 10974. | 12,057.2 | 638,224 | 729,967 | 3,795,009 | 759,030 | 3,132,141 | 5,264,496 | 112.1192 | 182.9603 | |
| 100 | 175.38 | 63.4525 | 41439. | 3295.23 | 7828.72 | 975.210 | 20,964.8 | 3868.10 | 0.0032 | 0.0021 | |
| 100 | 0.13594 | 0.061212 | 0.04952 | 0.024015 | 1.906313 | 0.460056 | 13.37504 | 3.08149 | 0.0209 | 0.0065 | |
| 100 | −8086.74 | 155.346 | −3942.82 | 404.160 | −3662.05 | 214.163 | −6331.19 | 332.566 | −9.4068 × 103 | 545.8885 | |
| 100 | 92.6917 | 14.2239 | 152.844 | 18.5535 | 214.895 | 17.2191 | 236.82 | 19.03359 | 73.4391 | 24.2290 | |
| 100 | 6.84483 | 1.24998 | 19.1325 | 0.23852 | 14.5676 | 0.46751 | 17.8461 | 0.53114 | 0.1078 | 0.4614 | |
| 100 | 2.7160 | 0.72771 | 420.525 | 25.25612 | 69.65755 | 12.11393 | 179.9046 | 32.43956 | 0.0181 | 0.0151 | |
| 100 | 4.105339 | 1.043492 | 8,742,814 | 1,405,679 | 368,400.8 | 172,132.9 | 34,131,682 | 1,893,429 | 0.5711 | 0.6499 | |
| 100 | 62.3985 | 94.84298 | 1 × 108 | 0 | 5,557,661 | 1,689,995 | 1.08 × 108 | 3,849,748 | 0.0616 | 0.2539 | |
| Sr. # | 1st Peak | 2nd Peak | 3rd Peak | 4th Peak | 5th Peak | 6th Peak |
|---|---|---|---|---|---|---|
| Altitude (km) | 0.5 | 1 | 1.75 | 1 | 1 | 2 |
| Centre positions (x, y) | (10, 10) | (20, 20) | (30, 30) | (20, 5) | (30, 15) | (10, 30) |
| Slope decrease (x-axis) | 2 | 2 | 4 | 2 | 2 | 4 |
| Slope decrease (y-axis) | 2 | 2 | 4 | 2 | 4 | 4 |
| Sr. # | Leader UAV | 1st UAV | 2nd UAV | 3rd UAV | 4th UAV | 5th UAV | 6th UAV | 7th UAV | 8th UAV |
|---|---|---|---|---|---|---|---|---|---|
| Start point (x, y) | (0, 10, 0) | (0, 12, 0) | (0, 8, 0) | (0, 14, 0) | (0, 6, 0) | (0, 16, 0) | (0, 4, 0) | (0, 18, 0) | (0, 2, 0) |
| End point (x, y) | (30, 22, 3.2) | (25, 22, 2.5) | (25, 18, 2.5) | (25, 24, 2.5) | (25, 16, 2.5) | (25, 26, 2.5) | (25, 14, 2.5) | (25, 28, 2.5) | (25, 12, 2.5) |
| 1st Obstacle | 2nd Obstacle | 3rd Obstacle | |
|---|---|---|---|
| Position (x, y, z) | (8, 15, 2) | (15, 10, 3) | (20, 20, 2.5) |
| Obstacle radii | 2 | 2 | 2 |
| Dynamic Obstacle | |
|---|---|
| Position (x, y) | (10, 10) |
| Obstacle velocity | (0.05, 0.05) |
| Time | 0.5 |
| Objective Function | Total Flight Length | Mountain Terrain Cost | Collision Avoidance | FOVPPSO to PSO | FOVPPSO to VPPSO |
|---|---|---|---|---|---|
| Minimum flight length | 213.1238 km | 8.8504 | 0.9253 | 29.05% | 2.26% |
| Mountain terrain cost | 154.6367 km | 7.5153 | 0.5971 | 16.46% | 1.60% |
| Collision avoidance cost | 151.152 km | 7.3954 | 0.4082 | 55.88% | 31.63% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wadood, A.; Yousaf, A.-F.; Alatwi, A.M. An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach. Fractal Fract. 2024, 8, 334. https://doi.org/10.3390/fractalfract8060334
Wadood A, Yousaf A-F, Alatwi AM. An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach. Fractal and Fractional. 2024; 8(6):334. https://doi.org/10.3390/fractalfract8060334
Chicago/Turabian StyleWadood, Abdul, Al-Fahad Yousaf, and Aadel Mohammed Alatwi. 2024. "An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach" Fractal and Fractional 8, no. 6: 334. https://doi.org/10.3390/fractalfract8060334
APA StyleWadood, A., Yousaf, A.-F., & Alatwi, A. M. (2024). An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach. Fractal and Fractional, 8(6), 334. https://doi.org/10.3390/fractalfract8060334






