Identification of the Dynamic Trade Relationship between China and the United States Using the Quantile Grey Lotka–Volterra Model
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contribution and Organization
- (1)
- This work proposes using the quantile grey Lotka–Volterra (QGLV) model to identify the dynamic competitive relationship between the two populations. An optimization model is established based on the new model to solve the optimal quantile parameters.
- (2)
- Empirical results show that the QGLV model has higher fitting accuracy than the traditional model and reveals the trade relationships at different quantiles based on quarterly data on China–US trade from 1999 to 2019.
- (3)
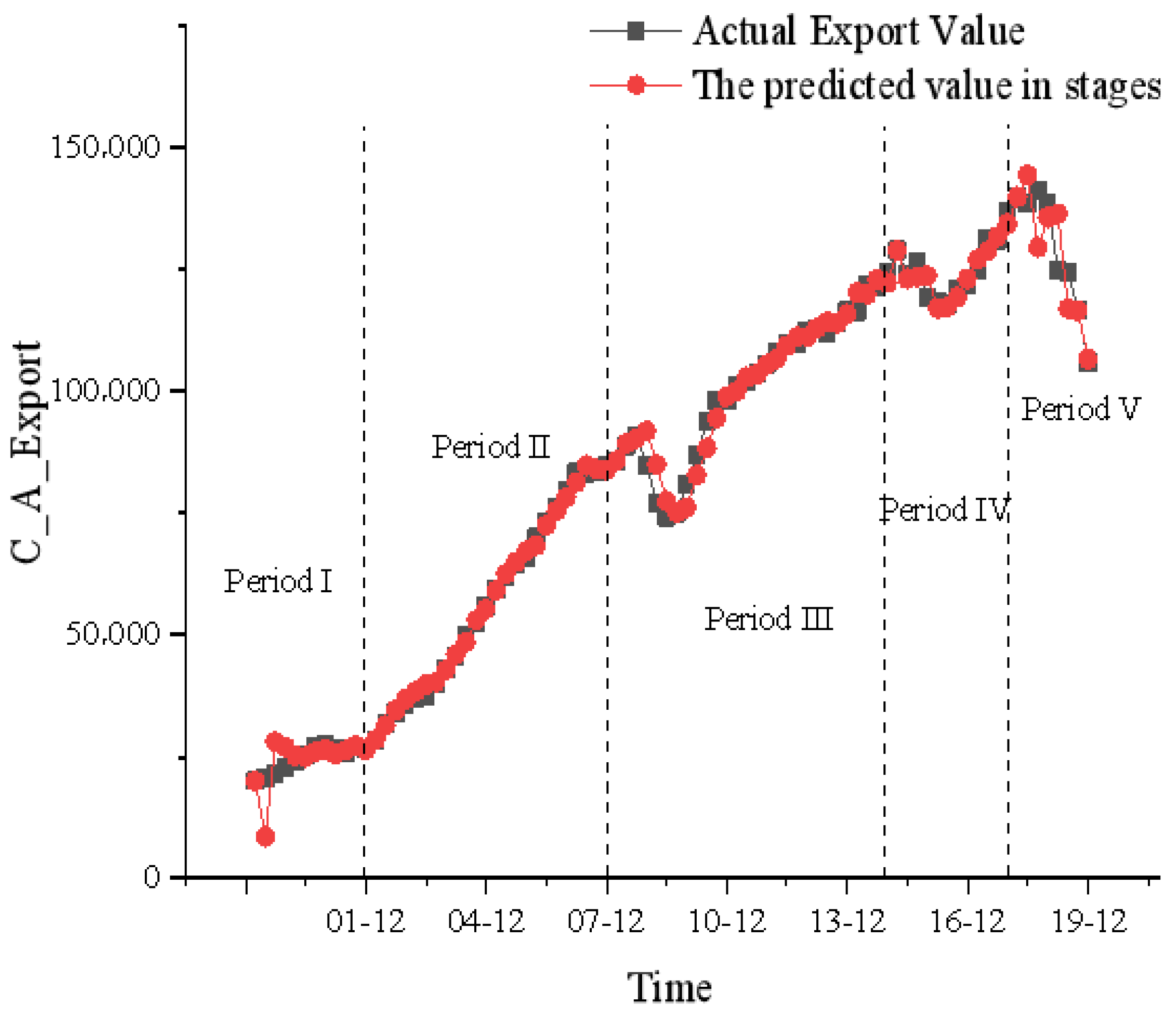
- The long-term China–US trade relationship exhibits a prominent predator–prey relationship. Moreover, we divide samples into five stages according to four key events, China’s accession to the WTO, the 2008 global financial crisis, the weak global economic recovery in 2015, and the 2018 China–US trade war, recognizing variation characteristics at different stages.
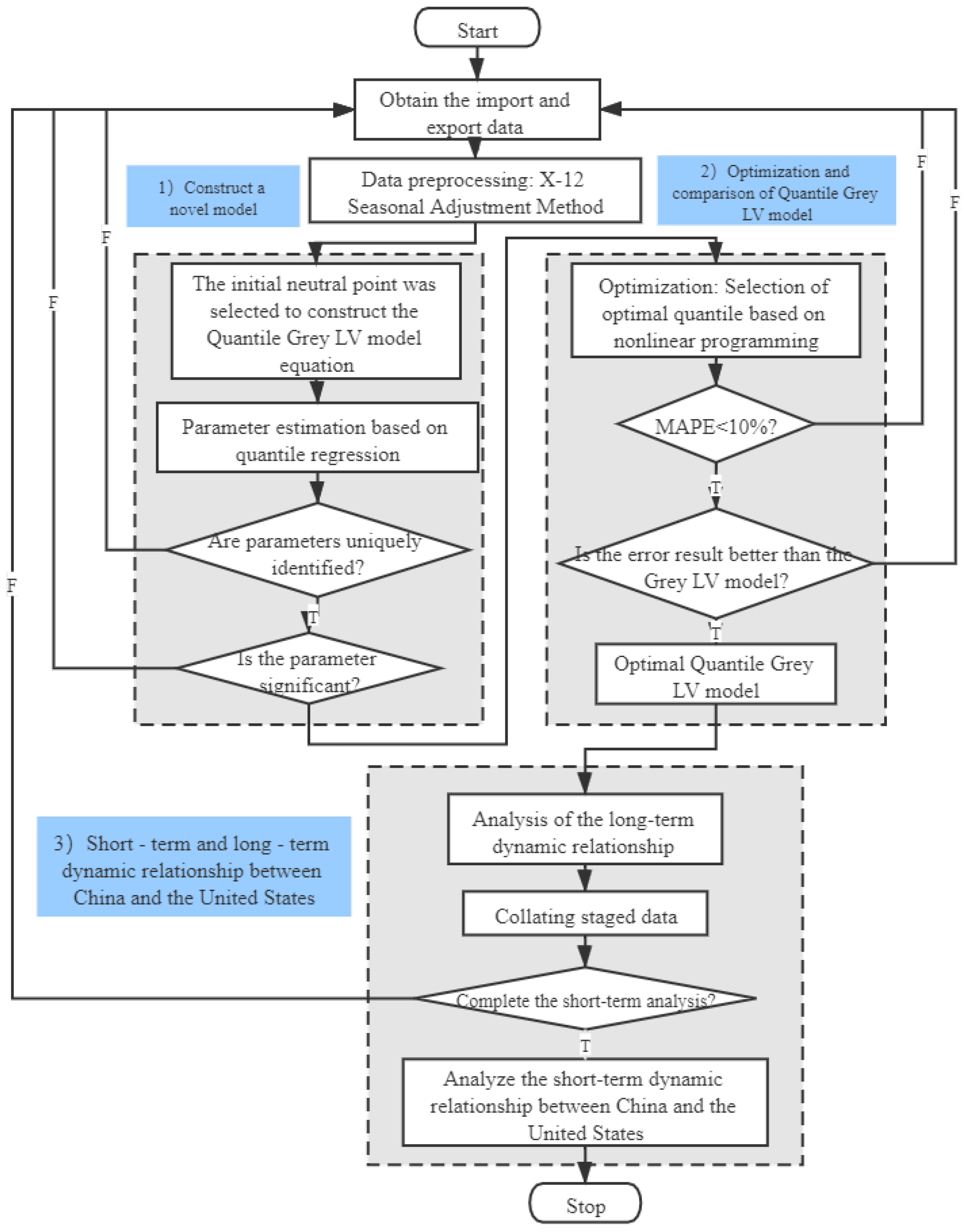
2. Methodology
2.1. The Existing GLV Model
2.2. The QGLV Model
2.3. Equilibrium Points and Stability
- (1)
- , which indicates that the two populations and disappear.
- (2)
- , which indicates that survives, but is gone.
- (3)
- , which indicates that only survives, while is gone.
- (4)
- , which indicates that during the process of competition, the two coexist in balance.
3. Modelling Results
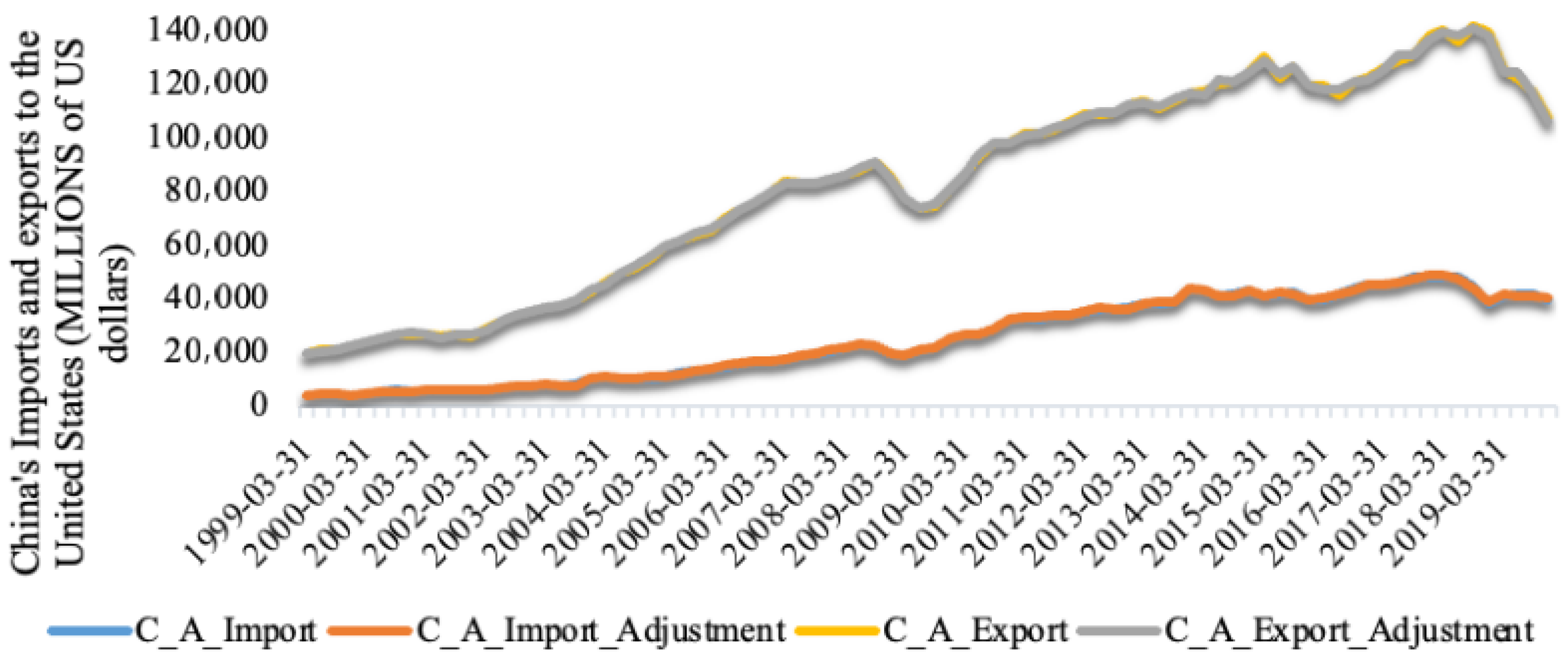
3.1. History of China–US Trade
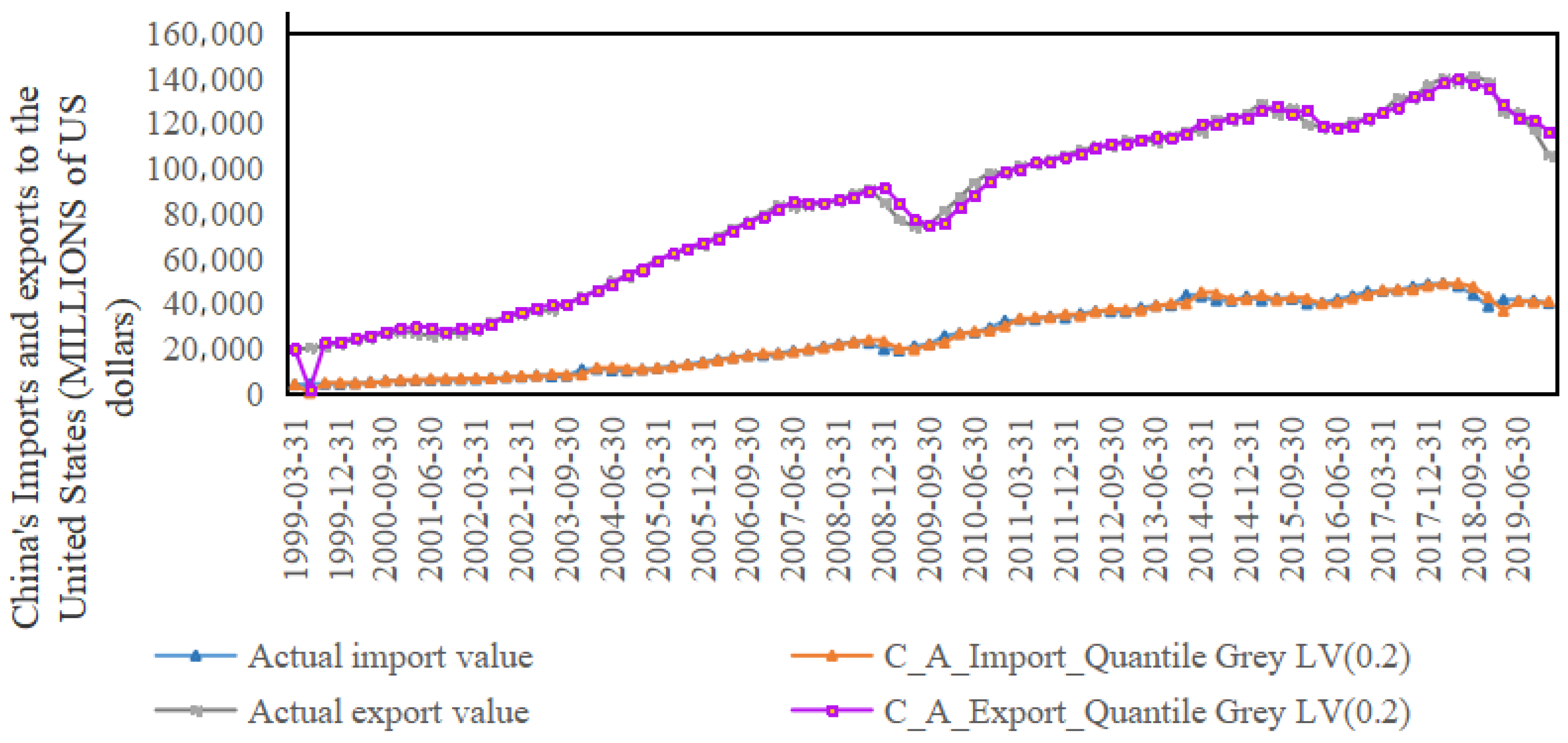
3.2. Simulation Using the QGLV Model
- (1)
- Comparison of export competitiveness. China’s imports of products and services from the United States meet the needs of the domestic population and partly replace the demand for domestic products and services, resulting in transporting domestic products and services abroad and promoting the development of China’s foreign trade. For the greater demand in the United States, China provides products at lower prices and complete services. Compared with the products exported by the United States to China, China’s exports to the US are more competitive, which has a considerable effect on the domestic market of the United States. For instance, after China acceded to the WTO, the significant reduction in export tariffs made its products and services competitive, and its global market share increased. The increased competitiveness of Chinese exports has affected the imports and exports of domestic companies in the United States. In addition, Athukorala and Yamashita [44] also believed that the China–US trade imbalance was a structural phenomenon caused by China’s critical role in the global production network as a final product assembly centre. Therefore, China’s imports to the US have become a driving mechanism to promote China’s exports to the US, and China’s export competitiveness to the US is more vital than that of the US to China.
- (2)
- Financial environment in the US. After financial liberalisation, the US financial supervision was relaxed, bank reserve ratios decreased, and loans increased. At the same time, the real estate and stock markets boomed, and the wealth effect stimulated household consumption and reduced the incentive to save. The US trade surplus equals the difference between US consumption and savings. To a certain extent, this change promotes imports from the US to China and restrains the trend of US trade exports to China, which changes the global economy. After the financial crisis, the international market as a whole was depressed. There was an inevitable interdependence between the two sides during the economic recovery. The China–US trade relationship evolved from a competitive relationship to a symbiotic and predator–prey relationship.
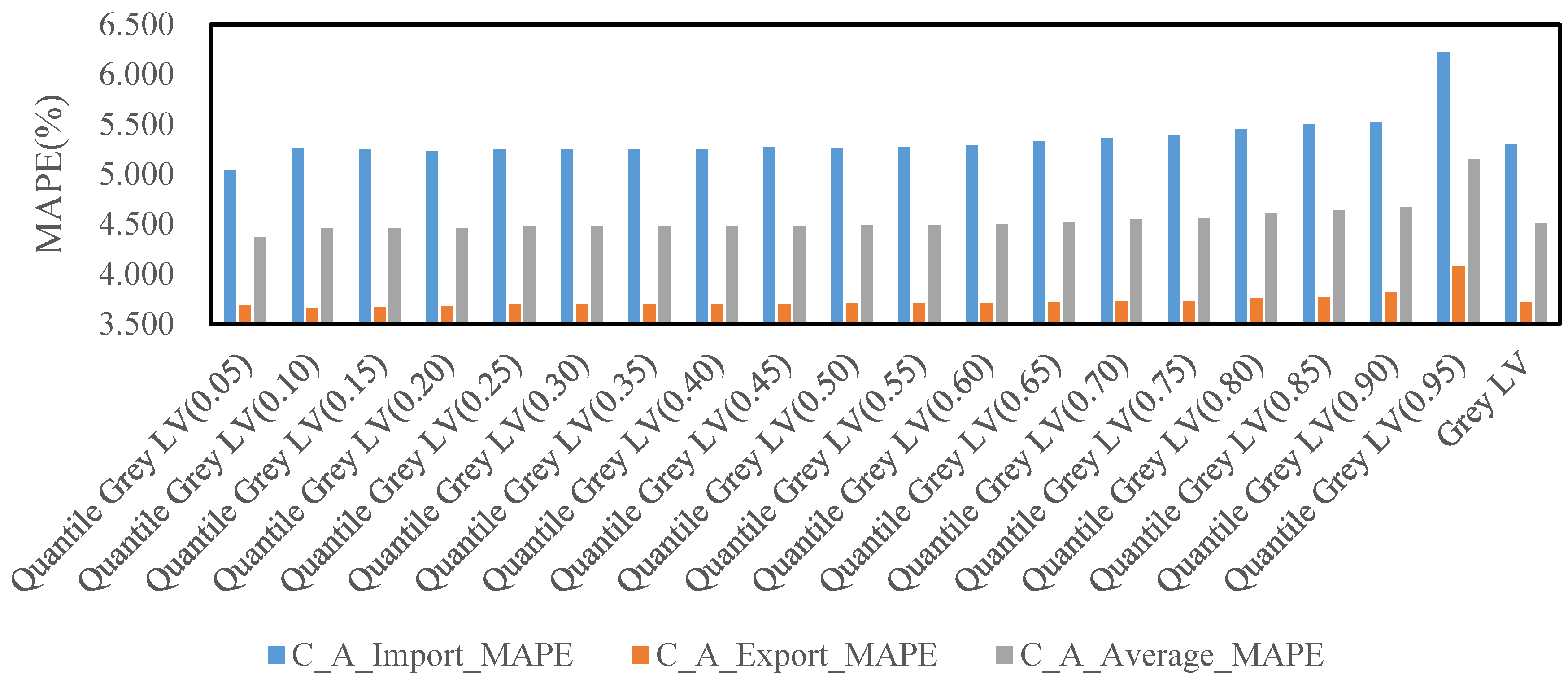
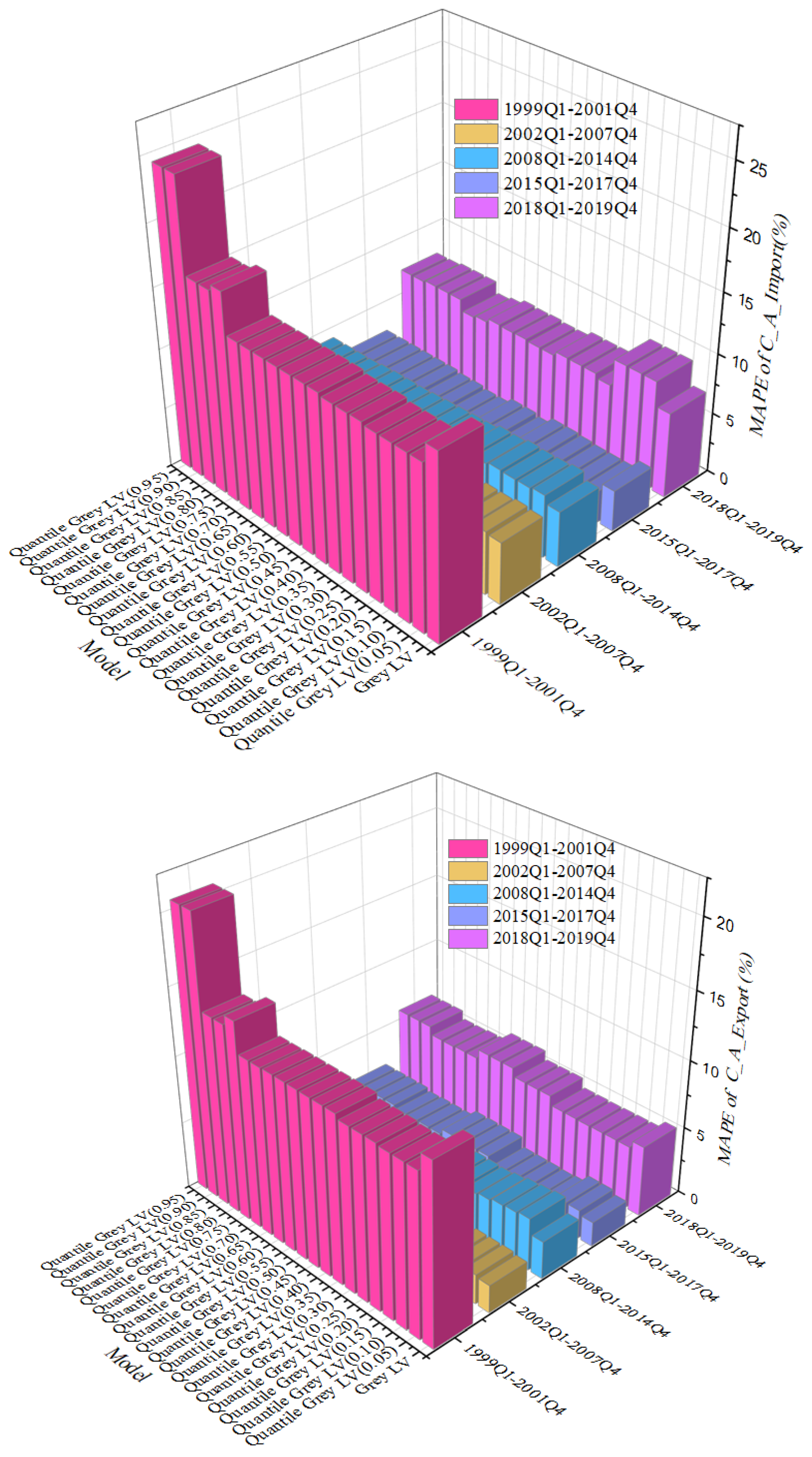
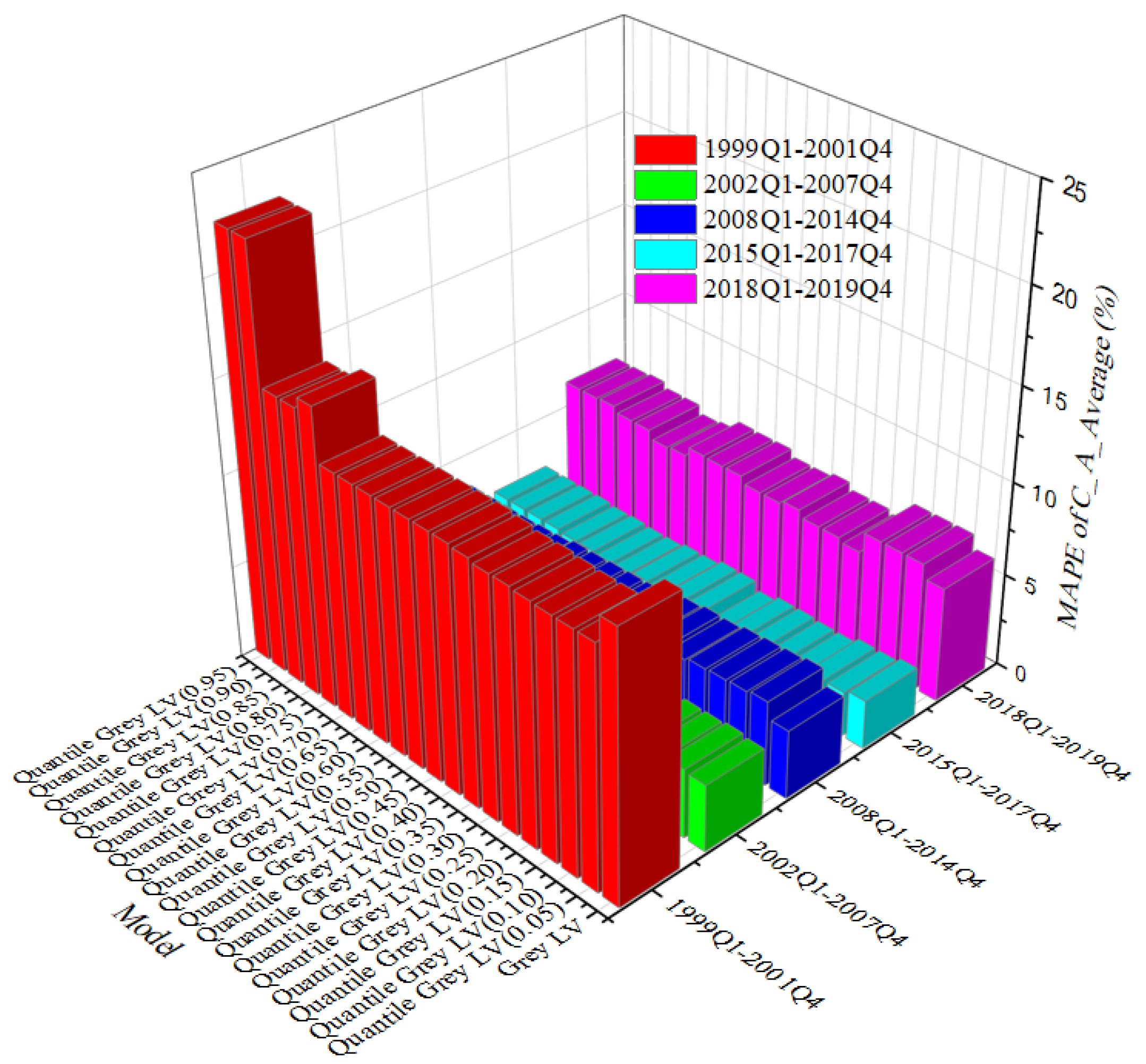
3.3. Comparison of the GLV and QGLV Models
3.4. Equilibrium Analysis
- (1)
- Explanation of ecosystem analysis. In ecosystem analysis, there are four possible outcomes of the rivalry. As shown in Table 5, trade in both countries has been suppressed at the first equilibrium point . Trade in one country wins, while trade in another country is suppressed at the second point and the third point . The import–export relationship will stabilise at the fourth equilibrium point , indicating that the cumulative volume of China’s imports to the United States will stabilise at million dollars, and the cumulative volume of China’s exports to the United States will stabilise at USD million dollars.
- (2)
- Explanation of economic model. Comparative advantage theory: China has a comparative advantage in labour-intensive products and can produce goods in large quantities at low cost. In contrast, the United States has a comparative advantage in technology-intensive and capital-intensive products. Via the trade cooperation between the two countries, the optimal allocation of resources and the improvement in efficiency can be achieved to achieve mutual benefit and win–win results. Absolute advantage theory: In China–US trade, China has the advantages of abundant labour and relatively low cost, while the United States has absolute advantages in high-tech fields and innovative industries. Because of their respective advantages, China has become the world’s factory, and the United States has become a leader in technology and innovation. However, when trade imbalance and bias gradually emerge, adjusting trade policies and balancing interests between the two sides will lead to trade friction.
3.5. Phased China–US Trade Relations Based on the QGLV Model
4. Conclusions and Policy Implications
- (1)
- The leading tone of China–US trade policy should be cooperation, not competition. Some trade frictions between China and the United States are sometimes not a collision of substantive interests but a misunderstanding caused by a lack of mutual understanding. China–US trade relations are mutually beneficial, with opportunities outstripping challenges and cooperation outstripping competition. Trade frictions can be effectively managed. With the development of China’s economy, the scale of China–US trade has been expanding, bringing tangible benefits to the economic development of the two countries and the lives of the two peoples. As major global trading countries, China and the United States have a profound basis for complementation. Bilateral trade is mutually beneficial and win–win, with massive potential for development and broad prospects. As a developed economy, the United States has long been a global leader in manufacturing and rich in high-tech resources. China has transformed from a traditional industrial structure to a modern industry as an emerging economy. The complementation of trade between significant countries is essential for China–US strategic trade cooperation. Amid the tortuous recovery of the global economy and trade, the two countries actively promote and shape the process of scientific and technological cooperation at the international level, which can further tap the potential of complementary trade structures, expand market cooperation space, and jointly improve the welfare of the people of the two countries and the world.
- (2)
- Promoting trade balance between China and the United States manifests high-quality foreign trade development. For a country’s foreign trade, export and import are like two sides of a coin, and any policies and measures that ignore one aspect will bring about the consequences of economic imbalance. It is found in this paper that China’s export to the United States inhibits China’s imports from the United States. China should have a deep and comprehensive understanding of the United States in many aspects such as politics, economy, society and culture. It should actively expand imports, promote trade balance, reduce trade surplus with the United States, promote the development of global multilateral trade, reduce trade friction, and promote international trade balance. The United States can appropriately liberalise export controls, reduce high tariffs, and promote trade balance. China and the United States need to take a step back and think before taking a step forward. The sustained and balanced development of China–US trade is necessary for the long-term economic and trade cooperation between the two countries.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Quantile | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 5.81 × 10−2 | −9.26 × 10−9 | 8.65 × 10−9 | 9.11 × 10−2 | 6.84 × 10−9 | −1.90 × 10−7 |
| 0.1 | 7.85 × 10−2 | −9.13 × 10−8 | 3.61 × 10−8 | 9.03 × 10−2 | 6.24 × 10−8 | −1.72 × 10−7 |
| 0.15 | 7.96 × 10−2 | −8.43 × 10−8 | 3.42 × 10−8 | 9.03 × 10−2 | 6.08 × 10−8 | −1.66 × 10−7 |
| 0.2 | 7.93 × 10−2 | −7.59 × 10−8 | 3.16 × 10−8 | 9.06 × 10−2 | 5.79 × 10−8 | −1.56 × 10−7 |
| 0.25 | 8.19 × 10−2 | −7.83 × 10−8 | 3.27 × 10−8 | 9.28 × 10−2 | 6.09 × 10−8 | −1.65 × 10−7 |
| 0.3 | 8.24 × 10−2 | −7.57 × 10−8 | 3.20 × 10−8 | 9.31 × 10−2 | 6.15 × 10−8 | −1.67 × 10−7 |
| 0.35 | 8.26 × 10−2 | −7.65 × 10−8 | 3.23 × 10−8 | 9.28 × 10−2 | 6.07 × 10−8 | −1.65 × 10−7 |
| 0.4 | 8.25 × 10−2 | −7.45 × 10−8 | 3.16 × 10−8 | 9.29 × 10−2 | 6.02 × 10−8 | −1.63 × 10−7 |
| 0.45 | 8.50 × 10−2 | −8.17 × 10−8 | 3.41 × 10−8 | 9.29 × 10−2 | 6.01 × 10−8 | −1.63 × 10−7 |
| 0.5 | 8.46 × 10−2 | −7.89 × 10−8 | 3.33 × 10−8 | 9.32 × 10−2 | 6.03 × 10−8 | −1.63 × 10−7 |
| 0.55 | 8.55 × 10−2 | −8.11 × 10−8 | 3.40 × 10−8 | 9.36 × 10−2 | 6.05 × 10−8 | −1.64 × 10−7 |
| 0.6 | 8.73 × 10−2 | −8.61 × 10−8 | 3.58 × 10−8 | 9.38 × 10−2 | 6.06 × 10−8 | −1.64 × 10−7 |
| 0.65 | 9.04 × 10−2 | −9.55 × 10−8 | 3.91 × 10−8 | 9.43 × 10−2 | 6.14 × 10−8 | −1.66 × 10−7 |
| 0.7 | 9.30 × 10−2 | −1.03 × 10−7 | 4.17 × 10−8 | 9.53 × 10−2 | 6.25 × 10−8 | −1.70 × 10−7 |
| 0.75 | 9.45 × 10−2 | −1.08 × 10−7 | 4.34 × 10−8 | 9.52 × 10−2 | 6.23 × 10−8 | −1.69 × 10−7 |
| 0.8 | 9.90 × 10−2 | −1.20 × 10−7 | 4.77 × 10−8 | 9.82 × 10−2 | 6.61 × 10−8 | −1.81 × 10−7 |
| 0.85 | 1.02 × 10−1 | −1.30 × 10−7 | 5.11 × 10−8 | 9.95 × 10−2 | 6.76 × 10−8 | −1.85 × 10−7 |
| 0.9 | 1.03 × 10−1 | −1.33 × 10−7 | 5.22 × 10−8 | 1.03 × 10−1 | 7.17 × 10−8 | −1.97 × 10−7 |
| 0.95 | 1.37 × 10−1 | −2.49 × 10−7 | 9.20 × 10−8 | 1.21 × 10−1 | 9.28 × 10−8 | −2.58 × 10−7 |
| Quantile | ||||||
|---|---|---|---|---|---|---|
| 0.05 | 1.06 × 100 | 1.10 × 100 | −9.53 × 10−9 | 7.16 × 10−8 | 8.91 × 10−9 | −1.99 × 10−7 |
| 0.1 | 1.08 × 100 | 1.09 × 100 | −9.50 × 10−8 | 6.53 × 10−8 | 3.76 × 10−8 | −1.80 × 10−7 |
| 0.15 | 1.08 × 100 | 1.09 × 100 | −8.77 × 10−8 | 6.36 × 10−8 | 3.56 × 10−8 | −1.74 × 10−7 |
| 0.2 | 1.08 × 100 | 1.09 × 100 | −7.90 × 10−8 | 6.06 × 10−8 | 3.29 × 10−8 | −1.63 × 10−7 |
| 0.25 | 1.09 × 100 | 1.10 × 100 | −8.16 × 10−8 | 6.38 × 10−8 | 3.41 × 10−8 | −1.73 × 10−7 |
| 0.3 | 1.09 × 100 | 1.10 × 100 | −7.89 × 10−8 | 6.45 × 10−8 | 3.34 × 10−8 | −1.75 × 10−7 |
| 0.35 | 1.09 × 100 | 1.10 × 100 | −7.97 × 10−8 | 6.36 × 10−8 | 3.37 × 10−8 | −1.73 × 10−7 |
| 0.4 | 1.09 × 100 | 1.10 × 100 | −7.77 × 10−8 | 6.31 × 10−8 | 3.29 × 10−8 | −1.71 × 10−7 |
| 0.45 | 1.09 × 100 | 1.10 × 100 | −8.53 × 10−8 | 6.30 × 10−8 | 3.56 × 10−8 | −1.71 × 10−7 |
| 0.5 | 1.09 × 100 | 1.10 × 100 | −8.23 × 10−8 | 6.32 × 10−8 | 3.47 × 10−8 | −1.71 × 10−7 |
| 0.55 | 1.09 × 100 | 1.10 × 100 | −8.47 × 10−8 | 6.34 × 10−8 | 3.55 × 10−8 | −1.72 × 10−7 |
| 0.6 | 1.09 × 100 | 1.10 × 100 | −9.00 × 10−8 | 6.35 × 10−8 | 3.74 × 10−8 | −1.72 × 10−7 |
| 0.65 | 1.09 × 100 | 1.10 × 100 | −9.99 × 10−8 | 6.44 × 10−8 | 4.09 × 10−8 | −1.74 × 10−7 |
| 0.7 | 1.10 × 100 | 1.10 × 100 | −1.08 × 10−7 | 6.56 × 10−8 | 4.37 × 10−8 | −1.78 × 10−7 |
| 0.75 | 1.10 × 100 | 1.10 × 100 | −1.13 × 10−7 | 6.54 × 10−8 | 4.55 × 10−8 | −1.77 × 10−7 |
| 0.8 | 1.10 × 100 | 1.10 × 100 | −1.26 × 10−7 | 6.95 × 10−8 | 5.01 × 10−8 | −1.90 × 10−7 |
| 0.85 | 1.11 × 100 | 1.10 × 100 | −1.37 × 10−7 | 7.11 × 10−8 | 5.38 × 10−8 | −1.95 × 10−7 |
| 0.9 | 1.11 × 100 | 1.11 × 100 | −1.40 × 10−7 | 7.55 × 10−8 | 5.50 × 10−8 | −2.08 × 10−7 |
| 0.95 | 1.15 × 100 | 1.13 × 100 | −2.67 × 10−7 | 9.87 × 10−8 | 9.86 × 10−8 | −2.74 × 10−7 |
References
- Jiang, Z.; Yoon, S. Dynamic co-movement between oil and stock markets in oil-importing and oil-exporting countries: Two types of wavelet analysis. Energy Econ. 2020, 90, 104835. [Google Scholar] [CrossRef]
- Mahmood, H.; Alkhateeb, T.; Furqan, M. Exports, imports, Foreign Direct Investment and CO2 emissions in North Africa: Spatial analysis. Energy Rep. 2020, 6, 2403–2409. [Google Scholar] [CrossRef]
- Lotka, A. The law of evolution as a maximal principle. Hum. Biol. 1945, 17, 167–194. [Google Scholar]
- Volterra, E. On the dynamic stress-strain relationship for plastic and elastic materials. In Proceedings of the 6th International Congress for Applied Mechanics, Paris, France, 22–29 September 1946. [Google Scholar]
- Rouvinen, P. Diffusion of Digital Mobile Telephony: Are Developing Countries Different? Telecommun. Policy 2006, 30, 46–63. [Google Scholar] [CrossRef]
- Ma, Z.S. Chaotic populations in genetic algorithms. Appl. Soft Comput. 2012, 12, 2409–2424. [Google Scholar] [CrossRef]
- Tseng, F.M.; Yu, J.R. A two stage fuzzy piecewise logistic model for penetration forecasting. Appl. Soft Comput. 2014, 21, 149–158. [Google Scholar] [CrossRef]
- Hong, J.; Koo, H.; Kim, T. Easy, reliable method for mid-term demand forecasting based on the Bass model: A hybrid approach of NLS and OLS. Eur. J. Oper. Res. 2016, 248, 681–690. [Google Scholar] [CrossRef]
- Kreng, V.; Wang, T.; Wang, H.T. Tripartite dynamic competition and equilibrium analysis on global television market. Comput. Ind. Eng. 2012, 63, 75–81. [Google Scholar] [CrossRef]
- Michalakelis, C.; Christodoulos, C.; Varoutas, D.; Sphicopoulos, T. Dynamic estimation of markets exhibiting a prey–predator behavior. Expert Syst. Appl. 2012, 39, 7690–7700. [Google Scholar] [CrossRef]
- Wang, Y.S.; Wu, H. Global dynamics of Lotka-Volterra equations characterizing multiple predators competing for one prey. J. Math. Anal. Appl. 2020, 491, 124293. [Google Scholar] [CrossRef]
- Mao, S.H.; Zhu, M.; Wang, X.P.; Xiao, X.P. Grey-Lotka-Volterra model for the competition and cooperation between third-party online payment systems and online banking in China. Appl. Soft Comput. 2020, 95, 106501. [Google Scholar] [CrossRef]
- Guo, D.; Yan, W.; Gao, X.; Hao, Y.; Xu, Y.; Wenjuan, E.; Tan, X.; Zhang, T. Forecast of passenger car market structure and environmental impact analysis in China. Sci. Total Environ. 2021, 772, 144950. [Google Scholar] [CrossRef]
- Grabner, C.; Hahn, H.; Leopold-Wildburger, U.; Pickl, S. Analyzing the sustainability of harvesting behavior and the relationship to personality traits in a simulated Lotka-Volterra biotope. Eur. J. Oper. Res. 2009, 193, 761–767. [Google Scholar] [CrossRef]
- Neokosmidis, I.; Avaritsiotis, N.; Ventoura, Z. Modeling gender evolution and gap in science and technology using ecological dynamics. Expert Syst. Appl. 2013, 40, 3481–3490. [Google Scholar] [CrossRef]
- Modis, T. US Nobel laureates: Logistic growth versus Volterra–Lotka. Technol. Forecast. Soc. Chang. 2011, 78, 559–564. [Google Scholar] [CrossRef]
- Chiang, S. An application of Lotka–Volterra model to Taiwan’s transition from 200 mm to 300 mm silicon wafers. Technol. Forecast. Soc. Chang. 2012, 79, 383–392. [Google Scholar] [CrossRef]
- Hung, H.C.; Tsai, Y.S.; Wu, M.C. A modified Lotka–Volterra model for competition forecasting in Taiwan’s retail industry. Comput. Ind. Eng. 2014, 77, 70–79. [Google Scholar] [CrossRef]
- Agrrawal, P.; Clark, J.M.; Agarwal, R.; Kale, J.K. An inter-temporal study of etf liquidity and underlying factor transition (2009–2014). J. Trading 2014, 9, 69–78. [Google Scholar] [CrossRef]
- Ditzen, J. Cross-country convergence in a general Lotka-Volterra model. Spat. Econ. Anal. 2018, 13, 191–211. [Google Scholar] [CrossRef]
- Marasco, A.; Picucci, A.; Romano, A. Market share dynamics using Lotka–Volterra models. Technol. Forecast. Soc. Chang. 2016, 105, 49–62. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.L.; Feng, Y.G. Study on the parameter grey estimation of logistic and Lotka-Volterra model. Coll. Math. 2004, 20, 82–87. [Google Scholar]
- Deng, J.L. The Basis of Grey Theory; Huazhong University of Science & Technology Press: Wuhan, China, 2002. [Google Scholar]
- Wu, L.F.; Liu, S.F.; Wang, Y.N. Grey Lotka–Volterra model and its application. Technol. Forecast. Soc. Chang. 2012, 79, 1720–1730. [Google Scholar] [CrossRef]
- Gatabazi, P.; Mba, J.C.; Pindza, E.; Labuschagne, C. Grey Lotka–Volterra models with application to cryptocurrencies adoption. Chaos Solitons Fractals 2019, 122, 47–57. [Google Scholar] [CrossRef]
- Hung, H.; Chiu, Y.; Huang, H. An enhanced application of Lotka–Volterra model to forecast the sales of two competing retail formats. Comput. Ind. Eng. 2017, 109, 325–334. [Google Scholar] [CrossRef]
- Zhang, S.; Meng, X.Z.; Feng, T.; Zhang, T.H. Dynamics analysis and numerical simulations of a stochastic non-autonomous predator–prey system with impulsive effects. Nonlinear Anal. Hybrid Syst. 2017, 26, 19–37. [Google Scholar] [CrossRef]
- Amore, P.; Fernández, F.M. On the application of the Lindstedt-Poincaré method to the Lotka-Volterra system. Ann. Phys. 2018, 396, 293–303. [Google Scholar] [CrossRef]
- Shi, L.L.; Chen, Y.Q. Existence and Iterative Algorithms of Solutions for Lotka-Volterra Competition Model. IAENG Int. J. Appl. Math. 2023, 53, 1–6. [Google Scholar]
- Zhao, K.; Yu, S.J.; Wu, L.F.; Wu, X.; Wang, L. Carbon emissions prediction considering environment protection investment of 30 provinces in China. Environ. Res. 2024, 224, 117914. [Google Scholar] [CrossRef]
- Morris, S.; Pratt, D. Analysis of the Lotka-Volterra competition equations as a technological substitution model. Technol. Forecast. Soc. Chang. 2003, 70, 103–133. [Google Scholar] [CrossRef]
- Lazzús, J.A.; Vega-Jorquera, P.; López-Caraballo, C.H.; Palma-Chilla, L.; Salfate, I. Parameter estimation of a generalized Lotka–Volterra system using a modified PSO algorithm. Appl. Soft Comput. 2020, 96, 106606. [Google Scholar] [CrossRef]
- Zhou, J.; Fang, R.; Li, Y.; Zhang, B. Parameter optimization of nonlinear grey Bernoulli model using particle swarm optimization. Appl. Math. Comput. 2009, 207, 292–299. [Google Scholar] [CrossRef]
- Agrrawal, P. An automation algorithm for harvesting capital market information from the web. Manag. Financ. 2009, 35, 427–438. [Google Scholar]
- Wang, C.; Hsu, L. Using genetic algorithms grey theory to forecast high technology industrial output. Appl. Math. Comput. 2008, 195, 256–263. [Google Scholar] [CrossRef]
- Wu, L.F.; Wang, Y.N. Estimation the parameters of Lotka-Volterra model based on grey direct modelling method and its application. Expert Syst. Appl. 2011, 38, 6412–6416. [Google Scholar] [CrossRef]
- Wang, Z.X.; Jv, Y.Q. A novel grey prediction model based on quantile regression. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105617. [Google Scholar] [CrossRef]
- Marinakis, Y.D.; White, R.; Walsh, S.T. Lotka–Volterra signals in ASEAN currency exchange rates. Phys. A Stat. Mech. Its Appl. 2020, 545, 123743. [Google Scholar] [CrossRef]
- Leslie, P. A Stochastic Model for Studying the Properties of Certain Biological Systems by Numerical Methods. Biometrika 1958, 45, 16–31. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, J. Regression Quantiles. Econometrica 1978, 46, 33–50. [Google Scholar] [CrossRef]
- Barrodale, I.; Roberts, F.D.K. An improved algorithm for discrete L1 linear approximation. SIAM J. Numer. Anal. 1973, 10, 839–848. [Google Scholar] [CrossRef]
- Pei, L.L.; Wang, Z.X.; Ye, D.J. Estimation of the Competitive Relationships between Amazon, Alibaba, and Suning Based on a Grey Tripartite Lotka-Volterra Model. J. Grey Syst. 2017, 29, 30–48. [Google Scholar]
- Agrrawal, P.; Skaves, M. Seasonality in stock and bond etfs (2001–2014): The months are getting mixed up but santa delivers on time. Soc. Sci. Electron. Publ. 2015, 24, 129–143. [Google Scholar] [CrossRef]
- Athukorala, P.; Yamashita, N. Global Production Sharing and China–US Trade Relations. China World Econ. 2009, 17, 39–56. [Google Scholar] [CrossRef]


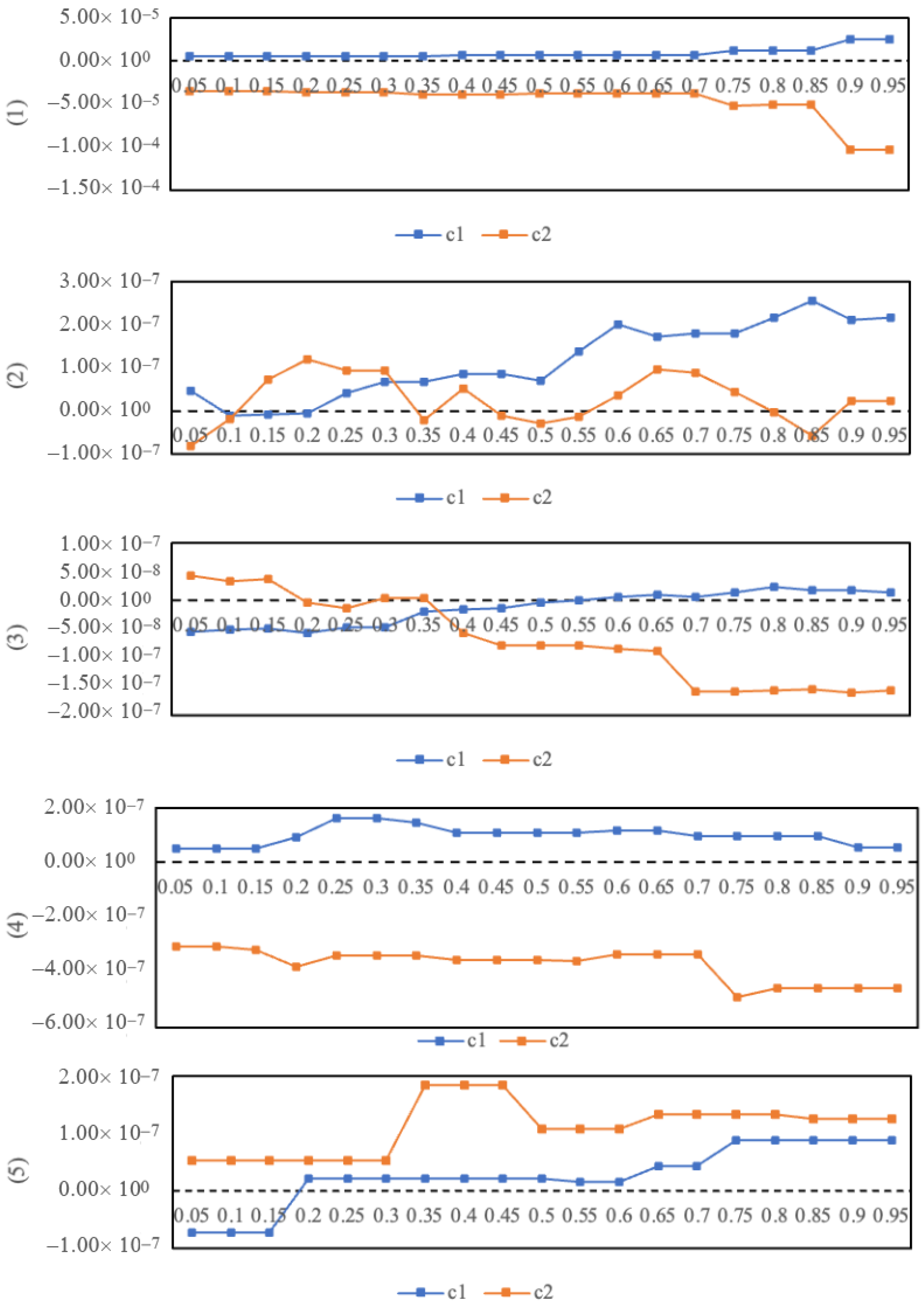
| c1 | c2 | Type of Competition | Implication |
|---|---|---|---|
| Pure competitive | The two groups are in a competitive relationship. | ||
| Predator–prey | Population 2 preys on population 1, which is not conducive to the survival of population 1 but beneficial to the survival of population 2. | ||
| Symbiotic | The two groups promote and support each other. | ||
| 0 | Commensalism | One-way promotion effect; population 2 has a good effect on the development of population 1. | |
| 0 | Amenity | One-way inhibition; population 2 exerts a negative effect on the development of population 1. | |
| 0 | 0 | Neutrality | The two groups develop independently. |
| Quantile | China’s Imports from the US (%) | China’s Exports to the US (%) | Quantile | China’s Imports from the US (%) | China’s Exports to the US (%) |
|---|---|---|---|---|---|
| 0.05 | 5.045 | 3.689 | 0.55 | 5.273 | 3.706 |
| 0.10 | 5.262 | 3.660 | 0.60 | 5.294 | 3.709 |
| 0.15 | 5.254 | 3.664 | 0.65 | 5.333 | 3.718 |
| 0.20 | 5.236 | 3.680 | 0.70 | 5.364 | 3.725 |
| 0.25 | 5.253 | 3.699 | 0.75 | 5.385 | 3.724 |
| 0.30 | 5.251 | 3.700 | 0.80 | 5.453 | 3.755 |
| 0.35 | 5.254 | 3.696 | 0.85 | 5.503 | 3.770 |
| 0.40 | 5.247 | 3.698 | 0.90 | 5.524 | 3.813 |
| 0.45 | 5.271 | 3.697 | 0.95 | 6.226 | 4.080 |
| 0.50 | 5.268 | 3.705 |
| China’s Import Trade Volume to the US | China’s Exports to the US | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | t | p | Parameter | Value | t | p |
| 23.72 | 0.00 | 47.86 | 0.00 | ||||
| −4.65 | 0.00 | 14.07 | 0.00 | ||||
| 5.93 | 0.00 | −11.83 | 0.00 | ||||
| Parameter | Estimated Value | Parameter | Estimated Value |
|---|---|---|---|
| 1.08 × 100 | 6.06 × 10−8 | ||
| 1.09 × 100 | 3.29 × 10−8 | ||
| −7.90 × 10−8 | −1.63 × 10−7 |
| Equilibrium | Eigenvalue | Equilibrium Value | Stability |
|---|---|---|---|
| Unstable | |||
| Unstable | |||
| Unstable | |||
| Stable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-X.; Li, Y.-T.; Gao, L.-F. Identification of the Dynamic Trade Relationship between China and the United States Using the Quantile Grey Lotka–Volterra Model. Fractal Fract. 2024, 8, 171. https://doi.org/10.3390/fractalfract8030171
Wang Z-X, Li Y-T, Gao L-F. Identification of the Dynamic Trade Relationship between China and the United States Using the Quantile Grey Lotka–Volterra Model. Fractal and Fractional. 2024; 8(3):171. https://doi.org/10.3390/fractalfract8030171
Chicago/Turabian StyleWang, Zheng-Xin, Yue-Ting Li, and Ling-Fei Gao. 2024. "Identification of the Dynamic Trade Relationship between China and the United States Using the Quantile Grey Lotka–Volterra Model" Fractal and Fractional 8, no. 3: 171. https://doi.org/10.3390/fractalfract8030171
APA StyleWang, Z.-X., Li, Y.-T., & Gao, L.-F. (2024). Identification of the Dynamic Trade Relationship between China and the United States Using the Quantile Grey Lotka–Volterra Model. Fractal and Fractional, 8(3), 171. https://doi.org/10.3390/fractalfract8030171







