1. Introduction
With the rapid development of information technology and the advent of the digital age, smart justice is becoming a prominent frontier in the contemporary judicial system. The rise of advanced technologies such as social media, big data analytics, and artificial intelligence bring unprecedented opportunities and challenges to judicial practice. We witnessed the great progress of smart justice at an unprecedented pace with the advent of big data technology. Legal translation software, automatic generation systems of legal documents, and online dispute handling systems have improved judicial efficiency, and great progress has been made in the construction of smart courts centered on court trials in terms of courtroom speech transcription, optical character recognition, clerical error correction, and document generation. Similar case similar judgment [
1,
2], providing judges with more comprehensive information, can automatically make legal judgments and legal reasoning according to the input case information and relevant laws and regulations, and reach the judgment result of the case. A legal prediction for a similar case is the most challenging task in smart justice.
In 2018, China’s Supreme People’s Court launched the “intelligent push system for class cases”, and many local courts followed suit and launched a series of systems for class cases and judgments. Many attempts have been made, from expert systems to unsupervised big data processing systems; however, judges have to spend a lot of time and energy on identifying similar cases from the amount of recommended cases and the accuracy of legal predictions needs to be improved. The reasons for the unactuated predictions lie in the incomplete legal data and in the technical deficiency. First, the structure of judicial case documents is not clear, the judicial cases belonging to the hierarchy of courts is not clear, the lack of cleaning makes a large amount of case information that needs to be manually marked, and there are problems such as the over-reliance on manual intervention and low recognition accuracy. Second, the judicial adjudication process is the process of personal value selection of judges, and the adjudication system is disguised as technical neutrality, but it cannot escape the value choice. How to solve the value choice of the judicial discretion model is an important topic to be solved. Third, the algorithm black box is a major reason for the criticism of artificial intelligence technology, and only by strengthening the judicial discretion system audit and disambiguation procedures so that legal professionals understand the type of case and judgment model can artificial technology truly integrate into the current judicial system. Therefore, the establishment of a complex system judicial intelligence system with a comprehensive analysis ability is a future development direction.
The current model based on artificial intelligence basically does not have common sense and analytical ability, and there is still a long way to go to establish a judicial discretion model with cognitive function. In order to improve the prediction accuracy of the judicial discretion model, we need to solve the following three problems in establishing the judicial discretion model: First, strengthen the description of the case to make it clearer. In the case where the structure of the current legal case documents is incomplete, it is better to use the combination of manual experts and automatic extraction to better extract the relevant information of the case. Second, the establishment process of the judicial discretion model is more transparent. At present, the most common-used algorithm to predict is the deep learning method, which can mine valuable information and establish a correlation from massive data, but its calculation process is completely unknown. If users can intervene in the process of the judicial discretion model, it will undoubtedly increase the transparency of the model. Third, judicial decisions are often combined with specific situations, and it is difficult to give a specific optimal value of the judgment. The judgment is often not a definite number, but limited within a certain range, as long as the final judgment is acceptable within a certain range.
The goal of the judiciary is to maintain fairness and justice, and judicial reasoning has always been known for its rigor, but there are often vague words in legislative documents and judgment documents [
3], such as using a “reasonable” approach, the social impact is “bad”, resulting in “serious” consequences, and how can it be considered “reasonable”, “serious”, “bad”? These kinds of words have a certain emotional color, different people come to a large difference in conclusions, and judicial interpretation is diverse. The analysis of previous cases to obtain the majority of people’s specific treatments of this fuzzy problem has become the current research progress of the artificial intelligence judicial discretion model. Fuzzy systems [
4,
5] significantly enhance the “similar case similar judgment” principle in law, offering nuanced and consistent evaluations of cases. These systems adapt to changes in legal standards and societal values, ensuring ongoing relevance and fairness. They foster transparency, mitigate biases, and strengthen public trust in the judiciary. Also crucial for legal research and education, fuzzy systems [
6,
7] deepen the understanding of legal reasoning. However, their integration demands a careful consideration of legal theory and practice to maintain justice. Ultimately, fuzzy systems [
8,
9,
10] promise a more sophisticated and equitable legal decision-making process. In 2011, we used fuzzy mathematics to establish a criminal sentencing model and control the range of sentencing within the degree of membership, which had a better effect on resolving the differences in judicial decisions [
11].
Law, as established by a nation or region in the form of legal texts, consists of a series of rules and principles that regulate social behavior and organize social order. Due to the different historical, cultural, political, and social backgrounds of various countries and regions, laws also vary accordingly. A judicial decision is a judgment made by a judge based on the specific circumstances of various cases and his own experience. This judgment is based on long-term legal knowledge, but it is closely related to the judge’s religion, family background, educational background, and work experience; so, it is difficult to give an objective description of the reasons for the judgment. Predicting compensation amounts in defamation cases is challenging due to the inherent complexity of cases and the ambiguity and uncertainty of the involved data. Fractional calculus has the unique advantages of long-term memory, non-locality, and weak singularity, and it has special advantages for solving nonlinear problems. Fractional calculus [
12,
13] has played a pivotal role in advancing the development of fuzzy systems, introducing a new dimension to the complexity and adaptability of these systems. Unlike traditional calculus, fractional calculus involves differentiation and integration to non-integer orders, offering a nuanced approach to modeling real-world phenomena that exhibit memory and hereditary properties [
13,
14]. This mathematical framework aligns harmoniously with the principles of fuzzy systems, which are designed to handle imprecision and ambiguity. The integration of fractional calculus into fuzzy systems enhances their modeling capabilities, particularly in systems where dynamics are influenced by past states or where processes are inherently complex and non-local. The memory characteristic of fractional operators allows fuzzy systems to incorporate a more extensive range of information, considering not only the current state but also the influence of past states, leading to more accurate and comprehensive models. In 2022, Bansal et al. applied fractional calculus to the study of crime dynamics by dividing the person into four clusters, and they discussed the well-posedness and stability of the proposed fractional model [
15].
Furthermore, the flexibility offered by fractional calculus in adjusting the order of differentiation or integration enables the fine-tuning of the fuzzy system’s response, allowing it to mirror the intricate and often fractional nature of human reasoning and natural processes [
16,
17,
18]. This adaptability is crucial in diverse fields such as control systems, signal processing, and bioengineering, where systems exhibit complex, non-linear behaviors that traditional integer-order models cannot adequately capture. In addition to enhancing system dynamics [
19,
20], fractional calculus contributes to the stability and robustness of fuzzy systems. By meticulously adjusting fractional orders, system designers can achieve a delicate balance between responsiveness and stability [
21], ensuring that the system can handle rapid changes in input or the environment while maintaining consistent performance. Compared to traditional neural network models without fractional-order fuzzy systems, the integrated model exhibits higher prediction accuracy in the compensation prediction of defamation cases. This is because the fractional-order fuzzy system provides a more complex and refined data processing mechanism, allowing the model to better understand and interpret the underlying relationships and patterns in the data.
With the popularity of social media and the internet, an individual’s speech and information can quickly spread to a global scope, resulting in a surge in reputation infringement cases. In this digital age, reputation infringement has become one of the focuses of social attention, seriously affecting the reputations and images of individuals, enterprises, and public figures. Therefore, research on predicting and preventing reputation infringement acts is particularly important. China enacted the “Civil Code of the People’s Republic of China” in 2020. Although the Tort Liability section of the code stipulates the compensation liability for damages caused by tortious acts, Chinese society is undergoing rapid economic, social, and cultural transformations, and the formulation and implementation of the Civil Code may face challenges in responding to these changes. Reputation infringement cases involve a balance between freedom of speech and the right to reputation. Freedom of speech is a fundamental right, but it must respect the right to reputation when expressing opinions. Therefore, courts need to weigh the conflict between these two rights to ensure fair handling of cases. The protection of the right to reputation is a subjective right, often involving the feelings and evaluations of individuals or organizations. This makes the facts and evidence in reputation infringement cases somewhat ambiguous, requiring a meticulous investigation and analysis.
In order to better describe the legal phenomenon and analyze the process of judicial judgment, in this paper, the method of fuzzy mathematics and fractional calculus is used to establish the prediction model of the judicial discretion model. The combination of fractional calculus with fuzzy logic not only deepens our understanding of complex systems but also opens new avenues for innovation in modeling, control, and decision-making. This paper combines the method of expert learning to structure the judicial judgment documents in advance. Then, fuzzy mathematics and fractional calculus are used to establish a model of the infringement of reputation rights, which can describe the case more carefully on the one hand and reduce the “black box” problems caused by deep learning and other methods. The introduction of fractional-order fuzzy systems helps to some extent in enhancing the model’s interpretability. This is due to the rules and membership functions of the fuzzy system providing an intuitive way to understand how the model processes and interprets input data.
The main research content and contributions of this article are listed below.
Construction of a Reputation infringement Case Dataset in China: This study has collected data on reputation infringement cases using publicly available judgment documents from the China Judgments Online. The data have been cleansed, and key information regarding penalties in reputation infringement cases has been organized to form a structured dataset. This dataset can be used for in-depth studies on the types, frequency, and influencing factors of reputation infringement cases. The case information and compensation amounts can be utilized to establish predictive models, assisting in the prediction of compensation amounts in reputation infringement cases. It also provides insights into the main points of dispute and hot topics in reputation infringement cases, offering references and a basis for the formulation of related legal policies.
Development of a Fractional Fuzzy Neural Network for the Prediction of Compensation Amounts in Reputation infringement Cases: Reputation infringement cases inherently possess a high degree of ambiguity. Firstly, the act of infringement often involves speech and assessment, requiring a balance between freedom of speech and the infringement of the right to reputation. Secondly, the ambiguity of language means that the information in judicial documents from China Judgments Online cannot accurately describe the severity of various infringement acts. The same statements or remarks can be understood differently in different contexts, leading to ambiguity in case conclusions. Lastly, there is ambiguity in the amount of compensation, as judges have a certain degree of discretion, and the civil case laws are not as detailed as the sentencing guidelines in criminal cases. For the same case, different judges, influenced by their subjective factors, may issue different penalties, indicating a certain level of ambiguity in judicial sentencing. Therefore, a fuzzy system is used to describe the elements in reputation infringement cases, addressing these ambiguities effectively.
Applying fractional calculus to the processing of judicial information is a new way to solve vague information, which has advantages in improving the accuracy of the judicial discretion model. Fractional calculus has great advantages in describing nonlinear fuzzy problems, and as social information such as legal information is vague, the potential for fractional-order fuzzy systems to solve intricate and dynamic problems becomes increasingly apparent, marking a significant stride in the evolution of intelligent systems.
3. Reputation Infringement Case Dataset
Civil compensation liability is based on the “Interpretation of Several Issues Concerning the Determination of Civil Liability for Compensation for Mental Damages” by the Supreme People’s Court of the People’s Republic of China (
Table 1). Article 10—The amount of compensation for mental damages is determined based on the following factors:
- (1)
The degree of fault of the infringer, except as otherwise provided by law;
- (2)
Specific circumstances such as the purpose, manner, and occasion of the infringement;
- (3)
The consequences caused by the infringement act;
- (4)
The profit situation of the infringer;
- (5)
The economic ability of the infringer to bear the liability;
- (6)
The average standard of living in the location where the court handling the lawsuit is situated.
Table 1.
Chinese legal basis for compensation in reputation infringement cases.
Table 1.
Chinese legal basis for compensation in reputation infringement cases.
| Interpretation of China Supreme People’s Court on Several Issues Concerning the Determination of Compensation Liability for Mental Damage in Civil Torts |
|---|
Article 10—The amount of compensation for mental damage shall be determined according to the following factors: - (1)
The extent of the infringer’s fault, except as otherwise provided by law; - (2)
The purpose, manner, occasion and other specific circumstances of the infringing act; - (3)
The consequences of the infringing act; - (4)
The profit of the infringer; - (5)
The economic ability of the infringer to bear responsibility; - (6)
The average standard of living in the place where the court for accepting litigation is located.
|
Therefore, constructing a dataset for predicting compensation for reputation infringement cases in China involves key features based on the aforementioned legal provisions. These include the location of the infringement, the identities of the plaintiff and the defendant, the method of infringement, the scope of impact, the consequences of the damage, the degree of the process, the per capita income level of the location where the court is situated, the amount of compensation for mental damage, and additional remarks.
We collected final judgment cases of reputation infringement from the publicly available legal document platform China Judgments Online. After data cleansing and privacy protection of the reputation infringement cases, we obtained the explanatory table of elements involved in reputation infringement cases shown below (
Table 2).
In the table above, elements such as the infringement location, plaintiff’s identity, defendant’s identity, infringement method, court’s location average income, and mental damage compensation amount are clearly defined and can be precisely represented. On the other hand, factors like the impact range, damage consequences, and degree of fault are described in natural language, exhibiting a certain level of ambiguity and making it challenging to provide precise and quantitative descriptions.
The constructed dataset provides crucial information about cases involving infringements of the right to honor, including elements such as the location of the infringement, the identity of the plaintiff, the identity of the defendant, the mode of infringement, the scope of impact, the consequences of the harm, the degree of fault, the average income level in the jurisdiction of the court, the amount of compensation for mental damages, and additional remarks. These details are invaluable for researching the types, frequency, and influencing factors of honor infringement cases, and predicting compensation for mental damages.
As shown in
Figure 2, this is the statistical relationship between the average annual income per capita in the jurisdiction of the court and the fines in cases of infringement of the right to honor in the dataset. Through a preliminary analysis of the dataset, several trends and correlations can be observed.
- (1)
There is a positive correlation between the compensation amount and the average income level in the jurisdiction of the court. As the regional average income increases, the compensation amount also tends to increase.
- (2)
The identity of the plaintiff and the identity of the defendant may have a significant impact on the type of cases and the compensation amount. Public figures and corporate users may face different types of infringement actions and compensation amounts.
- (3)
Descriptions of the mode of infringement, scope of impact, and consequences of harm exhibit some level of vagueness and require further natural language processing and text analysis for quantification and classification.
- (4)
The description of the degree of fault can be used for the court’s qualitative assessment of infringement actions, but a more in-depth analysis is needed to understand its relationship with compensation amounts.
- (5)
These initial observations provide valuable insights for further research into the characteristics of honor infringement cases and compensation prediction. Machine learning and statistical analysis methods can be employed to delve deeper into the dataset.
4. Fractional-Order Fuzzy Neural Network
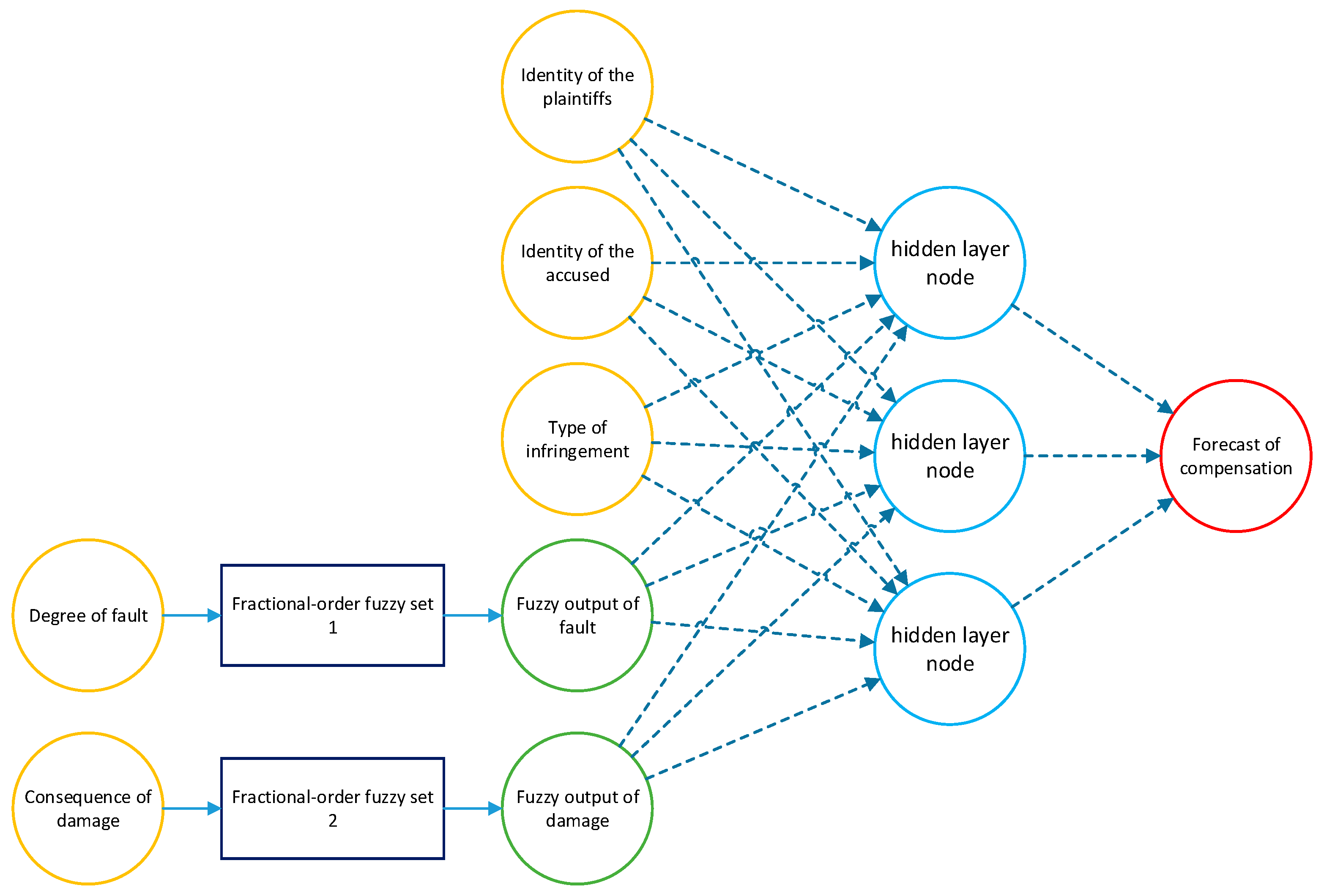
The fractional-order fuzzy neural network system is designed to address the fuzziness in describing the impact scope, consequences, and degrees of fault in cases of infringement within the dataset of the right to honor. In judicial documents, these descriptions often exhibit ambiguity, making it challenging for traditional neural networks to handle such unstructured and fuzzy input features. Therefore, fractional-order fuzzy membership functions are utilized to depict the infringement behaviors, consequences, and degrees of fault in the infringement dataset. The outputs of fractional-order fuzzy membership functions serve as inputs for neural network predictions, enabling the prediction of judgments in cases of infringement of the right to honor. The overall structure of the system is illustrated in the following diagram (
Figure 3).
In the diagram above, the fractional-order fuzzy interface is primarily used to perform fuzzy modeling of factors that are difficult to precisely describe in reputation infringement cases, such as the extent of impact, consequences of harm, and degree of fault. This modeling aims to generate structured input information that can be used for regression and prediction by the neural network.
4.1. Fractional-Order Fuzzy Membership Functions
The fractional-order fuzzy interface consists of two key components. Firstly, there is the fractional-order fuzzy membership function constructed by an expert system. This expert system is composed of legal experts in the field of reputation infringement who compile essential information based on current legal regulations and judicial precedents. This information is used to create appropriate fractional-order membership functions.
The second crucial component is the adaptive adjustment algorithm for fractional-order fuzzy membership functions. This algorithm automatically adjusts the fractional-order membership functions based on input data to ensure their adaptability and accuracy. Together, these two components form the fractional-order fuzzy interface, which is employed to handle fuzzy data and provide input information for the neural network’s regression and prediction tasks.
In cases of infringement, there are often fuzzy descriptions regarding aspects like the scope of influence, the consequences of the harm, and the degree of fault. To handle such fuzzy information, we use fractional-order fuzzy membership functions for representation. For situations where there are clear legal definitions of the severity of circumstances, we construct corresponding fuzzy membership functions based on legal provisions.
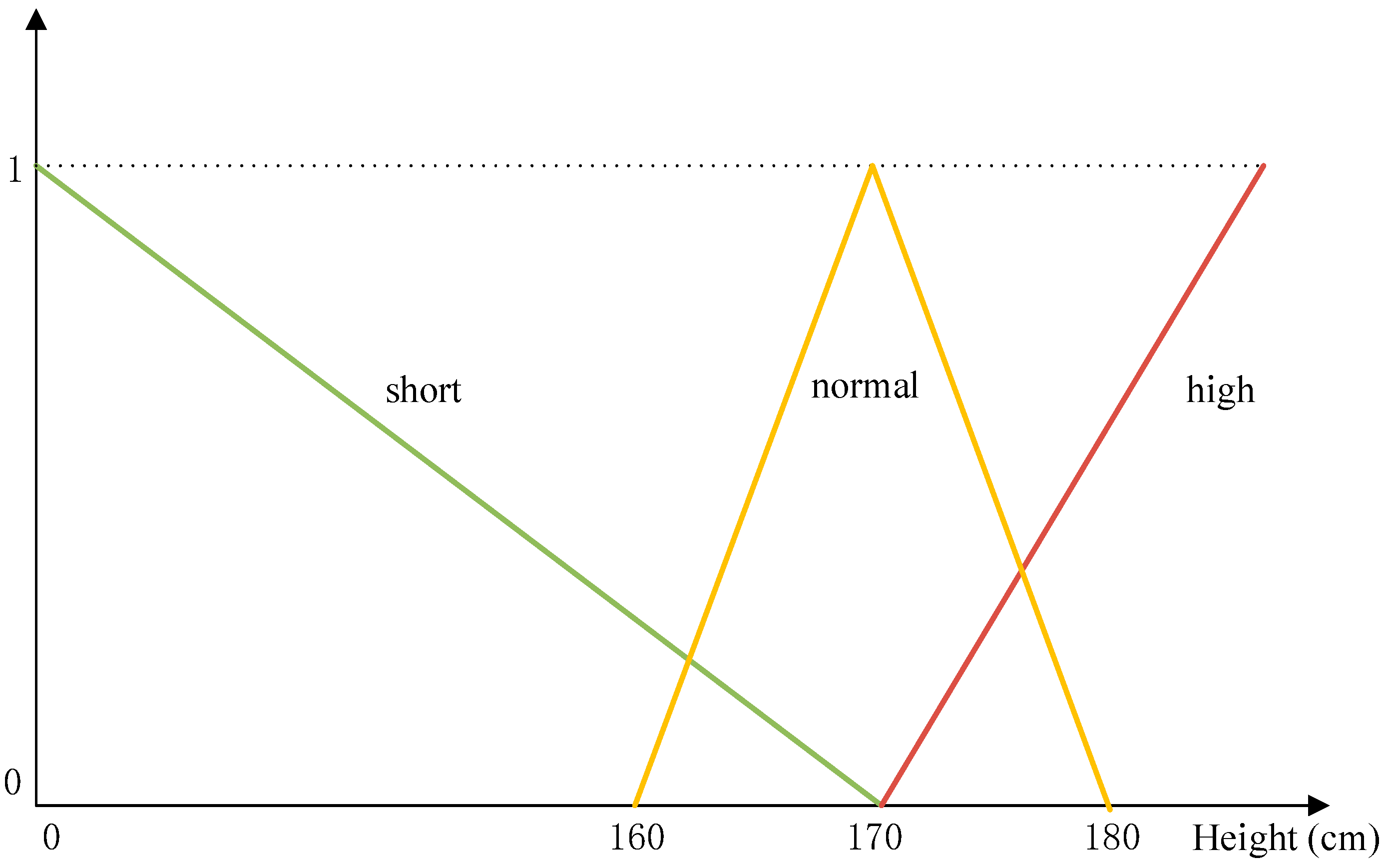
As shown in
Table 3, according to the interpretation by the Supreme People’s Court of the People’s Republic of China regarding crimes committed via information networks, the degree of forwarding defamatory and infringing information on the internet can serve as a reference. We can create a fuzzy membership function to represent the “degree of seriousness” of reputation infringement, where the input variable
represents the number of times defamatory information is viewed on the internet.
The construction of this fuzzy membership function
can be tailored according to specific legal provisions and relevant data, ensuring a more accurate quantification of the severity of forwarding infringement information on the internet.
The trapezoidal membership relationship function graph depicting the relationship between the qualitative classification of reputation infringement severity in online reputation cases and the number of views of defamatory information is shown below [
22,
23] (
Figure 4).
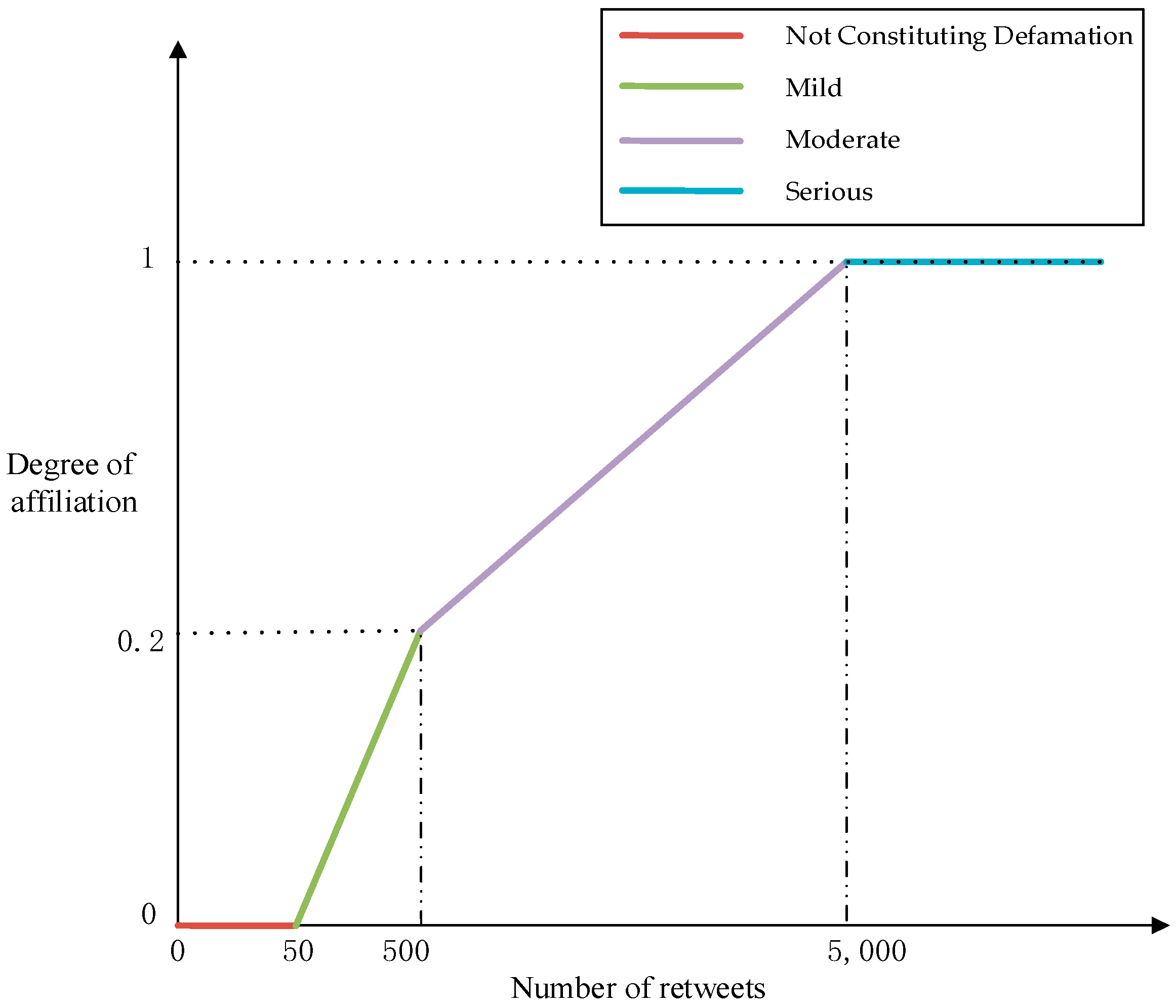
Similar to Formula (7), we can construct a fuzzy membership function for the “severity of the offense” of forwarding defamatory information on the internet, where x represents the number of times defamatory information is forwarded on the network.
In Equation (8), represents the fuzzy membership function for the impact of forwarding on reputation rights infringement, and represents the number of times information is forwarded.
In traditional fuzzy set operations, the range of values for the union of the number of times reputation infringement information is viewed and the number of times reputation infringement information is forwarded still belongs to the set . This is different from the way we handle it in legal contexts.
For example, if reputation infringement information posted by person A is viewed 5000 times and forwarded 500 times, traditional fuzzy set union processing would result in a value of
, which is the same as if A’s reputation infringement information was viewed 5000 times and forwarded 10 times
. This does not align with our intuitive understanding. Therefore, this paper introduces fractional-order fuzzy set operations, where the information from each fuzzy membership function contributes to the final result. Therefore, we define the defuzzification process of fractional-order membership functions as shown in the equation below.
where
represents fractional-order membership union operation and
is the fractional order.
represent the first and
kth membership functions, respectively. It must be noted that the range from
to
is ordered fuzzy membership functions. It satisfies the following inequalities:
and
is the difference coefficient in the fractional-order Grünwald–Letnikov definition.
represents the operation result of
k interrelated fuzzy set membership functions system under the fractional-order fuzzy union operation. From the Equation (9), it can be deduced that
, but the numerical upper limit is not restricted to 1 and may take values greater than 1.
is the difference coefficient that influences multiple fuzzy membership functions in a non-linearly decreasing manner in the fractional-order fuzzy operation system.
When defamatory information published by A is viewed 5000 times and forwarded 500 times, the
v-order fuzzy membership function is shown in Equation (11):
The most commonly used defuzzification operation for fuzzy sets, as shown in Equation (12), is taking the maximum value:
When the defamatory information posted by A has been viewed 5000 times and forwarded 100 times, the
v-order fuzzy membership function is shown in Equation (13):
The most commonly used defuzzification operation for fuzzy sets is shown in Equation (14):
From the above equations, it can be observed that the defuzzification function for fractional-order fuzzy sets provides a more detailed representation of different membership function scenarios. By utilizing the non-locality of the fractional order, it can reveal subtle differences within the fuzzy membership functions. In contrast, traditional fuzzy sets’ defuzzification typically selects the membership function with the highest value as the output, neglecting the less prominent membership functions.
After constructing the fractional-order fuzzy membership defuzzification function, it is necessary to perform parameter optimization to select the appropriate fractional order v that will yield the best results for the fractional-order fuzzy membership operations.
The determination of the fractional order v is achieved using a grid search method, with reference to known results from judicial decisions made by judges. Although factors like the extent of impact, damage consequences, and the degree of fault possess a degree of fuzziness, according to the judicial interpretations of the Supreme People’s Court of the People’s Republic of China, these factors should exhibit a certain degree of positive correlation with the final judgment outcome. A range of fractional-order parameters is considered, ranging from v = −1.5 to v = 1.5, with equidistant sampling intervals. This process allows us to obtain the weighted coefficients for various fractional-order parameters within the fractional-order fuzzy system.
The fractional-order weighted coefficients vary with the change in fractional order
v as shown in the following
Table 4 [
24].
Since there are approximately 7 categories of infringement methods in the judgment dataset of reputation infringement cases, these 7 categories of data, according to legal experts, are arranged from mild to severe as follows: public verbal abuse, verbal dissemination of insulting defamatory information, posting textual materials, reposting infringing articles, posting insulting defamatory information on social media circles, spreading insulting defamatory information on microblogs and blogs, and unauthorized use of photos for commercial promotion. Considering the methods of dissemination, the scope of influence, and the purpose of infringement, these overall trends are observed, but they are not absolute. For example, in the case where only 10 people view a post on a microblog or social media circle and 1000 posts of textual materials are distributed, we use fractional-order fuzzy sets to handle such situations. Within the 7 categories of infringement methods, experts have constructed fuzzy membership functions based on legal information. Between the 7 major categories, fractional calculus is used to combine multiple fuzzy membership functions, thereby obtaining a fractional-order defuzzification function. The value range of the fractional-order fuzzy membership function is , and is not limited to the range of .
4.2. Fractional-Order Fuzzy Neural Network
The previous section obtained the defuzzification function of the fractional-order fuzzy system. With this function, we can output the quantified impact range, degree of fault, and consequences of the infringement, which results in a continuous function value. Using this value in conjunction with the previous classification information, as well as the per capita income level, we input it into a backpropagation (BP) neural network [
25,
26,
27] to predict the verdict in reputation infringement cases. The entire fuzzy neural network structure is shown in the following diagram.
The
Figure 5 illustrates the predictive model of the BP neural network, which primarily consists of four layers.
The first layer is the fractional-order fuzzy interface, utilized for calculating the scope of impact, consequences of damage, degree of fault, and other information expressed in natural language, which are challenging to quantify precisely. This is performed through the application of the fractional-order fuzzy membership function, resulting in numerical data that can be input into the BP neural network.
The second layer encompasses factors such as the location of the tort, the identities of the plaintiff and defendant, the average income level in the jurisdiction of the court, as well as the output values of the fuzzy membership function. These pieces of information can be directly input into the BP neural network. Data types like the location of the tort and the identities of the plaintiff and defendant are encoded using one-hot encoding, while the fuzzy membership outcomes for the scope of impact, consequences of damage, and degree of fault, as well as the average income level of the court’s location, are numerical values.
The third layer is the hidden layer of the BP neural network, where the neurons are tasked with capturing abstract features from the input data.
The fourth layer delivers the final output, which is the predicted result concerning the infringement of the right to reputation.
Within this BP neural network, the activation function employed is the sigmoid function:
The error function is the square of the difference between the result of forward propagation and the actual fine. This is typically used in neural networks to quantify the difference between the predicted value and the actual value, guiding the optimization of the model during the training process.