Abstract
This study employs multifractal detrended fluctuation analysis to investigate the impact of fuel cell introduction in the Korean electricity market via the lens of multifractal scaling behavior. Using multifractal analysis, the research delineates discrepancies between peak and off-peak hours, accounting for the daily cyclicity of the electricity market, and proposes a crossover point detection method based on the Chow test. Furthermore, the impacts of fuel cell introduction are evidenced through various methods that encompass multifractal spectra and market efficiency. The findings initially indicate a higher degree of multifractality during off-peak hours relative to peak hours. In particular, the crossover points emerged solely during off-peak hours, unveiling short- and long-term dynamics predicated on a near-annual cycle. Additionally, the average Hurst exponent for the short-term was 0.542, while the average for the long-term was 0.098, representing a notable discrepancy. The introduction of fuel cells attenuated the heterogeneity in the scaling behavior, which is potentially attributable to the decreased volatility in both the supply and demand spectra. Remarkably, after the introduction of fuel cells, there was a discernible decrease in the influence of long-range correlation within multifractality, and the market exhibited an increased propensity toward random-walk behavior. This phenomenon was also detected in the market deficiency measure, from an average of 0.536, prior to the introduction, to an average of 0.267, following the introduction, signifying an improvement in market efficiency. This implies that the introduction of fuel cells into the market engendered increased supply stability and a consistent increase in demand, mitigating volatility on both the supply and demand sides, thus increasing market efficiency.
1. Introduction
Following World War II, the electric power industry underwent significant expansion in response to the increasing demand driven by economic growth, operating under the centralized monopoly of the central government with a focus on ensuring stable supply. However, this centralized structure resulted in inefficiencies such as overinvestment in supply infrastructure and the decoupling of supply and demand. To mitigate these inefficiencies, the global electricity market has been subject to deregulation and structural reforms since the 1990s, which aimed at achieving decentralization and promoting market competition to improve overall efficiency [1,2]. This regulatory trend, initially observed in Western nations, gradually extended to the BRICs during the 1990s and 2000s, with South Korea also pursuing the advantages of market restructuring.
The electricity market demonstrates pronounced seasonality in annual, weekly, and daily intervals and is distinguished by phenomena such as significant price spikes and elevated volatility, which are atypical compared to other commodities [3]. These seasonal dynamics are predominantly influenced by meteorological conditions, ambient temperatures, and variations in commercial activity, which led researchers to segment the electricity market temporally for detailed analysis [4,5,6]. The inherent challenges of accommodating abrupt demand fluctuations in the electricity market precipitate sharp price movements and increased volatility [7,8]. The substantial volatility and non-linear characteristics inherent in the electricity market introduce significant complexity to market pricing mechanisms, rendering multifractal analyses particularly effective.
Fama introduced the efficient market hypothesis (EMH), which posits that all available information is reflected in prices [9]. According to EMH, in an efficient market, all existing and historical information is already factored into prices, causing price movements to be random and excluding arbitrage opportunities. However, EMH does not account for phenomena such as long-range dependence, self-similarity, and fat tails in financial markets [10,11,12]. These market characteristics can be elucidated by the fractal market hypothesis (FMH), which is based on the theory of complex systems [13]. FMH posits that these irregular attributes, designated as fractal properties, are inherent in prices. Initially, these properties were probed using the rescaled range method (R/S) [14], although R/S has limitations with non-stationary time series. To overcome these limitations, detrended fluctuation analysis (DFA) [15] and multifractal detrended fluctuation analysis (MFDFA) [16] were developed. These methodologies have been applied to a variety of financial time series, including the stock market [17,18,19,20,21], the cryptocurrency market [22,23], and the commodity market [24,25,26,27]. The numerous studies, which assess market efficiency, are based on MFDFA. For example, Lee et al. [28] utilized the degree of market inefficiency to examine the efficiency of global stock indices. In [29], a market deficiency measure (MDM) was used to evaluate the efficiency of Dow Jones sector ETFs, while [30] applied the same approach to examine the efficiency of the Islamic stock market.
In the 21st century, the increased focus on sustainable development and climate change has catalyzed a paradigm shift in the energy sector. This transformation has exerted both direct and indirect influence on the electricity market. For example, the implementation of policies such as carbon credits, which impose opportunity costs on the utilization of carbon-based fuels, alongside an increase in the production ratio of renewable energy sources, underscores some of the significant changes underway. Numerous nations, including the United States, Germany, France, and the United Kingdom, are increasing their investments in renewable energy, with Spain being notable for achieving a renewable energy production ratio exceeding 50% by 2013. Generation of electricity through renewable sources, including hydrogen fuel cells, has been empirically shown to exert downward pressure on electricity prices [4,31,32]. Hydrogen fuel cells, in particular, exhibit resilience against natural environmental fluctuations, compared to traditional renewable sources such as solar and wind energy, and they do not encounter storage constraints. Consequently, they are emerging as a next-generation green energy solution. Fuel cells facilitate distributed electric power generation and can function as autonomous power systems, extending their utility to various sectors. The market penetration of electric vehicles powered by fuel cells is expanding rapidly on a global scale, which accounts for approximately 4.2% in 2020, rising to over 10% within two years and exceeding 14% by 2023. In South Korea, the market share for such vehicles increased from approximately 2.5% in 2020 to more than 8% in 2023, driven by technological advances and improvements in infrastructure.
The operational reliability of electric power networks has been improved by the deployment of independent fuel cell-based power systems, which is critical to maintaining uninterrupted services in essential domains. Ensuring a reliable electric power supply is paramount in settings such as data centers where even brief power outages can inflict substantial losses, thus necessitating dedicated backup power systems. In 2019, Microsoft (Redmond, WA, USA) began the deployment of fuel cell-based backup power systems for data centers, successfully demonstrating continuous 48-h operation in 2020. The evolution and integration of fuel cell technology are exerting a pervasive influence across various fields, attracting substantial investments aimed at advancing the technology’s practical applications. Similarly, in South Korea, fuel cells were introduced into electricity generation in 2008 and have gradually increased their share in power generation, with applications in a variety of fields. Recently, the volume of renewable energy transactions has exceeded 5%, which represents a significant change in the share of the electricity market. This change in the market structure is likely to affect the behavior of market prices.
In this study, we investigate the multifractal scaling behavior of the Korean electricity market, with an emphasis on the ramifications of integrating fuel cells on market stability and efficiency. Our analysis considers the seasonal daily dynamics of the electricity market, which is shaped by fluctuations in business demand, and delineates the variances in multifractal properties between peak and off-peak hours. Through the application of statistical methods-based crossover point detection, we elucidate the distinctions in multifractal scaling behavior between these temporal intervals. It is noteworthy that the multifractality in the off-peak hours is relatively high, and the crossover point is also only present in the off-peak hours. The crossover point, which is 52.4 weeks on average, aligns with the findings of other studies, which distinguish between short- and long-term electricity markets based on a one-year horizon. Furthermore, we evaluated the transformation within the electricity market induced by the introduction of fuel cells from a fractal viewpoint and probed the efficiency of the market to explain the implications of fuel cell integration. The findings suggest that the introduction of fuel cells results in a more efficient market, which may be attributed to a reduction in volatility on both the supply and demand sides.
This paper is organized as follows. Section 2 provides a historical overview of the Korean electricity market, with a particular focus on the changes that have occurred since the introduction of fuel cells; Section 3 offers a detailed description of the MF-DFA and subsequent methods; Section 4 presents a comprehensive summary of the experimental results; and Section 5 concludes.
2. Evolution of the Korean Electricity Market and the Impact of Fuel Cell
Historically, South Korea’s electricity market, administered through the Korea Electric Power Corporation (KEPCO), operated as a government monopoly. Following the 1997 economic crisis, a privatization plan was enacted, leading to the participation of six independent electric power generation companies by 2001. Although there were intentions to extend this privatization to the transmission and distribution stages, the plan was ultimately abandoned due to contemporaneous political issues, infrastructure deficiencies, and storage costs [33]. Consequently, the Korean electricity market continues to exhibit a coexistence of market mechanisms and regulatory controls. This hybrid market structure induces price distortions between production costs and retail rates, resulting in unnecessary economic losses and diminished market flexibility during peak times of demand and supply [34]. Similarly to the European Energy Exchange (EEX), KEPCO administers a day-ahead market in which hourly electricity consumption is predicted a day in advance; then hourly contracts are established. In this day-ahead market, the feasibility and bids of the market participants (power plants) are disclosed, allowing the operator to pre-contract electricity based on data from 24 h in advance. Accurate prediction of electricity consumption and production is of paramount importance, prompting extensive research in this area [35,36,37].
Concurrently, as the 21st century progresses and technology advances, there has been considerable development of renewable energy sources, which are more environmentally friendly than traditional fossil fuels. In light of the agreement on Sustainable Development (SD), numerous countries have been engaged in research and investment in renewable energy technologies. Likewise, South Korea has been rapidly expanding efforts in this field, with the dual objective of cost savings and sustainability. Consequently, a variety of renewable energy sources have been developed and implemented, with fuel cells representing a notable advancement. Since their inception in electricity generation in 2008, fuel cells have progressively amplified their contribution to electricity generation in South Korea. Table 1 summarizes the proportions of each fuel source in the average monthly volumes of electrical power transactions, showing that the proportion of renewables had increased from 0.88% in 2002–2006 to 5.12% in the period 2018–2023. Specifically, the ratios within renewable energy sources are summarized in Table 2. The volume of electricity transactions generated by fuel cells has increased consistently, currently comprising 14.26% of renewable energy transactions. The advent and expansion of renewable energy sources and fuel cells are reshaping the electricity market in multifaceted ways [5,38], culminating in a transformed landscape of market price behavior.

Table 1.
Proportions of fuels in the average monthly volumes of electrical power transactions in Korean electricity market. Fuels comprise nuclear (NUC), bituminous coal (BC), liquefied natural gas (LNG), anthracite coal (AC), oil, pumped storage (PSH), and renewable.

Table 2.
Proportions of each source in the average monthly volumes of electrical power transactions in renewable energy. The sources of renewable energy comprise integrated gasification combined cycle (IGCC), solar, wind, hydro, marine, biomass, waste, and fuel cell (FC).
3. Methods
Figure 1 presents a block diagram of the entire research procedure. First, this study aims to conduct a multifractal analysis of the Korean electricity market, for which relevant price series data were obtained from open source. By applying the MF-DFA to the data, we investigate the fluctuation function and dynamics of the electricity market, identifying differences between peak and off-peak hours. To achieve this, the generalized Hurst exponent and crossover point detection are utilized. Additionally, an analysis of the impact of fuel cell introduction into the Korean electricity market is performed using the Rényi exponent, Hölder spectrum, and market deficiency measure.
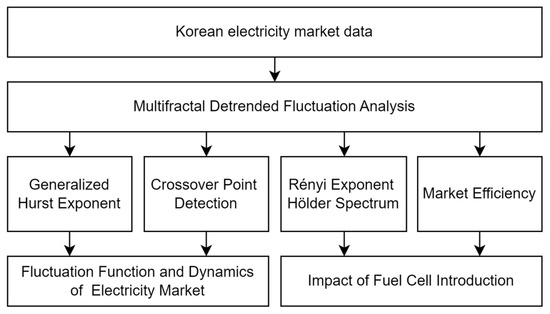
Figure 1.
A block diagram of the entire research procedure.
3.1. Multifractal Detrended Fluctuation Analysis
The multifractality and market efficiency of a time series can be investigated through MF-DFA [16]. Let be a logarithmic return of a price at time t as follows:
Then, MF-DFA for of length N can be defined in the following five steps.
- Step 1: Decide on the profile, .where is the average of the entire time series.
- Step 2: Divide the profile into non-overlapping segments.Divide the profile into segments of equal length k. If the profile does not exactly divide by k, repeat the process from the back to create a total of segments. This study uses as suggested in [15].
- Step 3: Calculate the local trend of each segment using the OLS method.Calculate the local trend of each segment using linear regression with the least squares method and compute the detrended variance. Let be the fitting first order polynomials in segment w, then represents the average of the square sum of the residuals associated with each segment for each segment such that,and for each segment ,
- Step 4: Calculate the qth order fluctuation function, , by averaging all detrended segments.
- Step 5: Determine the scaling behavior of fluctuations and derive the generalized Hurst exponent (GHE).If exhibits long-range dependence, then increases with s due to the scaling behavior of the power law. The GHE, , can be expressed as follows:Equation (6) is equivalent to where C is an arbitrary constant. By taking the logarithm of both sides, the GHE can be re-defined as follows:
is related to the autocorrelation of the time series. If is constant regardless of q, the time series is considered monofractal, and if not, it is considered multifractal. If the Hurst exponent H is in the range , the time series is persistent, indicating a high likelihood that positive rates of change will continue to be positive, while negative rates will continue to be negative. Conversely, if , the time series is anti-persistent, suggesting a high likelihood that positive rates of change will turn negative, and vice versa. Furthermore, if , the time series follows a random walk.
3.2. Crossover Point Detection
In the context of multifractal analysis, the heterogeneity of the scaling exponents underscores the complexity inherent in time series data, manifested as variations at discrete points along the temporal axis. A crossover point denotes a change in the fractal scaling behavior of the time series, frequently associated with a structural change in the Hurst exponent [39,40]. The Hurst exponent, which quantifies the long-range dependence of a time series, can be determined by the slope on a log–log plot. Consequently, a structural change in the Hurst exponent signifies a change in the log–log plot’s slope, reflecting a shift in the scaling dynamics of the time series. Despite this, the identification of crossover points often relies on subjective techniques, such as visual assessment of the log–log plot for slope change [41]. These approaches lack methodological rigor and reproducibility, indicating the need for a statistical validation procedure. To address this, we advocate for a crossover point test based on the Chow test [42].
The Chow test constitutes a rigorous statistical procedure for detecting structural changes between two distinct linear regression models. It involves two separate regressions on bifurcated segments of the dataset and evaluating the homogeneity of the resultant regression equations. The principal objective of this method is to test the null hypothesis, which implies that there is no difference in the regression coefficients between the segmented models. The rejection of this hypothesis signals the presence of structural change within the temporal series under examination. The procedural steps for conducting the Chow test can be defined below:
- Step 1: Establish a linear regression equation for all data.where , , and are the intercept, slope, and error term, respectively.
- Step 2: Divide the total data at a specific point and establish a linear regression equation for each segment.
- Step 3: Under the assumption that is a Gaussian noise, the null hypothesis of the Chow test is and . The test statistic of the Chow test follows an F-distribution under the null hypothesis such that,where , and represent the sum of squared residuals of Equations (8)–(10), respectively. and are the number of data points in each segment. k is the total number of parameters. A significance in F statistics in the Chow test indicates a structural change in point .
Based on the Chow test, the crossover point test can be defined as follows:
- Step 1: Divide the log–log plot into the left and right segments.If and are the lengths of the left and right segments, and and are the maximum and minimum values of s used in MFDFA, then always holds.
- Step 2: Set the minimum length (T) of a segment.In this experiment, to ensure the robustness of the trend, the minimum length was chosen as 5% of the log–log plot: .
- Step 3: Initially, set the length of the left segment to T.To find the point for each segment, designate the corresponding s as and calculate it as follows:
- Step 4: Conduct a Chow test to calculate the test statistic and p-value.If the p-value is smaller than the significance level, include the corresponding in the crossover set.
- Step 5: Increment by 1 and adjust the lengths of the left and right segments.
- Step 6: Conduct the Chow test for each .Based on the Chow test, the significance level and the p-value are compared to define the crossover set. The process continues until to verify the final crossover set.
- Step 7: If a crossover set exists, select the with the lowest p-value as the crossover point ().
3.3. Rényi Exponent and Hölder Spectrum
The multifractality of a time series can also be investigated through the Rényi exponent and the Hölder spectrum. Using the GHE, the Rényi exponent, , ref. [43] can be defined as follows:
where . If is not linear with respect to q, then the time series is considered multifractal.
From Equation (12), the Hölder exponent, , can be defined through the Legendre transform such that,
Then, the Hölder spectrum, , can be defined as follows:
The of a multifractal time series typically shows a single bell-shaped peak. Moreover, the width of the multifractal spectrum is used as a measure of the degree of multifractality, with a wider width indicating stronger multifractality.
3.4. Source of Multifractality and Market Efficiency
To investigate the source of multifractality within the electricity market, we analyze the degree of multifractality. It is well established that the multifractality of a time series typically arises from long-range correlations or fat-tailed distributions [44]. Long-range correlations can be probed by comparing the original time series with a randomly shuffled series, whereas fat-tailed distributions can be examined by comparing the original time series with a surrogate series. Randomly shuffled and surrogate series can be generated as follows:
- Randomly shuffled series
- When the length of the original series is N, randomly generate pairs where .
- Swap the values at the and positions in the original series.
- Repeat the above process times.
- Surrogate series
- Generate from a Gaussian distribution using the mean and variance of the original series.
- Rearrange to match the same rank pattern as .
Then, the degree of multifractality, , can be defined as follows [45,46]:
Let be the for the original, shuffled, and surrogate series, respectively, then if , the main source of multifractality is the fat-tailed distribution. If , the main source is the long-range correlation. If is 0, the time series is monofractal, and a larger indicates a stronger degree of multifractality.
Market efficiency can be evaluated under the postulate of the efficient market hypothesis (EMH), which asserts that all extant information is fully incorporated into asset prices, rendering them inherently unpredictable and subject to stochastic fluctuations. In scenarios where prices adhere to a random walk process, the metric would not exhibit a dependence on different q, consistently producing a value of 0.5. Evaluation of market efficiency can be performed using the MDM such that
If both large and small fluctuations follow a random walk, the market is efficient and MDM will be close to 0. Conversely, a high MDM indicates an inefficient market.
4. Results & Discussion
4.1. Data and Experimental Set-Up
The electricity price data used in this study are the marginal prices of the hourly system in the Korean electricity market obtained from the Electric Power Statistics Information System (EPSIS) [47]. The daily data for each hour are converted into weekly average prices, and the data period covers from 1 May 2001 to 31 December 2023, totaling 1183 weeks.
Figure 2 displays the heatmap of the correlation matrix for each hour. Note that h represents the hour, indicating each hour of the day. Through the correlation matrix, we can see that the hours of the day are divided into two groups, which allows us to define peak hours and off-peak hours as follows: peak hours (9 am to midnight), off-peak hours (1 am to 8 am). Meanwhile, fuel cells were introduced to the Korean electricity market in September 2008. The period before the introduction is referred to as the Pre-intro period, spanning from 1 May 2001 to 31 August 2008, totaling 383 weeks, and the period after the introduction is referred to as the Post-intro period, from 1 September 2008 to 31 December 2023, totaling 800 weeks. Figure 3 presents the log return series for the entire period, illustrating a notable change in the shape of the series between the Pre-intro and Post-intro periods.
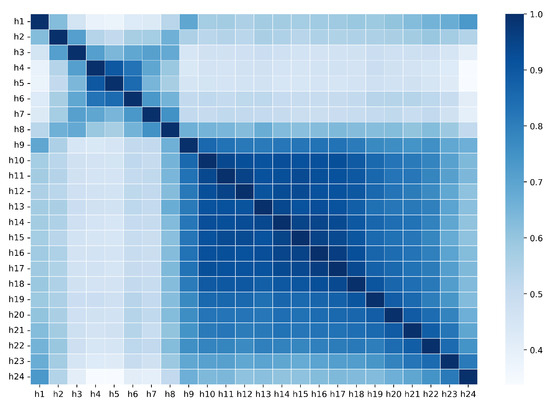
Figure 2.
Heatmap of each hour’s weekly log return correlation matrix.
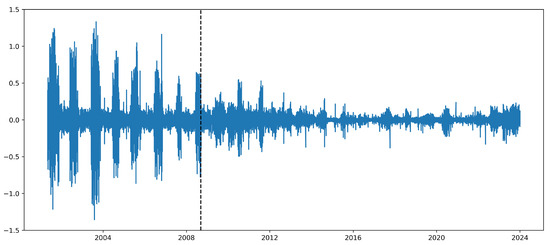
Figure 3.
Weekly log return series of electricity price.
In this study, we first examine the multifractality within each group of hours and investigate the daily seasonal characteristics of the electricity market. Furthermore, we examine the impact of the introduction of fuel cells on the electricity market from a fractal perspective through multifractality and market efficiency.
4.2. Fluctuation Function and Dynamics of Electricity Market
Figure 4 shows the GHE for each hour for the specified period as a function of the parameter q. In a monofractal time series, the function would remain invariant with respect to changes in q. In contrast, the observed decrement in GHE with increasing q across all hours demonstrates the multifractal nature of the electricity market. Furthermore, the GHE exhibits a more pronounced decline during off-peak hours compared to peak hours as q increases. In fact, the average degree of multifractality during off-peak hours is 0.6811, whereas during peak hours, it is 0.4737. A marked decrease in is indicative of significant multifractality in the time series, reflecting heterogeneity in the scaling exponents. This is corroborated by the average kurtosis values, which are 16.37 for off-peak hours and 14.25 for peak hours, with a higher kurtosis observed during off-peak hours. The relatively stronger multifractality during off-peak hours can be attributed to the uncertainty of demand [48]. In these periods of low consumption, even minor variations can substantially influence prices, complicating demand forecasting and amplifying price volatility. In addition, instability in renewable energy supply, such as wind and solar, can further exacerbate price heterogeneity. Thus, off-peak hours exhibit greater heterogeneity compared to peak hours.
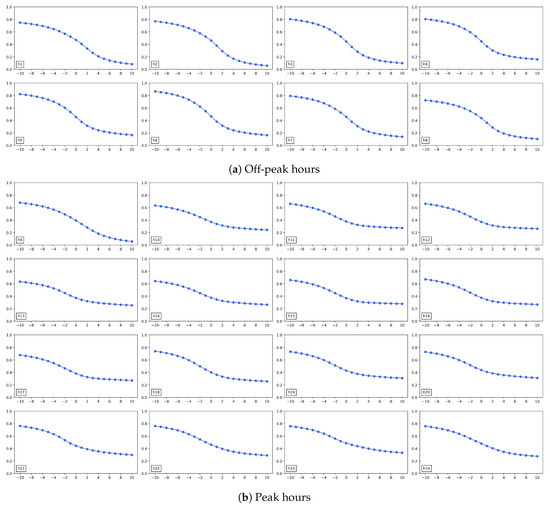
Figure 4.
Generalized Hurst exponent of entire period at each hour.
Then, we conducted the crossover point test at various significance levels, with the findings encapsulated in Table 3. This method facilitates the determination of the most appropriate significance level for the dataset. At the 0.01 significance level, no crossover points (CPs) were observed throughout all hours, while at the 0.1 level, CPs were manifested even at unrelated points. Significance levels of 0.025 and 0.05 yielded a suitable number of CPs, aligning with the results illustrated in Figure 4, which captures the heterogeneity of the scaling exponent during the off-peak hours. Significantly, at a significance level of 0.025, CPs were identified during all off-peak hours except 1 AM, leading this study to select 0.025 as the optimal significance level. Figure 5 presents these results on a log–log plot. The crossover point evaluation, employing the Chow test at a significance level of 0.025, accurately pinpointed the pertinent points, with the log–log plot further elucidating the scaling behavior disparities between off-peak and peak hours. Interestingly, CPs were located 52.4 weeks on average, approximately one year, indicating substantial moments of change in scaling behavior within the electricity market. The electricity market frequently displays annual cyclic patterns that include seasonal variations, yearly contracts, and analogous phenomena. Factors such as fluctuating power demand during winter and summer, policy changes, and price adjustments can precipitate this cyclicality. Hence, a one-year crossover point can be interpreted as reflecting the structural attributes of the electricity market, which fluctuates distinctly in short-term (less than one year) and long-term (more than one year) frameworks. These results are consistent with other studies [49,50,51], which have examined the electricity market over different short-term and long-term periods, frequently defining the long-term period as spanning one year.

Table 3.
Crossover point of each hour in different significance levels at .
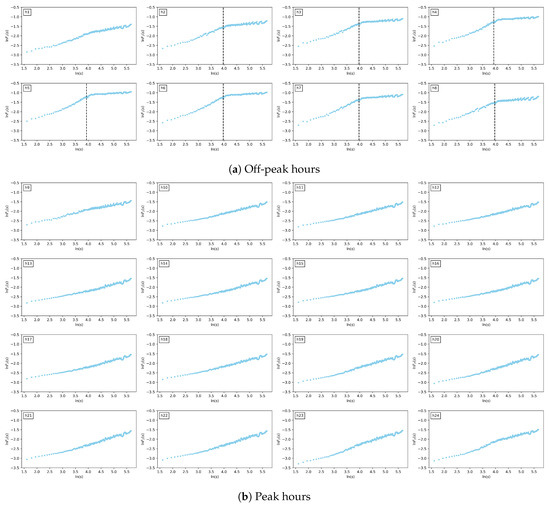
Figure 5.
Log–log plots of vs. with detected crossover point by MFDFA.
CPs identified during off-peak hours and their corresponding short-term and long-term Hurst exponents are summarized in Table 4. Initially, at 2 AM, the short-term Hurst exponent exhibits weak anti-persistence at a value of 0.4942, maintaining weak persistence under 0.6 at other times. In particular, the short-term Hurst exponent is approximately 0.5 during off-peak periods. In contrast, the long-term Hurst exponents exhibit strong anti-persistence across all hours, converging around 0.1. The proximity of the short-term Hurst exponent to 0.5 suggests that the electricity market adheres to a near-random walk, indicating market efficiency. This infers that price dynamics encapsulates various elements, such as supply-demand imbalances, short-term supply disruptions, and abrupt demand fluctuations. In contrast, the long-term Hurst exponent indicates a mean-reverting trend within the electricity market over extended periods, implying insubstantial price alterations over the long term and periodic adjustments in accordance with enduring trends. Such behavior may be driven by changes in policy and long-term imposed adjustments, suggesting gradual stabilization and equilibrium maintenance within the market through mean-reverting tendencies. Therefore, understanding and addressing long-term market trends is paramount, in contrast to short-term focus.

Table 4.
Hurst exponent behavior of off-peak hours.
4.3. Impact of Fuel Cell Introduction
To investigate the impact of the introduction of fuel cells in the electricity market, the analysis is segmented into intervals that precede and follow this technological adoption. The multifractality inherent in the time series is evaluated through the Hölder exponent and the Hölder spectrum. The Hölder exponent serves as a localized metric to assess the volatility and roughness of the time series; an elevated value signifies a decrease in volatility, while a reduced value correlates with increased volatility [52]. The Hölder spectrum delineates the distribution of Hölder exponents extracted from time series, exhibiting a peak at the most prevalent . A narrow peak suggests homogeneity in scaling behaviors, while a broad peak indicates various scaling behaviors [53]. Furthermore, an expansive spectrum denotes pronounced multifractality; a width of less than 0.05 categorizes the time series as monofractal [54]. The width of the multifractal spectra is computed as .
Figure 6 presents the multifractal spectra corresponding to Pre-intro and Post-intro periods, while Table 5 summarizes the hourly spectrum width. Initially, the width for all hours exceeds 0.05, signifying that the electricity market exhibits multifractality independent of the introduction of fuel cells. Note that the average spectrum width for off-peak hours in the Pre-intro period is 1.5696, compared to an average of 0.7467 for peak hours. Furthermore, the Post-intro period produced values of 1.1643 and 0.5518, respectively, which is in agreement with the results presented in Figure 4, which illustrate stronger multifractality in the off-peak hours. The spectrum width decreased after the introduction of fuel cells, from an average of 1.2994 to 0.6168, indicating a homogenization of the characteristics of the time series. This suggests that multifractality was more pronounced Pre-intro period, implying that the introduction of fuel cells attenuated the heterogeneity of scaling behavior, potentially improving the stability and reducing the volatility of the electricity market. This phenomenon may be attributed to the inherent advantages of fuel cells [55]. According to [56], power generation via fuel cells does not produce waste in addition to thermal energy, incurs lower generation costs, and is less susceptible to environmental conditions, thus facilitating consistent power production. In this regard, the implementation of fuel cells reinforces scalability and viability in the electricity market, attenuating supply-side volatility. Currently, as fuel cell technology advances, the deployment of electric vehicles is gaining momentum, leading to a burgeoning demand for electric vehicles. In 2022, electric vehicles accounted for nearly 10% of global automobile sales. In South Korea, where electric vehicles were initially introduced in 2013, their numbers surpassed 200,000 units in 2022, representing more than 2% of the total passenger car fleet. [57] employed the Gompertz model, factoring in the growth rate of the domestic electric vehicle market, to forecast a demand of approximately 1 million units by 2030. As the electric vehicle market expands precipitously, the proliferation of charging stations ensues, ultimately resulting in a sustained increase in electric demand. Therefore, the progression and adoption of fuel cell technology in the electricity market mitigates volatility from both the supply and demand perspectives.
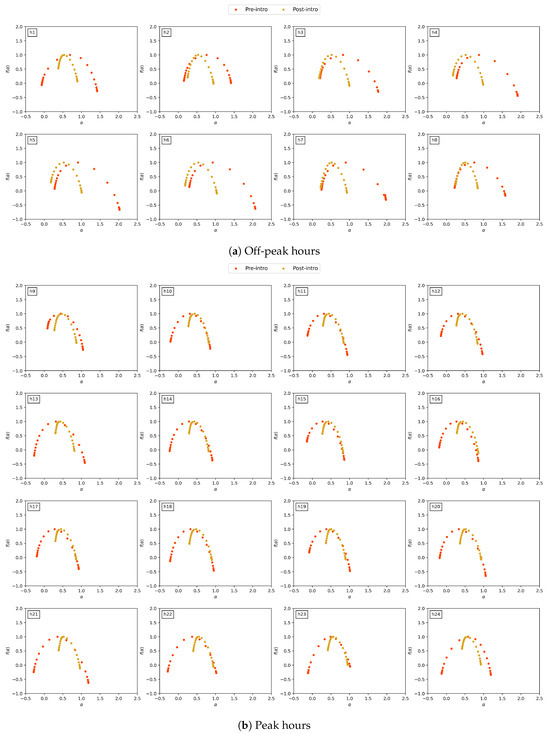
Figure 6.
Plots of vs for each period using MFDFA.

Table 5.
Multifractal spectrum width of each hour by period.
Table 6a,b show the degree of multifractality for all hours, during off-peak and peak hours, respectively. For robustness in the experiment, average values from 30 repetitions are used, and the values in parentheses represent the rate of change in , calculated as and . The values in bold indicate the main source of multifractality. For all hours, a fat-tailed distribution is identified as the main source of multifractality in the Korean electricity market. Moreover, of the original series exhibits stronger multifractality in the Pre-intro period compared to the Post-intro period, as shown in Figure 4. These results align with the log-return dynamics illustrated in Figure 3. It is evident that the Korean electricity market frequently experiences substantial price fluctuations associated with extreme events. This observation supports the plausible conclusion that the main source of multifractality derives from fat-tailed distributions. Furthermore, after the introduction of fuel cells, there is a noticeable reduction in price fluctuations associated with extreme events, suggesting that electricity prices have become relatively more stable. Furthermore, as shown in Figure 6, the degree of multifractality during off-peak hours in the original series is significantly higher compared to peak hours in the Pre-intro period. However, the difference in degrees of multifractality between off-peak and peak hours significantly decreases in the Post-intro period, indicating the stabilizing effect of fuel cells on the volatility of the Korean electricity market.

Table 6.
of the original, shuffled, and surrogate series in each hour for different periods.
4.4. Market Efficiency
The findings of the MDM analysis are presented in Table 7. In particular, at all hours, the MDM values were lower during the Post-intro period, indicating a reduction in the influence of long-range correlations and thereby enhanced market efficiency, corroborated by the results of the degree of multifractality. Furthermore, the MDM values were analyzed during off-peak and peak hours, revealing a notable decline in the average MDM value from 0.5364 during off-peak hours to 0.2673 during peak hours, implying increased market efficiency and reduced volatility during peak hours. In contrast, off-peak hours exhibit a relatively lower level of market efficiency and higher volatility [48]. During peak hours, due to the elevated level of electricity demand, there tends to be a notable prevalence of transactions and a discernible pattern of activity. In contrast, during off-peak hours, the volatility in supply and demand increases, leading to a reduction in market liquidity. Substantial fluctuations also imply that policy changes can be relatively more pronounced. These political changes and supply instability can further decrease market liquidity and precipitate pronounced price fluctuations. This market is more susceptible to external shocks, and consistent patterns can dissipate, leading to greater heterogeneity and, ultimately, to a less efficient market. This is also associated with the fact that the crossover point manifests itself only during off-peak hours, as illustrated in Figure 5. The deployment of fuel cells has influenced both the supply and demand dynamics. Enhanced supply stability, due to scalability and continuous applicability, coupled with stabilized demand from consistent usage, has collectively mitigated market volatility, thus improving market efficiency. This phenomenon parallels the observations made by [4], who assessed the impact of renewable energy integration on electricity prices. Ref. [4] posited that a stable and increasing share of renewable energy generation decreases the probability of price jumps, which consequently reduces market volatility and the disparity in expected prices among market participants. Similarly, the introduction of fuel cells reduces volatility on both the supply and demand sides, leading to a comparable reduction in the likelihood of price jumps. As market participants’ perspectives converge, they are incentivized to incorporate all available information, resulting in an efficient market where prices fully reflect all pertinent information.

Table 7.
Market deficiency measure of each hour by period.
4.5. Discussions
This research examines the evolution of the Korean electricity market over two distinct periods, each marked by the advent of a transformative technology, namely the introduction of fuel cells. This approach is consistent with existing studies that analyze and compare market characteristics based on specific technological turning points or policy changes. Ref. [5] investigates the influence of renewable energy expansion on market volatility and prices in the Danish and German electricity markets. The impact of the Renminbi exchange reform on exchange rates in China and Hong Kong is analyzed in [40], while [58] examines the impact of the global financial crisis on BRICS and developed stock markets. Similarly, analyzing market changes by setting a clear turning point, such as the introduction of fuel cells, has proven to be an effective method for measuring the impact of a specific event on market dynamics. The findings indicate that the market has become less volatile and more efficient following the introduction of fuel cells. In contrast to conventional renewable energy sources such as solar and wind, fuel cells are not significantly influenced by climatic and weather conditions, thereby facilitating a more stable power supply. This attribute positively impacts the reduction of volatility on the supply side of the market, enabling more reliable demand forecasts and contributing to a more efficient market.
Furthermore, multifractal analysis has been extensively employed to examine the intricate dynamics of electricity and other energy markets. For instance, ref. [27] employed MF-DFA in their analysis of the Spanish electricity market. Their findings highlighted the pronounced volatility and nonlinear characteristics inherent to the electricity market. In addition, multifractal analysis has been used to investigate the complex dynamics generated by various sources, including carbon, solar, and natural gas [59,60,61,62,63]. In light of the aforementioned studies, this research aims to examine the impact of the introduction of fuel cells in the Korean electricity market on the multifractal structure of the market. In particular, high multifractality was identified in off-peak hours, and the difference in dynamics before and after the crossover point was examined based on statistical methods. Furthermore, it was found that multifractality decreased after the introduction of fuel cells, suggesting that the introduction of fuel cells reduces market heterogeneity and improves the stability of the power supply, thereby making the market more efficient.
5. Conclusions
In this study, we investigated the multifractality and market efficiency of the Korean electricity market, based on MFDFA. Given the inherent characteristics of the electricity market, which are manifested through price spikes, increased volatility, and seasonality at weekly and daily levels driven by demand fluctuations, we initially evaluated the disparities in scaling behavior between peak and off-peak hours. Moreover, with the advent and increasing integration of fuel cells as a type of renewable energy that influences both electricity demand and supply, we conducted an analysis of the market impacts resulting from the introduction of fuel cells, particularly from a multifractal perspective.
At first, we examined seasonality at the daily level instigated by demand dynamics. A pronounced decline in GHE during off-peak periods relative to peak periods indicates a high degree of multifractality, suggesting the presence of heterogeneity in the scaling exponents. To statistically validate this observation, we applied the Chow test to perform a crossover point test on the log–log plot and determined that a significance level of 0.025 was the most appropriate for this study. In particular, the crossover point predominantly emerged around a 52-week cycle, with scaling behavior during off-peak periods displaying distinct patterns that aligned with an approximate annual cycle. The electricity market revealed markedly different behavior of the Hurst exponent in the short term versus the long term, signifying that diverse factors affect the market in these temporal frameworks. In the short term, the market exhibits characteristics similar to a random walk, reflecting price repercussions of short-term supply imbalances, supply disruptions, and sudden demand shifts. Conversely, in the long term, prices undergo periodic adjustments, which gravitate toward a stabilized state influenced by governmental policy alterations. Consequently, it is prudent to adopt divergent strategies for market engagement on short- and long-term horizons.
Secondly, we investigated the impact of the introduction of fuel cells on the electricity market. Multifractal spectral analysis illuminated a diminution in the heterogeneity of the scaling behavior after the introduction of the fuel cell compared to that in the preceding period. This phenomenon can be attributed to the intrinsic advantages of fuel cells, which lower production costs and exhibit reduced susceptibility to environmental variables, thus facilitating consistent energy output. These factors inherently support scalability. Moreover, the burgeoning demand for electric vehicles, propelled by advancements in fuel cell technology, has engendered a stable demand in comparison to previous levels. In summary, the development and deployment of fuel cell technology have demonstrably attenuated volatility on both the supply and demand sides.
Lastly, an inquiry into the origins of multifractality revealed that the primary contributor within the electricity market is the fat-tailed distribution. Notably, while long-range correlation was previously a significant factor, its influence has markedly waned, following the introduction of fuel cells. This attenuation suggests that fuel cells have mitigated this effect, leading to a time series with a diminished long-term memory that more closely approximates a random walk, thereby enhancing market efficiency. This is corroborated by an analysis of market efficiency from a multifractal perspective. Examining the values of before and after the introduction of fuel cells, during the Pre-intro and Post-intro periods, reveals a clear improvement in market efficiency. The advent of fuel cells has increased the stability of the supply side and catalyzed a steady escalation in demand, thereby reducing market volatility. The expanding market share of fuel cells reduces market volatility and converges expected prices among market participants, effectively minimizing the likelihood of abrupt price fluctuations. As the disparity in perspectives among market participants contracts, all available information is assimilated, culminating in a more efficient market where prices accurately reflect information.
Despite the novelty in this paper, there exist limitations that need to be addressed in future work. The initial analysis was mainly confined to the temporal dimension. An integration of spatial analyses, such as those focused on regional or country-specific electricity markets, could produce more comprehensive findings. Furthermore, additional research is needed on the prolonged impacts of fuel cells. Specifically, this study examined the market in the context of fuel cell introduction, but significant criteria such as technological advancements and fuel cell mechanisms warrant exploration. In addition, monitoring the long-term ramifications of market share expansion and evaluating its impact on market efficiency will be crucial areas for future research. Such multidimensional analyses can provide profound insight for market participants and foster the formulation of novel policy implications.
Author Contributions
Conceptualization, S.E.O., M.L., and J.W.S.; Methodology, M.L. and J.W.S.; Software, S.E.O.; Validation, M.L. and J.W.S.; Formal analysis, S.E.O.; Investigation, S.E.O. and J.W.S.; Data curation, S.E.O.; Writing—original draft preparation, S.E.O.; Writing—review and editing, M.L. and J.W.S.; Visualization, S.E.O.; Supervision, M.L. and J.W.S.; Project administration, M.L.; Funding acquisition, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2021R1I1A3049656).
Data Availability Statement
The data presented in this study are openly available in [Electric Power Statistics Information System] https://epsis.kpx.or.kr/epsisnew/selectEkccIntroEn.do?menuId=090101 (accessed on 23 August 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bierbrauer, M.; Menn, C.; Rachev, S.T.; Trück, S. Spot and derivative pricing in the EEX power market. J. Bank. Financ. 2007, 31, 3462–3485. [Google Scholar] [CrossRef]
- Bushnell, J.B.; Mansur, E.T.; Saravia, C. Vertical arrangements, market structure, and competition: An analysis of restructured US electricity markets. Am. Econ. Rev. 2008, 98, 237–266. [Google Scholar] [CrossRef]
- Matsumoto, T.; Yamada, Y. Simultaneous hedging strategy for price and volume risks in electricity businesses using energy and weather derivatives. Energy Econ. 2021, 95, 105101. [Google Scholar] [CrossRef]
- Ballester, C.; Furió, D. Effects of renewables on the stylized facts of electricity prices. Renew. Sustain. Energy Rev. 2015, 52, 1596–1609. [Google Scholar] [CrossRef]
- Rintamäki, T.; Siddiqui, A.S.; Salo, A. Does renewable energy generation decrease the volatility of electricity prices? An analysis of Denmark and Germany. Energy Econ. 2017, 62, 270–282. [Google Scholar] [CrossRef]
- Bâra, A.; Oprea, S.V. Predicting day-ahead electricity market prices through the integration of macroeconomic factors and machine learning techniques. Int. J. Comput. Intell. Syst. 2024, 17, 10. [Google Scholar] [CrossRef]
- Hwang, B.H.; Lee, H.S.; Park, K.H.; Shin, Y.S. A case study for determining system marginal price in Korea electricity market. In Proceedings of the KIEE Conference, Pyeongchang, Gangwon-do, Republic of Korea, 20–22 July 2011; The Korean Institute of Electrical Engineers: Seoul, Republic of Korea, 2011; pp. 634–635. [Google Scholar]
- Härdle, W.K.; Trück, S. The Dynamics of Hourly Electricity Prices. 2010. Available online: https://hdl.handle.net/10419/39311 (accessed on 23 August 2024).
- Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Ball, R. The global financial crisis and the efficient market hypothesis: What have we learned? J. Appl. Corp. Financ. 2009, 21, 8–16. [Google Scholar] [CrossRef]
- Aloui, C.; Mabrouk, S. Value-at-risk estimations of energy commodities via long-memory, asymmetry and fat-tailed GARCH models. Energy Policy 2010, 38, 2326–2339. [Google Scholar] [CrossRef]
- Lahmiri, S.; Uddin, G.S.; Bekiros, S. Nonlinear dynamics of equity, currency and commodity markets in the aftermath of the global financial crisis. Chaos Solitons Fractals 2017, 103, 342–346. [Google Scholar] [CrossRef]
- Peters, E.E. Fractal Market Analysis: Applying Chaos Theory to Investment and Economics; John Wiley & Sons: Hoboken, NJ, USA, 1994; Volume 24. [Google Scholar]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Ikeda, T. Multifractal structures for the Russian stock market. Phys. A Stat. Mech. Its Appl. 2018, 492, 2123–2128. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos Solitons Fractals 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Bai, M.Y.; Zhu, H.B. Power law and multiscaling properties of the Chinese stock market. Phys. A Stat. Mech. Its Appl. 2010, 389, 1883–1890. [Google Scholar] [CrossRef]
- Aslam, F.; Mohti, W.; Ferreira, P. Evidence of intraday multifractality in European stock markets during the recent coronavirus (COVID-19) outbreak. Int. J. Financ. Stud. 2020, 8, 31. [Google Scholar] [CrossRef]
- Lee, K.E.; Lee, J.W. Probability distribution function and multiscaling properties in the Korean stock market. Phys. A Stat. Mech. Its Appl. 2007, 383, 65–70. [Google Scholar] [CrossRef]
- da Silva Filho, A.C.; Maganini, N.D.; de Almeida, E.F. Multifractal analysis of Bitcoin market. Phys. A Stat. Mech. Its Appl. 2018, 512, 954–967. [Google Scholar] [CrossRef]
- Mnif, E.; Jarboui, A.; Mouakhar, K. How the cryptocurrency market has performed during COVID 19? A multifractal analysis. Financ. Res. Lett. 2020, 36, 101647. [Google Scholar] [CrossRef]
- Arshad, S. Analysing the relationship between oil prices and Islamic stock markets. Econ. Pap. A J. Appl. Econ. Policy 2017, 36, 429–443. [Google Scholar] [CrossRef]
- Pal, M.; Rao, P.M.; Manimaran, P. Multifractal detrended cross-correlation analysis on gold, crude oil and foreign exchange rate time series. Phys. A Stat. Mech. Its Appl. 2014, 416, 452–460. [Google Scholar] [CrossRef]
- Telli, Ş.; Chen, H. Multifractal behavior in return and volatility series of Bitcoin and gold in comparison. Chaos Solitons Fractals 2020, 139, 109994. [Google Scholar] [CrossRef]
- Norouzzadeh, P.; Dullaert, W.; Rahmani, B. Anti-correlation and multifractal features of Spain electricity spot market. Phys. A Stat. Mech. Its Appl. 2007, 380, 333–342. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Kim, S.; Chang, W. Asymmetric market efficiency using the index-based asymmetric-MFDFA. Phys. A Stat. Mech. Its Appl. 2018, 512, 1278–1294. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Albulescu, C.T.; Yoon, S.M. A multifractal detrended fluctuation analysis of financial market efficiency: Comparison using Dow Jones sector ETF indices. Phys. A Stat. Mech. Its Appl. 2017, 483, 182–192. [Google Scholar] [CrossRef]
- Bouoiyour, J.; Selmi, R.; Wohar, M.E. Are Islamic stock markets efficient? A multifractal detrended fluctuation analysis. Financ. Res. Lett. 2018, 26, 100–105. [Google Scholar] [CrossRef]
- Paraschiv, F.; Erni, D.; Pietsch, R. The impact of renewable energies on EEX day-ahead electricity prices. Energy Policy 2014, 73, 196–210. [Google Scholar] [CrossRef]
- Maciejowska, K. Assessing the impact of renewable energy sources on the electricity price level and variability–A quantile regression approach. Energy Econ. 2020, 85, 104532. [Google Scholar] [CrossRef]
- Lee, B.H.; Ahn, H.H. Electricity industry restructuring revisited: The case of Korea. Energy Policy 2006, 34, 1115–1126. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y.; Shin, J.S. The Korean electricity market: Stuck in transition. In Evolution of Global Electricity Markets; Elsevier: Amsterdam, The Netherlands, 2013; pp. 679–713. [Google Scholar]
- Li, G.; Liu, C.C.; Mattson, C.; Lawarrée, J. Day-ahead electricity price forecasting in a grid environment. IEEE Trans. Power Syst. 2007, 22, 266–274. [Google Scholar] [CrossRef]
- Yang, A.; Li, W.; Yang, X. Short-term electricity load forecasting based on feature selection and Least Squares Support Vector Machines. Knowl.-Based Syst. 2019, 163, 159–173. [Google Scholar] [CrossRef]
- Sideratos, G.; Ikonomopoulos, A.; Hatziargyriou, N.D. A novel fuzzy-based ensemble model for load forecasting using hybrid deep neural networks. Electr. Power Syst. Res. 2020, 178, 106025. [Google Scholar] [CrossRef]
- Mulder, M.; Scholtens, B. The impact of renewable energy on electricity prices in the Netherlands. Renew. Energy 2013, 57, 94–100. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Gu, R. Analysis of efficiency for Shenzhen stock market based on multifractal detrended fluctuation analysis. Int. Rev. Financ. Anal. 2009, 18, 271–276. [Google Scholar] [CrossRef]
- Qin, J.; Lu, X.; Zhou, Y.; Qu, L. The effectiveness of China’s RMB exchange rate reforms: An insight from multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2015, 421, 443–454. [Google Scholar] [CrossRef]
- Ge, E.; Leung, Y. Detection of crossover time scales in multifractal detrended fluctuation analysis. J. Geogr. Syst. 2013, 15, 115–147. [Google Scholar] [CrossRef]
- Chow, G.C. Tests of equality between sets of coefficients in two linear regressions. Econom. J. Econom. Soc. 1960, 28, 591–605. [Google Scholar] [CrossRef]
- Koscielny-Bunde, E.; Kantelhardt, J.W.; Braun, P.; Bunde, A.; Havlin, S. Long-term persistence and multifractality of river runoff records: Detrended fluctuation studies. J. Hydrol. 2006, 322, 120–137. [Google Scholar] [CrossRef]
- Norouzzadeh, P.; Rahmani, B. A multifractal detrended fluctuation description of Iranian rial–US dollar exchange rate. Phys. A Stat. Mech. Its Appl. 2006, 367, 328–336. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhuang, X.T.; Jin, X. Measuring multifractality of stock price fluctuation using multifractal detrended fluctuation analysis. Phys. A Stat. Mech. Its Appl. 2009, 388, 2189–2197. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.; Pan, Z. Multifractal detrending moving average analysis on the US Dollar exchange rates. Phys. A Stat. Mech. Its Appl. 2011, 390, 3512–3523. [Google Scholar] [CrossRef]
- Exchange, K.P. Electric Power Statistics System. 2020. Available online: https://epsis.kpx.or.kr (accessed on 23 August 2024).
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Bello, A.; Bunn, D.W.; Reneses, J.; Muñoz, A. Medium-term probabilistic forecasting of electricity prices: A hybrid approach. IEEE Trans. Power Syst. 2016, 32, 334–343. [Google Scholar] [CrossRef]
- Bello, A.; Bunn, D.; Reneses, J.; Muñoz, A. Parametric density recalibration of a fundamental market model to forecast electricity prices. Energies 2016, 9, 959. [Google Scholar] [CrossRef]
- Ziel, F.; Steinert, R. Probabilistic mid-and long-term electricity price forecasting. Renew. Sustain. Energy Rev. 2018, 94, 251–266. [Google Scholar] [CrossRef]
- Fu, X.L.; Gao, X.L.; Shan, Z.; Ma, Y.J.; Jiang, Z.Q.; Zhou, W.X. Multifractal characteristics and return predictability in the Chinese stock markets. Ann. Oper. Res. 2023, 1–26. [Google Scholar] [CrossRef]
- Zhou, W. A Guide to Econophysics; Shanghai University of Finance and Economics Press: Shanghai, China, 2007. [Google Scholar]
- Makowiec, D.; Fuliński, A. Multifractal detrended fluctuation analysis as the estimator of long-range dependence. Acta Phys. Pol. B 2010, 41, 1025. [Google Scholar]
- Stambouli, A.B. Fuel cells: The expectations for an environmental-friendly and sustainable source of energy. Renew. Sustain. Energy Rev. 2011, 15, 4507–4520. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Elsaid, K.; Wilberforce, T.; Kamil, M.; Sayed, E.T.; Olabi, A. Environmental aspects of fuel cells: A review. Sci. Total Environ. 2021, 752, 141803. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Lim, S.; Shin, J.; Lee, C.Y. How much hydrogen should be supplied in the transportation market? Focusing on hydrogen fuel cell vehicle demand in South Korea: Hydrogen demand and fuel cell vehicles in South Korea. Technol. Forecast. Soc. Chang. 2022, 181, 121750. [Google Scholar] [CrossRef]
- Ali, S.; Shahzad, S.J.H.; Raza, N.; Al-Yahyaee, K.H. Stock market efficiency: A comparative analysis of Islamic and conventional stock markets. Phys. A Stat. Mech. Its Appl. 2018, 503, 139–153. [Google Scholar] [CrossRef]
- Shahzad, S.J.H.; Bouri, E.; Kayani, G.M.; Nasir, R.M.; Kristoufek, L. Are clean energy stocks efficient? Asymmetric multifractal scaling behaviour. Phys. A Stat. Mech. Its Appl. 2020, 550, 124519. [Google Scholar] [CrossRef]
- Kristjanpoller, W.; Minutolo, M.C. Asymmetric multi-fractal cross-correlations of the price of electricity in the US with crude oil and the natural gas. Phys. A Stat. Mech. Its Appl. 2021, 572, 125830. [Google Scholar] [CrossRef]
- Cao, G.; Xu, W. Nonlinear structure analysis of carbon and energy markets with MFDCCA based on maximum overlap wavelet transform. Phys. A Stat. Mech. Its Appl. 2016, 444, 505–523. [Google Scholar] [CrossRef]
- Castro, A.L.; Marcato, A.L.M.; De Aguiar, E.P. Multifractal Analysis of the Brazilian Electricity Market. IEEE Access 2023, 11, 98939–98957. [Google Scholar] [CrossRef]
- Khurshid, A.; Khan, K.; Cifuentes-Faura, J.; Chen, Y. Asymmetric multifractality: Comparative efficiency analysis of global technological and renewable energy prices using MFDFA and A-MFDFA approaches. Energy 2024, 289, 130106. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).