Day of the Week Effect on the World Exchange Rates through Fractal Analysis
Abstract
1. Introduction
2. Materials and Methods
- •
- Step 1: Construct the profilewhere represents the series average of time series .
- •
- Step 2: Divide the profiles into non-overlapping windows of equal length s. Because the length of the series N is not necessarily a multiple of the time scale s, parts of the profile may remain at the end; thus, the same procedure is applied from the end of the series as well. The final result is segments.
- •
- Step 3: The trend for each of the segments is estimated using a linear regression as . This process precedes the determination of the detrended variance, calculated asfor each segment v, andfor each segment v, v = ,…, .
- •
- Step 4: By averaging all segments, the qth order fluctuation function can be obtained for the different behaviors of trends in the time series , as follows:when andfor . Here, and are the number of sub-time series with positive and negative trends. We assume that for all , such that .The traditional MF-DFA is implemented by computing the average fluctuation function for asand for as
- •
- Step 5: The scaling behavior of the fluctuations is analyzed by observing the log–log plots of versus s for each value of q. In the case where the two series are long-range cross-correlated, will increase for large values of s as a power law.
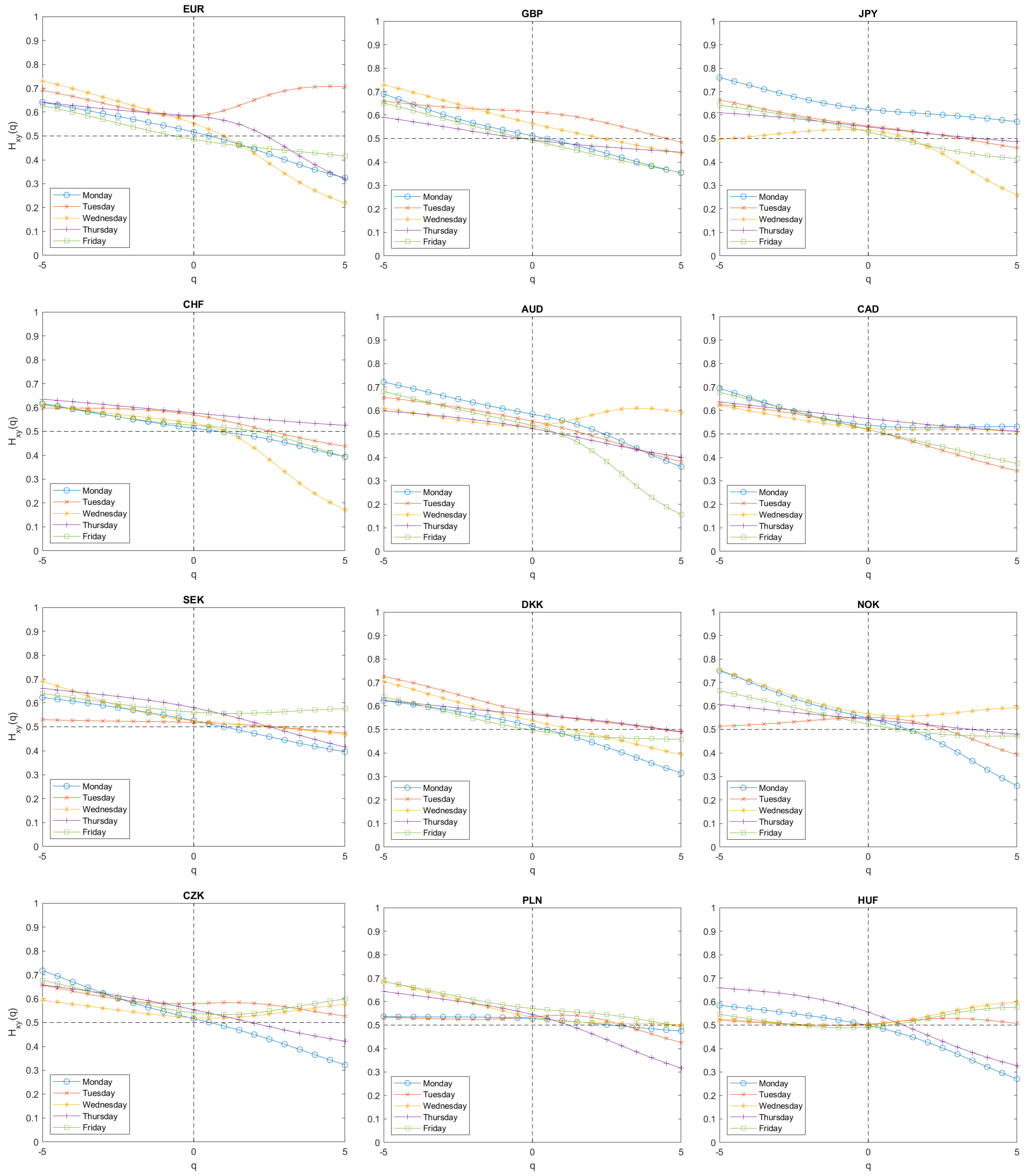
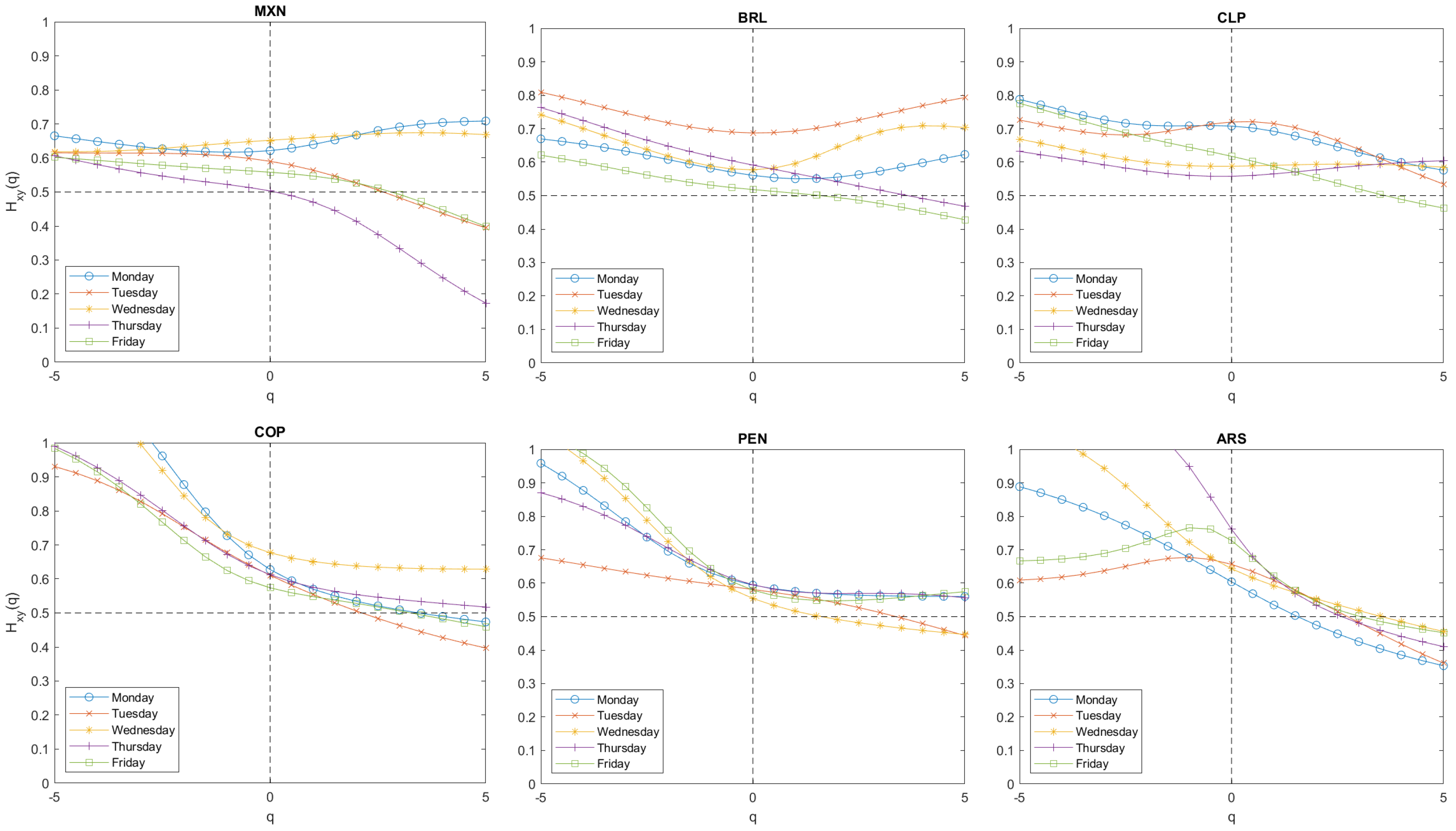
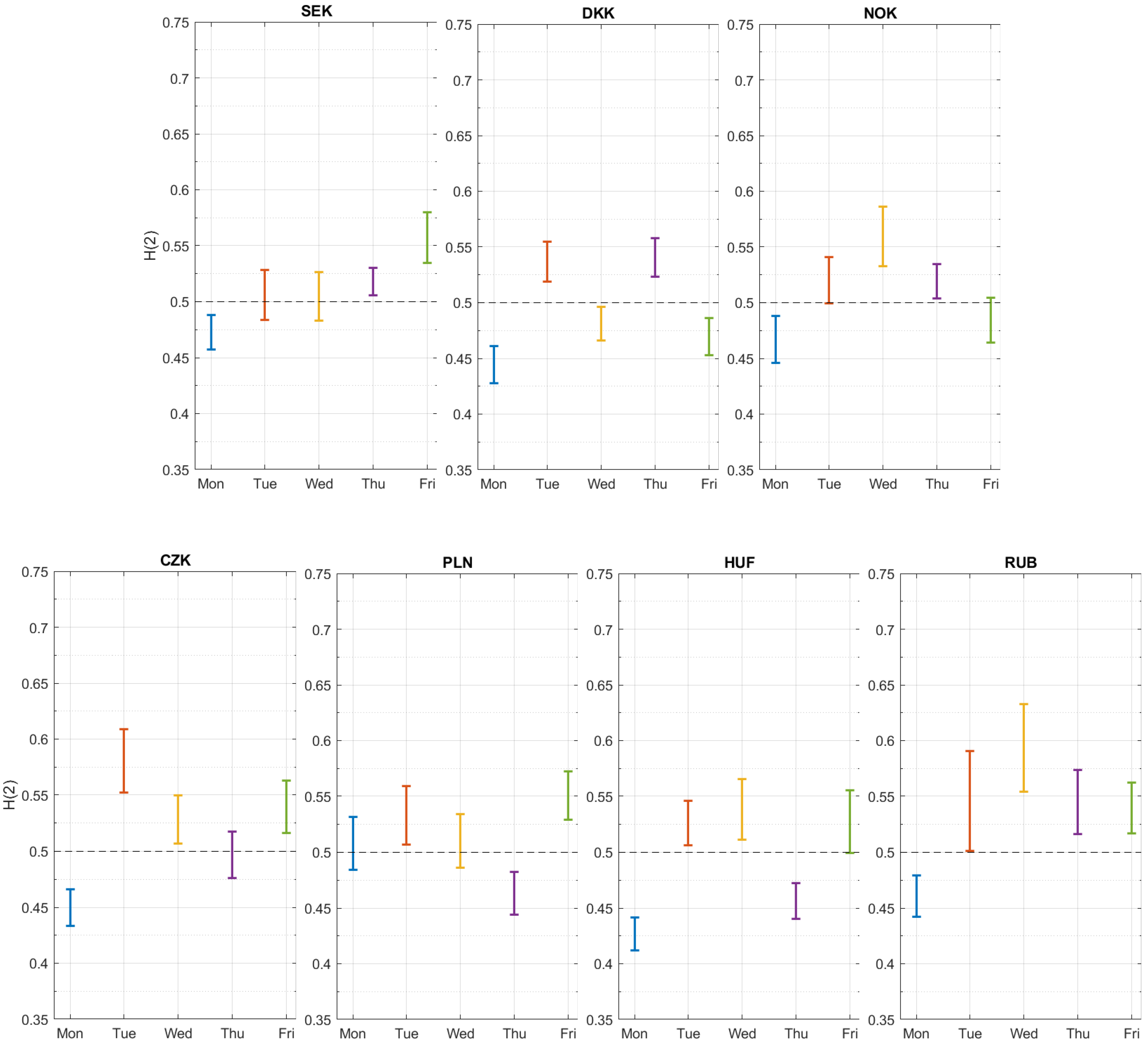
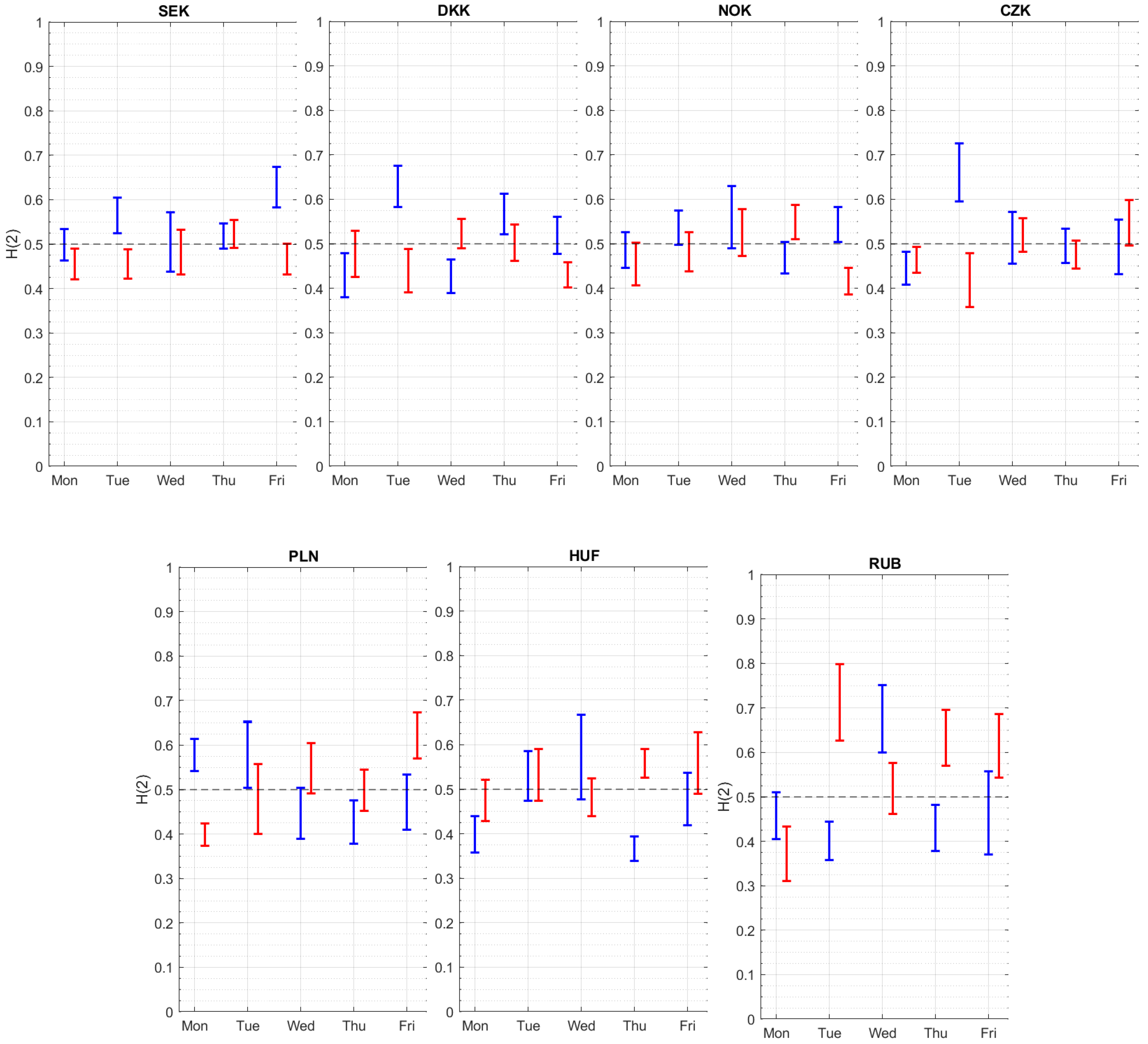
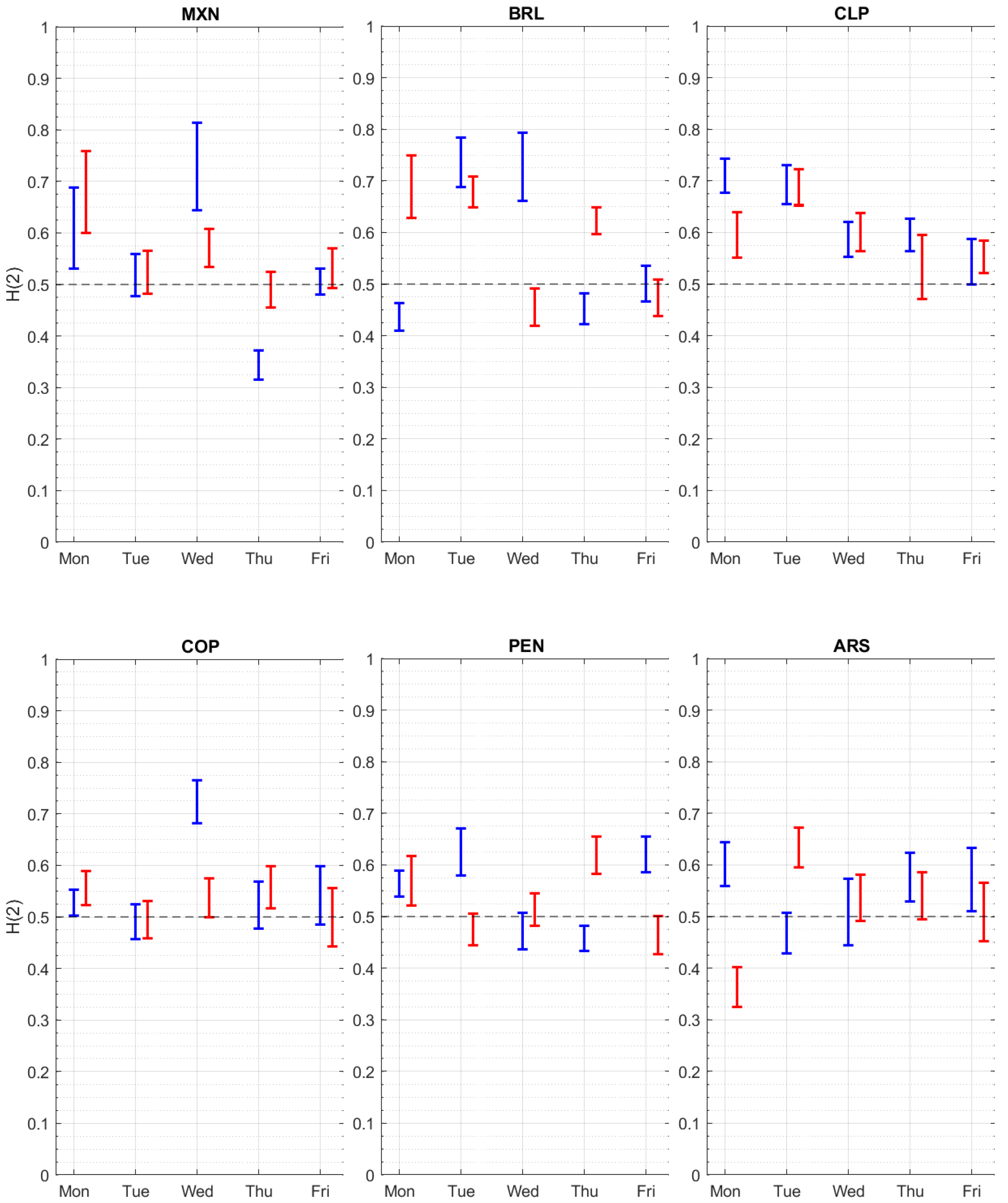
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
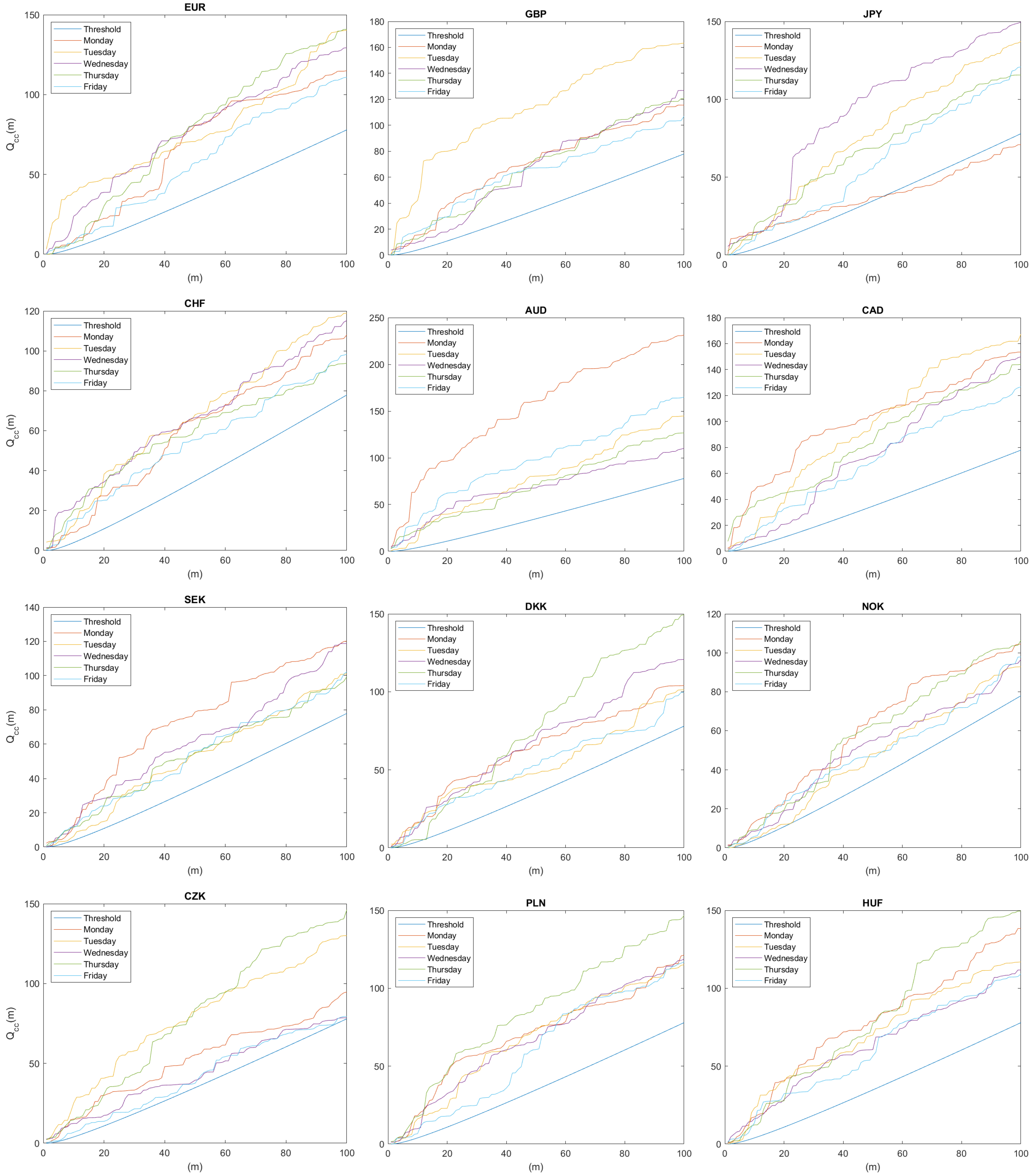


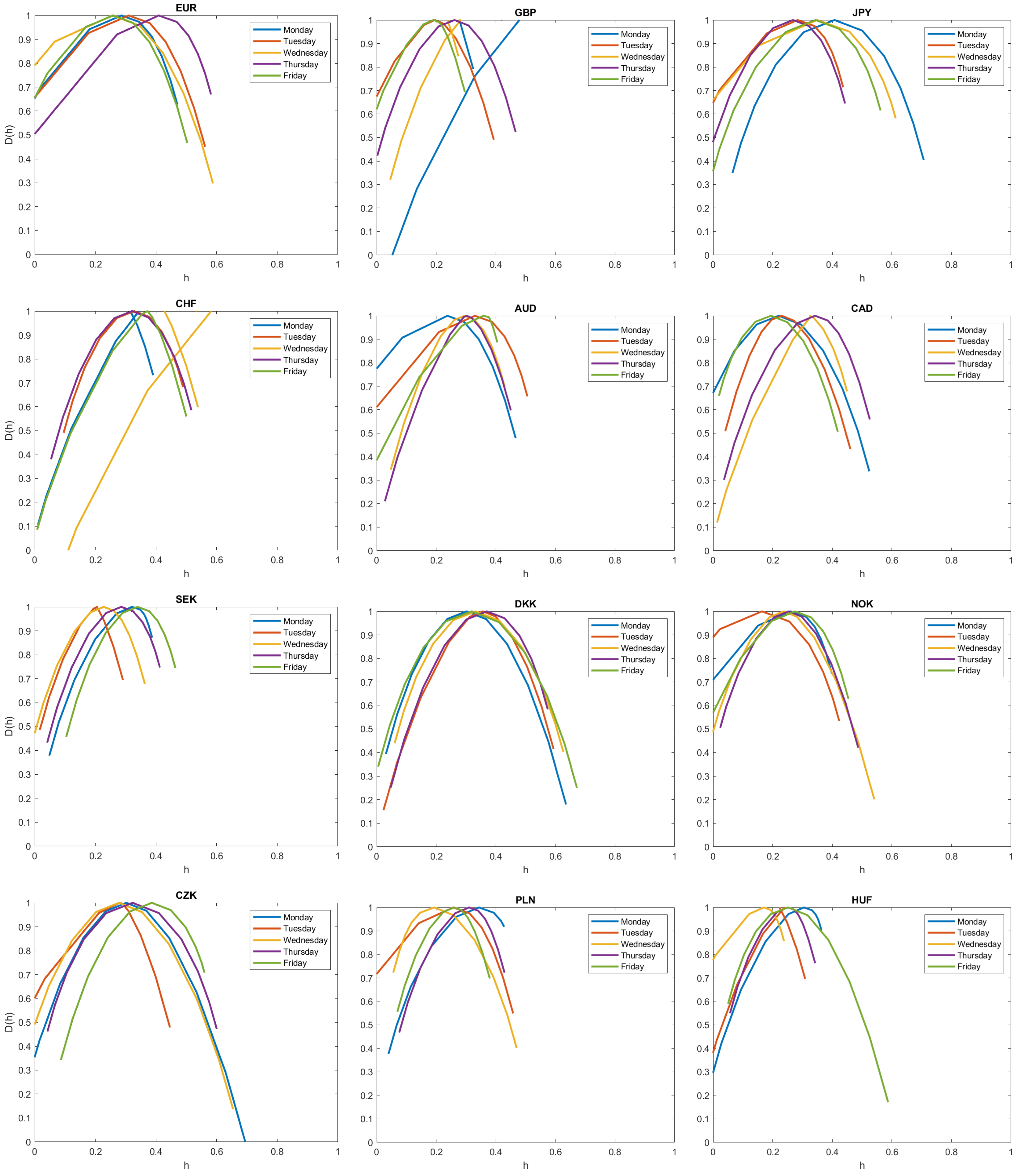

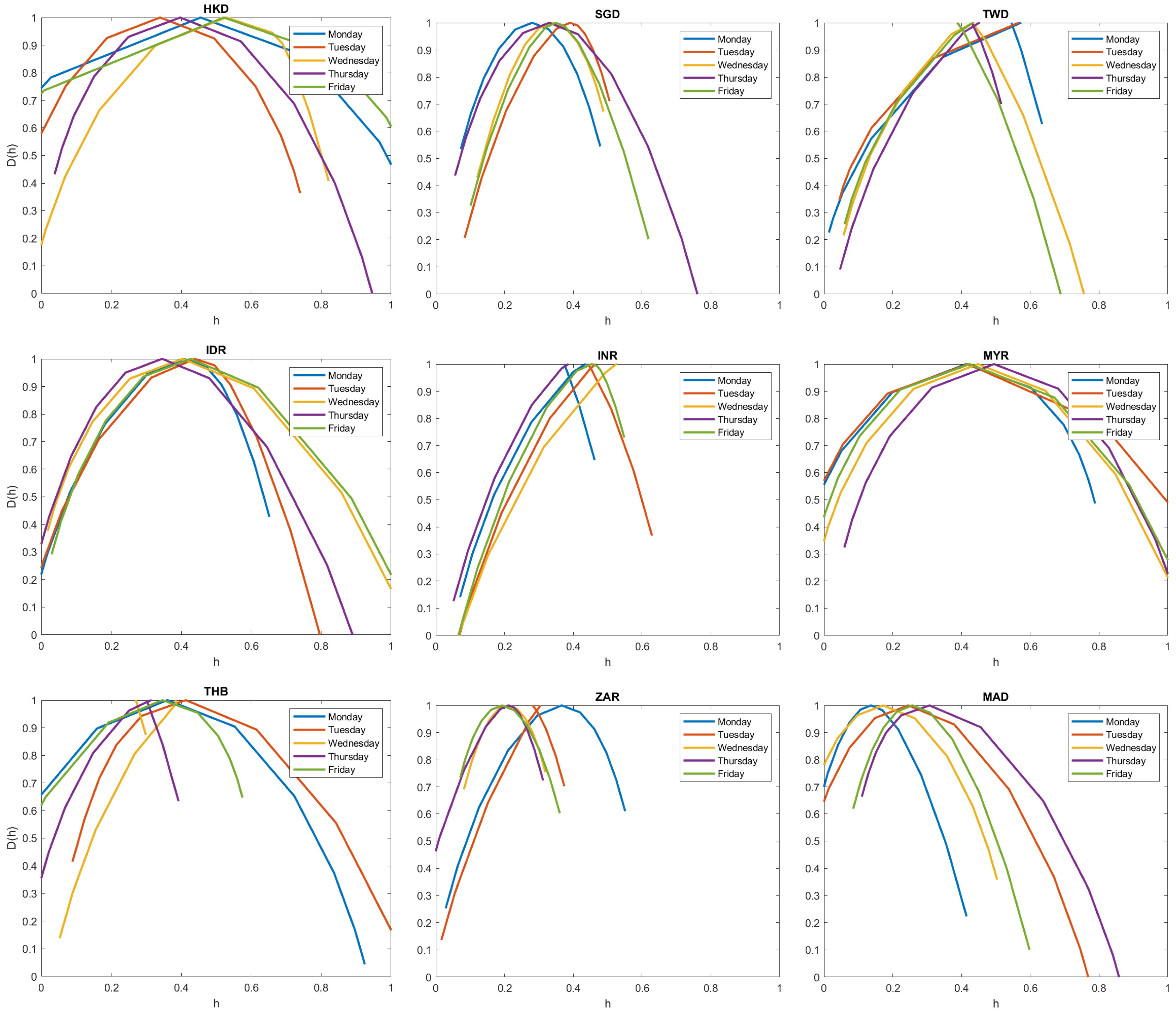
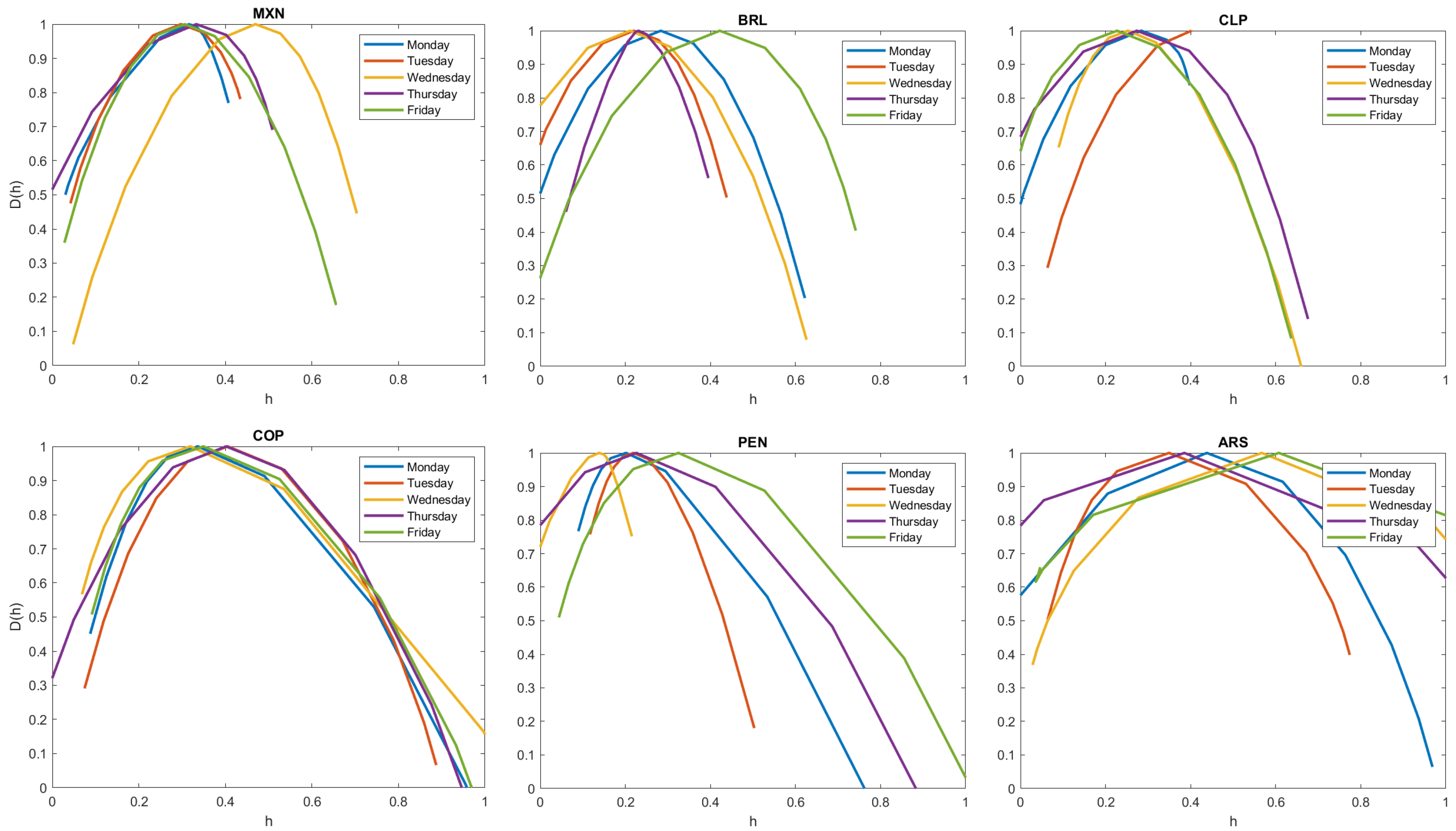


References
- Goodell, J.W.; Kumar, S.; Rao, P.; Verma, S. Emotions and stock market anomalies: A systematic review. J. Behav. Exp. Financ. 2023, 37, 100722. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Gold, currencies and market efficiency. Phys. A Stat. Mech. Appl. 2016, 449, 27–34. [Google Scholar] [CrossRef]
- Azzam, I.; El-Masry, A.A.; Yamani, E. Foreign exchange market efficiency during COVID-19 pandemic. Int. Rev. Econ. Financ. 2023, 86, 717–730. [Google Scholar] [CrossRef]
- Katusiime, L.; Shamsuddin, A.; Agbola, F.W. Foreign exchange market efficiency and profitability of trading rules: Evidence from a developing country. Int. Rev. Econ. Financ. 2015, 35, 315–332. [Google Scholar] [CrossRef]
- Oh, G.; Kim, S.; Eom, C. Market efficiency in foreign exchange markets. Phys. A Stat. Mech. Appl. 2007, 382, 209–212. [Google Scholar] [CrossRef]
- Lee, N.; Choi, W.; Pae, Y. Market efficiency in foreign exchange market. Econ. Lett. 2021, 205, 109931. [Google Scholar] [CrossRef]
- Aroskar, R.; Sarkar, S.K.; Swanson, P.E. European foreign exchange market efficiency: Evidence based on crisis and noncrisis periods. Int. Rev. Financ. Anal. 2004, 13, 333–347. [Google Scholar] [CrossRef]
- Yamani, E. Foreign exchange market efficiency and the global financial crisis: Fundamental versus technical information. Q. Rev. Econ. Financ. 2021, 79, 74–89. [Google Scholar] [CrossRef]
- Al-Khazali, O.M.; Leduc, G.; Pyun, C.S. Market efficiency of floating exchange rate systems: Some evidence from Pacific-Asian countries. Glob. Financ. J. 2011, 22, 154–168. [Google Scholar] [CrossRef]
- Wang, G.J.; Xie, C.; Han, F. Multi-scale approximate entropy analysis of foreign exchange markets efficiency. Syst. Eng. Procedia 2012, 3, 201–208. [Google Scholar] [CrossRef]
- Gkillas, K.; Vortelinos, D.I.; Babalos, V.; Wohar, M.E. Day-of-the-week effect and spread determinants: Some international evidence from equity markets. Int. Rev. Econ. Financ. 2021, 71, 268–288. [Google Scholar] [CrossRef]
- Ariss, R.T.; Rezvanian, R.; Mehdian, S.M. Calendar anomalies in the Gulf Cooperation Council stock markets. Emerg. Mark. Rev. 2011, 12, 293–307. [Google Scholar] [CrossRef]
- Shehadeh, A.A.; Zheng, M. Calendar anomalies in stock market returns: Evidence from Middle East countries. Int. Rev. Econ. Financ. 2023, 88, 962–980. [Google Scholar] [CrossRef]
- Lai, D.; Bai, A.; Chang, K.C.; Wei, H.; Luo, L. Nonparametric analysis of the Shenzhen Stock Market: The day of the week effect. Math. Comput. Model. 2012, 55, 1186–1192. [Google Scholar] [CrossRef]
- Chhabra, D.; Gupta, M. Calendar anomalies in commodity markets for natural resources: Evidence from India. Resour. Policy 2022, 79, 103019. [Google Scholar] [CrossRef]
- Qadan, M.; Idilbi-Bayaa, Y. The day-of-the-week-effect on the volatility of commodities. Resour. Policy 2021, 71, 101980. [Google Scholar] [CrossRef]
- Li, W.; Cheng, Y.; Fang, Q. Forecast on silver futures linked with structural breaks and day-of-the-week effect. N. Am. J. Econ. Financ. 2020, 53, 101192. [Google Scholar] [CrossRef]
- Gayaker, S.; Yalcin, Y.; Berument, M.H. The day of the week effect and interest rates. Borsa Istanb. Rev. 2020, 20, 55–63. [Google Scholar] [CrossRef]
- Ryu, I.; Jang, H.; Kim, D.; Ahn, K. Market efficiency of US REITs: A revisit. Chaos Solitons Fract. 2021, 150, 111070. [Google Scholar] [CrossRef]
- Bassiouny, A.; Kiryakos, M.; Tooma, E. Examining the adaptive market hypothesis with calendar effects: International evidence and the impact of COVID-19. Glob. Financ. J. 2023, 56, 100777. [Google Scholar] [CrossRef]
- Reboredo, J.C.; Rivera-Castro, M.A.; Miranda, J.G.; García-Rubio, R. How fast do stock prices adjust to market efficiency? Evidence from a detrended fluctuation analysis. Phys. A Stat. Mech. Appl. 2013, 392, 1631–1637. [Google Scholar] [CrossRef]
- Assaf, A.; Kristoufek, L.; Demir, E.; Mitra, S.K. Market efficiency in the art markets using a combination of long memory, fractal dimension, and approximate entropy measures. J. Int. Financ. Mark. Institutions Money 2021, 71, 101312. [Google Scholar] [CrossRef]
- Rodriguez, E.; Aguilar-Cornejo, M.; Femat, R.; Alvarez-Ramirez, J. US stock market efficiency over weekly, monthly, quarterly and yearly time scales. Phys. A Stat. Mech. Appl. 2014, 413, 554–564. [Google Scholar] [CrossRef]
- Sukpitak, J.; Hengpunya, V. The influence of trading volume on market efficiency: The DCCA approach. Phys. A Stat. Mech. Appl. 2016, 458, 259–265. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Aye, G.C.; Gupta, R. Stock market efficiency analysis using long spans of data: A multifractal detrended fluctuation approach. Financ. Res. Lett. 2019, 28, 398–411. [Google Scholar] [CrossRef]
- Fan, X.; Lv, X.; Yin, J.; Tian, L.; Liang, J. Multifractality and market efficiency of carbon emission trading market: Analysis using the multifractal detrended fluctuation technique. Appl. Energy 2019, 251, 113333. [Google Scholar] [CrossRef]
- Rejichi, I.Z.; Aloui, C. Hurst exponent behavior and assessment of the MENA stock markets efficiency. Res. Int. Bus. Financ. 2012, 26, 353–370. [Google Scholar] [CrossRef]
- Khurshid, A.; Khan, K.; Cifuentes-Faura, J.; Chen, Y. Asymmetric multifractality: Comparative efficiency analysis of global technological and renewable energy prices using MFDFA and A-MFDFA approaches. Energy 2024, 289, 130106. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Park, J.H.; Chang, W. Asymmetric multi-fractality in the US stock indices using index-based model of A-MFDFA. Chaos Solitons Fract. 2017, 97, 28–38. [Google Scholar] [CrossRef]
- Lee, M.; Song, J.W.; Kim, S.; Chang, W. Asymmetric market efficiency using the index-based asymmetric-MFDFA. Phys. A Stat. Mech. Appl. 2018, 512, 1278–1294. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, C.; Yang, X.; Yan, L.; Lai, Y. Analysis of the efficiency of Hong Kong REITs market based on Hurst exponent. Phys. A Stat. Mech. Appl. 2019, 534, 122035. [Google Scholar] [CrossRef]
- Choi, S.Y. Analysis of stock market efficiency during crisis periods in the US stock market: Differences between the global financial crisis and COVID-19 pandemic. Phys. A Stat. Mech. Appl. 2021, 574, 125988. [Google Scholar] [CrossRef]
- Stosic, D.; Stosic, D.; Vodenska, I.; Stanley, H.E.; Stosic, T. A New Look at Calendar Anomalies: Multifractality and Day-of-the-Week Effect. Entropy 2022, 24, 562. [Google Scholar] [CrossRef] [PubMed]
- Plastun, A.; Kozmenko, S.; Plastun, V.; Filatova, H. Market anomalies and data persistence: The case of the day-of-the-week effect. J. Int. Stud. 2019, 12, 122–130. [Google Scholar] [CrossRef]
- Sakalauskas, V.; Kriksciuniene, D. Evaluation the day-of-the-week effect using long range dependence measures. In Proceedings of the IEEE 2012 12th International Conference on Intelligent Systems Design and Applications (ISDA), Kochi, India, 27–29 November 2012; pp. 143–148. [Google Scholar]
- Bolek, M.; Gniadkowska-Szymańska, A.; Lyroudi, K. COVID-19 pandemic and day-of-the-week anomaly in Omx markets. Cent. Eur. Econ. J. 2022, 9, 158–177. [Google Scholar] [CrossRef]
- Ramos-Requena, J.; Trinidad-Segovia, J.; Sánchez-Granero, M. Introducing Hurst exponent in pair trading. Phys. A Stat. Mech. Appl. 2017, 488, 39–45. [Google Scholar] [CrossRef]
- Guasoni, P.; Mishura, Y.; Rásonyi, M. High-frequency trading with fractional Brownian motion. Financ. Stochastics 2021, 25, 277–310. [Google Scholar] [CrossRef]
- Garcin, M. Forecasting with fractional Brownian motion: A financial perspective. Quant. Financ. 2022, 22, 1495–1512. [Google Scholar] [CrossRef]
- Dewandaru, G.; Masih, R.; Bacha, O.I.; Masih, A.M.M. Developing trading strategies based on fractal finance: An application of MF-DFA in the context of Islamic equities. Phys. A Stat. Mech. Appl. 2015, 438, 223–235. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Berument, H.; Kiymaz, H. The day of the week effect on stock market volatility. J. Econ. Financ. 2001, 25, 181–193. [Google Scholar] [CrossRef]
- Choudhry, T. Day of the week effect in emerging Asian stock markets: Evidence from the GARCH model. Appl. Financ. Econ. 2000, 10, 235–242. [Google Scholar] [CrossRef]
- Olowe, R.A. Exchange Rate Volatility, Global Financial Crisis and the Day-of-the-Week Effect. KCA J. Bus. Manag. 2011, 3, 138–149. [Google Scholar] [CrossRef]
- Giovanis, E. A Study on the Day-of-The-Week Effect in Fifty Five Stock Markets: Evidence from Asymmetric GARCH Models. Int. Rev. Bus. Financ. 2010, 2, 103–120. [Google Scholar]
- Kiymaz, H.; Berument, H. The day of the week effect on stock market volatility and volume: International evidence. Rev. Financ. Econ. 2003, 12, 363–380. [Google Scholar] [CrossRef]
- Aharon, D.Y.; Qadan, M. Bitcoin and the day-of-the-week effect. Financ. Res. Lett. 2019, 31, 415-424. [Google Scholar] [CrossRef]
- Podobnik, B.; Grosse, I.; Horvatić, D.; Ilic, S.; Ivanov, P.C.; Stanley, H.E. Quantifying cross-correlations using local and global detrending approaches. Eur. Phys. J. B 2009, 71, 243–250. [Google Scholar] [CrossRef]
- Wendt, H.; Abry, P.; Jaffard, S. Bootstrap for empirical multifractal analysis. IEEE Signal Process. Mag. 2007, 24, 38–48. [Google Scholar] [CrossRef]
- Abry, P.; Jaffard, S.; Wendt, H. Irregularities and scaling in signal and image processing: Multifractal analysis. In Benoit Mandelbrot: A Life in Many Dimensions; World Scientific: Singapore, 2015; pp. 31–116. [Google Scholar]
- Wendt, H.; Jaffard, S.; Abry, P. Multifractal analysis of self-similar processes. In Proceedings of the 2012 IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 August 2012; pp. 69–72. [Google Scholar]
- Wendt, H.; Roux, S.G.; Jaffard, S.; Abry, P. Wavelet leaders and bootstrap for multifractal analysis of images. Signal Process. 2009, 89, 1100–1114. [Google Scholar] [CrossRef]





| Major Currencies | Polish Zloty (PLN) | Thai Baht (THB) |
| Euro (EUR) | Hungarian Forint (HUF) | African currencies |
| British Pound Sterling (GBP) | Russian Ruble (RUB) | South African Rand (ZAR) |
| Japanese Yen (JPY) | Asian currencies | Moroccan Dirham (MAD) |
| Swiss Franc (CHF) | Korean Won (KRW) | American currencies |
| Australian Dollar (AUD) | Israeli New Shekel (ILS) | Mexican Peso (MXN) |
| Canadian Dollar (CAD) | Hong Kong Dollar (HKD) | Brazilian Real (BRL) |
| European currencies | Singapore Dollar (SGD) | Chilean Peso (CLP) |
| Swedish Krona (SEK) | New Taiwan Dollar (TWD) | Colombian Peso (COP) |
| Danish Krone (DKK) | Indonesian Rupiah (INR) | Peruvian Sol (PEN) |
| Norwegian Krone (NOK) | Indian Rupee (INR) | Argentine Peso (ARS) |
| Czech Koruna (CZK) | Malaysian Ringgit (MY) |
| Return Average | Standard Deviation | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mon. | Tue. | Wed. | Thu. | Fri. | Mon. | Tue. | Wed. | Thu. | Fri. | |
| EUR | 0.04% | −0.01% | −0.01% | −0.01% | −0.01% | 0.66% | 0.62% | 0.65% | 0.66% | 0.68% |
| GBP | 0.06% | −0.02% | 0.01% | −0.03% | −0.03% | 0.67% | 0.55% | 0.57% | 0.59% | 0.61% |
| JPY | 0.00% | 0.00% | 0.01% | 0.01% | 0.01% | 0.65% | 0.61% | 0.69% | 0.63% | 0.66% |
| CHF | 0.02% | −0.01% | −0.01% | −0.02% | −0.02% | 0.62% | 0.55% | 0.66% | 0.59% | 0.71% |
| AUD | 0.04% | −0.03% | 0.00% | −0.01% | −0.01% | 0.85% | 0.73% | 0.77% | 0.80% | 0.79% |
| CAD | 0.03% | −0.01% | 0.01% | −0.01% | −0.01% | 0.58% | 0.50% | 0.56% | 0.58% | 0.56% |
| SEK | 0.06% | −0.01% | −0.03% | −0.02% | −0.02% | 0.78% | 0.75% | 0.75% | 0.76% | 0.76% |
| DKK | 0.04% | −0.02% | −0.01% | −0.01% | −0.01% | 0.59% | 0.55% | 0.54% | 0.58% | 0.62% |
| NOK | 0.03% | 0.01% | −0.01% | −0.03% | −0.03% | 0.86% | 0.83% | 0.81% | 0.86% | 0.78% |
| CZK | 0.02% | 0.02% | −0.02% | −0.02% | −0.02% | 0.72% | 0.78% | 0.69% | 0.77% | 0.78% |
| PLN | 0.04% | 0.00% | −0.03% | 0.02% | 0.02% | 0.91% | 0.91% | 0.83% | 0.90% | 0.84% |
| HUF | 0.04% | 0.03% | −0.03% | 0.01% | 0.01% | 0.92% | 0.91% | 0.87% | 0.96% | 0.87% |
| RUB | 0.11% | 0.04% | −0.01% | −0.05% | −0.05% | 1.10% | 1.14% | 0.96% | 1.17% | 1.08% |
| KRW | −0.12% | 0.15% | −0.02% | −0.01% | −0.01% | 0.94% | 0.97% | 0.83% | 0.85% | 0.77% |
| ILS | −0.01% | 0.01% | −0.01% | −0.02% | −0.02% | 0.54% | 0.53% | 0.55% | 0.48% | 0.50% |
| HKD | 0.01% | 0.00% | 0.00% | 0.00% | 0.00% | 0.10% | 0.03% | 0.04% | 0.03% | 0.10% |
| SGD | 0.01% | 0.00% | −0.02% | −0.01% | −0.01% | 0.35% | 0.30% | 0.31% | 0.36% | 0.33% |
| TWD | −0.09% | 0.14% | −0.02% | −0.02% | −0.02% | 0.86% | 0.78% | 0.60% | 0.61% | 0.67% |
| IDR | −0.09% | 0.14% | −0.01% | 0.01% | 0.01% | 0.88% | 0.84% | 0.68% | 0.66% | 0.68% |
| INR | −0.03% | 0.10% | 0.00% | −0.01% | −0.01% | 0.51% | 0.49% | 0.50% | 0.46% | 0.48% |
| MYR | 0.02% | 0.04% | 0.00% | −0.03% | −0.03% | 0.60% | 0.68% | 0.56% | 0.53% | 0.55% |
| THB | −0.21% | 0.22% | −0.01% | −0.01% | −0.01% | 0.83% | 0.78% | 0.51% | 0.50% | 0.52% |
| ZAR | 0.07% | 0.02% | −0.04% | 0.00% | 0.00% | 1.09% | 1.03% | 1.02% | 1.12% | 1.01% |
| MAD | 0.17% | 0.31% | 0.05% | −0.08% | −0.08% | 1.76% | 1.42% | 1.10% | 1.08% | 1.37% |
| MXN | 0.05% | 0.03% | 0.01% | 0.00% | 0.00% | 0.80% | 0.72% | 0.81% | 0.81% | 0.73% |
| BRL | −0.15% | 0.24% | −0.02% | −0.02% | −0.02% | 1.25% | 1.17% | 1.05% | 1.05% | 1.09% |
| CLP | −0.06% | 0.22% | 0.00% | −0.02% | −0.02% | 1.21% | 1.25% | 1.06% | 1.07% | 1.05% |
| COP | −0.07% | 0.18% | −0.01% | −0.08% | −0.08% | 1.20% | 1.26% | 1.15% | 1.18% | 1.16% |
| PEN | −0.46% | 0.47% | 0.06% | −0.03% | −0.03% | 1.32% | 1.37% | 1.10% | 1.13% | 1.18% |
| ARS | −0.07% | 0.21% | 0.04% | 0.09% | 0.09% | 0.78% | 0.86% | 0.72% | 0.74% | 0.72% |
| EUR | 0.0002 | −0.0004 | * | −0.0001 | 0.0000 | 0.0001 | ||||
| GBP | 0.0005 | ** | −0.0001 | −0.0001 | −0.0003 | 0.0000 | ||||
| JPY | 0.0001 | 0.0001 | 0.0004 | * | 0.0001 | 0.0002 | ||||
| CHF | −0.0001 | −0.0001 | 0.0000 | −0.0001 | 0.0000 | |||||
| AUD | 0.0003 | −0.0002 | −0.0001 | 0.0000 | 0.0001 | |||||
| CAD | 0.0002 | −0.0002 | 0.0002 | 0.0000 | −0.0002 | |||||
| SEK | 0.0007 | ** | −0.0004 | −0.0003 | 0.0000 | 0.0002 | ||||
| DKK | 0.0002 | −0.0003 | * | 0.0000 | 0.0000 | 0.0001 | ||||
| NOK | 0.0002 | −0.0002 | −0.0001 | −0.0001 | 0.0002 | |||||
| CZK | 0.0002 | −0.0001 | −0.0002 | 0.0000 | −0.0001 | |||||
| PLN | 0.0002 | −0.0003 | −0.0003 | 0.0003 | 0.0000 | |||||
| HUF | 0.0004 | 0.0001 | −0.0002 | 0.0002 | −0.0003 | |||||
| RUB | 0.0002 | ** | −0.0003 | ** | −0.0001 | −0.0002 | ** | −0.0004 | ** | |
| KRW | −0.0005 | ** | 0.0004 | * | 0.0000 | −0.0003 | 0.0000 | |||
| ILS | −0.0002 | * | 0.0001 | 0.0001 | −0.0002 | −0.0001 | ||||
| HKD | 0.0000 | ** | 0.0000 | ** | 0.0000 | ** | 0.0000 | ** | 0.0000 | |
| SGD | 0.0001 | 0.0000 | −0.0002 | * | −0.0002 | * | −0.0001 | |||
| TWD | 0.0003 | ** | −0.0004 | ** | −0.0006 | ** | −0.0003 | ** | −0.0007 | ** |
| IDR | −0.0006 | ** | 0.0008 | ** | 0.0001 | −0.0002 | * | 0.0000 | ||
| INR | 0.0001 | 0.0006 | ** | 0.0002 | ** | −0.0005 | ** | −0.0002 | ** | |
| MYR | 0.0000 | 0.0001 | ** | −0.0003 | ** | 0.0004 | ** | −0.0005 | ** | |
| THB | −0.0013 | ** | 0.0003 | ** | 0.0000 | 0.0000 | −0.0001 | |||
| ZAR | 0.0005 | 0.0004 | −0.0004 | −0.0001 | 0.0001 | |||||
| MAD | −0.0006 | * | 0.0015 | ** | 0.0007 | ** | −0.0002 | −0.0028 | ** | |
| MXN | 0.0004 | * | 0.0002 | −0.0001 | −0.0002 | −0.0009 | ** | |||
| BRL | −0.0009 | ** | 0.0017 | ** | −0.0002 | −0.0006 | ** | 0.0001 | ||
| CLP | −0.0007 | ** | 0.0017 | ** | 0.0007 | ** | −0.0003 | −0.0005 | ** | |
| COP | −0.0024 | ** | 0.0004 | * | 0.0002 | −0.0004 | * | −0.0015 | ** | |
| PEN | −0.0067 | ** | 0.0016 | ** | 0.0024 | ** | 0.0008 | ** | −0.0008 | ** |
| ARS | −0.0001 | 0.0016 | ** | 0.0007 | ** | 0.0008 | ** | 0.0000 | ||
| Monday | Tuesday | Wednesday | Thrusday | Friday | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| EUR | 0.317 | ** | −0.016 | 0.512 | ** | 0.322 | ** | 0.211 | ** | |
| GBP | 0.336 | ** | 0.175 | ** | 0.292 | ** | 0.149 | ** | 0.296 | ** |
| JPY | 0.188 | ** | 0.205 | ** | 0.237 | ** | 0.123 | ** | 0.228 | ** |
| CHF | 0.223 | ** | 0.160 | ** | 0.440 | ** | 0.109 | ** | 0.221 | ** |
| AUD | 0.360 | ** | 0.274 | ** | 0.018 | 0.197 | ** | 0.525 | ** | |
| CAD | 0.163 | ** | 0.282 | ** | 0.114 | ** | 0.125 | ** | 0.303 | ** |
| SEK | 0.227 | ** | 0.056 | * | 0.224 | ** | 0.246 | ** | 0.064 | * |
| DKK | 0.308 | ** | 0.237 | ** | 0.311 | ** | 0.133 | ** | 0.180 | ** |
| NOK | 0.489 | ** | 0.121 | ** | 0.159 | ** | 0.128 | ** | 0.193 | ** |
| CZK | 0.395 | ** | 0.129 | ** | 0.016 | 0.236 | ** | 0.078 | * | |
| PLN | 0.061 | * | 0.108 | ** | 0.185 | ** | 0.326 | ** | 0.194 | ** |
| HUF | 0.313 | ** | 0.014 | −0.071 | * | 0.331 | ** | −0.030 | ||
| RUB | 0.433 | ** | 0.430 | ** | 0.127 | * | 0.355 | ** | 0.521 | ** |
| KRW | 0.225 | ** | −0.022 | 0.342 | ** | 0.293 | ** | 0.429 | ** | |
| ILS | 0.056 | 0.310 | ** | 0.049 | 0.202 | ** | 0.372 | ** | ||
| HKD | 0.714 | ** | 0.593 | ** | 0.692 | ** | 0.245 | ** | 0.452 | ** |
| SGD | 0.309 | ** | 0.276 | ** | 0.147 | ** | 0.246 | ** | 0.332 | ** |
| TWD | 0.264 | ** | −0.002 | 0.538 | ** | 0.234 | ** | 0.373 | ** | |
| IDR | 0.406 | ** | 0.165 | ** | 0.725 | ** | 0.454 | ** | 0.812 | ** |
| INR | 0.499 | ** | 0.264 | ** | 0.225 | ** | 0.114 | ** | 0.212 | ** |
| MYR | 0.309 | ** | 0.839 | ** | 0.557 | ** | 0.560 | ** | 0.471 | ** |
| THB | 0.217 | ** | 0.119 | ** | 0.158 | ** | 0.096 | ** | 0.497 | ** |
| ZAR | 0.187 | ** | 0.131 | ** | −0.005 | 0.195 | ** | 0.152 | ** | |
| MAD | 0.161 | ** | 0.210 | ** | 0.532 | ** | 0.614 | ** | 0.179 | ** |
| MXN | −0.043 | 0.220 | ** | −0.050 | 0.433 | ** | 0.203 | ** | ||
| BRL | 0.047 | 0.016 | 0.038 | 0.295 | ** | 0.193 | ** | |||
| CLP | 0.212 | ** | 0.192 | ** | 0.084 | * | 0.027 | 0.313 | ** | |
| COP | 0.804 | ** | 0.533 | ** | 0.597 | ** | 0.473 | ** | 0.524 | ** |
| PEN | 0.398 | ** | 0.232 | ** | 0.603 | ** | 0.314 | ** | 0.476 | ** |
| ARS | 0.535 | ** | 0.248 | ** | 0.624 | ** | 0.760 | ** | 0.215 | ** |
| Monday | Tuesday | Wednesday | Thrusday | Friday | Monday | Tuesday | Wednesday | Thrusday | Friday | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EUR | 0.215 | ** | −0.128 | 0.542 | ** | 0.365 | ** | 0.025 | 0.457 | ** | ** | 0.355 | ** | 0.164 | ** | 0.433 | ** | |||
| GBP | 0.238 | ** | 0.124 | ** | 0.247 | ** | 0.168 | ** | 0.285 | ** | 0.286 | ** | 0.331 | ** | 0.369 | ** | 0.145 | ** | 0.341 | ** |
| JPY | 0.247 | ** | 0.183 | ** | 0.004 | 0.161 | ** | 0.358 | ** | 0.110 | ** | 0.223 | ** | 0.236 | ** | 0.116 | ** | 0.147 | ** | |
| CHF | 0.296 | ** | 0.044 | 0.425 | ** | 0.081 | * | 0.286 | ** | 0.381 | ** | 0.346 | ** | 0.423 | ** | 0.133 | ** | 0.264 | ** | |
| AUD | 0.255 | ** | 0.186 | ** | 0.108 | 0.250 | ** | 0.574 | ** | 0.328 | ** | 0.404 | ** | 0.162 | ** | 0.183 | ** | 0.291 | ** | |
| CAD | 0.031 | 0.481 | ** | 0.117 | 0.168 | ** | 0.313 | ** | 0.255 | ** | 0.179 | ** | 0.171 | ** | 0.078 | 0.310 | ** | |||
| SEK | 0.181 | ** | 0.018 | 0.211 | ** | 0.260 | ** | −0.059 | 0.267 | ** | 0.181 | ** | 0.324 | ** | 0.222 | ** | 0.297 | ** | ||
| DKK | 0.195 | ** | 0.028 | 0.439 | ** | 0.076 | 0.113 | * | 0.349 | ** | 0.430 | ** | 0.140 | ** | 0.215 | ** | 0.276 | ** | ||
| NOK | 0.033 | 0.103 | * | 0.235 | ** | 0.097 | ** | 0.051 | 0.647 | ** | 0.136 | ** | 0.187 | ** | 0.214 | ** | 0.381 | ** | ||
| CZK | 0.450 | ** | 0.193 | ** | 0.062 | 0.272 | ** | 0.188 | ** | 0.228 | ** | 0.323 | ** | 0.044 | 0.212 | ** | 0.090 | |||
| PLN | 0.097 | * | 0.081 | 0.460 | ** | 0.309 | ** | 0.184 | * | 0.207 | ** | 0.137 | 0.039 | 0.330 | ** | 0.313 | ** | |||
| HUF | 0.330 | ** | 0.185 | ** | −0.142 | 0.414 | ** | 0.041 | 0.184 | ** | −0.061 | 0.139 | ** | 0.239 | ** | 0.005 | ||||
| RUB | 0.592 | ** | 0.588 | ** | 0.251 | ** | 0.522 | ** | 0.597 | ** | 0.586 | ** | 0.332 | ** | 0.073 | 0.293 | ** | 0.457 | ** | |
| KRW | 0.241 | ** | 0.337 | ** | 0.620 | ** | 0.048 | 0.497 | ** | 0.304 | ** | −0.057 | 0.052 | 0.585 | ** | 0.347 | ** | |||
| ILS | −0.018 | 0.289 | ** | 0.086 | 0.231 | ** | 0.286 | ** | 0.105 | ** | 0.328 | ** | 0.312 | ** | 0.134 | ** | 0.455 | ** | ||
| HKD | 0.789 | ** | 0.338 | ** | 1.023 | ** | 0.421 | ** | 1.064 | ** | 1.632 | ** | 0.711 | ** | 0.445 | ** | 0.144 | * | 0.596 | ** |
| SGD | 0.185 | ** | 0.319 | ** | 0.237 | ** | 0.348 | ** | 0.453 | ** | 0.425 | ** | 0.231 | ** | 0.125 | * | 0.155 | ** | 0.218 | ** |
| TWD | 0.402 | ** | 0.610 | ** | 0.652 | ** | 0.351 | ** | 0.535 | ** | 0.686 | ** | 0.218 | ** | 0.414 | ** | 0.180 | ** | 0.264 | ** |
| IDR | 0.574 | ** | 0.099 | * | 0.859 | ** | 0.550 | ** | 1.102 | ** | 0.249 | ** | 0.171 | ** | 0.335 | ** | 0.331 | ** | 0.075 | |
| INR | 0.567 | ** | 0.340 | ** | 0.154 | * | −0.010 | 0.249 | ** | 0.320 | ** | 0.081 | * | 0.258 | ** | 0.292 | ** | 0.110 | * | |
| MYR | 0.456 | ** | 0.430 | ** | 0.552 | ** | 0.593 | ** | 0.459 | ** | 0.352 | ** | 0.812 | ** | 0.570 | ** | 0.157 | ** | 0.494 | ** |
| THB | 0.226 | ** | −0.028 | 0.099 | 0.123 | ** | 0.397 | ** | 0.086 | * | 0.350 | ** | 0.185 | ** | 0.078 | 0.594 | ** | |||
| ZAR | 0.158 | ** | 0.168 | ** | 0.130 | ** | 0.155 | ** | 0.211 | ** | 0.205 | ** | 0.078 | * | 0.010 | 0.224 | ** | 0.168 | ** | |
| MAD | 0.062 | −0.036 | 0.465 | ** | 0.526 | ** | 0.345 | ** | 0.303 | ** | 0.270 | ** | 0.515 | ** | 0.559 | ** | −0.009 | |||
| MXN | −0.093 | 0.249 | ** | 0.043 | 0.384 | ** | 0.274 | ** | 0.162 | * | 0.246 | ** | 0.023 | 0.195 | ** | 0.065 | ||||
| BRL | 0.384 | ** | −0.120 | * | 0.015 | 0.246 | ** | 0.286 | ** | −0.121 | * | 0.165 | ** | 0.370 | ** | 0.315 | ** | 0.147 | ** | |
| CLP | 0.212 | ** | 0.171 | ** | −0.049 | −0.034 | 0.189 | ** | 0.345 | ** | 0.226 | ** | 0.241 | ** | 0.193 | ** | 0.404 | ** | ||
| COP | 0.930 | ** | 0.261 | ** | 0.505 | ** | 0.600 | ** | 0.117 | 0.466 | ** | 0.575 | ** | 0.574 | ** | 0.202 | ** | 0.799 | ** | |
| PEN | 0.527 | ** | −0.145 | ** | 0.276 | ** | 0.518 | ** | 0.409 | ** | 0.016 | 0.461 | ** | 0.766 | ** | 0.230 | ** | 0.483 | ** | |
| ARS | 0.441 | ** | 0.397 | ** | 0.613 | ** | 0.743 | ** | 0.257 | * | 0.474 | ** | 0.176 | ** | 0.801 | ** | 0.928 | ** | 0.402 | ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kristjanpoller, W.; Miranda Tabak, B. Day of the Week Effect on the World Exchange Rates through Fractal Analysis. Fractal Fract. 2024, 8, 340. https://doi.org/10.3390/fractalfract8060340
Kristjanpoller W, Miranda Tabak B. Day of the Week Effect on the World Exchange Rates through Fractal Analysis. Fractal and Fractional. 2024; 8(6):340. https://doi.org/10.3390/fractalfract8060340
Chicago/Turabian StyleKristjanpoller, Werner, and Benjamin Miranda Tabak. 2024. "Day of the Week Effect on the World Exchange Rates through Fractal Analysis" Fractal and Fractional 8, no. 6: 340. https://doi.org/10.3390/fractalfract8060340
APA StyleKristjanpoller, W., & Miranda Tabak, B. (2024). Day of the Week Effect on the World Exchange Rates through Fractal Analysis. Fractal and Fractional, 8(6), 340. https://doi.org/10.3390/fractalfract8060340






