Multi-Peak and Propagation Behavior of M-Shape Solitons in (2 + 1)-Dimensional Integrable Schwarz-Korteweg-de Vries Problem
Abstract
:1. Introduction
2. MS
3. HB
4. -Shape Solitons
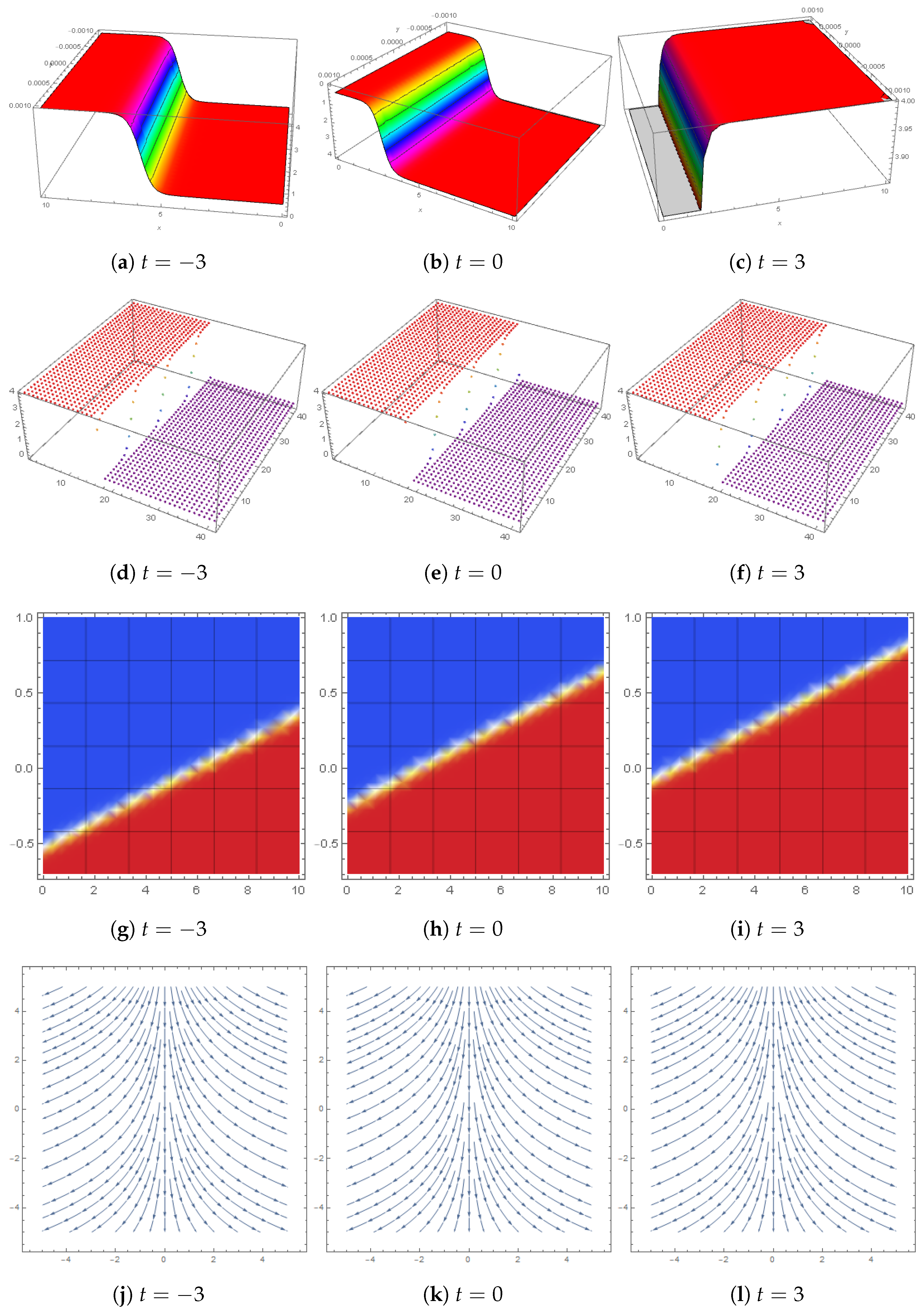
5. -Shape Soliton Interaction with One Kink
6. -Shape Soliton Interaction with Two Kinks
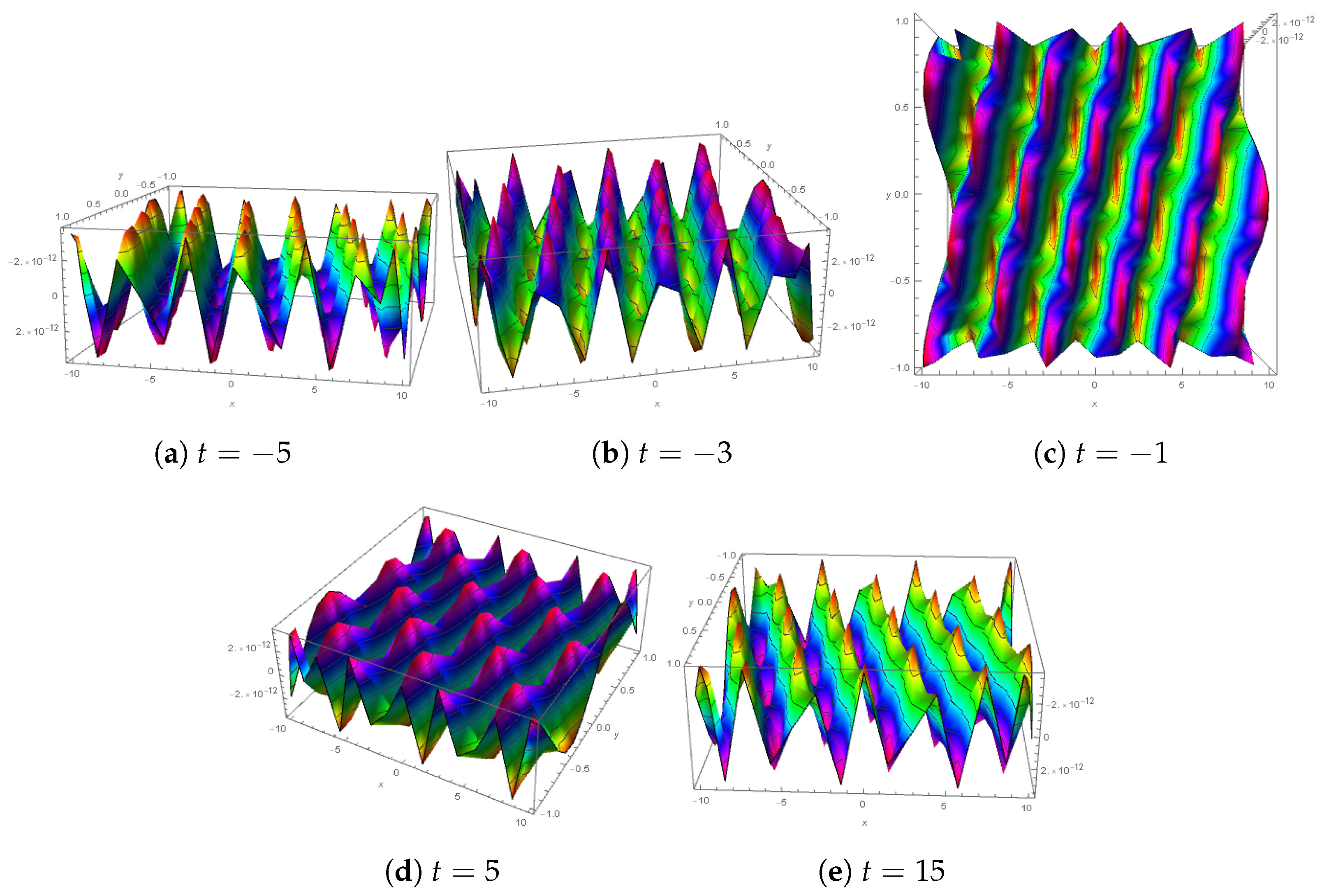
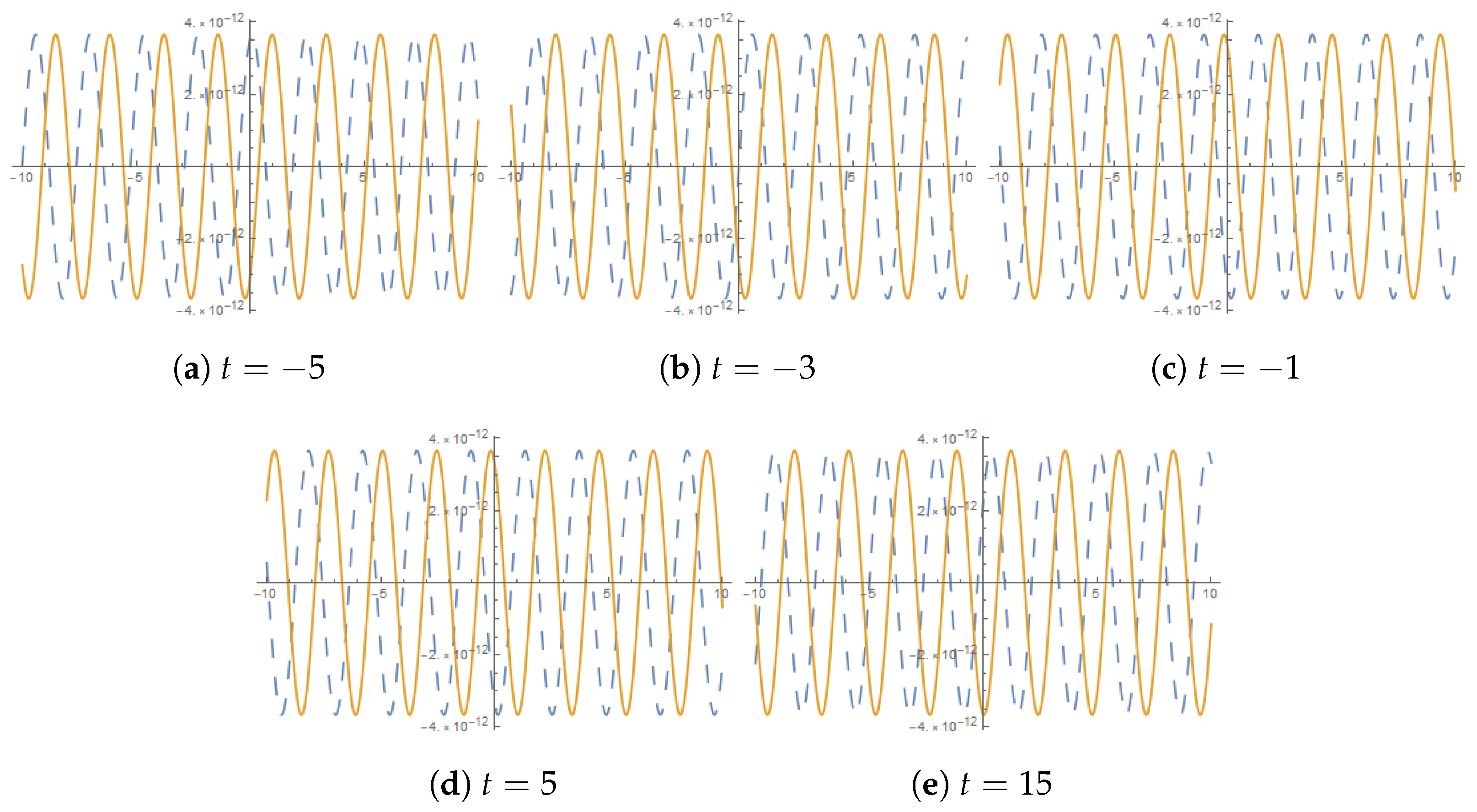
7. Stability Characteristic of Solutions
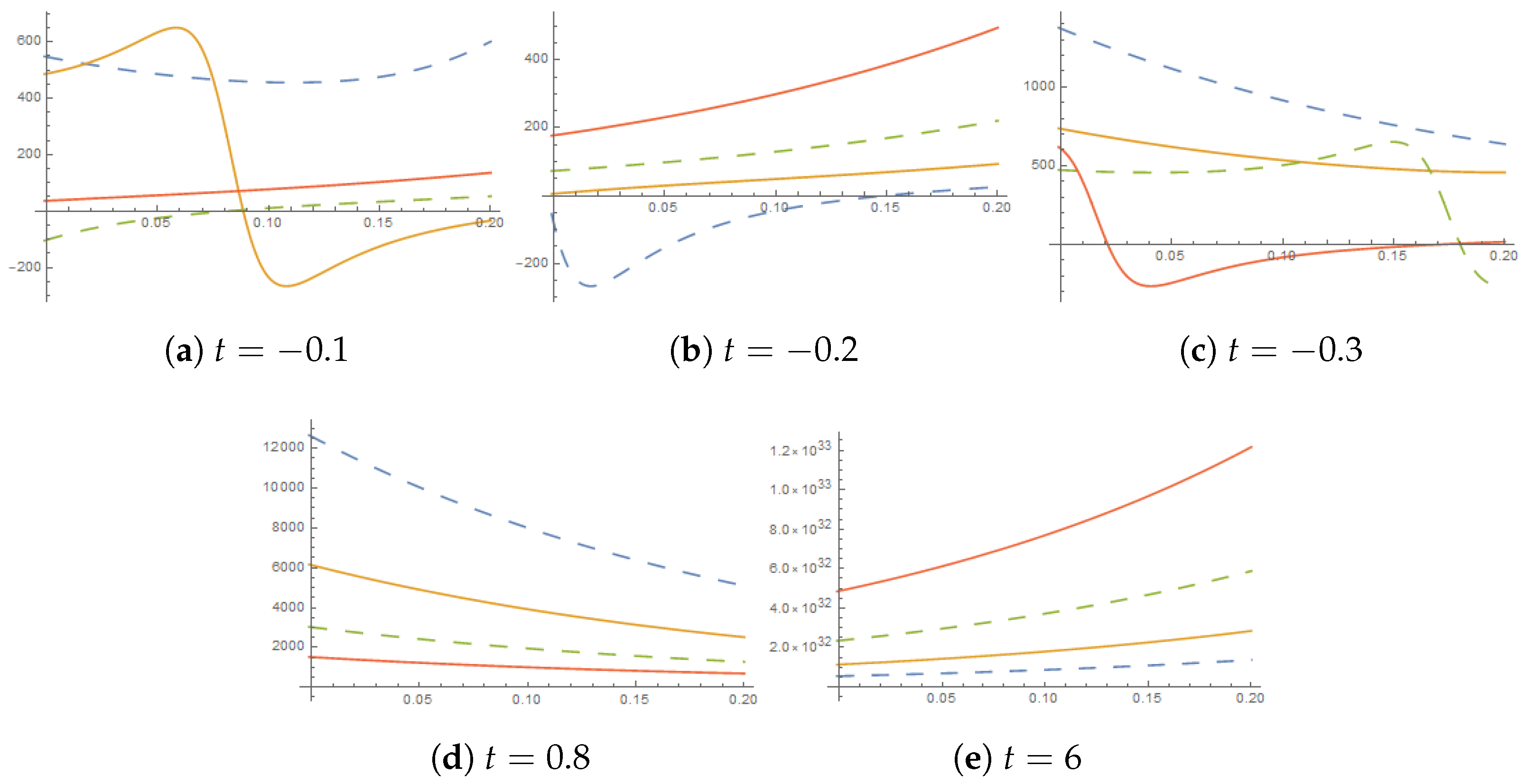
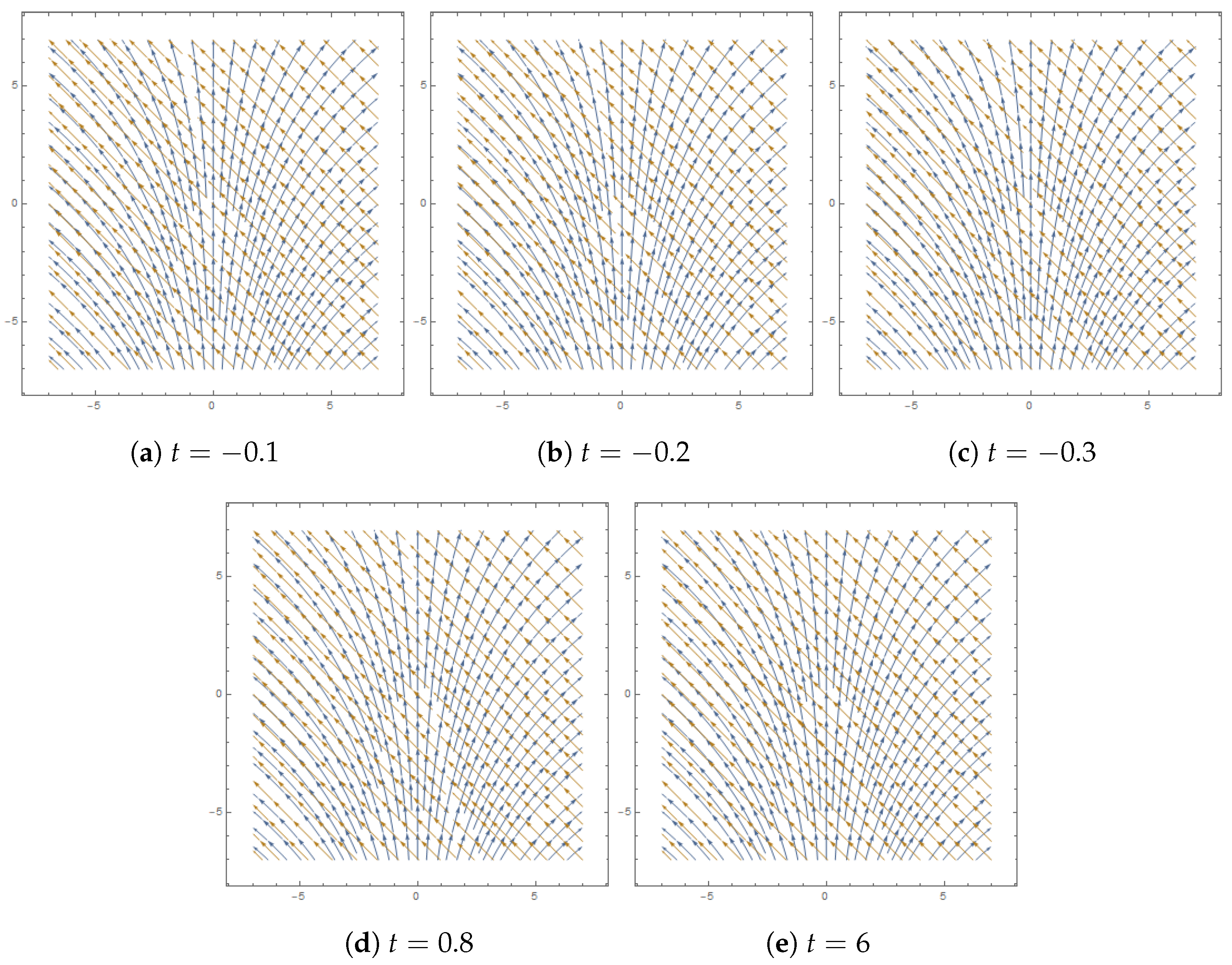
8. Results and Discussions
9. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Akinyemi, L. Shallow ocean soliton and localized waves in extended (2 + 1)-dimensional nonlinear evolution equations. Phys. Lett. 2023, 463, 128668. [Google Scholar] [CrossRef]
- Ali, K.; Seadawy, A.R.; Ahmed, S.; Rizvi, S.T. Discussion on rational solutions for Nematicons in liquid crystals with Kerr Law. Chaos Solitons Fractals 2022, 160, 112218. [Google Scholar] [CrossRef]
- Akinyemi, L.; Morazara, E. Integrability, multi-solitons, breathers, lumps and wave interactions for generalized extended Kadomtsev–Petviashvili equation. Nonlinear Dyn. 2023, 111, 4683–4707. [Google Scholar] [CrossRef]
- Akinyemi, L.; Şenol, M.; Tasbozan, O.; Kurt, A. Multiple-solitons for generalized-dimensional conformable Korteweg-de Vries-Kadomtsev-Petviashvili equation. J. Ocean. Eng. Sci. 2022, 7, 536–542. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ahmed, S.; Rizvi, S.T.; Ali, K. Lumps, breathers, interactions and rogue wave solutions for a stochastic gene evolution in double chain deoxyribonucleic acid system. Chaos Solitons Fractals 2022, 161, 112307. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Ahmad, S.; Younis, M.; Baleanu, D. Lump, lump-one stripe, multiwave and breather solutions for the Hunter–Saxton equation. Open Phys. 2021, 19, 1–10. [Google Scholar] [CrossRef]
- Liu, Y.; Li, B.; Wazwaz, A.M. Novel high-order breathers and rogue waves in the Boussinesq equation via determinants. Int. J. Mod. Phys. 2020, 43, 3701–3715. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov-Kuznetsov and dispersive long wave equations. Results Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multi-soliton rational solutions for some nonlinear evolution equations. J. Opt. 2022, 232, 162227. [Google Scholar]
- Triki, H.; Milovic, D.; Belic, M.; Biswas, A. Chirped femtosecond pulses in the higher-order nonlinear Schrödinger equation with non-Kerr nonlinear terms and cubic–quintic–septic nonlinearities. Optiks 2018, 326, 332–349. [Google Scholar] [CrossRef]
- Taghizadeh; Mirzazadeh, N.; Farahrooz, F. Exact solutions of the nonlinear Schrödinger equation by the first integral method. J. Math. Anal. Appl. 2011, 374, 549–553. [Google Scholar] [CrossRef]
- Chen, J.; Luan, Z.; Zhou, Q.; Alzahrani, A.K.; Biswas, A.; Liu, W. Periodic soliton interactions for higher-order nonlinear Schrödinger equation in optical fibers. Nonlinear Dyn. 2020, 100, 2817–2821. [Google Scholar] [CrossRef]
- Savaissou, N.; Gambo, B.; Rezazadeh, H.; Bekir, A.; Doka, S.Y. Exact optical solitons to the perturbed nonlinear Schrödinger equation with dual-power law of nonlinearity. Opt. Quantum Electron. 2020, 52, 318. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Almost general solution of the reduced higher-order nonlinear Schrödinger equation. Optik 2021, 230, 166347. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Optical solitons of the resonant nonlinear Schrödinger equation with arbitrary index. Optik 2021, 235, 166626. [Google Scholar] [CrossRef]
- Ma, G.; Zhao, J.; Zhou, Q.; Biswas, A.; Liu, W. Soliton interaction control through dispersion and nonlinear effects for the fifth-order nonlinear Schrödinger equation. Nonlinear Dyn. 2021, 106, 2479–2484. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, G.D. Variational theory and new abundant solutions to the (1+ 2)-dimensional chiral nonlinear Schrödinger equation in optics. Phys. Lett. A 2021, 412, 127588. [Google Scholar] [CrossRef]
- Mo, Y.; Ling, L.; Zeng, D. Data-driven vector soliton solutions of coupled nonlinear Schrödinger equation using a deep learning algorithm. Phys. Lett. A 2022, 421, 127739. [Google Scholar] [CrossRef]
- Jiang, C.; Cui, J.; Qian, X.; Song, S. High-order linearly implicit structure-preserving exponential integrators for the nonlinear Schrödinger equation. J. Sci. Comput. 2022, 90, 66. [Google Scholar] [CrossRef]
- Weng, W.; Zhang, G.; Zhang, M.; Zhou, Z.; Yan, Z. Semi-rational vector rogon-soliton solutions and asymptotic analysis for any n-component nonlinear Schrödinger equation with mixed boundary conditions. Phys. D Nonlinear Phenom. 2022, 432, 133150. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Rasoulizadeh, M.N. Soliton solutions of the nonlinear sine-Gordon model with Neumann boundary conditions arising in crystal dislocation theory. Nonlinear Dyn. 2021, 106, 783–813. [Google Scholar] [CrossRef]
- Asjad, M.I.; Ullah, N.; Rehman, H.; Baleanu, D. Optical solitons for conformable space-time fractional nonlinear model. J. Math. Comput. Sci. 2022, 27, 28. [Google Scholar] [CrossRef]
- Ngondiep, E. A novel three-level time-split approach for solving two-dimensional nonlinear unsteady convection-diffusion-reaction equation. J. Math. Comput. Sci. 2022, 26, 222–248. [Google Scholar] [CrossRef]
- Lax, P.D. Periodic solutions of the KdV equation. Commun. Pure Appl. Math. 1975, 28, 141–188. [Google Scholar] [CrossRef]
- Krichever, I.M.; Novikov, S.P. Holomorphic bundles over algebraic curves and non-linear equations. Russ. Math. Surv. 1980, 35, 53. [Google Scholar] [CrossRef]
- Shah, K.; Seadawy, A.R.; Arfan, M. Evaluation of one dimensional fuzzy fractional partial differential equations. Alexandria Eng. J. 2020, 59, 3347–3353. [Google Scholar] [CrossRef]
- Toda, K.; Yu, S.J. The investigation into the Schwarz–Korteweg–de Vries equation and the Schwarz derivative in (2 + 1)-dimensions. J. Math. Phys. 2000, 41, 4747–4751. [Google Scholar] [CrossRef]
- Bruzón, M.S.; Gandarias, M.L.; Muriel, C.; Ramirez, J.; Romero, F.R. Traveling-wave solutions of the Schwarz–Korteweg–de Vries equation in 2 + 1 dimensions and the Ablowitz–Kaup–Newell–Segur equation through symmetry reductions. Theor. Math. Phys. 2003, 137, 1378–1389. [Google Scholar] [CrossRef]
- Ramirez, J.; Romero, J.L.; Bruzón, M.S.; Gandarias, M.L. Multiple solutions for the Schwarzian Korteweg–de Vries equation in (2 + 1)-dimensions. Chaos Solitons Fractals 2007, 32, 682–693. [Google Scholar] [CrossRef]
- Seadawy, A.S.; Iqbal, I.; Lu, D. Applications of propagation of long-wave with dissipation and dispersion in nonlinear media via solitary wave solutions of generalized Kadomtsive-Petviashvili modified equal width dynamical equation. Comput. Math. Appl. 2019, 78, 3620–3632. [Google Scholar]
- Wang, J.; Shehzad, K.; Seadawy, A.R.; Arshad, M.; Asmat, F. Dynamic study of multi-peak solitons and other wave solutions of new coupled KdV and new coupled Zakharov-Kuznetsov systems with their stability. J. Taibah Univ. Sci. 2023, 17, 2163872. [Google Scholar] [CrossRef]
- Wang, K.J. Resonant multiple wave, periodic wave and interaction solutions of the new extended (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Nonlinear Dyn. 2023, 111, 16427–16439. [Google Scholar] [CrossRef]
- Gandarias, M.L.; Bruzón, M.S.; Ramirez, J. Classical symmetry reductions of the Schwarz–Korteweg–de Vries equation in 2 + 1 dimensions. Theor. Math. Phys. 2003, 134, 62–71. [Google Scholar] [CrossRef]
- Li, X.; Zhang, M. Darboux transformation and soliton solutions of the (2 + 1)-dimensional Schwarz–Korteweg–de Vries equation. Mod. Phys. Lett. B 2020, 34, 2050270. [Google Scholar] [CrossRef]
- Li, Z. Diversity soliton excitations for the (2 + 1)-dimensional Schwarzian Korteweg-de Vries equation. Therm. Sci. 2018, 22, 1781–1786. [Google Scholar] [CrossRef]
- Aslan, I. Analytic investigation of the (2 + 1)-dimensional Schwarzian Korteweg–de Vries equation for traveling wave solutions. Appl. Math. Comput. 2011, 217, 6013–6017. [Google Scholar] [CrossRef]
- Ahmed, I.; Seadawy, A.R.; Lu, D. Kinky breathers, W-shaped and multi-peak solitons interaction in (2+1)-dimensional nonlinear Schrödinger equation with Kerr law of nonlinearity. Eur. Phys. J. Plus 2019, 134, 120. [Google Scholar] [CrossRef]
- Ahmed, I.; Seadawy, A.R.; Lu, D. M-shaped rational solitons and their interaction with kink waves in the Fokas–Lenells equation. Phys. Scr. 2019, 94, 055205. [Google Scholar] [CrossRef]



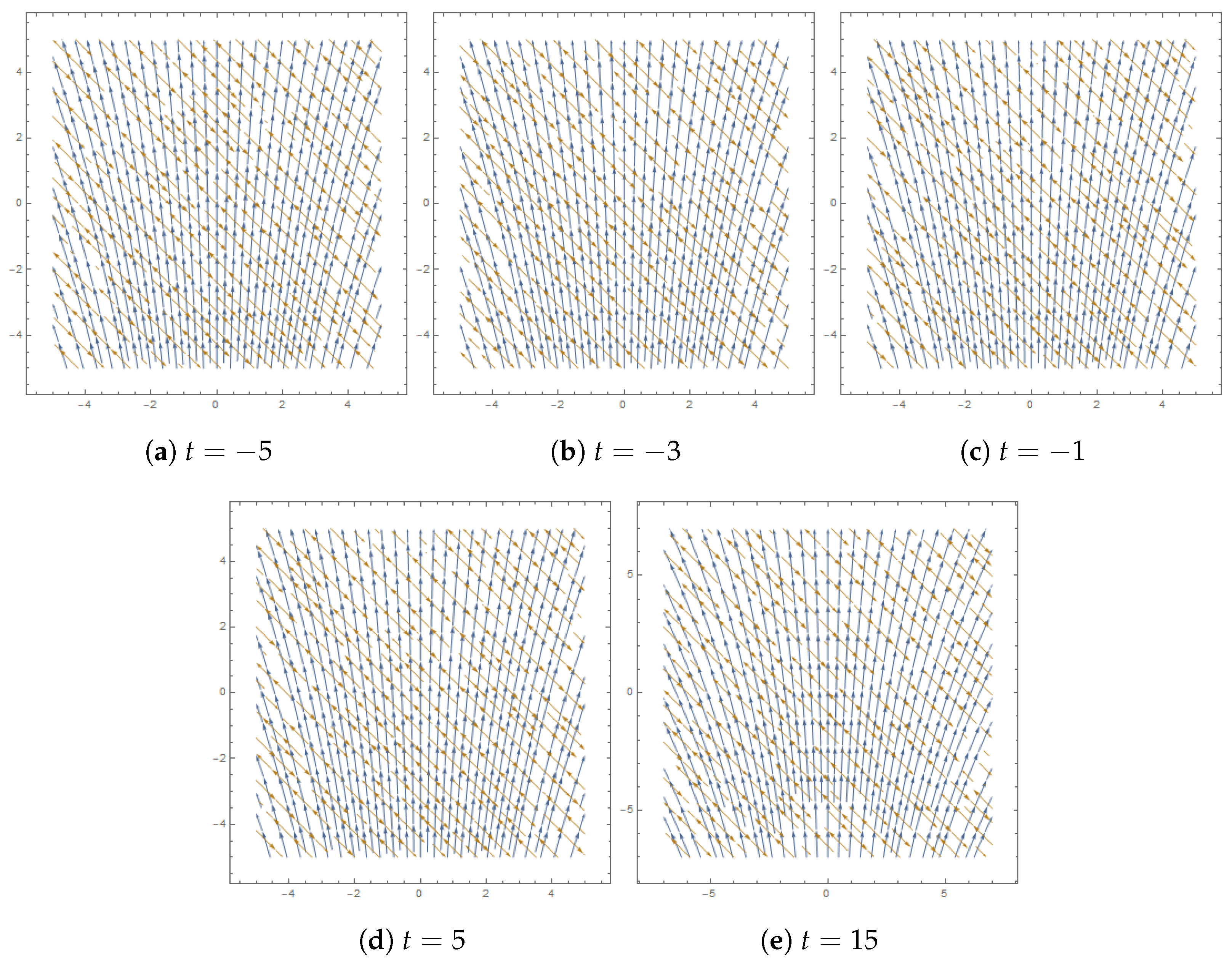

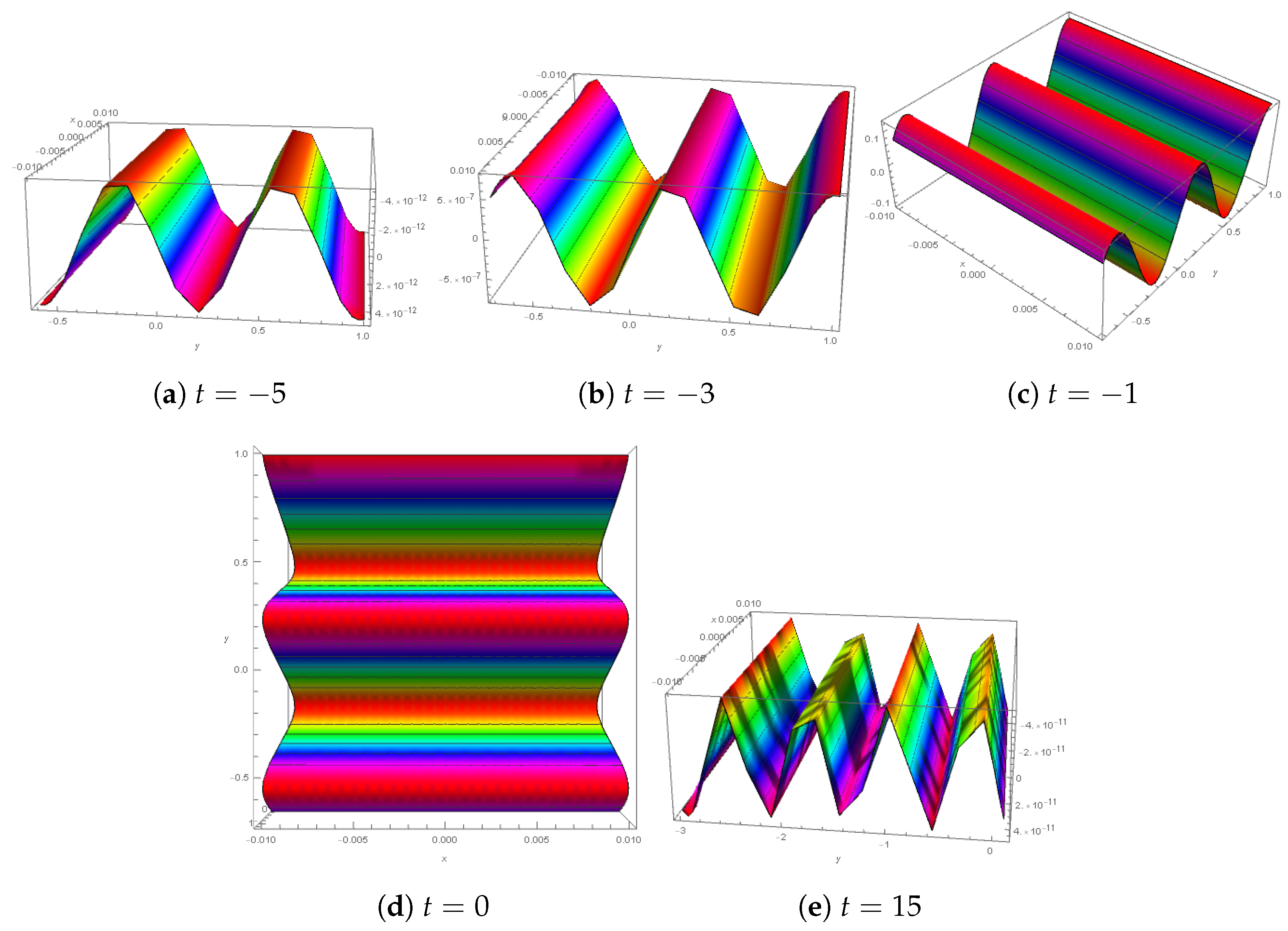

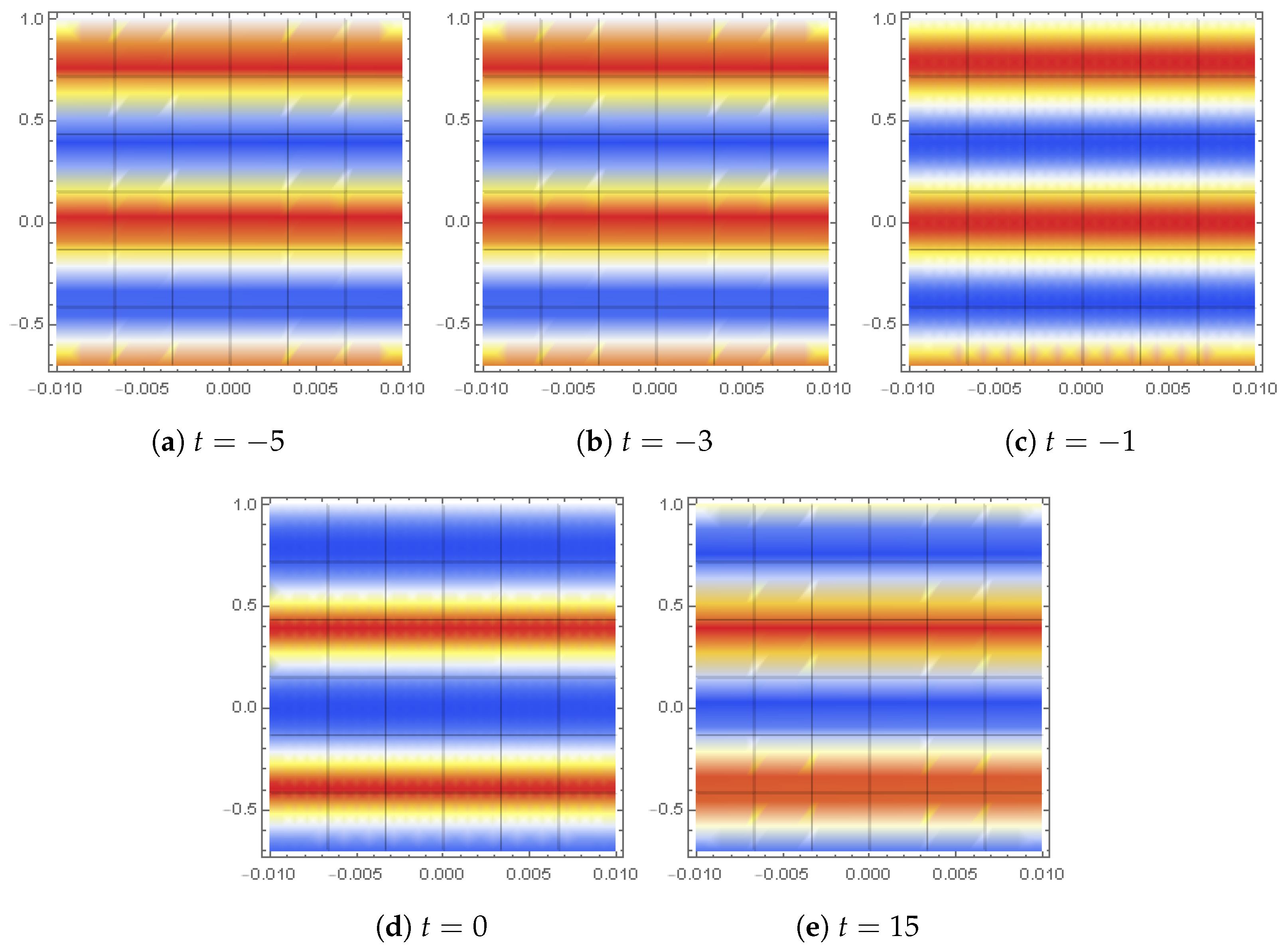
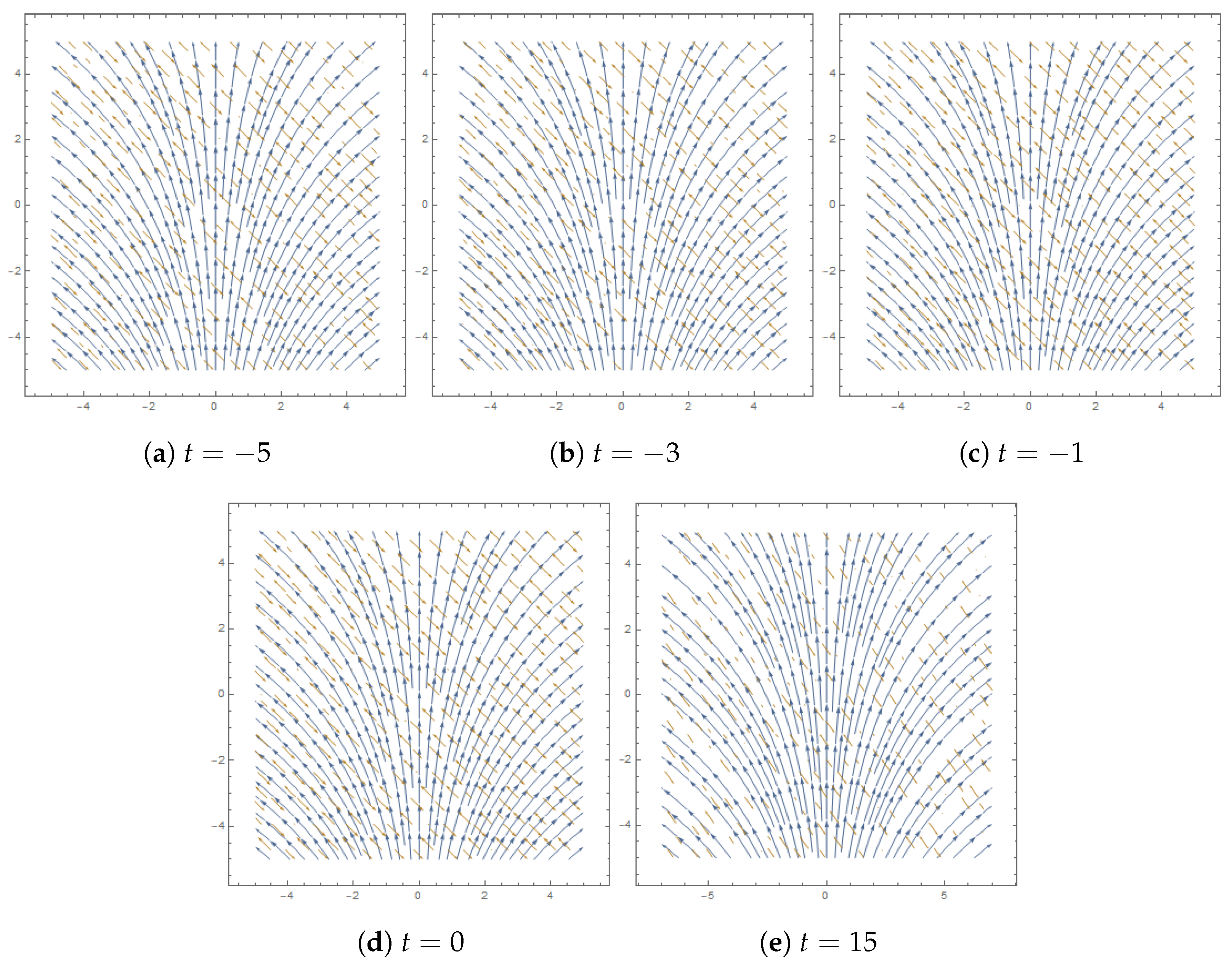
| Solution | Stability | Values of Variables |
|---|---|---|
| Stable | ||
| Stable | ||
| Unstable | Singular solution | |
| Stable | ||
| Stable | ||
| Stable | ||
| Unstable | Singular solution | |
| Stable | ||
| Stable | ||
| Stable | ||
| Unstable | Singular solution | |
| Unstable | Singular solution | |
| Stable | ||
| Stable |
| Solution | Type of Solution | Values of Variables |
|---|---|---|
| MS | ||
| MS | ||
| M-shape | . | |
| Interactional solution | . | |
| Interactional solution | . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Seadawy, A.R.; Rizvi, S.T.R.; Raza, U. Multi-Peak and Propagation Behavior of M-Shape Solitons in (2 + 1)-Dimensional Integrable Schwarz-Korteweg-de Vries Problem. Fractal Fract. 2023, 7, 709. https://doi.org/10.3390/fractalfract7100709
Ahmed S, Seadawy AR, Rizvi STR, Raza U. Multi-Peak and Propagation Behavior of M-Shape Solitons in (2 + 1)-Dimensional Integrable Schwarz-Korteweg-de Vries Problem. Fractal and Fractional. 2023; 7(10):709. https://doi.org/10.3390/fractalfract7100709
Chicago/Turabian StyleAhmed, Sarfaraz, Aly R. Seadawy, Syed T. R. Rizvi, and Umar Raza. 2023. "Multi-Peak and Propagation Behavior of M-Shape Solitons in (2 + 1)-Dimensional Integrable Schwarz-Korteweg-de Vries Problem" Fractal and Fractional 7, no. 10: 709. https://doi.org/10.3390/fractalfract7100709
APA StyleAhmed, S., Seadawy, A. R., Rizvi, S. T. R., & Raza, U. (2023). Multi-Peak and Propagation Behavior of M-Shape Solitons in (2 + 1)-Dimensional Integrable Schwarz-Korteweg-de Vries Problem. Fractal and Fractional, 7(10), 709. https://doi.org/10.3390/fractalfract7100709








