1. Introduction
The term “fractal” was proposed for the first time by Mandelbrot [
1], derived from the Latin root “fract” (lat. “Fractare”—break, fraction; “fractus”—dismembered, broken; English “fractal”—fractional). According to Mandelbrot’s definition, a set is denoted as ‘fractal’ if its Hausdorff–Besikovich dimension is strictly greater than its topological dimension. Simply put, a fractal set is a set of dimensions different from what is usually called a topological dimension, represented by a number as a whole. Mandelbrot [
1] also provided another definition: “a fractal is a structure made up of parts that resemble a whole in some way”. However, there is no strict and specific definition of a fractal today. A fractal structure is created by any infinitely repeating (iterating) initial shape, say H, in decreasing (or increasing) proportions, in a specific algorithm. This relatively simple feedback process provides a surprisingly diverse morphogenesis that often resembles the emergence of natural forms. Fractals are therefore characterized by self-similarity or large-scale invariance. Traditional geometric objects have integer dimensions: lines are one-dimensional, planes are two-dimensional, and spheres are three-dimensional. A fractal object is characterized by a fractal dimension. Such dimensions were introduced by F. Hausdorff. If a smooth Euclidean line just fills one-dimensional space, then the fractal line goes beyond it and partially fills two-dimensional space—its dimension is broken, and it lies between the original dimension of the line and the two-dimensional space of the fractal form Happened yes. The motivation of our research is presenting a new method for determining network fractality.
For example, fractal coastlines have dimensions between 1 and 2; fractal surfaces (mountains, clouds) have dimensions between 2 and 3. The fractal dimension [
2] is a topological invariant of every fractal structure, which is a special symmetry. So, as mentioned earlier, fractal lines go beyond one-dimensional space into two-dimensional space. Their dimensions are broken, and lie between the original dimension of lines and the two-dimensional space of morphogenesis—fractal genesis. Likewise, fractal planes extend partially into three-dimensional space; theoretically, we also believe that the output of a three-dimensional surface is the result of its fractalization into higher-dimensional spaces. For example, coastlines and many other natural structures and processes are fractal (or, more accurately, quasi-fractal): rivers and their tributaries, lightning, mountain surfaces, cloud cover, the distribution of galaxies, solar activity. The natural landscape around us is created by the dynamic chaos of natural processes. The fractal properties of natural objects demonstrate the ability to construct very realistic computer landscapes, virtual worlds, in relatively simple fractal programs, where the resemblance to reality is achieved through randomization and a certain degree of irregularity achieved through random number management. However, fractals can also be indistinguishable, such as scaly, granular, fibrous fractals, etc. The self-similarity of fractal structures as a result of functional iteration with reverse communication (self-referential feedback) determines near (local) connections to distant (global) orders and enables concise mathematical descriptions of structures and processes. These structures and processes are hardly suitable for mathematical description and mathematical understanding. Simple mathematical rules generate self-similar structures with respect to nonlinear transformations, thus enabling fairly complex shapes. This means that simple laws are at the very heart of complex systems and processes. The application of fractal structures in the field of mechanical engineering is most developed in fractal systems. Brittle iron is relatively weak, Mandelbrot also said. Fractal geometry has been successfully used for the detailed analysis of various mechanical properties of materials such as molybdenum, stone, concrete, steel, and composite materials of various lengths. The values obtained from the analyzed fracture sites confirm the concept of a global fracture measurement, independent of the fracture analysis obtained by scientific researchers for this type of material. This approach also facilitates product integration.
Robot laser hardening (RLH) belongs to the group of modern and highly effective methods for hardening the surface layers of materials [
3]. Thermal hardening of metals and alloys occurs locally when a portion of the radiation surface is heated followed by the fast cooling of this surface portion due to the removal of heat to the internal cold metal layers. Important advantages of laser hardening also include the reduction in the additional processing of the material, the eliminated need for a separate cooling process, and the ability to process inhomogeneous 3D blanks and complex geometries. Robot systems that provide not only heat treatment, but also positioning, the automatic feeding of workpieces, results measurement, etc., are becoming more relevant. The complex control system analyzes this data stream in real-time and, if necessary, corrects the parameters of laser radiation. This is important in the conditions of practical work when the workpiece warms up in the process of heat hardening. If the radiation power is not proportionally adjusted, overheating will occur, causing deterioration in the results of the heat-hardening process. The control system provides automatic calibration in the framework of the service tasks and makes appropriate corrections in the technological operations performed.
Heat-treatment processes, including the hardening and tempering of tool steels to achieve a desired microstructure with improved mechanical properties, is one of the last production steps which determines the final bulk residual stresses within the workpiece [
4]. Babič et al. [
5] presented a procedure based on the calculation of the FD complexity index. It was developed to assess the complex geometry of RLH materials’ microstructures upon changing the process parameters, and the obtained results were in agreement with experimental data.
Modeling of thermo-mechanical–metallurgical interactions during heat treatment is quite important in order to predict the evolution of internal stresses and distortions as a consequence of the process [
6].
Babič et al. [
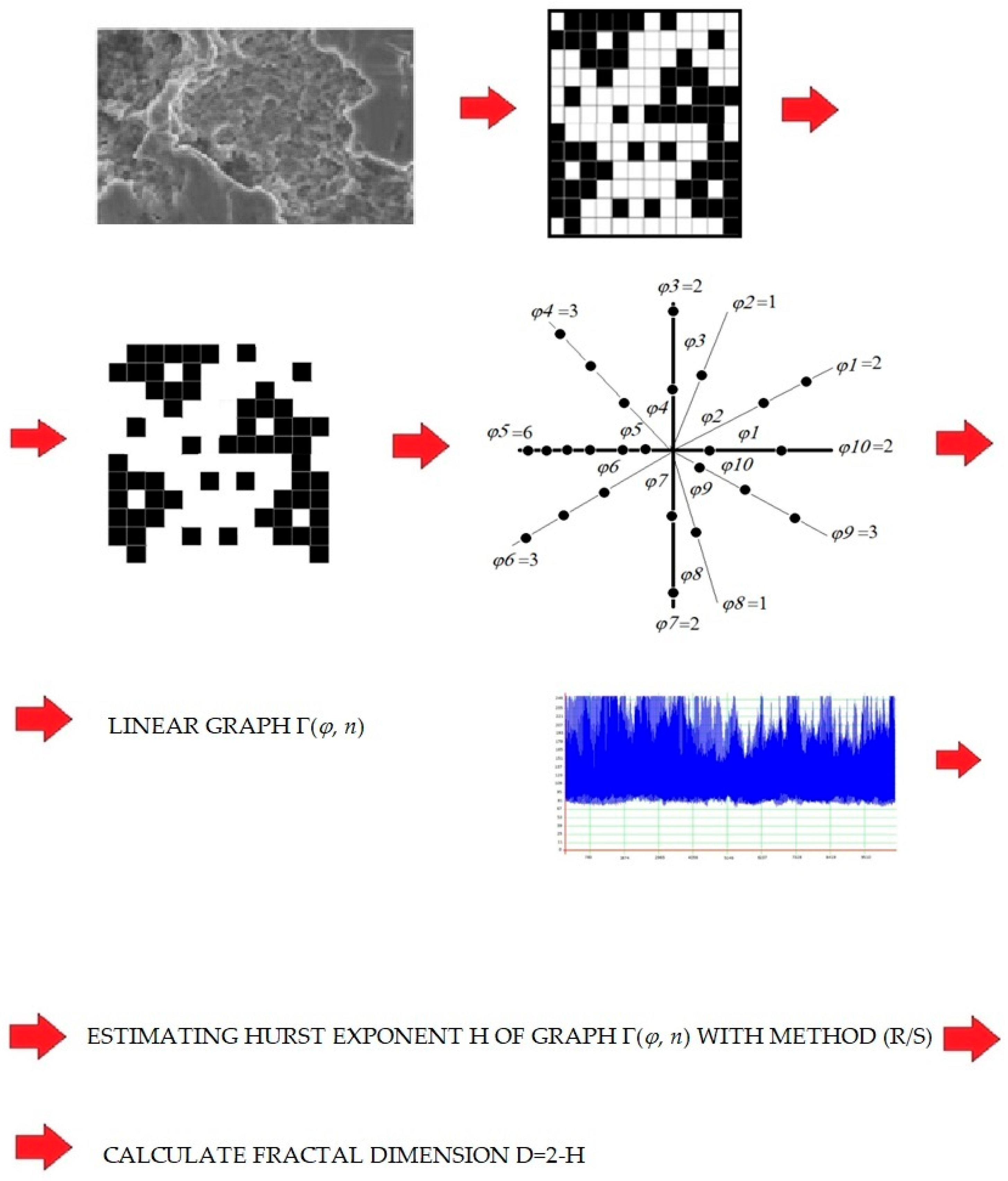
7] introduced a new method for quantifying the complexity of networks based on the network nodes given in Cartesian coordinates. The nodes were mapped to polar coordinates, and fractal dimensions were computed using the ReScaled Ranged (R/S) method. This work revealed various challenges, thus calling for further research in this field.
The aim of this manuscript is to propose a new approach to determining network fractality, with an application to robot-laser-hardened surfaces of materials, and to modeling the fractal networks of RLH specimens’ microstructures depending on the process parameters of the robot laser cell.
Section 2 presents the preparation of materials, methodology and data mining, and
Section 3 gives the results and discussion, while conclusions are given in the last section.
3. Results, Discussion, GP and CNN Approach
In
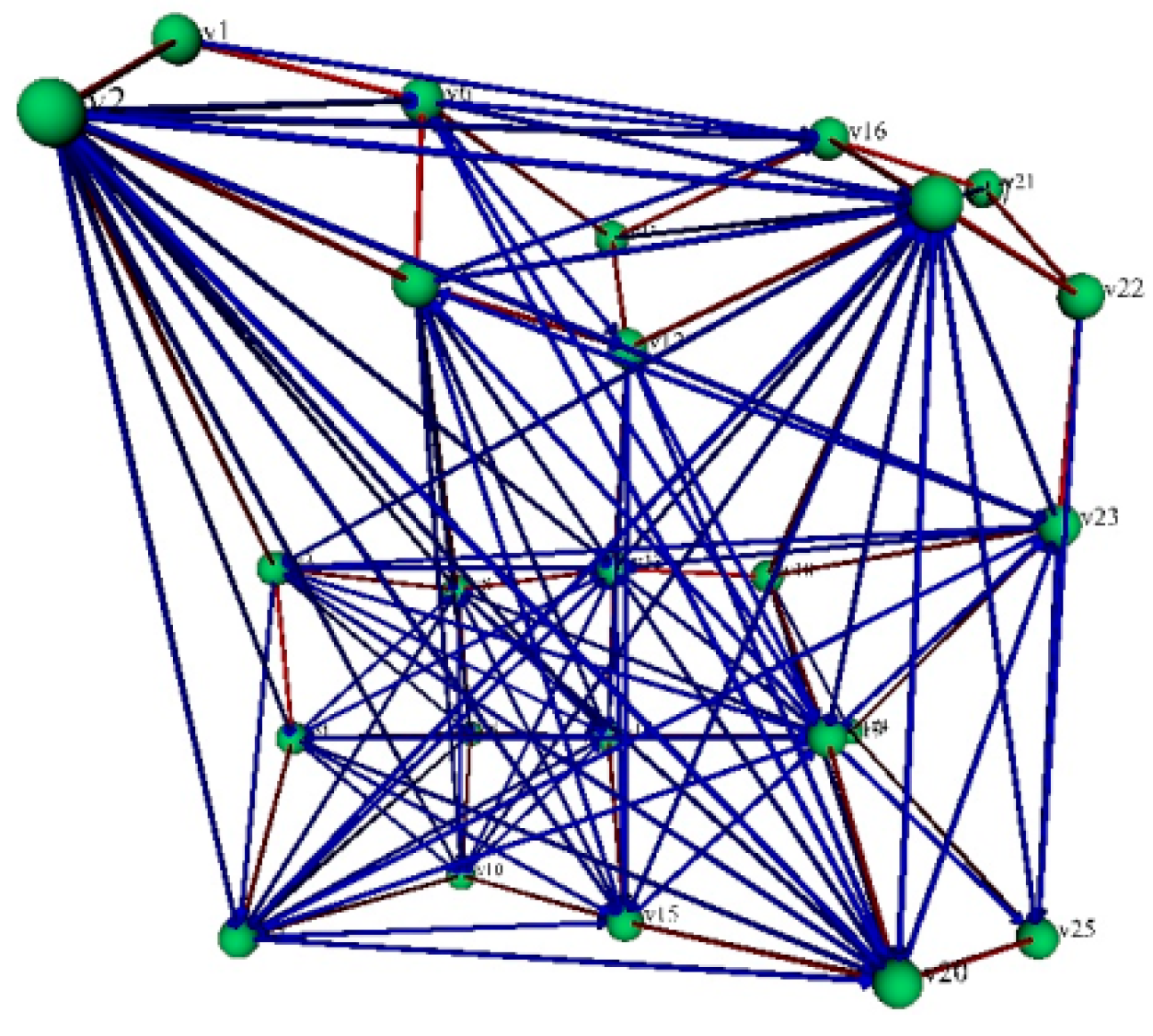
Table 2, the parameters and the network fractality of RLH specimens are presented. We mark specimens from S1 to S22. The parameter X1 represents the temperature [°C], X2 is the speed of hardening (mm/s), X3 is the angle (°) of hardening, X4 is the number of nodes of the fractal network and Y represents the network fractality of the RLH specimens. S1–S4 are the specimens hardened using the process presented in
Figure 1. Specimens S5–S8 represent the material next to the hardened zone. S9–S11 represent the results of the robot laser hardening under the following conditions: the variation in the angle φ ∈ (45, 60, 75)° between the left side of the laser beam and the material surface. S12–S14 represent the results of the robot laser hardening under these conditions: the variation in the incidence angle φ ∈ (45, 60, 75)° between the right side of the laser beam and the material surface. S15–S17 represent the results of the robot laser hardening under another set of conditions: the angle was changed in the plane defined by the direction of the laser beam φ ∈ [45°, 60°, 75°]. S18–S20 represent the results of robot laser hardening under the final set of variable conditions: the angle was changed in the plane perpendicular to the direction of the laser beam φ ∈ [105°, 120°, 135°]. S21 represents the results of the point-robot-laser-hardened specimens. Finally, specimen S22 represents the material before using the process of hardening.
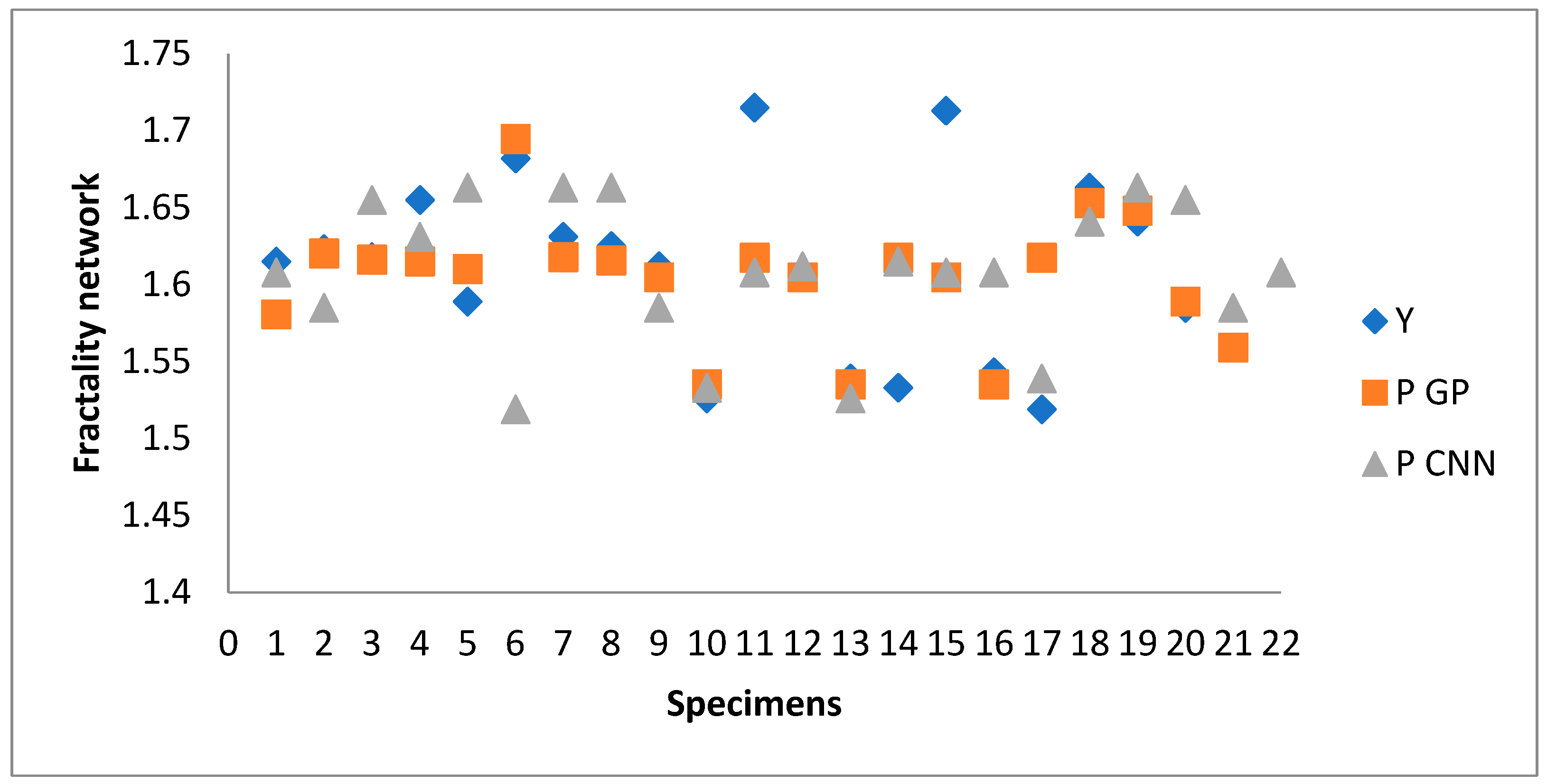
Table 3 gives the measured and predicted network fractality of RLH specimens, while
Figure 8 gives the predicted network fractality of RLH specimens by using GP and CNN.
The laser heat treatment technique for robots is straightforward, but this study reveals that the evolution of the microstructure during the laser-hardening process is an important aspect that needs to be addressed. It shows that the changing laser beam angles affect the intricate networks that make up the microstructure of specimens that were laser-hardened by means of robots. The proposed technique allows identifying the complicated network structure discovered in the microstructure of laser-hardened specimens at various angles. The maximum complexity specification is obtained for specimen S11: 1.715. This specimen was hardened at a rate of 4 mm/s at 1000 °C with the variation in the incidence angle φ ∈ 75° between the left side of the laser beam and the material surface. The minimal complexity was observed for the specimen S22, which represents the material before the robot-laser-hardening process. Hence, the complexity of the microstructure of the robot-laser-hardened specimens indicates how the heat treatment of a material alters its microstructure’s geometry.
Furthermore, the network complexity of microstructural materials hardened at various speeds, temperatures, and laser beam angles is modeled using genetic programming (GP). The measured data and the genetic programming model data yield a high agreement of 98.4%. As a result, the complexity network parameter X3 (angle) has a greater effect on the model. In order to create 100 different predictions based on the various parameters employed in the robot laser cell, the internal GP system was executed 100 times. On an I7 Intel processor (Intel Corporation, Santa Clara, CA, USA) with 8 GB of RAM, each run lasted roughly 2.5 h. Using an internal genetic programming system written in AutoLISP and connected with AutoCAD (v24.2), we used 100 separate models for forecasting network fractality of RLH specimens. The mean square of errors from the monitored data was used to measure the model’s fitness. It is given by
where
i is the square of the error of a single sample of data, and
n is the size of the monitored data.
Simply put, an individual organism’s single sample data variance is
where Ei and Gi are the projected and actual scrap fractions, respectively, and they only depend on the surface flaws.
The developed optimal model of genetic programming is given as follows:
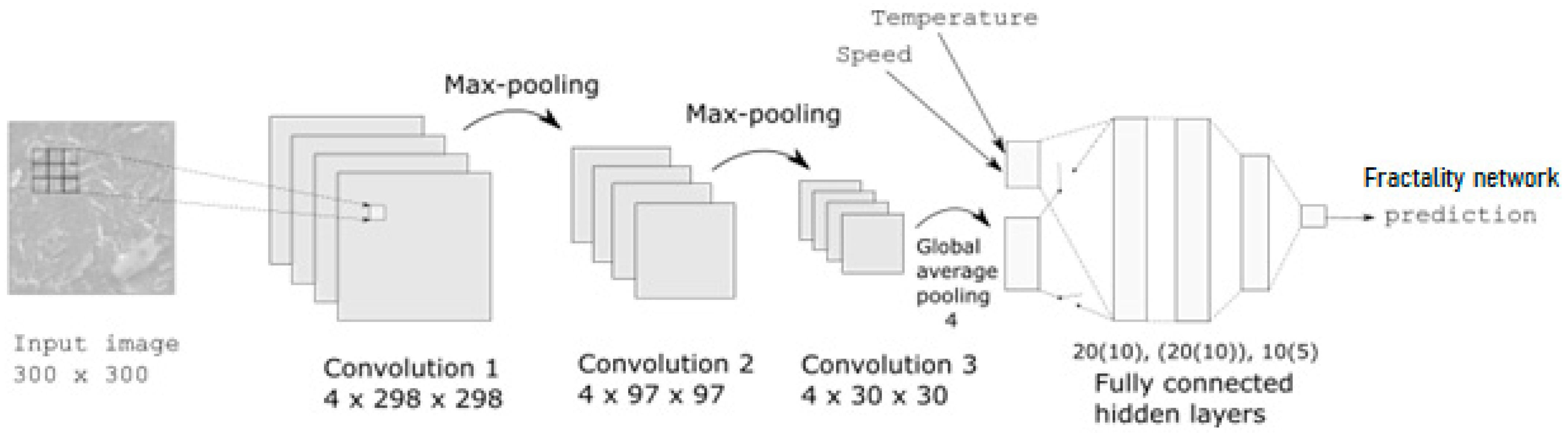
The specimen photos were reduced to a standard of 300 × 300 pixels. There was just one channel needed because they were given as grayscale. The values were scaled from the [0, 255] interval to the [0, 1] interval. To reduce the image size further, a two-dimensional max-pooling (3 × 3) layer was applied after a two-dimensional convolution layer with a filter size of 3 × 3 and four kernels. The 2D conv-layer and max-poling combination were used once more to obtain more compression. The third convolutional layer and an average pooling layer, whose output was flattened so that it could be combined with the non-image data, were then applied.
Figure 9 presents the microstructure of one example of 22 specimens characterized by speed treatments of 2 mm/s (S1), 3 mm/s (S2), 4 mm/s (S3), and 5 mm/s (S4) at 1000 °C.
The RMSprop learning method was used to train the CNNs over 1200 iterations at a learning rate of 0.001 error in the mean square (MSE). Both examined cases, those without photographs and those with images, had their mean squared error (MSE) recorded. Eight training configurations were tested for each setting, including two and three hidden layers, two different layer sizes (i.e., the number of artificial neurons), and two different activation modes for the neurons (sigmoid vs. relu). The output neuron’s activation function was always sigmoid, and it was utilized to predict the surface roughness.
Table 4 represents the findings. The average of 10 runs, along with the standard deviation, is the outcome for each round of training. For each parameter set (speed, temperature), two of the three photos were utilized for training, and the third one was used for testing. Therefore, we also have test results in the “image” setting. Because testing would produce identical results for the training in the “no-image” mode, only the training’s findings are provided. The bold numbers in
Table 4 are the best results obtained by means of CNN. The CNN model delivers a precision of 96.5%.
4. Conclusions
With the aim of analyzing the invariance property of the network fractality of real microstructure images (and fractography), it was necessary to develop a new method for determining the object complexity that can be seen in the microstructures of RLH specimens. In order to predict the complexity of robot-laser-hardened specimens, we applied an AI method, namely genetic programming. The genetic programming delivered an accuracy of above 98%.
The highest complexity specification was found for the specimen S11: 1.715. This specimen was hardened at a rate of 4 mm/s, at 1000 °C, with the variation in the incidence angle of φ ∈ 75° between the left side of the laser beam and the material surface. The minimal network fractality was found in the specimen before the RLH process. Finally, because the microstructure of RLH specimens is very chaotic and complex, it is clear that for the use of fractal-based analysis for the evaluation of the microstructure of RLH materials, careful calibrations are required to develop a technological tool for real-life application. There are a number of aspects that remain to be investigated to obtain a complete understanding of the fractal behavior of microstructures of RLH specimens using images and in order to implement its application for the evaluation of materials.
Furthermore, we successfully applied a convolutional neural network (CNN) to predict the surface roughness also using the photos of the materials’ surfaces. The mean squared error was in the range from 0.021 ± 0.002 to 0.015 ± 0.001 when images were also used. A t-test was applied to compare the means, yielding t = 0.023/0.017 = 1.35 at 16 degrees of freedom. This implies that the p-value is equal to 0.18. Hence, the prediction using images noticeably improved compared to the case when images were not used. The CNN model delivered a precision of 96.5%.
Making sprockets extremely hard throughout the hardening process is a very significant issue. In this study, we described a novel technique for hardening materials under various laser beam angles using a robot laser cell to address the issue of sprocket hardening (the idea of two laser-beam RLH). We split the laser beam into two parts using a prism. In the future, we intend to investigate the effects of different laser beam angles and characteristics on the topography of various materials using two laser beams for RLH.
An important advantage of the proposed method is its applicability in a wide range of fields such as in medicine, in the analysis of biochemical interactions, in the analysis of biomedical images in technical science, in the analysis of the influence of process parameters on a material’s mechanical properties, and even in social sciences. Of course, until more knowledge is acquired about its application in various fields, the method is to be used with special care.