1. Introduction
The exploration of solitary waves and solitons has been always at the forefront of modern nonlinear science topics. They have been gradually applied to various fields of natural science [
1,
2,
3,
4,
5,
6]. Research shows that most nonlinear physical phenomena can be expressed as corresponding mathematical models under specific approximate conditions and finally simplified as nonlinear evolution equations (NLEEs) varying with time and space. Thus, how to find the exact solutions of NLEEs using analytical and numerical methods is of great physical and practical value for understanding their characteristics and supplying wave parameter data and their applications. It is very important to construct exact solutions for various nonlinear models in the interdisciplinarity of mathematics and physics and to understand the exact solutions of NLEEs for finding out the dynamic mechanisms and their processes in different fields of scientific research. Through these exact solutions, we can understand the composition and propagation of various complex nonlinear wave phenomena from the perspective of physical images, such as the shape of waves, the appearance of peaking states, the steady state, instability or coexistence under certain conditions, and the space–time positioning of the propagation process.
Since NLEEs are widely used in natural science and their solutions can clarify the dynamic behavior of complex nonlinear phenomena, it is necessary to analyze and study them with effective and powerful methods. In recent years, remarkable advances have been made in solving nonlinear equations. Many strong and effective methods have been developed, and abundant solutions have been obtained, for example, the F-expansion method in Refs. [
7,
8], the tanh-sech method and its extension in Refs. [
9,
10,
11], the Jacobi elliptic function method in Refs. [
12,
13], the auxiliary equation method in Refs. [
14,
15,
16,
17,
18], the (G′/G)-expansion method and its extension in Refs. [
19,
20,
21,
22], and so on. These methods can construct a large number of exact solutions when dealing with some types of NLEEs. However, there are still many problems to be solved, such as developing a universal and simple method to construct complex and diverse exact analytical solutions. Theoretically, NLEEs have infinite solutions. In Refs. [
23,
24], a Bäcklund transformation is used to construct new infinite-series soliton-like solutions of NLEEs. For this kind of method, the auxiliary equation is the key to construct infinite-series solutions of NLEEs. An optimal auxiliary equation can greatly simplify the solving progress of NLEEs and can also provide various complex and diverse infinite-series exact solutions.
Because of its simple structure, the Riccati equation is an ideal auxiliary equation, which can greatly simplify the solving process, so it has a very wide range of applications for solving NLEEs. In the present work, we propose a new method to construct infinite-series solutions of NLEEs using the Riccati equation as an auxiliary equation. After the Riccati equation is treated in this way, we obtain many new infinite-series solutions. Then, as an application, this method is used to deal with the standard KDV equation, i.e.,
which is one of the most well-known models in fluid physics [
25] and in plasmas [
26], where
u(
x,
t) is a real differential wave function depending on one-dimensional space variable
x and one-dimensional time variable
t. It is a kind of one-way shallow-water wave partial differential equation discovered when studying small-amplitude long-wave motion in shallow water. It is also the first equation used to study soliton phenomena. Several methods have been proposed to solve this equation and KDV-type equations, for example, the tanh function method [
27,
28], the variable separation method [
29,
30], the simplified Hirota method [
31], the homotopy perturbation method [
32], and some other methods [
33,
34,
35]. In these literature works, different types of KDV equations have been studied, and many new exact solutions and solitary wave structures have been obtained. Although these methods, including those described above, are very effective in solving the KDV equation and KDV-type equations, under certain conditions, the structure of the solution of the KDV equation has some commonness with the Benjamin equation [
36], the Boussinesq equation [
37], the Benjamin–Bona–Mahony (BBM) equation [
38], the (2 + 1)-dimensional KDV equation [
39], the asymmetrical Nizhnik–Novikov–Veselov (aNNV) system [
40], etc. Therefore, the exploration of new exact solutions and complex wave phenomena of the KDV equation is not only important for understanding the dynamic behavior of the KDV equation, but it also provides reference for solving the above equations and analyzing their dynamic behavior. At the same time, it also provides some ideas for solving other NLEEs. The method we use in this paper, that is, the construction of solutions by squaring infinitely and extracting the square root infinitely, is a new method that has not been previously reported in other literature studies. It is also quite different from the above Bäcklund transformation method for constructing infinite-series solutions. After the KDV equation is treated using this method, many new forms of exact solutions and solitary wave structures are obtained.
The manuscript is organized in the following way: In
Section 2, the new infinite-series exact solutions of the Riccati equation are constructed, which gives abundant hyperbolic function solutions. This part is the theoretic basis of this paper. In
Section 3, the main steps of the scheme are described in detail. As an application, this method is used to solve the KDV equation to prove the wider applicability of handling NLEEs with a simplified process. Finally, the conclusion and discussion are given in
Section 4.
2. Construction of Infinite-Series Solitary Wave Solutions
To construct new infinite-series exact solitary wave solutions for NLEEs, the following form of a 0-order auxiliary equation is introduced:
where
p0 and
q0 are constants that can be obtained later. It is obvious that Equation (1) has the following solutions:
Next, we introduce the 1-order equation of Equation (2), which satisfies the following relationship:
where
p1 and
q1 are constants that can be obtained later. We first assume that 1-order Equation (6) and 0-order Equation (2) have the following relationship:
where
a0 is a constant. We substitute Equation (7) into Equation (6) and use Equation (2) to obtain
These equations were solved using MATLAB 2014a and 2021b software (so were the following; these software applications were used to plot all the figures and check all the results), obtaining the following results:
,
, and
. Then, we can obtain
For the second case, we adopt the following transformation:
where
a0 is a constant. We substitute Equation (12) into Equation (6) and use Equation (2) to obtain
By solving them, we can obtain
,
, and
. Then, we can obtain
Next, we introduce the
n-order equation of Equation (2), which satisfies the following relationship:
Moreover, it satisfies the following relations with the (
n − 1)-order equation:
According to Equations (6)–(8), (12) and (13), we can obtain the following infinite-series hyperbolic function solutions:
To simplify the process as much as possible, we choose the following simple Riccati equation [
17,
41,
42,
43]:
To find the new infinite-series hyperbolic function solutions, it is assumed that Equation (22) has the solution in the following transformation:
where
r,
k0, and
k1 are constants to be determined; and
. By substituting Equation (23) into Equation (22), using Equation (17), and then setting each coefficient of
(
) as zero, the following equations can be obtained:
By solving them, we can obtain
In
Case 1, when
, although
owing to
, the infinite-series hyperbolic function solutions of
are the same as those of
when
n > 1. So, in this case, we have new infinite-series hyperbolic function solutions in the following forms:
In
Case 2, the infinite-series hyperbolic function solutions of
are the same as Equation (27). So, in this case, we have new infinite-series hyperbolic function solutions in the following forms:
Next, we use the following formula transformation to solve Equation (28):
where
r,
k0, and
k1 are constants to be determined; and
. We substitute Equation (29) into Equation (22) and use Equation (17). The following equations can be obtained:
By solving them, we can obtain
So, we can obtain the following new infinite-series hyperbolic function solutions:
In
Case 2, because
the infinite-series hyperbolic function solutions of
and
are the same as Equation (28). Moreover, the infinite-series hyperbolic function solutions of
are also the same as Equation (33).
It is obvious that
also satisfies Equation (22) when
. Therefore, the following equations are also new infinite-series hyperbolic function solutions of Equation (22):
Compared with other published literature studies [
17,
41,
42,
43], the solutions of Equation (22) obtained are novel. In these infinite groups of solutions, except for a few low-
n-order solutions that have been reported in other literature studies, the rest are all our newly discovered solutions. Compared with Refs. [
23,
24], the infinite solutions in this paper are also quite different from those constructed using a Bäcklund transformation in the structure, especially the solutions obtained by extracting the square root infinitely.
3. Main Steps of the Scheme and Application
A (1 + 1)-dimensional nonlinear equation can be expressed as follows:
To find the exact solutions, we assume that Equation (40) has the following traveling wave transformation:
where
k and
c are pending wave parameters. The following ordinary differential equation can be obtained by substituting the above formula into Equation (40):
where
represents
. We assume that the solution of Equation (42) satisfies the following form:
where
are constants,
is the solution of Equation (22). and
n can be obtained using the homogeneous balance. In the present method, the predetermined complex formal solution can be put in the solving process of Riccati Equation (22), because its solving process is relatively much simpler. Following this procedure is of great benefit. First, it can greatly simplify the solving process of NLEEs. Second, many complex solutions are actually the same group of solutions after simplification. However, the simplification process is extremely complicated, and we can exclude the same solutions to the maximum extent by doing so.
In the following, we deal with Equation (1) using of this method. The traveling wave of Equation (41) is substituted into Equation (1) and integrated once, and the constant obtained using integration is zero. We can obtain
Considering the homogeneous balance, the solutions of Equation (44) can be shown as
Equation (45) is then iterated into Equation (44), and a set of algebraic equations is generated for
,
,
,
k, and
c. We collect all terms with the identical power of
and set each coefficient equal to zero. Finally, we can obtain
By solving the algebraic equations,
,
,
,
k, and
c can be shown as follows:
The parameters given in Equation (47) are consistent with the corresponding solutions of the KDV equation in Refs. [
28,
44]. The solutions obtained using the method in this paper include some existing solutions, and on this basis, they are extended to an infinite number of solutions in different ways. Thus, the new infinite-series solitary wave solutions of Equation (44) can be expressed as follows:
where
In this set of infinite solutions, owing to
, these two cases represent the same infinite-series solutions when
. Owing to
and
,
and
, so
does not converge. In fact, because there are some negative components in the denominator of
, even if the
n-order is not high enough,
tends to infinity in a small space–time range. This means that stable solitary wave structures only exist in those solutions with lower
n-order values. Since
includes so many solutions of the KDV equation, due to space limitation, we only give examples of solitary wave solutions when
and discard the imaginary number solutions. These four groups of solutions are as follows:
where
This set of solutions is consistent with one of solutions in Equation (31) of the KDV equation in Reference [
27].
where
If
, this set of solutions is consistent with Equation (29) in Reference [
28], while if
, it is consistent with Equation (31) in Reference [
28].
where
This set of solutions is a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained.
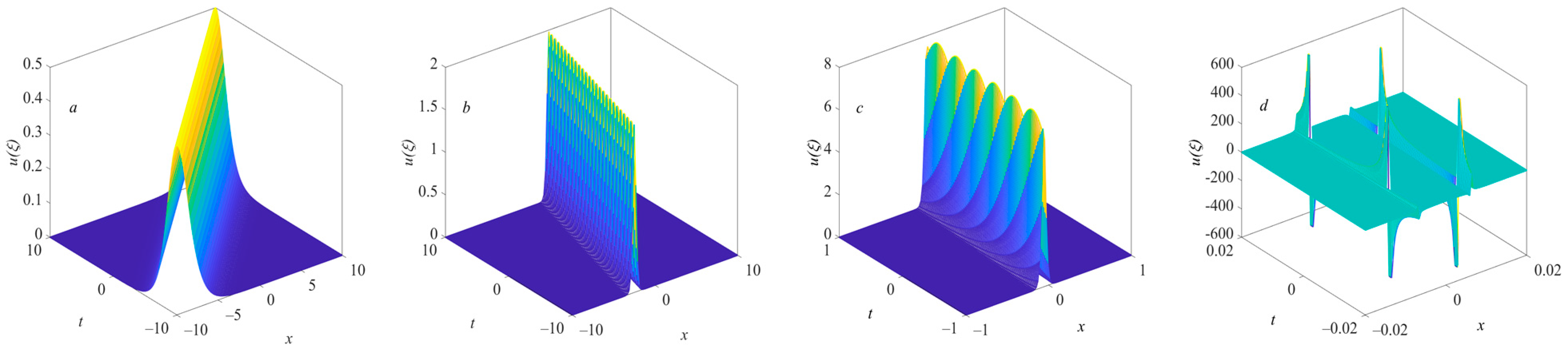
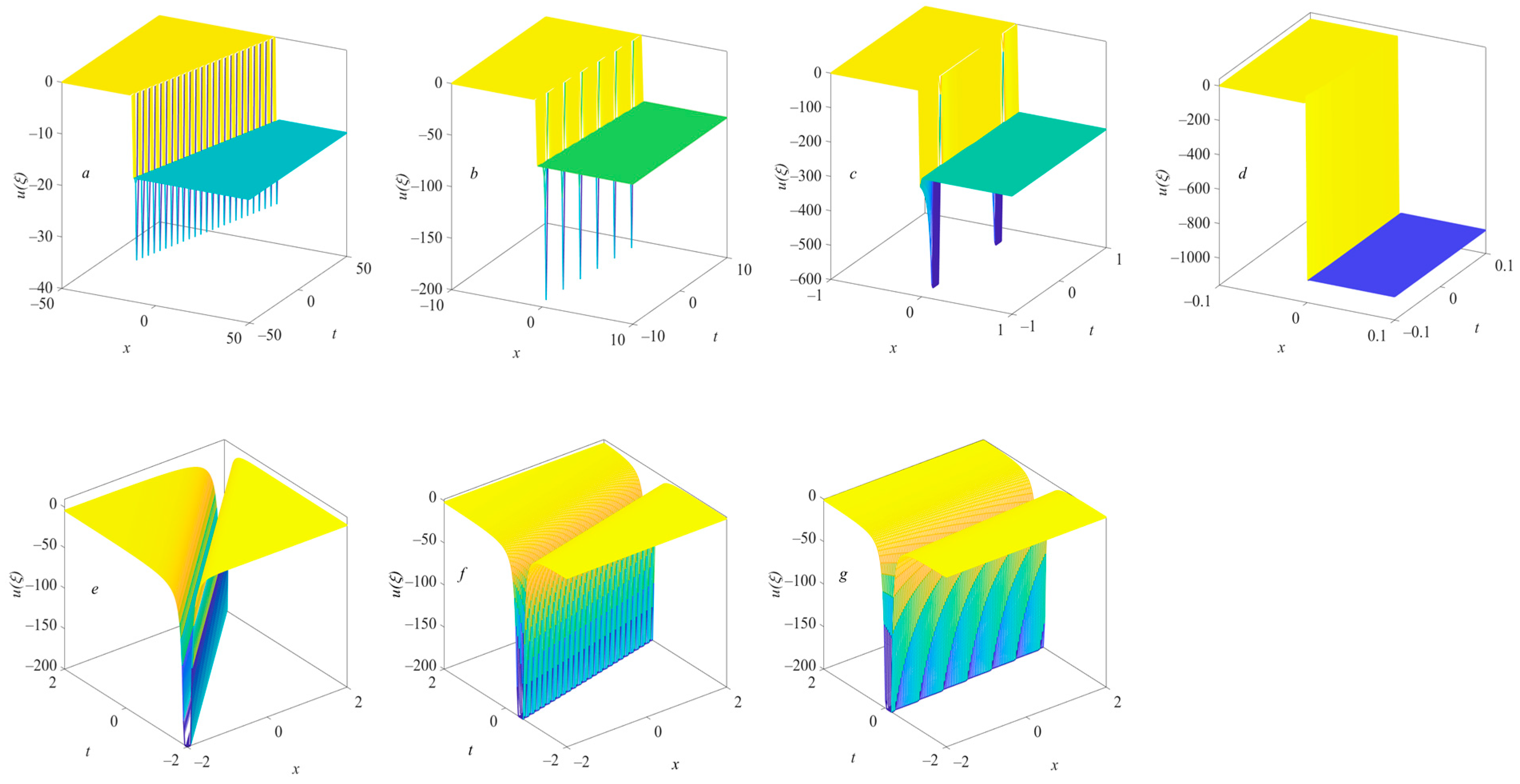
These four groups of solutions represent the bright solitary wave of the KDV equation (see
Figure 1). We apply a 3D plot to the image of function
changing with time and space, so that we can obtain the amplitude change of
for different space–time positions. From this, we can know the local wave structure of each solution and its evolution over time. The increase in
n in
increases the amplitude of the solitary wave and decreases the bandwidth in space–time. When
, there are two rows of singularities in a very small space–time region. It can be seen that, in this case, stable solitary wave structures only exist for
n = 1, 2, 3. When
n > 3, solitary waves become unstable.
where
This set of solutions contains a large number of integral, fractional, and irrational solitary wave solutions, which are determined by different values of
k,
λ,
ν,
n,
ε, and
r. If
, and
n = 1, this set of solutions is consistent with Equation (24) in Ref. [
44]. Under other conditions, it is the new solution we found for the first time. When
,
. When
,
changes slowly in a large space–time region. If
or
,
can tend to infinity in a certain space–time range. Therefore, stable solitary wave structures also only exist in some special solutions with lower
n-order values.
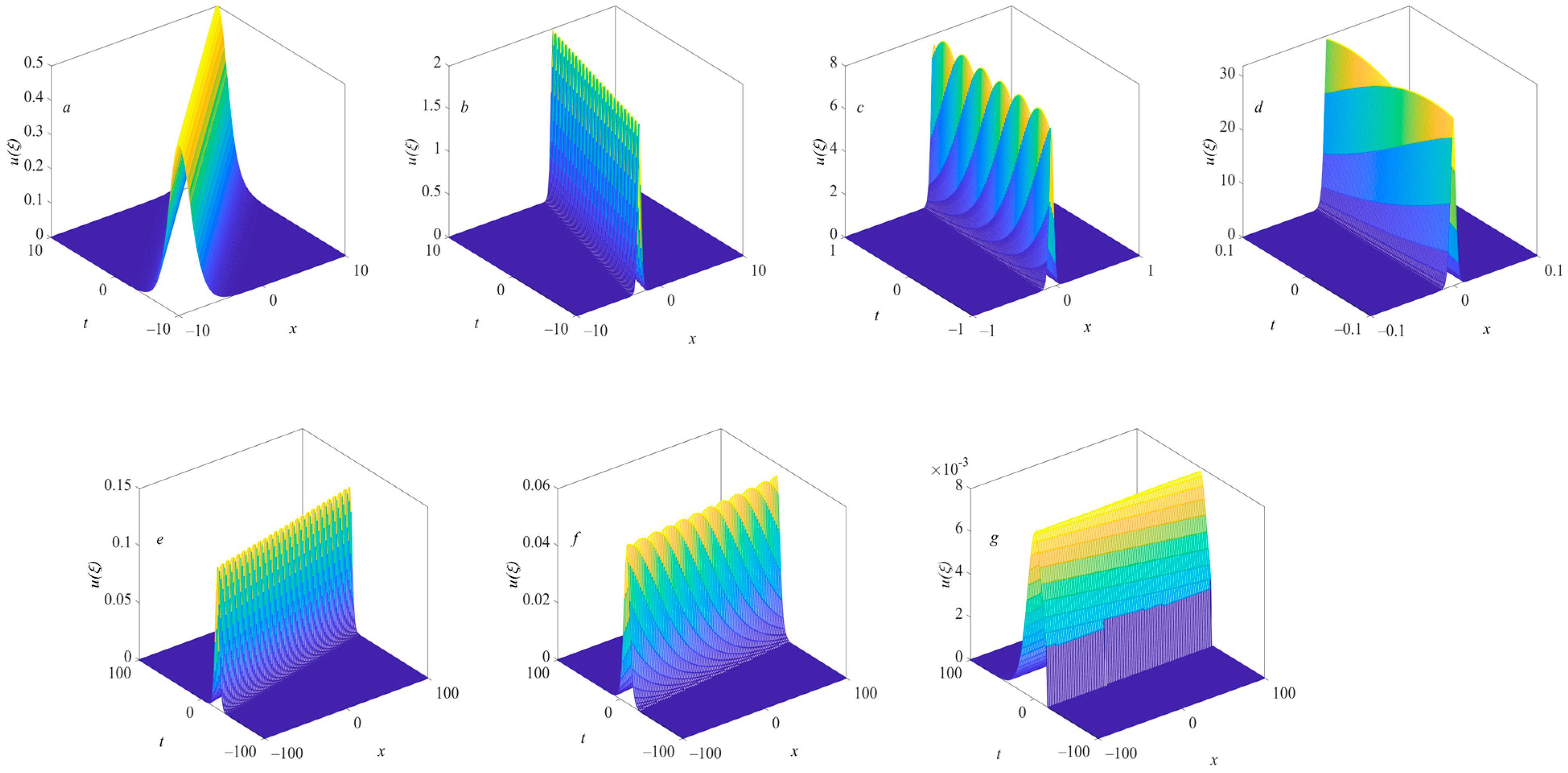
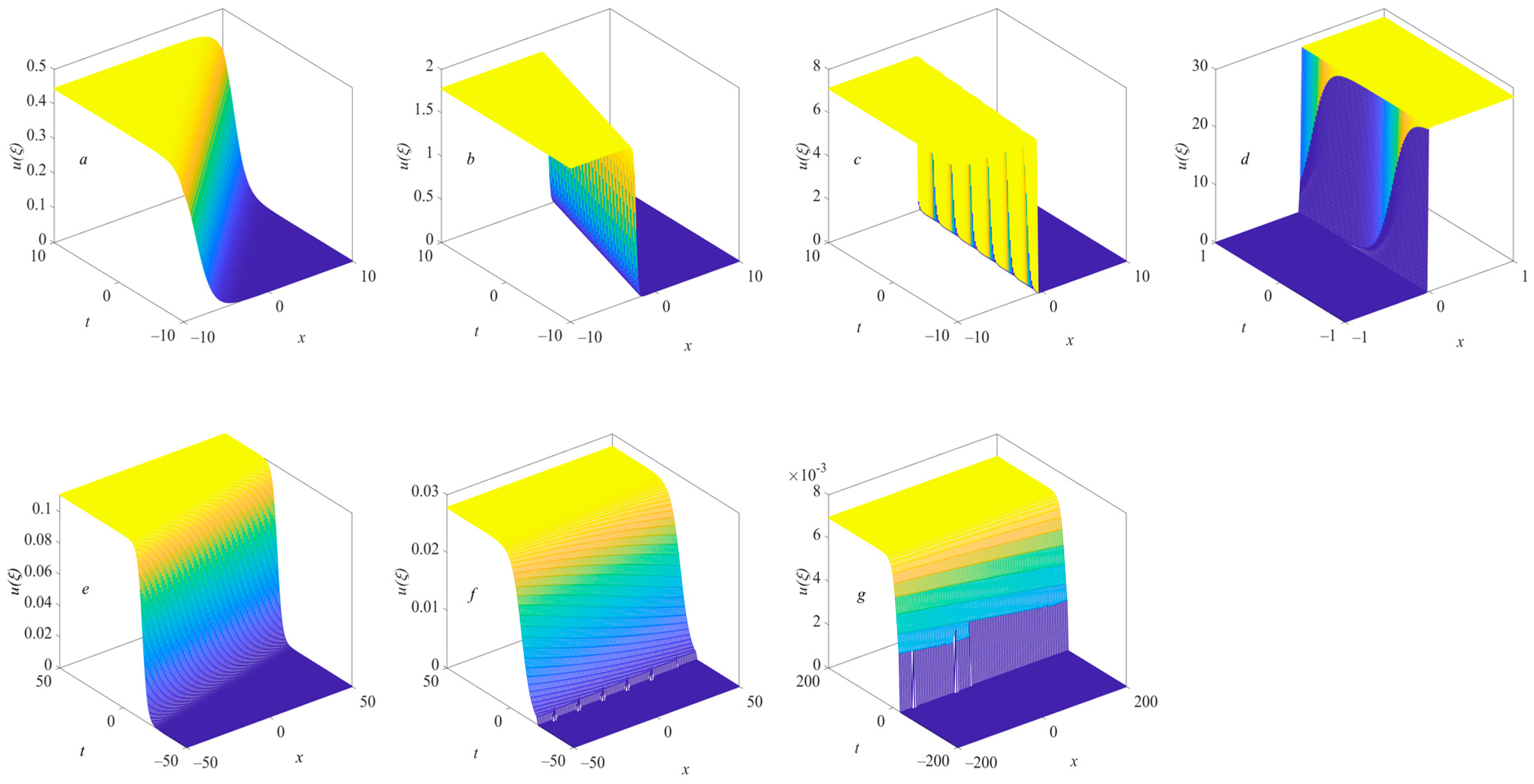
Figure 2 shows the images of bright solitary waves changing with
n when
. Under these conditions, the amplitude of the bright solitary wave increases with the increase in
n, while the bandwidth in space–time is the opposite. It can be seen that in this case, the solitary wave structure is relatively stable under low-
n conditions, but under very-high-
n conditions,
increases sharply in a small space–time range and becomes unstable.
where
This is a set of infinite-series solutions obtained by extracting the square root infinitely. Owing to
and
,
and
, so
with high-
n-order values can change slowly in a large space–time region. Since the solutions corresponding to
belong to the imaginary number range, we only give the examples corresponding to
. The solitary wave solutions of the four groups of examples are as follows:
where
This set of solutions is the same as Equation (49).
where
This set of solutions is a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained.
where
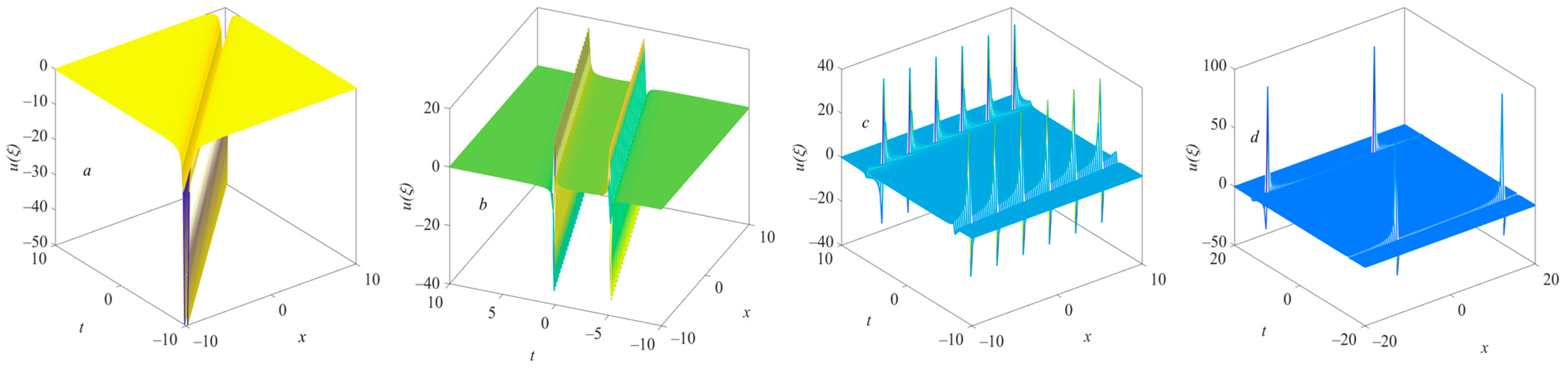
This set of solutions is also a new one of the KDV equation that we obtained. The solitary wave evolution images corresponding to these four groups of solutions are shown in
Figure 3, which represents the bright solitary wave solutions of the KDV equation. In this set of infinite-series solutions, it can be seen that the larger the square root number is, the smaller the amplitude of the corresponding bright solitary wave is, and the larger the space–time width is. In this case, all the solitary waves have relatively stable structures.
where
In this set of infinite-series solutions, although
, owing to being zero at the denominator for some values,
has singularities in some space–time positions. In this case, these four groups of examples are shown as follows:
where
This set of solutions is consistent with Equation (31) in Ref. [
28].
where
This set of solutions is a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained. The solitary wave evolution images corresponding to these four groups of solutions are shown in
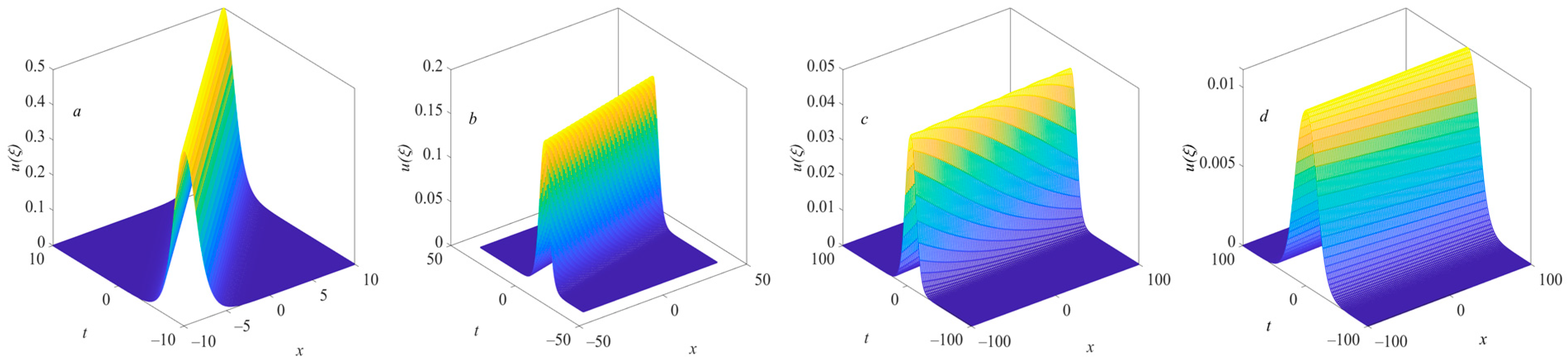
Figure 4, which represents the dark solitary wave solutions of the KDV equation. Furthermore, the space–time width of the solitary wave decreases with the increase in
n. However, because
under certain conditions, this set of infinite solutions has singularities in some specific space–time positions, which makes the solitary wave structure unstable.
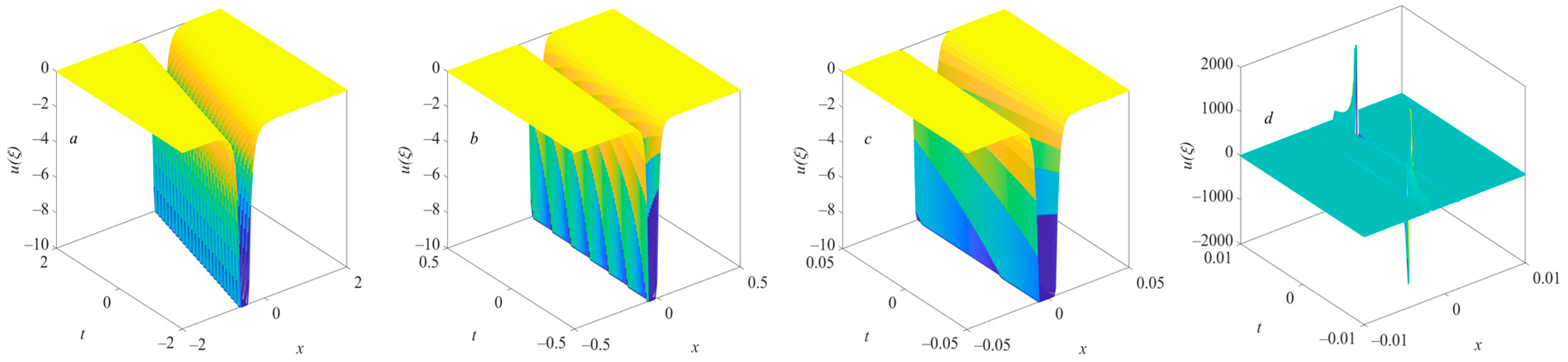
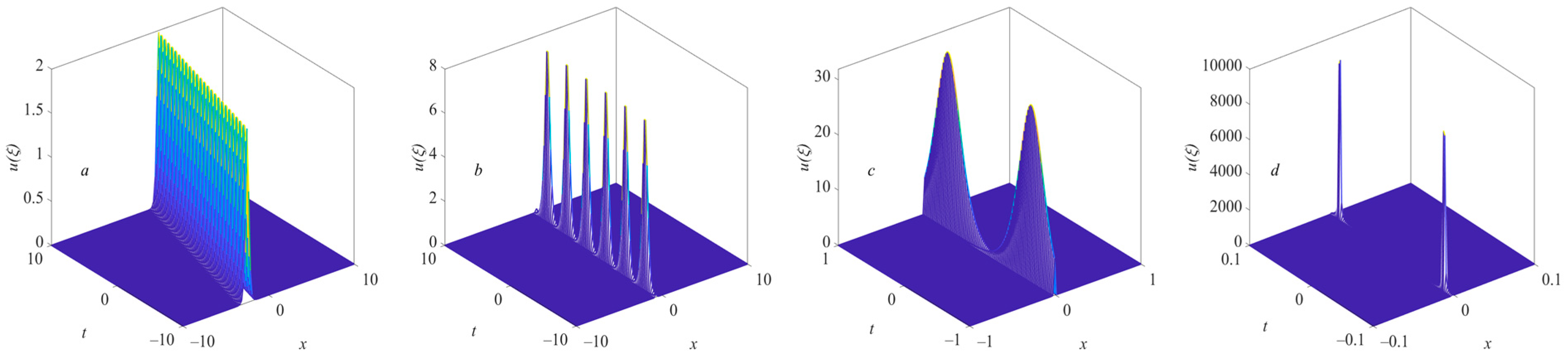
where
. This set of solutions is a new one of the KDV equation that we obtained. It does not converge when
. However, the different values of
and
can make
have singularities in some space–time positions. This set of solutions represents an anti-kink-type solitary wave with many singular points when
, as shown in
Figure 5. When
n increases, the amplitude of the solitary wave increases, while the bandwidth in space–time decreases. These solutions all have relatively stable solitary wave structures. When 0 <
n < 1, the solitary wave becomes a combined wave of an anti-kink solitary wave and a dark solitary wave with singularities. Then, the solitary wave becomes unstable near the singularities.
where
This set of solutions tends to infinity when
because
. In this case, these four groups of examples are shown as follows:
where
This set of solutions is consistent with Equation (20) in Reference [
27].
where
In this set of solutions, if
, it is consistent with Equation (35), and it is consistent with Equation (35) in Reference [
28], while if
, it is consistent with Equation (33) in Reference [
28].
where
This set of solutions is a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained. The solitary wave evolution images corresponding to these four groups of solutions are shown in
Figure 6, which represents the dark solitary wave solutions of the KDV equation. Owing to the existence of singularities, the solitary wave structure of each solution is completely unstable.
where
This set of solutions is a new one of the KDV equation that we obtained. In this set of solutions,
increases with
n until infinity. These solutions represent a kink-type solitary wave with many singular points when
, as shown in
Figure 7. Different values of
n can make the amplitude, space–time width, kink direction, and singularity position of the solitary wave different. In this case, all the solitary waves have relatively stable structures.
where
. In this set of solutions, although
, owing to being zero at the denominator for some values, many singularities could exist in some space–time positions. The solitary wave solutions of the four groups of examples are as follows:
where
This set of solutions is the same as Equation (66).
where
This set of solutions is a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained. The solitary wave evolution images of these four groups of solutions with
n are shown in
Figure 8. It can be seen that the value of
n can change the shape of the solitary wave and the space–time position of singular points.
represents a dark solitary wave. With the increase in
n, it gradually evolves into a traveling wave with two rows of singular points. So, the solitary wave structure becomes unstable under high-
n conditions.
where
As can be seen in Equation (76), the value of
increases with
n until infinity. In this set of solutions, the four groups of examples are as follows:
where
This set of solutions is consistent with Equation (29) in Reference [
28].
where
. This set of solutions is a new one of the KDV equation that we obtained.
where
. This set of solutions is also a new one of the KDV equation that we obtained.
where
This set of solutions is also a new one of the KDV equation that we obtained. The solitary wave evolution images corresponding to these four groups of solutions are shown in
Figure 9. In this case, the increase in
n reduces the space–time width of the solitary wave and changes the space–time position of the singularity.
represents a bright solitary wave. With the increase in
n, it gradually evolves into a traveling wave with many singular points. In this case, stable solitary wave structures only exist under low-
n conditions, while they become unstable under high-
n conditions.
where
. This set of solutions is also a new one of the KDV equation that we obtained. As shown in Equation (81),
, so stable solitary wave structures only exist in those solutions with lower
n-order values. This set of solutions represent a mixed type of solitary wave when
, as shown in
Figure 10. The change in
n can change the amplitude, space–time width, singularity position, and propagation direction of the solitary wave. In this case, under low-
n conditions, there are very stable mixed solitary wave structures, while under very-high-
n conditions, the wave structures become unstable.