Escape Criteria for Generating Fractals of Complex Functions Using DK-Iterative Scheme

Abstract

Fractals are essential in representing the natural environment due to their important characteristic of self similarity. The dynamical behavior of fractals mostly depends on escape criteria using different iterative techniques. In this article, we establish an escape criteria using DK-iteration as well as complex sine function $(sin\left(z^m\right)+c;m\ge 2,c\in \mathbb{C})$ and complex exponential function $(e^{z^m}+c;m\ge 2,c\in \mathbb{C})$. We use this to analyze the dynamical behavior of specific fractals namely Julia set and Mandelbrot set. This is achieved by generalizing the existing algorithms, which led to the visualization of beautiful fractals for $m=2,3$ and 4. Moreover, the image generation time in seconds using different values of input parameters is also computed.

1. Introduction

Fractals are common in nature because they adequately describe: tree branches, leaf patterns, lightning, electricity, clouds, crystals, rivers, and so on. Fractals play an important role in surveying or examining various natural or living frameworks, such as microorganism culture. Fractals are also used in liquid mechanics to determine and comprehend violent streams. Fractal geometries are important in the design of modern telecommunications systems, particularly antennas, for reasons such as smaller size, improved gain, and efficiency when operating in multi-frequency bands [1]. In addition, computational architectural design, radar frameworks, and engineering models fall into the areas in which fractal theory is widely used [2]. Cryptography [3], image compression [4], as well as encryption [5] are also common applications. Using these facts as inspiration, the authors establish an escape criteria for generating fractals of complex functions using the DK-iterative scheme. Thus, before presenting the findings of our research, it’s indeed necessary that we review and understand some fundamental terms in the subsequent paragraphs.

A fractal can be characterized as “a mathematical figure whose every point shows the same similarity as the entirety” or “an extremely irregular shape for which any appropriate focused part is like another larger or more modest part when amplified or diminished”. The word “fractal” is a Latin word that means broken or fractured. This terminology was first used by B. Mandelbrot [6] and later on he became famous as the “father of fractal geometry”. In the beginning of 20th century, P. Fatou and G. Julia tried to find the progressive estimate of $P:x⟶x^2+b$ where $x,b\in \mathbb{C}$ but they were unable to draw the graph of the proposed function. In 1985, B. Mandelbrot started work on this and successfully sketched the graph of complex function $f:x⟶x^2+b$. He defined Mandelbrot set by changing the values of complex parameter b and variable x [7]. M-sets for $P:x\to x^p+b$ where $p\ge 2$ and $x,b\in \mathbb{C}$ are elaborated in [8]. The images like J-set and M-set using rational and transcendental complex functions are discussed in [9]. Later on anti J-sets and anti M-sets were defined by Crow et al. [10], and they generated graphs of ${\overline{x}}^2+b$ where $x,b\in \mathbb{C},$ which are tri-corns.

Fixed point theory is playing an important role in the generation of fractals using different iterative schemes. For instance, implicit iterations with s-convexity are mainly discussed in [11,12,13,14,15]. Biological images and their characteristics are presented in [16,17,18,19]. Moreover, J-sets and M-sets of transcendental complex functions using diverse iterations are visualized by the authors of [20,21]. Fractals with high dimensions are elaborated in [22,23,24]. Specific fractals of general nature have been also created by applying diverse iterative techniques like Mann [25], Ishikawa [26], Noor [27], S and CR [28,29] iterations. Hence, the behavior of these fractals is discussed in [30,31,32,33,34,35] as well. In this research article, we use DK-iteration to generate the J-sets and M-sets using complex sine $\tau \left(z\right)=sin\left(z^m\right)+c$ as well as exponential $\tau \left(z\right)=e^{z^m}+c$ functions, where $m\ge 2c\in \mathbb{C}$.

The rest of the article is as follows. Some basic definition of M-set, J-set and some iterative schemes are explained in Section 2. We prove main results in Section 3. Section 4 presents algorithms and examples of fractals (i.e., J-sets and M-sets). We conclude these results by highlighting future applications in Section 5.

2. Basic Definitions and Preliminaries

This section contains basic notions and terms required for this research.

Definition 1. 

(J-set [36]): A set containing the end points of the following

$$f_{\tau }:=\{z\in \mathbb{C}:\{|{\tau }^m\left(z\right)\left|\right\}{}_{m=0}^{\infty }isbounded\}.$$

(1)

forms a basic J-set, where τ is a polynomial having degree 2 or greater than 2 with domain and range consisting of complex numbers, $\mathbb{C}$. Moreover, the set $f_{\tau }$ itself is named as filled J-set.

Definition 2. 

(M-Set [7]): M-set is a well-defined collection of connected J-sets and following to [37], we have

$$M:=\{c\in \mathbb{C}:\left\{{\tau }^m\left(0\right)\right\}\nrightarrow \infty asm\to \infty \}.$$

(2)

Moreover, zero is chosen as an initial point because it is a unique critical point.

Definition 3. 

(Noor Iteration [38]) Let $z_0\in \mathbb{C}$ and $\tau :\mathbb{C}\to \mathbb{C}$ be a complex mapping then Noor iterative scheme is defined as

$$\left\{\begin{array}{c}{z}_{i+1}=(1-{\alpha }_1)z_i+{\alpha }_1\tau \left(y_i\right),\hfill \\ y_i=(1-{\alpha }_2)z_i+{\alpha }_2\tau \left(x_i\right),\hfill \\ x_i=(1-{\alpha }_3)z_i+{\alpha }_3\tau \left(z_i\right),\hfill \end{array}\right.$$

(3)

where ${\alpha }_1,{\alpha }_2,{\alpha }_3\in (0,1]$ and $i=0,1,2,\dots .$

Definition 4. 

(DK-iteration [39]) For any $z_0\in \mathbb{C}$, Dogan and Karakaya introduced a new three step iteration (i.e., DK-iteration), which is defined as

$$\left\{\begin{array}{c}{z}_{i+1}=(1-\alpha )\tau \left(x_i\right)+\alpha \tau \left(y_i\right),\hfill \\ y_i=(1-\beta )\tau \left(z_i\right)+\beta \tau \left(x_i\right),\hfill \\ x_i=\tau \left(z_i\right),\hfill \end{array}\right.$$

(4)

where $\alpha ,\beta ,\in (0,1]$ and $i=0,1,2,\dots .$

3. Main Results

Escape criterion is an important tool to generate complex fractals. In this section, we present results for complex sine and exponential function via DK-iteration. Since DK-iteration have three steps, one can easily notice that $z_{i+1}$ depends on $y_i$, $y_i$ depends on $x_i$ and $x_i$ depends on $z_i$ for all $x,y,z\in \mathbb{C}$. So, for $i=0$ we assume $x_0=x$, $y_0=y$ and $z_0=z$ throughout this article.

3.1. Escape Criterion of DK-Iteration for Sine Function

Let $\tau \left(z\right)=sin\left(z^m\right)+cwherem\ge 2,c\in \mathbb{C}$ be a complex sine function, then the Maclaurin expansion for sine function is

$$\begin{array}{cc}|sin(z^m\left)\right|\hfill & =\left|z^m-\frac{z^{3m}}{3!}+\frac{z^{5m}}{5!}-\frac{z^{7m}}{7!}+\dots \right|\hfill \\ \hfill & =|z^m|\left|1-\frac{z^{2m}}{3!}+\frac{z^{4m}}{5!}-\frac{z^{6m}}{7!}\dots \right|\hfill \\ \hfill & \ge |z^m\left|\right|h_1|,\hfill \end{array}$$

(5)

where $|h_1|\in (0,1]$ satisfying the bound $|h_1|\le \left|1-\frac{z^{2m}}{3!}+\frac{z^{4m}}{5!}-\frac{z^{6m}}{7!}+\dots \right|;z\in \mathbb{C},$ and similarly,

$$\begin{array}{cc}|sin(y^m\left)\right|\hfill & =\left|y^m-\frac{y^{3m}}{3!}+\frac{y^{5m}}{5!}-\frac{y^{7m}}{7!}+\dots \right|\hfill \\ \hfill & =|y^m|\left|1-\frac{y^{2m}}{3!}+\frac{y^{4m}}{5!}-\frac{y^{6m}}{7!}\dots \right|\hfill \\ \hfill & \ge |y^m\left|\right|h_2|,\hfill \end{array}$$

(6)

where $|h_2|\in (0,1]$ satisfying the bound $|h_2|\le \left|1-\frac{y^{2m}}{3!}+\frac{y^{4m}}{5!}-\frac{y^{6m}}{7!}+\dots \right|;y\in \mathbb{C},$ and consequently,

$$\begin{array}{cc}|sin(x^m\left)\right|\hfill & =\left|x^m-\frac{x^{3m}}{3!}+\frac{x^{5m}}{5!}-\frac{x^{7m}}{7!}+\dots \right|\hfill \\ \hfill & =|x^m|\left|1-\frac{x^{2m}}{3!}+\frac{x^{4m}}{5!}-\frac{x^{6m}}{7!}\dots \right|\hfill \\ & \ge |x^m\left|\right|h_3|,\hfill \end{array}$$

(7)

where $|h_3|\in (0,1]$ satisfying the bound $|h_3|\le \left|1-\frac{x^{2m}}{3!}+\frac{x^{4m}}{5!}-\frac{x^{6m}}{7!}+\dots \right|;x\in \mathbb{C}.$

Theorem 1. 

Assume that ${\left\{z_i\right\}}_{i\in \mathbb{W}}$ be the sequence of iterates defined in (4) and ${\tau }_c\left(z\right)=sin\left(z^m\right)+c$, where $m\ge 2,c\in \mathbb{C}$ be a complex sine function with $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{|h_1|}\right)}^{\frac{1}{m-1}}$, $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\beta |h_3|}\right)}^{\frac{1}{m-1}}$ and $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\left(\alpha \right)|h_2|-|h_3|}\right)}^{\frac{1}{m-1}}$. Then $|z_i|\to \infty$, as $i\to \infty$.

Proof. 

By making use of the given information and fixing $x_0=x$, $y_0=y$ and $z_0=z$, the initial step of DK-iteration can be written as

$$|x_i|=|\tau \left(z_i\right)|\Rightarrow |x_0|=|\tau \left(z_0\right)|.$$

Next, by using  (5), and the given fact $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{|h_1|}\right)}^{\frac{1}{m-1}}\Rightarrow \left(\right|h_1\left|\right|z^{m-1}|-1)>1,$ we obtain

$$\begin{array}{cc}\hfill \left|x\right|& =\left|\tau \left(z\right)\right|=|sin\left(z^m\right)+c|\hfill \\ \hfill & \ge |sin(z^m\left)\right|-\left|c\right|\hfill \\ \hfill & \ge |h_1\left|\right|z^m|-|z|;|z|\ge \left|c\right|\hfill \\ \hfill & \ge \left|z\right|\left(|h_1\left|\right|z^{m-1}|-1\right)\hfill \\ \hfill & \ge \left|z\right|.\hfill \end{array}$$

Now, we consider the second step of DK-iteration

$$|y_i|=|(1-\beta )\tau \left(z_i\right)+\beta \tau \left(x_i\right)|\Rightarrow |y_0|=|(1-\beta )\tau \left(z_0\right)+\beta \tau \left(x_0\right)|.$$

Hence, by using (7), and $\left|x\right|\ge \left|z\right|\ge \left|c\right|>{\left(\frac{2}{\beta |h_3|}\right)}^{\frac{1}{m-1}}\Rightarrow \left(\beta \right|h_3\left|\right|x^{m-1}|-1)>1$ $\left|y\right|\ge \left|x\right|$, we obtain

$$\begin{array}{cc}\hfill \left|y\right|& =\left|\right(1-\beta \left)\tau \right(z)+\beta \tau (x\left)\right|\hfill \\ \hfill & \ge \left|\beta \tau \right(x\left)\right|-\left|\right(1-\beta \left)x\right|,\because x=\tau \left(z\right)\hfill \\ \hfill & \ge |\beta (sin\left(x^m\right)+c)\left)\right|-(1-\beta )\left|x\right|\hfill \\ \hfill & \ge \beta |sin(x^m\left)\right|-\beta \left|c\right|-\left|x\right|+\beta \left|x\right|\hfill \\ \hfill & \ge \beta |h_3\left|\right|x^m|-\beta |z|-|x|+\beta |z|.\hfill \end{array}$$

Now for final step of DK-iterative scheme, we have

$$|z_{i+1}|=|(1-\alpha )\tau \left(x_i\right)+\alpha \tau \left(y_i\right)|\Rightarrow |z_1|=|(1-\alpha )\tau \left(x\right)+\alpha \tau \left(y\right)|.$$

Hence, by neglecting $\alpha |sin(x^m\left)\right|$, and using (6) and (7), we obtain successively

$$\begin{array}{cc}\hfill |z_1|& =|(1-\alpha )(sin\left(x^m\right)+c)+\alpha sin\left(y^m\right)+c|\hfill \\ \hfill & =|(1-\alpha )sin\left(x^m\right)+\alpha sin\left(y^m\right)+(1-\alpha )\left|c\right|+\alpha \left(c\right)|\hfill \\ \hfill & =|(1-\alpha )sin\left(x^m\right)+\alpha sin\left(y^m\right)+c|\hfill \\ \hfill & \ge \alpha |sin\left(y^m\right)|-|sin\left(x^m\right)|+\alpha |sin\left(x^m\right)|-|c|\hfill \\ \hfill & \ge \alpha |sin\left(y^m\right)|-|sin\left(x^m\right)|-|c|\hfill \\ \hfill & \ge \alpha |h_2\left|\right|\left(y^m\right)|-|h_3\left|\right|\left(x^m\right)|-|c|\hfill \\ \hfill & \ge \alpha |h_2\left|\right|\left(z^m\right)|-|h_3\left|\right|\left(z^m\right)|-|z|,\because \left|y\right|\ge \left|x\right|\ge \left|z\right|\ge \left|c\right|\hfill \\ \hfill & \ge \left(\alpha |h_2|-|h_3|\right)|\left(z^m\right)|-|z|\hfill \\ \hfill & \ge \left|z\right|\left(\left(\alpha \right|h_2|-|h_3\left|\right)|\left(z^m\right)|-1\right).\hfill \end{array}$$

Continuing in this way, for $i=1$, we have

$$\begin{array}{cc}\hfill |z_2|& \ge \left|z\right|{\left(\left(\alpha \right|h_2|-|h_3\left|\right)|\left(z^m\right)|-1\right)}^2\hfill \end{array}$$

next, for $i=2$, we have

$$\begin{array}{cc}\hfill |z_3|& \ge \left|z\right|{\left(\left(\alpha \right|h_2|-|h_3\left|\right)|\left(z^m\right)|-1\right)}^3\hfill \end{array}$$

and so on, iterating upto the general term we get

$$\begin{array}{cc}\hfill |z_4|& \ge \left|z\right|{\left(\left(\alpha \right|h_2|-|h_3\left|\right)|\left(z^m\right)|-1\right)}^4\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill |z_{i+1}|& \ge \left|z\right|{\left(\left(\alpha \right|h_2|-|h_3\left|\right)|\left(z^m\right)|-1\right)}^i.\hfill \end{array}$$

Since $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\left(\left(\alpha \right)\right|h_2|-|h_3\left|\right)}\right)}^{\frac{1}{m-1}}\Rightarrow (\left(\alpha |h_3-|h_3|\right)|z^{m-1}|-1)>1$ and therefore, $|z_i|\to \infty$ as $i\to \infty .$    □

Corollary 1. 

For some $n\ge 0$, assume that

$$\{\begin{array}{c}\hfill \begin{array}{c}|z_i|>z_0>max\{\left|c\right|,{(\frac{2}{|h_1|})}^{\frac{1}{m-1}},{(\frac{2}{\beta |h_3|})}^{\frac{1}{m-1}},{(\frac{2}{\alpha |h_2|-|h_3|})}^{\frac{1}{m-1}}\}\hfill \end{array}\end{array}\},$$

then there exits a positive number $\theta >0$ such that

$$\left|z\right|\left(\left(\right|h_1\left|\right)\left(\beta \right|h_3\left|\right)\left(\alpha \right|h_2|-|h_3\left)\right|z^{m-1}|-1\right)>1+\theta \Rightarrow |z_{n+i}|>|z_n|{\left(1+\theta \right)}^{n+i}$$

and therefore, $|z_i|\to \infty$ as $i\to \infty .$

3.2. Escape Criterion of DK-Iteration for Exponential Function

Let us expand $\tau \left(z\right)=e^{z^m}+cwherem\ge 2,c\in \mathbb{C}$ as a Maclaurin series as follows

$$\begin{array}{cc}|e^{z^m}|\hfill & =\left|1+z^m+\frac{z^{2m}}{2!}+\frac{z^{3m}}{3!}+\frac{z^{4m}}{4!}+\dots \right|\hfill \\ \hfill & >\left|z^m+\frac{z^{2m}}{2!}+\frac{z^{3m}}{3!}+\frac{z^{4m}}{4!}+\dots \right|\hfill \\ \hfill & =|z^m|\left|1+\frac{z^m}{2!}+\frac{z^{2m}}{3!}+\frac{z^{3m}}{4!}+\dots \right|\hfill \\ \hfill & >|z^m\left|\right|k_1|,\hfill \end{array}$$

(8)

where $|k_1|\in (0,1]$ such that $|k_1|<\left|1+\frac{z^m}{2!}+\frac{z^{2m}}{3!}+\frac{z^{3m}}{4!}+\dots \right|;z\in \mathbb{C}.$

Similarly,

$$\begin{array}{cc}|e^{y^m}|\hfill & =\left|1+y^m+\frac{y^{2m}}{2!}+\frac{y^{3m}}{3!}+\frac{y^{4m}}{4!}+\dots \right|\hfill \\ \hfill & >\left|y^m+\frac{y^{2m}}{2!}+\frac{y^{3m}}{3!}+\frac{y^{4m}}{4!}+\dots \right|\hfill \\ \hfill & =|y^m|\left|1+\frac{y^m}{2!}+\frac{y^{2m}}{3!}+\frac{y^{3m}}{4!}+\dots \right|\hfill \\ \hfill & >|y^m\left|\right|k_2|\hfill \end{array}$$

(9)

where $|k_2|\in (0,1]$ such that $|k_2|<\left|1+\frac{y^m}{2!}+\frac{y^{2m}}{3!}+\frac{y^{3m}}{4!}+\dots \right|;y\in \mathbb{C}.$

Continuing in this way, we have

$$\begin{array}{cc}|e^{x^m}|\hfill & =\left|1+x^m+\frac{x^{2m}}{2!}+\frac{x^{3m}}{3!}+\frac{x^{4m}}{4!}+\dots \right|\hfill \\ \hfill & >\left|x^m+\frac{x^{2m}}{2!}+\frac{x^{3m}}{3!}+\frac{x^{4m}}{4!}+\dots \right|\hfill \\ \hfill & =|x^m|\left|1+\frac{x^m}{2!}+\frac{x^{2m}}{3!}+\frac{x^{3m}}{4!}+\dots \right|\hfill \\ & >|x^m\left|\right|k_3|,\hfill \end{array}$$

(10)

where $|k_3|\in (0,1]$ such that $|k_3|<\left|1+\frac{x^m}{2!}+\frac{x^{2m}}{3!}+\frac{x^{3m}}{4!}+\dots \right|;x\in \mathbb{C}.$

Theorem 2. 

Assume that ${\left\{z_i\right\}}_{i\in \mathbb{W}}$ be the sequence of iterates defined in (4) and ${\tau }_c\left(z\right)=e^{z^m}+c$, where m≥ 2, $c\in \mathbb{C}$ be a complex exponential function with $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{|k_1|}\right)}^{\frac{1}{m-1}}$, $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\beta |k_3|}\right)}^{\frac{1}{m-1}}$ and $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\left(\alpha \right)|k_2|-|k_3|}\right)}^{\frac{1}{m-1}}$. Then $|z_i|\to \infty$, as $i\to \infty$.

Proof. 

Since ${\tau }_c\left(z\right)=e^{z^m}+c$ and $x_0=x$, $y_0=y$ and $z_0=z$ then the initial step of DK-iteration is

$$|x_i|=|\tau \left(z_i\right)|\Rightarrow |x_0|=|\tau \left(z_0\right)|.$$

By using (8) and the given fact that $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{|k_1|}\right)}^{\frac{1}{m-1}}\Rightarrow \left(\right|k_1\left|\right|z^{m-1}|-1)>1,$ we obtain the criteria

$$\begin{array}{cc}\hfill \left|x\right|& =\left|\tau \right(z\left)\right|\hfill \\ \hfill & =|e^{z^m}+c|\hfill \\ \hfill & \ge |e^{z^m}|-|c|\hfill \\ \hfill & \ge |k_1\left|\right|z^m|-|z|,\because \left|z\right|\ge \left|c\right|\hfill \\ \hfill & \ge \left|z\right|\left(|k_1\left|\right|z^{m-1}|-1\right)\hfill \\ \hfill & \ge \left|z\right|.\hfill \end{array}$$

Now, for the second step of DK-iteration we have,

$$|y_i|=|(1-\beta )\tau \left(z_i\right)+\beta \tau \left(x_i\right)|\Rightarrow |y_0|=|(1-\beta )\tau \left(z_0\right)+\beta \tau \left(x_0\right)|.$$

Hence, by making use of (10) and $\left|x\right|\ge \left|z\right|\ge \left|c\right|>{\left(\frac{2}{\beta |k_3|}\right)}^{\frac{1}{m-1}}\Rightarrow \left(\beta \right|k_3\left|\right|x^{m-1}|-1)>1,$ we have

$$\begin{array}{cc}\hfill \left|y\right|& =\left|\right(1-\beta \left)\tau \right(z)+\beta \tau (x\left)\right|\hfill \\ \hfill & \ge |\beta .\tau (x\left)\right|-\left|\right(1-\beta \left)x\right|,\because x=\tau \left(z\right)\hfill \\ \hfill & \ge |\beta (e^{x^m}+c)\left)\right|-(1-\beta )\left|x\right|\hfill \\ \hfill & \ge \beta |e^{x^m}|-\beta |c|-|x|+\beta |x|,\hfill \\ \hfill & \ge \beta |k_3\left|\right|x^m|-\beta |z|-|x|+\beta |z|\because \left|x\right|\ge \left|z\right|\ge \left|c\right|\hfill \\ \hfill & \ge \beta |k_3\left|\right|x^m|-|x|\hfill \\ \hfill & \ge \left|x\right|\left(\beta |k_3\left|\right|x^{m-1}|-1\right)\hfill \\ & \ge \left|x\right|.\hfill \end{array}$$

Now for the final step of DK-iteration we have

$$|z_{i+1}|=|(1-\alpha )\tau \left(x_i\right)+\alpha \tau \left(y_i\right)|.$$

Taking $i=0$, then neglecting $\alpha |e^{x^m}|$, and using (9) and (10), respectively, we have

$$\begin{array}{cc}\hfill |z_1|& =|(1-\alpha )e^{x^m}+\alpha e^{y^m}+(1-\alpha )\left|c\right|+\alpha \left(c\right)|\hfill \\ \hfill & =|(1-\alpha )e^{x^m}+\alpha e^{y^m}+c|\hfill \\ \hfill & \ge \alpha |e^{y^m}|-|e^{x^m}|+\alpha |e^{x^m}|-|c|\hfill \\ \hfill & \ge \alpha |e^{y^m}|-|e^{x^m}|-|c|\hfill \\ \hfill & \ge \alpha |k_2{\left|\right|}^{y^m}|-|k_3\left|\right|x^m|-|c|\hfill \\ \hfill & \ge \alpha |k_2\left|\right|\left(z^m\right)|-|k_3\left|\right|\left(z^m\right)|-|z|,\because \left|y\right|\ge \left|x\right|\ge \left|z\right|\ge \left|c\right|\hfill \\ \hfill & \ge \left(\alpha |k_2|-|k_3|\right)|\left(z^m\right)|-|z|\hfill \\ \hfill & \ge \left|z\right|\left(\left(\alpha \right|k_2|-|k_3\left|\right)|\left(z^m\right)|-1\right).\hfill \end{array}$$

Continuing in this way, for $i=1$, we have

$$\begin{array}{cc}\hfill |z_2|& \ge \left|z\right|{\left(\left(\alpha \right|k_2|-|k_3\left|\right)|\left(z^m\right)|-1\right)}^2\hfill \end{array}$$

and for $i=2$, we have

$$\begin{array}{cc}\hfill |z_3|& \ge \left|z\right|{\left(\left(\alpha \right|k_2|-|k_3\left|\right)|\left(z^m\right)|-1\right)}^3\hfill \end{array}$$

and so on iterating upto the general term we get

$$\begin{array}{cc}\hfill |z_4|& \ge \left|z\right|{\left(\left(\alpha \right|k_2|-|k_3\left|\right)|\left(z^m\right)|-1\right)}^4\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill & .\hfill \\ \hfill |z_{i+1}|& \ge \left|z\right|{\left(\left(\alpha \right|k_2|-|k_3\left|\right)|\left(z^m\right)|-1\right)}^i.\hfill \end{array}$$

Since $\left|z\right|\ge \left|c\right|>{\left(\frac{2}{\left(\left(\alpha \right)\right|k_2|-|k_3\left|\right)}\right)}^{\frac{1}{m-1}}\Rightarrow (\left(\alpha |k_2|-|k_3|\right)|z^{m-1}|-1)>1$ and therefore, $|z_i|\to \infty$ as $i\to \infty .$    □

Corollary 2. 

For some $n\ge 0$, assume that

$$\begin{array}{c}\hfill \{\begin{array}{c}|z_i|>z_0>max\{\left|c\right|,{(\frac{2}{|k_1|})}^{\frac{1}{m-1}},{(\frac{2}{\beta |k_3|})}^{\frac{1}{m-1}},{(\frac{2}{\alpha |k_2|-|k_3|})}^{\frac{1}{m-1}}\}\hfill \end{array}\},\end{array}$$

then there exits a positive number $\theta >0$ such that

$$\left|z\right|\left(\left(\right|k_1\left|\right)\left(\beta \right|k_3\left|\right)\left(\alpha \right|k_2|-|k_3\left)\right|z^{m-1}|-1\right)>1+\theta \Rightarrow |z_{n+i}|>|z_n|{\left(1+\theta \right)}^{n+i}$$

and then $|z_i|\to \infty$ as $i\to \infty .$

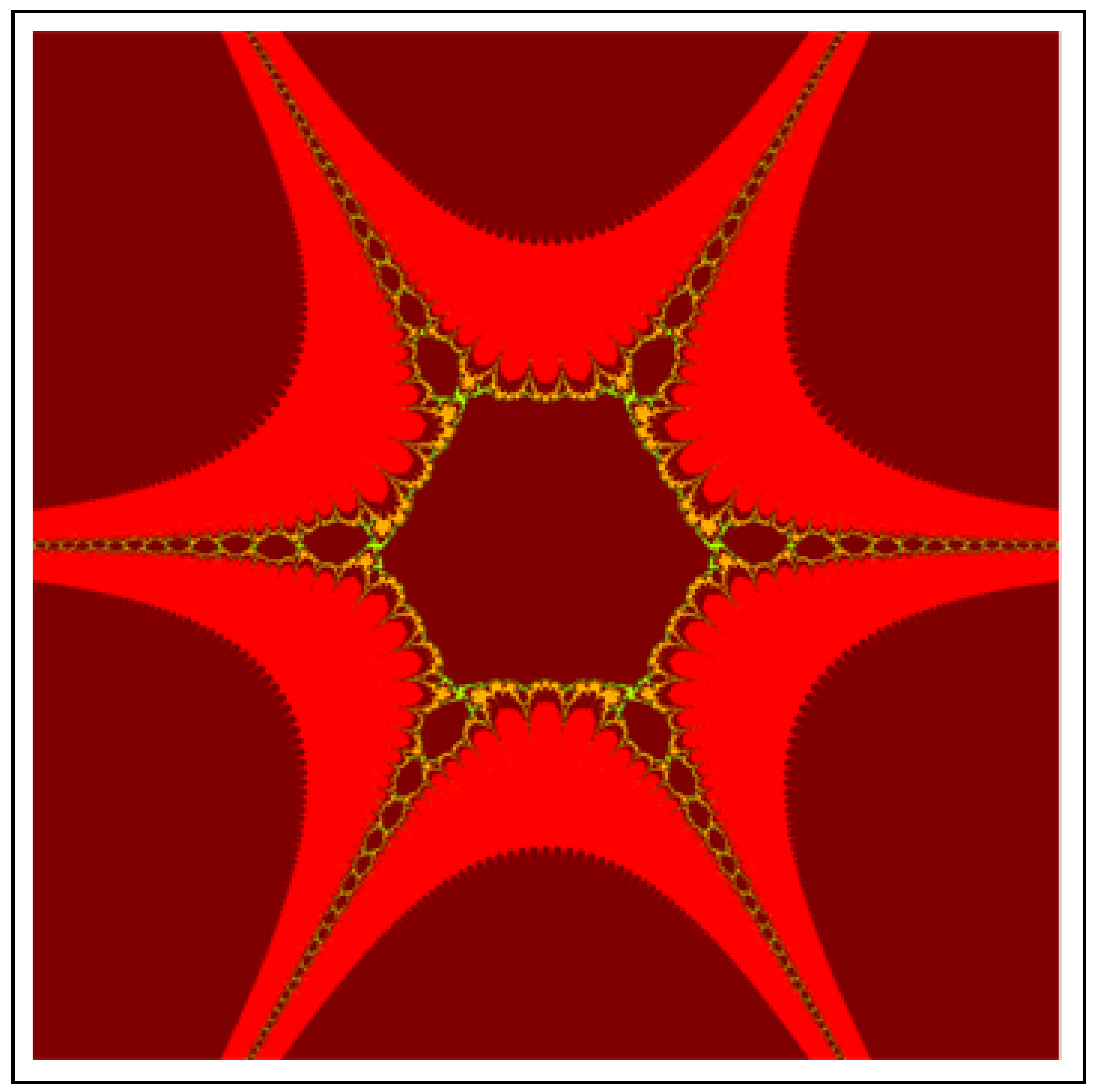
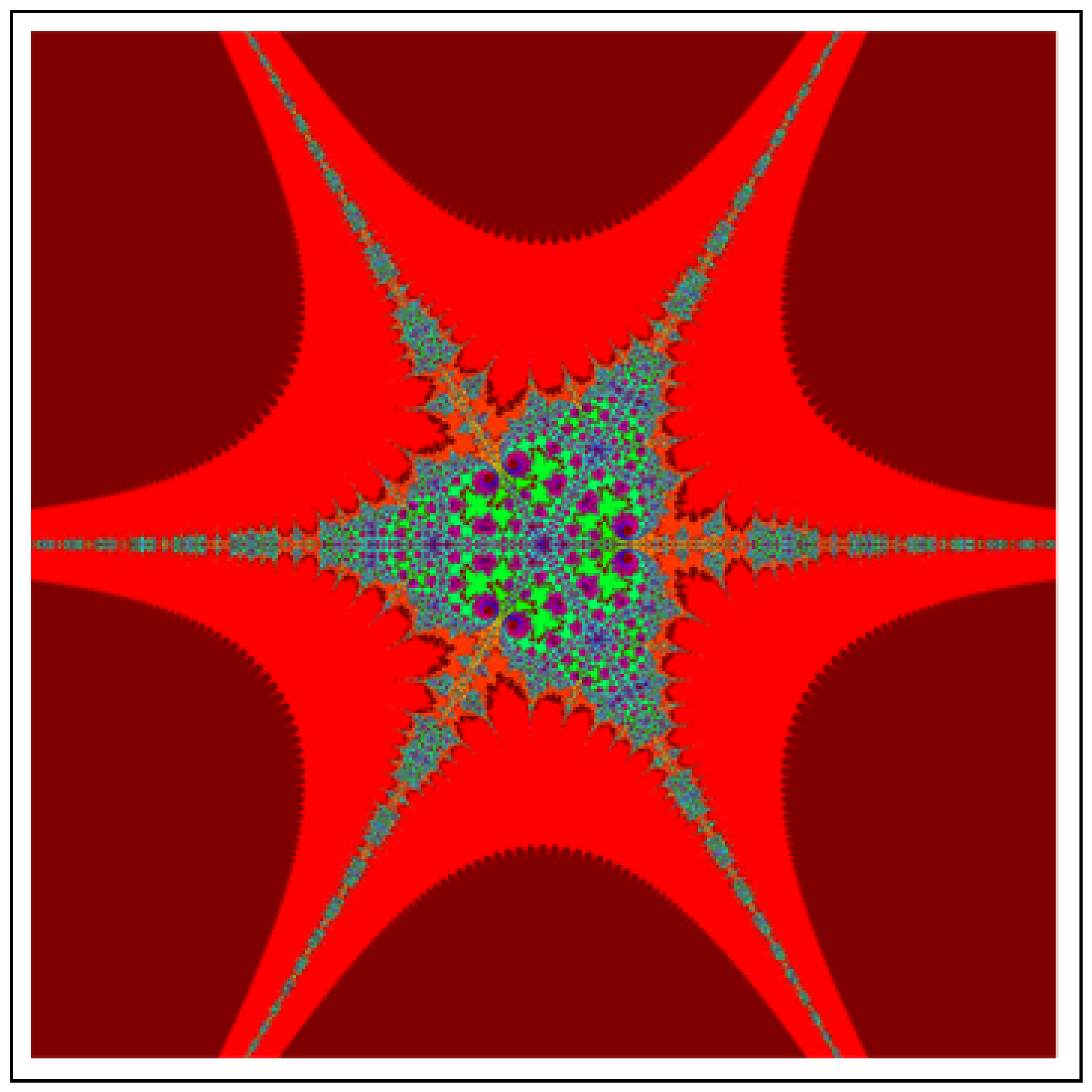
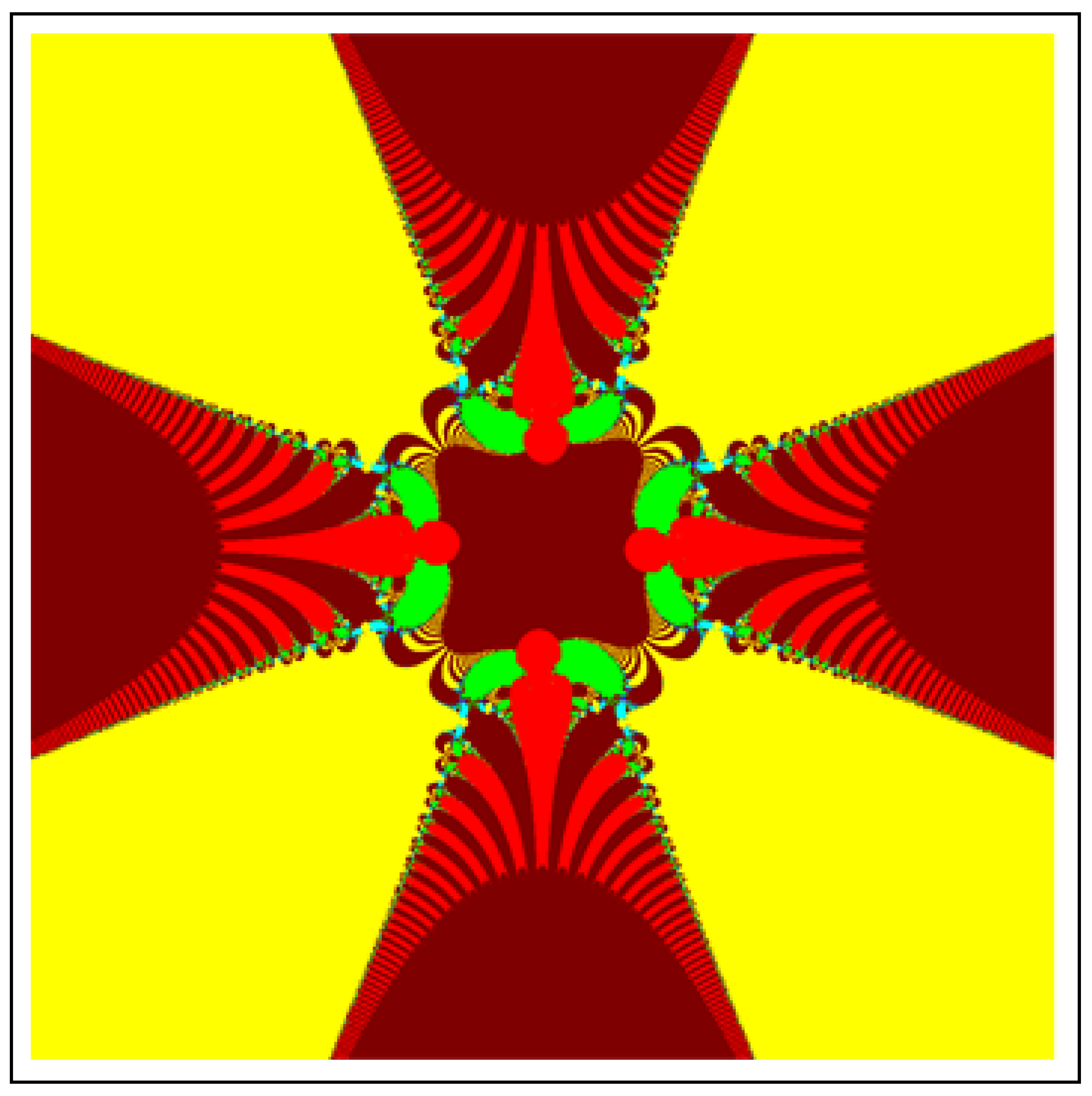
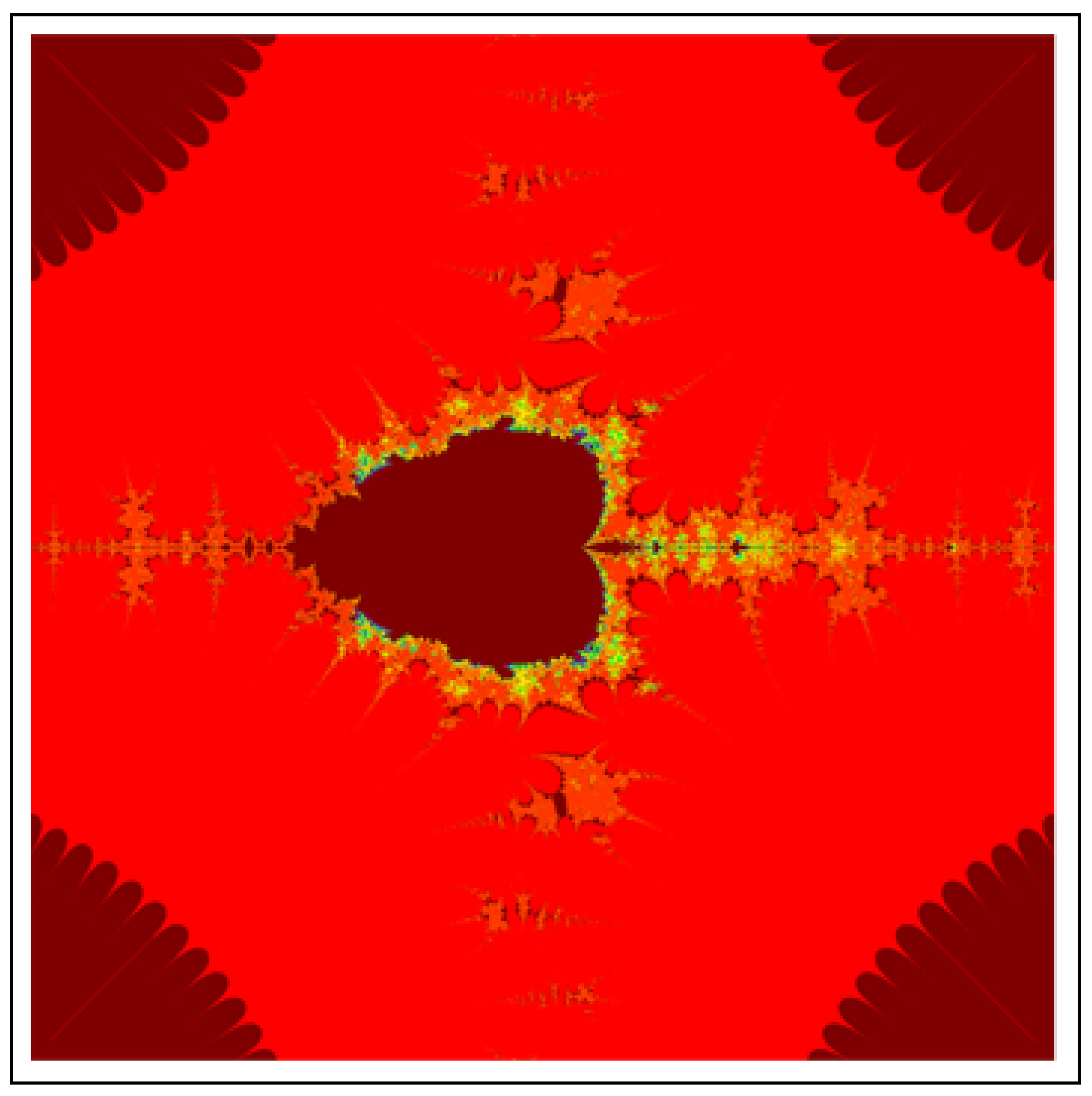
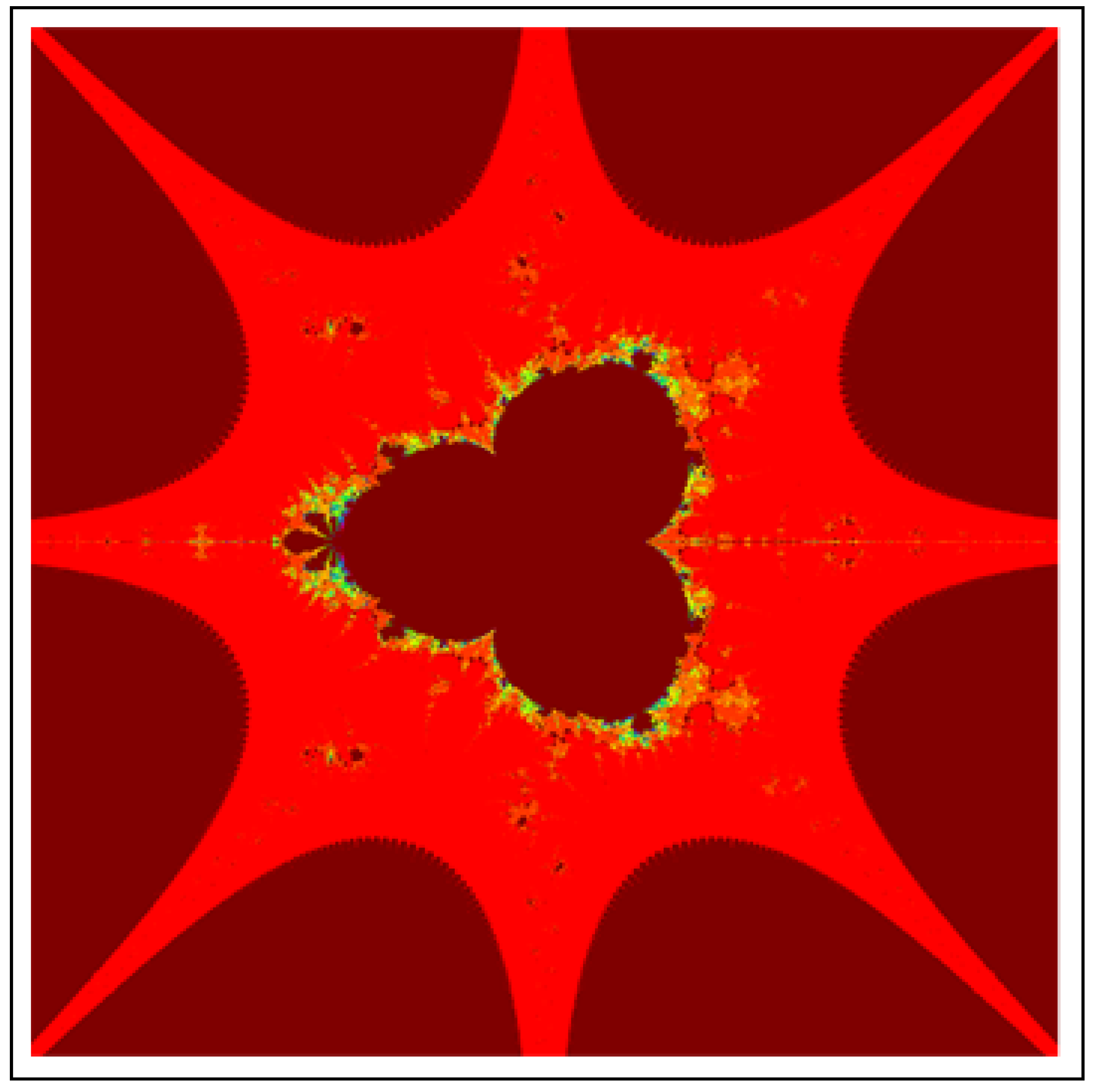
4. Applications in Fractals

This section presents fractals (i.e., J-sets and M-sets) using DK-iterative scheme. Mainly, the fractals are generated by following a criterion to execute images by an algorithm. There are some popular algorithms to generate the fractals:

• Distance Estimator [40],
• Potential Function Algorithm [41]
• Escape Criteria [42].

From the above listed methods, escape criterion is used here in the following Algorithms 1 and 2 to create the J-sets and M-sets in graphs. We use Mathematica 9.0 in computer “Intel(R) Core(TM) i7-7500U CPU @ 2.70 GHz 2.90 GHz” to obtain our desire results. In this section we use abbreviation DKIS for DK-iterative scheme.

4.1. Julia Set

J-set is a set of points for which the orbit of $f_{\tau }\nrightarrow \infty$ as $i\to \infty$. So, here we discuss some J-sets of functions $\tau \left(z\right)=sin\left(z^m\right)+c;\tau \left(z\right)=e^{z^m}+c;m=2,3,4$ using DK-iteration. Maximum number of iterations are considered 30 (i.e., $L=30$) and $A={[-3,3]}^2$ in Algorithm 1.

Algorithm 1: Geometry of J-Set

Example 1. 

J-sets for ${\tau }_c\left(z\right)=sin{z}^m+c;m=2,3,4$ are generated here with the following inputs

• Figure 1, Figure 2 and Figure 3: $|h_1|=0.05$, $|h_2|=0.09$, $|h_3|=0.03$, $\alpha =0.02$, $\beta =0.01$, $c=-0.005$$\mathbf{i}$,
• Figure 4, Figure 5 and Figure 6: $|h_1|=0.5$, $|h_2|=0.29$, $|h_3|=0.23$, $\alpha =0.2$, $\beta =0.1$, $c=-0.015$$\mathbf{i}$,
• Figure 7, Figure 8 and Figure 9: $|h_1|=0.5$, $|h_2|=0.8$, $|h_3|=0.6$, $\alpha =0.7$, $\beta =0.7$, $c=-0.1$$\mathbf{i}$.

All J-sets for $m=2$ have 4 attractors appears on main body of each. From 4 attractors, two are symmetrical to x-axis and other two are symmetrical to y-axis. Furthermore, each attractor has an angle $\frac{K\pi }{2}$, where K represents the position of each attractor form standard or initial attractor. For $m=3$, Images of J-sets have 6 attractors. All six attractors have an angle $\frac{K\pi }{3}$ and two of them have symmetry about x-axis. The J-sets for $m=4$ have 8 attractors and each have an angle $\frac{K\pi }{4}$. We observe that in the image of all J-sets, each attractor have infinite many lashes. All figures ${\tau }_c\left(z\right)=sin\left(z^m\right)+c$ look similar to each other but have difference in Julia points.

Example 2. 

J-sets for ${\tau }_c\left(z\right)=e^{z^m}+c;m=2,3,4$ are generated here with the following inputs

• Figure 10, Figure 11 and Figure 12: $|k_1|=0.7$, $|k_2|=0.9$, $|k_3|=0.3$, $\alpha =0.8$, $\beta =0.5$, $c=0.01-0.5$$\mathbf{i}$,
• Figure 13, Figure 14 and Figure 15: $|k_1|=0.7$, $|k_2|=0.5$, $|k_3|=0.4$, $\alpha =0.8$, $\beta =0.7$, $c=-0.005+0.4$$\mathbf{i}$,
• Figure 16, Figure 17 and Figure 18: $|k_1|=0.5$, $|k_2|=0.7$, $|k_3|=0.4$, $\alpha =0.5$, $\beta =0.7$, $c=-0.5$$\mathbf{i}$.

All J-sets for $m=2$ have two bunches of lashes. The size of lashes gradually decrease from the center of the bunch. The angle between two bunches is $\frac{\pi }{2}$. The images for $m=3$ and $m=4$ have three and four bunches, respectively. We notice that for $m=3$, the angle between every two bunches is $\frac{\pi }{3}$ and for $m=4$, the angle is $\frac{\pi }{4}$.

4.2. Mandelbrot Set

Here we discuss some M-sets for the function $\tau \left(z\right)=sin\left(z^m\right)+c$ and $\tau \left(z\right)=e^{z^m}+c$ at different m in the orbit of proposed iteration. We have generated M-sets for $m=2,3,4$ via DK-iteration. In all graphs we set the value of L as 30 (i.e., Fixed number of iterations) and $A={[-3,3]}^2$ in Algorithm 2.

Algorithm 2: Geometry of M-Set

Example 3. 

M-sets for ${\tau }_c\left(z\right)=sin{z}^m+c;m=2,3,4$ are generated here with the following inputs:

• Figure 19, Figure 20 and Figure 21: $|h_1|=0.05$, $|h_2|=0.09$, $|h_3|=0.03$, $\alpha =0.02$, $\beta =0.01$,
• Figure 22, Figure 23 and Figure 24: $|h_1|=0.5$, $|h_2|=0.29$, $|h_3|=0.23$, $\alpha =0.2$, $\beta =0.1$,
• Figure 25, Figure 26 and Figure 27: $|h_1|=0.5$, $|h_2|=0.8$, $|h_3|=0.6$, $\alpha =0.7$, $\beta =0.7$.

All M-sets for $m=2$ have 4 attractors on their main bodies and a classical quadratic Mandelbrot set at their centers. From 4 attractors, two are symmetrical to x-axis and other two are symmetrical to y-axis. For $m=3$, Images of M-sets have 6 attractors and a classical cubic Mandelbrot set at their centers. All six attractors have an angle $\frac{K\pi }{3}$ and two of them have symmetry about x-axis. The M-sets for $m=4$ have 8 attractors and a bi-quadratic classical Mandelbrot set at their centers. The angle of attractor $\frac{K\pi }{4}$ from the initial attractor. Moreover, here we also observe that in the images of all M-sets, attractors have infinite many lashes.

Example 4. 

M-sets for ${\tau }_c=e^{z^m}+c;m=2,3,4$ are generated here with the following inputs:

• Figure 28, Figure 29 and Figure 30: $|k_1|=0.7$, $|k_2|=0.9$, $|k_3|=0.3$, $\alpha =0.8$, $\beta =0.5$,
• Figure 31, Figure 32 and Figure 33: $|k_1|=0.7$, $|k_2|=0.5$, $|k_3|=0.4$, $\alpha =0.8$, $\beta =0.7$, and
• Figure 34, Figure 35 and Figure 36: $|k_1|=0.5$, $|k_2|=0.7$, $|k_3|=0.4$, $\alpha =0.5$, $\beta =0.7$.

All M-sets for $m=2$ have two bunches of lashes and two junctions of quadratic Mandelbrot sets. In each Junction infinite many large bulbs of quadratic Mandelbrot sets emerge on the main body. On the other hand, each lash of bunches is attract towards the Mandel-bulb of the junctions of quadratic Mandelbrot sets. The images for $m=3$ and $m=4$ have three and four bunches along with three and four junctions (i.e., Junctions of cubic and bi-quadratic Mandelbrot sets), respectively.

5. Conclusions

Escape criteria is proved by considering the complex sine, $\tau \left(z\right)=sin\left(z^m\right)+c$ as well as exponential, $\tau \left(z\right)=e^{z^m}+c$ functions using DK-iteration. These results are implemented in Algorithms 1 and 2 to visualize the Jsets and M-sets in DK-orbit. We discussed the generated Quadratic, Cubic, Bi-quadratic, J-sets and M-sets with detailed explanation. We observed that the attractors of J-sets for $\tau \left(z\right)=sin\left(z^m\right)+c$ originated from the center with an angle of $\frac{K\pi }{m}$ where K represented the positions of attractors from the initial attractor and same argument for M-sets with an extra characteristic that image of M-sets contains m type of Mandelbrot set at center for every m. We also observed that J and M-sets for $\tau \left(z\right)=e^{z^m}+c$ had m bunches of lashes and each M-set had junctions of m Mandelbrot sets between the bunches. Furthermore, we calculated the image execution time in seconds that showed, for any change in inputs the images had different execution time.

We hope that these findings are useful to study different types of fractals which were mentioned initially. The results of this paper can also be used in cloth industry for designing and printing purposes.