An Implicit Difference Scheme for the Fourth-Order Nonlinear Evolution Equation with Multi-Term Riemann–Liouvile Fractional Integral Kernels

Abstract

In this paper, an implicit difference scheme is proposed and analyzed for a class of nonlinear fourth-order equations with the multi-term Riemann–Liouvile (R–L) fractional integral kernels. For the nonlinear convection term, we handle implicitly and attain a system of nonlinear algebraic equations by using the Galerkin method based on piecewise linear test functions. The Riemann–Liouvile fractional integral terms are treated by convolution quadrature. In order to obtain a fully discrete method, the standard central difference approximation is used to discretize the spatial derivative. The stability and convergence are rigorously proved by the discrete energy method. In addition, the existence and uniqueness of numerical solutions for nonlinear systems are proved strictly. Additionally, we introduce and compare the Besse relaxation algorithm, the Newton iterative method, and the linearized iterative algorithm for solving the nonlinear systems. Numerical results confirm the theoretical analysis and show the effectiveness of the method.

1. Introduction

Partial integro-differential equations (PIDEs) have been applied widely in physical models, chemistry and biology [1,2,3,4]. Additionally, the fractional reaction–subdiffusion equation is believed to provide a powerful tool for the modeling plenty of natural phenomena in physics, biology, and chemistry [5,6,7]. Many numerical methods have been extensively studied. In [8], Sanz-Serna was the first to propose the difference scheme for nonlinear integro-differential equations; then, Lopez-Marcos [9] made a direct extension and considered the difference method for a class of nonlinear partial integro differential equations. Tang [10] considered a finite difference scheme for nonlinear PIDEs, approximated the differential term using the Crank–Nicolson scheme, and dealt with the integral term with the product trapezoidal method. Fairweather and Pani [11] used the backward Euler–Galerkin method for some partial integral differentials and derived the prior error estimates. Xu [12,13,14] also completed a series of studies for nonlinear integro-differential equations. A class of fractional convection–diffusion equations with variable coefficients are solved with the Sinc–Legendre collocation method [15], and nonlinear fractional convection–diffusion equations are solved using the homotopy analysis method [16]. For more development of numerical methods and analysis of the fractional reaction–subdiffusion equations, we refer the readers to [17,18,19].

This paper is devoted to the study of an implicit difference scheme for the nonlinear fourth-order equation with the multi-term Riemann–Liouvile fractional integral kernels

$$\begin{array}{ccc}\hfill & & u_t(x,t)+u(x,t)u_x(x,t)-{\mathfrak{L}}_{1}u(x,t)+{\mathfrak{L}}_{2}u(x,t)=f(x,t),\hfill \\ \hfill & & 0<t\le T,0<x<L,\hfill \end{array}$$

(1)

the initial condition and the boundary value conditions are

$$\begin{array}{c}\hfill u(x,0)=u^0\left(x\right),0\le x\le L,\end{array}$$

(2)

$$\begin{array}{c}\hfill u(0,t)=u(L,t)=u_{xx}(0,t)=u_{xx}(L,t)=0,0<t\le T,\end{array}$$

(3)

respectively, where $f(x,t)$ and $u^0\left(x\right)$ are the given smooth functions. Additionally, the ${\mathfrak{L}}_{1}u$ and ${\mathfrak{L}}_{2}u$ are defined by

$$\begin{array}{ccc}\hfill & & {\mathfrak{L}}_{1}u(x,t)=u_{xx}(x,t)+{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x,t),0<{\alpha }_1<1,\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & {\mathfrak{L}}_{2}u(x,t)=u_{xxxx}(x,t)+{\mathcal{I}}^{{\alpha }_2}{u}_{xxxx}(x,t),0<{\alpha }_2<1,\hfill \end{array}$$

(5)

where for $\gamma ={\alpha }_1,{\alpha }_2$, $0<\gamma <1$, ${\mathcal{I}}^{\gamma }$ denote the R–L fractional integral operator [2] defined by

$$\begin{array}{c}\hfill {\mathcal{I}}^{\gamma }\phi \left(t\right)={\int }_0^t\beta (t-s)\phi \left(s\right)ds=\frac{1}{\mathrm{\Gamma }\left(\gamma \right)}{\int }_0^t{(t-s)}^{\gamma -1}\phi \left(s\right)ds,t>0.\end{array}$$

(6)

For the fourth-order nonlinear partial differential equations, many scholars have carried out extensive research [9,20,21,22,23]. In the paper, we propose the backward Euler scheme and convolution quadrature finite difference method for (1)–(3). The nonlinear convective term in our equation deals with Galerkin method, which attains an advantage over the scheme in [23]. We also introduce and compare three nonlinear iterative methods, including the Besse relaxation algorithm, the Newton iterative method, and the linearized iterative algorithm, to solve the nonlinear systems. We also discuss the advantages and disadvantages of three kinds of methods. The existence and uniqueness of numerical solutions for nonlinear systems are proved strictly. The stability and convergence are rigorously proved by the discrete energy method.

The outline of the paper is as follows. In Section 2, the backward Euler implicit difference scheme is derived. In Section 3, it is proved that the stability of the difference scheme under the $L^2$ and $H^1$ norms. In particular, the existence of the backward Euler implicit difference scheme is proved by the Leray–Schauder Theorem. In the Section 4, convergence is proved, and the uniqueness of solution is also proved. The numerical examples are given to check our analysis in Section 5. Finally, this paper ends with a brief conclusion in Section 6.

2. The Construction of the Fully Discrete Scheme

Let J be a positive integer, define the space-step size $h:=\frac{L}{J}$, and $x_j:=jh(0\le j\le J)$ is the mesh points. For a positive integer N, we introduce the time-step size $k:=\frac{T}{N}$, the nodes $t_n:=nk(0\le n\le N)$, and the intermediate nodes $t_{n-\frac{1}{2}}:=t_n-\frac{1}{2}(1\le n\le N)$.

Additionally, we define the following grid functions:

$$\begin{array}{c}\hfill U_j^n:=u(x_j,t_n),f_j^n:=f(x_j,t_n),0\le j\le J,0\le n\le N.\end{array}$$

Giving grid function $U=\{U_j^n|0\le j\le J,0\le n\le N\}$. Some notations are defined as follows

$$\begin{array}{cc}\hfill & {\delta }_t{U}_j^n=\frac{1}{k}(U_j^n-U_j^{n-1}),{\delta }_x{U}_j^n=\frac{1}{h}(U_j^n-U_{j-1}^n);\hfill \\ \hfill & \Delta U_j^n=U_{j+1}^n-U_{j-1}^n,{\Delta }_{+}{U}_j^n=U_{j+1}^n-U_j^n;\hfill \\ \hfill & {\Delta }_{-}{U}_j^n=U_j^n-U_{j-1}^n,{\Delta }_x{U}_j^n=\frac{1}{2h}(U_{j+1}^n-U_{j-1}^n);\hfill \\ \hfill & \nabla U_j^n=\frac{1}{3}(U_{j+1}^n+U_j^n+U_{j-1}^n),{\delta }_x^2{U}_j^n=\frac{1}{h}({\delta }_x{U}_{j+1}^n-{\delta }_x{U}_j^n);\hfill \\ \hfill & {\delta }_x^4{U}_j^n=\frac{1}{h^2}({\delta }_x^2{U}_{j+1}^n-2{\delta }_x^2{U}_j^n+{\delta }_x^2{U}_{j-1}^n).\hfill \end{array}$$

(7)

To construct the scheme fully, we first introduce the first-order quadrature rule [20,21] to approximate the R–L fractional integral ${\mathcal{I}}^{\gamma }\phi \left(t\right)$

$$\begin{array}{c}\hfill {\mathcal{I}}^{\gamma }\phi \left(t_n\right)\approx {\widehat{q}}_n^{\gamma }\left(\phi \right)=k^{\gamma }\sum _{p=1}^n{\omega }_{n-p}^{\gamma }{\phi }^p=k^{\gamma }\sum _{p=0}^{n-1}{\omega }_p^{\gamma }{\phi }^{n-p},\end{array}$$

(8)

by the generating power series ${\left(\delta \left(\zeta \right)\right)}^{-\gamma }={(1-\zeta )}^{-\gamma }$, the quadrature weights ${\omega }_p^{\gamma }$ can be attained by

$$\begin{array}{ccc}\hfill & & \sum _{p=0}^{\infty }{\omega }_p^{\gamma }{\zeta }^p={(1-\zeta )}^{-\gamma }.\hfill \end{array}$$

(9)

Further, the quadrature weights ${\omega }_p^{\gamma }$ can be computed by

$$\begin{array}{c}\hfill {\omega }_0^{\gamma }=1,{\omega }_p^{\gamma }=\frac{\gamma (\gamma +1)\cdots (\gamma +p-1)}{p!},p=1,2,\cdots .\end{array}$$

(10)

Let $E\left(\phi \right)\left(t_n\right)={\mathcal{I}}^{\gamma }\phi \left(t_n\right)-{\widehat{q}}_n^{\gamma }\left(\phi \right)$, we can obtain the quadrature error in the next lemma.

Lemma 1

([3,14]). Let $\phi \left(t\right)$ be a real and continuously differentiable function in $0<t\le T$, and ${\phi }_t\left(t\right)$ is continuous and integrable for $0<t\le T$. Then, based on the Equation (9), the error of the convolution quadrature is bounded by

$$\begin{array}{c}\hfill |E\left(\phi \right)\left(t_n\right)|\le Ck{t}_n^{\gamma -1}|\phi \left(0\right)|+Ck{\int }_0^{t_{n-1}}{(t_n-s)}^{\gamma -1}|{\phi }_t\left(s\right)|ds\\ \hfill +C{k}^{\gamma }{\int }_{t_{n-1}}^{t_n}|{\phi }_t\left(s\right)|ds,\end{array}$$

where the constant C does not rely on k.

Lemma 2.

Let $u(x,t)\in C_{x,t}^{4,2}([0,L]\times (0,T])$, for $1\le j\le J-1,1\le n\le N$; it holds that

$$\begin{array}{ccc}& & |{\left(R_1\right)}_j^n|=|{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)-{\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{U}_j\right)|\le C(k^{{\alpha }_1}{n}^{{\alpha }_1-1}+h^2).\hfill \end{array}$$

Proof. 

By using the Taylor expansion with integral remainder [24,25,26], we obtain

$$\begin{array}{ccc}\hfill & & \frac{{\partial }^{2}u}{\partial x^2}(x_j,t_n)={\delta }_x^2{U}_j^n-\frac{1}{6}{h}^2{\int }_0^1[\frac{{\partial }^{4}u}{\partial x^4}(x_j+sh,t_n)\hfill \\ \hfill & & +\frac{{\partial }^{4}u}{\partial x^4}(x_j-sh,t_n)]{(1-s)}^{3}ds,1\le j\le J-1,1\le n\le N,\hfill \end{array}$$

(11)

by triangle inequality, we obtain

$$\begin{array}{ccc}\hfill |{\left(R_1\right)}_j^n|& =& |{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)-{\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{U}_j\right)|\hfill \\ \hfill & \le & |{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)-{\widehat{q}}_n^{{\alpha }_1}\left(u_{xx}(x_j,·)\right)|\hfill \\ \hfill & & +|{\widehat{q}}_n^{{\alpha }_1}\left(u_{xx}(x_j,·)\right)-{\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{U}_j\right)|,1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

Since ${\widehat{q}}_n^{{\alpha }_1}\left(1\right)=k^{{\alpha }_1}{\displaystyle \sum _{p=0}^{n-1}}{\omega }_p^{{\alpha }_1}=\frac{1}{\mathrm{\Gamma }\left({\alpha }_1\right)}{\int }_0^{t_n}{(t_n-s)}^{{\alpha }_1-1}·1ds=\frac{t_n^{{\alpha }_1}}{\mathrm{\Gamma }({\alpha }_1+1)}$, then

$$\begin{array}{ccc}\hfill |{\left(R_1\right)}_j^n|& \le & {\widehat{q}}_n^{{\alpha }_1}\left(1\right)\frac{h^2}{6}|{\int }_0^1[\frac{{\partial }^{4}U}{\partial x^4}(x_j+sh,t_{n-i})\hfill \\ \hfill & & +\frac{{\partial }^{4}U}{\partial x^4}(x_j-sh,t_{n-i})]{(1-s)}^{3}ds|+|{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)-{\widehat{q}}_n^{{\alpha }_1}\left(u_{xx}(x_j,·)\right)|,\hfill \\ \hfill & \le & C{h}^2\frac{t_n^{{\alpha }_1}}{\mathrm{\Gamma }({\alpha }_1+1)},1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

By Lemma 1, we obtain

$$\begin{array}{c}\hfill |{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)-{\widehat{q}}_n^{{\alpha }_1}\left(u_{xx}(x_j,·)\right)|\le C{n}^{{\alpha }_1-1}{k}^{{\alpha }_1},1\le j\le J-1,1\le n\le N.\end{array}$$

The proof is finished.  ☐

Lemma 3.

Let $u(x,t)\in C_{x,t}^{6,2}([0,L]\times (0,T])$, for $1\le j\le J-1,1\le n\le N$, we know

$$\begin{array}{ccc}\hfill & & |{\left(R_2\right)}_j^n|=|{\mathcal{I}}^{{\alpha }_2}{u}_{xxxx}(x_i,t_n)-{\widehat{q}}_n^{{\alpha }_2}\left({\delta }_x^4{U}_j\right)|\le C(n^{{\alpha }_2-1}{k}^{{\alpha }_2}+h^2).\hfill \end{array}$$

Proof. 

By using the Taylor expansion with integral remainder, we have

$$\begin{array}{ccc}\hfill & & \frac{{\partial }^{4}u}{\partial x^4}(x_j,t_n)={\delta }_x^4{U}_j^n-\frac{1}{6}{h}^2{\int }_0^1[\frac{{\partial }^{6}u}{\partial x^6}(x_j+sh,t_n)\hfill \\ \hfill & & +\frac{{\partial }^{6}u}{\partial x^6}(x_j-sh,t_n)]{(1-s)}^{3}ds,1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

(12)

Similarly to Lemma 2, we can complete the proof of the Lemma 3.  ☐

We now derive the backward Euler implicit difference scheme for the problem (1)–(3). Considering (1) at the point $(x_j,t_n)$, we obtain

$$\begin{array}{ccc}\hfill & & u_t(x_j,t_n)+u(x_j,t_n)u_x(x_j,t_n)-{\mathfrak{L}}_{1}u(x_j,t_n)+{\mathfrak{L}}_{2}u(x_j,t_n)\hfill \\ \hfill & & =f(x_j,t_n),1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

(13)

Next, we discretize the (13) one by one. First, from Lemmas 2 and 3, we obtain

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)={\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{U}_j\right)+{\left(R_1\right)}_j^n,1\le j\le J-1,1\le n\le N,\hfill \\ {\mathcal{I}}^{{\alpha }_2}{u}_{xxxx}(x_j,t_n)={\widehat{q}}_n^{{\alpha }_2}\left({\delta }_x^4{U}_j\right)+{\left(R_2\right)}_j^n,1\le j\le J-1,1\le n\le N,\hfill \end{array}\right.\end{array}$$

(14)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_{xx}(x_j,t_n)={\delta }_x^2{U}_j^n+{\left(R_3\right)}_j^n,\hfill \\ u_{xxxx}(x_j,t_n)={\delta }_x^4{U}_j^n+{\left(R_4\right)}_j^n,\hfill \end{array}\right.\end{array}$$

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left(R_3\right)}_j^n=-\frac{1}{6}{h}^2{\int }_0^1[\frac{{\partial }^{4}u}{\partial x^4}(x_j+sh,t_n)+\frac{{\partial }^{4}u}{\partial x^4}(x_j-sh,t_n)]{(1-s)}^{3}ds,\hfill \\ {\left(R_4\right)}_j^n=-\frac{1}{6}{h}^2{\int }_0^1[\frac{{\partial }^{6}u}{\partial x^6}(x_j+sh,t_n)+\frac{{\partial }^{6}u}{\partial x^6}(x_j-sh,t_n)]{(1-s)}^{3}ds.\hfill \end{array}\right.\end{array}$$

Thus, we have

$$\begin{array}{ccc}\hfill {\mathfrak{L}}_{1}u(x_j,t_n)& =& u_{xx}(x_j,t_n)+{\mathcal{I}}^{{\alpha }_1}{u}_{xx}(x_j,t_n)\hfill \\ \hfill & =& {\delta }_x^2{U}_j^n+{\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{U}_j\right)+{\left(R_1\right)}_j^n+{\left(R_3\right)}_j^n,\hfill \\ \hfill & & 1\le j\le J-1,1\le n\le N,\hfill \end{array}$$

(15)

and

$$\begin{array}{ccc}\hfill {\mathfrak{L}}_{2}u(x_j,t_n)& =& u_{xxxx}(x_j,t_n)+{\mathcal{I}}^{{\alpha }_2}{u}_{xxxx}(x_j,t_n)\hfill \\ \hfill & =& {\delta }_x^4{U}_j^n+{\widehat{q}}_n^{{\alpha }_2}\left({\delta }_x^4{U}_j\right)+{\left(R_2\right)}_j^n+{\left(R_4\right)}_j^n.\hfill \\ \hfill & & 1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

(16)

Second, for the nonlinear convection term $u{u}_x$, we discretize it by the Galerkin method with piecewise linear test functions

$$\begin{array}{ccc}\hfill u(x_j,t_n)u_x(x_j,t_n)& =& \frac{U_{j+1}^n+U_j^n+U_{j-1}^n}{3}\frac{U_{j+1}^n-U_{j-1}^n}{2h}+{\left(R_5\right)}_j^n\hfill \\ \hfill & =& \frac{1}{6h}(U_j^n\Delta U_j^n+\Delta {\left(U_j^n\right)}^2)+O\left(h^2\right),\hfill \\ & & 1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

(17)

Third, for $u_t(x_j,t_n)$, we have

$$\begin{array}{c}\hfill u_t(x_j,t_n)={\delta }_t{U}_j^n+{\left(R_6\right)}_j^n,1\le j\le J-1,1\le n\le N,\end{array}$$

(18)

where

$$\begin{array}{c}\hfill {\left(R_6\right)}_j^n=-k{\int }_0^1\frac{{\partial }^{2}u}{\partial t^2}(x_j,t_{n-1}+sk)sds.\end{array}$$

Substituting (14)–(18) into (13), we obtain

$$\begin{array}{ccc}\hfill & & {\delta }_t{U}_j^n+\frac{1}{6h}(U_j^n\Delta U_j^n+\Delta {\left(U_j^n\right)}^2)-k^{{\alpha }_1}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}{\delta }_x^2{U}_j^p\hfill \\ \hfill & & +k^{{\alpha }_2}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}{\delta }_x^4{U}_j^p-{\delta }_x^2{U}_j^n+{\delta }_x^4{U}_j^n=f_j^n+R_j^n,\hfill \\ & & 1\le j\le J-1,1\le n\le N,\hfill \end{array}$$

(19)

in which

$$\begin{array}{ccc}\hfill & & R_j^n={\left(R_1\right)}_j^n-{\left(R_2\right)}_j^n-{\left(R_3\right)}_j^n-{\left(R_4\right)}_j^n-{\left(R_5\right)}_j^n-{\left(R_6\right)}_j^n,\hfill \\ & & 1\le j\le J-1,1\le n\le N.\hfill \end{array}$$

By Lemmas 1–3, there is a constant C independent of h and k, which satisfies

$$\begin{array}{c}\hfill |R_j^n|\le C(n^{{\alpha }_1-1}{k}^{{\alpha }_1}+n^{{\alpha }_2-1}{k}^{{\alpha }_2}+h^2),1\le j\le J-1,1\le n\le N.\end{array}$$

(20)

The following initial and boundary value conditions can be attained

$$\begin{array}{ccc}\hfill & & U_0^n=U_J^n=0,{\delta }_x^2{U}_0^n={\delta }_x^2{U}_J^n=O\left(h^2\right),1\le n\le N.\hfill \\ & & U_j^0=u^0\left(x_j\right),0\le j\le J.\hfill \end{array}$$

(21)

Omitting the small terms in (19) and (21), and replacing $U_j^n$ with its numerical approximation $u_j^n$, $1\le j\le J-1,1\le n\le N$, we obtain the backward Euler implicit difference scheme

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\delta }_t{u}_j^n+\frac{1}{6h}(u_j^n\Delta u_j^n+\Delta {\left(u_j^n\right)}^2)-{\mathfrak{L}}_1{u}_j^n+{\mathfrak{L}}_2{u}_j^n=f_j^n,\hfill \\ \\ u_0^n=u_J^n=0,{\delta }_x^2{u}_0^n={\delta }_x^2{u}_J^n=0,\hfill \\ \\ u_j^0=u^0\left(x_j\right),\hfill \end{array}\right.\end{array}$$

(22)

and

$$\begin{array}{c}\hfill {\mathfrak{L}}_1{u}_j^n={\delta }_x^2{u}_j^n+{\widehat{q}}_n^{{\alpha }_1}\left({\delta }_x^2{u}_j\right),1\le j\le J-1,1\le n\le N,\end{array}$$

$$\begin{array}{c}\hfill {\mathfrak{L}}_2{u}_j^n={\delta }_x^4{u}_j^n+{\widehat{q}}_n^{{\alpha }_2}\left({\delta }_x^4{u}_j\right),1\le j\le J-1,1\le n\le N,\end{array}$$

where

$$\begin{array}{c}\hfill {\delta }_x^4{u}_j^n=\left\{\begin{array}{c}(-2{\delta }_x^2{u}_1^n+{\delta }_x^2{u}_2^n)/h^2,j=1,1\le n\le N,\hfill \\ \\ ({\delta }_x^2{u}_{j-1}^n-2{\delta }_x^2{u}_j^n+{\delta }_x^2{u}_{j+1}^n)/h^2,2\le j\le J-2,1\le n\le N,\hfill \\ \\ ({\delta }_x^2{u}_{J-2}^n-2{\delta }_x^2{u}_{J-1}^n)/h^2,j=J-1,1\le n\le N.\hfill \end{array}\right.\end{array}$$

3. Existence and Stability

In this section, we analyze the $L^2$ stability, $L^{\infty }$ stability, and existence of the backward Euler implicit difference scheme (22).

Firstly, we shall introduce some notations and lemmas that will be used for the proof of the stability. Let $V_h=\{s|s=(s_0,s_1,\dots ,s_J),s_0=s_J=0\}$. For any grid functions $s,g\in V_h$, we denote

$$\begin{array}{c}\hfill ⟨s,g⟩=h\sum _{j=1}^{J-1}{s}_j{g}_j{,||s||}_{\infty }=\underset{1\le j\le J-1}{\max }\{|s_j|\},\parallel s\parallel =\sqrt{⟨s,s⟩}.\\ \hfill \end{array}$$

(23)

Lemma 4

([27,28]). For any function s defined on $V_h$, we obtain

$$\begin{array}{c}\hfill {||s||}_{\infty }\le \frac{\sqrt{L}}{2}||{\delta }_{x}s||.\end{array}$$

Lemma 5

([9,29]). Let $s,g\in V_h$; then

$$\begin{array}{ccc}& & ⟨{\delta }_x^{2}s,g⟩=-\sum _{j=0}^{J-1}h\left({\delta }_x{s}_{j+1}\right)\left({\delta }_x{g}_{j+1}\right).\hfill \end{array}$$

Lemma 6

([24,25,30]). For any $s,g\in V_h$, such that ${\delta }_x^2{s}_0={\delta }_x^2{s}_J=0$; then, we have

$$\begin{array}{c}\hfill ⟨{\delta }_x^{4}s,g⟩=\sum _{j=1}^{J-1}h\left({\delta }_x^2{s}_j\right)\left({\delta }_x^2{g}_j\right).\end{array}$$

Lemma 7

([31]). Let $\beta \left(t\right)=t^{\alpha -1}/\mathrm{\Gamma }\left(\alpha \right)$ be defined in Equation (6); $\beta \left(t\right)\in L^{1,loc}(0,\infty )$ is a positive type if and only if

$$\begin{array}{c}\hfill Re\left(\widehat{\beta }\left(t\right)\right)\ge 0,fort\in C,Re\left(t\right)>0,\end{array}$$

where $Re$ denotes the real part, $\widehat{\beta }$ denotes the Laplace transform of $\beta \left(t\right)$.

Lemma 8

([24,25]). If {$b_0,b_1,\dots ,b_n,\dots$} is a real-valued sequence such that $\widehat{b}\left(z\right)={\displaystyle \sum _{n=0}^{\infty }}{b}_n{z}^n$ is analytic in $D=\{z\in C:|z|\le 1\}$, then for any positive integer N and any $(V^1,V^2,\dots$, $V^N)\in R^N$,

$$\begin{array}{c}\hfill \sum _{n=1}^N\left(\sum _{p=1}^n{b}_{n-p}{V}^p\right)V^n\ge 0,\end{array}$$

if and only if

$$\begin{array}{c}\hfill Re\widehat{b}\left(z\right)\ge 0,forz\in D.\end{array}$$

It is noticed that the generating function (9) satisfies the condition of Lemma 8.

3.1. Stability

Theorem 1.

($L^2$-stability) Assume that $\{u_j^n|1\le j\le J-1,1\le n\le N\}$ is the solution of the backward Euler implicit difference scheme (22). We can obtain

$$\begin{array}{c}\hfill \parallel u^n\parallel \le \parallel u^0\parallel +2k{\displaystyle \sum _{i=1}^n}\parallel f^i\parallel ,1\le n\le N.\end{array}$$

Proof. 

Taking the inner product of (22) with $u^n$, for $1\le n\le N$, we obtain the following formula

$$\begin{array}{cc}\hfill & ⟨{\delta }_t{u}^n,u^n⟩+\frac{1}{6h}⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2,u^n⟩-k^{{\alpha }_1}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,u^n⟩\hfill \\ \hfill & -⟨{\delta }_x^2{u}^n,u^n⟩+k^{{\alpha }_2}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^p,u^n⟩+⟨{\delta }_x^4{u}^n,u^n⟩=⟨f^n,u^n⟩.\hfill \end{array}$$

(24)

From [9,22,32], we have

$$\begin{array}{c}\hfill ⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2,u^n⟩=0,\end{array}$$

then for $N\ge 1$, (24) can be rearranged

$$\begin{array}{ccc}\hfill & & 2k\sum _{n=1}^N⟨{\delta }_t{u}^n,u^n⟩-2k^{{\alpha }_1+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,u^n⟩\hfill \\ \hfill & & -2k\sum _{n=1}^N⟨{\delta }_x^2{u}^n,u^n⟩+2k\sum _{n=1}^N⟨{\delta }_x^4{u}^n,u^n⟩\hfill \\ \hfill & & +2k^{{\alpha }_2+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^n,u^n⟩=2k\sum _{n=1}^N⟨f^n,u^n⟩,1\le n\le N.\hfill \end{array}$$

(25)

Next, we estimate the terms in (25) one by one. First, it is clear that

$$\begin{array}{ccc}\hfill ⟨{\delta }_t{u}^n,u^n⟩& =& \frac{1}{2k}⟨u^n-u^{n-1},u^n-u^{n-1}+u^n+u^{n-1}⟩\hfill \\ \hfill & \ge & \frac{1}{2k}(\parallel u^n{\parallel }^2-\parallel u^{n-1}{\parallel }^2),\hfill \end{array}$$

we arrive at

$$\begin{array}{c}\hfill 2k\sum _{n=1}^N⟨{\delta }_t{u}^n,u^n⟩\ge \parallel u^N{\parallel }^2-{\parallel u^0\parallel }^2.\end{array}$$

(26)

Second, utilizing Lemmas 4, 5, 7, and 8, we have

$$\begin{array}{ccc}\hfill & & -2k\sum _{n=1}^N⟨{\delta }_x^2{u}^n,u^n⟩-2k^{{\alpha }_1+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,u^n⟩\hfill \\ \hfill & =& 2k\sum _{n=1}^{N}h\sum _{j=1}^{J-1}\left({\delta }_x{u}_j^n\right)\left({\delta }_x{u}_j^n\right)+2k^{{\alpha }_1+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}h\sum _{j=1}^{J-1}\left({\delta }_x{u}_j^p\right)\left({\delta }_x{u}_j^n\right)\hfill \\ \hfill & =& 2kh\sum _{n=1}^N\sum _{j=1}^{J-1}\left({\delta }_x{u}_j^n\right)\left({\delta }_x{u}_j^n\right)+2k^{{\alpha }_1+1}h\sum _{j=1}^{J-1}\left[\sum _{n=1}^N\left(\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}{\delta }_x{u}_j^p\right){\delta }_x{u}_j^n\right]\hfill \\ \hfill & \ge & 0,1\le n\le N.\hfill \end{array}$$

(27)

Additionally,

$$\begin{array}{ccc}\hfill & & 2k\sum _{n=1}^N⟨{\delta }_x^4{u}^n,u^n⟩+2k^{{\alpha }_2+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^p,u^n⟩\hfill \\ \hfill & =& 2k\sum _{n=1}^N\sum _{j=1}^{J-1}h\left({\delta }_x^2{u}_j^n\right)\left({\delta }_x^2{u}_j^n\right)+2k^{{\alpha }_2+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}\sum _{j=1}^{J-1}h\left({\delta }_x^2{u}_j^p\right)\left({\delta }_x^2{u}_j^n\right)\hfill \\ \hfill & =& 2k\sum _{n=1}^N\sum _{j=1}^{J-1}h\left({\delta }_x^2{u}_j^n\right)\left({\delta }_x^2{u}_j^n\right)+2k^{{\alpha }_2+1}h\sum _{j=1}^{J-1}[\sum _{n=1}^N\left(\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}{\delta }_x^2{u}_j^p\right){\delta }_x^2{u}_j^n\hfill \\ \hfill & \ge & 0,1\le n\le N.\hfill \end{array}$$

(28)

Substituting (26)–(28) into (25), and using the Cauchy–Schwarz inequality, we have

$$\begin{array}{c}\hfill \parallel u^N{\parallel }^2\le \parallel u^0{\parallel }^2+2k{\displaystyle \sum _{n=1}^N}\parallel f^n\parallel \parallel u^n\parallel .\end{array}$$

(29)

Taking $\parallel u^M\parallel =\underset{0\le n\le N}{\max }\parallel u^n\parallel$, we obtain

$$\begin{array}{c}\hfill \parallel u^N\parallel \le \parallel u^M\parallel \le \parallel u^0\parallel +2k{\displaystyle \sum _{i=1}^M}\parallel f^i\parallel \le \parallel u^0\parallel +2k{\displaystyle \sum _{i=1}^N}\parallel f^i\parallel .\end{array}$$

(30)

The proof of the Theorem 1 is finished.

 ☐

Theorem 2.

($H^1$-stability) Assume that $\{u_j^n|1\le j\le J-1,1\le n\le N\}$ is the solution of the backward Euler implicit difference scheme (22). Then, it holds that

$$\begin{array}{c}\hfill |u^n{|}_1\le |u^0{|}_1+2k{\displaystyle \sum _{n=1}^N}{|f^n|}_1,1\le n\le N.\end{array}$$

Proof. 

Taking the inner product of (22) with $-2k{\delta }_x^2{u}^n$, for $1\le n\le N$, we have

$$\begin{array}{cc}\hfill & -2k⟨{\delta }_t{u}^n,{\delta }_x^2{u}^n⟩-\frac{k}{3h}⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & +2k^{1+{\alpha }_1}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,{\delta }_x^2{u}^n⟩+2k⟨{\delta }_x^2{u}^n,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & -2k^{1+{\alpha }_2}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^p,{\delta }_x^2{u}^n⟩-2k⟨{\delta }_x^4{u}^n,{\delta }_x^2{u}^n⟩=-2k⟨f^n,{\delta }_x^2{u}^n⟩.\hfill \end{array}$$

(31)

Since

$$\begin{array}{c}\hfill \begin{array}{c}-⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2,{\delta }_x^2{u}^n⟩=⟨{\delta }_x(u^n\Delta u^n+\Delta \left(u^n{u}^n\right)),{\delta }_x{u}^n⟩\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x(u_j^n\Delta u_j^n+\Delta \left(u_j^n{u}_j^n\right)){\delta }_x{u}_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x(u_j^n(u_{j+1}^n-u_{j-1}^n)+(u_{j+1}^n{u}_{j+1}^n-u_{j-1}^n{u}_{j-1}^n)){\delta }_x{u}_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x((u_j^n+u_{j+1}^n)u_{j+1}^n-(u_j^n+u_{j-1}^n)u_{j-1}^n){\delta }_x{u}_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x(u_j^n+u_{j+1}^n){\delta }_x{u}_{j+1}^n{\delta }_x{u}_j^n-{\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x(u_j^n+u_{j-1}^n){\delta }_x{u}_{j-1}^n{\delta }_x{u}_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h{\delta }_x(u_j^n+u_{j+1}^n){\delta }_x{u}_{j+1}^n{\delta }_x{u}_j^n-{\displaystyle \sum _{j=0}^{J-2}}h{\delta }_x(u_j^n+u_{j+1}^n){\delta }_x{u}_{j+1}^n{\delta }_x{u}_j^n\hfill \\ =h{\delta }_x(u_{J-1}^n+u_J^n){\delta }_x{u}_J^n{\delta }_x{u}_{J-1}^n-h{\delta }_x(u_0^n+u_1^n){\delta }_x{u}_1^n{\delta }_x{u}_0^n\hfill \\ =0.\hfill \end{array}\end{array}$$

Then, we have

$$\begin{array}{c}\hfill -\frac{k}{3h}⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2,{\delta }_x^2{u}^n⟩=0.\end{array}$$

For $N\ge 1$, (31) can be rearranged

$$\begin{array}{cc}\hfill & -2k\sum _{n=1}^N⟨{\delta }_t{u}^n,{\delta }_x^2{u}^n⟩+2k^{1+{\alpha }_1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & +2k\sum _{n=1}^N⟨{\delta }_x^2{u}^n,{\delta }_x^2{u}^n⟩-2k^{1+{\alpha }_2}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^p,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & -2k\sum _{n=1}^N⟨{\delta }_x^4{u}^n,{\delta }_x^2{u}^n⟩=-2k\sum _{n=1}^N⟨f^n,{\delta }_x^2{u}^n⟩,1\le n\le N.\hfill \end{array}$$

(32)

Since

$$\begin{array}{c}\hfill -⟨{\delta }_t{u}^n,{\delta }_x^2{u}^n⟩\ge \frac{1}{2k}(|u^n{|}_1^2-|u^{n-1}{|}_1^2),\end{array}$$

then

$$\begin{array}{c}\hfill -2k\sum _{n=1}^N⟨{\delta }_t{u}^n,{\delta }_x^2{u}^n⟩\ge |u^N{|}_1^2-{|u^0|}_1^2.\end{array}$$

(33)

By Lemma 8, we have

$$\begin{array}{ccc}\hfill & & 2k\sum _{n=1}^N⟨{\delta }_x^2{u}^n,{\delta }_x^2{u}^n⟩+2k^{{\alpha }_1+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}⟨{\delta }_x^2{u}^p,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & \ge & 0,1\le n\le N.\hfill \end{array}$$

(34)

Further, by Lemmas 4, 5, 7, and 8, we have

$$\begin{array}{ccc}\hfill & & -2k\sum _{n=1}^N⟨{\delta }_x^4{u}^n,{\delta }_x^2{u}^n⟩-2k^{{\alpha }_2+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}⟨{\delta }_x^4{u}^p,{\delta }_x^2{u}^n⟩\hfill \\ \hfill & =& 2k\sum _{n=1}^N\sum _{j=0}^{J-1}h\left({\delta }_x^3{u}_j^n\right)\left({\delta }_x^3{u}_j^n\right)+2k^{{\alpha }_2+1}\sum _{n=1}^N\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}\sum _{j=0}^{J-1}h\left({\delta }_x^3{u}_j^p\right)\left({\delta }_x^3{u}_j^n\right)\hfill \\ \hfill & =& 2k\sum _{n=1}^N\sum _{j=0}^{J-1}h\left({\delta }_x^3{u}_j^n\right)\left({\delta }_x^3{u}_j^n\right)+2k^{{\alpha }_2+1}h\sum _{j=0}^{J-1}[\sum _{n=1}^N\left(\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}{\delta }_x^3{u}_j^p\right){\delta }_x^3{u}_j^n\hfill \\ \hfill & \ge & 0,1\le n\le N.\hfill \end{array}$$

(35)

Substituting (33)–(35) into (32), and using the Cauchy–Schwarz inequality, we have

$$\begin{array}{c}\hfill |u^N{|}_1^2\le |u^0{|}_1^2+2k{\displaystyle \sum _{n=1}^N}|f^n{|}_1{|u^n|}_1.\end{array}$$

(36)

Similarly to Equation (30), we finish the proof of the Theorem 2.  ☐

3.2. Existence

Next, we will use the Leray–Schauder Theorem [33] to prove the existence of numerical solutions for the scheme (22).

Theorem 3.

Giving two positive integers J, N, and $u^0\in R^{J-1}$, the Equation (22) has a solution $u^n$ for $1\le n\le N.$

Proof. 

We can employ the mathematical induction to prove the Theorem 3. Since $u^0\in R^{J-1}$, for given $u^m$, $1\le m\le n-1$, we will prove that Equation (22) has a solution for $u^n$.

At the beginning, we define the mapping $\mathfrak{X}:R^{J-1}\to R^{J-1}$ by

$$\begin{array}{c}\hfill \mathfrak{X}\left(v\right):=-\frac{k}{6h}(v\Delta v+\Delta {\left(v\right)}^2)+k{\delta }_x^{2}v+k^{{\alpha }_1+1}{\omega }_0^{{\alpha }_1}{\delta }_x^{2}v-k^{{\alpha }_2+1}{\omega }_0^{{\alpha }_2}{\delta }_x^{4}v-k{\delta }_x^{4}v.\end{array}$$

Then, $u^n$ is a solution of (22) if and only if

$$\begin{array}{c}\hfill u^n=\mathfrak{X}\left(u^n\right)+\tilde{f},\end{array}$$

in which

$$\begin{array}{c}\hfill \tilde{f}=u^{n-1}+k^{{\alpha }_1+1}\sum _{p=1}^{n-1}{\omega }_{n-p}^{{\alpha }_1}{\delta }_x^2{u}^p-k^{{\alpha }_2+1}\sum _{p=1}^{n-1}{\omega }_{n-p}^{{\alpha }_2}{\delta }_x^4{u}^p+k{f}^n.\end{array}$$

Next, we need to prove that the mapping $\mathfrak{G}(·)=\mathfrak{X}(·)+\tilde{f}$ has a fixed point. We consider an open ball $\mathcal{L}=A(0,r)$ in $R^{J-1}$ endowed with the norm $\parallel ·\parallel$ in (23). Suppose that for $\lambda >1$ and $u^n$ in the boundary of $\mathcal{L}$,

$$\begin{array}{c}\hfill \lambda u^n=\mathfrak{G}\left(u^n\right)=\mathfrak{X}\left(u^n\right)+\tilde{f}.\end{array}$$

(37)

Since $⟨v\Delta v+\Delta {\left(v\right)}^2,v⟩=0$, using Lemmas 5 and 6, we obtain

$$\begin{array}{c}\hfill ⟨\mathfrak{X}\left(u^n\right),u^n⟩\le 0.\end{array}$$

Taking the inner product of (37) with $u^n$, we have

$$\begin{array}{c}\hfill \lambda \parallel u^n{\parallel }^2\le ⟨\tilde{f},u^n⟩\le \parallel \tilde{f}\parallel \parallel u^n\parallel \le \frac{1}{2}(\parallel \tilde{f}{\parallel }^2+\parallel u^n{\parallel }^2).\end{array}$$

Thus,

$$\begin{array}{c}\hfill \lambda \le \frac{1}{2}\frac{\parallel \tilde{f}{\parallel }^2+{\parallel u^n\parallel }^2}{\parallel u^n{\parallel }^2}=\frac{1}{2}(\frac{\parallel \tilde{f}{\parallel }^2}{\parallel u^n{\parallel }^2}+1)\le \frac{\parallel \tilde{f}{\parallel }^2}{2r^2}+\frac{1}{2}.\end{array}$$

It is noted that the above inequality contradicts with hypothesis $\lambda >1$ for large r. Hence, (37) has no solution on $\partial \mathcal{L}$. By the Leray–Schauder Theorem [33], there is a fixed point of $\mathfrak{G}$ in the closure of $\mathcal{L}$. The proof of existence Theorem is finished.  ☐

4. Uniqueness and Convergence

4.1. Convergence

Let

$$\begin{array}{c}\hfill e_j^n=U_j^n-u_j^n,0\le j\le J,1\le n\le N.\end{array}$$

Subtracting (22) from (19), we obtain the following error equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\delta }_t{e}_j^n+\frac{1}{6h}(e_j^n\Delta e_j^n+\Delta {\left(e_j^n\right)}^2)-{\mathfrak{L}}_1{e}_j^n+{\mathfrak{L}}_2{e}_j^n={\left(R_1\right)}_j^n-{\left(R_2\right)}_j^n\hfill \\ -{\left(R_3\right)}_j^n-{\left(R_4\right)}_j^n-{\left(R_5\right)}_j^n-{\left(R_6\right)}_j^n-\frac{1}{6h}({\left(R_7\right)}_j^n+{\left(R_8\right)}_j^n),\hfill \\ 1\le j\le J-1,1\le n\le N\hfill \\ \\ e_0^n=e_J^n=0,1\le n\le N,\hfill \\ \\ e_j^0=0,0\le j\le J,\hfill \end{array}\right.\end{array}$$

(38)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left(R_7\right)}_j^n=U_j^n\Delta e_j^n+\Delta \left(e_j^n{U}_j^n\right),\hfill \\ {\left(R_8\right)}_j^n=e_j^n\Delta U_j^n+\Delta \left(e_j^n{U}_j^n\right).\hfill \end{array}\right.\end{array}$$

(39)

To complete the proof of convergence, we provide the following Lemmas.

Lemma 9

([34]). (Discrete Gronwall’s inequality) If $A_n$ is a non-negative real sequence and satisfies

$$\begin{array}{c}\hfill A_n\le {\tilde{c}}_n+\sum _{m=0}^{n-1}{\tilde{d}}_m{A}_m,n\ge 0,\end{array}$$

where ${\tilde{c}}_n$ is non-descending and non-negative sequence, ${\tilde{d}}_m\ge 0$, then it holds that

$$\begin{array}{c}\hfill A_n\le {\tilde{c}}_{n}exp\left(\sum _{m=0}^{n-1}{\tilde{d}}_m\right),n\ge 0.\end{array}$$

Lemma 10.

For $\forall s,g\in V_h$, it holds that

$$\begin{array}{ccc}& & \left(i\right)⟨g\Delta s,g⟩+⟨\Delta {\left(g\right)}^2,s⟩=0;\hfill \\ & & \left(ii\right)⟨g\Delta g,s⟩+⟨\Delta \left(gs\right),g⟩=0.\hfill \end{array}$$

Proof. 

(i) By the definition of $⟨·,·⟩$, we have

$$\begin{array}{ccc}& & ⟨g\Delta s,g⟩+⟨\Delta {\left(g\right)}^2,s⟩\hfill \\ & & =h\sum _{j=1}^{J-1}{g}_j(s_{j+1}-s_{j-1})g_j+h\sum _{j=1}^{J-1}(g_{j+1}{g}_{j+1}-g_{j-1}{g}_{j-1})s_j\hfill \\ & & =h\sum _{j=2}^J{g}_{j-1}{s}_j{g}_{j-1}-h\sum _{j=1}^{J-1}{g}_j{s}_{j-1}{g}_j+h\sum _{j=2}^J{g}_j{g}_j{s}_{j-1}\hfill \\ & & -h\sum _{j=1}^{J-1}{g}_{j+1}{g}_{j+1}{s}_j\hfill \\ & & =h{g}_{J-1}{s}_J{g}_{J-1}-h{g}_0{s}_1{g}_0+h{g}_J{s}_{J-1}{g}_J-h{g}_1{s}_0{g}_1\hfill \\ & & =0.\hfill \end{array}$$

The proof of (ii) are similar to (i). Thus, Lemma 10 is proved.  ☐

Lemma 11.

When $U_0=U_J=0$ and $e_0=e_J=0$, then it holds that

$$\begin{array}{ccc}\hfill & & k\sum _{n=1}^N(\parallel {\left(R_1\right)}_j^n\parallel +\parallel {\left(R_2\right)}_j^n\parallel +\parallel {\left(R_3\right)}_j^n\parallel +\parallel {\left(R_4\right)}_j^n\parallel +\parallel {\left(R_5\right)}_j^n)\parallel \hfill \\ \hfill & & +\parallel {\left(R_6\right)}_j^n\parallel )\le C\left(T\right)(k+h^2).\hfill \end{array}$$

Proof. 

Utilizing the conditions $U_0=U_J=0$ and $e_0=e_J=0$.

Firstly, by (15), Lemmas 1 and 2, we have

$$\begin{array}{ccc}\hfill & & k\sum _{n=1}^N\parallel {\left(R_1\right)}_j^n\parallel +k\sum _{n=1}^N\parallel {\left(R_3\right)}_j^n\parallel \hfill \\ \hfill & & \le k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left[C(n^{{\alpha }_1-1}{k}^{{\alpha }_1}+h^2)\right]}^2}\hfill \\ \hfill & & \le Ck\sum _{n=1}^N(k^{{\alpha }_1}{n}^{{\alpha }_1-1}+h^2)\le Ck\left(\sum _{n=1}^N{t}_n^{{\alpha }_1-1}k\right)+C\left(Nk\right)h^2\hfill \\ \hfill & & \le Ck\left({\int }_{t_0}^{t_N}{s}^{{\alpha }_1-1}ds\right)+C\left(T\right)h^2\le Ck\left(\frac{T^{{\alpha }_1}}{{\alpha }_1}\right)+C\left(T\right)h^2\le C\left(T\right)(k+h^2).\hfill \end{array}$$

(40)

Secondly,

$$\begin{array}{ccc}\hfill & & k\sum _{n=1}^N\parallel {\left(R_5\right)}_j^n\parallel =k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left({\left(R_5\right)}_j^n\right)}^2}\le k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left(C{h}^2\right)}^2}\hfill \\ \hfill & & \le C\left(T\right)h^2.\hfill \end{array}$$

(41)

Thirdly,

$$\begin{array}{c}\hfill k\sum _{n=1}^N\parallel {\left(R_6\right)}_j^n\parallel =k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left({\left(R_6\right)}_j^n\right)}^2}\le k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left(Ck\right)}^2}\le C\left(T\right)k.\end{array}$$

(42)

Finally, by (16), Lemmas 1 and 3, we have

$$\begin{array}{ccc}\hfill & & k\sum _{n=1}^N\parallel {\left(R_2\right)}_j^n\parallel +k\sum _{n=1}^N\parallel {\left(R_4\right)}_j^n\parallel \hfill \\ \hfill & & \le k\sum _{n=1}^N\sqrt{\sum _{j=1}^{J-1}h{\left[C(n^{{\alpha }_2-1}{k}^{{\alpha }_2}+h^2)\right]}^2}\hfill \\ \hfill & & \le Ck\left({\int }_{t_0}^{t_N}{s}^{{\alpha }_1-1}ds\right)+C\left(T\right)h^2\hfill \\ \hfill & & Ck\left(\frac{T^{{\alpha }_2}}{{\alpha }_2}\right)+C\left(T\right)h^2\le C\left(T\right)(k+h^2).\hfill \end{array}$$

(43)

Combining (40)–(43), we have

$$\begin{array}{ccc}\hfill & & k\sum _{n=1}^N(\parallel {\left(R_1\right)}_j^n\parallel +\parallel {\left(R_2\right)}_j^n\parallel +\parallel {\left(R_3\right)}_j^n\parallel +\parallel {\left(R_4\right)}_j^n\parallel +\parallel {\left(R_5\right)}_j^n\parallel \hfill \\ \hfill & & +\parallel {\left(R_6\right)}_j^n\parallel )\le C\left(T\right)(k+h^2).\hfill \end{array}$$

(44)

Therefore, we are done with this proof.  ☐

Lemma 12.

Set $\widehat{c_0}:=\underset{(x,t)\in [0,L]\times (0,T]}{\max }$$\{|u(x,t)|,|u_x(x,t)|\}$, for $U_0=U_J=0$, $e_0=e_J=0$, $1\le n\le N$, we have

$$\begin{array}{c}\hfill |⟨{\left(R_8\right)}^n,e^n⟩|\le 3\widehat{c_0}h{\parallel e^n\parallel }^2.\end{array}$$

Proof. 

By Lemma 10, for $\forall s,g\in V_h$, it holds that

$$⟨\Delta \left(gs\right),s⟩=\frac{1}{2}⟨s_{j+1}{\Delta }_{+}g+s_{j-1}{\Delta }_{-}g,s⟩,$$

then, we obtain

$$\begin{array}{ccc}\hfill & & ⟨\Delta \left(e^n{U}^n\right),e^n⟩=\frac{1}{2}⟨e_{j+1}^n{\Delta }_{+}{U}^n+e_{j-1}^n{\Delta }_{-}{U}^n,e^n⟩,1\le n\le N.\hfill \end{array}$$

(45)

Utilizing the boundary conditions $U_0=U_J=0,e_0=e_J=0$ and using the Cauchy–Schwarz inequality, we obtain

$$\begin{array}{ccc}\hfill |⟨e_{j+1}^n{\Delta }_{+}{U}^n,e^n⟩|& \le & \parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }|⟨e_{j+1}^n,e^n⟩|\hfill \\ \hfill & =& \parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }|\sum _{j=1}^{J-1}h{e}_{j+1}^n{e}_j^n|\hfill \\ \hfill & \le & \parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }\sum _{j=1}^{J-1}\frac{h}{2}({\left(e_{j+1}^n\right)}^2+{\left(e_j^n\right)}^2)\hfill \\ \hfill & =& \frac{1}{2}\parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }(\sum _{j=1}^{J-1}h{\left(e_{j+1}^n\right)}^2+\parallel e^n{\parallel }^2)\hfill \\ \hfill & \le & \frac{1}{2}\parallel {\Delta }_{+}{U}^{\infty }{\parallel }_{\infty }(\sum _{j=2}^{J}h{\left(e_j^n\right)}^2+\parallel e^n{\parallel }^2)\hfill \\ \hfill & \le & \parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }{\parallel e^n\parallel }^2,1\le n\le N.\hfill \end{array}$$

Additionally, we can get

$$\begin{array}{c}\hfill |⟨e_{j-1}^n{\Delta }_{-}{U}^n,e^n⟩|\le \parallel {\Delta }_{-}{U}^n{\parallel }_{\infty }{\parallel e^n\parallel }^2,1\le n\le N.\end{array}$$

Thus, we obtain

$$\begin{array}{ccc}\hfill |⟨{\left(R_8\right)}^n,e^n⟩|& =& |⟨e^n\Delta U^n+\Delta \left(e^n{U}^n\right),e^n⟩|\hfill \\ \hfill & =& |⟨e^n\Delta U^n,e^n⟩+\frac{1}{2}⟨e_{j+1}^n{\Delta }_{+}{U}^n+e_{j-1}^n{\Delta }_{-}{U}^n,e^n⟩|\hfill \\ \hfill & \le & \parallel \Delta U^n{\parallel }_{\infty }\parallel e^n{\parallel }^2+\frac{1}{2}(\parallel {\Delta }_{+}{U}^n{\parallel }_{\infty }+\parallel {\Delta }_{-}{U}^n{\parallel }_{\infty })\parallel e^n{\parallel }^2\hfill \\ \hfill & \le & 3\widetilde{c_0}h{\parallel e^n\parallel }^2,1\le n\le N.\hfill \end{array}$$

The proof is proved.  ☐

Theorem 4.

($L^2$-convergence) Suppose that the problem (1)–(3) has smooth solution $u(x,t)\in C_{x,t}^{4,2}([0,L]\times (0,T])$, $\{u_j^n|0\le j\le J,1\le n\le N\}$ is the solution of difference scheme (22). We can obtain

$$\begin{array}{c}\hfill \underset{1\le n\le N}{\max }\parallel U^n-u^n\parallel \le C\left(T\right)(k+h^2).\end{array}$$

Proof. 

Taking the inner product of the (38) with $e^n$, summing up for n from 1 to N, utilizing (26) and Lemma 8, and noting

$$⟨e^n\Delta e^n+\Delta {\left(e^n\right)}^2,e^n⟩=0$$

we can obtain

$$\begin{array}{ccc}\hfill & & \parallel e^N{\parallel }^2\le \parallel e^0{\parallel }^2+2k{\displaystyle \sum _{n=1}^N}⟨R_1^n-R_2^n-R_3^n-R_4^n\hfill \\ \hfill & & -R_5^n-R_6^n-\frac{1}{6h}(R_7^n+R_8^n),e^n⟩,1\le n\le N.\hfill \end{array}$$

(46)

It is noted that when $e^0=0$, we have

$$\begin{array}{ccc}\hfill & & \parallel e^N{\parallel }^2\le 2k\sum _{n=1}^N(\parallel R_1^n\parallel +\parallel R_2^n\parallel +\parallel R_3^n\parallel +\parallel R_4^n\parallel +\parallel R_5^n\parallel \hfill \\ \hfill & & +\parallel R_6^n\parallel e^n\parallel -2k\sum _{n=1}^N⟨\frac{1}{6h}(R_7^n+R_8^n),e^n⟩,1\le n\le N.\hfill \end{array}$$

(47)

Since

$$\begin{array}{c}\hfill \begin{array}{c}⟨R_7^n,e^n⟩=⟨U^n\Delta e^n+\Delta \left(e^n{U}^n\right),e^n⟩\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h(U_j^n\Delta e_j^n+\Delta \left(e_j^n{U}_j^n\right))e_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h(U_j^n(e_{j+1}^n-e_{j-1}^n)+(e_{j+1}^n{U}_{j+1}^n-e_{j-1}^n{U}_{j-1}^n))e_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h((U_j^n+U_{j+1}^n)e_{j+1}^n-(U_j^n+U_{j-1}^n)e_{j-1}^n)e_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h(U_j^n+U_{j+1}^n)e_{j+1}^n{e}_j^n-{\displaystyle \sum _{j=1}^{J-1}}h(U_j^n+U_{j-1}^n)e_{j-1}^n{e}_j^n\hfill \\ ={\displaystyle \sum _{j=1}^{J-1}}h(U_j^n+U_{j+1}^n)e_{j+1}^n{e}_j^n-\sum _{j=0}^{J-2}h(U_j^n+U_{j+1}^n)e_{j+1}^n{e}_j^n\hfill \\ =h(U_{J-1}^n+U_J^n)e_J^n{e}_{J-1}^n-h(U_0^n+U_1^n)e_1^n{e}_0^n\hfill \\ =0,1\le n\le N.\hfill \end{array}\end{array}$$

(48)

Combining (48), Lemma 12 and inequality (40), (47) can be written as

$$\begin{array}{ccc}& & \parallel e^N{\parallel }^2\le 2k\sum _{n=1}^N(\parallel R_1^n\parallel +\parallel R_2^n\parallel +\parallel R_3^n\parallel \hfill \\ \hfill & & +\parallel R_4^n\parallel +\parallel R_5^n\parallel +\parallel R_6^n\parallel )\parallel e^n\parallel +\widehat{c_0}k\sum _{n=1}^N{\parallel e^n\parallel }^2,1\le n\le N.\hfill \end{array}$$

Taking appropriate M such that $\parallel e^M\parallel =\underset{0\le n\le N}{\max }\parallel e^n\parallel$ and using Lemma 11, we obtain

$$\begin{array}{ccc}\hfill & & \parallel e^N\parallel \le \parallel e^M\parallel \hfill \\ \hfill & \le & 2k\sum _{n=1}^N(\parallel R_1^n\parallel +\parallel R_2^n\parallel +\parallel R_3^n\parallel +\parallel R_4^n\parallel +\parallel R_5^n\parallel +\parallel R_6^n\parallel )+\widehat{c_0}k\sum _{n=1}^N\parallel e^n\parallel \hfill \\ \hfill & \le & C\left(T\right)(k+h^2)+\widehat{c_0}k\sum _{n=1}^N\parallel e^n\parallel .\hfill \end{array}$$

(49)

Further

$$\begin{array}{c}\hfill (1-\widehat{c_0}k)\parallel e^N\parallel \le C\left(T\right)(k+h^2)+\widehat{c_0}k\sum _{n=0}^{N-1}\parallel e^n\parallel .\end{array}$$

(50)

Using discrete Gronwall inequality, for $k<\frac{\widehat{c_0}}{2}$, we obtain

$$\begin{array}{c}\hfill \parallel e^N\parallel \le 2\exp \left\{2\widehat{c_0}Nk\right\}C\left(T\right)(k+h^2)\le C\left(T\right)(k+h^2).\end{array}$$

 ☐

4.2. Uniqueness

Theorem 5.

Under the assumptions in Theorem 4—for h is small enough and $k=o\left(h^{\frac{3}{4}}\right)$—then the difference scheme (22) has a unique solution.

Proof. 

Set $u^n\in R^{n-1}$ and $v^n\in R^{n-1}$, $0\le n\le N$ to be the solutions of (22). Since $u^0=v^0$, we assume $u^m=v^m$ for $0\le m\le n-1$. Next, we need to prove $u^n=v^n$.

First, using (22), we have

$$\begin{array}{ccc}\hfill & & {\delta }_t(u_j^n-v_j^n)-{\delta }_x^2(u_j^n-v_j^n)+{\delta }_x^4(u_j^n-v_j^n)+\frac{1}{6h}(u_j^n\Delta u_j^n\hfill \\ \hfill & & +\Delta {\left(u_j^n\right)}^2-v_j^n\Delta v_j^n-\Delta {\left(v_j^n\right)}^2)\hfill \\ & & =k^{{\alpha }_1}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_1}{\delta }_x^2(u_j^p-v_j^p)-k^{{\alpha }_2}\sum _{p=1}^n{\omega }_{n-p}^{{\alpha }_2}{\delta }_x^4(u_j^p-v_j^p).\hfill \end{array}$$

(51)

Second, taking the inner product of (51) with $u^n-v^n$, and using Lemmas 5, 6, and 8, we obtain

$$\begin{array}{ccc}& & \frac{1}{2k}(\parallel u^n-v^n{\parallel }^2-\parallel u^{n-1}-v^{n-1}{\parallel }^2)\hfill \\ \hfill & & \le -\frac{1}{6h}⟨u^n\Delta u^n+\Delta {\left(u^n\right)}^2-v^n\Delta v^n-\Delta {\left(v^n\right)}^2,u^n-v^n⟩\hfill \\ & & =-\frac{1}{6h}⟨u^n\Delta (u^n-v^n)+(u^n-v^n)\Delta v^n+\Delta (u^n-v^n)(u^n+v^n),u^n-v^n⟩.\hfill \end{array}$$

Since

$$\begin{array}{ccc}& & ⟨u^n\Delta (u^n-v^n)+(u^n-v^n)\Delta v^n+\Delta (u^n-v^n)(u^n+v^n),u^n-v^n⟩\hfill \\ & & =⟨(u^n-v^n)\Delta v^n+\Delta \left(v^n(u^n-v^n)\right),u^n-v^n⟩.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill & & \parallel u^n-v^n{\parallel }^2\le {\parallel u^{n-1}-v^{n-1}\parallel }^2\hfill \\ \hfill & & -\frac{k}{3h}⟨(u^n-v^n)\Delta v^n+\Delta \left(v^n(u^n-v^n)\right),u^n-v^n⟩\hfill \\ & & \le \frac{k}{3h}|⟨(u^n-v^n)\Delta v^n+\Delta \left(v^n(u^n-v^n)\right),u^n-v^n⟩|.\hfill \end{array}$$

(52)

Further, we have

$$\begin{array}{ccc}\hfill & & |⟨(u^n-v^n)\Delta v^n+\Delta \left(v^n(u^n-v^n)\right),u^n-v^n⟩|\hfill \\ \hfill & & \le \parallel \Delta v^n{\parallel }_{\infty }\parallel u^n-v^n{\parallel }^2+\frac{1}{2}(\parallel {\Delta }_{+}{v}^n{\parallel }_{\infty }+\parallel {\Delta }_{-}{v}^n{\parallel }_{\infty })\parallel u^n-v^n{\parallel }^2.\hfill \end{array}$$

(53)

Rearranging, we have

$$\begin{array}{ccc}\hfill \parallel \Delta v^n{\parallel }_{\infty }& =& \underset{1\le j\le J-1}{\max }\{|u_{j+1}^n-v_{j-1}^n|\}\hfill \\ \hfill & \le & \underset{1\le j\le J-1}{\max }\{|v_{j+1}^n-V_{j+1}^n|+|V_{j+1}^n-V_{j-1}^n|+|V_{j-1}^n-v_{j-1}^n|\}\hfill \\ \hfill & \le & 2\parallel V^n-v^n{\parallel }_{\infty }+Ch\le 2h^{-\frac{1}{2}}\parallel V^n-v^n\parallel +Ch\hfill \\ \hfill & \le & C{h}^{-\frac{1}{2}}(k+h^2)+Ch.\hfill \end{array}$$

(54)

Additionally,

$$\begin{array}{ccc}\hfill & & |⟨(u^n-v^n)\Delta v^n+\Delta \left(v^n(u^n-v^n)\right),u^n-v^n⟩|\hfill \\ \hfill & & \le C[h^{-\frac{1}{2}}(k+h^2)+h]{\parallel u^n-v^n\parallel }^2.\hfill \end{array}$$

(55)

Thus, we ottain

$$\begin{array}{c}\hfill \parallel u^n-v^n\parallel \le C(k^2{h}^{-\frac{3}{2}}+k{h}^{\frac{1}{2}}+k)\parallel u^n-v^n\parallel .\end{array}$$

(56)

Using inequality (56), we have $\parallel u^n-v^n{\parallel }^2=0$ for $k=o\left(h^{\frac{3}{4}}\right)$ as $h\to 0$ and finish the proof.  ☐

5. Numerical Results

In this section, we solve this problem (1)–(3) with $L=T=1$ by difference scheme (22). We provide three iterative methods [32,35,36]: the Besse relaxtion algorithm (Besse), the Newton iterative method (Newton), and the linearized iterative algorithm (linearized), to solve the nonlinear system (22). Let $MaxStep=300$ and $eps=1.0\times {10}^{-5}$ and

$$\begin{array}{ccc}& & E(h,k)=\sqrt{h\sum _{j=1}^{J-1}{(U_j^N-u_j^N)}^2},\hfill \\ & & rat{e}^x=lo{g}_2\left(\frac{E(2h,k)}{E(h,k)}\right),rat{e}^t=lo{g}_2\left(\frac{E(h,2k)}{E(h,k)}\right).\hfill \end{array}$$

Example 1.

In the first example, we consider the initial condition $\phi \left(x\right)=\sin \pi x$, the source term

$$\begin{array}{ccc}& & f(x,t)=sin2\pi x(-\frac{2\alpha t^{\alpha -1}}{\mathrm{\Gamma }(\alpha +1)}-\frac{2(\alpha +1)t^{\alpha }}{\mathrm{\Gamma }(\alpha +2)})\hfill \\ & & +\pi sin4\pi x{(1-\frac{2t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}-\frac{t^{\alpha +1}}{\mathrm{\Gamma }(\alpha +2)})}^2\hfill \\ & & +4{\pi }^{2}sin2\pi x(\frac{t^{{\alpha }_1}}{\mathrm{\Gamma }({\alpha }_1+1)}-\frac{2t^{{\alpha }_1+\alpha }}{\mathrm{\Gamma }(\alpha +{\alpha }_1+1)}-\frac{t^{{\alpha }_1+\alpha +1}}{\mathrm{\Gamma }(\alpha +{\alpha }_1+2)})\hfill \\ & & +16{\pi }^{4}sin2\pi x(\frac{t^{{\alpha }_2}}{\mathrm{\Gamma }({\alpha }_2+1)}-\frac{2t^{{\alpha }_2+\alpha }}{\mathrm{\Gamma }(\alpha +{\alpha }_2+1)}-\frac{t^{{\alpha }_2+\alpha +1}}{\mathrm{\Gamma }(\alpha +{\alpha }_2+2)})\hfill \\ & & (16{\pi }^{4}sin2\pi x+4{\pi }^{2}sin2\pi x)(1-\frac{2t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}-\frac{t^{\alpha +1}}{\mathrm{\Gamma }(\alpha +2)}).\hfill \end{array}$$

and the exact solution is

$$\begin{array}{c}\hfill u(x,t)=\sin 2\pi x(1-\frac{2t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}-\frac{t^{\alpha +1}}{\mathrm{\Gamma }(\alpha +2)}),\end{array}$$

where α, $0<\alpha <1$ is the regular parameter.

Table 1 lists the $L^2$ norm errors; the corresponding spatial convergence rate; and the total number of iterations of our scheme under different parameters ${\alpha }_1$ and ${\alpha }_2$, respectively. Taking the temporal step $k=1/1024$ and $\alpha =0.50$, we can know from Table 1 that the spatial convergence order is about order 2. Through comparison, it can be seen that the numerical results of the three iterative methods have a small gap in the spatial direction.

Table 1. The errors and convergence rates when $k=1/1024$ and $\alpha =0.50$, for Example 1.

Methods	${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$	J	Error	${\mathit{r}\mathit{a}\mathit{t}\mathit{e}}^{\mathit{x}}$	Iterative
$Besse$		16	$2.3245\times {10}^{-2}$	−	−
	${\alpha }_1=0.30$	32	$1.1700\times {10}^{-2}$	$0.9904$	−
	${\alpha }_2=0.70$	64	$5.7776\times {10}^{-3}$	$1.0179$	−
		128	$2.7732\times {10}^{-3}$	$1.0589$	−
		16	$2.1483\times {10}^{-2}$	−	−
	${\alpha }_1=0.35$	32	$1.0779\times {10}^{-2}$	$0.9950$	−
	${\alpha }_2=0.65$	64	$5.3063\times {10}^{-3}$	$1.0224$	−
		128	$2.5347\times {10}^{-3}$	$1.0659$	−
		16	$1.8288\times {10}^{-2}$	−	−
	${\alpha }_1=0.75$	32	$9.1218\times {10}^{-3}$	$1.0035$	−
	${\alpha }_2=0.55$	64	$4.4609\times {10}^{-3}$	$1.0320$	−
		128	$2.1079\times {10}^{-3}$	$1.0816$	−
$Newton$		16	$2.3456\times {10}^{-2}$	−	46
	${\alpha }_1=0.30$	32	$1.1747\times {10}^{-2}$	$0.9977$	87
	${\alpha }_2=0.70$	64	$5.7882\times {10}^{-3}$	$1.0211$	155
		128	$2.7753\times {10}^{-3}$	$1.0605$	259
		16	$2.1633\times {10}^{-2}$	−	46
	${\alpha }_1=0.35$	32	$1.0811\times {10}^{-2}$	$1.0007$	87
	${\alpha }_2=0.65$	64	$5.3130\times {10}^{-3}$	$1.0249$	155
		128	$2.5358\times {10}^{-3}$	$1.0671$	259
		16	$1.8353\times {10}^{-2}$	−	45
	${\alpha }_1=0.75$	32	$9.1346\times {10}^{-3}$	$1.0066$	86
	${\alpha }_2=0.55$	64	$4.4631\times {10}^{-3}$	$1.0333$	154
		128	$2.1078\times {10}^{-3}$	$1.0823$	259
$Linearized$		16	$2.3455\times {10}^{-2}$	−	46
	${\alpha }_1=0.30$	32	$1.1747\times {10}^{-2}$	$0.9976$	87
	${\alpha }_2=0.70$	64	$5.7879\times {10}^{-3}$	$1.0212$	154
		128	$2.7751\times {10}^{-3}$	$1.0605$	259
		16	$2.1632\times {10}^{-2}$	−	46
	${\alpha }_1=0.35$	32	$1.0812\times {10}^{-2}$	$1.0006$	87
	${\alpha }_2=0.65$	64	$5.3132\times {10}^{-3}$	$1.0250$	154
		128	$2.5357\times {10}^{-3}$	$1.0672$	259
		16	$1.8353\times {10}^{-2}$	−	45
	${\alpha }_1=0.75$	32	$9.1347\times {10}^{-3}$	$1.0066$	86
	${\alpha }_2=0.55$	64	$4.4626\times {10}^{-3}$	$1.0335$	153
		128	$2.1077\times {10}^{-3}$	$1.0822$	259

Fix the spatial step $h=1/J=1024$ and $\alpha =0.50$. Table 2 shows that the temporal convergence order is about order one. Through the comparison of three iteration methods, we can find that the temporal convergence order of the Basse relaxation algorithm is not very stable. In addition, the total number of iterations of the linear iterative algorithm is less than the Newton iterative method.

Table 2. The errors and convergence rates when $h=1/1024$ and $\alpha =0.50$, for Example 1.

Methods	${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$	N	Error	${\mathit{r}\mathit{a}\mathit{t}\mathit{e}}^{\mathit{t}}$	Iterative
$Besse$		16	$2.3245\times {10}^{-2}$	−	−
	${\alpha }_1=0.30$	32	$1.1700\times {10}^{-2}$	$0.9904$	−
	${\alpha }_2=0.70$	64	$5.7776\times {10}^{-3}$	$1.0179$	−
		128	$2.7732\times {10}^{-3}$	$1.0589$	−
		16	$2.1483\times {10}^{-2}$	−	−
	${\alpha }_1=0.35$	32	$1.0779\times {10}^{-2}$	$0.9950$	−
	${\alpha }_2=0.65$	64	$5.3063\times {10}^{-3}$	$1.0224$	−
		128	$2.5347\times {10}^{-3}$	$1.0659$	−
		16	$1.8288\times {10}^{-2}$	−	−
	${\alpha }_1=0.75$	32	$9.1218\times {10}^{-3}$	$1.0035$	−
	${\alpha }_2=0.55$	64	$4.4609\times {10}^{-3}$	$1.0320$	−
		128	$2.1079\times {10}^{-3}$	$1.0816$	−
$Newton$		16	$2.3456\times {10}^{-2}$	−	46
	${\alpha }_1=0.30$	32	$1.1747\times {10}^{-2}$	$0.9977$	87
	${\alpha }_2=0.70$	64	$5.7882\times {10}^{-3}$	$1.0211$	155
		128	$2.7753\times {10}^{-3}$	$1.0605$	259
		16	$2.1633\times {10}^{-2}$	−	46
	${\alpha }_1=0.35$	32	$1.0811\times {10}^{-2}$	$1.0007$	87
	${\alpha }_2=0.65$	64	$5.3130\times {10}^{-3}$	$1.0249$	155
		128	$2.5358\times {10}^{-3}$	$1.0671$	259
		16	$1.8353\times {10}^{-2}$	−	45
	${\alpha }_1=0.75$	32	$9.1346\times {10}^{-3}$	$1.0066$	86
	${\alpha }_2=0.55$	64	$4.4631\times {10}^{-3}$	$1.0333$	154
		128	$2.1078\times {10}^{-3}$	$1.0823$	259
$Linearized$		16	$2.3455\times {10}^{-2}$	−	46
	${\alpha }_1=0.30$	32	$1.1747\times {10}^{-2}$	$0.9976$	87
	${\alpha }_2=0.70$	64	$5.7879\times {10}^{-3}$	$1.0212$	154
		128	$2.7751\times {10}^{-3}$	$1.0605$	259
		16	$2.1632\times {10}^{-2}$	−	46
	${\alpha }_1=0.35$	32	$1.0812\times {10}^{-2}$	$1.0006$	87
	${\alpha }_2=0.65$	64	$5.3132\times {10}^{-3}$	$1.0250$	154
		128	$2.5357\times {10}^{-3}$	$1.0672$	259
		16	$1.8353\times {10}^{-2}$	−	45
	${\alpha }_1=0.75$	32	$9.1347\times {10}^{-3}$	$1.0066$	86
	${\alpha }_2=0.55$	64	$4.4626\times {10}^{-3}$	$1.0335$	153
		128	$2.1077\times {10}^{-3}$	$1.0822$	259

Taking $\alpha =0.5$ fixed, Figure 1 shows the spatial convergence order for $N=1024$, and Figure 2 shows the convergence order in the time direction for $J=1024$. It can be seen that the numerical results of the convergence order are in good agreement with the theoretical analysis.

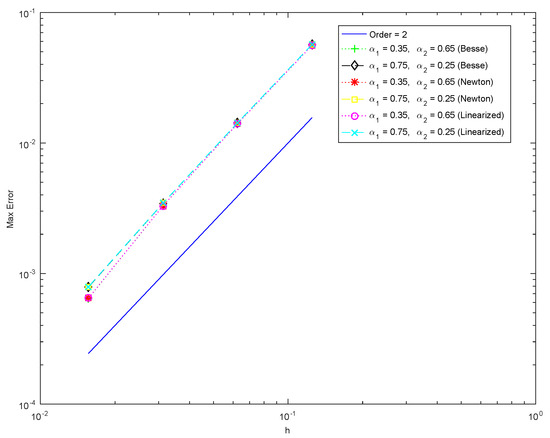
Figure 1. The error and convergence orders in space with $\alpha =0.50$ and $k=1/1024$, for Example 1.

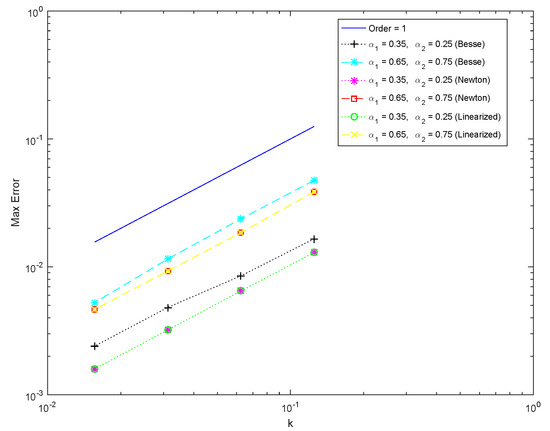
Figure 2. The error and convergence orders in time with $\alpha =0.50$ and $h=1/1024$, for Example 1.

Example 2.

In the second Example, we take the exact solution

$$\begin{array}{c}\hfill u(x,t)=\sin \pi x\frac{2t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)},0<\alpha <1.\end{array}$$

Correspondingly, the initial condition is $u^0\left(x\right)=0$ and the inhomogeneous term is

$$\begin{array}{ccc}& & f(x,t)=\hfill \\ & & \sin \pi x\frac{2\alpha t^{\alpha -1}}{\mathrm{\Gamma }(\alpha +1)}+2\pi \sin 2\pi x{\left(\frac{t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}\right)}^2+\frac{2{\pi }^2\sin \left(\pi x\right)t^{\alpha +{\alpha }_1}}{\mathrm{\Gamma }(\alpha +{\alpha }_1+1)}\hfill \\ & & +\frac{2{\pi }^4\sin \left(\pi x\right)t^{\alpha +{\alpha }_2}}{\mathrm{\Gamma }(\alpha +{\alpha }_2+1)}+({\pi }^4\sin \pi x+{\pi }^2\sin \pi x)\frac{2t^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}.\hfill \end{array}$$

It can be seen from Table 3 and Table 4 that the spatial convergence order is about order two and the temporal convergence order is about order one, respectively. It can be seen that the numerical results are the same as Example 1 and the convergence order is in good agreement with the theoretical analysis.

Table 3. The errors and convergence rates when $k=1/1024$ and $\alpha =0.50$, for Example 2.

Methods	${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$	J	Error	${\mathit{r}\mathit{a}\mathit{t}\mathit{e}}^{\mathit{x}}$	Iterative
$Besse$	${\alpha }_1=0.30$	16	$9.6163\times {10}^{-3}$	−	−
	${\alpha }_2=0.70$	32	$2.2743\times {10}^{-3}$	2.092	−
		64	$4.4453\times {10}^{-4}$	2.423	−
	${\alpha }_1=0.35$	16	$9.7560\times {10}^{-3}$	−	−
	${\alpha }_2=0.65$	32	$2.3922\times {10}^{-3}$	$2.073$	−
		64	$5.5698\times {10}^{-4}$	$2.315$	−
$Newton$	${\alpha }_1=0.30$	16	$9.6292\times {10}^{-3}$	−	2048
	${\alpha }_2=0.70$	32	$2.2840\times {10}^{-3}$	2.076	2048
		64	$4.5341\times {10}^{-4}$	2.333	2048
	${\alpha }_1=0.35$	16	$9.6486\times {10}^{-3}$	−	2048
	${\alpha }_2=0.65$	32	$2.3005\times {10}^{-3}$	2.068	2048
		64	$4.6915\times {10}^{-4}$	2.294	2048
$Linearized$	${\alpha }_1=0.30$	16	$9.6291\times {10}^{-3}$	−	2048
	${\alpha }_2=0.70$	32	$2.2839\times {10}^{-3}$	2.076	2048
		64	$4.5330\times {10}^{-4}$	2.333	2048
	${\alpha }_1=0.35$	16	$9.6484\times {10}^{-3}$	−	2048
	${\alpha }_2=0.65$	32	$2.3004\times {10}^{-3}$	2.068	2048
		64	$4.6904\times {10}^{-4}$	2.294	2048

Table 4. The errors and convergence rates when $h=1/1024$ and $\alpha =0.50$, for Example 2.

Methods	${\mathit{\alpha }}_1,{\mathit{\alpha }}_2$	N	Error	${\mathit{r}\mathit{a}\mathit{t}\mathit{e}}^{\mathit{t}}$	Iterative
$Besse$	${\alpha }_1=0.30$	16	$1.2909\times {10}^{-2}$	−	−
	${\alpha }_2=0.70$	32	$6.4875\times {10}^{-3}$	0.993	−
		64	$3.2196\times {10}^{-3}$	1.011	−
	${\alpha }_1=0.35$	16	$1.1689\times {10}^{-2}$	−	−
	${\alpha }_2=0.65$	32	$5.8697\times {10}^{-3}$	$0.994$	−
		64	$2.9127\times {10}^{-3}$	$1.011$	−
$Newton$	${\alpha }_1=0.30$	16	$1.2818\times {10}^{-2}$	−	62
	${\alpha }_2=0.70$	32	$6.4717\times {10}^{-3}$	0.986	109
		64	$3.2142\times {10}^{-3}$	1.010	192
	${\alpha }_1=0.35$	16	$1.1588\times {10}^{-2}$	−	62
	${\alpha }_2=0.65$	32	$5.8495\times {10}^{-3}$	0.986	110
		64	$2.9036\times {10}^{-3}$	1.011	192
$Linearized$	${\alpha }_1=0.30$	16	$1.2813\times {10}^{-2}$	−	48
	${\alpha }_2=0.70$	32	$6.4754\times {10}^{-3}$	0.985	96
		64	$3.2101\times {10}^{-3}$	1.012	192
	${\alpha }_1=0.35$	16	$1.1580\times {10}^{-2}$	−	48
	${\alpha }_2=0.65$	32	$5.8529\times {10}^{-3}$	0.984	96
		64	$2.9054\times {10}^{-3}$	1.010	192

6. Concluding Remarks

In this paper, we propose an implicit difference scheme for a class of nonlinear fourth-order equations with the multi-term Riemann–Liouvile fractional integral kernels. For the nonlinear convection term, we use the Galerkin method based on piecewise linear test functions. The Riemann–Liouvile fractional integral terms are treated by convolution quadrature. The standard central difference approximation is used to discretize the spatial derivative. The stability and convergence are rigorously proved by the discrete energy method. The existence and uniqueness of the numerical solutions for nonlinear systems are proved strictly. Lastly, we introduce and compare three iterative methods for solving the nonlinear systems.